Note: Descriptions are shown in the official language in which they were submitted.
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
MULTIPLE NUMBER BASE ENCODER/DECODER USING CORRESPONDING XOR
FIELD OF THE INVENTION
The present invention relates to apparatus and methods for encryption and
decryption wherein a ciphertext is generated. More particularly, the present
invention
is related to the use of symmetrix private key encryption. Once the sender and
receiver have exchanged key information, encryption of a message by the sender
and
decryption by the receiver is accomplished in a direct manner.
BACKGROUND OF THE INVENTION
In 1917 Vernan created a telegraphic cipher system (U.S. patent No.
1,310,719; issued July 22, 1919) which used the addition of the value of a
message
character on a paper tape with another character on a looped key tape; the sum
of the
values was transmitted as the cipher character. It was soon recognized that
the
security of the method relied on a very long key tapes. Later to eliminate
excessively
long key tapes, Morehouse (1918) connected two Vernan telegraphic machines
IS together employing two separate looped key tapes so that the output of the
first
modified the output of the second and this combined output encoded the message
tape
to create an enciphered message. These two loops had non-equal lengths such
that all
the permutations of the characters on one would occur with all the characters
on the
other. Thus, two shorter tapes could mimic the employment of a single much
larger
2o tape. Mauborgne showed that the Morehouse system was crypto<~raphically
secure
only when the key tape (or the permutation of two tapes) was comparable in
length to
the clear text to be encrypted and was used only one time. Any repetition of
any kind
of the key either within that message or its use to encrypt other messages
would
compromise the key tape. It was also shown that a ciphertext made using an
25 encryption key the same size as the message itself but consisting of
coherent text
could be broken, but not if the key were a collection of random characters.
Dr. Man ~'oung Rhee, in his book Cryptography and Secure
Communications (McGraw-Hill, 1994) states on page 12: "A cryptosystem which
SUBSTITUTE SHEET (RULE 26)
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
2
can resist any cryptanalytic attack, no matter how much computation is allowed
is
said to be unconditionally secure. The one time pad is the only
unconditionally
secure cipher in use. One of the most remarkable ciphers is the one-time pad
in
which the ciphertext is the bit-by-bit modulo-2 sum of the plaintext and a
nonrepeating keystream of the same length. However, the one-time pad is
impractical
for most applications because of the large size of the nonrepeating key."
US patent 5,113,444 issued May 12, 1992 entitled ''RANDOM CHOICE
CIPHER SYSTEM AND METHOD" states ''First random number strings are a
relatively scarce commodity. Second, the receiver must have at hand exactly
the
same random number sequence the sender used or must be able to reproduce it.
The
first of these alternatives requires the sharing of an enormous amount of key
material.
The sharing of an enormous amount of key material is impractical. The second
alternative is impossible." The first and second conclusions to these
statements are
inaccurate. Statistical analysis of the sampling of digital sources
(specifically 16 bit
I S sound files) shows that random or arbitrary numbers or bytes are readily
available in
the digital/computer environment. This ready availability of random numbers is
contrary to the teachings and opinions of those skilled in the art as well as
those
expert in the art of cryptography.
US Patent 5,113,444, issued May 12, 1992 entitled "RANDOM CHOICE
CIPHER SYSTEM AND METHODS," states "First random number strings are a
relatively scarce commodity. Second, the receiver must have at hand exactly
the
same random number sequence the sender used or must be able to reproduce it.
The
first of these alternatives requires the sharing of an enormous amount of key
material.
The sharing of an enormous amount of key material is impractical. The second
alternative is impossible." The first and second conclusions to these
statements are
inaccurate. Statistical analysis of the sampling of digital sources
(specifically 16 bit
sound files) shows that random or arbitrary numbers or bytes are readily
available in
the digital/computer environment. This ready availability of random numbers is
contrary to the teachings and opinions of those skilled in the art as well as
those
3o expert in the art of cryptography.
Another prevailing view of those skilled in the art is that most pseudo-
random numbers have an inherent weakness because they are generated by a
formula
CA 02371446 2001-11-02
WO 00/70818 PCT/LJS99/10929
3
and that it may be possible to reconstruct the formula and then predict the
numbers
in the series.
Another encryption technique is disclosed in US Patent 5,113,444, entitled
"RANDOM CODING CIPHER SYSTEM AND METHODS," and US Patent NO.
5,307,412, teach the use of a thesaurus and/or synonyms together with
arithmetic/logic operations to combine data and masks to accomplish
encoding/decoding. These patents are thus limited by the use of the thesaurus
and
synonyms.
US. PATENT 5,077,793 entitled "RESIDUE NUMBER ENCRYPTION
to AND DECRYPTION SYSTEM" teaches (column 3 lines 40 to column 4 lines 8): "If
the moduli are chosen to be mutually prime, then all integers with the range
of zero to
the product of the moduli minus one can be uniquely represented. The
importance of
the residue number system to numerical process is that the operations of
addition,
subtraction, and multiplication can be performed without the use of carry
operations
between the moduli. In other words, each digit in the n-tuple can be operated
on
independently and in parallel." And shows that for the sum Z of the digits X
and Y,
the ith digit may be given by: z;=(x;+y;) mod m; and that "a sixteen bit
binary number
can be represented in the residue number system using five moduli
5,7,11,13,17."
The moduli (m;) are chosen to be relatively prime to each other. In Columns 5
and 6
the description goes on to define Z=(X+Y) mod M (where is the product of all
of the
moduli, i.e., M=m~ x m2 ... m",) is a generalization of the Vigenere cipher.
If Z=(X-
Y) mod M is used to encrypt X using Y then X may be recovered from Z by X=(Y-
Z)
mod M, which is a generalization of the Beaufort cipher. The method described
by
this patent requires that multiple and different moduli must be used at the
same time
to calculate different residues which are transmitted to a receiver to
uniquely define
the number which was encrypted. The encryption method described herein does
not
use multiple moduli and is different from this patent. Because different
moduli are
not used, the encryption/decryption apparatus may be simpler in design.
Pages 13 through 15 in "Applied Cryptography, Second Edition" by Bruce
3o Schneier, John Wiley & Sons, Inc. 1996, provide a critique on the security
inherent in
the Vigenere encryption method. "The simple-XOR algorithm is really an
embarrassment; it's nothing more than a Vigenere polyalphabetic cipher."
"There is
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
4
no real security here. This kind of encryption is trivial to break, even
without
computers. It will take only a few seconds with a computer. Assume the
plaintext is
English. Furthermore, assume the key length is any small number of bytes.
Here's
how to break it:
1. Discover the length of the key by a procedure known as counting
coincidences. XOR the ciphertext against itself shifted various number of
bytes, and
count those bytes that are equal. If the displacement is a multiple of the key
length,
then something over 6 percent of the bytes will be equal. if it is not, then
less than
0.4 percent will be equal (assuming a random key encrypting normal ASCII text;
other plaintext will have different numbers). This is called the index of
coincidence.
The smallest displacement that indicates a multiple of the key length is the
length of
the key.
2. Shift the ciphertext by that length and XOR it with itself. This removes
the
key and leaves you with the plaintext XORed with the plaintext shifted the
length of
the key. Since English has 1.3 bits of real information per byte, there is
plenty of
redundancy for determining a unique decryption."
The above method for breaking a Vigenere cipher relies on the fact that
XOR (base 2) is its own inverse and that the encrypting key (masking bytes)
are
repeated many times. The XOR is its own inverse because A XOR B XOR B=A. It
is an object of the present invention to improve upon the security of the
Vigenere and
Variant Beaufort cipher methods by applying them not to characters directly
but
rather to digits representing that character in another number base.
Pages 70 and 71 in "Cryptography: An Introduction to Computer Security"
by Jennifer Seberry and Josef Pieprzyk, Prentice Hall, 1989 - "The Vigenere
cipher.
The key is specified by a sequence of letters: K= k, kd where k1, (i=1,...,d)
gives the
amount of shift in the ith alphabet, that is: f, (a)=a + ki (mod n)." "Variant
Beaufort
cipher. Here we use: f (a)=a + k,) (mod n). Since a - k~ = a + (n - ki) (mod
n) the
Variant Beaufort cipher is equivalent to the Vigenere cipher with the key
character n -
k,. The Variant Beaufort cipher is, in fact, the inverse of the Vigenere
cipher since if
one is used to encipher the other is used to decipher."
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
Historically the Vigenere and Variant Beaufort ciphers have been applied
to whole letters or characters. That is, the value (position in the alphabet)
of a
character has a number either added or subtracted to it (modulo the length of
the
alphabet) and the resultant number is used to specify a character position in
the
alphabet and the character in that position is sent as the ciphered character.
Herein BCN refers to the binary to base n conversion of a number and the
representation of the base n number as a digit shown in binary. A common
example
(base 10) is BCD (binary coded decimal) where the values 0 through 9 are
represented by 4 binary bits.
Herein a byte is defined as two or more bits. In typical usage a byte is
considered to be, but is not limited to, eight bits.
Herein, arrays (or masks) are described as being comprised of elements.
Such elements are defined as any actual or logical grouping, for example: a
bit, a
nibble, a byte or word of any length.
It is an object of the present invention to provide an encryption/decryption
apparatus and method that does not depend upon the use of thesaurus's and/or
synonyms and/or other forms of look-up tables.
It is yet another object of the present invention to provide an
encryption/decryption scheme wherein the presentation of a character in one
number
2o base is transformed into a corresponding representation in another number
base.
SUMMARY OF THE INVENTION
The foregoing objects are met in an encryption/decryption apparatus where
a message or information expressed as elements or characters is to be
encrypted from
transmission or sending to another where the message will be decrypted. A mask
of
elements or characters is defined and utilized in the encryption/decryption.
The
message elements and mask elements are converted into corresponding elements
in
another new number base system, where this new number base system is not
binary.
The converted message and mask elements are combined, element by element,
respectively, thus forming a new set of elements, which are defined as a
ciphertext.
CA 02371446 2001-11-02
WO 00/70818 PCTNS99/10929
6
This ciphertext may be sent or transformed into a set of elements in yet
another
number base that is suitable for transmission.
To decode the ciphertext, mask elements, identical to those used for
encryption, are converted into corresponding elements in another number base
(the
same number base as that of the digits of ciphertext. Then these elements are
combined, element by element, respectively using the inverse from that which
was
used for encryption, thus forming a new set of elements which when converted
to a
number in the original message number base is the plaintext message.
Herein XORn (XOR+ and XOR-) describes an exclusive-or operation (base
n) defined as: let the numbers A and B base n be defined (for m digits) as:
nt-I nt-1
A=~n'a; and B=~n'b;
r=o .=o
Then, in a preferred embodiment, the elements A and B may be combined
according
to the following equations.
m-I
C=Axor+ B= ~n'((n+a;+b;~modn) Eq. 1
r=o
m-I
and C = A xor - B = ~ n' ((n + a; - b; ) mod n) Eq. 2
.=o
For base 2, XORn is identical to the standard XOR operation. The conversion of
a
binary number to j digits (base n) is done by the successive division of the
number by
n where the remainder of each division becomes the ith digit for i=0 to j-1.
The digits
of a number (base n) are converted back to binary by: setting sum=0, then for
i j-1 to
0 perform sum=(sum * n) + digit;. When done the result is in sum.
An advantage of the present invention is that an encryption method
employing an XOR (base 2) is strengthened by the use of a base greater than 2.
This
is because A XORn B XORn B does not equal A.
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
7
Another advantage of the present invention is that each byte to be
encrypted and each masking byte (key byte) in a preferred embodiment are
converted
from binary into a string of digits or elements base n (rv2) and the
operations of
equation 1 and 2 are applied to these digits in a systematic manner. Only one
number
base, or moduli, is used at a time.
In a preferred embodiment of the present invention the equation 1 and 2 are
used to advantage since there is no repeating key (as a key to usually thought
of)
because the key is now the sequence of digits resulting from the conversion of
binary
masking bytes to digits of another number base. The masking byte string is now
not
limited to a few characters, but can be a very long series of bytes. Though it
would
still be possible to have a repeating series of digits if the masking bytes
followed a
repeating sequence, the ready availability of arbitrary masking bytes in the
computer
environment should lessen this occurrence. These bytes may be derived from any
of
several digital sources including, but not limited to, the sampling of digital
sources,
the application of numeric hashing functions, pseudo-random number generation
and
other numeric operations.
In a preferred embodiment the equation I is used for encryption and
equation 2 is used for decryption. Since these are inverse ciphers, in another
preferred embodiment equation 2 is used instead for encryption and equation 1
is
used for decryption. For simplicity, only the first method is shown, but the
implementation of the second scheme will be understood by someone skilled in
the
art.
Arbitrary and random numbers are created by normal digital processes.
Most digitized music, which comes on a CD-ROM, is 16 bits of Stereo sampled at
a
44.1 kilohertz rate. This produces approximately 10.5 million bytes per
minute. Of
these about one half may be used as arbitrary data bytes, or about 5 million
bytes per
minute. Reasonably random data byte are generated by reading in the digital
data
stream which makes up the music and throwing away the top 8 bits and sampling
only the lower eight bits of sound to produce an arbitrary or random number.
Fourier
3o analysis on the resultant byte stream shows no particular patterns. It
should be kept in
mind that silent passages are to be avoided. If taking every byte of music in
order is
undesirable, then using every nth byte should work quite well for small values
of n
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
8
between 11 and 17. Please note, the error correction inherent with a music CD-
ROM is not perfect and the user might want to convert the CD-ROM music format
to
a WAVE (.WAV) file format and then send the WAVE (.WAV) file to someone by
either modem, large capacity removable drive, digital magnetic tape cartridge,
or by
making a digital CD-ROM containing the WAVE (.WAV) file.
Another source of arbitrary or random digital numbers may be found in the
pixel by pixel modification (ex-clusive oring, adding, subtracting) of several
pictures
from a PHOTO CD-ROM, again looking at the low order bytes. Computer Zipped
(.ZIP) files and other compressed file formats can be used.
The sender and receiver must agree ahead of time on the sources to be used
for the masking bytes and how these sources will be sampled and/or combined to
create the masking bytes to be used to encrypt and decrypt a message.
In other preferred embodiments, the intelligent sampling of digital sources
can be used to advantage to lessen the reconstruction of the byte stream used
for
encryption. In addition, encryption and hashing algorithms may be used to
modify
the digital sources prior to their use. Moreover, the modification of pseudo-
random
numbers for tables, arrays and/or masks may also be used to advantage.
Other objects, features and advantages will be apparent from the following
detailed description of preferred embodiments thereof taken in conjunction
with the
2o accompanying drawing.
BRIEF DESCRIPTION OF THE DRAWINGS
Fig. 1 A is a flow chart outlining an encoder process of a preferred
embodiment of the
present invention;
Fig. 1 B is a flow chart outlining a decoder process of a preferred embodiment
of the
present invention;
Fig. 2 is a block diagram of the encoder/decoder.
DETAILED DESCRIPTION OF PREFERRED EMBODIMENTS
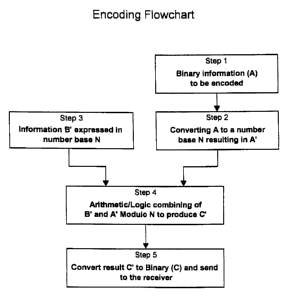
Fig. 1 A shows a preferred embodiment of the steps for encoding a binary
value. In step 1, binary information to be encoded (A) is p[resented to an
encoder for
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
9
step 2. In step 2, the binary information is converted into digits of
characters (A')
expressed in another number base N. In step 3, the digits or characters (B')
are
combined in step 4 according to Eq. l, resulting in digits C' expressed in
number base
N. The C' digits are an encrypted form of the original information A. In step
5, these
digits C', are converted to a binary number (C) which is a convenient base for
sending to a receiver.
Fig. 1B shows the steps needed for a receiver of the digits sent as described
in Fig. 1 A to decode the received encoded digits. In step 6, the encoded
binary digits
C are received for decoding. In step 7, the C digits are converted into digits
in the
number base N forming digits C'. In step 8, the digits B' are stored . The
digits C'
and B' are combined in step 9 according the Eq. 2 which results in the digits
A'. In
step l0,the digits of A' are converted back into the original binary A.
In the process illustrated in Figs. 1 A and 1 B, the order of use of Eq. 1 and
Eq. 2 may be reversed, where Eq. 2 is used in step 4 of Fig. 1 A, and Eq. 1 is
used in
step 9 of Fig. 1 B.
Still referring to Figs. 1 A and 1 B, the binary information A may be
exprtessed as 8 bit bytes, but any size byte may be used. A', B' and C' are
numbers
expressed as digits in a nyumber base N. Also, source B' information may be
form
any random, pseudo-random. Or arbitrary source, as describe herein. Moreover,
other
logic/arithmetic operations may be used to provide additional security as
substantially
and step of Figs. 1 A and 1 B.
Fig. 2 shows a basic block diagram of the Encoder/Decoder. The next
description will be for processing binary input (N3 = 2) to binary output (N2
= 2)
with binary masking bytes (N4 = 2). N 1 will be any value greater than 2. M
bytes of
plaintext are loaded into the INPUT DATA BUFFER, 2, via line 21. In addition,
M
masking bytes are loaded into the DATA MASK BUFFER, 3, via line 22. The
address counters, DATA ADDRESS COUNTER, l, MASK ADDRSS COUNTER,
14, and the OUTPUT ADDRESS COUNTER, 15, are all initialized to 0. These
counters will be clocked M times to process a whole buffer. ED is a 1 bit
binary flag
used to indicate which equation (#1 or #2) will be utilized by the
encoder/decoder.
For encoding ED is set =0, while for decoding, ED is set =1. N1, 7, is the
number
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
base to be used for the XOR operation. N2, 10, is the number base to be used
for
the conversion of the digits (based N 1 ) back into a byte to be put into the
output
buffer. Normally N2 would be 2 for binary outputs bytes. N3, 13, is the number
base
for the input data bytes and is normally 2 for binary input bytes. The number
of
5 internal digits for the DIGIT CONVERTERS (4 and 5) and the NUMBER
CONVERTER, 9, are supplied by DIGITS (the number of digits), 12, via line 32.
The number of digits needed is determined by the number base for the XOR
operation
and the bit width of the bytes to be processed. The value of DIGITS is
calculated as
follows: DIGITS>_(In(2~N~.ofB~'S3 -1)/(In(N1)). Ifthe number of bits is 8 (28-
1=255) and
the number base for the XORn is 15, then 3 digits will be required because
In(255)/In(15) is 2.04 which is rounded up to the next integer value of 3.
The DATA ADDRESS COUNTER, 1 is sent via 20 to the INPUT DATA
BUFFER, 2. The MASK ADDRESS COUNTER, 14, is sent via 36 to the DATA
MASK BUFFER, 3. THE OUTPUT ADDRESS COUNTER, 15, is sent via line 37
to the OUTPUT DATA BUFFER, 11. These counters are used to specify which
bytes will be selected from the INPUT DATA BUFFER, 2, and DATA MASK
BUFFER, 3, and where the resultant byte will be placed in the OUTPUT DATA
BUFFER, 11. A byte from the INPUT DATA BUFFER, 2, is sent via line 24 to the
DIGIT CONVERTER, 5. Similarly, a byte from the DATA MASK BUFFER, 3, is
2o sent via line 23 to the DIGIT CONVERTER, 4. N1 (the number base for the
XORn
operation), 7, via line 25 is sent to the "base" inputs for DIGIT CONVERTERS 4
and
5 and the "i base" input of the NUMERIC CONVERTER, 9. N3, 13, (the number
base for the input data byte) in this case is set equal to 2 (for binary) and
is sent via 34
to DIGITS CONVERTER, 5. Similarly, N4, 16, (the number base for the mask byte)
in this case is also set equal to 2 (for binary) and is sent via 35 to DIGITS
CONVERTER, 4. The number of DIGITS, 12, is sent via 32 to the "# dig" inputs
for
the DIGITS CONVERTERS 4 & 5 and the NUMERIC CONVERTER 9.
The binary input data byte is converted into digits base N 1 in the DIGITS
CONVERTER, 5, and the resulting digits are sent via line 27 to the "A in"
input of
3o the MODULO N ADDER/SUBTRACTER, 6. The conversion of a binary number to
j digits (base n) is done by the successive division of the number by n where
the
remainder of each division becomes the ith digit for I-0 to j-1. Or this
conversion
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
11
may also be accomplished by table look up using tables calculated ahead of
time.
Similarly, the binary mask byte is converted in digits base N1 in the DIGITS
CONVERTER, 4, and the resulting digits are sent via line 26 to the "B in"
input of
the MODULO N ADDER/SUBTRACTER, 6. ED, 8, is sent via line 28 to the "e/d"
input of the MODULO N ADDER/SUBTRACTER, 6. If ED=0, then for each "j"
digit, C~ _ (A~ + B~) Mod N1. If ED=1 then for each digit, C~ =(N1+A~ - B~ )
Mod N1.
The digits (C~ ) resulting from the operations within the MODULO N
ADDER/SUBTRACTER, 6, are sent via line 29 to the input of the NUMBER
CONVERTER, 9. Optionally, the output digits of the MODULO N
1o ADDER/SUBTRACTER, 6, can be considered as a series of ciphertext output
digits
(instead of being converted back to a binary value). These digits may be used
by
some other process for transmission to a receiver. If ED=1, the output of the
MODULO N ADDER/SUBTRACTER, 6, can be considered as a series of ciphertext
output digits (instead of being converted back to a receiver. If ED=l, the
output of
the MODULO N ADDER/SUBTRACTER, 6, would be digits representing the
original plaintext. And for this illustration wold be the binary plaintext
only after
conversion to binary in the Number converter, 9.
The value of the output number base N2, 10, is sent via line 30 to the "ok
base" input for the NUMBER CONVERTER, 9. When N2=2, the digits sent to the
2o NUMBER CONVERTER, 9, are converted back to binary by: setting sum=0, then
for
j=DIGITS-1 to 0 perform sum=(sum * Nl) +C~ where C~ is the result of A~XORn
B~.
When done the result in sum. This number base conversion may also be
accomplished by table lookup using tables calculated ahead of time. If N2=2
(binary)
the resultant binary value in sum is sent via line 31 to the OUTPUT DATA
BUFFER,
11.
If N2 is not equal to 2, then the binary value of sum is converted to digits
based N2 (by the method described above) and these digits are used to form BCN
digits in the output byte and the output byte (in BCN format) is then sent via
line 31
to the OUTPUT DATTA BUFFER, 11.
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
12
These steps are repeated until all of the bytes in the input buffer have
been processed and placed in the output buffer. Then the ciphertext is sent
via line 33
to the user. If ED=l, then the output buffer contains plaintext.
The use of number bases (other than binary) for input and output c an alter
the operation of the encoder/decoder. The following examples all use number
bases
greater than 2.
If N2 (the number base for output result) is equal to N1 (the number base
for the XORn calculations) then the digits, resulting from the XORn
calculation, are
placed in the OUTPUT DATA BUFFER, 11, via line 31, without change. This
requires that the size of the OUTPUT DATA BUFFER, 11, must be greater than the
INPUT DATA BUFFER in order to hold the digit values in output bytes. Also, the
OUTPUT ADDRESS COUNTER, 1 ~, must send more addresses to the OUTPUT
DATA BUFFER to handle the extra information being stored. The resulting
Ciphertext can be in digit or BCN format depending upon the implementation.
If either the Plaintext, 21, or the Data Masks, 22, are in digit or BCN
format and the number base for either of these inputs is the same as the
number base
for the XORn calculation (N3 or N4 ~ N I ), then these digits ( ~N 1 ) are
passed
through the respective DIGIT CONVERTER (4 or 5) without change. This case
requires that the respective address counter must be incremented an
appropriate
number of extra times to cause the required number of digits to be sent to the
MODULO N ADDER/SUBTRACTER, 6.
If either the Plaintext, 21, or the Data Masks, 22, are in either a BCN or
digit format and N3 or N4 = N 1, then the appropriate input (=N 1 ) is first
converted by
the respective DIGIT CONVERTER (4 or 5) internally to binary before being
converted to base N 1 digits.
In some preferred embodiments the conversion of bytes into digits based n
is achieved by table lookup instead of by repetitive division of the byte by
n. In
CA 02371446 2001-11-02
WO 00/70818 PCT/US99/10929
13
addition, the conversion of the digits (based n) into binary or another number
base
is also accomplished by table lookup.
In another preferred embodiment, not shown, the input data and masking
data bytes are 16 bites wide, and other counters, tables, variable or arrays
are used to
modify the e/d input of the MODULO N ADDER/SUBTRACTER causing the
method of combining digits to be altered (between equation 1 and 2 forms)
while the
buffers are being processed. In another preferred embodiment, the data bytes
in the
input and output buffers are processed as if all of the bits in the buffer
constitute one
very large byte. Other preferred embodiments use a byte width, which is larger
than
t o 16 bits.
It will now be apparent to those skilled in the art that other embodiments,
improvements, details and uses can be made consistent with the letter and
spirit of the
foregoing disclosure and within the scope of this patent, which is limited
only by the
following claims, construed in accordance with the patent law, including the
doctrine
of equivalents.