Note: Descriptions are shown in the official language in which they were submitted.
CA 02413573 2002-12-05
-1-
Title: SYSTEM AND METHOD FOR MEASURING AND MANAGING
OPERATIONAL RISK
FIELD OF THE INVENTION
(0001] The present invention relates generally to risk management
systems and methods, and is more specifically directed to systems and
methods for measuring and managing operational risk.
BACKGROUND OF THE INVENTION
[0002] Risk management systems are commonly employed by firms,
which may include financial institutions, resource-based corporations, trading
organizations, governments, and other users, for example, to make informed
decisions in assessing and managing the risks associated with the operations
of these users.
[0003] In modern financial and regulatory environments, effectively
measuring and managing market risk, credit risk and operational risk is vital
in
the development of a comprehensive risk management system. Many
organizations have implemented procedures that successfully address market
risk and, to some extent, credit risk. However, managing operational risk
presents special challenges, since the sources of data required to measure
operational risk are often limited, and since there is a lack of industry-
accepted methodologies to measure such risk.
[0004] Operational risk is defined as the risk of loss resulting from
inadequate or failed internal processes, people, systems or external events.
This definition may be extended for non-regulatory purposes to encompass
legal risk and strategic risk (i.e. the risk of making a poor business
decision).
Some of the most important types of operational risk involve breakdowns in
internal controls and corporate governance. Such breakdowns can lead to
financial losses through error, fraud, or failure to perform (i.e. address
risk
events) in a timely manner or cause the interests of a financial institution
to be
compromised in some other way (e.g. staff exceeding their authority or
conducting business in an unethical or risky manner). Major publicized losses
at financial institutions in recent years illustrate fhe enormity of loss
events
CA 02413573 2002-12-05
resulting from the failure of or non-existence of operational risk management
systems. Major losses caused by information technology systems failures,
disasters, and rogue trading, for example, have cost financial institutions
and
firms vast sums of money, diminished shareholder value, and tarnished their
reputation with the general public.
[0005] Recent studies have suggested that the operational risk
exposure in the banking industry is substantial and growing. For instance,
KPMG Consulting Inc. published an analysis entitled "Operational Risk
Becomes a Capital Problem" (May 10, 2000) which found that operational risk
accounts for approximately 40% of a financial institutions overall risk.
Reflecting the growing importance of operational risk, the Basle Committee on
Banking Supervision (BCBS) has recently established new capital proposals
that will require financial institutions to implement robust systems for the
collection and monitoring of operational risk data. The BCBS is part of The
Bank of International Settlements (BIS), an international organization which
fosters international monetary and financial cooperation, and serves as a
bank for central banks. The BCBS proposes implementing three new
methods for calculating the operational risk capital charge for financial
institutions, namely:
(a) Basic Indicator Approach;
(b) Standardized Approach; and
(c) Advanced Measurement Approach (AMA).
[0006] Under the Basic Indicator Approach, financial institutions must
hold capital for operational risk equal to a fixed percentage of an indicator
of
size, or risk, such as gross income. Under the Standarized Approach, the
required capital for a financial institution as a whole is the aggregate of
the
required capital amounts for all business lines within the organization, as
calculated individually using a similar methodology to the Basic Indicator
Approach. The AMA is a more sophisticated method that allows each
institution to implement its own measurement method for operational risk. As
CA 02413573 2002-12-05
-3-
an incentive for implementing operational risk management systems, B1S has
proposed that as financial institutions move from the Basic Indicator method
along the continuum of increasingly sophisticated models for calculating the
operational risk, they will be rewarded with a lower capital charge. Further,
BIS mandates that failure to comply with its new policies will be result in a
variety of supervisory actions, including increased oversight, seni~r
management changes, and the requirement of additional capital.
[0007 In theory, the desire not to tie up capital should provide a
powerful incentive for financial institutions to monitor and reduce
operational
risk. Despite being aware that operational risk has been increasing in the
banking industry, many banks are only in the early stages of developing a
framework for measuring and managing operational risk. This reluctance to
adopt operational risk management systems may be largely be attributed to
the tack of effective risk measurement models and methodologies.
[00081 Various approaches have been developed for modeling
operational risk. The majority of these models provide only a firm-wide view
of operational risk, and are unable to effectively manage risk exposure at the
business unit level. For example, the Capital Asset Pricing Model (CAPM) is
a top-down model which provides an overview of a firm's operational risk
exposure by focusing only on major operational failures (e.g. disasters).
[0009) A further hindrance to the development and adoption of
operational risk management systems is the limited availability of loss
process
data. While a growing number of financial institutions are collecting and
analyzing operational loss event data, it is clear that there has been no
industry standard for the accumulating such data. Such data collection is
vital
for the assessment of operational risk at individual institutions.
[0010] Accordingly, there is a need for a system and method of
measuring and managing operational risk that is capable of providing an
assessment of risk exposure throughout all levels of a firm. There is a
further
need for a flexible operational risk management system that can be adapted
CA 02413573 2002-12-05
to support new operational risk capital calculation models and methodologies,
and new sources of loss process data, as they appear.
SUMMARY OF THE INVENTION
[0011] The present invention relates generally to risk management
systems and methods, and is more specifically directed to systems and
methods for measuring and managing operational risk. According to a first
aspect of the invention, there is provided a system for measuring and
managing operational risk, comprising: a database, wherein operational risk
data is stored therein, wherein said operational risk data includes data
associated with a plurality of first loss events; a first calibration engine
coupled
to said database, wherein said calibration engine generates a plurality of
loss
processes, and estimates a plurality of loss process attributes; a second
reporting hierarchy engine coupled to said database, wherein said reporting
hierarchy engine associates each of said plurality of loss processes to one or
more operational units; a third simulation engine connected to said
calibration
engine for performing simulation-based computations, wherein said third
simulation engine forecasts a plurality of second toss events using said
plurality of loss processes, wherein said second loss events are estirr~ates
of
future loss events; and a fourth risk engine coupled to said second reporting
hierarchy engine and said third simulation engine for computing at least one
risk measure using said plurality of first or said second loss events, wherein
said risk measure is a measure of operational risk.
[0012] According to another aspect of the invention, there is provided a
method of measuring and managing operational risk within a firm, comprising
the steps of: defining a plurality of reporting hierarchies, wherein said
reporting hierarchies are composed of operational units; associating
operational risk data to one or more of said operational units, Wherein said
operational risk data includes data associated with a plurality of first loss
events; defining a plurality of scenarios, wherein said plurality of scenarios
include a plurality of loss process attributes; computing a plurality of
second
loss events using said plurality of loss processes and said plurality of loss
CA 02413573 2002-12-05
-5-
process attributes; storing data associated with one or more of said plurality
of
second loss events in a storage medium; and aggregating said plurality of
second loss events to produce at least one risk measure, wherein said risk
measure is a measure of operational risk.
[0013] According to another aspect of the invention, there is provided a
method of modeling operational risk comprising the steps of: defining one or
more reporting hierarchies, wherein said reporting hierarchies are composed
of operational units; associating operational risk data to one or more of said
operational units, wherein said operational risk data includes data associated
with a plurality of first loss events; and calibrating a plurality of loss
processes
and a plurality of loss process attributes using said plurality of first loss
events, wherein a plurality of loss processes are generated for use in at
least
one of risk management, operations management, and financial
management.
BRIEF DESCRIPTION OF THE DRAWINGS
[0014] For a better understanding of the present invention, and to show
more clearly how it may be carried into effect, reference will now be made, by
way of example, to the accompanying drawings, in which:
[0015] Figure 1 is a schematic diagram illustrating a system for valuing
and managing operational risk in an embodiment of 'the present invention;
Figure 2 is diagram illustrating a standard Mark-ta-Future (MtF)
Cube;
Figure 3 is a diagram illustrating a modified MtF Cube for
operational risk measurement and management;
Figure 4 a flowchart illustrating the steps in a modified MtF
methodology for operational risk;
Figure 5 is a diagram illustrating a first type of reporting
hierarchy;
CA 02413573 2002-12-05
-6-
Figure 6 is a diagram illustrating a second type of reporting
hierarchy;
Figure 7 is a diagram illustrating a third type of reporting
hierarchy; and
Figure 8 is a graph modeling an annual loss distribution using an
enterprise-wide approach to operational risk capital; and
Figure 9 is a graph modeling an annual loss distribution using a
hierarchy-based approach to operational risk capital.
DETAILED DESCRIPTION OF THE INVENTION
[0016] The present application claims priority from Canadian Patent
Application No. 2,364,425, the contents of which are herein incorporated by
reference.
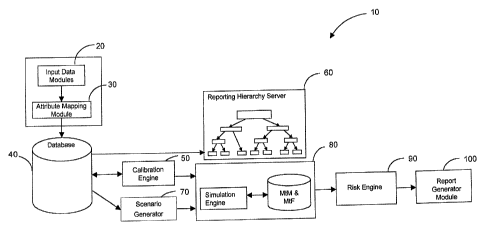
[0017] Referring to Figure 1, a schematic diagram of a system for
measuring and managing operational risk capital in an embodiment of the
present invention is shown generally as 10.
[0018] System 10 comprises a set of integrated components in modular
form used to provide for the hierarchical structuring, Mark-to-Future (MtF)
valuation, simulation and risk management, and reporting of operational risk
capital based on a variety of loss processes. Operational risk capital is
typically defined as the regulatory capital amount that a firm must maintain
to
sufficiently absorb losses resulting from the failure of internal systems,
people
or external events, for example, so as not to cause a financial collapse
andlor
disrupt the orderly functioning of financial markets. Operational risk capital
may also have an internal aspect which would allow a firm to assess and
manage its operational risk exposure.
[0019] System 10 comprises a set of input data modules 20 and
attribute mapping modules 30 to support the loading and managing of large
volumes of data. Input data modules 20 receive loss event data and related
information from a variety of sources, including, for example, manual input
through a computer keyboard or web-browser interfaces. The data received
CA 02413573 2002-12-05
- 7 -
by input data modules 20 may be in various formats, including, for example,
text files, spreadsheets and web-based interfaces.
(0020] Attribute mapping modules 30 may be used to convert
information obtained from input data modules 20 into a consistent format for
storage in database 40. For example, data may be mapped into a desired
format and used to create text files with a prescribed layout that can be read
by standard database block copy tools
[0021] Database 40 may be used to store various data types, including,
for example, internal loss events, indicators, internal near-miss events,
scenarios, external consortium losses, and external public domain losses (to
be described in further detail with reference to Figure 5). It will be obvious
to
those skilled in the art that data to be stored in database 40 may exist in a
single database or other storage means, or distributed across multiple
databases ar other storage means. Database 40 may be a known relational
database, as manufactured by Oracle and Sybase, for example.
[0022] Additionally, database 40 may have a canonical structure
comprising, for example:
(a) event tables (e.g. loss amount, monetary amount, data, event
identification);
(b) classification structure (e.g. name, node identification, parent
identification);
(c) join tables linking events and classifications (i.e. node identification,
event identification); andlor
(d) Foreign exchange rates (monetary amounts, value, date).
[0023] Alternatively, the present invention may utilize object-oriented
databases, wherein the loss events, reporting hierarchies and foreign
exchange rates are stared as objects. Other databases as known in the art
may also be used.
[0024] Database 40 is used to input and extract the operational risk
data and reporting hierarchy information into a calibration engine 50.
CA 02413573 2002-12-05
_ $ -
Generally, reporting hierarchies are representations of the physical or
logical
structure of a firm. Most firms are already logically or physically organized
in
a hierarchical structure for risk reporting and management purposes, which
may make the task of defining operational units in implementing the present
invention less complicated. Reporting hierarchies within a firm may be
defined according to the firm's physical units (e.g. trading desks),
geographic
locations (e.g. regional offices), reporting lines, generic organizational
units, or
risk classes, for example. Risk class-based reporting hierarchies may also be
structured according to "event-based" or "effect-based" categorizations. Input
data obtained from external data sources is also often structured in a
hierarchical manner, and can be easily incorporated into the subject firm's
reporting hierarchy along side internal input data.
[0025] The calibration engine 50 uses the input data and reporting
hierarchy information from the database 40 to determine an appropriate set of
loss processes. In the simplest case, this is done by bucketing (i.e.,
grouping)
aN available data associated with each node of a reporting hierarchy
(operational unit), then examining the data within each bucket. More complex
methods are also used. For example, when two (or more) reporting
hierarchies are to be used simultaneously, it is the pair-wise combination of
leaf nodes of the hierarchies that determines a set of initial data buckets. A
leaf node is an operational unit with no child units for example in Figure 5,
leaf nodes are 154, 158, 160 and in Figure 6 leaf nodes are 164, 166, 168,
170.
[0026] Beyond the reporting hierarchy analysis, loss processes may be
determined using knowledge of real-world processes (e.g., trade settlement)
or statistical data analysis.
[0027] A loss process is a model that can produce or describe a set of
hypothetical future loss events. A loss event is an occurrence having a
quantifiable financial impact on a firm (e.g. a monetary loss). A future loss
event is a plausible or possible loss event that has not or will not
necessarily
occur in the future. A loss process may be modeled using a frequency
CA 02413573 2002-12-05
_g_
distribution (number of events) and severity distribution (size of event), or
using a complete loss distribution (total losses over a specified period) or
in
other ways. Typically the first approach, referred to as an actuarial model,
is
used. For ease of discussion, this approach is discussed herein since it is
the
most common. Actuarial models are typically designed to produce loss
distributions which estimate the expected value of one or more economic
variables, such as would be generated by loss processes, that are distributed
in a random manner. A characteristic of a typical actuarial model is that the
annual loss is not a single loss caused by a single event, but is the result
of
the aggregation of a number of losses.
[0028] A variety of parametric and non-parametric distributions may be
used to determine the frequency and severity distribution models. Table 1
contains a list of possible frequency and severity actuarial models which may
be used by calibration engine 50 to produce the loss distributions:
Frequency DistributionsSeverity Distributions
Poisson Normal
Binomial Lo normal
Bernoulli Student's t
UserDefined Non- arametric
__ Dirac Delta
Non-parametric (correlated)
Table 1: Frequency and Severity Distributions
Possible non-parametric distributions which may be used by calibration
engine 50 include, for example, various histogram or bucketed
representations, or a simple resampling of the input data.
[0029) Calibration engine 50 may present a user with a list of possible
models and allow the user to select one or more models to be used in the
calibration process. Alternatively, calibration engine 50 may also permit a
user
to add additional actuarial models andlor distributions to system 10 by, for
example, specifying a discrete distribution function, or by creating a Visual
Basic or C++ module that is used by calibration engine 50.
[0030] Once the set of loss processes and distributions for the
frequency and severity of each loss process have been selected, calibration
CA 02413573 2002-12-05
-10-
engine 50 utilizes a "fitting method" to calibrate the models. Note that if an
actuarial model is not used, the steps of choosing one or more distributions
and then calibrating proceed in the same fashion. Fitting methods are used to
compare the frequency results from actuarial toss distributions to the
expected
frequencies of theoretical statistical distributions, such as a Chi-square
goodness of fit test. Alternatively, calibration engine 50 may utilize more
sophisticated fitting methods as known in the art, such as the Maximum
Likelihood and Bayesian methods, for example.
[0031] Given the limited supply of operational risk data in financial and
business markets, it is usually not possible to calibrate loss process data
using mark-to-market methods. In order to assess whether the loss
processes are adequate, it is beneficial to provide the user with feedback
regarding the "level of fit" of the selected models. Calibration engine 50 is
capable of providing goodness of fit feedback (e.g. statistical ratios,
graphical
representations) to a user. The user then can use this feedback to decide
whether the level of fit of the selected models to the loss process data is
acceptable.
(0032] The definition, sorting, and aggregation of different reporting
hierarchies across business units, geographic locations, industries,
instruments, risk classes, regulatory requirements, or other sorting criteria
are
performed by a reporting hierarchy engine 60.
(0033] Scenario generator module 70 is used to generate a plurality of
scenarios, coNectively known as a scenario set. The number of scenarios
must be large enough to provide an acceptable statistical representation of
the model. In practice, scenario sets typically contain thousands of
scenarios.
A scenario is a hypothetical value for an attribute of a loss process that may
occur during a given risk time horizon. An attribute of a loss process may
include the frequency of loss events per risk time horizon or the average
severity of such a loss event, for example. A scenario is typically the
realization of a set of random variables representing attributes of a lass
process. Alternatively, a scenario may be the value of one or more
CA 02413573 2002-12-05
-11-
independent risk factors that can be used to infer the value of an attribute
of a
loss process.
[0034j Subsequent output from calibration engine 50, reporting
hierarchy engine 60, and scenario generator module 70 may be stored in
database 40, to be used by simulation engine 80. Simulation engine 80 may
use scenario sets having loss processes with attributes or risk factors to
generate scenarios of loss events. Scenarios of loss events rnay be a set of
loss events experienced in a given risk time horizon by modeling a plurality
loss processes according to the model specified by the user in the calibration
engine 50. For example, for a risk time horizon of one year, the unit of
simulation is the sum of losses for the period of one year. In practice, any
risk
horizon may be used, however, the one year period is commonly used by risk
managers in measuring and managing credit and operational risk. Simulation
engine 80 performs the following steps for each loss process in the reporting
hierarchy:
1. Simulate the number of loss events in each of the scenarios,
and where applicable, each time horizon (i.e. the frequency, n).
2. Sample fram the distribution of absolute loss amounts, the result
being a set of h losses as indicated in the scenario.
3. Sum the losses to form the (simulated) loss at each time horizon
for each scenario.
4. Collect and analyze the simulated losses to provide risk
measures (e.g. the largest expected boss every hundred years).
The output from simulation engine 80, such as MtF valuations, may be stored
in directly database 40 or in a temporary data storage medium.
[0035j Outputs from simulation engine 80 and reporting hierarchy
engine 60 are provided to risk engine 90. Risk engine 90 is used to determine
loss distributions and risk measures associated with each loss process, and
with each operational unit in a reporting hierarchy. The risk measures can be
used to support decision-making and the management of operational risk, and
CA 02413573 2002-12-05
-12-
may include, for example, expected loss, unexpected loss at a confidence
level, value-at-risk (VaR) at a confidence level, marginal VaR at a confidence
level, measures of frequency and severity of loss events, and arrival times of
loss events. Risk engine 90 may also be programmed to perform real-time
"what-if' scenario simulations for new and existing loss process data.
[0036] Output from risk engine 90 may be stored in database 40, and
may be used to generate reports using report generator 100. Report
generator 100 can be used to define and generate standard andlor user-
defined reports. Report generator 100 is able to query databases (e.g.
database 40), extract values directly from the risk engine 90, and utilize
functions of the reporting hierarchy server 60 (e.g. assigning the loss
distribution results to specific units in the reporting hierarchy) Report
generator 100 may be a standard database reporting tool, such as Crystal
Decision's "Crystal Reports" application, for example. In a preferred
embodiment of the present invention, report generator 100 may create user
reports that enable the user to "drill down" or incrementally review each
level
within a reporting hierarchy. Additionally, report generator 100 is capable of
producing and reporting risk measures internally based on more than one
reporting hierarchy.
[0037] The present invention may be implemented in systems designed
to provide distributed, desktop capabilities to support firm-wide operational
risk management. Such systems are also preferably designed to be
computationally efficient and scalable to the largest hierarchical firm
structures and loss processes. In preferred embodiments of invention, the
systems comprise analysis and reporting tools that include the ability to
attribute the marginal operational risks and capital contributions of each
constituent unit (i.e. departments, trading desks) fio the firm-wide
regulatory
andlor internal capital amount. When calibrated to a set of loss processes,
the system may compute MtF operational risk capital valuations for known
and hypothetical loss processes. The system may be adapted to support new
CA 02413573 2002-12-05
-13-
operational risk capital calculation models and methodologies, and new
sources of loss process data, as they appear.
[0038] Application to a Mark-to-Future Methodology
As indicated with reference to Figure 1, system 10 can be adapted to
generate MtF data for use in simulation and risk management applications,
both by components within system 10 of the present invention, and external
applications. MtF data can be generated from the output of various
components of system 10, including reporting hierarchy engine 60, and
scenario generator module 70. In an application of the present invention to
the MtF framework, reporting hierarchy server 60 can work in parallel to
produce a variant of the standard MtF Cube far use in the context of
operational risk.
(0039] The generation of the standard MtF Cube is at the core of the
MtF framework. Key to the MtF framework is the premise that knowledge of
portfolio holdings is not required to generate a MtF Cube: a single MtF Cube
accommodates the risk/reward assessment of multiple portfolios
simultaneously. Figure 2 illustrates an example of a standard MtF Cube,
shown generally as 110, comprising of a set of scenarios 112, time steps 114,
and instruments 116 (e.g. loans). For market and credit risk systems, the NItF
framework creates an instrument MtF Cube containing all of the necessary
information about the values of individual instruments. All market and credit
risklreward analyses and portfolio dynamics for any set of holdings can be
derived by post-processing the contents of the MtF Cube. Further details on
the Mark-to-Future Cube can be found in Dembo et al., Mark-to-Future: A
Framework for Measuring Risk and Reward (Toronto: Algorithmics
Publications, 2000), the contents of which are herein incorporated by
reference. An example of an implementation of this method and why it
represents a standard for simulation-based risk/reward measurement and
management can be found in pending United Mates Patent Application
091811,684, the contents of which are herein incorporated by reference.
CA 02413573 2002-12-05
- 14-
Mark-to-Future is a framework designed not merely to measure risk and
reward, but also to manage the trade-off of risk and reward.
[00401 Mark-to-Future Methodology for Operational Risk
The application of the MtF framework to operational risk hinges on developing
a variant of the standard MtF Cube for use with reporting hierarchies and loss
process data. Figure 3 illustrates an example of a variant of the standard MtF
Cube, shown generally as 118, for use in measuring and managing
operational risk. The variant MtF Cube comprises of scenarios 120, time
series 122, and loss processes 124. The MtF methodology for operational risk
assessment can be summarized by the following seven steps, each of which
can be explicitly configured as an independent component of the overall
process.
The first four steps build the Mtf Cube:
1. Define the reporting hierarchies and loss processes.
2. Define the scenario paths and time step(s).
3. Define the loss processes.
4. Simulate the loss processes over scenarios and time steps to
generate a MtF Cube.
The next three steps apply the MtF Cube:
5. Map the MtF Cube into loss distributions to produce a foes
distribution MtF table.
6. Aggregate the loss distribution MtF table values to produce risk
measures and/or statistics.
7. Incorporate loss distribution MtF tables into (other) advanced
applications.
A key aspect of the modified MtF Cube methodology for use in operational
risk measurement is the addition of Step 1 in which reporting hierarchies and
CA 02413573 2002-12-05
-15-
loss processes are defined. Defining loss processes in the MtF framework
enables the resulting loss distributions and MtF values to be computed
efficiently and consistently.
[0041] The simulation of the operational risk MtF Cube in Steps 1 to 4
above represents a computationally intensive stage of the process and need
be performed only once. These steps represent the pre-Cube stage of MtF
processing. In contrast, Steps 5 to 7 represent post-processing exercises,
which can be performed with minimal additional processing (Step 5 and Step
6) or slightly more complex processing (Step 7). These steps represent the
post-Cube stage of MtF processing. Figure 4 provides a flowchart illustrating
the seven steps of the modified MtF methodology, as applied to operational
risk management, explained in further detail below.
[0042] The decoupling of the post-Cube stage from the pre-Cube stage
is a key architectural benefit of the Mark-to-Future framework. A single risk
service may generate a MtF Cube (pre-Cube) that can be distributed to
internal business units or departments (post-Cube) for a variety of customized
business applications. This generates leverage as a common risk framework
and can be widely distributed throughout the financial institution or firm as
well
as to external organizations for user-specific analyses.
[0043] Referring to Figure 4, the details of this MtF framework and the
underlying methodology as it is applied to operational risk are shown
generally as 126, and explained in further detail below.
[0044] Steo 1 (marked as 128 in Figure 4): Define reaortina hierarchies
Reporting hierarchies represent the structure of a firm in a plurality of
operational units (e.g. business units, regional offices, trading desks)(to be
described in further detail with reference to Figures 5, 6 an 7) and loss
processes. Defining the reporting hierarchies allows the MtF values for the
loss processes to be attributed to a specific operational unit for risk
management purposes and/or aggregated to determine the firm-wide
operational risk capital. Reporting hierarchies are also used in the
definition
CA 02413573 2002-12-05
-16-
of the set of loss processes, a key requirement in the use of Mark to Future
for operational risk measurement and management.
[0045] Step 2 (marked as 130 in Figure 4): Define the scenarios and
time steps
In the MtF framework, scenarios represent the joint evolution of risk factors
through time, and are, thus, the ultimate determinant of future uncertainty.
The explicit choice of scenarios is the key input to many analyses. The
scenarios may be realizations of the number of loss events per period (i.e. a
year) for each operational loss process. Alternatively, scenarios may be
realizations of attributes or abstract risk factors affecting the overall loss
distribution. Far example, a linear combination of loss frequencies may be
used, taking into account any correlations between loss events in the finro
processes? As a further example, parameters of the frequency or severity
distributions associated with a loss process, such as. the average frequency
over one year, may constitute risk factors, and hence realizations of the
parameter values would constitute scenarios. The information generated from
the scenarios, such as, the frequency of tosses and the total amount of loss
for all operational loss processes in the firm, for example, can be used to
populate a three-dimensional Mark-to-Future (MtF). Accordingly, scenarios
directly or indirectly determine the estimated future distributions of MtF
values.
[0046] Stea 3 (marked as 132 in Figure 4): Define the loss processes
Reporting hierarchies consist of various loss processes, both internal and
external to the firm. A loss process may represent an actual loss process or a
statistical (e.g. hypothetical) loss process. Typically, loss processes are
defined using the defined reporting hierarchies from Step 1 (marked as 128 in
Figure 4) and data analysis, conducted in calibration engine 50. The MtF
Cube is a package of MtF tables, each table corresponding to an individual
loss process with realizations across time and scenario 120 (as illustrated in
Figure 3).
CA 02413573 2002-12-05
-17-
[0047] Stea 4 (marked as 134 in Figure 4~ Simulate the loss
processes over the scenarios and time steps
The MtF Cube consists of a set of MtF tables each associated with a given
loss process. The cells of the MtF table contain the MtF values of that loss
process as simulated over a set of scenarios and a number of time steps.
Each loss process has a single loss value on the current risk horizon (e.g.
one
year) assigned to a plurality of cells in the MtF tables. Determining these
loss values is the act of simulation.
[0048] Step 5 (marked as 136 in Figure 4): Map the MtF Cube into a
hierarchical portfolio reporting structures
From the MtF Cube, multiple hierarchical MtF tables can be generated as
functions ( or combinations) of the MtF tables associated with each loss
process. The MtF framework allows a MtF Cube to be generated
independently of reporting hierarchy loss events. Any reporting hierarchy or
hierarchy regime can be represented by mapping the MtF Cube into static or
dynamically changing reporting hierarchies.
[0049] Step 6 (marked as 138 in Figure 4): Actgreaate loss distribution
MtF values to produce risk statistics
The reporting hierarchy-based MtF table resulting from the mapping of the
MtF Cube into a given reporting hierarchy contains a full description of
future
uncertainty. Each cell of the reporting hierarchy MtF table contains a MtF
value for a specific node or level within the reporting hierarchy under a
given
scenario and time step. The actual risk measures chosen to characterize this
uncertainty can be arbitrarily defined and incorporated strictly as post-
processing functionality in the post-Cube stage.
[0050] Step 7 (marked as 140 in Figure 4): Incorporate loss distribution
values into other aanlications
MtF Cube may serve as input for applications more complex than calculating
simple risk measures. The properties of linearity and conditional
independence on each scenario and risk time horizon can be used to obtain
CA 02413573 2002-12-05
-18-
computationally efficient methodologies. For example, conditional
independence within a particular scenario is a powerful tool that allows the
MtF framework to incorporate effectively processes such as joint counterparty
migration. In addition, reporting hierarchy or loss process MtF cubes may be
used as input to a wide variety of scenario-based risk management and
reporting hierarchy optimization applications.
[0051] The MtF methodology was designed to enable a new generation
of risk quantification and management software, and it has a number of key
features that make it an excellent choice for operational risk measurement
and management purposes. Most importantly for operational risk, the MtF
framework is efficient for marginal risk calculation within a reporting
hierarchy.
For example, in a simulation a position can be reset to zero and the risk
statistics recalculated without revaluing the loss processes. Furthermore, it
allows multiple reporting hierarchies to be constructed from the same
simulation results (the pre-Cube stage occurs once while the post-Cube
processing may be repeated). This feature is particularly useful for
operational risk managers to allow capital (and other risk measures) to be
reported in a number of reporting hierarchies (i.e. business units, classes,
geographical locations, process elements, etc.).
[0052] Given that credit risk and market risk measurement systems
may also utilize the MtF framework, the present invention is capable of being
quantified in conjunction with market and credit risk within the same
framework, on the same platform, and using the same software architecture.
This integration of market, credit and operational risk has significant
potential
benefits through the use of common risk factors, instruments and risk
measurement methodologies.
[0053] Reporting hierarchies
An aspect of the MtF methodology, as applied in accordance with the present
invention, is defining the organizational and management structures of a firm
into reporting hierarchies. In order to calculate the operational risk capital
and
related risk measures, it is necessary to first describe a firm's reporting
CA 02413573 2002-12-05
-19-
hierarchy in terms of operational units and loss processes. As described
earlier with reference to Figure 1, most firms are organized in a hierarchical
structure according to physical or logical structure ~e.g. geographic location
and lines of business, respectively). Alternatively, reporting hierarchies may
be prescribed by regulators or set by a governing body. For example, in the
2001 working paper on Regulatory Treatment of Operational Risk issued by
the Basel Committee on Bank Supervision and the Capital Accord, two
reporting hierarchies are proposed for use in the financial services industry
in
determining operational risk capital, namely, business lines and risk
classification hierarchies.
[0054] Referring to Figure 5, an example of a reporting hierarchy in
accordance with an embodiment of the present invention is illustrated and
shown generally as 150. Reporting hierarchy 150 comprises of operational
units 152, 154, 156, 158 and 160. A reporting hierarchy represents the
physical or logical structure of a firm and may comprise of a plurality of
operational units in a variety of configurations. Figures 6 and 7 illustrate
two
examples of reporting hierarchies defined in accordance with variant
embodiments of the present invention. Referring to Figure 6, a simplified risk
class-based reporting hierarchy is shown generally as 162. Reporting
hierarchy 162 comprises four operational units 164, 166, 168, and 170,
Figure 7 illustrates a detailed reporting hierarchy 172 comprising a plurality
of
primary operational units 174, 176, 178, 180, 182, 184, 186, 188, 190 and
192.
(0055] In an alternative embodiment of the present invention, system
10 may combine reporting hierarchies to calculate operational risk capital. In
principle, the combination of hierarchies is useful to obtain accurate
measurements when sources of data are limited, or when "shallow"
hierarchies are combined. Other alternate reporting hierarchies may also be
defined as required.
(0056] Codependence Between Operational Units
CA 02413573 2002-12-05
-20-
Once a reporting hierarchy has been defined, certain additional issues may
become easier to articulate. For example, one serious concern is the
correlations or more general relationships between losses experienced by
diverse operational units, referred to as the codependence between
operational units. Codependence between operational units may arise in at
least two ways: First, codependence may arise °°naturally" as a
result of
internal or external causal influences which affect distinct loss events. For
example, two loss events might be reported in geographically distinct
locations, but have a common causal influence, such as an extreme market
movement that creates stress and leads to human errors. If the decision has
been made to hold capital against such events separately in the two
geographical locations, the calculation of the amount of capital to hold will
be
affected by the correlation between some of the events.
[0057] Codependences may also arise "artificially°° if a single
loss event
has effects which are shared throughout the hierarchy of the firm. For
example, if the financial impact of a single loss event is shared between two
operational units, then that loss is effectively split into two events.
However,
there is an implied correlation because the events are derived from a single
underlying loss (i.e. the events are not independent). The capital held by the
two operational units and by operational units higher up the hierarchy
depends on this correlation.
[0058] The codependent relations between primary operational units
can be expressed within the actuarial framework in the form of the joint
frequency distribution of all m primary operational units. Suppose operational
unit k has nk events per year, then the required distribution is h~m~(nl,
n2,...,n"~
with
(m)
~7=h (n l,n2,...,nm
equal to the probability of n~ events at the first operational unit n2 events
at
the second operational unit, and so on. The marginal distributions are
determined using the following equation:
CA 02413573 2002-12-05
-21 -
hx~"k~ =~h~m~(n,,n2,...,n,~)
~ jx k
(0059] Because the joint distribution must be specified, the frequency
and codependence models are linked in the framework.
[0060] Loss processes
Quantifying operational risk may be challenging because large volumes of
input data are required to properly calibrate both loss process distributions
and scenario generators for risk factors. The term model is used generally to
refer to any item requiring calibration, including loss process frequencies
and
severities, and scenario generators. The present invention can utilize several
different types of input data in the calibration of its models. It is often
useful to
assign more than one loss process to an operational unit. For instance, if
loss
processes correspond to distinct physical processes within a firm (e.g.
manual and automatic settlement of financial instruments), representing the
two loss processes separately is more intuitive and likely to more accurately
reflect reality. However, loss processes need not be independent of one
another in any sense (e.g. statistical). The following is a description of
some
examples of various loss processes that may be used in system 10.
[0061] Internal loss event data includes; for example, information
regarding monetary loss amounts and dates. The Basel Capital Accord
regulatory proposals indicate that these types of data should form the basis
of
all capital calculations under the Advanced Measurement Approach. The
proposals also require that operational risk loss event data be collected and
maintained in a robust, systematic way using well-defined and documented
internal processes.
(0062] Indicators are (a time series of) internal or external numeric
factors that may influence losses. In accordance with the present invention,
indicators are used as predictors of operational risk. For example, if the
volume of financial transactions by a firm increases (e.g. introduction of a
new
product on the market) while the number of staff and availability of new
technology decreases (e.g. layoffs or budget cutbacks), the number of loss
CA 02413573 2002-12-05
-22-
processes during that period would likely increase. Such numerical
correlations between indicators and losses can assist in calibrating loss
distributions and operational risk capital. Indicators can also be useful in
assessing the frequency and severity of loss events. Since indicators may
also serve as risk factors, time series data may contribute to the calibration
of
scenario generators.
[0063] Indicators, both internal and external, also provide static data
that are important for developing defensible scaling models. The
development of defensible scaling models using indicators allows an
organization to scale its internal loss event data according to the
operational
(e.g. external) market. This ability to scale internal loss event data using
indicators is useful when an organization is changing its business focus,
expanding, merging and/or operating in inflationary economies. External data
(e.g. public domain and consortium) may also need to be scaled before it can
applied rationally to the calibration of internal loss distribution models.
[0064] "Near-miss" or "close calls" data typically include event dates
and monetary exposures. A "near-miss" situation is one that could have
resulted in a loss process but failed to occur despite the non-existence of
preventive risk avoidance measures. Monetary exposures are loss amounts
that may have been experienced had the situation occurred. Near-miss data
can be used by organizations to understand the potential for loss events, and
to help prevent similar mistakes or occurrences from leading to losses in the
future. Additionally, near-misses may be used to augment internal loss data
in the calibration of the capital calculation models.
[0065] issues include a set of frequency and approximate monetary
amounts of hypothetical loss events (e.g. "what if' risk assessments). Issue
data is increasingly becoming the subject of regulatory proposals. As a
result,
many firms have established practices for collecting this form of data. In
many instances, issue data can be used to identify processes within a firm
that have a high degree of ,risk. Issue data may also be useful for assessing
the operational risk of new business endeavours, which typically do not have
CA 02413573 2002-12-05
-23-
large amounts of loss process data, or to augment the tails of loss
distributions. In the risk management industry, issues are often referred to
as
scenarios. Since these are not necessarily the same as scenarios in the MtF
context, we have used the term issue herein.
[0066j External public domain loss event data commonly comprises a
set of monetary amounts and dates of events experienced by external firms,
taken from the public domain. Such loss event data includes, for example,
the Zurich IC Squared- Financial Institutions Risk Scenario Trends (FIRST)
database. External loss process data from loss data consortia, such as data
obtainable from the Multinational Operational Risk Exchange or the British
Banker's Association Operational Risk Data Association, for example, may
also be used.
[0067] Detailed classification of all the above, i.e. the assignment of
each datum to one or more nodes or operational units in a reporting
hierarchies.
[0068] System 10 may utilize various types and forms of data and is not
limited solely to the data types described above. Furthermore, in any given
situation, not all of the above data may be available or necessary for system
10. It is possible that system 10 may utilize different procedures, for
example,
if the required output is regulatory capital, the procedure may be different
than
that for internal economic capital. The Basel Capital Accord proposals do not
explicitly specify a procedure for making such decisions, except in the case
of
the simpler approaches to capital calculation. Nevertheless, the present
invention is highly flexible and extensible, and is capable of evaluating and
adopting new data sources, models and methodologies as they appear.
[0069] In the following sections, two examples of simulations have
been provided to illustrate the application of the present invention to
operational risk management problems. The first example shows the
calculation of operation risk capital at the firm-wide level using an
aggregate
loss distribution approach. The second example illustrates aggregation of
operational risk using the hierarchy in Figure 5. In both instances, the data
CA 02413573 2002-12-05
-24-
utilized is purely hypothetical, and the examples are intended to explain the
simulation of operational risk in the Mark-to-Future framework.
[0070] Example 9: Enterprise-wide Capital Calculation
In this example, the goal is to calculate operational risk capital at the firm-
wide
level. It is assumed the subject firm has a reporting hierarchy identical to
the
hierarchy described in Figure 5. For ease of understanding, the operational
units in reporting hierarchy 150 will be referred by number (e.g. operational
unit 152 will have a loss distribution of f,52(z)). The desired output value
is a
figure for the annual capital for firm 152 with a one-year risk horizon. A
list of
internal loss event data and a set of indicator time series data is presumed
to
be available. The data are associated with a corresponding loss process (a,
b, c, d, e, or f) attached to an operational unit directly (154, 158 or 160)
or
indirectly (156, 152). The loss events can be summed year-by-year to create
a series of total annual losses for each operational unit.
[0071] It is also presumed that the data collection is consistent with the
Basel Capital Accord. in a more complex example, a very different result may
be obtained if self assessment scenarios, external data, near misses, or other
inputs were included. Table 2 contains a summary of the input data collected
for the entire firm, consisting of six years of losses totaling 316 losses.
The
number of loss events n for each year in the range 2000-2005 is listed, along
with the total loss z, the mean ~,(x) and standard deviation ~(x) of the
severity
(individual loss amounts).
Year n Z ~,(x) a(x)
(US$ millions)US$ thousands)US$ thousands
20_00_ 64 7.55 117.9 109.6
2001 57 6.35 111.3 106.2
2002 52 5.14 98.8 93.7
2003 55 5.29 96.1 88.0
2004 43 3.86 89.7 78.5
2005 45 3.41 75.7 68.5
Table 2: Summary of input data for firm-wide capital calculation
CA 02413573 2002-12-05
-25-
A Poisson distribution for the frequency of loss, and an empirical
distribution
for the severity of the loss are selected, requiring both the estimation of
the
parameters of the distributions and the assessment of the appropriateness of
the assumptions based on the assumed input data.
[0072] The frequency, whose probability distribution function is given by
~"e ''
h(re) nt
is calibrated using a calibration engine (e.g. calibration engine 50 of Figure
1 ).
The parameter 7~ can be estimated by the average number of events per year
over the six years. For this example, the result is 52.67. The Poisson
distribution is likely to be appropriate because of the clustering of the
number
of losses about the mean. This indicates a low variance, much in line with the
effects of a Poisson distribution. A more detailed back-testing analysis would
have to be carried out to formally determine the appropriateness of the model.
[0073] To construct severity distributions, calibration engine 50 uses
the given 316 individual loss events, with severity ~x;~, i= 1, 2,...,316.
Their
broad statistical properties can be deduced from the data in the table, viz
mean p.=USD 99.9K and standard deviation a=USD 93:6K. Assuming that all
previous losses are equally likely to reappear, sampling, with replacement,
can be conducted directly from the vector of past loss severities. In more
forma! terms, the implied assumption is that the toss processes are
conditionally independent, given n.
[0074] Where codependences exist between loss processes, a latent
variable model (e.g. the Merton model) may be used to represent a
frequency-codependence structure which is equivalent to specifying the joint
frequency distribution. The latent variable model is based on covariate
normal risk factors, with the loss event frequency determined by a threshold
model.
CA 02413573 2002-12-05
-26-
[0075] Using a latent variable model approach, a set of m risk indexes
~yk} at the operational units are random variables with a covariate normal
joint
distribution. An event at operational unit k is deemed to have occurred if yk
crosses a threshold rlk. Using the latent variable model, the marginal
distribution of frequencies at each operational unit is a Bernoulli
distribution
(or binomial of order 1 ). The distribution has a probability given by:
p= ~N(1,0)(x~dx
k
Possible values of N are 0 or 1.
[0076] If identical related uncorrelated operational units with probability
p are grouped together, a binomial marginal frequency distribution is obtained
for the group. When the group has v members, the maximum frequency is v,
and the probability of a single event is p". In the event that p is very
small, but
pu =~, remains finite, the distribution tends to a Poisson distribution with
intensity ~,.
[0077] Additionally, generalizations of the covariate normal approach
are possible involving rank correiations and marginal distributions of yk
which
are not normal. Furthermore, dependencies between different severity
modules (basic risk) can be handled by the MtF framework in the present
invention.
[0078] Based on the assumption that the loss processes are
conditionally independent, the annual distributions can be determined as
follows:
n
Z = x.
i=1
where {x~} is a sample (with replacement) of size r~ from the input data {x;}.
Note that an explicit choice was made not to fit a smooth parametric model to
the data to obtain the annual loss distribution, but to simple resample the
input
data.
CA 02413573 2002-12-05
-27-
[0079] Having determined and calibrated the distributions, a scenario
generator module (e.g. scenario generator 70 of Figure 1 ) creates scenarios
for the input data. First, N is equal to 1000 scenarios (i.e. 1000 simulated
years are created). This results in 1000 scenarios for one quantity: the
number of events, firm-wide, n. For every scenario on n, an annual loss is
generated using the selected actuarial model, with a different sample of ~z~~.
With 1000 scenarios, there will be 1000 samples of annual losses (with
different values of n). This is the way that the most simulation-based
aggregation methods work in market and credit risk systems.
[0080 A simulation engine (e.g. simulation engine 80 of Figure 1 )
utilizes the selected actuarial model where the annual loss z is not a single
loss caused by a single event, but rather is the result of the aggregation of
a
number of losses. For example, where in a particular year, there are n events
that each cause a loss and have monetary values given by:
x., i=1,.., n
then
n
z=~,~
[0081] Understanding the composition of z is facilitated by viewing both
x and n as random variables. Thus x has a distribution g such that
dp= g(x)dx
is the conditional probability of experiencing a loss with value in the range
[x,
x+dx] given that an event has occurred. Event n has a distribution h such that
p"= h(n)
is the probability of experiencing n loss events in a year. When no
operational
risk events have occurred p ~ 0. In actuarial terms, x is the "severity" of an
event, g is the "severity distribution°', n is the "frequency'°,
and h is the
"frequency distribution" of the operational unit.
CA 02413573 2002-12-05
-28-
(0082] In preferred embodiments of the invention, system 10 calculates
the loss distribution fk(x) for each operational unit (e.g. 152, 154, 156, 158
and
160 of Figure 5) in a consistent manner. Generally, loss distribution fk(x) is
the probability that a loss of magnitude x will occur over a specified period
(e.g. one year) in operational unit k. The annual loss distribution may be
written as follows:
f(z)= ~hCn)g'°'(z)
n=o
where g~"~ is the distribution of annual losses, given that there were
precisely n
events.
[0083] The actuarial model approach is advantageous when used in
operational risk applications because it is operable when the number of
events n is small. Although the estimation of h is affected when there is a
limited number of years of data, the actuarial model approach is generally
more ready to accept assumptions about h. Principal among these
assumptions is that the independent events have a Poisson distribution, as
follows
_ 7v" a ~
h(n) nt
which has a single parameter ~., the average number of events per year.
Another choice is the negative binomial distribution
Ci+n-1 1
h(n) -
n 1+~ ~i +l
with a > 0, ~3 > 0. It is interesting to note that the negative binomial
distribution can be derived as a mixture of Poisson distributions with
different
frequencies ~.. The negative binomial distribution is obtained when ~, has a
gamma distribution. The above equation represents a process where there
CA 02413573 2002-12-05
-29-
are expected to be A=a[i loss events per year, however there can be more
or less than this number. The standard deviation of the event frequency is
given by [ice .
[0084) Additionally, the annual loss distribution equation may be
exploited to derive the statistical properties of f from the properties of g
and h.
The expected value and variance of g and h can be written as follows:
Es(x)=P~ v~'s(x~=~x~
Fi(n) =~.n, var h(n)=an
[0085] The expected value of x over g~"~ is n~, and the variance is nax.
Thus, the expected value of z over f is,
Ef (x) _ ~h(n)np,x= pnp,x
n
and the second moment of z is
Ef(z2)=~h(n)(n~X +n2~,X),
n
so the variance of z is
Zz
V8T f (z~ = I,t,nQ x + Qn E.tx
[0086) The usual assumption is that the loss events at a given
operational unit are conditionally independent given the value of n. Given
this
assumption gin' is equal to g convolved with itself n time. This convolution
expression can be written iteratively as,
g~n~(x~ ~g~n ~~(y x~g(Y)dy
g~°~( x) = a ( x)~
where a is the Dirac delta : a(x) = 0 for x~ 0.
The advantage of assuming independence is that there are efficient analytic
and numerical techniques for evaluating g(°~. The assumption can be
relaxed
in special cases, at the expense of additional complication.
CA 02413573 2002-12-05
-30-
[0087] Each aggregate operational unit also requires a loss distribution.
These distributions are created by aggregation of the constituent operational
units. Aggregation consists of identifying all of the operational loss
processes
belonging to the operational unit and all of its descendants in the hierarchy.
The annual loss in each scenario for the operational unit is simply the sum of
all annual losses in the constituent operational loss processes.
[0088] For aggregate operational units 152 and 156, different methods
of calculating the loss distributions are required because no operational loss
processes are directly attached to these operational units. For example, the
information available to operational unit 156 is comprised of all of the data
from constituent primary operational units 158 and 160, together with their
loss distributions flsa and f160~ and any intermediate results that have been
stored in database 40. If losses in operational unit 158 are independent of
losses in operational unit 160, then f"6fx) may be determined as the
convolution of fls8 and fi6o.
[0089] In many situations the losses experienced by the operational
units 158 and 160 are related in some fashion. For example, if the hierarchy
is based on a line of business reporting structure, operational units 158 and
160 may both experience losses due to the same event, such as a technology
failure. This example illustrates a powerful reason to believe that
operational
risk will be correlated between operational units. In such situations, the
loss
distributions fs8 and fl6o Of operation units 158 and 160 are not sufficient.
Further information containing the relations between the two operational units
will also be required.
(0090] While in this example, only one sample of z is constructed per
frequency scenario, but it would also be possible to construct more than one;
the results are equivalent for a large enough number of scenarios. Figure 8
shows the firm-wide annual loss distribution calculated using the assumed
input data in Table 2. The results of loss distribution results have been
summarized in Table 3. The simulated results in Figure 8 represent one
severity sample per frequency scenario. Simulation curve 194 is formed
CA 02413573 2002-12-05
-31 -
using a simulation approach with resampling. For cornparison, the results are
also shown after applying the Central Limit Theorem. The expected loss p is
given along with the standard deviation a. VaR (p) is defined as the
difference between thepth percentile and the expected loss.
Method N. o . VaR VaR VaR
USD, millionsUSD; millions95% X99% 99.9%
Resampling 5.28 1.00 1.72 2.35 3.47
Central 5.26 0.99 1.63 2.31 3.07
Limit
Theorem
Table 3: Firm-wide risk measures using a non-parametric simulation
approach
[0091] In this example, the expected loss is 5.26M USD, and the
standard deviation is 0.99M USD. The difference in the two results of risk
statistics is largely due to sampling error owing to the small number of
scenarios used.
(0092] For comparison, since a large number of events per year
are expected, the results of a semi-analytic convolution are also provided. In
this case, suppose that the severity distribution does not appear to have an
ultra-heavy tail, so the Central Limit Theorem can be applied to the
convolution. With this approximation the frequencies are simulated as before,
and the firm-wide annual loss distribution can be effectively calculated to a
high degree of accuracy.
(0093] Example 2: Capital Calculation in a Hierarchy
In an embodiment of the present invention, system 10 determines
distributions for each of the operational loss processes and utilizes this
information to derive distributions for the operational units. In the first
example, the amount operational risk capital was calculated for the firm as a
whole. In the second example the amount operational risk capital is
determine for each operational unit within the reporting hierarchy. As will be
discussed below, the basis of the capital calculation is scenario input data
used in assessing operational risk.
CA 02413573 2002-12-05
-32-
(0094] In this example of an embodiment of the present invention, it is
assumed that each of the primary operational units 154; 158 and 160 has
been through a risk profiling exercise. Table 4 summarizes the scenario data
used for this example.
Operational Scenario X
Unit (USD) (per year)
154 Retail T ical 100 iC 1
Bankin Worst case 10 M 0.01
158 Custody T ical 1 M 0.1
Worst case 100 M 0.01
160 CorporateT ical 200 iC 5
A enc Worst case 40 M 0.01
Table 4: Summary of Scenario Data
The data relates to a fictitious risk profiling of the operational units in
Figure 5.
Each primary operational unit has provided a '°typical'° and a
'°worst case"
scenario for loss events. Each scenario has a loss amount and an estimated
average frequency.
[0095] Capital for these risks is not necessarily regulated directly, but
economic capital may be held by the firm as a buffer. An economic capital
figure is also an efficient way of prioritizing the contra) and mitigation
actions.
Action plans to control and mitigate the unacceptable risks may be
implemented based on the results of the capital calculations.
[0096] Using a simulation engine (e.g. simulation engine 80 of Figure
1 ), the modified MtF framework is used to calculate the economic capital for
the identified risks, and to aggregate the capital to the firm level. For
simplicity, the events in each of the six scenarios are assumed to be
independent. This means that operational units 154, 158 and 160 each have
two separate operational loss processes (i.e. typical and worst case), with
each having a separate severity and frequency distribution.
CA 02413573 2002-12-05
-33-
[0097] Further, it is assumed that all operational loss processes have a
Poisson frequency distribution in accordance with the following equation:
~n a A
h(n)=
n!
with intensity equal to the estimated average frequency in Table 4. All
severity distributions are modeled as a simple spike at the value of the
estimated loss. Either the frequency or severity distributions could be
extended to more complex models without altering the remainder of the
example.
[0098] Simulation engine 80 simulates N=10000 scenarios over one
time step, with one simulated quantity (frequencies) per operational loss
process (six in total), the dimensions of the MtF Cube are 10000 x 1 x 6. The
results are summarized in Table 5 below and in Figure 9. The quantiles may
be estimated using any method as known in the art (e.g. Kernel method)
which improves their stability and reliability. Kernel method estimators are
useful for applications where the severity distribution is composed of spikes
because the cumulative distribution of annual losses is not continuous.
Unit 1u o VaR (99%) VaR (99.9%)MVaR (99.9%)
(USD) (USD) (USD) (USD) (USD)
152 2.75 M 10.9 68.7 M 99.2 M 100%
M
154 2.54 M 10.8 68.7 M 99.2 M 86%
M
156 216K 1.07M 8.18M 10.0M 14%
158 1.11 M 10.0 49.9 M 98.9 M 67%
M
160 1.43 M 4.13 24.9 M 40.2 M 19%
M
Table 5: Summary of Simulation Results
[0099] The marginal Value-at-Risk of an operational unit is the
contribution at the margin of that operational unit to the overall Value-at-
Risk
of the firm, or of the parent of the unit. A useful property of mVaR is that
the
sum of all values of mVaR for operational units at the same level in the
CA 02413573 2002-12-05
-34-
reporting hierarchy (i.e. "child" operational units) would total the mVaR of
an
operational unit at the next highest level in the reporting hierarchy (i.e. a
'°parent" operational unit). MVaR contributions are calculated by
approximating the partial derivative of the firm-wide VaR with respect to the
overall scale of the loss distribution at each operational unit. This is very
efficient to calculate within the MtF framework because it does not require a
re-simulation. Most of the VaR for the firm can be traced to operational unit
158, hence this operational unit would be deemed to be consuming the most
capital. With this information, a business decision can be made as to whether
the return on the capital for operational unit 158 is acceptable to the firm
as a
whole.
[00100] In accordance with an embodiment of the present invention, the
above examples describe several approaches far performing firm-wide and
hierarchy-based measurements of operational risk capital. System 10 may
also be used to perform simpler day-to-day models or impact measures that
are intended to improve the quality of workflow, reduce losses caused by
process failure, change the risk culture the firm, and provide early warning
of
deterioration in systems or management.
[00101 ] The use of a simulation approach to operational risk overcomes
many of the above-mentioned complications. An advantage of using a
simulation approach to determine the operational risk capital is that no
particular model is mandated for either frequency or severity distributions.
Hence, the simulation approach provides the flexibility to specify the precise
forms and calibration methods of both distributions, and most particularly the
severity distribution.
[00102] The simulation approach also accommodates special forms of
dependence between frequency and severity distributions. For example,
consider an operational unit that experiences only toss events of five
amounts: critical, very high, high, moderate and low. If a critical loss
occurs,
the operational unit will cease operations. This means that after a critical
loss,
the probability of further losses is zero. If a very high loss occurs, the
CA 02413573 2002-12-05
-35-
operational unit manager may obtain insurance or enforce a policy change,
thus affecting the probability of future losses at each level or the number of
future losses, respectively. The consequence is that g~"~(z) has no explicit
functional form. In such instances, a simulation engine (e.g. simulation
engine 80 of Figure 1) would simulate these extreme cases by assigning zero
sensitivities to subsequent events.
(00103) Lastly, in an alternative embodiment of the present invention,
the frequency distribution h(n) can be re-expressed as the distribution of
arrival times of an event. For example, the simple Poisson distribution
equation can be written in terms of the arrival time t as follows:
q(t) _ ~ a x~
where q(t)dt is the probability of the next event arriving after t years. The
arrival time formulation is particularly convenient for certain applications
(e.g.
forecasting loss processes), and can help with the specification of the
codependence between the different event types.
[00104) Writing the joint frequency distribution in terms of arrival times
requires q~'"~ (t!, t2, ..., t") with
dp = q~ "'' (t, , t2,..., tm )dt, dtZ...dtm
equal to the probability of the arrival times being in the infinitesimal range
of
(t~, t2, ..., tm). The marginal distribution qk is given by:
m
Rk(tkO t j 9~ ) (tl,t2,..., tm )dtldtZ...dtm
jxk
Extending the concepts above, arrival time modeling facilitates the inclusion
of
more complicated ideas in a simulation framework. For instance, instead of
q~m~ being constant, it could be dependent on the most recent event. An
important and convenient mechanism for specifying joint distributions is
through the use of copulas. Copulas are a special farm of joint distribution
of
continuous variables, which, in this context, would be used to specify q~'"~.
CA 02413573 2002-12-05
-36-
(00105] Whife simulation is an approach to estimating the loss
distribution based on the calibrated loss distribution, other techniques are
available. Specifically, analytic convolution and numerical convolution
methods, including for example Fast Fourier Transforms and Panjer's
Algorithm, can be employed. These techniques provide computational
efficiency, but generally rely on more restrictive assumptions.
[00106 The present invention has been described with regard to specific
embodiments. However, it will be obvious to persons skilled in the art that a
number of variants and modifications can be made without departing from the
scope and spirit of the invention defined in the claims appended hereto.
i . ., . ... .. M . ~~ .. ...,:~~~~~,. .~ n~. :~~~rw _. ,Y..L~e
~~~:~.~:~.~~.,..F3 ~~,~~. .~rt~~N~