Note: Descriptions are shown in the official language in which they were submitted.
CA 02431094 2003-06-04
1
IRREGULAR PRT DECONVOLUTION METHOD AND SYSTEMS, AND ITS
USES
This invention relates to radar signal processing. In particular, this
invention concerns Doppler processing and clutter filtering on irregular Pulse
Repetition Time (PRT) sampled signal.
Description of the Prior Art
In conventional radar, Doppler processing uses discrete Fourier
transform (DFT) on regularly sampled signals because the pulse repetition
time is constant within a burst. So, such conventional processing using
discrete Fourier transform (DFT) is not applicable to irregular Pulse
Repetition Time (PRT) sampled signal.
Irregular Pulse Repetition Time (PRT) is usually meant to prevent
blind speeds (velocity ambiguity), the jammers from locking on the radar 's
Pulse Repetition Time (PRT), and also to solve Doppler ambiguities.
Current work on irregular sampling is mostly motivated by image
processing. Efficient algorithms based on frame operations have been
developed as Efficient numerical methods in non-uniform sampling theory"
written by Feichtinger, H.G. and al in Numerische M'athematik 69 (NUHAG).
Wavelet transform in digital filter banks as uMultirate systems and filter
banks" written by Vaidyanathan, P.P. Prentice-Hall Publishers (1993)
illustrates efficient 1 D applications with irregular samples obtained by
integer
decimation or expansion of uniform samples.
In Doppler radar signal processing, Pulse Repetition Time (PRT)
staggering has been studied, but with emphasis on the Fourier analysis,
rather than on solving the irregular-sampling problem.
An exception is the NSSL algorithm proposed in the American patent
US 6,081,221 for Doppler weather radar. This NSSL algorithm offers a non-
ambiguous solution in Doppler speed and does only ground clutter filtering.
Such ground clutter has a mean frequency equal to zero because it does not
move. So, clutter with any mean frequency like: sea clutter or rain clutter...
can not be filtered with this proposed NSSL algorithm.
CA 02431094 2003-06-04
2
Summary of the invention
This invention solves the above-mentioned drawbacks, in particular
solving the velocity ambiguity and filtering any type of clutter, providing a
deconvolution method which filter any kind of clutter even varying clutter
like
sea clutter, rain clutter...
An object of this invention is a deconvolution method of irregular pulse
repetition time sampled signal x(tm), which comprises the following steps:
[S1 J conversion of the irregular samples x(t,,,) to regular samples r(iTe);
io - [S2] computation of the spectrum dft(r) of these regular samples;
- [S3] isolation of the clutter spectra in dft(r) by assuming clutter spreads
over more than a few range gates;
[S4] estimation of the clutter spectral lines from the mean and the width of
the isolated clutter spectra,
is - [S5] subtraction of the estimated clutter spectra from the total spectrum
dft(r);
- [S6] deconvolution of the remaining spectra.
In a first embodiment of the deconvolution method, the computation in
the steps of subtraction [S5] and deconvolution [S6] is adjusted to the
clutter
20 type by the clutter spectra given by step [S3J.
A further object of this invention is deconvolution system of irregular
pulse repetition time sampled signal x(fm), which comprises:
Mean for converting the irregular samples x(t,,,) to regular samples niT,.);
25 - Mean for computing the spectrum dft(r) of these regular samples;
Mean for isolating the clutter spectra in dit(r) by assuming clutter spreads
over more than a few range gates;
- Mean for estimating the clutter spectral lines from the mean and the width
of the isolated clutter spectra;
3o - Mean for subtracting the estimated clutter spectra from the total
spectrum
dft(r);
- Mean for deconvolving of the remaining spectra.
Moreover, another object of this invention is the use of such
35 deconvolution method in radar system.
CA 02431094 2010-08-11
3
A further object to this invention is the use of such deconvolution
method as clutter filtering, in particular as sea clutter filtering.
According to an aspect of the present invention there is provided a
deconvolution method of irregular pulse repetition time sampled signal x(tm)
wherein the method comprises the following steps:
converting of the irregular samples x(tm) to regular samples r(iTe);
computing of a spectrum dft(r) of these regular samples;
isolating of a clutter spectra in dft(r) by assuming clutter spreads over more
than a few range gates;
estimating of clutter spectral lines from the means and the width of the
isolated clutter spectra;
subtracting of estimated clutter spectra from total spectrum dit(r);
deconvoluting of remaining spectra,
wherein, in said subtracting and deconvoluting steps, the computations are
adjusted to the clutter type by the clutter spectra given by the isolating
step.
According to another aspect of the present invention there is provided
a deconvolution system of irregular pulse repetition time sampled signal x(tm)
comprising:
converting means for converting the irregular samples x(tm) to regular
samples r(iTe);
computing means for computing the spectrum dft(r) of these regular samples;
isolating means for isolating the clutter spectra in dft(r) by assuming
clutter
spreads over more than a few range gates;
estimating means for estimating the clutter spectral lines from the means and
the width of the isolated clutter spectra;
subtracting means for subtracting the estimated clutter spectra from the total
spectrum dft(r); and
deconvolving means for deconvolving of the remaining spectra,
wherein the computation in the means for subtracting and the means for
deconvolving are adjusted to the clutter type by the clutter spectra given by
the
means for isolating.
Brief description of the drawings
Further features and advantages of the invention will be apparent from
the following description of examples of embodiments of the invention with
reference to the drawing, which shows details essential to the invention, and
from the claims. The individual details may be realised in an embodiment of
the invention either severally or jointly in any combination.
CA 02431094 2010-08-11
3a
Figure 1a, 1b, tc and 1 d, Spectra obtained from irregular Pulse
Repetition Time (PRT) sampled signal with four different prior art
techniques: respectively, NSSL, NUHAG, wavelet and LSP methods,
- Figure 2a and 2b, Clutter of, respectively, land and sea given
by NSSL,
- Figure 3, Flow chart of significant steps in the method to filter
clutter according to the invention.
Figure 4a, 4b, 4c, 4d and 4e, Illustration of the method
according to the invention, respectively, by spectra of the used irregular
sampling, the simulated signal, the simulated sea clutter, the clutter filter
input and output for a signal which is a noise-free complex exponential at
frequency 1.2, and a Gaussian-shaped sea clutter with mean and
bandwidth corresponding to sea state 5 when PRF and RF would be
respectively 1 kHz and 1 GHz,
- Figure 5a, 5b, 5c, 5d and 5e, Illustration of the method
according to the invention applied to target echo and sea clutter from
Figure 4 with added Gaussian noise and Weibull-distributed amplitude,
respectively, by spectra of the used irregular sampling, the simulated
signal, the simulated sea clutter, the clutter filter input and output for a
signal which is a complex exponential at frequency 1.28, a Gaussian-
shaped sea clutter with mean and bandwidth corresponding to sea state 5
when PRF and RF would be respectively f kHz and 1 GHz, and a target
frequency at 1.28.
CA 02431094 2003-06-04
4
More detailed description
Irregular sampling has not been used as widely as uniform sampling
because the time and frequency analyses of irregular samples are rather
involved.
Random sampling usually involves random numbers added to regular
sampling times. The DFT-based power spectrum of random samples
consists of the power spectrum of signal plus additive uncorrelated noise. For
1o example, even with a noise-free signal sampled at the Nyquist sampling
rate,
the output signal-to-noise ratio could be 1 only.
Deterministic irregular sampling involves repeating periodically the
same sequence of K irregular intervals with the mean sampling interval T.
The sampling is usually called interlaced when K=2, and multirate or bunch
when K has an arbitrary length. Since such a sampling set contains K regular
sampling sets, DFT gives K peaks (per one frequency component of a signal)
within the range limited by the sampling frequency 1/T,.
For any regular sampling set (nT), such that T<1/(213), a real signal x(t)
limited to a frequency band B, writes as x(t) = En x(nT).sin c(2B(z - nT)).
Irregular samples are well understood in theory, but their method are usually
too complicated. For an irregular sampling set (tn}, the reconstruction with
bi-
orthogonal bases (sin c[2B(r-nT)]) and (`f'i(r):}, writes as:
X(r) = Z.csinc(2B(t-tõ)) = E,x(rõ)'=',,(r)where cõ is the inner product of
x(t)
with (Tw(t) j. If the set {tJ is limited as jr - tnJ < 1/ (8B), Y,,(t) is a
Lagrange
interpolation function. Basis functions can also be frames, i.e. bases whose
orthogonality is not required. The frame conditions are much weaker and
more useful for practical purpose.
The following prior art techniques illustrate the state of the art in the
spectral analysis from irregular samples.
The Lomb-Scargle periodogram (LSP) is the classical DFT-based
periodogram corrected by preserving the statistical behaviour and time-
translation invariance. If the samples are irregular, the Lamb-Scargle
CA 02431094 2003-06-04
periodogram (LSP) on multirate samples reveals the deterministic pattern as
shown by Figure I d.
The wavelet transform of x(t) is given as X(aj) with a wavelet shifted
s by 'r and scaled by a. The spectrum is represented by I X(c,z) 12, so-called
scalogram. Current efficient wavelet transform algorithms support the uniform
sampling with dyadic scaling and shifting (a= f and x= n2"'). In this study,
any irregular sampling is implemented in an existing Morlet wavelet. The
wavelet transform is more robust, but its frequency resolution is very poor as
io shown by Figure 1c. In general, wavelet transform is not applicable because
radar echoes are periodic signals and, thus, wavelets can hardly serve as
their convenient basis functions.
In the NUHAG frame decomposition, a complex band-limited signal
x(t) of finite energy, given by M irregular samples, is first rewritten as
trigonometric polynomials p(f) of period 1 and degree K, K<M/2. The solution
for the Fourier coefficients ak, I k I < K, x(r) = X , aexp(j2;2f,.r) , I &1:5
B, is
based on properties of the frame operator: M p(tm).DX(t -r,õ) where
DK{t) = Zkexp(j2.,-d,,.r), represents the frame. The NUHAG method illustrated
by Figure lb is applicable for any sampling type but only up to the sampling
frequency, what is unfortunately, not application for the radar applications.
The NSSL magnitude deconvolution is used for the ground radar
Doppler processing of interlaced sampling scheme. In general, an NSSL
sampling set Ãtm} is multirate with rate K and the mean interval TK. An NSSL
time interval (tm+1 - tm), as well as the whole sequence KTs, are integer
multiples of the largest common time interval T,, KT6 = LT,, so that the
smallest regular set {f7 } can contain {t,, J, (tm} c {iT}.
Thus, the irregular samples x(tm) are converted to the zero-padded
samples r(iTe) being product of a sampling scheme c,, c,= c(jTE - t n), and
the
regular samples x(iTf). Based on this relation: r = diag(c).x (in the vector
form), the spectrum of x, can be derived as follows:
dft(r) = dfi(c) * dfi(x) = C - dfr(x)
Idt(x)( = Iq-1, Id
h(r)I
CA 02431094 2003-06-04
6
where C is a Toeplitz matrix whose row vectors are cyclically shifted
dft(c). Since C is singular and, thus not invertible, the NSSL idea is to use
the
magnitudes instead. It is applicable only if there are no complex additions in
the product C C. dit(x). This condition implies the bandwidth of x, but it is
not a
constraint for most radar.
The spectrum Idfr(r)I contains L replicas of the spectrum fdit(x)J that
are weighted by coefficient from Idft(c)I, in a frequency range which is UK
times wider than the mean sampling frequency fE. The deconvolution gives
the strongest replica, i.e. the signal spectrum Idfr(x)I
As shown by Figure la, NSSL method is comparable with NUHAG
method (Figure 1b) for multirate samples. Furthermore, NSSL method
enables solving the radar problems of Doppler ambiguity and ground clutter
filtering. Unfortunately, the NSSL method is applicable only for ground radar
applications.
Only the NSSL method supports frequencies above the Nyquist
frequencies, namely up to LX times the sampling frequency.
In track radar, where expected Dopplers are reasonably known, the
signal spectra supported by NSSL may suffice. Namely, using the
magnitudes in
dft(r) = dfr (c) * dit (x) = C = dfx (x)
Idf(x)l -ICj-' =Idt(r)I
implies that the spectrum of the signal x cannot be broader than NIL spectral
lines, where N and L are the number of regular samples (i.e. the length of the
vectors r and x) and the length of the basic irregular sequence, respectively,
It can also work in the cases where the signal spectrum is broader than NIL,
but no distance between the spectral lines can be an integer multiple of NfL.
The range of unambiguous frequencies may expand limitlessly, but
clutter filtering becomes more involved with increasing 'complexity of the
sampling.
According to the invention, if the clutter bandwidth Bj is known, the
complex clutter amplitudes can be estimated, and filtered from Idfi`(r)I,
before
the deconvolution. Thus, the filter according to the invention is adapted to
the
CA 02431094 2003-06-04
7
particular clutter type of the environment in which the signal is transmitted,
e.g. sea clutter as shown by Figures 2 and 3.
Any kind of clutter can be estimated. A set {i) is then centred at an
integer corresponding to the mean Doppler as shown by Figures 3a and 3b
for, respectively, land clutter and sea clutter.
In general, the amplitudes .c(i, k) of the i-th clutter spectral
component, f, e Bd, i E- [-i, J] repeated at the k-th non-zero-line of the
code
spectrum, k= f, L, can be estimated as follows:
dkZd` - z fori>O
Ci.k! at.Lal.L.z N fori<O
t l+l+f L
where vectors d and at contain L non-zero spectral components from dit(c),
di = {dit(c)}a+c--i)Nf , ldft(c)1=1, at. -[d2 d3 ... dL, dTJ, and z = dff (r)
In general, the integer interval i e [-1, JJ is unknown. For estimating
the clutter spectral lines, f e B1, by using the correlation, the clutters are
assumed to have a Gaussian shape and the received signals to be complex
exponentials.
The Gaussian shape implies that the- spectrum width crci can be
estimated from the correlation coefficients p(z) at the first two lags, as
follows:
al CrC1_'.?Crf
The clutter spectrum o,6, of three times crt from the mean frequency to
the left and to the right implies 99,7% of the spectrum. An optimum cry, is a
compromise between taking as much as possible of clutter spectra and
leaving as much as possible signal spectra, and as such it should be treated
as adaptive to a particular radar echo.
The mean Doppler frequency f. can be estimate from the argument
of the a utocorrelationat the first lag p(r) exp(m }, as follows:
f a = Srg[r(r, )V (2, r')
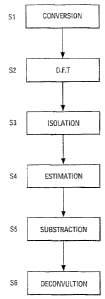
The deconvolution method according to the invention is illustrated by
Figure S. This method can be summarised by the following steps:
[Si: conversion step) The irregular samples x(f,,,) are converted to
regular samples r(1T:);
CA 02431094 2003-06-04
E
(S2: DFT step] The spectrum dft(r) of these regular samples is
computed;
(S3: isolation step) The clutter spectra are isolated by assuming clutter
spreads over more than a few range gates;
(S4: estimation] The clutter spectral lines are estimated from the mean
and the width of the isolated clutter spectra;
[S5: subtraction] The clutter spectra are subtracted from the total
spectrum dft(r);
(S6: deconvolution] The remaining spectra are deconvolved,
Wherein the steps S5 and S6, the computation are adjusted to the
clutter type by the clutter spectra given by step S3.
In a second embodiment, the spectrum dft(c) can also be computed
and its L non-zero components found in step S2. In third embodiment, the
is amplitudes of the clutter spectra can be estimated in step S4. So, the
convolution operations can be reduced, based on the L non-zero spectral
components between the steps S5 and S6. In other embodiments, these
second and third embodiments can be combined.
Furthermore, the clutter spectral lines can be estimated from the mean
in f d = arg[r(Zi) (2wt,) and/or the width in Q. _ = acr> acct
of the isolated spectra (84). Moreover, the amplitudes of the clutter spectra
d'-Ed, .z A, Pori>_O
I r+1+cr-ti L
can be estimated by g r (i, k:) = a. L E a:.L . Z L for i < 0 (S4]' The
tit+lL
convolution operation can be reduced in
dft(r) = dit(c) *dit(x) = C dfx(x)
1 before the remaining spectra in
Idft(x)(= IG_=Jdit(r)i
dff (r) = dff(c) * dfr(x) = C = dft(x)
t are deconvolved (S6).
The deconvoiution method according to the invention is illustrated in
Figures 4a, 4b, 4c, 4d and 4e when the multirate sampling contains five non-
zero spectral components as shown by Figure 4a which modulate the input
CA 02431094 2003-06-04
9
signal of Figure 4d containing the noise-free target echo of Figure 4b and
non-random sea clutter of Figure 4c. All these spectra are given in dB in
function of normalised Doppler. The power spectral density (psd) of the sea
clutter is assumed to be Gaussian shaped. The clutter filtering and
deconvolution result in the frequency contents of the target echo as shown by
Figure 4e.
This deconvolution method in any of its embodiments is applied in
radar system by a deconvolution system, which comprises:
- A mean for converting the irregular samples x(t,,) to regular samples
r(iTg);
- A mean for computing the spectrum dft(r) of these regular samples;
- A mean for isolating the clutter spectra in dft(r) by assuming clutter
spreads over more than a few range gates;
- A mean for estimating the clutter spectral lines from the mean and the
width of the isolated clutter spectra;
- A mean for subtracting the estimated clutter spectra from the total
spectrum dit(r);
A mean for deconvolving of the remaining spectra.
in Figures 5a, 5b, Sc, 5d and 6e, the deconvolution method according
to the invention is applied to a more realistic scenario. Gaussian noise is
added to the target echo as shown by Figure 5b, and the sea clutter of Figure
5c is made random. The clutter is normally distributed over irregular pulse
repetition time (PRT) sampled signal having the correlation determined by
the Gaussian shaped power spectral density, and with amplitude per range
assumed to be Weibull distributed. The same sampling (Figure 5a)
modulates the input signal of Figure 5d containing a noisy target echo (Figure
5b) and a random sea clutter (Figure 5c). All these spectra are given in dB in
function of normalised Doppler. The deconvolution method according to the
invention works better if the normalised Doppler frequency is adjusted to
frequency 1,28. Changing the sampling frequency can do it. The clutter
estimation and subtraction, which are followed by the deconvolution, result
again in the frequency contents of the target echo as shown by Figure Se.
CA 02431094 2003-06-04
Other irregular sequences may be used which could be optimal for the
Doppler range extension but also for the clutter filtering.
One advantage of the deconvolution method according to the
5 invention is that it works above the Nyquist frequencies and offers
filtering
method for any kind of clutter, in particular: any "varying" clutter as sea
clutter
or rain clutter, but also non varying clutter as land clutter.
So, another application to the proposed method and filter may be
io "rain" clutter filtering, or even any clutter filtering (for "varying" and
"not
varying" clutter). So, it allows the use of this clutter filter in any kind of
radar
whatever the environment is. This because clutter filtering according to the
invention is possible for clutter whose spectral lines are not necessarily
centred at zero.
More generally, such deconvolution system may be used to
deconvolve any kind of irregular sampled signal not only radar one.