Note: Descriptions are shown in the official language in which they were submitted.
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
SYSTEM AND METHOD FOR QUANTITATIVE ASSESSMENT OF CANCERS
AND THEIR CHANGE OVER TIME
Reference to Related Applications
The present application claims the benefit of U.S. Provisional Application No.
60/322,427, filed September 17, 2001, whose disclosure is hereby incorporated
by reference
in its entirety into the present disclosure.
Field of the Invention
The present invention is directed to a system and method for quantifying
cancers and
their change over time and is more particularly directed to such a system and
method wluch
use biomarlcers related to cancers, or oncomarkers.
Description of Related Art
Malignant tumors, including cancers of the lungs, abdominal organs, bones, and
central nervous system, afflict a sigW ficant percent of the population. In
assessing those
conditions, and in tracking their change over time, including improvements due
to new
therapies, it is necessary to have quantitative information. Manually obtained
and imprecise
measures of tumor growth, traditionally assessed through manual tracings or by
caliper
measurements of an image, have been used in the past. Such measures lack
sensitivity and
are typically useful only for gross characterization of tumor behavior.
Examples of
measurements that are taken from MRI or CT examinations of cancer patients
include: lesion
volmne, lesion surface area within one slice, maj or and minor axes within one
slice, and the
cross product of major and minor axes within one slice.
Some references for the prior work include: Therasse, P., et al. "New
Guidelines to
Evaluate the Response to Treatment in Solid Tumors," .Tourhal of National
Cafzce~ Institute,
Feb. 2000(92)3: 205-216. That paper describes the standard (RECIST) for
unidimensional
tumor measurement.
1
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
Also, for an example of the awl~wardness of the conventional mouse-driven
manual
outlining of lesions, see: Barseghian, T. "Uterine Fibroid Embolization Offers
Alternative to
Surgery," Diagnostic Imaging, Sept. 1997, 11-12.
Other references include:
Pieterman, R. et al. "Preoperative Staging of Non-Small-Cell Lung Cancer with
Positron-Emission Tomography," New Ezzgland Journal ofMedicine, 2000 Jul. 27,
343(4)
290-2.
Yang, W., et al., "Comparison of Dynamic Helical CT and Dynamic MR Imaging in
the Evaluation of Pelvic Lymph Nodes in Cervical Carcinoma, " Anze>"ican
Journal of
Roentgenology, 2000 Sep; 175(3) 759 - 766.
Lilleby, W., et al. "Computed Tomography/Magnetic Resonance Based Volume
Changes of the Primary Tumour in Patients with Prostate Cancer with or without
Androgen
Deprivation," Radiotherapy azzd Oncology, 2000 Nov; 57(2): 195 -200.
Ward, R., et al. "Phase I Clinical Trial of the Chimeric Monoclonal Antibody
(C30.6)
in Patients with Metastatic Colorectal Cancer," Clinical Cance>" Resea>"ch,
2000 Dec; 6(12):
4674 - 4683.
Hermans, R., et al. "The Relation of CT-Determined Tumor Parameters and Local
and
Regional Outcome of Tonsillar Cancer after Definitive Radiation Treatment,"
International
Journal ofRadiation Oncology Biology-Physics. 2001 May 1; 50(1): 37-45.
Stolckel, M., et al. "Staging of Lymph Nodes with FDG Dual-Headed PET in
Patients
with Non-Small-Cell Lung Cancer," Nuclear Medicine Communications, 1999 Nov;
20(11):1001-1007.
Sahani, D., et al. "Quantitative Measurements of Medical Images for
Pharmaceutical
Clinical Trials: Comparison Between On and Off Site Assessments," American
Journal of
Roentgenology, 2000 Apr; 174(4): 1159-1162.
2
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
Couteau, C, et al., "A Phase II Study of Docetaxel in Patients with Metastatic
Squamous Cell Carcinoma of the Head and Neclc," Bf°itish
Jouf°rzal of Caracer~, 1999 Oct;
81 (3):457-462.
Padhani, A., et al. "Dynamic Contrast Enhanced MRI of Prostate Cancer:
Correlation
with Morphology and Tumour Stage, Histologic Grade and PSA," Cliraical
Radiology, 2000
Feb; 55(2): 99-109.
Yanl~elevitz, D., et al. "Small Pulomonary Nodules: Volumetrically Determined
Growth Rates Based on CT Evaluation," Radiology, 2000 Oct; 217: 251-256:
Those measurements require manual or semi-manual systems that require a user
to
identify the structure of interest and to trace boundaries or areas, or to
initialize an active
contour.
The prior art is capable of assessing gross changes over time. However, the
conventional measurements are not well suited to assessing and quantifying
subtle changes in
lesion size, and are incapable of describing complex topology or shape in an
accurate manner
or of addressing finer details of tumor biology. Furthermore, manual and semi-
manual
measurements from raw images suffer from a high inter-observer and infra-
observer
variability. Also, manual and semi-manual measurements tend to produce ragged
and
irregular boundaries in 3D when the tracings are based on a sequence of 2D
images.
3
CA 02459557 2004-03-03 i -i / ti v v ~-'~~ '~
~~~r ~ /~~G ~
~mmary of the Invention
It will be apparent from the above that a need exists in the art to identify
features of
__mors such as their boundaries and sub-components. It is therefore a primary
object of the
invention to provide a more accurate quantification of solid tumors and other
cancerous
tissues. It is another object of the invention to provide a more accurate
quantification of
changes in time of those tissues. It is a further object of the invention to
address the needs
noted above.
To achieve the above and other objects, the present invention is directed to a
technique for identifying characteristics of cancerous tissue, such as tumor
margins, and
..._.
identifying specific sub-components such as necrotic core, viable perimeter,
and development
of tumor vasculature (angiogenesis), which are sensitive indicators of disease
progress or
response to therapy. The topological, morphological, radiological, and
pharmacokinetic
characteristics of tumors and their sub-structures are called biomarkers, and
specific
measurements of the biomarkers serve as the quantitative assessment of disease
progress.
Biomarkers specific to tumors are also called oncomarkers.
The inventors have discovered that the following new biomarkers are sensitive
indicators of the progress of diseases characterized by solid tumors and other
cancerous
~.* .
tissues in humans and in animals. In addition to tumor surface area and tumor
3D volume,
the biomarkers are:
~ tumor compactness (surface-to-volume ratio);
~ tumor surface curvature;
~ tumor surface roughness;
~ necrotic core volume;
~ necrotic core compactness;
~ necrotic core shape;
116741.00201/35589871v1
4
~~E~D~d ~IH,
CA 02459557 2004-03-03 ( '
~ viable periphery volume;
~ volume of tumor vasculature;
~ change in tumor vasculature over time;
~ tumor shape, as defined through spherical harmonic analysis;
~ morphological surface characteristics;
~ lesion characteristics;
~ tumor characteristics;
~ tumor peripheral characteristics;
~ tumor core characteristics;
ri'_,
~ bone metastases characteristics;
~ ascites characteristics;
~ pleural fluid characteristics;
~ vessel structure characteristics;
~ neovasculature characteristics;
~ polyp characteristics;
~ nodule characteristics;
t
°~ rv ~ angiogenisis characteristics;
~ tumor length; and
~ tumor width.
A preferred method for extracting the biomarkers is with statistical based
reasoning as
defined in Parker et al (US Patent 6,169,817), whose disclosure is hereby
incorporated by
reference in its entirety into the present disclosure. A preferred method for
quantifying shape
and topology is with the morphological and topological formulas as defined by
the following
references:
5
116741.00201/35589871v1
4 .r~'"
~'.3~~~L ~~~:?~ -~~ ~-.d~r ~'~'~"~~s
f~. ~ 'n'-' ' _
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
Curvature Analysis: Peet, F.G., Sahota, T.S. "Surface Curvature as a Measure
of
Image Texture" IEEE Transactions on Pattern Analysis and Machine Itatelligence
1985 Vol
PAMI-7 6:734-738;
Struik, D.J., Lectures oh Classical Differential Geometry, 2nd ed., Dover,
1988.
Shape and Topological Descriptors: Duda, R.O, Hart, P.E., Pattern
Classification and
Scene Analysis, Wiley & Sons, 1973.
Jain, A.I~, Fundamentals ofDigitallnZage Processing, Prentice Hall, 1989.
Spherical Harmonics: Matheny, A., Goldgof, D. "The Use of Three and Four
Dimensional Surface Harmonics for Nonrigid Shape Recovery and Representation,"
IEEE
Transactions on Pattern Analysis and Machine Intelligence 1995, 17: 967-981;
Chen, C.W, Huang, T.S., Anot, M. "Modeling, Analysis, and Visualization of
Left
Ventricle Shape and Motion by Hierarchical Decomposition," IEEE Transactions
o3a Pattern
Analysis and Machine Intelligeyzce 1994, 342-356.
Those morphological and topological measurements have not in the past been
applied
to onco-biomarkers.
The quantitative assessment of the new biomarkers listed above provides an
objective
measurement of the state of progression of diseases characterized by solid
tumors. It is also
very useful to obtain accurate measurements of those biomarkers over time,
particularly to
judge the degree of response to a new therapy. Manual and semi-manual
assessments of
conventional biomarkers (such as major axis length or cross-sectional area)
have a high
inherent variability, so that as successive scans are traced, the variability
can hide subtle
trends. That means that only gross changes, sometimes over very long time
periods, can be
verified using conventional methods. The inventors have discovered that
extracting the
biomarker using statistical tests and treating the biomarker over time as a 4D
object, with an
automatic passing of boundaries from one time interval to the next, can
provide a highly
6
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
accurate and reproducible segmentation from which trends over time can be
detected. That
preferred approach is defined in the above-cited patent to Parker et al. Thus,
the combination
of selected biomarlcers that themselves capture subtle pathologies with a 4D
approach to
increase accuracy and reliability over time, creates sensitivity that has not
been previously
obtainable.
The quantitative measure of the tumor can be one or more of tumor shape, tumor
surface morphology, tumor surface curvature and tumor surface roughness.
7
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
Brief Description of the Drawings
A preferred embodiment of the present invention will be set forth in detail
with
reference to the drawings, in which:
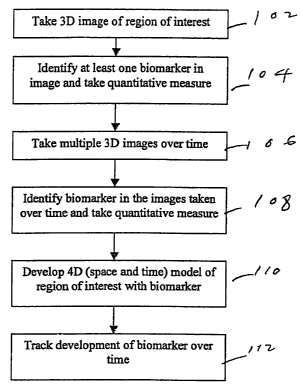
Fig. 1 shows a flow chart of an overview of the process of the preferred
embodiment;
Fig. 2 shows a flow chart of a segmentation process used in the process of
Fig. l;
Fig. 3 shows a process of tracl~ing a segmented image in multiple images taken
over
time; and
Fig. 4 shows a block diagram of a system on which the process of Figs. 1-3 can
be
implemented.
8
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
Detailed Description of the Preferred Embodiment
A preferred embodiment of the present invention will now be set forth with
reference
to the drawings.
Fig. 1 shows an overview of the process of identifying biomarkers and their
trends
over time. In step 102, a three-dimensional image of the region of interest is
taken. In step
104, at least one biomarker is identified in the image; the technique for
doing so will be
explained with reference to Fig. 2. Also in step 104, at least one
quantitative measurement is
made of the biomarker. In step 106, multiple three-dimensional images of the
same region of
the region of interest are taken over time. In some cases, step 106 can be
completed before
step 104; the order of the two steps is a matter of convenience. In step 108,
the same
biomarker or biomarkers and their quantitative measurements are identified in
the images
taken over time; the technique for doing so will be explained with reference
to Fig. 3. The
identification of the biomarkers in the multiple image allows the development
in step 110 of a
model of the region of interest in four dimensions, namely, three dimensions
of space and one
of time. From that model, the development of the biomarker or biomarkers can
be tracked
over time in step 112.
The preferred method for extracting the biomarkers is with statistical based
reasoning
as defined in Parker et al (US Patent 6,169,817), whose disclosure is hereby
incorporated by
reference in its entirety into the present disclosure. From raw image data
obtained through
magnetic resonance imaging or the like, an obj ect is reconstructed and
visualized in four
dimensions (both space and time) by first dividing the first image in the
sequence of images
into regions through statistical estimation of the mean value and variance of
the image data
and joining of picture elements (voxels) that are sufficiently similar and
then extrapolating
the regions to the remainder of the images by using known motion
characteristics of
components of the image (e.g., spring constants of muscles and tendons) to
estimate the rigid
9
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
and deformational motion of each region from image to image. The object and
its regions
can be rendered and interacted with in a four-dimensional (4D) virtual reality
environment,
the four dimensions being three spatial dimensions and time.
The segmentation will be explained with reference to Fig. 2. First, at step
201, the
images in the sequence are tal~en, as by an MRI. Raw image data are thus
obtained. Then, at
step 203, the raw data of the first image in the sequence are input into a
computing device.
Next, for each voxel, the local mean value and region variance of the image
data are
estimated at step 205. The connectivity among the voxels is estimated at step
207 by a
comparison of the mean values and variances estimated at step 205 to form
regions. Once the
connectivity is estimated, it is determined which regions need to be split,
and those regions
are split, at step 209. The accuracy of those regions can be improved still
more through the
segmentation relaxation of step 211. Then, it is determined which regions need
to be merged,
and those regions are merged, at step 213. Again, segmentation relaxation is
performed, at
step 215. Thus, the raw image data are converted into a segmented image, which
is the end
result at step 217. Further details of any of those processes can be found in
the above-cited
Parker et al patent.
The creation of a 4D model (in three dimensions of space and one of time) will
be
described with reference to Fig. 3. A motion tracking and estimation algorithm
provides the
information needed to pass the segmented image from one frame to another once
the first
image in the sequence and the completely segmented image derived therefrom as
described
above have been input at step 301. The presence of both the rigid and non-
rigid components
should ideally be taken into account in the estimation of the 3D motion.
According to the
present invention, the motion vector of each voxel is estimated after the
registration of
selected feature points in the image.
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
To take into consideration the movement of the many structures present in the
region
of interest, the approach of the present invention takes into account the
local deformations of
soft tissues by using a priori knowledge of the material properties of the
different structures
found in the image segmentation. Such knowledge is input in an appropriate
database form at
step 303. Also, different strategies can be applied to the motion of the rigid
structures and to
that of the soft tissues. .Once the selected points have been registered, the
motion vector of
every voxel in the image is computed by interpolating the motion vectors of
the selected
points. Once the motion vector of each voxel has been estimated, the
segmentation of the
next image in the sequence is just the propagation of the segmentation of the
former image.
That technique is repeated until every image in the sequence has been
analyzed. The
definition of time and the order of a sequence can be reversed for convenience
in the analysis.
Finite-element models (FEM) are known for the analysis of images and for time-
evolution analysis. The present invention follows a similar approach and
recovers the point
correspondence by minimizing the total energy of a mesh of masses and springs
that models
the physical properties of the anatomy. In the present invention, the mesh is
not constrained
by a single structure in the image, but instead is free to model the whole
volumetric image, in
which topological properties axe supplied by the first segmented image and the
physical
properties are supplied by the a p~io~i properties and the first segmented
image. The motion
estimation approach is an FEM-based point correspondence recovery algorithm
between two
consecutive images in the sequence. Each node in the mesh is an automatically
selected
feature point of the image sought to be tracked, and the spring stiffness is
computed from the
first segmented image and a p~io~i lcnowledge of the human anatomy and typical
biomechanical properties for the tissues in the region of interest.
Many deformable models assume that a vector force field that drives spring-
attached
point masses can be extracted from the image. Most such models use that
approach to build
11
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
semi-automatic feature extraction algorithms. The present invention employs a
similar
approach and assumes that the image sampled at t = ~z is a set of three
dynamic scalar fields:
~(x~t) _ {gyt(x)~ Ivg»(x)h o2g~t(x»~
namely, the gray-scale image value, the magnitude of the gradient of the image
value, and the
Laplacian of the image value. Accordingly, a change in ~(x, t) causes a
quadratic change in
the scalar field energy U~(x) oc (0(x))2. Furthermore, the structures
underlying the image
are assumed to be modeled as a mesh of spring-attached point masses in a state
of
equilibrium with those scalar fields. Although equilibrium assumes that there
is an external
force field, the shape of the force field is not important. The distribution
of the point masses
is assumed to change in time, and the total energy change in a time period Ot
after time t = h
is given by
D U" (fix)
~ ~(a(g,~ Cx) - g,~+i (x + ~1x)))z + (~(~ogn (x)~ - ~og,~+~ (x + dx)I))Z +
dXEg"
(~(v2gn (x) + v2gn+1 (x -+- ~)))2 + ~ ~~T K~l
where a, j3, and y are weights for the contribution of every individual field
change, r~ weighs
the gain in the strain energy, K is the FEM stiffness matrix, and 0~ is the
FEM node
displacement matrix. Analysis of that equation shows that any change in the
image fields or
in the mesh point distribution increases the system total energy. Therefore,
the point
correspondence from g" to gt+i is given by the mesh configuration whose total
energy
variation is a minimum. Accordingly, the point correspondence is given by
X =X+OX
where
t1~ = mini DU" (~).
In that notation, mine q is the value ofp that minimizes c~.
12
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
While the equations set forth above could conceivably be used to estimate the
motion
(point correspondence) of every voxel in the image, the number of voxels,
which is typically
over one million, and the complex nature of the equations malee global
minimization difficult.
To simplify the problem, a coarse FEM mesh is constructed with selected points
from the
image at step 305. The energy miumization gives the point correspondence of
the selected
points.
The selection of such points is not trivial. First, for practical purposes,
the number of
points has to be very small, typically = 104; care must be taken that the
selected points
describe the whole image motion. Second, region boundaries are important
features because
boundary traclcing is enough for accurate region motion description. Third, at
region
boundaries, the magnitude of the gradient is high, and the Laplacian is at a
zero crossing
point, making region boundaries easy features to track. Accordingly, segmented
boundary
points are selected in the construction of the FEM.
Although the boundary points represent a small subset of the image points,
there are
still too many boundary points for practical purposes. In order to reduce the
number of
points, constrained random sampling of the boundary points is used for the
point extraction
step. The constraint consists of avoiding the selection of a point too close
to the points
already selected. That constraint allows a more uniform selection of the
points across the
boundaries. Finally, to reduce the motion estimation error at points internal
to each region, a
few more points of the image are randomly selected using the same distance
constraint.
Experimental results show that between 5,000 and 10,000 points are enough to
estimate and
describe the motion of a typical volumetric image of 256x256x34 voxels. Of the
selected
points, 75% are arbitrarily chosen as boundary points, while the remaining 25%
are interior
points. Of course, other percentages can be used where appropriate.
13
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
Once a set of points to track is selected, the next step is to construct an
FEM mesh for
those points at step 307. The mesh constrains the kind of motion allowed by
coding the
material properties and the interaction properties for each region. The first
step is to find, for
every nodal point, the neighboring nodal point. Those skilled in the art will
appreciate that
the operation of finding the neighboring nodal point corresponds to building
the Voronoi
diagram of the mesh. Its dual, the Delaunay triangulation, represents the best
possible
tetrahedral finite element for a given nodal configuration. The Voronoi
diagram is
constructed by a dilation approach. Under that approach, each nodal point in
the discrete
volume is dilated. Such dilation aclueves two purposes. First, it is tested
when one dilated
point contacts another, so that neighboring points can be identified. Second,
every voxel can
be associated with a point of the mesh.
Once every point xi has been associated with a neighboring point x~, the two
points are
considered to be attached by a spring having spring constant k~ ~', where l
and m identify the
materials. The spring constant is defined by the material interaction
properties of the
connected points; those material interaction properties are predefined by the
user in
accordance with known properties of the materials. If the connected points
belong to the
same region, the spring constant reduces to k~ ~ and is derived from the
elastic properties of
the material in the region. If the connected points belong to different
regions, the spring
constant is derived from the average interaction force between the materials
at the boundary.
In theory, the interaction must be defined between any two adjacent regions.
In
practice, however, it is an acceptable approximation to define the interaction
only between
major anatomical components in the image and to leave the rest as arbitrary
constants. In
such an approximation, the error introduced is not significant compared with
other errors
introduced in the assumptions set forth above.
14
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
Spring constants can be assigned automatically, particularly if the region of
interest
includes tissues or structures whose approximate size and image intensity are
known a priori,
e.g., bone. Segmented image regions matching the a p~ior~i expectations are
assigned to the
relatively rigid elastic constants for bone. Soft tissues and growing or
shrinking lesions are
assigned relatively soft elastic constants.
Once the mesh has been set up, the next image in the sequence is input at step
309,
and the energy between the two successive images in the sequence is minimized
at step 311.
The problem of minimizing the energy II can be split into two separate
problems:
minimizing the energy associated with rigid motion and minimizing that
associated with
deformable motion. While both energies use the same energy function, they rely
on different
strategies.
The rigid motion estimation relies on the fact that the contribution of rigid
motion to
the mesh deformation energy (OXTK~1X)/2 is very close to zero. The
segmentation and the a
pYiori knowledge of the anatomy indicate which points belong to a rigid body.
If such points
are selected for every individual rigid region, the rigid motion energy
minimization is
accomplished by finding, for each rigid region RZ, the rigid motion rotation
RZ and the
translation TZ that minimize that region's own energy:
rigid = mini ~rlgid - ~ (~ = mini. Un (~Xi ))
b'lerigid
where OXi = Ri~Xi + TtXi and ~zi is the optimum displacement matrix for the
points that
belong to the rigid region Rl. That minimization problem has only six degrees
of freedom for
each rigid region: three in the rotation matrix and three in the translation
matrix. Therefore,
the twelve components (nine rotational and three translational) can be found
via a six-
dimensional steepest-descent technique if the difference between any two
images in the
sequence is small enough.
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
Once the rigid motion parameters have been found, the deformational motion is
estimated through minimization of the total system energy U. That minimization
cannot be
simplified as much as the minimization of the rigid energy, and without
further
considerations, the nmnber of degrees of freedom in a 3D deformable object is
three times the
number of node points in the entire mesh. The nature of the problem allows the
use of a
simple gradient descent technique for each node in the mesh. From the
potential and kinetic
energies, the Lagrangian (or lcinetic potential, defined in physics as the
kinetic energy minus
the potential energy) of the system can be used to derive the Euler-Lagrange
equations for
every node of the system where the driving local force is just the gradient of
the energy field.
For every node in the mesh, the local energy is given by
UX;,n (~')
(a(g» (xc + ~) - ~~t+i (x~ ))) 2 + (~(IDg» (x~ + ~)I - I~gn+~ (x~ )I))2 +
r(vz~" (x~ + ~) + vZg»+~ (xa )>2 + 2 ~ ~ (k~ ~» (x~ _ x~ _ ~))2
x; eG,a ~~r )
where G", represents a neighborhood in the Voronoi diagram.
Thus, for every node, there is a problem in three degrees of freedom whose
minimization is performed using a simple gradient descent technique that
iteratively reduces
the local node energy. The local node gradient descent equation is
x~ (ra + 1) = x1 (h) - v4U~x ~"),") (fix)
where the gradient of the mesh energy is analytically computable, the gradient
of the field
energy is numerically estimated from the image at two different resolutions,
x(ya+1) is the
next node position, and v is a weighting factor for the gradient contribution.
At every step in the minimization, the process for each node takes into
account the
neighboring nodes' former displacement. The process is repeated until the
total energy
reaches a local minimum, which for small deformations is close to or equal to
the global
16
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
minimum. The displacement vector thus found represents the estimated motion at
the node
points.
Once the minimization process just described yields the sampled displacement
field
0X, that displacement field is used to estimate the dense motion field needed
to track the
segmentation from one image in the sequence to the next (step 313). The dense
motion is
estimated by weighting the contribution of every neighbor mode in the mesh. A
constant
velocity model is assumed, and the estimated velocity of a voxel x at a time t
is v(x, t) _
~x(t)lOt. The dense motion field is estimated by
c(x) kr,m~x~
v(x, t) _
0t 'd4x~EG,w(xi) Ix - xl
where
kl,m
c(x) = v~~~ x
".( ;> x-x.i
7~~"' is the spring constant or stiffness between the materials Z and m
associated with the voxels
x and xJ, ~t is the time interval between successive images in the sequence,
~x - x~~ is the
simple Euclidean distance between the voxels, and the interpolation is
performed using the
neighbor nodes of the closest node to the voxel x. That interpolation weights
the contribution
of every neighbor node by its material property k1 ~ ; thus, the estimated
voxel motion is
similar for every homogeneous region, even at the boundary of that region.
Then, at step 315, the next image in the sequence is filled with the
segmentation data.
That means that the regions determined in one image are carried over into the
next image. To
do so, the velocity is estimated for every voxel in that next image. That is
accomplished by a
reverse mapping of the estimated motion, which is given by
v(x, t + 0t) = H ~ v(x~ , t)
b'[x~+v(x~,t)]eS(x)
17
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
where H is the number of points that fall into the same voxel space S(x) in
the next image.
That mapping does not fill all the space at time t+0t, but a simple
interpolation between
mapped neighbor voxels can be used to fill out that space. Once the velocity
is estimated for
every voxel in the next image, the segmentation of that image is simply
L(x, t + Ot) = L(x - v(x, t + Ot)4t, t)
where L(x,t) and L(x,t+Ot) are the segmentation labels at the voxel x for the
times t and t+~t.
At step 317, the segmentation thus developed is adjusted through relaxation
labeling,
such as that done at steps 211 and 215, and fine adjustments are made to the
mesh nodes in
the image. Then, the next image is input at step 309, unless it is determined
at step 319 that
the last image in the sequence has been segmented, in which case the operation
ends at step
321.
The operations described above can be implemented in a system such as that
shown in
the bloclc diagram of Fig. 4. System 400 includes an input device 402 for
input of the image
data, the database of material properties, and the like. The information input
through the
input device 402 is received in the workstation 404, which has a storage
device 406 such as a
hard drive, a processing unit 408 for performing the processing disclosed
above to provide
the 4D data, and a graphics rendering engine 410 for preparing the 4D data for
viewing, e.g.,
by surface rendering. An output device 412 can include a monitor for viewing
the images
rendered by the rendering engine 410, a further storage device such as a video
recorder for
recording the images, or both. Illustrative examples of the workstation 304
and the graphics
rendering engine 410 are a Silicon Graplucs Indigo workstation and an Irix
Explorer 3D
graphics engine.
Shape and topology of the identified biomarkers can be quantified by any
suitable
techniques lniowil in analytical geometry. The preferred method for
quantifying shape and
18
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
topology is with the morphological and topological formulas as defined by the
references
cited above.
The data are then analyzed over time as the individual is scanned at later
intervals.
There are two types of presentations of the time trends that are preferred. In
one class,
successive measurements are overlaid in rapid sequence so as to form a movie.
In the
complementary representation, a trend plot is drawn giving the higher order
measures as a
function of time. For example, the mean and standard deviation (or range) of a
quantitative
assessment can be plotted for a specific local area, as a function of time.
The accuracy of those measurements and their sensitivity to subtle changes in
small
substructures are highly dependent on the resolution of the imaging system.
Unfortunately,
most CT, MRI, and ultrasound systems have poor resolution in the out-of plane,
or "z" axis.
While the in-plane resolution of those systems can commonly resolve objects
that are just
under one millimeter in separation, the out-of plane (slice thickness) is
cormnonly set at
l.Smm or even greater. For assessing subtle changes and small defects using
higher order
structural measurements, it is desirable to have better than one millimeter
resolution in all
three orthogonal axes. That can be accomplished by fusion of a high resolution
scan in the
orthogonal, or out-of plane direction, to create a lugh resolution voxel data
set (Pena, J.-T.,
Totterman, S.M.S., Parker, K.J. "MRI Isotropic Resolution Reconstruction from
Two
Orthogonal Scans," SPIE Medical Ifnaging, 2001, hereby incorporated by
reference in its
entirety into the present disclosure). In addition to the assessment of subtle
defects in
structures, that high-resolution voxel data set enables more accurate
measurement of
structures that are thin, curved, or tortuous.
In following the response of a person or animal to therapy, or to monitor the
progression of disease, it is desirable to accurately and precisely monitor
the trends in
biomarkers over time. That is difficult to do in conventional practice since
repeated scans
19
CA 02459557 2004-03-03
WO 03/025837 PCT/US02/29005
must be reviewed independently and the biomarkers of interest must be traced
or measured
manually or semi-manually with each time interval representing a new and
tedious process
for repeating the measurements. It is highly advantageous to talce a 4D
approach, such as was
defined in the above-cited patent to Parker et al, where a biomarker is
identified with
statistical reasoning, arid the biomarker is traclced from scan to scan over
time. That is, the
initial segmentation of the biomarker of interest is passed on to the data
sets from scans taken
at later intervals. A search is done to traclc the biomarlcer boundaries from
one scan to the
next. The accuracy and precision and reproducibility of that approach is
superior to that of
performing manual or semi-manual measurements on images with no automatic
tracking or
passing of boundary information from one scan interval to subsequent scans.
While a preferred embodiment of the invention has been set forth above, those
spilled
in the art who have reviewed the present disclosure will readily appreciate
that other
embodiments can be realized within the scope of the present invention. For
example, any
suitable imaging technology can be used. Therefore, the present invention
should be
construed as limited only by the appended claims.