Note: Descriptions are shown in the official language in which they were submitted.
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
A CRYPTOSYSTEM FOR IJATA SECURITY
Field of the Invention
The present invention relates to the field of data encoding and encryp-
tion, and in particular, to data encryption in v~hich statistical information
in the "plaintext" is removed in the transformation of the plaintext into
the "ciphertext" .
Background of the Invention
The need for sending messages secretly has led to the development of
the art and science of encryption, which has been used for millennia. Ex-
1o cellent surveys of the field and the state of the art can be found in
Menezes
et al. (Hezndbool~ of Applied Cryptography, CRC Press, (1996)), Stallings
( Cryptography ~ Netzvor7~ Security: Principles ~ Practice, Prentice Hall,
(1998)), and Stinson (Cryptography : Theory an,d Practice, CRC Press,
(1995)).
The hallmark of a perfect cryptosystem is the fundamental property
called Perfect Secrecy. Informally, this property means that for every
input data stream, the probability of yielding any given output data
stream is the same, and independent of the input. Consequently, there is
no statistical information in the output data stream or ciphertext, about
2o the identity and distribution of the input data or plaintext.
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
The problem of attaining Perfect Secrecy was originally formalized by
C. Shannon in 1949 (see Shannon (Communication Theory of Secrecy
Systems, Bell System Technical Journal, 28:656-715, (1949) ) ] who has
shown that if a cryptosystem possesses Perfect Secrecy, then the length of
the secret key must be at least as large as the plaintext. This restriction
makes Perfect Secrecy impractical in real-life cryptosystems. An example
of a system providing Perfect Secrecy is the Vernam One-time pad.
Two related open problems in the fields of data encoding and cryp-
tography are:
1. Optimizing the Output Probabilities
There are numerous schemes which have been devised for data com-
pression~encoding. The problem of obtaining arbitrary encodings of the
output symbols has been studied by researchers for at least five decades.
Many encoding algorithms (such as those of Huffman, Fano, Shannon,
the arithmetic coding and others) have been developed using different
statistical and structure models (e.g. dictionary structures, higher-order
statistical models and others). They are all intended to compress data,
but their major drawback is that they cannot control the probabilities
of the output symbols. A survey of the field is found in Hankerson et al.
(Introduction to Information Theory and Data Compression, CRC Press,
(1998)j, Sayood (Introd~cction to Data Compression, Morgan Kaufmann,
2nd. edition, (2000)), and Witten et al. (Managing Gigabytes: Corrc-
~ressing and Indexing Documents and Images, Morgan Kaufmann, 2nd.
2
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
edition, (1999)).
Previous schemes have a drawback, namely that once the data ~com-
pression~encoding method has been specified, the user loses control of
the contents and the statistical properties of the compressed/encoded
s file. In other words, the statistical properties of the output compressed
file is outside of the control of the user - they take on their values as a
consequence of the statistical properties of the uncompressed file and the
data compression method in question.
A problem that has been open for many decades (see Hankerson et al.
(Introd~cction to Information Theory and Data Compression, CRC Press,
(1998) pp.75-79)), which will be referred to herein as the Distribution
Optimizing Data Compression (or "D~DC" ) problem, (or in a more
general context of not just compressing the plaintext, it will be referred
to herein as the Distribution Optimizing Data Encoding (or "DODE" )
problem), consists of devising a compression scheme, which when applied
on a data file, compresses the file and simultaneously makes the file
appear to be random noise. The formal definition of this problem is found
in Appendix A. If the input alphabet is binary, the input probability of
'0' and '1' could be arbitrary, and is fully dictated by the plaintext. The
2o problem of the user specifying the output probability of '0' and '1' in the
compressed file has been considered an open problem. Indeed, if the user
could specify the stringent constraint that the output probabilities of '0'
and '1' be arbitrarily close to 0.~, the consequences are very far-reaching,
3
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
resulting in the erasure of statistical information.
2. Achieving Statistical Perfect Secrecy
The problem of erasing the statistical distribution from the input data
stream and therefore the output data stream, has fundamental signifi
cance in cryptographic applications. It is well known that any good
cryptosystem should generate an output that has random characteris-
tics (see Menezes et al. (Handbool~ of Applied Cryptography, CRC Press,
(1996)), Stallings (Cryptography ~ Network Security: Principles ~ Prac-
tice, Prentice Hall, (1998)), Stinson (Cryptography : Theory and Practice,
1o CRC Press, (1995)), and Shannon (Communication Theory of Secrecy
Systems, Bell System Technical Jo~crnal, 28:656-715, ( 1949) ) ) .
A fundamental goal in cryptography is to attain Perfect Secrecy (see
Stinson, Cryptography : Theory and Practice, CRC Press, (1995))).
Developing a pragmatic encoding system that satisfies this property
is an open problem that has been unsolved for many decades. Shannon
(see Menezes (Handbool~ of Applied Cryptography, CRC Press, (1996)),
Stallings Cryptography ~ Networl~ Security: Principles ~ Practice, Pren-
tice Hall, (1998)), Stinson (Cryptography : Theory and Practice, CRC
Press, (1995)), and Shannon (Communication Theory of Secrecy Sys-
2o terns, Bell System Technical Journal, 28:656-715, (1949))) showed that
if a cryptosystem possesses Perfect Secrecy, then the length of the secret
key must be at least as large as the Plaintext. This makes the devel-
opment of a realistic perfect secrecy cryptosystem impractical, such as
4
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
demonstrated by the Vernam One-time Pad.
Consider a system in which x = ~(1~ . . . ~~M~ is the plaintext data
stream, where each x~7~~ is drawn from a plaintext alphabet, S = ~sl . . .
sm~,
and y = y(1~ . . . y~R~ is the ciphertext data stream, where each y~7~~ E ,,4
of cardinality r.
Informally speaking, a system (including cryptosystems, compression
systems, and in general, encoding systems) is said to possess Statistical
Perfect Secrecy if all its contiguous output sequences of length 1~ are
equally likely, for all values of 1~, independent of x. Thus, a scheme
to that removes all statistical properties of the input stream also has the
property of Statistical Perfect Secrecy. A system possessing Statistical
Perfect Secrecy maximizes the entropy of the output computed on a
symbol-wise basis.
More formally, a system is said to possess Statistical Perfect Secrecy if
for every input Xthere exists some integer j0 > 0 and an arbitrarily small
positive real number so such that for all j > j0, Pr(y~+1... y~+~ I x~ _ . r
~bofora111~,0.G1~<R-jo.
A system possessing this property is correctly said to display Statistical
Perfect Secrecy. This is because for all practical purposes and for all
2o finite-lengthed subsequences, statistically speaking, the system behaves
as if it, indeed, possessed the stronger property of Perfect Secrecy.
It is interesting to note that Statistical Perfect Secrecy is related to
the concept of Perfect Secrecy. However, since the property of Statistical
5
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Perfect Secrecy can characterize any system and not just a cryptosystem,
there is no requirement of relating the size of the key to the size of the
input, as required by Shannon's theorem.
Summary of the Invention
The object of the present invention is to provide an improved method
of encoding and decoding data, which permits the user to specify certain
statistical parameters of the ciphertext, and to control or remove statisti-
cal information during the process of encoding plaintext into ciphertext.
It is a further object of an embodiment of the present invention to pro-
1o vide an improved method of encoding and decoding data, which permits
the user to obtain Statistical Perfect Secrecy in the ciphertext.
It is a further object of an embodiment of the present invention to pro-
vide an improved method of encoding and decoding data, which ensures
that Statistical Perfect Secrecy in the ciphertext has been obtained..
It is a further object of an embodiment of the present invention to
provide an improved method of encryption and decryption:
It is a further object of an embodiment of the present invention to
provide an improved method of steganography.
It is a further object of an embodiment of the present invention to
2o provide an improved method of secure communications.
It is a further object of an embodiment of the present invention to
provide an improved method of secure data storage and retrieval.
6
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Accordingly, in one aspect, the present invention relates to a method
for creating ciphertext from plaintext comprising the steps of: (a) re-
ceiving a character of plaintext; (b) traversing an Oommen-Rueda Tree
between the root and that leaf corresponding to that character of plain-
s text and recording the Assignment Value of each branch so traversed; (c)
receiving a next character of plaintext; and repeating steps (b) and (c)
until the plaintext has been processed.
In another aspect, the present invention relates to a method for cre
ating ciphertext from plaintext comprising the steps of: (a) creating an
so Oommen-Rueda Tree; (b) receiving a character of plaintext; (c) travers
ing the Oommen-Rueda Tree between the root and that leaf correspond-
ing to that character of plaintext and recording the Assignment Value of
each branch so traversed; (d) receiving a next character of plaintext; and
(e) repeating steps (c) and (d) until the plaintext has been processed.
15 In another aspect, the present invention relates to a method for cre-
acing ciphertext from plaintext comprising the steps of: (a) receiving an
Oommen-Rueda Tree; (b) receiving a character of plaintext; (c) travers-
ing the Oommen-Rueda Tree between the root and that leaf correspond-
ing to that character of plaintext. and recording the Assignment Value of
2o each branch so traversed; (d) receiving a next character of plaintext; and
(e) repeating steps (c) and (d) until the plaintext has been processed.
In another aspect, the present invention relates to a method for cre-
ating ciphertext from plaintext comprising the steps of: (a) creating an
7
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Oommen-Rueda Tree, which Oommen-Rueda Tree has leaves associated
with the members of the alphabet of the plaintext, each member of the
alphabet of the plaintext being associated with at least one leaf, which
Oommen-Rueda Tree's internal nodes each have at least one branch de-
pending therefrom, which Oommen-Rueda Tree branches have associated
therewith an Assignment Value, which Assignment Value is associated
with a member of the alphabet of the ciphertext, which Oommen-Rueda
Tree's nodes each have associated therewith a quantity related to the fre-
quency weight (b) receiving a first character of plaintext; (c) traversing
the Oommen-Rueda Tree between the root and that leaf corresponding
to that character of plaintext and recording the Assignment Value of each
branch so traversed; (d) receiving the next symbol of plaintext; and (e)
repeating steps (c) and (d) until the~plaintext has been processed.
In another aspect, the present invention relates to a method for cre-
ating ciphertext from plaintext comprising the steps of: (a) receiving an
Oommen-Rueda Tree, which Oommen-Rueda Tree has leaves associated
with the members of the alphabet of the plaintext, each member of the
alphabet of the plaintext being associated with at least one leaf, which
Oommen-Rueda Tree's internal nodes each have at least one branch de-
2o pending therefrom, which Oommen-Rueda Tree branches have associated
therewith an Assignment Value, which Assignment Value is associated
with a member of the alphabet of the ciphertext, which Oommen-Rueda
Tree's nodes each have associated therewith a quantity related to the
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
frequency weight of each of the nodes and leaves dependant therefrom;
(b) receiving a first character of plaintext; (c) traversing the Oommen-
Rueda Tree between the root and that leaf corresponding to that char-
acter of plaintext and recording the Assignment Value of each branch so
traversed; (d) receiving the next symbol of plaintext; and (e) repeating
steps (c) and (d) until the plaintext has been processed.
In another aspect, the present invention relates to a method of decod-
ing ciphertext, comprising the steps of: (a) receiving a first character of
ciphertext; (b) utilizing an Oommen-Rueda Tree having a structure cor-
1o responding to the Oommen-Rueda Tree initially utilized by the encoder
and utilizing the same Branch Assignment Rule as utilized by the encoder
to provide the Assignment Values for the branches depending from the
root, traversing such Oommen-Rueda Tree from the root towards a leaf,
the first symbol character of ciphertext determining the branch to then
be traversed; (c) if a leaf has not been reached, utilizing the same Branch
Assignment Rule as utilized by the encoder to provide Assignment Val-
ues for the branches depending from the node that has been reached,
receiving the next character of ciphertext, and continuing to traverse the
Oommen-Rueda Tree from the node that has been reached towards a
2o leaf, the current symbol of ciphertext determining the branch to then be
traversed; (d) when a leaf is reached, recording the plaintext character
associated with the label of the leaf, the root becoming the node that has
been reached for the purpose of further processing; (e) repeating steps
9
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
(c) and (d) until all symbols of ciphertext have been processed.
In another aspect, the present invention relates to a method of decod-
ing ciphertext, comprising the steps of: (a) creating an Oommen-Rueda
Tree (b) receiving a first character of ciphertext; (c) utilizing an Oommen-
Rueda Tree having a structure corresponding to the Oommen-Rueda Tree
initially utilized by the encoder and utilizing the same Branch Assign-
ment Rule as utilized by the encoder to provide the Assignment Values for
the branches depending from the root, traversing such Oommen-Rueda
Tree from the root towards a leaf, the first character of ciphertext de-
to termining the branch to then be traversed; (d) if a leaf has not been
reached, utilizing the same Branch Assignment Rule as utilized by the
encoder to provide Assignment Values for the branches depending from
the node that has been reached, receiving the next character of cipher-
text, and continuing to traverse the Oommen-Rueda Tree from the node
that has been reached towards a leaf, the current symbol of ciphertext
determining the branch to then be traversed; (e) when a leaf is reached,
recording the plaintext character associated with the label of the leaf, the
root becoming the node that has been reached for the purpose of further
processing; repeating steps (d) and (e) until all symbols of ciphertext
2o have been processed.
In another aspect, the. present invention relates to a method of decod~
ing ciphertext, comprising the steps of: (a) receiving an Oommen-Rueda
Tree (b) receiving a first character of ciphertext; (c) utilizing an Oommen-
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Rueda Tree having a structure corresponding to the Oommen-Rueda Tree
initially utilized by the. encoder and utilizing the same Branch Assign-
ment Rule as utilized by the encoder to provide the Assignment Values for
the branches depending from the root, traversing such Oommen-Rueda
Tree from the root towards a leaf, the first character of ciphertext de-
termining the branch to then be traversed; (d) if a Leaf has not been
reached; utilizing the same Branch Assignment Rule as utilized by the
encoder to provide Assignment Values for the branches depending from
the node that has been reached, receiving the next character of cipher-
xo text, and continuing to traverse the Oommen-Rueda Tree from the node
that has been reached towards a leaf, the current symbol of ciphertext
determining the branch to then be traversed; (e) when a leaf is reached,
recording the plaintext character associated with the label of the leaf, the
root becoming the node that has been reached for the purpose of further
i5 processing; repeating steps (d) and (e) until all symbols of ciphertext
have been processed.
The advantage of an embodiment of the present invention is that it
provides a method of encoding and decoding data, which encoded data
has the Statistical Perfect Secrecy property.
2o A further advantage of an embodiment of the present invention is
that it guarantees that the encoded message has the Statistical Perfect
Secrecy property.
A further advantage of an embodiment of the present invention is
11
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
that it can be adapted to simultaneously provide optimal and lossless
compression of the input data stream in a prefix manner.
A further advantage of an embodiment of the present invention is that
it can also be adapted to simultaneously provide an output of the same
size or larger than the input data stream in a prefix manner.
A further advantage of an embodiment of the present invention is that
it provides an improved method of encryption and decryption.
A further advantage of an embodiment of the present invention is that
it provides an improved method of steganography.
1o A further advantage of an embodiment of the present invention is that
it provides an improved method of secure communications.
A further advantage of an embodiment of the present invention is that
it provides an improved method of secure data storage and retrieval.
Brief Description of the Figures
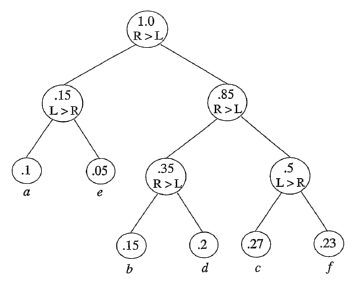
Figure .~ presents an Oommen-Rueda Tree in which the input alphabet
S = ~a, b, c, d, e, f ~ with probabilities P = ~0.1., 0.1~, 0.2'7, 0.2, 0.0~,
.23~,
and the output alphabet is ,A. = ~0,1~. The root points to two children.
Each node stores a weight, which is the sum of the weights associated with
its children. It also stores the ordering of the children in terms of their
2o weights, i.e., whether the weight of the left child is greater than that of
the
right child, or vice versa. Although, in this example, the encoding does
not achieve optimal data compression, using DODE, arbitrary output
12
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
probabilites can be achieved.
Figure ~ presents a Huffman tree constructed using Huffman's algo-
rithm with <S = ~a, b, c, d~, P = ~0.4, 0.3, 0.2, 0.1~, and .A = ~0,1~.
Figures 3 and l~ present a schematic diagram showing the Process
s D_S~i~m~2 used to encode an input data sequence. The input to the
process is the Static Huffman Tree, T, and the source sequence, x. The
output is the sequence, y. It is assumed that there is a hashing function
which locates the position of the input alphabet symbols ,as leaves in T.
Figures 5 and 6 present a schematic diagram showing the Process
to D_S~I~m ~ used to decode a data sequence encoded by following Process
D_S_H~m,2. The input to the process is the static Huffman Tree, T, and
the encoded sequence, y. The output is the decoded sequence, which is,
indeed, the original source sequence, ~.
Figure 7 depicts the two possible labeling strategies that can be done
15 in a Huffman tree constructed for Process D_S_H~~,2, where S = ~0,1~,
and P = ~p,1 - p~ with p > 0.5.
Figure ~ graphically plots the average distance obtained after running
D_S_H~m,2 on file bib from the Calgary Corpus, where f * = 0.5 and
O=2.
2o Figure 9 and 10 present a schematic diagram showing the Process
D~1.~I~m~2 used to encode an input data sequence. The input to the
process is an initial Adaptive Huffmam Tree, T, and the source sequence,
x. The output is the sequence, ~. It is assumed that there is a hashing
13
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
function which locates the position of the input alphabet symbols as
leaves in T.
Figure .~1 and 1~ present a schematic diagram showing the Process
DA~i~m,2 used to decode a data sequence encoded by following Process
D~~I~~,.L,~. The input to the process is the same initial Adaptive Hufl-
man Tree, T used by Process D~~I~m,2, and the encoded sequence;
y. The output is the decoded sequence, which is, indeed, the original
source sequence, x.
Figure 13 graphically plots the average distance obtained after running
1o DA~-I_E~~2 on file bib from the Calgary Corpus, where f * = 0.5 and
O=2.
Figures 1~ and 15 present a schematic diagram showing the Process
RV.A_H~m,2 used to encode an input data sequence. The input to the
process is an initial Hufiman Tree, T, and the source sequence, a.'. The
output is the sequence, y. It is assumed that there is a hashing function
which locates the position of the input alphabet symbols as leaves in T.
Figure .16 demonstrates how the decision in the Branch Assignment
Rule in Process RV~SI~r,t,2 is based on the value of f (n) and a~pseudo-
random number, c~.
2o Figure .17 and 1~ present a schematic diagram showing the Process
RV~_H~m,~ used to decode a data sequence encoded by following Pro-
cess RVA~I~~,2. The input to the process is the same initial Adaptive
Huffman Tree, T used by Process RVA_H_Em,2, and the encoded se-
14
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
quence, y. The output is the decoded sequence, which is, indeed, the
original source sequence, X.
Fig~cre 19 demonstrates how the decision in the Branch Assignment
Rule in Process RR_A~I~m,2 is based on the value of f (n) and two
pseudo-random number invocations.
Fig~cre ~0 graphically plots the average distance obtained after running
Process RV~.~I~m,2 on file bib from the Calgary Corpus, where f * = 0.~
and O = 2.
Figure ~1 graphically plots the average distance obtained after running
1o Process RV~._H_Em,,~ on file bib from the Calgary Corpus, where f * = 0.5
and O = 2, and where the transient behavior has been eliminated.
Figure ~~ graphically plots the average distance obtained after running
Process RR~~-L~m,2 on file bib from the Calgary Corpus, where f * _
0.~ and O = 2, and where the transient behavior has been eliminated.
~ 5 Figure ~3 displays the original carrier image, the well-known Lena im-
age, and the resulting image after applying steganographic techniques to
the output of the file f-ae~ds, c from the Canterbury corpus. The stegano-
graphic method used is a fairly simplistic one, but includes the message
encrypted as per Process RV.A~-T.~m,2.
2o Description of the Preferred Embodiments
The invention operates on a data structure referred to as the Oommen-
Rueda Tree defined as below for a plaintext alphabet of cardinality m
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
and an ciphertext alphabet of cardinality r, where the desired output
frequency distribution is .~'*, and its measured (estimated) value is .~.
The Oommen-Rueda Tree
An optimized Oommen-Rueda Tree is defined recursively as a set of
Nodes, Leaves and Edges as follows:
1. The tree is referenced by a pointer to the tree's root - which is a
unique node, and which has no parents.
2. Every node contains a weight which is associated with the sum of
the weights associated with its children (including both nodes and
leaves) .
3. In a typical Oommen-Rueda Tree, every node has r edges (or branches),
each edge pointing to one of its r children, which child could be a
node or a leaf. However, if any node has less_than r children, it can
be conceptually viewed as having exactly r children where the rest
of the children have axi associated weight of zero.
4. Every node maintains an ordering on its children in such a way that
it knows how the weights of the children are sorted.
~. Each plaintext alphabet symbol is associated with a leaf (where a
leaf is a node that does not have any children) . The weight as-
2o sociated with each leaf node is associated with the probability (or
16
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
an estimate of the probability) of the occurrence of the associated
plaintext symbol.
6. A hashing function is maintained which maps the source alphabet
symbols to the leaves, thus ensuring that when an input symbol
is received, a path can be traced between the root and the leaf
corresponding to that input symbol. An alternate approach is to
search the entire tree, although this would render the Oommen-
Rueda. Process less efficient.
7. If the input symbol probabilities are known a priori, the Oommen-
1o Rueda Tree is maintained statically. Otherwise, it is maintained
adaptively in terms of the current estimates of the input probabili-
ties, by re-ordering the nodes of the tree so as to maintain the above
properties.
Specific instantiations of the Oommen-Rueda Tree are the Huffman
tree, and the Fano tree, in which the ordering of the nodes at every
level obeys a sibling-like property (see Hankerson et al. (Introduction to
Information Theory and~Data Compression, CRC Press, (1998))).
It is to be understood that the Oommen-Rueda Trees referred to
herein, include those less optimal versions of the above-defined Oommen-
2o Rueda Tree which can be designed by introducing nodes, leaves and edges
which have no significant contribution, or whose significance can be min-
imized by merging them with other nodes, leaves and edges respectively,
17
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
resulting in a Oommen-Rueda Tree 'with a lesser number of nodes, leaves
and edges respectively.
It is further to be understood that if the sibling property is not main-
tamed in a left-to-right order, the corresponding assignments will not be
made in a left-to-right order.
It is to be understood that the term "plainteXt" encompasses all man-
ner of data represented symbolically and includes, but is not limited to,
data utilized in the processing of audio data, speech, music, still images,
video images, electronic mail, Internet communications and others.
Finally, it is to be understood that the combination of the Oommen-
Rueda Tree with the encoding and decoding processes described herein,
will provide, a solution of the Distribution Optimizing Data Encoding
problem in which the ouput may be compressed, of the same size, or
even expanded.
~5 The Encoding Process Utilizing Oommen-Rueda Trees
The encoding process related to Oommen-Rueda Trees involves travers-
ing (in accordance with a hashing function maintained for the Oommen-
Rueda Tree) the Oommen-Rueda Tree between the root and the leaf
corresponding to the current plaintext symbol, and recording the branch
2o assignment of the edges so traversed, which branch assignment is de-
termined in accordance with the Branch Assignment Rule. The actual
encoding of the current plaintext symbol is done by transforming the
plaintext input symbol into a string associated with the labels of the
l~
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
edges (determined as per the Branch Assignment Rule) on the path from
the root to the leaf associated with that plaintext symbol.
It is understood that the traversal of the Oommen-Rueda Tree (as dic-
tated by the Hashing function) in the Encoding Process can be achieved
either in root-to-leaf manner, or in a leaf to-root manner, in which latter
case the output stream is reversed for that particular plaintext symbol.
The Branch Assignment Rule
1. This Rule determines the assignment of labels on the edges of the
tree, the labels being associated with the symbols of the output
1o alphabet.
2. The assignment can be chosen either deterministically, or randomly
involving a fixed constant, or randomly by invoking random vari-
ables whose distributions do not depend on the current measurement
(or estimate), ~', or randomly by invoking at least one random vari-
able whose distribution depends on the current measurement (or
estimate), ,~.
3. The assignments can be made so as to converge to the predeter-
mined value of .~'*. Additionally, the Branch Assignment Rule can
be designed so that the Process converges to a probability distribu-
2o tion which simultaneously maintains the independence of the output
symbols. This can be achieved by utilizing the Markovian history,
for example, using fo~o, and foil to converge to fo~o, and fo~1 respec-
19
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
tively, when the output alphabet is binary.
The Tree Restructuring Rule
1. If the Oommen-Rueda Tree is updated adaptively, the updating of
the Oommen-Rueda Tree is done after the processing of each plain-
text symbol has been affected. For example, in the case of the Huff
man tree, the updating is achieved by using the technique described
by Knuth (Dynamic Huffman Coding, Journal of Algorithms, 6:163-
180, (1985)), or Vitter (Design and Analysis of Dynamic Huffman
Codes, Journal of the ACM, 34(4):825-845, (1987)), wherein the
to tree is updated so as to maintain the sibling property at every level
of the tree.
2. For other instantiations .of the Oommen-Rueda Trees, it is to be
understood that the Tree Restructuring Rule can be affected by ei-
ther re-creating the tree using an exhaustive search of all possible
Oommen-Rueda Trees characterizing that instantiation, or by incre-
mentally modifying them based on the properties of the particular
instantiation.
The Decoding Process Utilizing Oommen-Rueda Trees
The decoding process assumes that the Decoder can either create or
2o is provided with an Oommen-Rueda Tree, which Tree is identical to the
Oommen-Rueda tree utilized by the Encoder to encode the any pre-
specified plaintext symbol. The actual decoding process involves the
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
steps of
1. Traversing the Decoder's copy of the Oommen-Rueda Tree from the
root to a leaf, the traversal being determined by the same Branch
Assignment Rule utilized by the Encoder, and the ciphertext sym-
bols.
2. The label of the leaf is recorded as the decoded symbol.
3. If the Oommen-Rueda Tree is updated adaptively, the updating of
the Decoder's Oommen-Rueda Tree is done as per the Tree Restruc-
turfing Rule described above, after the source symbol associated with
to the current encoded string has been determined. This ensures that
after the decoding of each plaintext symbol has been affected, both
the Encoder and Decoder maintain identical Oommen-Rueda Trees.
It is to be understood that if the Encoder utilized a process that in-
volved a Branch Assignment Rule, the same Branch Assignment Rule
must also be utilized by the Decoder. Furthermore, if the Encoder uti-
lined a process that did not involve a Branch Assignment Rule, the De-
coder's process must also not involve a Branch Assignment Rule.
It is further to be understood that if the Encoder utilized a process
that involved a Tree Restructuring Rule, the same Tree Restructuring
2o Rule must also be utilized by the Decoder. Furthermore, if the Encoder
utilized a process that did not involve a Tree Restructuring Rule, the
Decoder's process must also not involve a Tree Restructuring Rule.
21
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Additional Instantiations of the Invention .
The Oommen-Rueda Tree may be used in a wide range of circum-
stances and is flexible to the needs of the user.
If the occurrence probabilities of the plaintext input symbols are
known a priori, the tree (and consequently, the associated processes)
are Static. On the other hand, if the occurrence probabilities of the
input symbols are not known a priori, the tree (and consequently, the
associated processes) are Adaptive.
As indicated above, this invention also utilizes an Branch Assignment
to Rule for the labels of the edges of .the Oommen-Rueda Tree. A process
manipulating the tree is termed Deterministic or Randomized depending
on whether the Branch Assignment Rule is Deterministic or Randomized
respectively, which is more fully described below for the specific instan-
tiations.
The various embodiments of the invention are specified herein by
first stating whether the Branch Assignment Rule is (D)eterministic or
(R)andomized. In the case of a randomized Branch Assignment Rule,
the effect of randomization on the branch assignment can be either
determined by a comparison with (F)ixed constant, a (V)ariable or a
~o (R) andom variable itself.
The second specification of a process details whether the tree is created
in a (S)tatic or (A)daptive manner.
The third specification of the embodiment details the specific instan-
22
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
nation of the Oommen-Rueda Tree (that is, whether the generalized
Oommen-Rueda Tree is being used, or ~ a specific instantiation such as
the Huffman or Fano tree is being used) .
The .fourth specification of a process informs whether it is an Encoding
or Decoding Process.
The last specification are the cardinalities of the input and output
alphabets.
The following sections describe specific embodiments of the invention
for the case when the size of the ciphertext alphabet is 2. It is easily seen
1o that when the size of the ciphertext alphabet is r, the corresponding
r-ary embodiment can be obtained by concatenating log2r bits in the
output and causing this binary string of length log~r to represent a single
symbol from the output r-ary alphabet. When r is not a power of two,
r symbols can be composed with probability f ractl, r, thus ignoring
~.5 the other strings of length log~r,. implying that this method assigns a
probability value of zero for the strings of length log2r that have been
ignored.
Using the above nomenclature, the following are some specific embod-
invents of the Invention:
23
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
a~ ~ c~c~c~ ~ c~ c~c~1 c~ c~ ~ c~ c~
'~~a II IIIIII IIII IIII II II II II II
N - _ _ _ _ _ _ _ _ _ _ _ _
.,-,
U
~
O II IIIIII IIII IIII II II II II II
,~
~.01~Db~0b~0I~0b~060b.0 bi0 6.0 L~0 ~0 END
~ , ~ , ~ ~ ~ -,
''drdr b r , ~ b ~ '"~ ~ . rd
O O rdO ''d''C~''dO ''d O '~ '~ O
O O O O O O O
U U U U U U U U U U U U U
W W f~W ~1W ~ W f~ W f~ W ~1
b
0
O
U N N N N N O N N N N N
U U
r, .-r~ ..a~ ,-~ ~ ,-.,
-1~'"~'~-V~+~+~ -1~+~ +~ ~ -~ -1~ +~
''dU.~U~'t~b '~ ''c3''ci ''d "d rd ''~ ''d
'zS ''~ "d ''d
'~''~''~-N '~...''~'+'N N N N N ~
,~ ,C'.~d
..-,. . . . .,-~N a~ ~, ~ ~, ~ cd~ cd
r,r-,r.,,-.~~ O 0 0 ~ O ~ O
~C 5C 0
N N N N ~ , ~ ~ ~ y ~ ~ '"d
~ ~ W Cd~
Cd
N ~ N N N N N ~
O ~ c~ c~ cV c~ cat~ cu
catc~c~ c~ico
~
~ W ~ W f~W ~ W ~ W f~ W
O x ~ ~ ~ w ~ x
24
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Throughout this document, unless otherwise specified, DDODE (for
Deterministic Distribution Optimizing Data Encoding) will be used as a
generic name for any Deterministic solution that yields Statistical Perfect
Secrecy. Specific instantiations of DDODE are D_S~I~m,2, D~1 II~,,~,2
etc. Similarly, RDODE (for Randomized Distribution Optimizing Data
Encoding)will be used as a generic name for any Randomized solution
that yields Statistical Perfect Secrecy. Specific instantiations of RDODE
are RF_S_H~m~~, RV.A~I_Em~2 etc.
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
D_S_H_Em,~ : The Deterministic Embodiment using
Static Huffman Coding
The Encoding Process : D_SSI~m,~
This section describes the process that provides a method of opti-
mining the distribution of the output by using the sibling property of
Huffman trees (see Hankerson et al. (Introduction to Information The-
ory and Data Compression, CRC Press, (1998)), Sayood (Introd~cction to
Data Compression; Morgan Kaufmann, 2nd. edition, (2000)), and Wit-
ten et al. (Managing Gigabytes: Corrzpressing and Indexing .Documents
1o and Images, Morgan Kaufmann, 2nd. edition, (1999))), and a determin-
istic rule that changes the labeling of the encoding scheme dynamically
during the encoding process.
This document uses the notation that f (n) represents the estimate
of the probability of 0 in the output at time 'n', and f (n) refers to the
actual probability of 0 in the output at time 'n'. The estimation of f (n)
uses a window that contains the last t symbols generated at the output,
arid f (n) is estimated as ~°tt~ , where co (t) is the number of 0's in
the
window. In the included analysis and implementation, the window has
been made arbitrarily Iarge by considering t = n, i.e. the window is the
2o entire output sequence up to time 'n'. The effect of the window size, 't',
will be discussed later..
The process D-S_H-Em,2 is formally given below and pictorially in
Figures 3 and 4.
26
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Schematic of D_S~I~m,2
The schematic chart of Process D_S~I~m,2 is explained here. The
figures begin with and Input/output block (block 100) in which (i) the
source sequence, x = ~ ~1~ . . . ~ ~M~, is the data to be encoded, (ii) r
is the root of the Huffman tree that has ~ been created using the static
Huffman coding approach (see Huffman (A Method for the Construction
o Minimum Redundancy Codes, Proceedings of IRE, 40(9), pp. 1098
1101, (1952))), (iii) h(s) is the hashing function that returns the pointer
to the node associated with any plaintext symbol s, and (iv) f * is the
1o requested probability of '0' in the output.
In block 110, the estimated probability of '0' in the output, f , is
initialized to 0, and. the counter of zeros in the output, ~co, is initialized
to 0 as well. The counter of bits in the output, n, is initialized to l, and
the counter of symbols read from the input is initialized to 1 too. Other
s5 straightforward initializations of these quantities are also possible.
A decision block is then invoked in block 120 which constitutes the
starting of a looping structure that is executed from 1 to the number
of symbols in the input, M. In block 130, a variable, q, which keeps
the pointer to the current node being inspected in the tree, is initialized
2o to the node associated with the current symbol, ~(1~~, by invoking the
hashing function h(~ ~1~~ ) . The length of the code word associated with
~(1~~, .~, is initialized to 0. The decision block 140 constitutes the
starting
'point of a looping that traces the path from the node associated with ~~1~~
27
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
to the root of the tree, r. Block 150 increments the length of the code
word associated with ~~1~~ by 1, since this length is actually the number of
edges in that path. The decision block 160 tests if the corresponding path
goes through the left or right branch, true for left (block 170) and false
for right (block 180). In block 185, the current pointer, q, moves up to its
parent towards the root of the tree. Connector 190 is the continuation of
the branch "No" of the decision block 140, i.e. when q reaches the root
of the tree (q = r) : Connector 200 is the continuation of the decision
"No" of block 120, which occurs when all the symbols of the input have
1o been read. Connector 210 is the continuation of block 310 and enters in
the decision block 120 to process the next symbol from the input.
In block 220, j is initialized to the length of the current path so as to
process that path from the root of the tree towards the leaf associated
Wlth ~~~]. Block 230 involves a decision on whether or not each node
in the path has been processed. The decision block 240 compares the
estimated probability of '0' in the output, f , to the probability of '0'
requested by the user, f *, so as to decide on the branch assignment
strategy to be applied. The branch "Yes" leads to block 250, which test
if .the path goes to the left (true) or to the right (false). The branch
"Yes" of block 250 goes to block 280 in which a '0' is sent to the output,
and the corresponding counter, c0, is thus increased. Block 280 is also
reached after deciding "No" in block 260, which implies that f > f *,
and hence the branch assignment 1-0 has been used. The branch "No"
28
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
of block 250, where the branch assignment 0-1 is applied and the path
goes to the right, leads to block 270 in which a '1' is sent to the output.
Block 270 is also reached by the branch "No" of block 250 in which the
0-1 branch assignment is used and the path goes to .the right.
In block 290, the estimated probability of '0' in the output is updated
using the current counter of zeros and the current value of n, and the
counter of bits in the output, n, is incremented. Block 300 decrements
the counter of edges in the path, j, and goes to the decision block 230,
which decides "No" when the node associated with ~~1~~ is reached. In this
1o case, block 310 is reached, where the counter of symbols in the input,
k, is increased and the process continues with the decision block 120
which ends the looping (decides "No" ~ when all the symbols of the input
have been processed, reaching the Input/output block 320 in which the
encoded sequence, y = y~l~ . . . y(R~, is stored. Block 330 returns the
control to the "upper-level" process which invoked Process D_S_H_E,~,,~,
and the process D_S~I_E,,",,~ terminates.
29
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Process D_S~i Em,~
Input: The Huffman Tree, T. The source sequence,. X. The re-
quested probability of 0, f *.
Output: The output sequence, y.
Assumption: It is assumed that there is a hashing function which
locates the position of the input alphabet symbols as leaves in T.
Method:
co(0) ~ 0; n E- 1; f (0) ~- 1
for 1~ ~- l to M do ~~ For all the symbols of the input sequence
to Find the Path for ~ (1~~
q ~ root(T)
vVhile q is not a leaf do
if f (n) G f * then // Assignment 0-1
if path is "left" then
15 g~n~ ~- 0; co(n) ~ co(n - 1) -I-1; q ~- left(q)
else
y~n~ ~ 1; q f- right(q)
endif
else ~/ Assignment 1-0
2o if path is "left". then
yLn~ ~ 1; q ~- left(q)
else
y~n~ ~ 0~ co(~) ~- co(n - 1) -I- l; q ~- right(q)
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
endif
endif
f ~n) ~ coin)
n ~- n -E-1
endwhile
endfor
End Process D_S~I~?.,.,,,~
31
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Rationale for the Encoding Process
In the traditional Huffman encoding, after constructing the Huffman
tree in a bottom-up manner, an encoding scheme is. generated which is
used to replace each symbol of the source sequence by its corresponding
code word. A labeling procedure is performed ,at each internal node,
by assigning a code alphabet symbol to each branch. Different labeling
procedures lead to different encoding schemes, and hence to different
probabilities of the output symbols. In fact, for a source alphabet of m
symbols there are 2m-~ such encoding schemes. It is easy to see (as from
1o the following example) how the labeling scheme can generate different
probabilities in the output.
Example 1. Consider <S = ~a, b, c, d~, P = ~0.4, 0.3, 0.2, 0.1~, ,A. _
~0,1~, and the encoding schemes ~A : S ~ CA = ~l, 00, 010, 011 and
~B : ~ -~ ~B = 0,10,. I10,1II~, generated by using different labeling
strategies on the Huffman tree depicted in Figure 1. The superior en-
coding scheme between c~A and c~B, such that .~* _ ~0.5, 0.5~, is sought
for.
First, the average code word length of bits per symbol is calculated
(see Hankerson et ad. (Introd~cction to Information Theory and .Data
2o Compression, CRC Press, (1998))) for the exact formula for computing
it) for both encoding schemes: .~A = .~B = 1(0.4) -~- 2(0.3) ~-- 3(0.2) -1-
3(0.1) = 1.9.
Second, the distance for ~A and ~B from the optimal distribution,
32
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
dA(.~'A, .~*) and dB (.~'B, .~'*) respectively, are calculated, by using (15)
where O = 2, as follows:
0(0.4)+2(0.3)+2(0.2)+1(0.1) N 0.57895 ,
f0a = 1.9
1(0.4)+0(0.3)+1(0.2)+2(0.l) N 0.42105 ,
.fly = 1.9
dlq(,~A, .~') = 10.57895 - 0.~~2 -I- ~0.4~20~ - 0.52 = 0.012466 ,
1(0.4)+1(0.3)+1(0.2)+0(0.l) r" 0.47368 ,
foB = 1.s
0(0.4)+1(0:3)+2(0.2)+3(0.l) ~, 0.52632 , and
= 1.s
dB(.~'B, .~') _ 0.47368 - 0.52 -~ 0.52632 - 0.52 = 0.001385 .
Third, observe that CA and GB are prefix, .~A and .~B are minimal, and
1o dB G dA. Therefore, ~B is better than ~A for .~'* _ ~0.5, 0.5~.
In order to solve the DODO Problem, a "brute force" technique is pro-
posed in Hankerson et al. (Introduction to Information Theory and Data
Compression, CRC Press, (1998)), which searches over the 2m-1 differ-
ent encoding schemes and chooses the scheme that achieves the minimal
distance. It can be shown that even with this brute force technique, it
is not always possible to obtain the requested output probability of 0.5.
The following example clarifies this.
Example 2. Consider <S = ~a, b, c, d~ and .A. _ ~0,1~. Suppose that the
requested probability of 0 in the output is f * = 0.5. There are 2'~-1 = 8
2o possible encoding schemes whose code word lengths are ~1, 2, 3, 3~ (those
generated from the Huffman tree depicted in Figure 1 obtained by using
different labeling strategies) .
The eight possible encoding schemes, their probabilities of 0 in the
33
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
output, and their distances, as defined in (I4) where O = 2, are given in
Table 1.
.7~~ : S --~ f d(.~,
C~ .~*)
1 ~0,10,110,111~0.47368 0.001385
2 0,10, I11,110~0.42105 0.012466
3 ~0,11,100,101~0.47368 0.001385
4 ~0, l1,101,100~0.42105 0.012466
~1, 00, 010, 0.57895 0.012466
011
6 ~1, 00, 011, 0.52632 0.001385
010
7 ~l, 01, 000, 0.57895 0.012466
001
8 ~1, 01, 001, 0.52632 0.001385
000
Table 1: All possible encoding schemes for the code word lengths
~1, 2, 3, 3~, where S = ~a, b, c, d~, ,A. _ ~0,1~, and P = (0.4, 0.3, 0.2,
0.1~.
Observe that none of these encodings yield the optimal value of f * _
0.5. Indeed, the smallest distance is 0.001385, obtained when using, for
5 example, ~1, in which the probability of 0 in the output is 0.47367.
As seen in Example 2, it is impossible to find the optimal requested
probability of 0 in the output even after exhaustively searching over all
possible encoding schemes. Rather than using a fixed labeling scheme
1o for encoding the entire input sequence, D_S_H~m,~ adopts a different
labeling scheme each time a bit is sent to the output. These labeling
schemes are chosen based on the structure of the Huffman tree and the
distribution of the output sequence encoded so far.
Basically, D_S~I_Em,2 works by taking advantage of the sibling rorop-
34
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
erty of the Huffman tree (see Gallager (Variations on a Theme by Huff
man,.IEEE Transactions on Information Theory, 24(6):668-674, (1978))).
From this property, it can be observed that the weight of the left child
is always greater than or equal to that of the right one. Consider a
Huffman tree, T. By keeping track of the number of 0's, co(n), and the
number of bits already sent to the output, n, the probability of 0 in the
output is estimated as f (n) _ ~°nn~ , whenever a node of T is visited.
D_S~I~m,2 takes f (n) and compares it with f * as follows: if f (n) is
smaller than or equal to f *, 0 is favored by the branch assignment 0-l,
so otherwise 1 is favored by the branch assignment 1-0. This is referred to
as the D_S_H~m,~ Rile.
Essentially, this implies that the process utilizes a composite Huffman
tree obtained by adaptively blending the exponential number of Huffman
trees that would have resulted from a given fired assignment. This blend-
ing, as mentioned, is adaptive and requires no overhead. The blending
function is not explicit, but implicit, and is done in a manner so as to
force f (n) to converge to the fixed point, f *.
D_S~i~m~2 also maintains a pointer, q, that is used to trace a path
from the root to the leaf in which the current symbol is located in T. This
2o symbol is then encoded by using the D_S~-I~,~,2 Rule. This division of
path tracing and encoding is done to maintain consistency between the
Encoder and the Decoder. A small example will help to clarify this
procedure.
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Example 3. Consider the source alphabet <S = ~a, b, c, d~ with respec-
tine probabilities of occurrence P = ~0.4, 0.3, 0.2, 0.1~ and the code al-
phabet ,A. _ ~0,1~. To encode the source sequence ~ = bacba, D_S~I~m,~,
the Huffman tree (shown in Figure 1) is first constructed using Huffman's
algorithm (see Huffman (A Method for the Construction of Minimum Re-
dundancy Codes, f Proceedings of IRE, 40(9):1098-1101, (1952))).
The encoding achieved by Process D_S~I~m,~ is detailed in Table 2.
First, co(0), n, and f (0) are all set to 0. The starting branch assignment
n ~ Path c0 f (n) Assign. Go y ~n
~1~~ (n) -I-
1
0 b LL 0 0.0000 0-1 L 0
1 1 1.0000 1-0 L 1
2 a R 1 0.5000 0-1 R 1
3 c LRL 1 0.3333 0-1 L 0
4 2 0.5000 0-1 R 1
5 2 0.4000 0-1 L 0
6 b LL 3 0.5000 0-1 L 0
7 4 0.5714 1-0 L 1
8 a R 4 0.5000 0-1 R 1
9 4 0.4444
Table 2: Encoding of the source sequence ~1.' = bacba using D_S_H_Em,2
and the Huffman tree of Figure 1. The resulting output sequence is
y = 011010011.
is 0-1. For each symbol of x, a path is generated; and for each element
1o of this path (column 'Go') using the current assignment, the output is
generated. Afterwards, no, n, and f (n) are updated.
From Example 3, the power of D_S_H~m,2 can be observed. The
3G
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
probability of 0 in the output, f (n), almost approaches f * = 0.~ after
generating only 9 bits in the output. Although this appears to be a
"stroke of luck", it is later shown, both theoretically and empirically,
that D_S~-I~m,2 'follows this behavior relatively rapidly.
The Decoding Process : D_SSI~m,2
The decoding process, D_S_H~m,~, is much more easily implemented.
For each bit received from the output sequence, f (n) is compared with
f *. If f (n) is smaller than or equal to f *, 0 is favored by the branch
assignment 0-l, otherwise 1 is favored by the branch assignment 1-0.
1o D_S~i_Dr",,~ also maintains a pointer, q, that is used to trace a path from
the root of T to the leaf where the symbol to be decoded is located.
The formal decoding procedure is given in Process D_S~-I~m,~, and
pictorially in Figures ~ and 6.
Schematic of D_SSI~m,~
15 The process D_S~I~m,2 (see Figures ~ and 6) begins with the In-
put~0utput block 100, where the encoded sequence, ~J = y~l~ . . . y(R~,
the root of the Huffman tree, r, and the requested probability of '0' in
the output, f *, are read. The Huffman tree must be the same as that
used by Process D_S~I_Em,2 if the original source sequence, ~, is to be
2o correctly recovered.
In block 110, the estimated probability of '0' in the output, f , and
the counter of zeros in the output, c0, are initialized to 0. The number
37
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
of bits processed from the input sequence, n, and the number of symbols
sent to the output, 1~, are both initialized to 1. As in D_S~I~,,',2, other
straightforward initializations of these quantities are also possible, but
the Encoder and Decoder must maintain identical initializations if the
original source sequence, x, is to be correctly recovered. The Process
also initializes a pointer to the current node in the tree, q, W111Ch is set
to the root of the tree, r.
The decision block 120 constitutes the starting of a looping structure
that ends (branch labeled "No" ) when all the bits from ~ are processed.
1o The decision block 130 compares the estimated probability of '0' in ~, f ,
with the desired probability, f *, leading to block 140 through the branch
"Yes" (branch assignment 0-1) if f G f *. The decision block 140 leads
to block 170 if the current bit is a '0' because the branch assignment
being used is 0-1 and the path must go to the left. Conversely, when
the current bit is a '1', the path must go to the right (block 160) . The
branch "No" of block 130 (when f > f *) leads to the decision block 150,
which compares the. current bit with '0'. If that bit is a '0', the "Yes"
branch goes to block 160, in which the current pointer, q, is set to its
right child. When the current bit is a '1' (the branch labeled "No" of
2o block 150), the process continues with block 170, which sets q to its left
child, and increments the counter of zeros in y, c0.
Connector 180 is the continuation of the process after block 160 or 170
have been processed. Connector 190 is the continuation of the branch
38
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
"No" of block 120, which implies that all the bits from y have been
processed. Connector 200 is ~ the continuation of the branch "Yes" of
block 230, and goes to block 130 to continue processing the current path.
Connector 210 is the continuation of the looping structure that process
all the bits of y.
In block 220, the estimated probability of '0' in y, f , is updated using
the current counter of zeros, and the counter of bits processed.
The next decision block (block 230), checks whether or not the current
pointer, q, is pointing to a leaf. In the case in which q is pointing to the
to leaf associated with the source symbol to be recovered (branch "No" ),
the process continues with block 240, in which the corresponding source
symbol, ~(1~~, is recovered, the counter of source symbols in x, 7~, is
incremented, and the current pointer, q, is moved to the root of the tree.
Block 250 occurs when all the bits from y.have been processed (branch
"No" of block 120). At this point, the original source sequence, X, is
completely recovered, and the Process D_S_H~r,z,2 terminates in block
260, where the control is returned to the "upper level" process which
invoked it.
39
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Process D_S~-I~,.,z,~
Input: The Huffman Tree, T. The encoded sequence, y. The
requested probability of 0, f *.
Output: The source sequence, X.
Method: '
c0 (0) f- '0; n f- 1; f (0) f- 1
q ~ root('7~; l~ = 1
for n ~ 1 to R do ~~ .F'or all the symbols of the output sequence
if f (n) < f * then ~~ Assignment 0-1
1o if y~n~ = 0 then
co(n) ~- co(n - 1) -I- 1; q ~ left(q)
else
q f- right(q)
endif
else // Assignment 1-0
if y(n~ = 0 then
q ~ right(q)
else
co(n) ~ co(n - 1) -E- 1; q f- left(q)
endif
endif
if q is a "leaf" then
~~1~~ ~ symbol(q); q ~- root(7~; k ~ 1~ -~- 1
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
endif
f (n~ ~ ~°nn~ ~~ Recalculate the probability of 0 irt the output
endfor
End Process D_S~I~r",,2
41
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Example 4. Consider the source alphabet ~S = ~a, b, c, d~ with prob-
abilities of occurrence P = ~0.4, 0.3, 0.2, 0_1~ and the code alphabet
,A _, ~0, l~. The output sequence y = 011010011 is decoded using
D_S~I~m,,2 and the Huffman tree depicted in Figure 1.
The decoding process is detailed in Table 3. As in D_S~-I~m~2, co(n)
and f (n) are set to 0, and the default branch assignment is set to be 0-1.
For each bit, y ~n~, read from y, the current branch assignment and y (n~
determine the direction of the path traced, or more informally, where
child q will 'Go': left (L) or right (R). Subsequently, co(n) and f (n) are
1o updated. Whenever a leaf is reached, the source symbol associated with
it is recorded as the decoded output. Finally, observe that the origi-
nal input, the source sequence of Example 3, ~1' = bacba, is completely
recovered.
Proof of Convergence of D_S.~I~m,~
The fundamental properties of D_S_H~m,~ are crucial in determining
the characteristics of the resulting compression and the encryptions which-
are constructed from it. To help derive the properties of D_S_H~m,~, the
properties of the binary input alphabet case are first derived, and later,
the result for the multi-symbol input alphabet case is inductively derived.
2o The Binary Alphabet Case
In this section, the convergence of D_S~I~?,,,~~ for a particular case
when the input has a binary source alphabet is proven. In this case,
42
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
n y~n -I- co(n) f (n) Assignment Go ~
1~
0 0 0 0.0000 0-1 L
1 1 1 1.0000 1-0 L b
2 1 1 0.5000 0-1 R a
3 0 1 0.3333 0-1 L
4 1 2 0.5000 0-1 R
0 2 0.4000 0-1 L c
6 0 3 0.5000 0-1 L
7 1 4 0.5'7141-0 L b
'
8 1 4 0.5000 0-1 R a
9 5 0.4444
Table 3: Decoding of the output sequence y = 011010011 using Process
D_S~-T~m,~2 and the HufFman tree of Figure 1. The source sequence of
Example 3 is completely recovered.
the Huffman tree has only three nodes - a root and two children. The
encoding process for this case is referred to as D_S_H_E~,2.
Consider the source alphabet, eS = ~0,1~. The encoding procedure
is detailed in Process D_S~i~~~2 given below. The symbol s, the most
5 likely symbol of S, is the symbol associated with the left child of the
root, and s is the complement of s (i.e. s is 0 if s is 1 and vice versa) is
associated with the right child.
43
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Process D_S~I~2,~
Input: The source alphabet, <S, and the source sequence, X. The
requested probability of 0, f *.
Output: The output sequence, y.
Method:
co(0) ~- 0; f (1) ~- 0; s E- The most likely symbol of S.
for n ~ 1 to M do ~~ For all the symbols of the input sequence
if f (n) G f * then ~~ Assignment D-1
if ~~n~ = 0 then
1o y~n~ ~ s; co(n) ~- co(n - 1) -I- s
else
y~n~ ~ s~ co(n) ~ co(n - 1) + s
endif
else ~~ Assignment 1-0
if ~(n~ = 0 then
y~n~ ~ s~ co(n) ~ co(n - 1) + s
else
~J~n~ ~ s~ co(n) ~ co(~ - 1) -I- s
endif
2o endif
f (n) ~ ~°nn~ ~~ Recalc~clate the probability of 0
endfor
End Process D_S~I~2,2
44
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
The Huffman tree for this case is straightforward, it has the root and
two leaf nodes (for 0 and 1). There are two possible labeling strategies
with this tree. The first one consists of labeling the left branch with 0 and
the right one with 1 (Figure 6(a)), which leads to the encoding scheme
~o : ~S -~ G = ~0,1~. The alternate labeling strategy assigns 1 to the left
branch and 0 to the right branch (Figure 6(b)), leading to the encoding
scheme ~1 : ~S -~ C = ~1, 0~. Rather than using a fixed encoding scheme
to encode the entire input sequence, a labeling strategy that chooses the
branch assignment (either 0-1 or 1-0) based on the estimated probability
of 0 in the output, f (n) is enforced.
In regard to the proof of convergence, it is assumed that the probabil-
ity of 0 in the input, p, is greater than or equal to 1- p, the probability
of 1 occurring in the input, and hence p > 0.~. This means that the most
likely symbol of ~ is 0. The case in which p, G 0.5, can be solved by sym-
metry and is straightforward. It is shown that any probability requested
in the output, f *, is achieved by the D_S~I~~~2, where 1- p G f * < p.
The statement of the result is given in Theorem ~ below. The rigorous
proof of this theorem is given in Appendix B.
Theorem 1 (Convergence of Process D_S~-I~2~~). Consider a sta-
2o tionary, memoryless source with alphabet S = ~0,1~, whose proba-
bilities are P - ~p,1 - p~, where p > 0.5, and the code alphabet,
,A. _ ~0,1~. If the source sequence x = x(l~, . . . , ~(n~, . . ., with ~(i~ E
~S, i = l, . . . , n, . . ., is encoded using the Process D_S_H~~,2 so as to
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
yield the output sequence ~ _ , y~l~, . . . , ~~n~, . . ., such that y~i~ E
,A.,
i = l, . . . , n, . . ., then
lim.Pr~f (n) = f *~ = 1, (1)
n-->oo
where f _* is the requested probability of 0 in the output (1- p G f * < p),
and f (n) _ ~°nn~ with co(n) being the number of 0's encoded up to time
n.
The result that D_S~I~~,2 guarantees Statistical Perfect Secrecy fol-
to lows.
Corollary 1 (Statistical Perfect Secrecy of Process D_S~I~~,2).
The Process D_S~I_E~,2 guarantees Statistical Perfect Secrecy.
Proof. The result of Theorem 1 states that the probability of 0 in the
output sequence, asymptotically converges to the requested value f *,
Where 1 - p < f * < p, with probability 1. In particular, this guarantees
convergence whenever f * is 0.~.
Since the value of f is guaranteed to be close to 0.5 after a finite num-
ber of steps, this, in turn, implies that for every input x, Pr~y~+l...y~+~~,
the probability of every output sequence of length l~ occurring, will be
2o arbitrarily close to ~k . The result follows.
Equation (57) (in Appendix B) also guarantees optimal and lossless
compression.
46
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Convergence Properties of D_S~I~2,2
Theorem 1 proves that f (n) converges with probability 1 to the value
f *. However, the issue of the transient behaviors is not clarified. It is
now shown that f (n) converges very quickly to the final solution. Indeed,
if the expected value of f (n) is considered, it can be shown that this
quantity converges in one step to the value 0.5, if f * is actually set to
0.5.
Theorem 2 (Rate of convergence of Process D_S~i~~,2). If f * is
set at 0.5, then E~ f (1)~ = 0.5, for D_S_H~2,2, implying a one-step con-
to vergence in the expected value. 0
The effect on the convergence (when using a window, which contains
the last t symbols in the output sequence, to estimate the probability of
0 in the output) is 11OW discussed.
When the probability of 0 in the output is estimated using the entire
sequence of size n, it is well known that f (n) converges to f *. Thus,
f (n) - ~ co (n) - f
n
i=o
Trivially, since the convergence is ensured, after 1~ more steps the
2o estimated probability of 0 in the output again becomes:
lThe transient behavior, its implications in solving the DODE, and how it can
be
eliminated in any given encryption are re-visited later.
47
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
f (n + k) - n+~ co (n) - f* .
n -I-1~
i=o
It is straightforward to see that, by estimating the probability of 0
in the output using the last k bits, the modified D_S~I~2,2 would still
converge to the same fixed point f *, since
n+k c0(~) - f*'i
i=n+1
1o were co(k) is the number of 0's in the last k bits of the output sequence.
In other words, this means that instead of using a window of size ~
to implement the learning, one can equivalently use the entire output
encoded sequence to estimate f (n) as done in D_S_H~~~2. The current
scheme will converge to also yield point-wise convergence:
1~ The lVlulti-Symbol Alphabet Gase
The convergence of D_S~i~m,2, where m > 2 is now discussed. For
this case, it can be shown that the maximum probability of 0 attainable
in the output is fma~ and the minimum is 1 - f max, where f max is the
probability of 0 in the output produced by an encoding scheme obtained
2o by labeling all the branches of the Huffman tree using the branch assign-
48
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
ment 0-1. This result is shown by induction on the number of levels of the
Huffman tree. It is shown that D_SlL~m,~ converges to the fixed point
f * at every level of the tree, using the convergence result of. the binary
case. The convergence of D_S~I~m,2 is stated and proved in Theorem 4
below.
Theorem 3 (Convergence of Process D_S~L~~,2). Consider a sta-
tionary, memoryless source with alphabet ~ _ ~sl, . . : , sm~ whose prob-
abilities are P = (p1, . . . , pm~, the code alphabet ,A. _ ~0, l~, and a bi-
nary Huffman tree, T, constructed using Huffman's algorithm. If the
to source sequence x = ~(1~ . . . ~(M~ is encoded by means of the Process
D_S~i_Em,~ and T,.to yield the output sequence y = y(1~ . . . y(R~, then
~~ Pr(f (n) = f *~ = 1
15 where f * is the requested probability of 0 in the output (1- fm~x < f * <
fmax)~ and f (n) _ ~°nn~ with ca(n) being the number of 0's encoded up
to time n. '
Corollary 2. The Process D_S~I~m~2 guarantees Statistical Perfect Se-
crecy.
49
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Empirical Results
One of the sets of files used to evaluate the performance of the en-
coding algorithms presented in this research work was obtained from the
University of Calgary. It has been universally used for many years as
a standard test suite known as the Calgary corpus2. The other set of
files was obtained from the University of Canterbury. This benchmark,
.known as Canterbury corpus, was proposed in 199'7 as a replacement
for the Calgary corpus test suite (see Arnold et al. (A Corpus for the
Evaluation of Lossless Compression Algorithms, Proceedings of the IEEE
so Data C'om~ression Conference pages 201-210, Los Alamitos,. CA, IEEE
Computer Society Press, (1997))). These files are widely used to test and
compare the efficiency of different compression methods. They represent
a wide range of different files and applications including executable pro
grams, spreadsheets, web pages, pictures, source code, postscript source,
etc.
Process D_S~I~m,2 has been implemented by considering the ASCII
set as the source alphabet, and the results have been compared to the
results obtained by traditional Huffman coding. The latter has been con-
sidered here as the fixed-replacement encoding scheme obtained by using
2o a binary Huffman tree and the branch assignment 0-1. This method
is referred to as the Traditional Static Huffman (TSH) method. The
requested frequency of 0, f *, was set to be 0.5 and O was set to be
ZAvailable at ftp. cpsc.ucalgary. ca/pub/projects/text. compression. corpus/.
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
2. The empirical results obtained from testing D_S~i~m~2 and TSH on
files of the Calgary corpus and the Canterbury corpus are given in Ta-
bles 4 and 5, respectively. The first column corresponds to the name of
the original file in the Calgary or Canterbury corpus. The second col-
umn fTS.H is the maximum probability of 0 attainable with the Huffman
tree, i.e. the probability of 0 in the output attained by TSH. fDSFrE
is the estimated probability of 0 in the output sequence generated by
D_S~i~m,2: The last column, d(,~', .~'*), is the distance calculated by
using (14), where fDSHE is the probability of 0 in the compressed file
to generated by D_S~I_E~,,2.
The last row of Tables 4 and ~, labeled "Average", is the weighted
average of the distance.
From Table 4, observe that D_S_H~m,~ achieves a probability of 0
which is very close to the requested one. Besides, the largest distance
(calculated with O = 2) is approximately 3.0E-08, and the weighted
average is less than 7.5E-09.
On the files of the Canterbury corpus, even better results (Table ~) are
obtained. Although the worst case was in the output of compressing the
file grammar.lsp, for which the distance is about 10E-08, the weighted
2o average distance was even smaller than ~.5E-10.
51
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File Name fTSH fD.SHE d(y .h*)
bib 0.5346281040.5000025776.64093E-12
bookl 0.5392741580.500000000O.OOOOOE-X00
book2 0.5362332370.5001736023.01377E-08
geo 0.5249782490.4999956931.85502E-11
news 0.5348629680.5000202934.11806E-10
ob j 1 0.5273736840.5000077886.06529E-11
obj2 0.5280486930.5000830786.90195E-09
paperl 0.5360352670.5000308669.52710E-10
progc 0.5340784650.5000577563.33576E-09
progl 0.5317065810.4999636971.31791E-09
progp 0.5350765260.4999921236.20471E-11
trans 0.5328034480.499999065~ 8.74225E-13
Average 7.44546E-09
Table 4: Empirical results obtained after executing D_S~I~m,~ and TSH
on files of the Calgary corpus, where f * = 0.5.
Graphical Analysis
The performance of D_S~I~m,2 has also been plotted graphically. The
graph for the distance on the file bib of the Calgary corpus is depicted
in Figure 7. The x-axis represents the number of bits generated in the
output sequence and the y-axis represents the average distance between
the probabilities requested in the output and the probability of 0 in the
output sequence.
The average distance mentioned above is calculated as follows. For
each bit generated, the distance, d( f , f *), is calculated by using (14),
1o where the probability of 0 requested in the output is f * = 0.5, and f
52
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File Name fTSH fDSHE d(~, ~*)
alice29.txt0.542500235 0.4999444053.09080E-09
asyoulik.txt0.538999222 0.4999860841.93647E-10
cp.html 0.5369'787330.500000000O.OOOOOE~-00
fields.c 0.536561933 0.5000889597.91361E-09
grammar.lsp0.538545748 0.4996542981.19510E-0'7
kennedy.xls0.535706989 0.500000278'7.'10618E-14
lcetl0.txt 0.535809446 0.4999892'741.15043E-10
plrabnl2.txt0.542373081 0.5000004542.05'153E-13
ptt5 0.'7378341570:50000058'73.44100E-13
xargs.l 0.532936146 0.4998798831.44281E-08
Average 5.42759E-10
Table 5: Empirical results of D_S~I~m~~ and TSH tested on files of the
Canterbury corpus, where f * = 0.5.
is estimated as the number of 0's, co(n), divided by the number of bits
already sent to the output. In order to calculate the average distance, the
output was divided into 500 groups of gi bits and the average distance is
calculated by adding d( f , f *) over each bit generated in the group, and
dividing it by gZ .
From the figure it can be seen that the distance drops quickly towards
0, and remains arbitrarily close to 0. Such 'convergence is typical for all
the files from both the Calgary corpus and Canterbury corpus.
53
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
D~~-I~~,2 : The Deterministic Embodiment using
Adaptive Huffman Coding
The Encoding Process
The technique for solving DODC by using Huffman's adaptive cod
s ing scheme is straightforward. Again, the design takes advantage of the
sibling property of the tree at every instant to decide, on the labeling
strategy used at that time. Apart from this, the process has to incorpo
rate the learning stage in which the probabilities of the source symbols
are estimated. This is a fairly standard method and well documented in
to the literature (see Hankerson et al. (Introd~cction to Information The-
ory and Data Compression, CRC Press, (1998)), Gallager (Variations
on a Theme by Huffman, IEEE Transactions on Information Theory,
24(6):668-674, (19'78)), Knuth (Dynamic Huffman Coding, Jo~crnal of
Algorithms, 6:163-180, (1985)), and Vitter (Design and Analysis of Dy-
15 namic Huffman Codes, Journal of the ACM, 34(4):825-845, (1987))).
The encoding procedure for the distribution optimizing algorithm us-
ing the Huffman coding in an adaptive manner is detailed in Process
D~~I~,~,2 given below, and pictorially in Figures 9 and 10.
Schematic of D_A.~i_Em,2
2o The schematic chart of Process DA_H~,~,~ is explained here. In
block 100, the source sequence to be encoded, x = ~(l~ . . . ~~M~, and
the requested probability of '0' in the output, f *, are read from the in-
54
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
put. In block 110, a Huffman tree is constructed following the procedure
presented in Huffman (A Method for the Construction o Minimum Re-
dundancy Codes, Proceedings of IRE, 40(9), pp. 1098-1101, (1952)), by
assuming a suitable probability distribution for the source symbols. This
procedure returns the Huffman tree by means of a pointer to the root,
r, and a hashing function, h(.), that is used later to locate the node
associated with the symbol being processed from the input.
In block 120, the estimated probability of '0' in the output, f , and
the counter of zeros in the output, co, are set to 0. The corresponding
Zo counters for the number of bits sent to the output, n, and for the number
of symbols processed from the input, l~, are set to 1. As in D_S_H_Em,~,
other straightforward initializations of these quantities are also possible,
but the Encoder and Decoder must maintain identical initializations if
the original source sequence, .~, is to be correctly recovered.
15 The decision block' 130 constitutes the starting of a looping structure
that processes the M symbols from the input. The branch "Yes" leads
to block 140, which sets the current pointer, q, to the node associated
with the current symbol being processed, ~~1~~, by invoking the hashing
function h(.). The length of the path from the root to the node associated
20 with ~~k~, .~, is set to 0, and a temporary pointer, q1, used later when
updating the Huffman tree, is set to q so as to store the pointer to the
node associated with ~~k~.
The decision block 150 constitutes the starting of a looping structure
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
that processes all the edges in the path. When the current pointer, q, is
not the root, the process continues by tracing the path towards r (branch
"Yes" ), going to block 160, which increments the length of the path, .~.
The next block in the process is the decision block 170, which checks if
the path comes from the left child (branch "Yes" where the path is set to
true in block 180), or from the right child, where the path is set to false
in block 190. The current pointer, q, is then moved to its parent (block
195). The branch "No" of block 150 indicates that the root of the tree
has been reached, and the branch assignment process starts in block 230
to (reached through Connector 200), which sets a counter of bits to be sent
to the output, j, to the length of the path, .~.
Connector 210 is the continuation of the branch "No" of the decision
block 130, and indicates that all the symbols coming from the input
have been processed. Connector 220 is the continuation of the looping
z5 structure that processes all the symbols of the input.
The decision block 240 constitutes the starting of a looping structure
that processes all the edges in the current path. When j > 0 (branch
"Yes" ), the process continues by performing a labeling of the current
edge (block 250). If the estimated probability of '0' in the output, f , is
20 less than or equal to the required probability, f *, the branch.assignment
0-1 is used, and hence when the path leads to the left (true or branch
"Yes" of block 260), a '0' is sent to the output and the counter of zeros
is incremented (block 290). Conversely, when the path goes to the right
56
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
(false or branch "No" of block 260), a '1' is sent to the output (block
280). The branch "No" of block 250 ( f > f *) indicates that the branch
assignment 1-0 is used, leading to the decision block 270, in which the
branch "Yes" leads to block 280 (a '1' is sent to the output), and the
branch "No" leads to block 290 (a '0' is sent to the output and the counter
of zeros, ca, is incremented) .
In block 300, the estimated probability of '0' in the output, f , is
updated using the current counter of zeros and the current counter of
bits. The counter of edges in the path, j, is decremented (block 310),
1o since the path is now being traced from the root to q1.
When all the edges in the path are processed (branch "No" of block
240), the counter of symbols processed from the input, k, is increased
(block 320), and the Huffman tree is updated by invoking the procedure
described in Knuth (Dynamic Huffman Coding; Journal of -Algorithms,
Vol. 6, pp. 163-180, (1985)), or Vitter (Design and Analysis of Dynamic
Huffman Codes, Journal of the AG'M, 34(4):825-845, (198'7)), returning
the updated hashing function, h(.), and the new root of the tree, r, if
changed.
When all symbols from the input have been processed (branch "No"
of block 130) the encoded sequence, y, is stored (Input~0utput block
340), the Process D_A~I~,~,2 terminates, and the control is returned to
the "upper-level" process (block 350) that invoked it.
57
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Process D~~I~' m,2
Input: The source alphabet, S. The source sequence, x. The
requested probability of 0, f *.
Output: The output sequence, y.
Assumption: It is assumed that there is a hashing function which
locates the position of the input alphabet symbols as leaves in T. It is
also assumed that the Process has at its disposal an algorithm (see ~~~,
(16~) to update the Huffman tree adaptively as the source symbols come.
Method:
to Construct a Huffman tree, T, assuming any suitable distribution
for the symbols of S. In this instantiation, it is assumed that the symbols
are initially equally likely.
co(0) f- 0; n f- l; f (1) ~- 0;
for 1~ f- 1 to M do ~/ For all the sgmbols of the inp~ct sequence
Find the path for ~~1~~; q ~- root(T)
while q is not a leaf do
if f (n) < f * then /~ Assignment 0-1
if path is "left" then
~J~n~ ~ 0~ co(n) ~ co(~ - 1) +n~ q ~ left(q)
2o else
y(n~ ~- 1; q ~ right(q)
endif
else ~~ Assignrrzent 1-0
58
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
if path is "left" then
y(n~ ~- 1; q f- left(q)
else
~J~n~ ~ ~~ co(~) f- co(~ - 1) + 1~ q ~ right(q)
endif
endif
f (n) ~ c~nn) i n ~- n'-I-1
endwhile
Update T by using the adaptive Huffman approach (5~, ~16~ .
1o endfor
End Process D_A II~r,.',2
The Decoding Process
The decoding process for the adaptive Huffman coding is also straight
forward. It only requires the encoded sequence, y, and some conventions
to initialize the Huffman tree and the associated parameters. This proce
dure is formalized in Process D~4~-I~m,~, and pictorially in Figures 11
and 12. Observe that, unlike in the static Human coding, the Decoder
does not require that any extra information is stored in the encoded
sequence. It proceeds "from scratch" based on prior established conven
~o tions.
Schematic of D_A~i~m,2
The Process DA_H_Dm,~, depicted in Figures 11 and 12, begins with
59
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
the Input~0utput block 100,~where the encoded sequence, y = y(l~ . . . y(R~,
and the requested probability of '0', f *, are read. In block 110, the pro-
cedure that constructs the Huffman tree is invoked using the same initial
probability distributions for the source symbols as those used in the Pro-
s cess D~~I~m,2 so as to recover the original source sequence, x. Again,
the tree is referenced by a pointer to its root, r.
In block 120, the estimated probability of '0' in y, f , and the counter
of zeros in y, ca, are both set to 0. The counter of bits processed, n,
and the counter of symbols sent to the output, l~, are set to 1, and the
1o current pointer, q, is set to the root of the tree, r. As in D_A~-I~m,~,
other straightforward initializations of these quantities are also possible,
but the Encoder and Decoder must maintain identical initializations if
the original source sequence, x, is to be correctly recovered.
The decision block 130 constitutes the starting of a looping structure
15 that processes all the bits from y. The next block is the decision block
140, which compares the estimated probability of '0' in y, f , to the
requested probability, f *. If f C f *, the branch assignment 0-I is used,
and hence in block 1~0, when a '0' comes from y, the branch "Yes"
moves q to its left child (block 130), and when y(n~ is a '1', the current
2o pointer, q, goes to its right child (block 170). The branch "No" of the
decision block 140 ( f > f *) indicates that the branch assignment 1-0 is
used, leading to the decision block 160. When the current bit is a '0',
the current pointer is set to its right child (block 170), and when y(n~
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
is a '1', the current pointer, q, is set to its left child, and the counter of
zeros in y, c0, is increased (block 180).
The. process continues through connector 190, leading then to block
230 in which the estimated probability of '0' in y, f , is updated using
the current counter of zeros, c0, and the counter of bits processed, n.
The process continues by performing the decision block 240, where the
current pointer, q, is tested. If q is not a leaf (i.e. its left child is riot
nil), the process continues with the next bit (the next edge in the path)
going to block 140 through connector 210. Otherwise the corresponding
1o source symbol, x(1~~, is recovered, and the counter of source symbols, l~,
is increased (block 250). The process continues with block 260, where
the tree is updated by invoking the same updating procedure as that of
the D~I~I~m 2 so that the same tree is maintained by both the Encoder
and Decoder. In block 270, the current pointer, q, is set to the root r,
and the process continues with the decision block 130 through connector
220 so that the next source symbol is processed.
The branch "No" of the decision block 130 indicates that all the bits
of y have been processed, going (through connector 200) to the In
putlOutput block 280 in which the original source sequence, x, is stored.
2o The Process DA~-I_Dm~2 terminates in block 290.
61
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Process D~~I~"r,,2
Input: The source alphabet, <S. The encoded sequence, y. The
requested probability of 0, f *.
Output: The source sequence, x.
Assumption: It is assumed that there is a hashing function which
locates the position of the input alphabet symbols as leaves in T. It is
also assumed that the Process has at its disposal an algorithm (see ~5~,
~16~) to update the Huffman tree adaptively as the source symbols come.
Method:
1o Construct a Huffman tree, T, assuming any suitable distribution
for the symbols of S. In this instantiation, it is assumed that the symbols
are initially equally likely.
c0(0) ~- 0; n ~ 1; f (1) f- 0
q f- root(7~; k ~ 1
for n ~- 1 to R do ~/ For all the symbols of the o~ctp~t seq~cence
if f (n) G f * then ~/ Assignment 0-1
if y~n~ = 0 then
co(n) ~ co(n - 1) -I-1; q ~ left(q)
else
2o q ~ right(q)
endif
else ~~ Assignment 1-0
if y(n~ = 0 then
62
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
q ~- right(q)
else
co(n) ~- co(n - 1) ~-- l; q ~- left(q)
endif
endif
if q is a "leaf" then
x~l~~ ~- symbol(q)
Update r by using the adaptive Huffman approach ~5~, (16~.
q f- root(T); 1~ ~ 1~ -I-1
~o endif
f (n) ~ ~°nn~ ~~ Recalculate the Probability of 0 in the outp~ct
endfor
End Process D_A~3~r,L,2
Proof of Convergence
The solution of DODO using DA_H_E2,~ works with a Huffman tree
which has three nodes: the root and two children. This tree has the
sibling property, hence the decision in the branch assignment rule is based
on the value of f (n) compared to the requested probability of 0 in the
output, f *. The proof of convergence for this particular case is given
2o below in Theorem 5.
Theorem 4 (Convergence of Process D_A~I~~,~). Consider a
memoryless source with alphabet ~S = ~0,1~, whose probabilities are
P = (p,1- p~, where p > 0.5, and the code alphabet, ,A. _ ~0,1~. If the
63
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
source sequence x = ~~1,, . . . , ~~72,, . . ., Wlth ~~Z, E cS, Z = 1, . . . ,
TL, . . ., 1S
encoded using the Process D~~i~2,2 so as to yield the output sequence
y = ~~1~, . . . , y~n~, . . ., such that ~~i~ E ,A., i = 1, . . . , n, . . .,
then
lim Pr~ f (n) = f *~ = 1, (0)
n-goo
Where f * is the requested probability of 0 in the output, (1- p < f * < p),
and f (n) _ ~°nn~ With co(n) being the number of 0's encoded up to time
n. 0
1o The Huffman tree maintained in DA_H~m,~ satisfies the sibling prop-
erty, even though its structure may change at every time 'n'. There-
fore, the convergence of D~4_H_Em,~ follows from the convergence of
DA_H~2,~. The convergence result is stated in Theorem 6, and proved
in Appendix B. Here, the fact that the estimated probability of 0 in the
15 output can vary on the range ~1 - f may, ,fmax~ is utilized. The final
result
that D-A_H~",, 2 yields Statistical Perfect Secrecy follows.
64
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Theorem 5 (Convergence of Process D_A~-I~m,~). Consider a mem-
oryless source with alphabet S =. ~s~, . . . , sm~ whose probabilities are
P = (p1, . . . , pm~, and the code alphabet .A _ ~0,1~. If the source~se-
quence X = x(1~ . . . x~M~ is encoded by means of the Process D_A~I~m,~,
generating the output sequence y = y(1~ . . . y~R~, then
lim Pr~f (n) = f *~ _ ~
n-300
where f * is the requested probability of 0 in the output (1- fma~ < f
1o fm,ax), and f (n) _ ~°nn~ with co(n) being the number of 0's encoded
up
to time 'w'.
Corollary 3. The Process DA~I~m,~ guarantees Statistical Perfect
Secrecy.
Empirical Results
In order to demonstrate the performance of D~~i~,.",,~, the latter
has been tested on files of the Calgary corpus. The empirical results
obtained are cataloged in Table 6, for which the requested probability of
0 in the output is f * = 0.5. The column labeled fTAH corresponds to
the estimated probability of 0 in the output after encoding the files using
2o the Tradition Adaptive Huffman (TAH) scheme. The column labeled
fl7AFIE .corresponds to the estimated probability of 0 in the output of
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
DA~I~m~2. Observe that D~~I~m,~ performs very well on these files,
and even sometimes attains the value 0.5 exactly. This is also true for
the average performance, as can be seen from the table.
File Name fTAH fDAHE d~~~ ~*~
bib 0.5348908850.500002567 6.59052E-12
bookl 0.5393829610.500000142 2.02778E-14
book2 0.5362874530.499.8180873.30923E-08
geo 0.5260899980.499985391 2.13437E-10
news 0.5347580200.500027867 7.76559E-10
objl 0.5278052170.497746566 5.07797E-06
obj2 0.5279448090.500000000 0.00000E+00
paperl 0.5352243210.500513626 2.63812E-07
progc 0.5351044550.500121932 1.48674E-08
progl 0.5355981400.500010118 1.02366E-10
progp 0.5354033850.500000000 O.OOOOOE-f-00
tr ans 0.5334958370.500001909 3.64352E-12
Average 6.46539E-08
Table 6: Empirical results obtained after running D_A~I~m,2 and TAH
on the files of the Calgary corpus, where f * = 0.5.
D~~I_Em,2 was also tested on files of the Canterbury corpus. The
empirical results are presented in Table 7, where, as usual, the optimal
probability of 0 in the output was set to be f * = 0.5. The power of
DA~-I~~,.,,,~ is reflected by the fact that the average distance is less
than 9.0E-10, and that D_A H~m~2 performed extremely well in all
the files contained in this benchmark suite. Observe that the perfor-
1o mance achieved by D~~I_Em,2 is as good as that of the static ver-.
66
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
sion D_S~I~?,z,2. Additionally, it is important. to highlight the fact that
the former does not require any overhead (statistical information of the
source) in the encoded data so as to proceed with the encoding and
decoding processes.
File Name fTAH fDAHE d(W ~*)
alice29.txt 0.5438885210.499945970 2.91922E-09
asyoulik.txt0.53837409'70.500012320 1.51787E-10
cp.html 0.5379929490.500003807 1.44948E-11
fields.c 0.5345407280.499878683 1.471'l9E-08
grammar.lsp 0.5373995580.499919107 6.54369E-09
kennedy.xls 0.5354774840.499999865 1.82520E-14
lcetl0.txt 0.5385926520.49994?023 2.8065?E-09
plrabnl2.txt0.542479'l090.499999531 2.19961E-13
ptt5 0.7367026570.500000000 O.OOOOOE+00
xargs.l 0.5368120410.500136005 1.84974E-08
Average 8.89609E-10
Table 7: Empirical results of D_A_H_Em 2 and TAH tested on the files of
the Canterbury corpus, where f * = 0.5.
In order to provide another perspective about the properties of D~lI~m,~,
a graphical display of the value of d(.~, .~) obtained by processing the
files bib of the Calgary corpus is included. The plot of the distance for
this file is shown in Figure 12.
Observe that the convergence of the estimated probability of 0 occurs
to rapidly, and the distance remains arbitrarily close to 0 as n increases.
From our experience, in general, DA~-I~m,~ converges faster than the
static version D_S~I~m,2. The results presented here are typical - anal-
67
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
ogous results are available for the other files of the Calgary corpus and
for files of the Canterbury corpus.
The Randomized Embodiments using Adaptive
Huffman Coding
This section describes a few randomized embodiments for solving the
Distribution Optimizing Data Compression problem. These processes
are obtained by incorporating various stochastic (or randomized) rules
in the decision of the labeling assignment. In general, the various em-
bodiments operate on the general Oommen-.Rueda Tree, but the embod-
1o invents described here specifically utilize a Huffman tree. Also, although
the Huffman tree can be statically or adaptively maintained, to avoid
repetition, the randomized embodiments are described in terms of the
Adaptive Huffman Tree.
The Encoding Process
The first embodiment described is RV~.~I~m,~. The underlying tree
structure is the Adaptive Huffman Tree. The Branch Assignment Rule
is randomized, and thus an branch assignment decision is made after
invoking a pseudo-random number. As per the nomenclature mentioned
earlier, it is referred to as RVA~I~m,2.
2o Consider the source alphabet,<S = ~sl, . . . , s~~ and the code alphabet
,A. _ ~0,1~. Consider also an input sequence .x = x(l~ . . . ~(M~, which
has to be encoded, generating an output sequence ~J = y~l~ . . . y~R~. The
68
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
formal procedure for encoding x into y by means of a randomized solu-
tion to the DODO, and utilizing the Huffman tree in an adaptive manner
is formalized in Process RV A~I~m~2 below. The process is also given
pictorially in Figure 14 and 1~. The decision on the branch assignment
to be used at time 'rc' is based on the current pseudo-random number
obtained from the generator, RNG(next~andom~.umber~, assumed to be
available for the system in which the scheme is implemented. In general,
any cryptographically secure pseudo-random number generator can be
used.
69
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Schematic of RV~~i~m,2
The Process RV~1.~I~"L,2, depicted in Figures 14 and 15, begins in
block 100, in which the input sequence, x = ~ (l~ . . . x (M~, the requested
probability of '0' in the output, f *, and a user-defined seed, ,Q, are read.
The initial seed must be exactly the same seed as used by the decoding
Process RV~I.~i~m,2 to correctly recover the plaintext. A Huffman tree
is then constructed in block 110 by following the procedure presented
in Huffman (A Method for the Construction o Minimum Redundancy
Codes, Proceedings of IRE, 40(9), pp. 1098-1101, (1952)), and assuming
a suitable initial probability distribution for the source symbols. This
procedure returns a pointer to the root of the tree, r, which serves as a
reference to the entire tree, and a hashing function, h(s), which is used
later to locate the node associated with s.
In block 120, a pseudo-random number generator (RNG) is initialized
using the user-defined seed, ,Q.
The next step consists of initializing the estimated probability of '0'
in the output, f , and the counter of zeros in the output, c0, both to 0
(block.130). In this block, the counter of bits sent to the output, n, and
the counter of source symbols processed from the input, l~, are set to 1.
2o Otherwise, the next decision block (block 140) constitutes the starting
point of an iteration on the number of source symbols coming from the
input. When there are symbols to be processed (the branch "Yes" ), the
process continues with block 150, where the current node, q, is set to the
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
corresponding value that the hashing function returns after being invoked
with the current source symbol as a parameter. The node associated with
x~l~~, q1, is set to the current node, q, and the length of the path from
that node to the root, .~, is set to 0. The decision block 160 evaluates if
the current pointer, q, has not .reached the root of the tree. In this case,
the process continues with block 170, where the length of the path, .~, is
increased. The next.block in the process is the decision block 180, which
evaluates if the current node, q, is~ a left child or a right child. The path
is set to true (block 190) in the former case, and to false (block 200) in
to the latter case. The process then continues with block 205, where the
current pointer, q, is moved to its parent.
The branch "No" of the decision block 160 indicates that the current
node has reached the root, and the process continues with block 240
through connector 210, where the counter of edges in the current path,
j, is initialized to .~, the length of the path. The decision block 250
constitutes the starting point of a looping structure that process all the
nodes in the current path. When there are edges remaining in the path
( j > 0), the nt~ random number obtained from RNG is compared to the
estimated probability of '0' in the output, f, (block 260). If RNG(n~ >
2o f , the branch assignment 0-1 is used, continuing the process with the
decision block 270, which leads to the left child if path(.~~ is true. In this
case, a '0' is sent to the output and the counter of zeros in the output,
c0, is incremented (block 310). If path~.~~ is false, the process continues
71
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
with block 290, where a '1' is sent to the output. The branch '~No" of
the decision block 260 implies that the branch assignment 1-0 is used,
continuing the process with the decision block 280. When path~.~~ is true,
a '1' is sent to the output (block 290), otherwise the process continues
with block 310. The next block in the process is block 320, where the
estimated probability of '0' in the output, f , is updated and the counter
of bits sent to the output, n, is increased. The next block (block 320)
decreases the counter of edges in the path, j, and continues with the next
edge in the path (the decision block 250).
to When all the edges in the current path have been processed, the pro-
cess continues with block 330, where the counter of source symbols pro-
cessed, 1~, is incremented. The next block in the process is block 340 in
which the Huffman tree is updated by invoking the procedure introduced
in I~nuth (Dynamic Huffman Coding, Journal of Algorithms, Vol. 6, pp.
163-180, (1980), or Vitter (Design and Analysis of Dynamic Huffman
Codes, Jo~crnal of the ACM, 34(4):82-84~, (198'7)), returning the up-
dated hash function, h(.), and the new root of the tree, r, if changed.
The process continues with the decision block 140 (through connector
230).
2o When all the source symbols have been processed (branch "No" of the
decision block 140), the process continues with the Input~0utput block
3~0 (through connector 220), where the encoded sequence, y, is stored.
The process then terminates in block 360.
72
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Process RV~.~I~m,~
Input: The source alphabet, ~. The source sequence, X. A user-
defined seed, ~3. It is assumed that we are converging to the value of
f * = 0.5.
Output: The output sequence, y.
Assumption: It is assumed that there is a hashing function which
locates the position of the input alphabet symbols as leaves in T. It
is also assumed that the Process has at its disposal an algorithm (see
Knuth ~~~ and Vitter ~16~) to update the Huffman tree adaptively as the
1o source symbols come.
Method:
Construct a Huffman tree, T, assuming any suitable distribution
for the symbols of S. In this instantiation, it is assumed that the symbols
are initially equally likely.
Initialize a pseudo-random number generator, RNG, using ,Q.
co(0) ~- 0; n ~ 1; f (1) ~- 0
for i ~- 1 to M do ~~ For all the symbols of the inp~ct sequence
Find the path for ~ ~i~
q ~ root(T')
2o while q is not a leaf do
if RNG~next~andommumber~ > f (n) then . // Assignment
0-1
if path is "left" then
73
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
~J~n~ ~ 0~ co(n) ~ co(n - 1) + 1; q ~- left(q)
else
g~n~ ~ 1; q ~ right(q)
endif
else ~~ Assignment 1-0
if bath is "left" then
y(n~ f- 1; q ~ left(q)
else
~J~n~ ~ 0~ co(n) ~.co(n -' 1) -I-1; q f- right(R')
to endif
endif
f (n) ~ c~nn~ i n ~- n -I- 1
endwhile
Update T by using the adaptive Huffman approach ~5~, ~16~.
endfor
End Process RV_A~I~,~,2
Rationale for the Encoding Process
Process RVA~I_Em~~ works by performing a stochastic rule, based on
a pseudo-random number, a Huffman tree, and the estimated probability
of 0 in the output at time 'n', ' f (n) . At time 'n', the next pseudo-random
number, cx, obtained from the generator is compared with the current
value of f (n) . Since c~ is generated by a uniformly distributed random
variable, the branch assignment 0-1 is chosen with probability 1- f (n),
74
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
and hence the branch assignment 1-0 is chosen with probability f (n) .
Let us denote p2 = ~,i+~i+1, where ~i is the weight of the its' node of
the Huffman tree, and ~i+r is the weight of its right sibling. Whenever
f (n) < 0.5, the branch assignment 0-1 implies that the output is to be
a 0 with probability pi, and a 1 with probability 1 - pi. Since p2 > 0.5
(because of the sibling 'property), the number of 0's in the output is
ri~.ore likely to be increased than the number of 1's. This rule causes
f (n) to move towards f * - 0.5. Conversely, when f (n) > 0.5, the
branch assignment 1-0 causes f (n) to move downwards towards f * = 0.~.
to This makes f (n) asymptotically converge to the fixed point f * = 0.~ as
n -~ oo. This is formally and empirically shown later in this section.
It is important to note that Process RV_A~i_Em,2works only when
the requested probability of 0 in the output is f * = 0.5. However,
RV.A~I~m,~ can easily be adapted to work with any value of f *, when-
ever 1- f m,ax ~ f * C fmax ~ This can be achieved by generating random
numbers from a random variable whose mean is the desired f *.
An example will clarify the above branch assignment rule.
Example 5. Suppose that, at time 'n', the decision on the branch as-
signment has to be made. Suppose also that cx = 0.59'12... is the returned
2o pseudo-random number, and that f (n) = 0.3. Both of these values are
used to make the decision on the assignment. These values, the interval
(0,1~, and the range corresponding to each branch assignment are de-
pitted in Figure 15. From these arguments, it is easy to see that since
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
f (n) G f * = 0.5, it is more likely to send a 0 to the output than a 1, thus
increasing f (n -I- 1) from 0.3 towards f *. This shows the way by which
RV~I.Si~m,~ works so as to asymptotically converge to f *.
The Decoding Process
The decoding process, RV~_H~m~~, follows from RVA~L~m,~, but
in the reverse manner. As in the case of the D.A_H~r,,,,~ decoding pro-
cess, RV~.~-I_Em,~ works by keeping track of the number of 0's already
read from the encoded sequence. These are used to estimate the probabil-
ity of 0, f (n), at each time instant. Also, it is assumed that RV_A~I~n,,,2
1o and RV~.~I_Dm,~ utilize the same sequence of pseudo-random numbers
to ensure that the encoded sequence is correctly decoded. Using this
information and the Huffman tree (which is adaptively maintained), the
stochastic rule is invoked so as to decide which branch assignment is to
be used (either 0-1 or 1-0) to decode the given string. The actual pro-
cedure for the decoding process that uses Huffman coding adaptively is
formalized in Process RV~. II_Dm ~ and given pictorially in Figures 17
and 18.
Schematic of RV.~1.~I_D",,~~
The schematic of Process RV~~I~m,2 given in Figures 1'7 and 18 is
2o explained below. The process starts with the Input/output block 100,
where the encoded sequence, y = yl~ . . . y~R~, the requested probability
of '0' in the output, f *, and a user-defined seed, ,~, are read. The initial
76
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
seed must be exactly the same seed as used by the Process RVA_H~,~,~
to correctly recover the plaintext.
The next block (block 110) generates a Huffman tree by invoking the
same procedure as that of the Process RV~_H~m,2 with the same initial
probabilities for the source symbols, returning the root of the tree, r.
The next block in the process is block 120 which initializes the same
pseudo-random number generator (RNG) as that of Process RV~1._H_Em,2,
using the user-defined seed ~. In block 125, the estimated probability
of '0' in ~, f , and the counter of zeros in y, c0, are both set to 0. The
1o counter of bits processed from y, n, and the counter of source symbols
processed, l~, are set to 1. As in the processes described earlier, other
straightforward initializations of these quantities are also possible, but
the Encoder and Decoder must maintain identical initializations if the
original source sequence, a.', is to be correctly recovered. In this block,
the pointer to the current node, q, is set to the root r.
The next block of the process is the decision block 130, which con-
stitutes the starting point of an iteration on the number of bits pro-
cessed. The "Yes" branch of this block indicates that more bits have to
be processed, continuing with the decision block 140, in which the cur-
2o rent pseudo-random number from RNG is compared with the estimated
probability of '0' in y. When RNG~n~ > f , the branch assignment 0-1 is
being used, and the process continues with the decision block 150, which
tests if the current bit is a '0'. In this case, the process continues with
77
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
block 180, where the current pointer, q, is moved to its left child and the'
counter of zeros in y is incremented. Conversely, when the current bit is
a '1', the process continues with block 170, in which the current pointer,
q, is moved to its right child.
s The branch "No" of block 140 continues with the decision block 160,
which tests the current bit. If this bit is a '0', the process continues with
block 170, otherwise, it goes to block 180.
The next block in the process is block 230 (reached through connector
190), where the estimated probability of '0' in y is re-calculated. The
to decision block 240 tests if the current pointer has not reached a leaf. In
.
this case, the process continues with the next edge in the path, going
to the decision block l40 (reached through connector 210) . The branch
"No" of the decision block 240 indicates that a leaf is reached, and the
corresponding source symbol, ~~1~~, is recovered (block 240). The counter
15 of source symbols, h, is thus incremented.
The next block in the process is block 250, in which the Huffman
tree is updated by invoking the same updating procedure as that of the
Process RV.A_H~m~2. In block 260, the current pointer, q, is moved to
the root r, and the process continues with the decision block 130 (reached
2o through connector 220).
When all the bits from y are processed (branch "No" of the deci-
sion block 130), the process continues with the Input~0utput~ block 270
(reached through connector 200). The source sequence X is stored, and
78
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
the process ends in block 280.
Process R~VA~-I~m,~
Input: The source alphabet, ~S. The encoded sequence, y. A user-
defined seed, ~3. It is assumed that we are converging to the value of
f* = 0.~.
Output: The source sequence, x.
Assumption: It is assumed that there is a hashing function which
locates the position of the input alphabet symbols as leaves in T. It
is also assumed that the Process. has at its disposal an algorithm (see
1o Knuth ~5~ and Vitter ~16~) to update the Huffman tree adaptively as the
source symbols come. In order to recover the original source sequence,
X, ,Q must be the same as the one used in Process RV~_H_Em,2.
Method:
Construct a Huffman tree, T, assuming any suitable distribution
1~ for the symbols of S. In this instantiation, it is assumed that the symbols
are initially equally likely.
Initialize a pseudo-random number generator, RNG, using Vii.
c0(0) ~ 0; n f- 1; f (1) ~- 0
q ~ root('T~; k f- 1
2o for n ~- 1 to R do ~~ For all the symbols of the output sequence
if RNG(next.~andom number > f (n) then /~ Assignrrzent 0-1
if y~n~ = 0 then
c0 (n) ~- c0 (n - 1) -I-1; q ~- left (q)
79
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
else
q ~ right(q)
endif
else ~~ Assignment 1-0
if y(n~ = 0 then
q ~- right(q)
else
co(n) f- co(n - 1) -I-1; q ~- left(q)
endif
1o endif
if q is a "leaf" then
x~h~ ~ symbol(q);
Update T by using the adaptive Huffman approach ~5~, ~16~.
q E- root(; h ~- k -~-1
endif
f (n) ~- ~°n~'~ ~~ Recalculate the probability of 0 in the o~tp~ct
endfor
End Process RV_A~~m,2
The Proof of Convergence
2o Prior to considering the more general case of RV_A~I~m,2 the con-
vergence of the binary-input case, RVA~I_E2,~ is first discussed. This
particular case uses an adaptively constructed Huffman tree which has
three nodes : the root and two children. This tree has the sibling prop-
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
erty, and hence the decision on the branch assignment is based on the
value of f (n) and the pseudo-random numbers generated. Consider the
case in which the requested probability in the output is f * = 0.5. The
proof of corivergence3 for this particular case is stated in Theorem '7, and
proven in the Appendix B.4
Theorem 6 (Convergence of Process RV_A~i~2 2). Consider a
memoryless source whose alphabet is S = ~0, l~ and a code alphabet,
,A. _ ~0, l~. If the source sequence x = ~~1~, . . . , x(n~, . . ., with ~(i~
E
S, i = l, . . . , n, . . ., is encoded using the Process RV~.~I_E~,~ so as to
1o yield the output sequence ~ = y~l~, . . . , y(n~, . . ., such that y~i~ E
,A.,
2 = 1, . . . , TL, . . ., then
lire E( f (n)~ - f * , and (8)
n->oo
lim Var( f (n)~ - 0 , (0)
n-goo
3The modus operandus of the proof is slightly different from that of Theorem
4. It
rather follows the proofs of the LRp scheme of automata learning (see
Lakshmivarahan
(Learning Algorithms Theory and Applications. Springer-Verlag, New York,
(1981)),
and Narendra et al. (Learning Automata. An Introduction, Prentice Hall,
(1989))).
The quantity E I f (n + 1) I ~ in terms of f (n) is first computed. The
expectation
L f (n)
is then taken a second time and E [ f (n + 1 )] is solved by analyzing the
difference
equation. It turns out that this difference equation is linear !
4The price that is paid for randomizing the solution to DODO is that the
complexity
of the analysis increases; f (n) is now a random variable whose rrcean
converges to f
and variance converges to zero. Mean square convergence, and consequently,
converge
in probability, are thus guaranteed.
81
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
where f * = 0.5 is the requested probability of 0 in the output, and f (n) _
~°~n~ with ca(n) being the number of 0's encoded up to time n. Thus f
(n)
converges to f * in the mean square sense, and in probability. D
When RV~~I~~,2 is generalized to the Huffman tree maintained in
RVA~I~m~2, the latter satisfies the sibling property even though its
structure may change at every time 'n'. As before, the proof of conver-
gence of RV~1SI_Em,2, relies on the convergence properties of the binary
input alphabet scheme, RVA~I~2~2. The convergence result is stated
and proved in Theorem ~. Crucial to the argument is the fact that
the estimated probability of 0 in the output can vary within the range
~1 -. fmax~ frrLax~.
Theorem 7 (Convergence of Process RV_A~I~m,2). Consider a
memoryless source whose alphabet is S = ~sl, . . . , sm~ and a code al-
phabet, ,A. _ ~0,1~. If the source sequence X = ~(1~, . . ., ~(M~, . . ., with
~(i~ E S, i = l, . . . , n, . . ., is encoded using the Process RV~4~i_Em,~ so
as to yield the output sequence ~J = y(1~, . . . , y~R~, . . ., such that y~z~
E .A.,
i = 1, . . . , R, . . ., then
lim E~ f (n)~ - f * , and (10)
n~ 00
lim Var~ f (n)~ - 0 , (11)
n-~ 00
~2
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
where f * = 0.5 is the requested probability of 0 in the output, and f (n) _
°nn~ with c0 (n) being the number of 0's encoded up to time n. Thus f
(n)
converges to f * in the mean square sense and in probability.
s Corollary 4. The Process RV~~i_E~.,,,2 guarantees Statistical Perfect
Secrecy.
RFA~I~m,2 : A Randomized Embodiment not Utilizing f (n)
The above randomized embodiment, RVA~i.Em,2, was developed by
comparing the invoked random number with ,f (n). Since the mean of
1o the random number is 0.5, and since convergence to a value f * = 0.5 is
intended, it is easy to modify RVA_H~m,,2 so that the random number
invoked is compared to the fired value 0.5, as opposed to the time-varying
value f (n) .
Indeed, this is achieved by modifying Process RV~~I_Em,~ by merely
15 changing the comparison:
if RNG~next~andommumber~ > f (n) then /~ Assignment 0-1
to:
if RNG~next~andommumber~ > 0.5 then ~~ Assignment 0-1.
Since the dependence of the branch assignment rule does not depend
~o on f (n) the convergence rate degrades. However, this modified process,
RF~,.~I~m,2, is computationally more efficient than RV~~I~m,~, since
it avoids the necessity to constantly update f (n).
83
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
The convergence and Statistical. Perfect Secrecy properties of the
RFA_H_Em,2 are easily proven.
The formal description of the processes RF_A~I~,~,2 and the
RFA_H~r,.t,2, and the corresponding proofs of their properties are omit-
ted to avoid repetition.
RR_ASI~~,,,2 : An Embodiment Utilizing an f (n)-based Ran-
dom Variable
'As observed, the above randomized embodiment, RV~1.SI_Er,L,2, was
developed by comparing the invoked random number, a, with f (n),
1o which comparison was avoided in RFC. II~m,2.
A new process, RR~~I~~,~, is now designed in which the random
number invoked, cx, is not compared to f (n) but to a second random
variable whose domain depends on f (n) .
Observe that the mean of the random number in ~0,1~ is 0.5. Since
convergence to a value f * = 0.~ is intended, RR.A H_Em,2 is developed
by forcing f (n) to move towards 0.5 based on how far it is from the fixed
point. But rather than achieve this in a deterministic manner, this is
done by invoking two random variables. The first, c~, as in RRA~i_Em,2
returns a value in the interval ~0,1~ . The second, c~~, is a random value
2o in the interval ~ f (n), 0.5~ (or ~0.5, f (n)~, depending on whether f (n)
is
greater than 0.5 or not) . The branch assignment is made to be either
0 - 1 or 1 - 0 randomly depending on where cx is with regard to rx~.
The rationale for this is exactly as in the case of RVA~I~m,2, except
~4
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
that the interval ~f (n), 0.5~ (or ~0.5, f (n)~) is amplified to ensure that
the
convergence is hastened, and the variations around the fixed point are
minimized. Figure 19 clarifies this.
These changes are achieved by modifying Process RVA~I~7,L,2 by
merely changing the comparisons
if RNG~next~andommumber~ > f (n)
then ~~ Assignment 0-1
to:
if RNG~next_random_number~ > RNG(next~andom..number ( f (n), 0.5)
1o a ~ then ~~ Assignment 0-1.
It should be observed that this process, RR~1~I~~,~, is computa-
tionally less e~.cient than RVA_H~r,z~2 because it requires two random
number invocations. However, the transient behavior is better, and the
variation around the fixed point is less than that of RVA_H~m,~.
The convergence and Statistical Perfect Secrecy properties of the
RRA~I~m,2 are easily proven.
The formal description of the processes RRA~I~m,~ and the
RRA_H_Dm,2, and the corresponding proofs of their properties are omit-
ted to avoid repetition. However, the experimental results involving these
2o processes will be included later.
Empirical Results
As before, the Processes RV~.4~i_E,~~~, RFA_H~m,2 and the
RRA~i_Em,~, and their respective decoding counterparts, have been rig-
~5
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
orously tested on files of the Calgary corpus and the Canterbury corpus.
The empirical results obtained for these runs for RV~4Si.Em,~ are shown
in Tables 8 and 9 respectively.
File Name fTAH ~VAHE d(~~ ~*)
bib 0.5348908850.499661985 1.14254E-07
bookl 0.5393829610.499823502 3.11515E-08
book2 0.5362874530.499586161 1.71263E-07
geo 0.5260899980.499553980 1.98933E-07
news 0.5347580200.500035467 1.25789E-09
objl 0.5278052170.498309924 2.85636E-06
obj2. 0.5279448090.499897080 1.05926E-08
paperl 0.5352243210.498786652 1.47221E-06
.
progc 0.5351044550.499165603 6.96219E-07
progl 0.5355981400.500651864 4.24927E-07
progp 0.5354033850.499089276 8.29419E-07
traps 0.5334958370.499352913 4.18722E-07
Average 1.77154E-07
Table 8: Empirical results obtained from RV_A~I~m,2 and TAH which
were tested files of the Calgary corpus, where f * = 0.5.
The second column, fTAH, corresponds to the estimated probability of
0 in the output obtained from the Traditional Adaptive Huffman scheme
(TAH). The third column, fRVAHE, contains the estimated probability
of 0 in the output obtained from running RVA~I~~,~~. The last column
corresponds to the distance between f * = 0.5 and f~YAHE, calculated as
in ( 14) .
to Observe the high accuracy of RV~.~I~m,~ for all the files. Although
86
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File Name fTAH fRVAHE d(~, ~*)
alice29.txt0.543888521 0.4998924671.15633E-08
asyoulik.txt0.538374097 0.4992238286.02443E-07
cp.html 0.537992949 0.5011003071.21068E-06
fields.c 0.534540728 0.4984575392.37919E-06
grammar.lsp0.537399558 0.5005662513.20641E-07
kennedy.xls0.535477484 0.5000157982.49567E-10
lcetl0.txt 0.538592652 0.5003119769.73291E-08
plrabnl2.txt0.542479709 0.5003259521.06245E-07
ptt5 0:736702657 0.5003393821.15180E-07
xargs.l 0.536812041 0.5001813403.28842E-08
Average 1.17159E-07
Table 9: Empirical results obtained from running RVA~-I~m,2 and TAH
on the files of the Canterbury corpus, where f * = 0.5.
the performance of RV~._H_Em,~ is comparable to that of D_ASI~m,2,
the average distance is less than 2.0E-07 for files of the Calgary corpus
and the Canterbury corpus. Note also that the largest value of the dis-
tance for the files of the Calgary corpus and the Canterbury corpus is
less than 1.5E-06.
A graphical analysis of the RV~4_H~,~,2 is presented by plotting the
value of d(.~', .~) obtained by processing the file bzb of the Calgary corpus.
The plot of the distance for this is depicted in Figure 20.
Note how the estimated probability of 0 converges very rapidly (al-
to though marginally slower than D~I~I~m,~ ) to 0.5. This is reflected, in
the fact that the distance remains arbitrarily close to 0 as n increases.
Similar results are available for the other files of the Calgary corpus and
~7
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
for files of the Canterbury corpus, and are omitted.
Encryption Processes Utilizing DDODE and
RDODE Solutions
This section describes how the deterministic and randomized embod-
s invents of DODE can be incorporated to yield various encryption strate-
gees.
As mentioned earlier, the notation used is that DDODE is a generic
name for any Deterministic encoding solution that yields Statistical Per-
fect Secrecy. Similarly, RDODE is a generic name for any Randomized
to encoding solution that yields Statistical Perfect Secrecy.
Elimination of Transient Behavior
There are two ways to eliminate the transient behavior of any DDODE
or RDODE process. These are explained below.
In the first method, the Sender and the Receiver both initialize n
15 to have a large value (typically about 1000) and also assign f (n) to be
0.~. Since the initial solution for f (n) is at the terminal fixed point, the
process is constrained by the updating rule to be arbitrarily close to it.
This eliminates the transient behavior.
In the second method, the input sequence x is padded in a prefix
2o manner with a simple key-related string. This string could be, in the
simplest case, a constant number of repetitions of the key itself. In more
elegant implementations, this prefix string could be multiple number of
88
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
predetermined variations of a string generated from the key. It should
be noted that since the Sender and the Receiver are aware of the key,
they are 'also aware of the prefix padded portion. This key-related prefix
is called the TransientPref-c~. The only requirement that is imposed on
s TransientPrefix is that it must be key related, known a priori to the
Sender and Receiver, and must be of sufficient length so that after it
is processed, the system enters into its steady state, or non-transient
behavior. Typically, a string of a few thousand bits guar antees this
phenomenon.
to The issue of eliminating the transient is solved as follows. The Sender
first pads X with TransientPrefi~, to generate a new message xTemp~
which is now processed by the encryption that utilizes either the process
DDODE or RDODE. Before transmitting its coded form, say, xTemp'
the Sender deletes TransientPrefix~, the prefix information in xTem '
P
15 which pertains to the encryption of TrrxnsientPrefi~, to yield the
resultant
string X,I,emp. xTemp does not have any transient characteristics - it
converges to 0.5 immediately. The Receiver, being aware of this padding
information and the process which yielded xTe~p, pads xTemp with
TransientPrefix~ to yield xZ,emp, whence the decryption follows. '
2o The formal procedure for achieving this is straightforward and omit-
ted in the interest of brevity. In future, whenever reference is made to
encryptions involving DDODE or RDODE, they refer to the versions in
which the transient behavior is eliminated.
89
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Serial use of DDODE or RDODE with Traditional Encryptions
Both DDODE and RDODE can be used to enhance encryption sys-
tems by utilizing them serially, in conjunction with any, already existing,
encryption mechanism.
Two encryption methods, DODE" and DODE+ respectively, based on
a solution to the DODE are presented. The solution to the. DODE can
be either deterministic.(DDODE) or randomized (RDODE).
1. DODE~ uses a DDODE or RDODE process as an encoding mecha
nism in conjunction with army encryption, say ENCNonPreserve, that
1o does not preserve the input-output random properties. Observe that
without a key specifying mechanism, both DDODE and RDODE
can be used~as encoding processes that guarantee Statistical Perfect
Secrecy. If this output is subsequently. encrypted, the system can-
not be broken by statistical methods because DDODE and RDODE
annihilate the statistical information found in the original plaintext,
and simultaneously provides Stealth. However, the output of the se-
rial pair will depend on the stochastic properties of ENC'~ronpres~rve.
E'NG'NonPreserve, the encryption operating in tandem with DDODE
or RDODE can be any public key cryptosystem or private key cryp-
2o tosystem (see Stinson ( Cryptography : Theory and Practice, CRC
Press, (1995))).
2. DODE+ uses a DDODE or RDODE process as an encoding mech-
anism in conjunction with any encryption that preserves the input-
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
output random properties, say, EN~rpreserve~ TYPically, any "good"
substitution or permutation encryption achieves this (one such str aight-
forward process for ENC'p,.eserve is given in Appendix C~ . From the
earlier discussions it is clear that without a key specifying mecha-
s nism, both DDODE and RDODE can be used as encoding processes
that guarantee Statistical Perfect Secrecy. If this output is subse-
quently encrypted by ENCP,.eserve, the system cannot be broken by
statistical methods because DDODE and RDODE annihilate the
statistical information found in the original plaintext. Observe that
to since ENCpr~serve Preserves the input-output random properties,
one can expect the output of the tandem pair to also guarantee Sta
tistical Perfect Secrecy. Thus, breaking DODE+ using statistical
based cryptanalytic methods is impossible, and necessarily requires
the exhaustive search of the entire key space. DODE+ also provides
m Stealth.
RDODE* : Encryption Utilizing RDODE
This section describes how RDODE, any randomized embodiment for
RODE, can be utilized for encryption. The encryption is obtained by
incorporating into RDODE a key specifying mechanism.
2o Unlike DODE" and DODE+, in which the two processes of com-
pression (expansion or data length specification in the case of general
Oommen-Ruedcz Trees) and encryption operate serially on each other, in
the case of RDODE*, it is not possible to decompose RDODE* into the
91
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
two composite mutually exclusive processes. They augment each other
in a non-decomposable manner.
RDODE* uses a private key. This keys is used to specify ~3, the initial
seed used by the Random Number Generator invoked by the specific
randomized solution, RDODE. The mapping from the key to the seed is
now described.
Formally, the key, 1C, is a sequence of symbols, 1~(1~ . . . l~(T~, where
di, 1~(i~ E x3 = ~bl, . . . , bt~. The key uniquely specifies the initial seed
used by the pseudo-random generator, by means of a transformation of 1C
1o into an integer. There are numerous ways by which this transformation
can be defined. First of all, any key, 1C, of length T can clearly be
transformed into an integer in the range (0, . . . , tT -1 ~ . Furthermore,
since
the symbols of the key can be permuted, there are numerous possible
transformations that such a key-to-integer mapping can be specified. One
such transformation procedure is proposed below.
Consider a key, IC = 1~(1~ . . . k(T~ (where 1~(i~ E ,~), which is to be
transformed into a seed, /3. First, 1C is transformed into an sequence of
integers, where each symbol of ,t3 is a unique integer between 0 and t -1.
This sequence is of the form 1C' - k'(1~ . . .1~'(T~, such that 'di, 1~'(i~ E
~0, . . . , t - 1~. After this transformation, the seed6, ~, is calculated as
SThe key alphabet can contain letters, numbers, special symbols (such as '*',
')',
'#'), the blank space, etc. In a developed prototype, the key alphabet
consists of
~a, . . . , z~ U ~A, . . . , Z~ U f 0, . . . , 9~ U space, '.'}.
sIt should be noted that this conversion yields the seed as an integer number.
If
the system requires a binary seed, the latter can be trivially obtained from
the binary
expansion of ,~.
92
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
follows:
T-1
,Q = ~ l~'~i -I-1~t2 . (12)
Z=O
s It can be trivially seen that for each transformed key, 1~'~l~ . . .1~'~T~,
there is a unique integer, ,~3 in the set ~0, . . . , tT - 1~, and hence if
~ Amax ~ Statistical Perfect Secrecy can be achieved, where Zmax is the
maximum possible seed of the pseudo-random number generator. Ob-
serve too that both the Sender and Receiver must have the same initial
1o seed, ~3, so as to recover the original source sequence
After invoking the RNG using ~3, the value of the seed ~, is updated.
This implies that the labeling branch assignment to yield the nth bit of the
output, is determined by the current pseudo-random number generated
using the current value of ,Q. Thus, same sequences of pseudo-random
15 numbers are utilized by the encryption and decryption mechanisms.
In any practical implementation, the maximum number that a seed
can take depends on the precision of the system being used.. When ,Q >
~max~ where Z~ax is the maximum seed that the system supports, /3
can be decomposed into J seeds, Z1, . . . , ZJ, so as to yield J pseudo-
2o random numbers. The actual. pseudo-random number, (say c~), to be
utilized in the instantiation of RDODE is obtained by concatenating the
J random numbers generated at time n, each of which 'invokes a specific
93
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
instantiation of the system's RNG. Thus, if the encryption guarantees
192-bit security, it would imply the invocation of four 48-bit pseudo-
random numbers, each being a specific instantiation of the system's RNG.
A small example will help to clarify this procedure.
Example 6. Suppose that a message is to be encrypted using the key
1C = "T he Moon" , which is composed of symbols drawn from the alpha-
bet Z3 that contains 64 symbols: decimal digits, the blank space, upper
case letters, lower case letters, and '.'. The transformation of 1C into ICS
is done as follows:
~ the digits from 0 to 9 are mapped to the integers from 0 to 9,
~ The blank space is mapped to 10,
~ the letters from A to 2 are mapped to the integers from 11 to 36,
~ the letters from a to z are mapped to the integers from 3'l to 62,
and
~ the period, '.', is mapped to 63.
Therefore,1C' =30 44 4110 23 515150. There are 648 = 281, 4'l4, 976, 710, 656
possible seeds, which are contained in the set ~0, . . . , 648 - l~.
The seed, ,Q, is calculated from 1C as follows:
,Q= (30)64°+(44)64~--~(41)64~+(10)643+(23)644+(51)645+(51)646
+(50)647
= 223, 462,168, 369, 950 .
94
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Observe that such a key-to-seed transformation is ideal for an RNG
implementation working with 4~-bit accuracy, as in the Java program-
ming language (jdk l.xx). In such a case, a key of length eight chosen
from the 64-symbol key space leads to a seed which is uniform in the
seed space.
We conclude this section by noting that by virtue of the previous
results, every instantiation of RDODE* guarantees Statistical Perfect
Secrecy. Thus, breaking RDODE* using statistical-based cryptanalytic
methods is impossible, and necessarily requires the exhaustive search of
1o the entire key space.
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Testing of Encryptions Utilizing RV~.~i~m,2 and RRA~I~m,2
To demonstrate the power of the encryption in which the transient
behaviour is eliminated, and the seed is key-dependent, RV~ ~I~m,2
and RR~ ~i~,,.,,,2 have been incorporated into a fully operational 48-
bit prototype cryptosystem. Both of these been rigouously tested for a
variety of tests, and these results are cataloged below. The key-to-seed
specifying mechanism is exactly as explained in the above example.
The results for testing RVA_H~m~~ on the Calgary Corpus and Can-
terbury are given in Tables 10 and 11 respectively. Observe that the value
to of distance as computed by (14) is arbitrarily close to zero in every case.
Similar results for RR_A~I~m~2 on the Calgary Corpus and Canterbury
Corpus are given in Tables 12 and 13 respectively.
The variation of the distance as a function of the encrypted stream
has also been plotted for various files. Figure 21 graphically plots the
average distance obtained after encrypting file bib (from the . Calgary
Corpus) using the Process RV.A~I~m~2 as the kernel. The similar figure
in which Process RR~~I~m,2 is used as the kernel is found in Figure
22. Observe that the graphs attains their terminal value close to zero
right from the outset - without any transient characteristics.
9G
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File Name fTAH fROHA l d(.~, .~*)
bib 0.5348908850.4989260521.15336E-06
bookl 0.5393829610.5004252191.80811E-07
book2 0.5362874530.5003494151.22091E-07
geo 0.5260899980.5013311831.77205E-06
news 0.5347580200.4997122128.28219E-08
objl 0.5278052170.4997762 5.00864E-08
obj2 0.52'79448090.4995214202.29039E-07
paperl 0.5352243210.5006327284.00345E-07
progc 0.5351044550.4999163217.00218E-09
progl 0.5355981400.4992'787585.20190E-07
progp 0.5354033850.4999466692.84420E-09
trans 0.53349583'70.4997843044.65248E-08
Average 2.?40'79E-07
Table 10: Empirical results obtained after encrypting files from the Calgary
Corpus using the Process RV~.~i~m~2 as the kernel. The results are also
compared with the Traditional Adaptive Huffman (TAH) scheme.
97
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File Name .~ .~
J TAH ,/ ROHA d (.~, .~
alice29.txt 0.5438885210.4993150304.69184E-07
asyoulik.txt0.5383740970.5004837732.34036E-07
cp.html 0.5379929490.4986940991.70538E-06
fields.c 0.5345407280.5014904682.22149E-06
grammar.lsp 0.5373995580.5056355552.22149E-06
kennedy.xls 0.5354774840.5005053923.17595E-05
lcetl0.txt 0.5385926520.4999137522.55421E-07
plrabnl2.txt0.5424797090.4999329337.43872E-09
ptt5 0.7367026570.5002387385.69958E-08
xargs.l 0.5368120410.5052135282.71809E-05
Average ~ 1.16081E-05
Table 11: Empirical results obtained after encrypting files from the Can-
terbury Corpus using the Process RV~~I_Em,2 as the kernel. The re-
sults are also compared with the Traditional Adaptive Huffman (TAH~
scheme.
Output Markovian Modeling and Independence Analysis
The theoretical analysis of convergence and the empirical results dis-
cussed for RV~~I~m,~ were done by merely considering the probabil-
ities of occurrence of the output symbols. The question of the depen-
dencies of the output symbols is now studied using a Markovian analysis
and a ~~ hypothesis testing analysis. To achieve this goal, the possibility
of the output sequence obtained by RV~.~I~m,~ being a higher-order
Markov model is analyzed. This model, which considers conditional prob-
abilities of a symbol given the occurrence of the k previous symbols, is
1o called a kt~-order model.
Consider the first-order model with the following conditional probabil-
98
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File Name fTAH fRROHA d(.~, J2*)
bib 0.5348908850.4987309441.61050E-06
bookl 0.5393829610.4994405913.12938E-07
book2 0.5362874530.4995936211.65144E-07
geo 0.5260899980.5003807071.44938E-07
news 0.5347580200.4997669325.43207E-08
ob j 1 0.5278052170.5004167311.73665E-07
obj2 ~ 0.5279448090.4993760453.89320E-07
paperl 0.5352243210.4989876361.02488E-06
'
progc 0.5351044550.50075?8915.74399E-07
progl 0.5355981400.4999580841.75695E-09
progp 0.5354033850.5001764023.11177E-08
trans 0.5334958370.4988184451.39607E-06
~
Average ~ 3.5628E-07
Table 12: Empirical results obtained after encrypting files from the Calgary
Corpus using the Process RR-A~I~m,~ as the kernel. The results are
also compared with the Traditional Adaptive Huffman (TAH) scheme.
ities, fo~o(n) and fl~o(n) (where the latter is equal to 1- fo~o(n)), fo~l(n),
and fl~l(n) (which in turn, is 1 - fo~1(n)). These probabilities can also
be expressed in terms of a 2 x 2 matrix form, the underlying transition
matrix. Since the asymptotic probabilities are (0.5, 0.5~, it is easy to see
b 1-b
that this matrix has to be symmetric of the form , where
s 1-b b
& = 0.5 is the case when there is no Markovian dependence. The value
of b is estimated from the output sequence in a straightforward manner.
In order to analyze the independence of the symbols in the output,
RV~l~i~m~~ has been tested on files of the Calgary corpus and the
99
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File Name fTAH
1 fRR~HA I d(.1~, .~~)
alice29.txt0.543888521 0.4996184791.45558E-07
asyoulik.txt0.538374097 0.499708422~ 8.50177E-08
cp.html 0.537992949 0.5000038071.44932E-11
fields.c 0.534540728 0.5029289438.57871E-06
grammar.lsp0.537399558 0.4994337483.20641E-07
kennedy.xls0.535477484 0.4995596891.93874E-07
lcetl0.txt 0.538592652 0.499937297.3.93167E-09
plrabnl2.txt0.542479709 0.5000825436.81335E-09
ptt5 0.736702657 0.5003920451.53699E-07
xargs.l 0.536812041 0.5044881682.01437E-05
Average 1.92746E-07
Table 13:~ Empirical results obtained after encrypting files from the Can-
terbury Corpus using the Process RR-A~I~m,~ as the kernel. The re-
sults are also compared with the Traditional Adaptive Huffman (TAH)
scheme.
Canterbury corpus. The requested probability of 0 in the output is f * -
0.5. The estimated probability of 0 given 0 in a file of R bits is obtained
as follows : fo~o = ~~o~R~~, where co~o(R) is the number of occurrences of
the sequence '00' in y, and c0 (R) is the number of 0's in y. Analogously,
fl~l is calculated.
Assuming that y is a sequence of random variables, the analysis of
independence in the output is done by using a Chi-square hypothesis test
(see Snedecor et al. (Statistical Methods, Iowa State University Press,
8th edition, . ( 1989) ) ) . The empirical results obtained from executing
1o RV.A~I~m,~ on files of the Calgary corpus and the Canterbury corpus
are shown in Tables 14 and 15 respectively.
100
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File namef~ 2 fl ~2 Decision (98%
bib . 0.4991533 0.00000726Indep.
bookl 0.4997611 0.00000166Indep.
book2 0.4995139 0.0000019.6Indep.
geo 0.4999662 0.00000096Indep.
news 0.4992'1390.00000423Indep.
objl 0.5008566 0.00000608Indep.
obj2 0.500571'70.00000315Indep.
paperl 0.4995268 0.00000367Indep.
progc 0.5009482 0.00001100Indep.
progl 0.4977808 0.00005315Indep.
progp 0.4994945 0.00002204Indep.
traps 0.4999502 0.00000060Indep.
Table 14: Results of the Chi-square test of independence in the output of
the encryption that uses RVA~I~~,,2 as the kernel. The encryption was
tested on files of the Calgary corpus with f * = 0.5.
The second column represents, the average between fo~o and f1~1 which
are calculated as explained above. The third column contains the value
of the Chi-square statistic for fai~a~, where ai, a~ are either 0 or l, and
the
number of degrees of freedom is unity. The last column stands for the
decision of the testing based on a 98°~o confidence level. Observe that
for
all the files of the Calgary corpus and the Canterbury corpus the output
random variables are independent. This implies that besides converging
to the value 0.5 in the mean square sense, the output of RV~I~I~m,~ is
also statistically independent as per the 98% confidence level.
to Similar results are also .available for higher-order Markovian models
101
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File name f~ 2 fl~l~~ Decision (98%
)
alice29.txt 0.50016500.00000032 Indep.
asyoulik.txt0.50049830.00001600 Indep.
cp.html 0.50080970.00001010 Indep.
fields.c 0.50181630.00001105 Indep.
grammar.lsp 0.50228180.00008135 Indep.
kennedy.xls 0.49989540.00000009 Indep.
lcetl0.txt 0.50066210.00000154 Indep.
plrabnl2.txt0.49993150.00000013 Indep.
ptt5 ' 0.49937040.00000320 Indep.
xargs.l 0.49156720.00057094 Indep.
Table 15: Results of the Chi-square test of independence in the output of
the encryption that uses RVA~I Em,~ as the kernel. The encryption was
tested on files of the Canterbury corpus with f * = 0.5.
up to level five, in which the output of RVA_H_E,~ ~ proves to be also
statistically independent as per the 98°~o confidence level.
The FIPS 140-1 Statistical Tests of Randomness of RDODE*
The results of the previous two subsections demonstrate the power of
the encryptions for Statistical Perfect Secrecy (convergence to f * = 0.5)
and the Markovian independence. However, it is well known that a good
cryptosystem must endure even most stingent statistical tests. One such
suite of tests are those recommended by the standard FIPS 140-1 (see
Menezes et al. (Handbool~ of Applied C'ry~tography, CRC Press, (1996))
1o pp. 181-183). These tests include the frequency test, the poker test, the
runs test, and the long runs test. As suggested these tests have been run
102
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
for encrypted strings of lengh 20000 bits with the corresponding statistics
for passing the tests are clearly specified. The empirical results obtained
after encrypting the files of the Calgary Corpus and the Canterbury
Corpus using RVA~i.~m, 2 as the kernel are cataloged in Tables 16, 17,
18, 19, 20, 21, 22, 23, 24, and 25, respectively. Notice that the encryption
passes all the tests. Similar results are available for the encryption which
uses RR_A~I~m, 2 as the kernel.
103
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File namenlmin ~ ~1 nlmax
~ I
bib 9,654 10,007 10,646
bookl 9,654 9,9'74 10,646
book2 9,654 9,991 10,646
geo 9,654 10,009 10,646
news 9,654 10,000 10,646
objl 9,654 10,053 10,646
obj2 9,654 9,866 10,646
paperl 9,654 9,958 10,646
progc 9,654 10,006 10,646
progl 9,654 10,072 10,646
progp 9,654 9,9?3 10,646
trans 9,654 10,046 10,646
Table 16: Results of the Monobit test in the output of the encryption that
uses RV~1.~I~m~2 as the kernel. The encryption was tested on files of
the Calgary corpus.
104
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File named nlmin C n1 nlmax
C
alice29.txt9,654 ~ 10,00810,646
asyoulik.txt9,654 10,029 10,646
cp.html 9,654 9,955 10,646
fields.c 9,654 9,974 10,646
kennedy.xls9,654 9,983 10,646
lcetl0.txt 9,654 10,131 10,646
plrabnl2.txt9,654 9,926 10,646
ptt5 9,654 10,13'710,646
sum 9,654 10,046 10,646
xargs.l 9,654 9,989 10,646
Table 17: Results of the Monobit test in the output of the encryption that
uses RV~.~I~m,2 as the kernel. The encryption v~ras tested on files of
the Canterbury corpus. .
10~
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
~ File ~3min C ~3 X3max
name ~
bib 1.03 6.25 57.4
bookl 1.03 28.74 57.4
book2 1.03 10.33 57.4
geo 1.03 13.50 57.4
news 1.03 18.65 57.4
objl 1.03 9.28 57.4
~
obj2 2.03 11.00 57.4
paperl 1.03 21.72 57.4
progc 1.03 11.15 57.4
progl 1.03 13.67 5'7.4
progp 1.03 7.71 57.4
traps 1.03 14.30 5'l.4
Table .18: Results of the Poker test (when m = 4) in the output of the
encryption that uses RV~.~LE.,,.z,~ as the kernel. The encryption was
tested on files of the Calgary corpus.
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File name -x3min ~ ~3 ~~3l~n.ax
C
alice29.txt1.03 12.34 57.4
asyoulik.txt1.03 18.19 57.4
cp.html 1.03 8.85 57.4
fields.c 1.03 17.81 57.4
kennedy.xls1.03 14.31 57.4
lcetl0.txt 1.03 12.16 57.4
plrabnl2.txt1.03 23.69 57.4
ptt5 1.03 11.45 57.4
sum 1.03 10.44 57.4
xargs.l 1.03 16.25 57.4
Table 19: Results of the Poker test (when m = 4) in the output of the
encryption that uses RV.~~~m,2 as the kernel. The encryption was
tested on files of the Canterbury corpus.
107
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File B2/G ~ Gi Bz < Bi/Gzmax
name
run ~ in
1 2, 267 _ 2, 445 2, 733
2,
482
2 1, 079 l, 1, 214 1, 421
241
3 502 612 672 748
bib 4 223 293 ~ 7 402
5 90 173 146 223
6 90 146 164 223
1 2, 267 2, 2, 539 2, 733
540
2 1, 079 l, 1, 336 l, 421
305
3 502 628 574 748
bookl 4 223 264 295 402
5 90 138 150 223.
6 90 143 149 223
1 2, 267 2, 2, 532 2, 733
463
2 1, 079 1, 1,184 1, 421
266
3 502 627 636 748
book2 4 223 328 322 402
5 90 165 169 223
6 90 170 170 223
1 2, 267 2, 2, 517 2, 733
494
2 l, 079 1, 1, 251 1, 421
226
3 502 660 613 748
geo 4 ~ 223 320 289 402
.
5 90 158 157 223
6 90 152 161 223
1 2, 267 2, 2, 579 2, 733
532
2 1, 079 1, 1, 261 1, 421
255
3 502 643 610 748
news 4 223 319 293 402
5 90 156 138 223
6 90 176 154 223
1 2, 267 2, 2, 510 2, 733
534
2 1, 079 1, ' 1, 1, 421
257 230 .
3 502 620 637 748
objl
4 223 313 344 402
5 90 149 158 223
6 90 156 168 223
Table 20: Results of the Runs test in the output of the encryption that
uses RV~_H~~,2 as the kernel. The encryption was tested on files of
the Calgary corpus.
108
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File run B2/Gzmin~ ~i Bi Bi~Gimax
name ~
1 2,267 2,406 2,494 2,733
2 1,079 1,277 1,241 1,421
3 502 640 618 748
obj2 4 223 313 287 402
5 90 143 164 223
6 90 177 135 223
1 2, 267 2, 2, 2, 733
427 476
2 1, 079 1, l, 1, 421
328 223
3 502 560 611 748
paperl 4 223 306 335 402
5 90 161 144 223
6 90 161 151 223
1 2, 267 2, 2, 2, 733
540 516
2 1, 079 1, 1, 1, 421
250 268
3 502 604 618 748
progc 4 223 300 292 402
5 90 152 167 223
6 90 159 169 223
1 2, 267 2, 2, 2, 733
550 494
2 l, 079 1, 1, . 1, 421
202 259
~
3 502 660 586 748
progl 4 223 287 333 402
5 90 146 176 223
6 90 147 142 223
1 2,267 2,582 2,576 2,733
2 1,079 1,291 1,288 1,421
3 502 580 601 748
progp 4 223 323 311 402
5 90 152 154 223
6 90 147 131 223
1 2, 267 2, 2, 2, 733
457 462
2 1, 079 1, 1, 1, 421
228 245
3 502 642 587 748
trans 4 223 316 312 402
5 90 146 187 ,223
6 90. 177 161 223
Table 21: Results of the Runs test in the output of the encryption that uses
RVA~i Em,2 as the kernel. The encryption was tested on files of the Calgary
cor-
pus.
109
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File namerun Bz/Gzmi < Gi Bi < BZ/Gimax
1 2, 267 2, 2, 502 2, 733
529
2 1, 079 l, 1, 292 l, 421
238
3 502 632 631 748
alice29.txt4 223 319 308 402
5 90 173 155 223
6 90 158 170 223
1 2, 267 2, 2, 467 2, 733
473
2 1, 079 1, 1, 268 1, 421
243 .
3 502 617 609 748
asyoulik.txt4 223 332 296 402
5 90 146 151 223
6 90 149 151 223
1 2, 267 2, 2, 604 2, 733
579
2 l, 079 1, 1, 266 1, 421
291
3 502 596 644 748
cp.html 4 223 294 274 402
- 5 90 155 146 223
6 90. 147 133 223
1 2, 267 2, 2, 593 2, 733
542
2 1, 079 1, 1, 232 l, 421
314
3 502 588 621 748
fields.c 4 223 307 311 402
5 90 161 170 223
6 90 161 162 223
1 2, 267 2, 2, 559 2, 733
532
2 1, 079 1, 1, 212 l, 421
259
3 502 626 624 748
kennedy.xls4 223 294 351 402
5 90 174 144 223
6 90 177 169 223
Table 22: Results of the Runs test in the output of the encryption that uses
RV~~-I~~,,2 as the kernel. The encryption was tested on files of the
Canterbury
corpus.
110
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File namerun Bi/G;min~ Gz Bi ) Bi/Gim~
C
1 2, 267 2, 513 2, 2, 733
443
2 1, 079 1,196 l, 1, 421
224
3 502 635 610 748
lcetl0.txt4 223 314 340 402
5 90 136 157 223
6 90 170 132 223
1 2,267 2,467 2,526 2,733
2 1, 079 1, 294 1, 1, 421
261
plrabnl2.txt3 502 601 619 748
4 223 316 296 402
5 90 161 140 223
6 90 170 150 223
1 2, 267 2, 513 2, 2, 733
468
2 1, 079 1, 239 1, 1, 421
230
3 502 653 619 748
ptt5 4 223 281 331 402
5 90 148 172 223
6 90 155 145 223
1 2, 267 2, 589.2, 2, 733
522
2 1, 079 1, 257 l, 1, 421
286
3 502 586 626 748
sum 4 223 298 308 402
5 90 150 149 223
6 90 159 158 223
1 2, 267 2, 502 2, 2, 733
508
2 1, 079 1, 241 1, 1, 421
264
xargs.l 3 502 654 629 748
4 223 301 304 402
5 90 152 149 223
6 90 159 153 223
Table 23: Results of the Runs test in the output of the encryption that uses
RV~.~I~r,.t 2 as the kernel. The encryption was tested on files of the
Canterbury
corpus.
111
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Fife namelV.~ax. run Runs > 34
length ~
bib 13 D
bookl . 12 . 0
book2 14 0
geo 14 0
neWS ~.6 0
objl. ~ 7.4 0
obj2 13 0
paperl ~.5 0
progc ~ 7 0
progl ~6 0
progp 17 0
trans 7.4 0 '
Table 24: Results of the Long Runs test in the output of the encryption
that uses RVA_H Em,~ as the kernel. The encryption was tested on files
off' the Calgary corpus.
~.z2
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File name Max. run lengthRuns > 34
alice29.txt15 0
asyoulik.txt16 0
cp.html 13 0
fields.c 17 0
kennedy.xls14 0
lcetl0.txt 17 0
plrabnl2.txt14 0
ptt~ 14 0
sum 13 0
xargs.1 15 0
Table 25: Results of the Long Runs test in the output of the encryption
that uses RVA~I_Em,2 as the kernel. The encryption was tested on files
of the Canterbury corpus.
113
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Statistical Tests of I~ey-Input-Output Dependency
Apart from 'the FIPS 140-1 tests described above, the encryption
which uses RVA~I~m,2 has also been rigorously tested to see how en-
crypted output varies with the keys and the input. In particular, the
probability of observing changes in the output when the key changes by
a single bit has been computed. This is tabulated in Table 26. Observe
that as desired, the value is, close to 0.5 for all the files of the Calgary
Corpus. Similarly, the probability of changing subsequent output bits
after a given input symbol has been changed by one bit has also been
to computed. This value is also close to the desired value of 0.5 in almost
czll
files. The results are tabulated in Table 27. Similar results are available
for files of the Canterbury Corpus also.
114
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
bile namep
bib . 0.499610
bookl 0.499955
book2 0.500052
geo 0.499907
news 0.499842
ob j 1 0.499463
ob j 2 0.500309
paperl 0.500962
progc 0.498403
progl 0.500092
progp 0.499961
trans 0.499244
Table 26: Statistical independence test between the key and the output
performed by modifying the key in one single bit on files of the Calgary
corpus. p is the estimated prob. of change.
115
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
File nam p
~
bib 0.492451
bookl 0.467442
book2 0.501907
geo 0.500798
news 0.500089
ob j 1 0.477444
ob j 2 0.496427
paperl 0.481311
progc 0.484270
progl 0.471639
progp 0.490529
traps 0.491802
Table 27: Statistical independence test between the input and the output
performed by modifying one single bit in the input on files of the Calgary
corpus. p is the estimated prob. of change.
ms
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Applications of DDODE and RDODE
With regard to applications, both DDODE and RDODE (and their
respective instantiations~ can be used as compressions~encodings in their
own right. They can thus be used in both data transmission, data storage
and in the recording of data in magnetic media. However, the major
applications are those that arise from their cryptographic capabilities
and include:
~ Traffic on the Internet
~ E-commerce~e-banking
~ E=mail
~ Video conferencing
~ Secure wired or wireless communications
~ Network security. To clarify this, let us assume that the files stored
in a network are saved using one of the schemes advocated by this
invention. In such a case, even if a hacker succeeds in breaking the
firewall and enters the system, he will not be able to "read" the files
he accesses, because they will effectively be stored as random noise.
The advantages of this are invaluable.
Appart from the above, the application of DDODE and RDODE in
2o steganography is emphasized.
117
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Steganography is the ancient art of hiding information, which dates
back from around 440 B.C (see Katzenbeisser et al. (Information Hiding
Techniques for S'teganography and Digital Watermarking, Artech House,
(2000) ) ) . One of the most common steganographic techniques consists
of hiding information in images. To experimentally demonstrate the
power of RV~._H~,~,2, the latter has been incorporated into a stegano-
graphic application by modifying 256-gray scale images with the output
of RDODE*. By virtue of the Statistical Perfect Secrecy property of
RV~~-I~m,2, its use in steganography is unique.
1o Rather than use a sophisticated scheme, to demonstrate a prima facie
case, the Least Significant Bit (LSB) substitution approach for image
"carriers" has been used. This technique consists of replacing the least
significant bit of the j~h pixel (or, to be more specific, the byte that
represents it) by the l~t~ bit of the output sequence. The set of indices,
~ j1, . . . , jR~, where R is the size of the output (R G ~I~, and ~I~ is the
size of the carrier image), can be chosen in various ways, including the,
so called, pseudo-random permutations. Details of this techniques can
be found in I~atzenbeisser et al. (Information Hiding Techniques for
Steganography and Digital Watermarking, Artech House, (2000) ) .
2o Although this is a fairly simplistic approach to applying RV~_H_Em,2
in steganography, it has been deliberately used so as to demonstrate its
power. An example will clarify the issue. In an experimental prototype,
the well known "Lena" image has been used as the carrier file, which
118
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
carries the output of RV_A~I_Em,2. The original Lena image and the
image resulting from embedding the output obtained from encrypting
the file fields. c of the Canterbury corpus are shown in Figure 23. Apart
from the two images being visually similar, their respective histograms
pass the similarity test with a very high level of confidence. Such results
are typical.
Observe that once the output of RVA~I-Em,2 has been obtained, it
can be easily embedded in the carrier by the most sophisticated steganog-
raphy tools (see Information Hiding Techniques for S'teganogra~hy and
.Digital Watermarl~ing, Artech House, (2000)) currently available, and
need not be embedded by the simplistic LSB pseudo-random permuta-
Lion scheme described above.
The present invention has been described herein with regard to pre-
ferred embodiments. However, it will be obvious to persons skilled in the
art that a number of variations and modifications can be made without
departing from the scope of the invention as described herein.
119
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
References
(1 ~ R. Arnold and T. Bell. A Corpus for the Evaluation of Lossless
Compression Algorithms. Proceedings of the IEEE Data Compres-
sion Conference pages 201-210, Los Alamitos, CA, 1997. IEEE
Computer Society Press.
(2 ~ R. Gallager. Variations on a Theme by Huffman. IEEE Transac-
tions on Informe~tion Theory, 24(6):668-6'74, 1978.
(3 ~ D. Hankerson, G. Harris, and P. Johnson Jr. Introduction to In-
formation Theory and Data Compression. CRC Press, 1998.
(4 ~ D.A. Huffman. A Method for the Construction of Minimum Re-
dundancy Codes. Proceedings of IRE, 40(9):1098-1101, 1952.
(5 ~ D. Knuth. Dynamic Huffman Coding. Journal of Algorithms,
6:163-180, 1985.
(6 ~ S. Lakshmivarahan. Learning Algorithms Theory and Applications.
Springer-Verlag, New York, 1981.
(? ~ A. Menezes, P. van Oorschot, and S. Vanstone. Handbool~ of Ap-
plied Cryptography. CRC Press, 1996.
(8 ~ K. Narendra and M. Thathachar. Learning Automata. An Intro-
duction. Prentice Hall, 1989.
120
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
(9 ~ K. Sayood. Introduction to Data Compression. Morgan Kaufmann,
2nd. edition, 2000.
(10 ~ G. Snedecor and W. Cochran. Statitical Methods. Iowa State
University Press, 8th edition, 1989.
s (11 J C. E. Shannon. Communication Theory of Secrecy Systems. Bell
System Technical Journal, 28:656-?15, 1949.
(12 j W. Stallings. Cryptography ~ Networl~ ,Security: Principles ~
Practice. Prentice Hall, 1998.
(13 ~ D. R. Stinson. Cyptography : Theory and Practice. CRC 'Press,
1995.
(14 ~ I. Witten, A. Moffat, and T. Bell. Managing Gigabytes: Compress-
ing and Indexing Documents and Images. Morgan Kaufmann, 2nd.
edition, 1999.
(15 ~ S. Katzenbeisser and F. Peticolas. Information Hiding Techn2q~ces
for Steganography and Digital Watermarl~ing. Artech House, 2000.
(16 ~ J. Vitter. Design and Analysis of Dynamic Huffman Codes. .Iour-
nal of the ACM, 34(4):825-845, 1987.
121
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Appendix A
Formal Statement of the RODE Open Problem
Assume that a code alphabet ,A _ ~al, . . . , aT~ is given, and that the
user' specifies the desired output probabilities (or frequencies) of each
rx~ E .,4 in the compressed file by .~* _ ~ f~ , . . . , fr ~. Such a
rendering
will be called an "entropy optimal" rendering. On the other hand, the
user also simultaneously requires optimal, or even sub-optimal lossless
data compression. Thus, if the decompression process is invoked on a
compressed a file, the file recovered must be exactly the same as the
original uncompressed file.
As stated in Hankerson et al. (Introduction to Informcztior~ Theory
cznd Data Compression, CRC Press, (1990 pp.'75-79), the Distribution
Optimizing Data Compression (DODO) problem? can be more formally
written as follows:
Problem 1. Consider the source alphabet, S = ~sl, . . . , s,~~, with prob-
abilities of occurrence, P = (p1, . . . , p,,.,.t~, where the input sequence
is
X = ~~1~ . . . ~(M~, the code alphabet, ,A. _ ~al, . . . , ar~, and the
optimal
frequencies, ~'* _ ~ f 1, . . . , fT ~, of each cc~ , j = 1, . . . , r,
required in the
output sequence. The output is to be a sequence, y = y(l~ . . . y~R~, whose
2o probabilities are ~ _ ~ fl, . . . , fr~, generated by the encoding scheme
~ : ~S ~ C = ~wl, . . . , wm~, where .~2 is the length of wi, such that:
?In general, outside the context of compression, this problem is referred to
as the Distribution
Optimizing Data Encoding (DODE) problem.
122
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
(i) C is prefix,
(ii) the average code word length of ~,
m
pi~i ~ (13)
i=1
is minimal, . and
(iii) the distance
r
d(~~ ~) _ ~ ~fj - f~ ~~ (14)
j=1
is minimal, where O > l is a real number.
1o The Distribution Optimization Data Oompression (DODO) problem
involves developing an encoding scheme in which d(.~, .~*) is arbitrarily
close to zero.
Given the source alphabet, the probabilities of occurrence of the source
symbols, and the encoding scheme, each f j can be calculated without
encoding x, as stated in the following formula for j = 1, . . . , r
m m
~i=1 ~jipi _ -1
fj - m
~i=1 pi~i - .~ ujipi ~ (
i=1
123
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
where aj occurs u~2 tunes in zuz, for i = 1, . . . , m and j = 1, . . . , r.
It is interesting to note that the problem is intrinsically difficult be-
cause the data compression requirements and the output probability re-
quirements can be contradictory. Informally speaking, if the occurrence
s of '0' is significantly lower than the occurrence of 'l' in the uncompressed
file, designing a data compression method which compresses the file and
which simultaneously increases the proportion of '0's to '1's is far from
trivial.
The importance of the problem is reflected in the following paragraph
1o as originally stated in Hankerson et al. (Introduction to Information
Theory and Data Compression, GRG Press, (1998)):
" It would be nice to have a slick algorithm to solve Problem 1, es-
pecially in the case r = 2, when the output will not vary Wlth different
definitions of d(.~',.~*). Also, the case r = 2 is distinguished by the fact
15 that binary channels are in widespread use in the real world.
We have no such algorithm! Perhaps someone reading this will supply
one some day..."
124
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Appendix B
Proof of Theorems
Theorem 1 (Convergence of Process D_S~I~2,2). Consider a sta-
tionary, memoryless source with alphabet S = ~0,1~, whose proba-
bilities are P - (~,1 - p~, where p > 0.~, and the code alphabet,
,A _ ~0,1~. If the source sequence X = ~(1~, . . . , ~(n~, . . ., with ~(i~ E
S, i = 1, . . . , n, . . ., is encoded using the Process D_S II_E2,~ so as 'to
yield the output sequence y = y(1~, . . . , y(n~, . . ., such that y(i~ E .,4,
i = 1, . . . , n, . . ., then
lim Pr( f (n) = f *~ = 1, (16)
n-boo
where f * is the requested probability of 0 in the output (1-.p < f * G p),
and f (n) _ ~°~n) with co(n) being the number of 0's encoded up to time
n.
Proof. By following the sequence of operations executed by the Process
D_S~-I~~,2, and using the fact that the most likely symbol of S is 0,
y(n -~ 1~ is encoded as follows:
125
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
0 if x (n -I-1~ = 0 and f (n) < f or
y(n -I- 1~ _ x(n + 1~ - 1 and f (n) > f (17)
1 if x (n -I-1 J = 0 and f (n) > f or
x(n -i-1~ = 1 and f (n) < f ,
where f (n) is the estimrxted probability of 0 in the output, obtained
as the ratio between the number of 0's in the output and n as follows:
~(n) - ~o(n).
For ease of notation, let f (n-I-1) ~ f(n) denote the conditional probability
Pr(~(n -I-1~ = 0 ~ f (n)~, which is, indeed, the probability of obtaining 0 in
the output at time n -I- 1 given f (n). Using (17) and the fact that f (n)
1o is given, f (n -I-1) ~ f(n) is calculated as follows:
co(n)+1 if x(n -I-1~ = 0 and f (n) < f * or
n-I-1 -
f ( + 1) ~ x(n -I-1~ = 1 and f (n) > f * (18)
n f(n) -
n+i if x(n -I- 1~ = 0 and f (n) > f * or
x(n -I- 1~ = 1 and f (n) .< f * ,
where co (n) is the number of 0's in the output at time n.
Since f (n) _ ~°~n), it implies that co(n) = n f (n). Hence, (1~)
can be
126
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
re-written as follows:
nfn++1 if ~~n + 1~ = 0 and f (n) < f * or ~(a)
f (n + ~) ~ ' - x~n + 1~ = 1 and f (n) > f * (b) (19)
f ~n~ of ~n~ if ~ ~n -I-1~ = 0 and f (n) > f * or (c)
n~-1
~~n -I- l~ = 1 and f (n) < f * . (d)
Since (16) has to be satisfied, the behavior of (19) is analyzed for an
arbitrarily large value of n. To be more specific,' the analysis consists of
considering the convergence of f (n -I- 1) ~ fin) as n ~ oo. This is accom-
plished by considering three mutually exclusive and exhaustive cases for
f (n)
The first one, deals with the situation in which f (n) = f *. As n -~ oo,
1o it is shown that f * is a fixed point. That is, f (n -I- 1) ~ f~n~- f* is
increased
by an increment whose limit (for n -~ oo) is 0, and hence f (n-I-1)~ f(n)-f*
will stay at a fixed point, f *.
The second case considers the scenario when f (n) < f *. The Process .
D_S~I~2,2 increments f (n -~ 1) ~ f~n)~ f* with a value proportional to the
difference p - f (n), causing f (n) to rapidly converge towards f * in the
direction of p. As it approaches p from f (n), it has to necessarily cross
the value f *, since f (n) < f *. It will be shown that this is done in a
finite number of steps, l~, for which f (n -I- k) ~ f(n)s f* > f *.
On the other hand, when f (n) > f *, f (n -I- 1) ~ f~n)~ f* decreases. This
decrement is by an amount proportional to the difference f (n) - ( 1- p) .
127
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
This, in turn, causes f (n) to rapidly converge towards 1 - p, and as
before, it intersects the value f *.
While the above quantities are proportional to p - f (n) and ( f (n) -
(1- p)), respectively, it will be shown that they are both inversely pro-
portional to n -~-1.
These two convergence phenomena, namely those of the second and
third cases, cause f (n -I- 1) ~ f(n) to become increasingly closer to f * as
n
is large, until ultimately f (n) is arbitrarily close to f *, whence the fixed
point result of the first case forces f (n) to remain arbitrarily close to f
*.
1o Observe that the combination of the convergence properties of the
three cases yields a strong convergence result, namely convergence with
probability one. The formal analysis for the three cases follows.
f (n) = f *.
The analysis of the asymptotic property of the probability of
y~n -I- l~ = 0 given f (n) = f * is required. In this case, this is
calculated using (19.(a)) and (19.(d)), and the fact that Pr~x(n-I-
l~ _ OJ = p, as follows:
n f (n) ~-1 n f (n~
f (n + ~) ~ f(rz,)- f* = rz -I- 1 p + n -~-1 (1 p)
nf~n) -~~
n -E- 1
_ of (n) + f (n~ + p - f (n~
2o n -f-1 n -I- 1
12~
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
- f(n) + P f(n) (20)
n -t-1
Since, in this case, f (n) = f *, (20) results in:
f (n + 1)I f(n)-f* _ f* + ~ 1 ~ (21)
-f-
This implies that f (n -I-1) ~ fin)- f* ~ f *, as n ~ oo and f * is a
fixed point. Therefore, the following is true:
~m~ Pr~ f (n -f- 1) ~ fin)' f* = f *~ = 1. (22)
Equation (22) is a very strong statement, since it implies that, as
n ~ oo, once f (n) arrives at f *, it stays at f * with probability
one.
(ii) f (n) < f *
In this case, the conditional probability of y~n -I- 1~ = 0 given
f (n) < f *, is calculated using (20). as follows:
f(n -I-1) I f~n)c f* = f(n) -~ p f (n) , (23)
n -~ 1
129
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Since f (n) < f * and f * G p, by our hypothesis, it is clear that
f (n) G p. Hence:
f (n -I- l)Lf(n)<f* - f (n) -I- O ~ (24)
s
where O = ~n+1n) > 0 for all finite values of n.
Prior to analyzing the number of steps, k, required to ensure
that f (n -I- 1~) ~ becomes greater than or equal to f *, a
.f (n) <.f
closed-form expression for f (n -I-1~) ~ f~n)< f* is first derived. Since
to (23) determines f (n -~- l ) ~ f(n)< f*, it will be shown below that
f (n -~ 1~) ~ f(n)< f* can be calculated as follows:
~ [p f (n))
f (n -I- ~) ~ f~n)< f* = f (n) -~- n + ~ ~ (25)
15 Equation (2~) is proven by induction on 7~.
Basis step: Clearly, (25) is satisfied for 1~ = 1 by the fact that
(23) is true.
Inductive hypothesis: Suppose that (25) is satisfied for any j > 1.
130
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
That is:
~ [p-f(n~,
f (n -E- ~) ~ f~n~< f* = f (n) -f- n + j ~ (
s Inductive ste~ro: It is required to prove that (25) is true for j -I-1.
Substituting n for n -I- j in (23):
.f(n+~+1)I f(n)<f* -.f(n+~)+~ .f(n+~) .
n -E- ,~ -I-1
1o Using the inductive hypothesis, (26), (27) can be rewritten as
follows:
f (n + j + 1) I f(n~< f* _
.~ p - f (n) p - f (n) +'~pn+jn)~
n
n + j + n -I- j -I-1
f(n) + ~p - jf (n) + P - f (n)
n -I- j n -~- ~ n -I- j -E-1 n -~- j -f- 1
131
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
' ~P + ~ f (n)
(n+.7)(n+j+1) (n~--~)(n+.7~-1)
- f (n) + nip + ~ 2~ + (n + .7 )~
(n+~)(n+~ + 1)
-n~f (n) +.7~f (n) -E- (~ + ~)f (n) (28)
(n+~)(n+.7 ~-1)
- f (n) -f- ~p + P - j f (n) + f (n)
n -I- j -~ 1 n -I- j -I-1
(~+f) [p-f(n),
- f (n) d- n + j + 1 . (29)
Hence, (25) is satisfied for all 7~ > 1.
On analyzing the conditions for 1~ so that f (n -I-1~) ~ f(n)<,f* > f *~
it is seen that the following must be true:
~~ - f (n)~
f (n) + n + ~ > f * ~ (30)
Subtracting f (n) from both sides
~ Cp _ f(n)~ * .
n~-~ ~f -f(n)~
132
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Multiplying both sides by '~~~ > 0 and dividing by f *- f (n) > 0,
(31) results in:
~ - f (n) > n -I - ~ - n .+ 1. (32)
f * - f (n) l~ ~, .
Solving for k yields:
1~ > ~- f(n) .
(33)
f*- f(n) - 1
1o Hence, for a finite n, after 1~ steps (7~ finite), (30) is satisfied with
probability one. More formally,
Pr~f (n -I- ~) ~ f(n~~ f* > f *~ - 1 ~ 1~ < oo . (34)
Observe that the convergence implied by (34) is very strong. It
implies that f (n -~- 7~) ~ f(n)s f* will be above (or equal to) f * in a
finite number of steps, 7~, with probability one. Moreover, since
the increment is inversely proportional to n -I- 1, f (n) converges
quickly towards f * for small values of n, and will stay arbitrarily
close to f *, as n -~ oo with probability one.
2o Since f (n-I-l~) ~ f~n)~ f* .urill sooner or later exceed f *, the
discussion
of this case is concluded by noting that when f (n -I-1~) ~ f(n>~ f* >
133
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
f *, the quantity f (n -I- I~ -I- 1) ~ f(n)s f* has to be calculated in a
different way since the hypothesis of Case (ii) is violated. Indeed,
in this scenario, the hypothesis of Case (iii) is satisfied, and the
following analysis comes into effect. Finally, if f (n-I-k)~ f~n~~ f* _-_.
f *, the quantity f (n -I- k -~- 1) ~ f(n)s f* is calculated using (21) as
in Case (i), converging to the fixed' point, f *, as n -~ oo.
(Zii) f (n) > f *.
In this case, the conditional probability of y(n -I- 1~ = 0 given
f (n) > f *, is calculated using (19. (b) ) and ( 19. (c) ), and the fact
1o that Pr~~~n -I- 1~ = 0~ = p, as follows:
f (n + 1) I f(n)> f* - of (n) + 1 (1 - p) + of (n)p
n -~-1 n -I-1
nf(n)-~-1-p
n -~-1
- of (n) + f (n) + (1 - p) - f (n)
n -~-1 n -I-1
- f(n) - f(n) - (1 - p) (3~)
n -~ 1
Since f (n) > f * and f * > 1 - p, it means that f (n) > 1 - p,
which implies that f (n) - (1 - p) > 0. Thus:
f (n + 1) ~ f(n)> f* = f (n) - 0 a (36)
134
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
where O = f inn+1 ~> > 0 for n finite. Hence, as n grows, f (n)
decreases by a positive value, O.
A closed-form expression for f (n -I-1~) ~ f(n)> f* is now derived. In-
deed, it is shown by induction that if f (n-I-1) ~ f~n)> f* is calculated
as in (35), f (n -I-1~) ~ f(n~> f* can be calculated as follows (1~ > 1):
~ [f (n) - (1 - p)],
f (n + ~) ~ f(n)> f* = f (n) - n -I- ~ ' (37)
so Basis step: Equation (37) is -clearly satisfied, by virtue of the
fact that (35) holds. Hence the basis step.
Inductive hypothesis: Assume that (37) is true for j' > 1. That
is:
j ~ f(n) - (Z - p),
~5 f (n +~)I f(~,,)>f* = f (n) - n ,~ j .
Inductive step: It is shown that (37) is satisfied for j -I- 1. Sub-
135
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
stituting n for n -I- j in (35) results in:
f (n '~ ~ + 1) ~ f(n), f* = f (n + j) - f (n n .~) - (1 - p)
+ ~ -I-1
Using the inductive hypothesis, (38), (39) can be re-written as
follows8:
f (n + .7 + 1) ~ f~n~~ f*
.? [f (n) - (1- 2~)]
f (n) n + j
f (n) - ~~f~n)+jl-~)~ - (1- ~
- (40)
n-~j+1 .
f (n) - .7 f (n) + .7 (1 - p) - f (n) +
n + ~ n ~-- j n -I- j -f- 1 n --~ j -~- 1
+ .7f (n) - ~ (1 - p)
(n+~)(n+j+1) (n+j)(n+~~-1)
f(n) - n~f (n) + ~2f (n) + (n + j)f (n)
1s (n+~)(n+.~ -f- 1)
+n.7(1 -p) +.72(1 -~) + (n+.7)(1-~)
(n + j ) (n -I- ~ + 1)
BThe algebra for this case mirrors the algebra of Case (ii). It is not
identical, though,
since ~ro and 1- p interchange places, and the sign for f (n) changes from
being positive
to negative in various places. The proof is included in the interest of
completeness.
13G
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
- f(n) - 9f (n) + f (n) + .7 (1 - P) + (1 - P)
n ~- j -E-1 n -I- j -~ 1
(~ + ~) [f (n) w(1- P),
f (n) _ n -I- j -I-1 . (41)
Therefore, (3'7) is satisfied for all 1~ > 1.
Observe now that f (n) monotonically decreases till it crosses f *.
To satisfy f (n -I-1~) ~ f(n)s f* < f *, the following must be true:
~ ~f (n) - (~ - ~)~
f (n) - n + ~ < f . (42)
1o Subtracting f (n), and reversing the inequality, yields:
f(n) - f* < n ~ ~ [f(n) - (1 - p) . (43)
-I-
Multiplying both sides by n~ ~ > 0 and dividing by f (n) - f * > 0,
(43) results in:
137
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
f(n)-(1-p)>n+~-n+1. 44
f (n) - f * 7~ 7~ .( )
As before, solving for 1~, yields:
I~ > f(n)_(1_p) - 1 ,
(4~)
.f (n)-.f
Thus, for a finite n, after 1~ steps (k finite), (42) is satisfied with
probability one. That is:
Pr~ f (n -I- 7~) ~ f(n)s f* < f *~ - 1. (46)
As in the case of (34), equation (46) represents a strong conver-
gence result. It implies that, starting from f (n) > f *, f (n -I-
. 1~) ~ f(n)s f* will be below (or equal to) f * in a finite number of
steps, 1~, with probability one. Moreover, since the decrement is
inversely proportional to n -I- 1, f (n) converges quickly towards
f * for small values of n, and will stay arbitrarily close to f *, as
138
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
n -~ oo with probability one.
Since f (n -~ 1~) ~ f(,~)~ f* will sooner or later become less than or
equal to f *, this case is terminated by noting that when f (n -I-
1~) ~ f(n)s f* < f *, the quantity f (n -~ 1~ -f- 1) ~ f(n)s f* has to be cal-
culated in a different way since the hypothesis of Case (iii) is
violated. At this juncture, the hypothesis of Case (ii) is sat-
isfied, and the previous analysis of Case (ii) comes into effect.
Clearly, if f (n ~- l~) ~ f(n)s f* = f *, the quantity f (n -I- l~ -I-1) ~
f(n)s f*
is calculated using (21) as in Case (i), converging to the fixed
1o point, f *, as n -~ oo.
To complete the proof, the analyses of the three cases are combined
to show that the total probability f (.), converges to f *.
From (34), there exists m > n such that
1'rLf (m) I f(n)< f* ~ f *~ = 1 ~ (47)
This means that f (m) ~ f(n)< f* > f *, but f (m-I-1) ~ f(n)< f* < f (m) ~
f(n)< f*,
since f (m)) f(n)< f* obeys (35). Equation (35) yields
f (m) ~ f (n) <.f * _ f * ~ (~ , (48)
139
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
where b ~ 0 as n -~ oo. Hence, there exists no > m, and E arbitrarily
small such that:
lim Pr~If (no) I f(n)<f* - f * ~ G E~ = 1. (49)
no-goo
In the contrary scenario of (46), it is known that there exists m > n
such that:
to PrLf (m) I f(n)>,f * ~ f *~ - 1 ' (50)
Hence f (m) ~ * G f *, but f (m -I- 1) ~ * > f (m) ~ *. From
f (n) >f f (n) > f f (n) > f
(23), it can be seen that:
15 f (m)~ f(n)>f* = f*.~ b, (51)
where b ~ 0 as n ~ oo. Again, there exists no = m, and E arbitrarily
small such that:
140
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
lim Pr~If (no)I f(n)> f* - f*~ G E~ = 1. (52)
no~oo
Combining (22), (49), and (52), yields:
t ~ 1'r~f (t) I f(n)- f* = f *~ - 1 ~ (53)
li ~ Pr( f (t) I f(n)< f* _ f *~ - l , and (54)
~ Pr~f (t) I f(n)>f* _ f *~ - l . (55)
From the three cases discussed above, the total probability f (t) = f *
1o is evaluated as:
Pr~f (t) = f *~ - Pr~f (t) I f(n)=f* = f *~ Pr~f (n) = f *~ -~-
Pr~f (t) I f(n)<f* = f *~ Pr(f (n) < f *~ -I-
Pr(f (t) I f(n)> f* = f *~ Pr~f (~) > f *~ ~ (5~)
Since the conditioning events are mutually exclusive and collectively
exhaustive, (53), (54), (55), and (56) are combined to yield:
141
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
t ~ Pr~f (t) _' f *~ = 1 ~ (57)
and the result is proven.
s Theorem 2 (Rate of Convergence of Process D_S~I~~~2). If f * is
set at 0.5, then E~ f (1)~=0.5, for Process D_S~I_E2,~, implying a one-step
convergence iri ~ the expected value.
Proof. From (23) it can be seen that f (n -I-1) has the value given below
to f (n + 1)I f(n)<f* _ f (n) -~- p .f (n) . (58)
n -I- 1
whenever f (n) G f *.
But independent of the value set for f (0) in the initialization process,
this quantity cancels in the computation of f (1), leading to the simple
15 expression (obtained by setting n = 0) that
f (1) = p whenever f (0) G 0.5 .
Similarly, using expression (35), it is clear that f (1) has the value
1 - p whenever f (0) > 0.5 .
142
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Initializing the value of f (0) to be less than f * with probability s,
leads to
f (1) - spf (0) + spLl - f (0)~'
which can be expressed in its matrix form as follows:
T
f(1) - sp s(1 - p) f(0) .
sp s(1 - p) 1 - f(0)
1- f(1)
The above, of course, implies that the value of f (0) can be initialized
to be greater than f * with probability 1- s. Thus,
f (~-) _ (1 ' s)(~ ' p)f (0) + (1 - s)pL1 ' f (0)~
which can also be expressed using the matrix form as follows:
to
T
f(1) - (1 ' s)(1 - p) (1 - s)p f(0) . (00)
I - f (~) (~ ' s) (~- - p) (1- s)p 1 - f (0)
From (59), (60), and using .~'(~) to denote the vector ~ f (~),1 - f (~)~,
the expected value of f ( 1) and 1 - f ( 1) becomes:
143
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
r ~.~~y~ - z~~T~ ~.~~o~] ,
where M is the Markov transition matrix given by:
T
T sp+(1-s)(1-p) s(1-p)+(Z-s)p
M - . (62)
sp-f-(1-s)(1-p) s(1 -p)-~-(1-s)p
Calculating the eigenvalues of M, yields al = 1 and .12 = 0, and hence
the Markov chain converges in a single step!!
1o Therefore, if f (0) is uniformly initialized with probability s = 0.~,
E( f (1)~ attains the value of f * = 0.5 in a single step. 0
Theorem 3 (Convergence of Process D_S~i~m,~). Consider a sta-
tionary, memoryless source with alphabet S = ~sl, . . . , sm~ whose prob-
abilities are P = (p1, . . . , pm~, the code alphabet ,A. _ ~0, l~, and a
binary
Huffman tree, 7r, constructed using Huffman's process. If the source se-
quence x = ~(1~ . . . x(M~ is encoded by means of the Process D_S~-I~m,2
and 'T~, generating the output sequence y = ~(1~ . . . y(R~, then
lim Pr( f (n) = f *~ = 1, (63)
n~o~
144
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
where f * is the requested probability of 0 in the output (1- fma~ < f * <_
fmczx) ~ and f (n) _ ~°n"~ with c0 (n) being the number of 0's encoded
up
to time n.
s Proof. Assume that the maximum number of levels in T is j. Since
different symbols coming from the input sequence are being encoded, it
is clear that the level j is not reached for every symbol. Observe that
the first node of the tree is reached for every symbol coming from x -
which is obvious, since ~ every path starts from the root of T. Using this
1o fact the basis step is proved, and assuming that the fixed point, f *, is
achieved at every level (up to j - 1) of T, the inductive step that f * is
also attained at level j can be proven.
Basis step: It has to be proved that the fixed point f * is achieved at the
first level of T. Note that the root node has the associated probability
15 equal to unity, and hence its left child has some probability p1, > 0.5
(because of the sibling property), and the right child has probability
1-pl. This is exactly a Huffman tree with three nodes as in Theorem 1.
Depending on the condition f (n) < f *, the value of f (n) will be
increased (Case (ii) of Theorem 1) or decreased (Case (iii) of Theorem 1)
20 by O1 as given in (24) or (36) respectively. Whenever f (n) asymptotically
reaches the value of f *, it will stay at this fixed point (Case (i) of
Theorem
1). By following the rigorous analysis of Theorem 1, omitted here for the
sake of~brevity, it is clear that f (n) asymptotically attains the fixed point
145
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
f * as n -~ oo, w.p.l.
Inductive hypothesis: Assume that the fixed point f * is attained by
Process D_S~i~,,.z~2 at level j -1 > 2, for n -~ oo with probability unity.
Inductive step: It is to be shown that the fixed point f * is asymptot
s ically achieved at level l = j . Since the level j may not reached for all
the symbols coming from the input sequence., the decision regarding the
assignment 0-1 or 1-0 for these symbols must have been taken at a level
1~ < j. In this case, the .argument is true for j, because of the inductive
hypothesis.
1o For the case in which the level j is reached, the decision concerning
the branch assignment is to be taken in a subtree, T, whose root '(at level
j ) has weight ~, and its two leafs have probabilities pal and p~2 . After
normalizing (i.e. dividing by ~), the root of T will have an associated
normalized probability l, the left child has the associated normalized
15 probability p~ _ ~~ , and the right child has probability 1 - p~ = p~ ,
where p1 > 0.~ because of the sibling property.
Since the decision on the branch assignment is being taken at the root
of ~, if f (n) < f *, the value of f (n) will be increased by an amount 0~
as given in (24). This corresponds to Case (ii) of Theorem 1. On the
20 other hand, if f (n) > f *, f (n) will be decrease by 0~ as given in (36),
which corresponds to Gase (iii) of Theorem 1. Finally, if f (n) = f *, f (n)
will asymptotically stay at the fixed point f *(Case (i) of Theorem 1). As
in the basis step, by following the rigorous analysis of Theorem 1, which
146
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
is omitted here for the sake of brevity, it follows that f (n) asymptotically
achieves the fixed point f * as n --~ oo, w.p.l.
The induction follows and the theorem is proved.
Theorem 4 (Convergence of Process D~~I~2,2). Consider a
s memoryless source with alphabet S = ~0,1~ and the code alphabet,
,A. _ ~0, l~. If the source sequence X = x(1~, . . . , ~(n~, . . ., with x(i~
E S,
i = 1, . . . , n, . . ., is encoded using the Process Process D~..~I~~,~ so as
to yield the output sequence y = y(1~, . . . , y(n~, . . ., such that y(i~ E
,A,
i = 1, . . . , n, . . ., then
io
lim Pr( f (n) = f *~ = 1, (64)
n~oo
where f * is the requested probability of 0 in the output, and f (n) _
~°~n~
n
with co(n) being the number of 0's encoded up to time n.
15 Proof. It is to be shown that the fixed point f * is asymptotically
achieved
by Process D.A~I_E2~~ as n -~ oo, with probability unity. Observe that
at each time instant, Process DA~I~2,2 maintains a HufFman Tree Tn,
which has the sibling property. 7rn has the root, whose probability or
weight is unity, the left child with probability ~(n), and the right child
2o whose probability is 1 - p(n), where w(n) > 0.5 because of the sibling
property.
The details of the proof follow the exact same lines as the proof of
147
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Theorem 1. They are not repeated here. However, it is clear that at
each time instant 'n', there are three cases for f (n):
(i) f (n) = f * : In this case, as n increases indefinitely, f (n) will
stay at the fixed point f *, by invoking Case (i) of Theorem 1,
where the probability of 0 in the input at time 'n' is p(n).
(ii) f (n) < f * : In this case, the value of f (n) will be increased by
O, as given in (24). This corresponds to Case (ii) of Theorem 1.
(iii) f (n) > f * : In this case, the value f (n) will be decreased by O;
as given in (36). This corresponds to Case (iii) of Theorem 1.
to With these three cases, and mirroring the same rigorous analysis done
in Theorem 1, one can conclude that the estimated probability of 0 in
the output, f (n), converges to the fixed point f *, as n -~ oo. This will
happens w. p. 1, as stated in (64) .
Theorem 5 (Convergence of Process I~_A~I~m~2). Consider a
memoryless source with alphabet ~S = ~sl, . . . , sm~ whose probabili-
ties are P = ~pl, . . . , pr,.,,~, and the code alphabet ,A. _ ~0, l~. If the
source sequence ~ = x(1~ . . . ~(M~ is encoded by means of the Process
D_A_H~m,2, generating the output sequence ~ = y(1~ . . . y(R~, then
lim Pr~ f (n) = f *~ = 1, (6~)
n-->oo .
14~
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
where f * is the requested probability of 0 in the output (1- fmax < f * <
fm,a~), and f (n) = ~°nn~ with co(n) being the number of 0's encoded up
to time n.
Proof. Considering an initial distribution for the symbols of ~, a Huffman
tree, ~, is created at the beginning of Process DA_H~~,L,2. As in Process
D_S~I~m,~, it is assumed that the maximum level of T is l = j. This
level will not be reached at a1 time instants. However, the first node
is reached for every symbol coming from ~1,', because every path starts
1o from the root of ~ . Assuming that the fixed point f * is achieved at
every level (up to j - 1) of T , it is shown by induction that f * is also
asymptotically attained at level j .
Basis step: The root node of ~ has the normalized weight of unity, its
left child has the normalized weight p(1~), and hence the right child has
Is the normalized weight 1 - p(1~), where p(7~) > 0.~ because of the sibling
property. There are again three cases for the relation between f (n) and
f*
(i) Whenever f (n) = f *, f (n) will asymptotically stay at the fixed
point f*as n -~ oo.
~o (22) If f (n) < f *, f (n) will be increased by C~1, as in Case (ii) of
Theorem 4.
(iii) If f (n) > f *, f (n) will be decreased by O1 (Case (iii) of Theorem
149
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
4) .
From these three cases and from the analysis done in Theorem 4, it
can be shown that f (n) will converge to f * as n ~ oo w. p. 1, and hence
(6~) is satisfied
Ind~cctive hypothesis: Assume that the fixed point f * is attained w.
p. 1 by D~~ Em~~ at any level j -1 > 2 of ~, for n ~ oo.
Inductive step: In order to show that f * is asymptotically achieved at
level l = j , two cases are considered. The first case is when the level j
is not reached by the symbol being encoded. In. this case, the labeling
1o strategy was considered in a level i < j, for which the result follows from
the inductive hypothesis.
For the case in which the level j is reached, the decision on the labeling
is being taken in a subtree, ~~, whose root has the estimated probability
~(1~), and its two leafs have estimated probabilities p31 (l~) and ~~2 (l~).
After normalizing (i.e. dividing by ~(7~)), the root of T~ has probability
unity, the Ieft child has probability ~~ (1~) _ ~,~~~~~ , and the right child
has
probability 1 - p~,(1~) _ ~~(~~~, where p~(l~) > 0.5 because of the sibling
property.
Again, there are three cases for f (n) for the local subtree. When
2o f (n) = f *, f (n) will asymptotically stay at the fixed point f *.
Whenever
f (n) < f *, f (n) will be increased by 0~ (1~), calculated as in (24), which
is positive, since it depends on p~ (1~) > 0.~. If f (n) > f *, f (n) will be
decreased by 0~ (l~) (again positive, because p~ (1~) > 0.~) as given in (36).
150
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
From these three cases 'and the analysis done in Theorem 5, it follows in
an analogous manner that Process DASI~m,~ achieves the fixed point
f * as n -~ oo w. p. 1, as stated in (6~).
Theorem 6 (Convergence of Process RV_A~I~~,~). Consider a
memoryless source whose alphabet is S = ~0,1~ and a code alphabet,
.A. _ ~0,1~. If the source sequence x = ~(1~, . . . , ~~n~, . . ., with x(i~ E
<S, i = 1, . . . , n, . . ., is encoded using the Process RV~.~i~2,2 s0 as to
yield the output sequence y = y(1~, . . . , y~n~, . . ., such that y(i~ E .A.,
i = 1, . . . , n, . . ., then
lim E~ f (n)~ - f * , and (00)
n~oo
~mo0 ~ar~f (n)~ - 0 ~ (
where f * = 0.5 is the requested probability of 0 in the output, and
f (n) _ ~°~n) with co(n) being the number of 0's encoded up to time n.
Thus f (n) converges to f * in the mean square sense, and in probability.
Proof. The estimated probability of 0 in the output at time 'n -I-1' given
the value of f (n), f (n -I-1 ) ~ f(n), is calculated as follows
f n+1)~° _ ~°(n) ify~n~-1~=0 ( )
( _ n+1 Og
.f (n) c°(n)+1 if y~~t + 1~ = 1
n+1
151
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
where f (n) is the estimated probability of 0 in the output, obtained as
the ratio between the number of 0's in the output and n ~as f (n) _
~°~n~ .
n
On the other hand, the output of Process RVA~-I~~,~ at time n + 1,
is generated as per the following probabilities:
~[ .+ ~, - 0 with probability (1- f (n)~p(n) + f (n)(1- p(n)) (00)
n
1 with probability ~1 - f (n)~ (1- p(n)) + f (n)p(n) ,
where p(n) is the estimated probability of 0 in the input at time 'n',
to and p(n) > 0.5 because of the sibling property.
Unlike in the convergence analysis of Process D_S_H~2,2 in which the
exact value of f (n + 1) ~ f(n) was calculated, here the expected value of
f (n + 1 ) ~ fin) is computed. For the ease of notation, let f (n + 1) be the
expected value of f (n -~ l) given f (n) . Replacing the value of c0 (n) by
n f (n) in (68), and using (69), all the quadratic terms disappear. Taking
expectations again f (n -I- 1) is evaluated as:
n_f(n)+1
f (n + 1) - n + 1 ~ ~1- f (n)~p(n) + f (n) (1- p(n))
+nf (n) ~1- f (n)~(1- p(n)) + f (n)p(n) ~ (70)
n -I- 1 ~ - -
152
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
After some algebraic manipulations, (70) can be written as:
f (n + 1) = f (n) + p(~)(~- - 2f (n)~ . (71)
_ n+1
The convergence of (76) can be paralleled by the convergence results
of Theorem 1 with the exception that instead of speaking of f (n) the con-
vergence of E( f (n)~ is investigated. This proof is achieved by analyzing
three mutually exclusive cases for f (n) .
~i~ f (n) = f
1o In this case, Equation (?1) asymptotically leads to f (n-I-1) = f *.
This implies that if f (n) is at the fixed point f *, it will remain
there as n ~ oo, and hence (66) is satisfied.
(22) f (n) < f *.
In this scenario, equation (71) can be written as:
f(n+ 1) = f(n) ~-0 ~ (
where O = ~~n»n+lf ~n» > 0, since f (n) < f *.
Note that (72) is similar to (24), where O > 0 again implying
153
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
that f (n) increases at time 'n' towards f
(iii) f (n) > f *.
For the analysis of this case, (71) is expressed as below:
f(n + 1) = f(n) - 0 ~ (73)
where O = p~n»n+~1 ~ ~~ > 0, because f (n) > f *.
For this case, (73) is analogous to (36),where O > 0 except that
f (n) replaces the term f (n) of (36).
to With these three cases, and following the rigorous analysis of Theorem
1 (omitted here for the sake of brevity), it can be seen that
lim E( f (n)~ = f * . (74)
n--Do0
15 Thus f (n) is a random variable whose expected value , f (n), converges
to the desired probability of 0 in the output, f *, as n ~ oo.~
To analyze the asymptotic variance of this random variable, f (n), the
calculation is as follows:
154
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Var(f (n + 1)~ = E(f 2(n + 1)~ - E(f (n + 1)~2 ~ (75)
To evaluate E ( f 2 (n -f-1), , the expression for the conditional expecta-
tion E [ f 2 (n -I-1) ~ f(n), from (68) is written as follows:
E f2 (n + 1) I f(~)~ - of (n) i 1 ~ (1- f (n)~p(n) + f (n) (1- p(n)~
n -I-
2
of (n) (1- f (n)~ (1- P(~)~ + f (n)P(n) ~ (7~)
n -I-1
1o On simplification, it turns out that all the cubic terms involving f (n)
cancel (fortunately). Taking expectations a second time yields E(f 2(n -~-
1)~ to be a linear function of E( f 2(n)~, E( f (n)~ and some constants not
involving f (n). More specifically, if f (n) represents E( f (n)~,
f~(n-~ 1) _
1 1 ~ ~ f ~ (n) (n2 - 2n -I- 4np~ -I- (gyp - 1-I- 2n - 2n~~ f (n) + ( 1- p) ~
(7'l )
(n ~- )
155
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Normalizing this equation by multiplying both sides by (n-~-1)2 yields
(n + ~)2~f~(n -f-1)~ _
-
f2 (n) ~n~ - 2n -I- 4np~ -I- (2p - 1--~ 2n - 2np~f (n) + (1- p) ~ ~ (78)
There are now two situations, namely the case when the sequence
converges and alternatively, when it does not. In the latter case, f (n)
1o converges slower than n2. Taking the limit as n -~ oo, this leads to the
trivial (non-interesting) result that f (oo) = f (oo). The more meaningful
result is obtained when f (n) converges faster ' than n2. In this case,
expanding both sides and setting f (n) to its terminal value f (oo) (which
is ultimately solved for, and hence moved to the LHS), yields
~~~n2 + ~n -I- 1 - n~ -I- 2n - 4np~f ~(°°) _ ('l9)
lim (2p - 1-I- 2n - 2np~ f (oo) -I- (1- p) . (80)
n-boo -
2o Observe that the n2 terms again cancel implying that a finite limit for
z5s
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
the solution exists. This leads to
f 2(00) = lim 2p 1 + 2n - 2npf (~) ~ (81)
4n -- 4np -I- 1 -
s or rather
f 2(°°) ~~ 4n(1- p) f (°°) = 0.25 . (82)
n( p)
Since f (00) is 0.5 and f 2 (oo) is 0.25, it follows that Var~ f ~ is zero.
Thus
1o f (n) converges to a random variable with mean f * and variance zero,
implying both mean square convergence and convergence in probability.
Hence the theorem. ~ ~ 0
Theorem 7 (Convergence of Process RV_A~I~m,2). Consider a
memoryless source whose alphabet is S = ~sl, . . . , sm~ and a code al-
ts phabet, ,A. _ ~0,1~. If the source sequence x' _ ~~1~, . . . , x~M~, . . .,
with
x(i~ E S, i = 1, . . . , M, . . ., is encoded using the Process RVASI_Em,2 so
as to yield the output sequence y = y~l~, . . . , y~R~, . . ., such that y~i~
E .A,
i = l, . . . , R, . . ., then
20 ~~ E~f (n)~ - f * , and (83)
157
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
lim Var( f (n)~ - 0 , (84)
n-3oo
where f * - 0.5 is the requested probability of 0 in the output, and
f (n) _ ~°,~n~ with co(n) being the number of 0's, encoded up to time
n.
Thus f (n) converges to f * in the mean square sense and in probability.
Proof. As per Process RV~1.~I~m,2, a Huffman tree, To, is initially cre-
ated based on the initial assumed distribution for the symbols of <S. As
in the proof of convergence of Process D~~-I~m,~ (Theorem 5), it is
again assumed that the maximum level of ~ is l = j . This level may not
1o be reached all the time instants. However, the fist node is reached for
every symbol coming from x, because every path starts from the root of
. The proof of Theorem 6 now completes the proof of the basis case.
For the inductive argument, the inductive hypothesis is used, i.e., that
the fixed point f * is achieved at every level (up to j -1) of T . By arguing
i5 in a manner identical to the proof of Theorem 5 (omitted here to avoid
repetition), the result follows by induction on the number of levels in the
tree ~ . D
158
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
Appendix C
A Simple Encryption Useful for DODE+
This Appendix contains a straightforward encryption that can be used
in DODE+ as a special ease of ENCpreserve.
Suppose that the input sequence X is encoded by using any deter-
ministic or randomized embodiment for DODE, generating an output
sequence ~. = ~(1~ . . . y(R~, where y(i~ E ,A = ~0,1~. y is parsed using
m = 2~~ source symbols, ~S. _ ~so,,. . . , sm_1~, whose binary representa-
tions are obtained in a natural manner (i.e. from 0000... to 1111...). The
to output, y', is generated by encoding each of the R div l~ symbols, s2, of
~ as the corresponding wi obtained from a particular encoding scheme,
~ : S = ~so, . . . , sm_1~ ~ C = ~wo, . . . , wm,-1~. The remaining R mod 1~
bits can be encoded by using a similar mapping for a smaller number of
bits.
Notice that there are m! different encoding schemes, and that each
encoding scheme has a ~cniq~ce key, 1C, which is an integer from 0 to
m! - 1. The Process to transform a given key into a mapping consists of
repeatedly dividing~the key by a number, ~, which starts at m! and is
decremented to unity. The remainder at every stage specifies the current
2o mapping, and the dividend is then divided by the decremented value of
Z.
More formally, let w~ow~1. . . zv~k refer to w~ E C.
15s
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
The mapping procedure proceeds as follows. It starts with eS =
~so, . . . , sm_1~. IC is divided by m obtaining the dividend, do, and the
reminder, j0. The code word of C, w0, is s~o, which is removed from <S.
Then, do is divided by m -1 obtaining d1 and j1, and it continues in the
same fashion until all the symbols of S have been removed.
The process is straightforward and explained in standard textbooks,
and omitted in the interest of brevity. However, a small example will
help to clarify this procedure.
Example 7. LetaS = 000, 001, 010, 011,100,101,110,111 be the source
to alphabet for the case when the output obtained from DODE is y =
011101001010110010110, and the key is JC = 2451.
The mapping construction procedure is depicted in Table 28. Dividing
1C by 8, we obtain do = 308, and io = 3, and hence s3 = 011 is assigned
to w0; s3 is removed from <S (in bold typeface in the table). Dividing 308
by 7, we obtain dl = 43 and i1 = 5, and hence ss = 110 is assigned to
wx; s5 is removed from S (in bold typeface in the table).
The mapping construction procedure continues in the same fashion
obtaining the following mapping shown in Table 29 below.
Finally, we parse y using this mapping, and hence we obtain y' -
100000110001101001101.
It is easy to see that if the symbols of ~S are equally likely (as it is,
since
the output of DODE and RDODE guarantee Statistical Perfect Secrecy),
the key specification capabilities presented above make DODE+ a truly
160
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
8 2451 ? 306 G 43
306 : 3 43 : 5 . 7 : 1
0 000 0 000 0 000
1 001 1 001 1 001
2 010 2 010 . 2 010
3 011 ~ 3 100 ~ 3 100
4 100 4 101 4 101
.
110 5 111
5 101
6 110 6 111
7 111
Table 2~: An example of a straightforward
mapping construction proce-
dure that can be used by DODE+.
In this case, the key 1C is
2451, and
the encryption is achieved by
transforming sequences of three
symbols at
a time.
~S binary C binary
so 000 -~ w0 011
s1 001 --~ w1 110
s2 O10 --~ w~ 001
s3 011 -~ w3 100
s4 100 --~ w4 010
s~ 101 --~ w5 000
s6 110 -~ w6 101
s7 111 -~ w7 111
Table 29: An example of orie possible encoding schemes
of the 8! from S
to C. In this case, the key and the encryption is achieved
1C is 2451, by
transforming sequences of threeols at a time.
symb
161
SUBSTITUTE SHEET (RULE 26)
CA 02460863 2004-03-17
WO 03/028281 PCT/CA01/01429
functional cryptosystem that also guarantees Statistical Perfect Secrecy.
Thus, the cryptanalysis of DODE+ using statistical means is impossible.
Breaking DODE+ necessarily requires the exhaustive search of the entire
key space.
162
SUBSTITUTE SHEET (RULE 26)