Note: Descriptions are shown in the official language in which they were submitted.
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
TOLERANCED DIGITIZING METHOD
Background Information
Digitizing is the process where by position data is gathered from the surface
of a physical model object with the aim of reconstructing one or more
duplicates of
the model object. A conventional digitizing system is a data collection device
by
which surface points on a physical model may be collected. This data
("Digitized
Data") is then used to produce a physical duplicate of the model object. This
is
achieved by using the Digitized Data to generate Computer Numerical Control
("CNC") part program, which may be executed on a machine tool. The objective
of
the digitizing process is to efficiently capture sufficient data to faithfully
reproduce
the model object.
A conventional digitizing system may consist of an actuated machine, a
controller, and a digitizing probe that are employed to collect data
representative of
points on the surface of the model object. The machine may also consist of a
table on
which a model object is placed and a head for mounting the data gathering
probe.
Relative motion between the probe and the model object is achieved when the
controller generates control signals to the machine's actuators (e.g.,
servomotors).
The controller orchestrates the relative motion between the probe and the
model
object by processing feedback information from the machine's actuators and by
processing the output signals from the data-gathering probe. The motions of
the
actuated machine may be, for example, orthogonal three-diinensional motions.
Those
skilled in the art will understand that systems may implement more or fewer
axes of
controllable motion. The feedback generated by the actuated axes may, for
example,
be in the form of encoder feedback indicating the relative displacement of
each axis
of motion form a known reference point.
Summary of the Invention
The present invention relates to a method of routing a probe of a digitizing
system on the surface of a model object for the purpose of copying that model
object
as a part are disclosed. When a tolerance nuinber is given, model surface data
can be
collected so that the geometrical difference between the model and the part is
within
the given tolerance for all touchable points on the model surface.
1
CA 02463895 2006-08-14
In a broad aspect, then, the present invention relates to a method for
collecting
position data in a digitizing system, the digitizing system including a
physical model and
a digitizing head with a probe stylus, the stylus having a radius, the stylus
being movable
in a three-dimensional space along a surface of the physical model to collect
the position
data, the method comprising the steps of: collecting first position data along
a first curve
comprising the intersection of a first plane with the surface of the physical
model;
collecting second position data along a second curve comprising the
intersection of a
second plane, which is parallel to the first plane, with the surface of the
physical model;
calculating a curve distance from point on the first curve to point on the
second curve;
comparing the curve distance with an allowable distance; if the curve distance
is greater
than the allowable distance, collecting third position data along a third
curve comprising
the intersection of a third plane with the surface of the physical model, said
third plane
located intermediate and parallel to said first and second planes; and storing
said first
and second position data.
la
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
Brief Description of Drawings
The above-mentioned and other features and objects of this invention, and the
mamer of attaining them, will become more apparent and the invention itself
will be
better understood by reference to the following description of embodiments of
the
invention taken in conjunction with the accompanying drawings, wherein:
Fig. 1 shows an exemplary diagram of a conventional digitizing system.
Fig. 2.1 shows an exemplary flow diagram for a conventional line digitizing
method.
Fig. 2.2 shows an exemplary flow diagram for a conventional rotation
digitizing method.
Fig. 3 shows the exemplary results of a conventional line digitizing method.
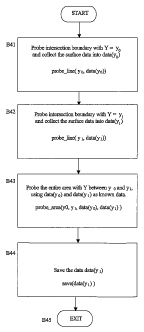
Fig. 4 shows an exemplary flow diagram detailing the Toleranced Digitizing
method according to the present invention.
Fig. 5 shows an exemplary flow diagram detailing the recursive sub procedure
used in the Toleranced Digitizing system according to the present invention.
Fig. 6 is an exeinplary illustration of the results of the Toleranced
Digitizing
inethod according to the present invention.
Corresponding reference characters indicate corresponding parts throughout
the several views. Although the drawings represent embodiments of the present
invention, the drawings are not necessarily to scale and certain features may
be
exaggerated in order to better illustrate and explain the present invention.
The
exemplification set out herein illustrates embodiments of the invention, in
several
forms, and such exemplifications are not to be construed as liiniting the
scope of the
invention in any manner.
Detailed Description of the Invention
2
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
The embodiments disclosed below are not intended to be exhaustive or limit
the invention to the precise forms disclosed in the following detailed
description.
Rather, the embodiments are chosen and described so that others skilled in the
art
may utilize their teachings. The present invention may be further understood
with
reference to the following description of exemplary embodiments and the
related
appended drawings, wlierein like elements are provided with the same reference
numerals.
A conventional digitizing system usually includes a table on which the model
object may be mounted for relative movement along the axes of an XYZ Cartesian
coordinate system between the model object and a head on which a probe is
mounted.
The probe is a precision sensor capable of generating output signals
indicative of
surface points from a model object. In its siniplest form, i.e., a touch
trigger probe,
the output signal is binary (i.e., either "ON" or "OFF"). A touch trigger
probe has a
stylus which consists of a slender rod with a spherical ball affixed to one
end. The
touch trigger probe is connected to a highly sensitive displacement switch.
Therefore,
when the ball of the stylus comes in contact with the surface, the probe
generates an
"ON" output signal. When the probe is no longer in contact with the surface,
an
"OFF" output signal is generated. By combining the output signal of the touch
trigger probe with the machine feedback, the controller generates and stores
coordinate values that are representative of an associate surface point on the
model
object.
Fig. 1 shows an exemplary diagram of a conventional digitizing system. The
digitizing system is controlled by a computer (or "control box"), which
monitors the
positions of the encoders of the XYZ axes and the probe output signals. In
addition,
while the control box computes and sends motion control signals to motors on
the
XYZ axes so that the probe stylus may move along the model surface according
to a
routing algorithm, the contacting positions are recorded. Later, if a CNC
program is
formed by transferring this position data to a program to run a CNC. machine
using a
spherical tool with the same diameter as the probe stylus, a part siinilar to
the model
may be obtained.
The digitizing process may be broken down into two parts: Data Gathering
and Digitizing Approach. Data Gathering details the method used by the
controller to
generate points representative of the surface of the model object within a
finite
3
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
region, typically the curve forined at the intersection of the surface of the
model
object with a plane. The data gathered during this step is referred to as a
Pass Data
Set and may be represented as:
data(Pass_Id)
The fiulction dataO is the Pass Data Set and Pass Id is an identifier that
refers
to the data collected (i. e., the definition of the intersecting plane).
The selection of an appropriate Data Gathering method is dependent on many
factors including the machine and the probe. For example, the Data Gathering
method described in U.S. Patent No. 6,052,628 is particularly suited for use
with a
three-axis touch trigger probe digitizing system, though other methods may
also be
employed to carry out the task of Data Gathering. Those skilled in the art
will be able
to select an appropriate Data Gathering method.
The Digitized Approach initiates multiple Data Gathering passes to collect
data that is representative of the model object, i.e., the Digitized Data. The
Digitizing
Approach defines the method which is utilized to determine where the instances
of
the Data Gathering are performed such that the collection of the Pass Data
Sets is
enough to faithfully reproduce the model object.
A common Digitizing Approach uses a set of cross-sections obtained by
intersecting the model object with a set of predetermined inutually parallel
and
equally distanced virtual planes. The coinputer controls the stylus motion so
that the
probe traces along each of the virtual plane-model object intersection
boundaries in
turn. Along each intersection boundary a sequence of points representing the
intersection boundary curve, i.e., the Pass Data Set, is gathered yielding the
Digitized
Data. If the norinal direction of the intersection planes is perpendicular to
the Z-axis,
the method is referred to as a Line Digitizing Approach. Fig. 2.1 shows an
exemplary
flow diagrain of a program utilizing Line Digitizing Approach. On the other
hand, if
the normal direction of the set of planes is parallel to the Z-axis, the
method is
referred to as a Rotational Digitizing Approach. Fig. 2.2 shows an exemplary
flow
diagram of a program utilizing Rotational Digitizing Approach.
4
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
The Line Digitizing Approach may be expressed in shorthand notation as:
probe_line(Plane_Id, data(Plane_Id))
The probe_line() function represents the Line Digitizing Approach. Plane Id
identifies the desired data-gathering plane and data(Plane Id) identifies the
Pass Data
Set as described above.
The Rotational Digitizing Approach may be expressed in shorthand notation
as:
probe_around(Plane_Id, data(Plane_Id))
The probe_aroundQ function represents the Rotational Digitizing Approach.
Plane_Id identifies the desired data-gathering plane and data(Plane_Id)
identifies the
Pass Data Set as described above.
For example, a model of the shorthand notation may describe a model object
that is a 2-inch sphere cut in half and placed on the table such that the semi-
sphere's
center is coincident with the machines (0, 1, 0) reference point. It may be
desired to
gather data using the Line Digitizing Approach along the intersection boundary
formed by the Y virtual plane with value y = 1, i. e., the plane bisecting the
semi-
sphere. This notation may be expressed in shorthand fonn as:
probe_line(1.0, data(1. 0))
Again, the probe_line() function represents the Line Digitizing Approach.
Plane Id was replaced by an expression identifying the desired plane, i.e., y
= 1.0 in
this current example. The function data(Plane Id) was replaced by data(Pass
Id)
with a Pass Id of y = 1.0 identifying the data from this plane.
As mentioned above, Fig. 2.1 shows a flow diagram of a program utilizing
Line Digitizing Approach starting with a virtual plane of y= 0 and successive
virtual
planes having a 0.2 inch positive displacement until the Digitized Data in the
region
between y = 0 and y = 1.0 have been gathered. The flow diagram assigns a
virtual
5
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
plane of y= 0 at B11, and then at B12 executes probe_line(y, data(y)). This
digitizes
a curve on the boundary of the intersection of the object model in the XZ
plane with
Y coordinate equal to y, and stores the Pass Data Set in data(y). At B13, y is
increased by a constant, 0.2 in this example, specifying the location of the
next virtual
plane. B 14 checks whether y is greater than the exit condition, 1.0 in the
present
example. If not, this newly computed virtual plane is used for data collection
as
indicated by the revisiting of step B 12. If the y-coordinate of the virtual
plane is
greater than 1.0, the flow diagram proceeds to B 15 and is finished.
Similarly, Fig. 2.2 shows a flow diagram of a Rotational Digitizing Approach.
The shorthand notation of probe_around(z, data(z)) directs the probing of the
boundary of the planar section in the XY plane witll Z-coordinate equal to a
constant
z and stores the collected surface position data in data(z). The flow diagram
assigns 0
to z at B21, and then at B22 executes probe_around(z, data(z)). This digitizes
a curve
on the boundary of the section of the model in the XY plane with Z-coordinate
equal
to z, and stores the collected data in data(z). At B23, z is increased by a
constant 0.2.
B24 checks whether z is greater than 1.0, the exit condition. If not, the
process
continues to B22 and repeats the steps until the exit condition is met, at
which it
proceeds to B25.
The exemplary flow diagram shown in Fig. 2.1 will generate six curves at the
sections with y = 0.0, 0.2, 0.4, 0.6, 0.8, and 1Ø The six curves are stored
in
data(0.0), data(0.2), data(0.4), data(0.6), data(0.8) and data(1.0),
respectively. If the
model is the same half sphere of the previous example, centered at (0.0, 1.0,
0.0) with
a radius of 1.0, the six cuives generated using the flow diagram of Fig. 2.1
are
illustrated in Fig. 3. Fig. 3 depicting both a top and side view is
representative of the
current art of digitizing. The curves have a height of 0.000, 0.8000, 0.9165,
0.9798,
and 1.000, respectively. The resulting distance between the six curves are
0.6325
(between data(0.0) and data(0.2)), 0.2828 (between data(0.2) and data(0.4)),
0.2315
(between data(0.4) and data(0.6), 0.2098 between data(0.6) and data(0.8)), and
0.2010
(between data(0.8) and data(1.0)).
A short coming of this approach is that despite the appearance of uniform
spacing of the sequential Pass Data Sets when viewed from above, i.e.,
data(0.0)
through data(1.0) in the above example, the use of equidistance virtual planes
results
in the non-uniform and unbounded 3-Dimensional ("3D") spacing between the Pass
6
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
Data Sets. Essentially, the maximum distance between any two adjacent Pass
Data
Sets is uncontrolled. For example, in Fig. 3, the distance between the Pass
Data sets
varies from a, minimum value of 0.2010 (between data (0.8) and data (1.0)) and
has a
maximum value of 0.6325 (between data(0.0) and data(0.2)). The maximuin
distance
between two adjacent Pass Data Sets is a measure of how accurately the
Digitizing
Data, captured the details of the model object's surface. By computing the
distance
between adjacent Pass Data Sets, the notion of quality of the Digitized Data
may be
introduced. As the distance between adjacent Pass Data Sets increases, the
fidelity by
which the data set captures the model object's essence decreases. This notion
of
controlled quality is missing in the art of digitizing today.
The present invention relates to an improved Digitizing Approach, Toleranced
Digitizing, by which the distance between any two digitized curves (or two
adjacent
Pass Data Sets) in the 3D space will be smaller than or equal to a
predetermined
distance.
A physical duplicate object may be machined according to the Digitized Data
utilizing a sphere tool with the same diameter as the probe stylus. The tool
sequentially visits each of the data points within a Pass Data Set, traversing
from one
point within the Pass Data Set to the next using straight line segments. When
the
geometrical difference between the duplicate object and the model object is
smaller
than or equal to a specified value, E, for all "touchable" surface points then
the
desired Global Tolerance value ("E") has been achieved. If a duplicate object
were
superiinposed with the model object and a second offset surface from the model
object is projected by a distance equal to the value E, all the surface points
of the
duplicate object are bound by the model object's surface and the offset
surface.
"Touchable" surface points includes all points on the model object's surface
that may be touched by the probe. A point on the back, under or inside the
object
model is not touchable, nor is a point inside a very narrow gap that the probe
cannot
reach. Although the nuinber of collected surface points from any object model
is
finite, the Global Tolerance is satisfied for the infinitely many touchable
points.
To ensure quality, the Global Tolerance E may be deterinined by the
following forinula:
7
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
E = 2*(R-sqrt(R*R-0.25*D*D)). (3.1)
Given the Global Tolerance, the maximum allowable distance ("D") between
Pass Data Sets may be generated, i.e., D is a fiulction of E. Therefore,
solving
equation (3.1) for E, results in the equation:
D = sqrt(4*E*R-E*E). (3.2)
In equations (3.1) and (3.2), the sqrt() function is the mathematical square
root
function. R is the radius of a probe stylus, and D is the maximum distance
between
two adjacent Pass Data Sets in 3D space. For a given Global Tolerance E and a
lcnown probe stylus radius R, one may calculate an allowable maximum distance
D
between two adjacent Pass Data Sets in 3D space.
By controlling the distance between any two adjacent Pass Data Sets to an
amount less than D, or by controlling the distance between the adjacent
virtual
intersection planes to an amount less than E, the Global Tolerance may be
controlled
to an amount less than E. It is important to compute the maximum distance
between
two adjacent digitized curves in 3D space controlled to an amount less than D.
For a first Pass Data Set represented by a sequence of points, data(yi) ={P11,
P12,...,Plm}, and a second Pass Data Set represented by a sequence of points,
data(y2) = {P21, P22,...,P2n}, the distance between any two points P1=(xl, yl,
zi) and
P2=(x2, y2, z2) is given by the following formula:
distance(P1, P2) = sqrt((xl-x2)*(xl-x2)+(Yl-Y2)*(Yi-Y2)+(zi-z2)*(zl-z2))=
(3.3)
The distance between the point P1 to a sequence of points, data(ya) ={P21,
P22,...,P2n} is given by the following formula:
distance(P1, data(y2)) = Min {distance(P1, P2i)}; for i=1,2,...,n,
(3.4)
8
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
i. e. , the minimum distance between P 1 and any point in data(y2). The
distance
between two Pass Data Sets data(yi) and data(y2) is given by:
distance(data(yi), data(y2)) = Max{distance(Plj, data(y2)}, for j=1,2,...,m,
(3.5)
i. e., the maximum distance from any point in data(yi) to curve data(y2). The
method of calculating the maximum and minimum number among a set of numbers
will be fainiliar to those skilled in the art.
The following details one exainple of applying the Toleranced Digitizing
method using a Line Digitizing Approach. Those skilled in the art will
understand
that the algorithm may easily be modified for a Rotational Digitizing Approach
as
well as other situations.
Fig. 4 illustrates an exemplary program according to the present invention for
routing the probe to guarantee a Global Tolerance of E while digitizing an
area yO is
less than or equal to Y and Y is less than or equal to yl. B41 in Fig. 4
digitizes the
intersection boundary curve in the XZ plane with Y= yo, where the points on
the
curve are collected and represented by data(yo). B42 digitizes the
intersection
boundary curve in the XZ plane with Y = yl, where the points on the curve are
collected and represented by data(yi). B43, probe_area(yo, yl, data(yo),
data(yi)) is a
recursive procedure detailed below which essentially checks two conditions.
First, it
determines whether two Pass Data Sets data(yo) and data(yi) satisfy the
allowable 3D
distance condition (see B52 of Fig. 5) and if they do, indicates that the job
is finished,
saves the data and exits the procedure. Next, if the two Pass Data Sets do not
satisfy
the allowable 3D distance condition, B43 inserts more virtual intersection
planes and
digitizes more intersection boundary curves there between and save them, until
the
allowable distance condition is satisfied by all pairs of adjacent Pass Data
Sets
scanned (see B54-B57 of Fig. 5). B44 saves the Pass Data Sets associated with
Y=y1,
represented as data(yi), into computer storage.
It may be necessary to repeatedly check whether the specified objective has
been met, i.e., the allowable distance between two adjacent Pass Data Sets and
the
tolerance constraint between two adjacent virtual planes. If neither condition
is met,
9
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
then an additional intersection boundary curve is obtained half way between
the first
curve and the second curve. The new curve is then tested with the first curve
to see if
the specified objective has been met. This bisecting and testing procedure is
repeated
as needed until the objective is met. The new curve is then tested with the
second
curve to check whether the specified objective is met. Those familiar with the
art of
algorithm application are familiar wit11 recursive procedures.
After the Data Gathering step is complete, the Digitizing Approach is
implemented. Fig. 5 details a recursive procedure probe_area(yo, yi, data(yo),
data(yi)) that implements this recursive bisecting. At B5 1, the distance
("dis")
between two Pass Data Sets data(yo) and data(yi) in 3D space is calculated as
described by formulas (3.3), (3.4) and (3.5). At B52, dis is compared with D,
the
allowable distance. If dis is smaller than or equal to D, or yl-yo is smaller
than or
equal to the tolerance number E, then data(yo) is saved at B53 and the
procedure is
exited at B58. Otherwise, the procedure continues to B54, wllere an
intermediate
value y= 0.5 *(yo+yl) is calculated. At B55, the probe is controlled to
digitize
another intersection boundary curve in the XZ plane where Y-coordinates equal
y and
the curve digitized produces the Pass Data Set data(y). Now the original
problem
(i.e., the execution of Toleranced Digitizing in area yO is less than or equal
to Y and
Y is less than or equal to yl) is divided into two similar but smaller
problems.~ First,
the execution of Toleranced Digitizing in the area yO is less than or equal to
Y and Y
is less than or equal to y, and second, the execution of Toleranced Digitizing
in the
area y is less than or equal to Y and Y is less than or equal to yl.
Therefore, at B56,
probe_area(yo, y, data(yo), data(y)) is called and at B57, probe_area(y, yi,
data(y),
data(yi)) is called. The procedure probe_area(yo, yl, data(yo), data(yi)) then
exits at
B58.
For example, assume that the model is a sphere centered at (0,0,0) with radius
0.75, a probe stylus having a radius 0.25, a digitizing area of -1 is less
than or equal
to X and X is less than or equal to 1, -1.1 is less than or equal to Y and Y
is less than
or equal to -0.9, and Z is greater than or equal to 0, and a Global Tolerance
set to E=
0.02. According to Formula (3.2), the allowable distance between the adjacent
curves
is:
D = sqrt(4*0.02*0.25-0.02*0.02) = 0.14
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
Since the radius of the probe stylus is 0.25 and the radius of the spherical
model is 0.75, the digitizing result is equivalent to a situation wherein a
sphere of
radius 1.0 is digitized with a zero radius probe stylus.
B41 of Fig. 4, executes procedure probe_line(-1.1, data(-1.1)). The model is
not touched, therefore obtaining a straight line Z = 0, saved and represented
as data(-
1.1). B42 executes procedure probe_line(-0.9, data(-0.9)), obtaining an arch
of height
0.4359. Now at B43, the recursive procedure probe_area(-1.1. -0.9, data(-1.1),
data(-
0.9)) is entered. The detailed execution of this recursive procedure is shown
as
follows:
1. At B51, dis = 0.4796 is calculated
2. At B52 : neither condition is satisfied, procedure proceeds to B54;
3. At B54 intermediate value y = -1.0000, is calculated;
4. At B55 probe_line(-1.0000,data(-1.0000)) is called, an intersection curve
with Y
coordinate = -1 is
probed and surface data is collected and represented as data(-1), wliich is a
straight
line Z=0.0000;
5. At B56 probe_area(-1.1000,-1.0000,data(-1.1000),data(-1.0000)) is called,
resulting
5.1. At B51 dis = 0.1000 is calculated;
5.2. At B52 condition dis<=D is satisfied, procedure proceeds to B53;
5.3. At B53, saves data(-1.1000);
5.4. At B58, exits procedure probe_area(-1.1000,-1.0000,data(-1.1000),data(-
1.0000));
6. At B57: probe_area(-1.0000,-0.9000,data(-1.0000),data(-0.9000)) is called,
resulting
6.1. At B51 dis = 0.4472 is calculated
6.2. At B52 neither condition is satisfied, procedure proceeds to B54;
6.3. At B54 intermediate value y = -0.9500, is calculated;
6.4. At B55 probe_line(-0.9500,data(-0.9500)) is called, a intersection curve
with
Y coordinate =
-0.95 is probed and surface data is collected and represented as data(-0.9500)
which is an arch of
11
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
6.5. At B56 procedure probe_area(-1.0000,-0.9500,data(-1.0000),data(-0.9500))
is called, resulting
6.5.1. At B51 dis = 0.3 162 is calculated;
6.5.2. At B52 neither condition is satisfied, procedure proceeds to B54;
6.5.3. At B54 intermediate value y = -0.9750, is calculated;
6.5.4. At B55: probe_line(-0.9750,data(-0.9750)) is called, an intersection
curve witli
Y coordinate = -0.975 is probed and surface data is collected and represented
as
data(-0.975), which is an arch of height 0.2222;
6.5.5. At B56 probe_area(-1.0000,-0.9750,data(-1.0000),data(-0.9750)) is
called, resulting
6.5.5.1. At B51 dis = 0.2236 is calculated;
6.5.5.2. At B52 neitlier condition is satisfied, procedure proceeds to B54;
6.5.5.3. At B54 intermediate value y = -0.9875, is calculated;
6.5.5.4. At B55 probe_line(-0.9875,data(-0.9875)) is called, an
intersection curve with
Y coordinate = -0.9875 is probed and surface data is collected and
represented as
data(-0.9875), which is an arch of height 0.1576;
6.5.5.5. At B56 probe_area(-1.0000,-0.9875,data(-1.0000),data(-0.9875))
is called, resulting
6.5.5.5.1. At B51 dis = 0.1581 is calculated;
6.5.5.5.2. At B52 condition yl-y0<E is satisfied, procedure proceeds
to B53;
6.5.5.5.3. At B53, saves data (-1.0000);
6.5.5.5.4. At B5 8, exits probe_area(-1.0000,-0.9875,data(-
1.0000),data(-0.9875));
6.5.5.6. At B57 probe_area(-0.9875,-0.9750,data(-0.9875),data(-0.9750))
is called, resulting
6.5.5.6.1. At B51 dis = 0.0658 is calculated;
6.5.5.6.2. At B52 condition yl-yO<E is satisfied, procedure proceeds
to B53;
6.5.5.6.3. At B53, saves data(-0.9875);
6.5.5.6.4. At B58, exits probe_area(-0.9875,-0.9750,data(-
0.9875),data(-0.975));
12
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
6.5.5.7. At B58 exits probe_area(-1.0000,-0.9750,data(-1.0000),data(-
0.9750));
6.5.6. At B57 probe_area(-0.9750,-0.9500,data(-0.9750),data(-0.9500)) is
called, resulting
6.5.6.1. At B51 dis = 0.0935 is calculated;
6.5.6.2. At B52 condition dis<=D is satisfied, procedure proceeds to B53
and
6.5.6.3. At B53, saves data(-0.9750),
6.5.6.4. At B58 exits probe_area(-0.9750,-0.9500,data(-0.9750),data(-
0.95));
6.5.7. At B58 exits probe_area(-1.0000,-0.9500,data(-1.0000),data(-0.9500));
6.6. At B57 probe_area(-0.9500,-0.9000,data(-0.9500),data(-0.9000)) is called,
resulting
6.6.1. At B51dis = 0.1334 is calculated;
6.6.2. At B52 condition dis<=D is satisfied, procedure proceeds to B53;
6.6.3. At B53, saves data(-0.9500),
6.6.4. At B58, exits probe_area(-0.9500,-0.9000,data(-0.9500),data(-0.9));
6.7. At B58 exits probe_area(-1.0000,-0.9000,data(-1.0000),data(-0.9));
7. At B58 exits probe_area(-1.1000,-0.9000,data(-1.1000),data(-0.9));
After exiting procedure probe_area(-1.1000,-0.9000,data(-1.1000),data(-0.9)),
the routine returns to B44 in FIG.4, saves data(-0.9000), and exits the whole
prograin
at B45.
The Pass Data Sets saved according to execution time is then:
data(-1.1000)
data(-1.0000)
data(-0.9875)
data(-0.9750)
data(-0.9500)
data(-0.9000)
13
CA 02463895 2004-04-16
WO 03/040651 PCT/US02/33185
The data order is consistent with the corresponding Y coordinates and is
different from the order in which they were digitized. For all these adjacent
pairs,
either their distance in 3D space is bounded by D= 0.14, or the distance
between
virtual intersection planes is bounded by E= 0.02. If a CNC inachine drives a
spherical tool of radius 0.25 exactly according to these trajectories, the
global
tolerance will be within E= 0.02, compared to the model (a sphere of radius
0.75) in
the digitized area (-1.1 < Y < -0.9).
One may see that the probe trajectories shown in FIG. 6 are more evenly
distributed in 3D space. Therefore, the predetermined tolerance is guaranteed.
This
method is not only useful for Line Digitizing, but also useful for Rotational
Digitizing
and other digitizing methods.
An advantage to the present invention is that the curves obtained from a
Digitizing program will be evenly distributed. This signifies that the global
tolerance
of the digitizing system is guaranteed.
While this invention has been described as having an exemplary design, the
present invention may be further modified within the spirit and scope of this
disclosure. This application is therefore intended to cover any variations,
uses, or
adaptations of the invention using its general principles. Further, this
application is
intended to cover such departures from the present disclosure as come within
known
or customary practice in the art to which this invention pertains. The
specification
and drawings are accordingly to be regarded in an illustrative rather than
restrictive
sense.
14