Note: Descriptions are shown in the official language in which they were submitted.
CA 02483361 2007-04-10
ICOSAHEXAHEDRON
A space structure usable in maw) structures; building construction, housing,
warehousing; and micro
= or molecular space structures and applications.
BACKGROUND OF THE INVENTION
The project began as an exploration of various existing known space structures
for possible use in
building construction applications, along the lines of the work that
Bucktninster Fn.tk:r achieved in his
explorations of the 3-frequency Geodesic Dome which eventually unexpectedly
led to the further
discovery of applications in micro and molecular structures, specifically the
discovery of the Carbon.60
molecule.
The project examined the feasibility of using the source structure of Fuller's
work, the lcosahcciron,
With various permutations applied to endeavour to discover new and novel uses
of the structure, either
through different mathematical transformations, or through fusion into newly
synthemived structures.
=
CA 02483361 2004-10-26
Research was done into the field of Geodesic Domes including Fuller's work and
publications such
as Domebook IT and Refried Domes. In Refried Domes is revealed many, many
technical
problems in using multi-frequency (high curvature) dome structures, summarized
as:
1) high variety of dimensional sizes and angles requiring much increased
labour.
2) as in item I whereby there is much material waste.
3) sound reflection problems due to the internal curved shape.
4) moisture problems in the roof due to no adequate ventilation strategy.
5) outward facing windows suffering from rain-shipping leakage problems.
6) difficulty in interface standard vertical internal walls to multi-angle
outer walls.
7) difficulty in installing insulation into many diverse gaps.
8) all the above causing an inherent specialization in the field regarding
Geodesic Structures.
In the world there have been many informal attempts to achieve an intangible
unclear goal of
using micro geodesic structures in a macro implementation that historically
have often failed
due to not completely and systematically meeting all of the above objectives.
There are some exceptions where various Geodesic Domes have been successfully
implemented
at World Fairs and various museums around the World, but albeit almost always
at very
greatly specialized expense and effort, hence failing several of the above
objectives.
The current construction code is based on an orthogonal methodology that does
not readily allow
a generali7ation of geodesic structures, keeping them highly specialized
because of the inherent
problem of dealing with many diverse non-orthogonal angles.
Traditionally, orthogonal approaches to building structures have been dictated
by the
orthogonal nature of gravity. In taking a different approach to offsetthig
loads under the force
of gravity one has to employ more complex geometric and mathematical formulas
to arrive at
orthogonal equivalents that are only available through very specialized, and
thus uncertain,
means.
This also requires more specialized knowledge and resources that may or may
not be available.
However the key uncertainty had lain in the fact that standard building
materials and
construction techniques are almost entirely oriented to the building
methodologies currently in
place. There was uncertainty in whether the Geometric Vectoring techniques
needing to be
employed would successfully arrive at values that match in efficient enough
fractions, the
standard dimensioning currently in use in the field of Building Construction.
2
CA 02483361 2004-10-26
A second uncertainty was in whether an efficient means of joining materials in
non-orthogonal
ways would require again, specialized joining mechanisms, defeating the
purpose of the
objectives, or whether a way of manipulating Geodesic Structures, perhaps
through fusion,
would lead to an efficient new way of joining elements with the required
strength.
The project set out and successfully solved these technical problems, as well
as making major
new unexpected discoveries. Work resulted in employing the native Icosahedron,
un-phased,
leaving the large planar surfaces intact. Next analysis led to implementations
whereby standard
building dimensions, specifically the 4x8 foot standard sheathing/drywall
panel, and the
standard 16", or 24" dimensions were mapped into effective implementations of
the
Icosahedron's native large triangular panels, to solve problem 1, 2, 3, 6, and
7. Problem 4 was
solved by employing a thick enough extrusion of the wall and roof system to
allow thick
enough insulation and air gap to meet building code for both. Problem 5 was
solved by
finding a window configuration that would see all windows slanted inward and
elegantly
configured doorways to be vertical.
Problem 8 was solved in solving problem 1 to 7 resulting in a successful de-
specialization, or
generalization, of a Geodesic Building Structure.
Further work led to discoveries a) of how to eliminate the roof-overhang
leading to many
advantages, b) an entirely new geometric shape known as the kosahexahedron
with one variation,
c) further repeatability in the design allowing high efficiency, and d) a way
of incorporating the
structural shape into macro, micro, and molecular applications which is the
basis for this
invention.
The project set out and successfully solved several diverse technical problems
in the Geodesic
Structures leading to a successful de-specialization, or generalization, as
well as making major
new unexpected discoveries. Work resulted in employing the native Icosahedron,
un-phased,
leaving the large planar surfaces intact. Next analysis led to implementations
whereby standard
building dimensions, specifically the 4x8 foot standard sheathing/drywall
panel, and the
standard 16", or 24" dimensions were mapped into effective implementations of
the
kosahedron's native large triangular panels, to solve problem 1, 2, 3, 6, and
7. Problem 4 was
solved by employing a thick enough extrusion of the wall and roof system to
allow thick
enough insulation and air gap to meet building code for both. Problem 5 was
solved by
finding a window configuration that would see all windows slanted inward and
elegantly
configured doorways to be vertical.
3
õ _____________________________________________________________________
CA 02483361 2004-10-26
Problem 8 was solved in solving problem 1 to 7 resulting in a successful de-
specialization, or
generalization, of a Geodesic Building Structure.
Further work led to discoveries a) of how to eliminate the roof-overhang
leading to many
advantages, b) an entirely new geometric shape known as the Icosahexahedron
with one variation,
c) further repeatability in the design allowing high efficiency, and d) a way
of incorporating the
structural shape into macro, micro, and molecular applications which is the
basis for this
invention.
What began as an investigation of a micro structure, the kosahedron, for use
as a macro structure
leading to the discovery of a new synthesized structure which is the result of
fusion between two
Icosahedrons, came full-circle in being applicable to micro and molecular
applications, in the
pattern of Buckrninster Fuller.
SUMMARY OF THE INVENTION
The invention is a Geometric shape which is the result of fusing or merging
two Icosahedrons into
one, along vertices and panels native to the kosahedron, retaining all
original vertices but
introducing new interface planes that are completely native only to the new
synthesized structure,
an Icosahexahedron.
The new structure has 3 unique internal planes that are of specific use in the
employment of the
shape as a macro structure, which also explicitly contribute to the definition
of the structure.
The original Icosahedron has 20 sides and 12 vertices, whereupon it is split
into two 10 sided half-
Icosahedrons, and fused together resulting in a shape that has the original 20
sides, but 6 new
interface panels which are: 2 of which are the same, another 2 different, and
2 quadrilaterals
different again, resulting in a structure that has 16 vertices.
There are several dimensional relationships in the structure that are based on
the mathematical
ratio PHI, otherwise known as the Fibonacci Sequence, and the Golden Ratio. Of
note is that the
ratio of the number of vertices of the Icosahexahedron to ifs number of
panels, 16/26, is a mid
increment ratio of PHI (between 13/21 and 21/34 in the sequence).
4
CA 02483361 2004-10-26
There is one variation of the shape where the 3 internal planes are not used
resulting in a structure
which is similar but less symmetrical, employing again the original 20
Icosahedron panels but
interfaced by 6 identical triangles, creating a pure Icosahexahedron. In
transforming the first form
of the Icosahedron into the second, the 2 pairs of different triangles and the
2 quadrilaterals,
become identical.
It is the first form of the Icosahexahedron having the 3 internal parallel
planes, and external
interface planes in 3 dimensions that is useful in macro building
applications.
The Icosahexahedron also has a staggering exact alignment with the left side
of the Star
Constellation Orion, and a Transformational Correspondence to the right side.
In the drawings forming a part of this specification are:
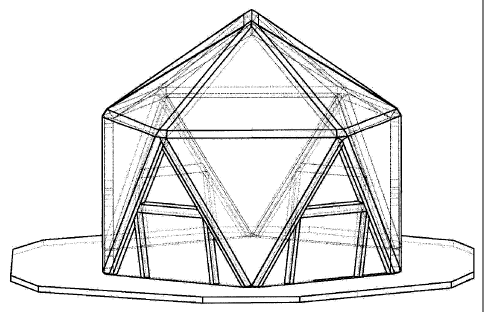
Fig.1-6 Solid views of the structure front and off-angle
Fig.7-12 Solid views of the structure side, top, and off-angle
Fig.13-18 Wireframe views of the structure, front, side, top, off-angle.
Fig.19-30 Wireframe views of the structure, varying off-angle.
Fig.31-36 Wireframe views upside down, front, side, top, off-angle.
Fig.37-48 Wireframe views upside down, varying off-angle.
Fig.49-60 Development of base component equilateral triangles and angles.
Fig.61-72 Views of single base component Icosahedron,front,side, top, off-
angle.
Fig.73-84 Views of interfaced base triangles to Icosahedron, varying.
Fig.85-87 Views of two base Icosahedrons aligned in proximity for fusing.
Fig.88-90 Views of base Icosahedron relevant alignment planes for fusing
Fig.91-93 Views of base Icosahedron key panels to be removed for fusing.
Fig.94-96 Development of major fusion interface planes and points.
Fig.97-99 Major fusion interface planes aligned and points connected.
Fig.100 Exploded View off-angle of structure with non-regular panels.
Fig.101-103 Views of resultant non-regular panels off-angle, front, top
Fig.104-115 Alternate views of structure derivation, front,top, off-angle.
Fig.116-126 Dimensional analysis of non-regular interface panels.
Fig.127-134 Development of structure major planes upper and lower.
Fig.135-149 Mathematical formulas for non-regular panels and upper plane.
Fig.150-158 Mathematical formulas for lower plane.of structure.
Fig.159-172 Mathematical formulas for vertical dimensions of structure.
- -
CA 02483361 2004-10-26
Fig.174-197 Development of alternate 26 sided structure subcomponents
Fig.198-209 Wireframe views of alternate structure with interface panels.
Fig.210-221 Solid views of alternate structure
Fig.221-236 Component substructure placement within fused structure.
Fig.237-248 Molecular external alignments and interface planes.
Fig.249-273 Views of substructures resulting from fused structure.
Fig.274 Wireframe off-angle view of the 3 major internal usable planes.
Fig.275 Solid exploded off-angle view of the 3 major internal planes.
Fig.276-277 Solid exploded front & off-angle view of the major equatorial.
Fig.278-284 Mathematical analysis of the 3 major internal usable planes.
Fig. 285-289 Solid views of upside-down upper-plane dissected structure.
Fig.290-294 Solid views of rightside-up lower-plane dissected structure.
Fig.295-301 Solid views of rightside-up equatorial dissected structure.
Fig.302-308 Solid views of updside-down equatorial dissected structure.
Fig.309-313 Solid views of rightside-up lower-planed window configuration.
Fig.314-315 Wireframe views of lower-planed window/roof/wall config.
Fig.316-319 Wireframe views of lower-planed 3 major internal planes.
Fig.320-325 Views of two structures interfaced to each other at side plane.
Fig.326-331 Views of two structures stacked at lower-to-upper planes.
Fig.332-337 Views of double-phased strut support in main panels.
Fig.338-343 Views of orthogonal-phased strut support in main panels.
Fig.344-349 Views of double-ortho-phased strut support mixed derivative.
Fig.350-384 Views of substructures resulting from double-ortho mix.
Fig.385-392 Mathematical analysis of double and ortho phase strut-works.
Fig.393-397 Mathematical analysis of standard 16" or 24" stud-works
Fig.398-399 Structural analysis of panel corner interface bolt-patterns.
Fig.400-404 Solid views of ventilated extruded wall and roof thickness.
Fig.405-410 Derivation of panel interface virtual beam structures. & bolts.
Fig.411-416 2.5 storey 2500 square foot free-standing house or warehouse.
Fig.417 Bottom view of structure showing bottom plane configuration.
Fig.418 Accurate sky view of Star Constellation Orion.
Fig.419 View of bottom view of structure aligning perfectly with Orion.
Fig.420 View of resulting interface matching Universal Symbol of Peace
6
CA 02483361 2004-10-26
DETAILED DESCRIPTION OF THE INVENTION
The 26 sided semi-regular polyhedron can be a planar solid, as in Fig. 1, a
wireframe, as in Fig. 13
or hollow solid with a shell thickness of varying depth defined by the
definition vertices of the
structure where all struts connect, extruded either inward toward inside the
structure or outward
away from the surface of the planes defined by the defining points of the
structure, defined further
in following discussion.
The structure is considered semi-regular for the reason that it is made up of
20 exact equilateral
triangles, which are regular, but also a non-regular family of 3 pairs
(another six) of isosceles
triangles, which are all linked in their characteristics mathematically, to
total 26 panels making up
the structure.
Further, the structure has a unique resulting paradoxical semi-symmetry, or
semi-asymmetry. From various
views the structure is very symmetrical, as in Fig. 7 & 8 and 9 & 10. In other
views it becomes very
graphically asymmetrical, as in Fig. 1 and Fig. 5. Various views in between
tend to show bizarre off-angle
variations of the two, as in Fig 2,3,4,6,11 & 12. In other cases a strange
kind of "hybrid-symmetry" can be
viewed like in Fig. 22 & 43.
A tangible asymmetry in one plane can serve as a directional means of
orientation of the structure.
In selecting one direction of the asymmetry as "rightside-up" it allows a
tangible method of
orienting the structure for identification and reference purposes. From this
orientation the
standard views of front, back, sides, top and underneath can be applied to the
rightside-up
orientation. A preferred orientation was selected based on a later developed
view of a certain
orientation identified as being most relevant to practical uses of the
structure, resulting in the
rightside-up orientation of Fig. 1.
This orientation was arrived at through the subsequent desire to remove the
bottom cap of the
structure shown in Fig. 257-260 in favour of using the top cap shown in Fig.
249-252 for the
purpose of eliminating the only non-triangular panels in the structure which
is desired for
construction purposes, leaving only triangular panels making up the primarily
useful structure as
defined further below. All front, side, top and bottom views of the structure
are based on this
orientation.
7
CA 02483361 2004-10-26
Views that are employed are: front, back, top, underneath, left and right.
They are identified in
the drawings with a cube present nearby the structure or other elements
identified respectfully: F
(front), B (back), L (left), R (right), T (top) and U (underneath).
In vvireframe drawings solid lines represent struts that are on the viewer
side of the structure,
whereas dotted lines represent struts that are on the opposite side of the
structure, as viewed
transparently.
All 3D views of the structure are with Zero Perspective, i.e. non-isometric,
so that the effect of
symmetric can be seen in cases where perfect symmetry in any wireframe view is
indicated by the
absence of any dotted lines, where it can be inferred that other associated
drawings that the dotted
line is hidden immediately behind the solid line indicating perfect symmetry,
as shown in Fig. 13,
15, & 31. Using any degree of perspective would introduce difficulty in
properly understanding
the degrees of symmetry throughout the structure.
Derivation of the structure begins in Fig. 49-60 starting with a simple
Equilateral Triangle in Fig.
49. This is a very important basic building block in deriving the structure,
and is given a unit
dimension called "T" for each equal side of the triangle 0 as in Fig. 121,
which can be any non-
zero size, and is described further below. By mathematical definition the
Angle U in Fig. 121
inside each corner of the triangle will always be 60 degrees
The same triangle is shown in Fig. 2 from Right View slightly elevated. A
second identical
triangle joined to the first along one edge is shown in Fig. 51 where the
joining edge becomes an
axis of rotation for the second triangle as in Fig. 52 identified as Axis A
forming Angle B between
the two triangles in Fig. 53.
Note that the use of the the equilateral triangle as a building block was
original derived from
analysis of the Regular Polyhedron structure known as the kosahedron, a 20
sided structure. The
Icosahexadron comes from the result of fusing two Icosahedrons together
according to a certain
protocol described further below. From that analysis it is established that
the correct angle of
rotation between the triangles in Fig. 53 to allow the pair to be used as a
subcomponent making
up an Icosahedron, is (rounded to one decimal place here and expanded further
below) 138.2
degrees and can be viewed in Fig. 54-60.
This dual triangle component can be employed empirically facing in and joining
only by its 3
vertices to adjacent identical components to arrive at the kosahedron
structure. Following these
8
CA 02483361 2004-10-26
rules will result in no other possible structure and will result in accuracy
of the overall structure
depending on the accuracy of size T and Angle B.
The characteristics of paradoxical-symmetry can be viewed in the Icosahedron
as in Fig. 61-72, for
which the invention amplifies into many new variations as though the two
parent fused
Icosahedrons result in a completely new unique variant characteristic
offspring that is similar yet
different.
The employment of the dual triangle component of Fig. 51 into the Icosahedron
is shown in Fig.
73-84 whereby each component interfaces to each adjacent one by connected
through the 3
vertices of each triangle at an angle of 138.2 degrees.
Note that there are other alternate mathematical methods of deriving the
Icosahedron but this one
is selected for it's simplicity and direct application in using 3D CAD tools
to construct the base
Icosahedron as a subcomponent to the invented Icosahexahedron.
Further, the invention can be created and modelled through various
mathematical methods but in
this case is presented in the same method as it was discovered, through
manipulation of 3D
representations of the level of vertice structure of two adjacent kosahedrons.
In other words the derivation assumes two perfect Icosahedron base units with
zero-width panel
thickness that will be connected together perfectly at various vertices shown
below.
To begin the process of fusing two kosahedrons together they need to be
roughly oriented as in
Fig. 85-87. Various experimental development was required to arrive at the
final successful joining
method that identified the various panels in Fig. 88 being removed as the
result of slicing the two
Icosahedron structures in Fig 85-87 to create the two new substructures STRI
and STR2 along
the respective planes DI and D2 shown in Fig. 88-89, resulting in key vertices
that can allow
logical interface points at VTX1-1 to 5 and VTX2-1 to 5 along planes D1 and D2
Next, the panel families E, F, and G need to be removed from, the structures
STRI and STR2 in
Fig. 91-93 which results in the two new derived structures STR1b and STR2b in
Fig. 94-96.
The two new structures then need to be aligned so that the plane PLN1 defined
by vertices VI-1
to 4 matches the plane PLN2 defined by vertices V2-1 to 4. And also so that
the plane PLN3
defined by vertices VI-5 to 7 and plane PLN4 defined by vertices V2-5-7 match
each other.
9
.=,......xwargrestzwmmi MilfflOMOI
CA 02483361 2011-01-24
The two structures STR1b and STR2b are then joined together at the two
interfaces il and i2 by
connecting the vertices V1-2 and V2-1 together, as well as the vertices V1-3
and V2-4, all the
while maintaining the planes PLN1 and PLN2 equal, as well as the planes PLN3
and PLN4 equal,
which results in the new single synthesized partially complete structure in
Fig. 97-99.
In Fig. 100 is an exploded view of all new panels created in fusing the two
Icosahedrals resulting in
panels J1-2, K1-2, and L1-2 making up the new panel types J, K, L, adding to
existing panel type
0. In Figure 101 the struts Si to 4 are created by creating a) strut Si
between the two top vertices
V1-9 and V2-9 at the top of the fused structure creating the new panels J1 and
J2, b) strut S3
between the bottom two vertices V1-8 and V2-8 creating the new panels Li and
L2, c) strut S2
between the two front vertices V1-5 and V2-5 creating the new panel Kl, and d)
strut S4 between
the two back vertices V1-6 and V2-6 creating the new panel K2, as in the panel
families J, L, K
shown at the bottom of Figure 100.
The connected vertices result in the completed invention, an Icosahexahedron,
in Fig. 101-103,
showing the regular panels in transparent (white) with the non-regular panels
in grey.
The non-regular panels are interestingly related to each other and displayed
viewed laterally from
the front for clarity in Fig. 116.
In Fig. 117-119 the non-regular panels are showed in various two-dimensional
special
relationships which can be summarized as following.
a) In Fig. 101, strut S1=S3, amazingly, b) strut S2=S4, and c) 52=S1 *2
In Fig. 120 forward the variable R is assigned to the length of Si and the
variable S is assigned to
S2. The variable T is as mentioned the overall system structure base unit,
which for practical
purposes can be set to the value 1 to simplify derivations.
Of extreme significance are the following relationships also summarized in
Fig. 125: a) R=S/2, b)
S=2R, c) the short edge of panel J in Fig. 120, R, is identical to the long
edge of Panel L in Fig.
123, as also shown graphically in Fig. 119, d) the long edge of Panel in Fig.
122, S, is identical to
the long edge of Panel L in Fig. 123, as also shown in Fig. 119, e) as the
overall structure is
oriented, the vertical oriented struts all are size T, whereas the horizontal
oriented struts Si to 4 all
follow the above relationships, f) 3 Panel J's in Fig. 123 fit perfecdy
dimensionally inside 1 Panel L
as in Fig. 124.
CA 02483361 2011-01-24
All internal angles are listed in Fig. 126 and can be calculated using
standard mathematical
geometry since all triangle side lengths are known.
Of structural significance is the orientation of the plane PLN5 in Fig. 97,
hereby known as the
Plane Top PT as shown in Fig. 274, and the plane PLN3/PLN4 (PLN3=PLN4) of Fig.
97
hereby known as Plane Bottom PB as shown in Fig. 274. In an analysis of these
two planes there is
a dual symmetry exists in that base components of each invert to create the
other, as explained
further in Pig. 127-134.
In an analysis of Plane Top PT first, in Fig. 127 & 131 looking down from
above are two identical
sided polygons known as pentagons, PN1 and PN2, which are the same as the two
top and
bottom planes of a regular kosahedron, as can be seen in Fig. 85 & 87.
Plane Top PT is derived as in Fig. 94 by connecting vertices V1-2 to V2-1 and
vertices V1-3 to
V2-4. This results in a geometric shape of Plane Top as in Fig. 129. The
location of V1-9 (and
V1-8) in STR1 is the same as vertex VTX1 in Fig. 128 which is also the
intersection of lines DL1
and 2, and the location of V2-9 (and V2-9) in STR2 is the same as VTX2 in Fig.
132 which is
also the intersection of the two lines DL3 and 4 resulting in the locations
for the vertices VTX1
and 2 in Fig. 129 & 130 (& 133).
Plane Bottom PB is made up of the same two Pentagon components in an inverse
way, as in Fig.
133 where the vertex in Fig. 94 V1-5 is connected to V2-5 by the distance S,
similarly for the
vertex V1-6 to V2-6, resulting in the pattern for Plane Bottom in Fig. 133
Looking down on the overall structure in Fig. 101-103 results in the same
pattern as in Fig. 134,
showing the overlapping views of Plane Top, and Plan Bottom, with the
interaction of R in Fig.
129, and S in Fig. 134, which is extremely novel and intriguing.
A further analysis of relevant parameters of the invented fused structure is
in Fig. 135-149, where
in Fig. 135 is shown Plane Top where the previously derived values R and T are
visible, and the
new values P in Fig. 136 which is the perpendicular line from T looking in the
downward plane
across to the vertex VTX2 in Fig. 132. The value Z in Fig. 137 is the line
segment from V1-2/V2-
1 in Fig. 94 to the extension of the line segment T which also defmes 1/2 the
length of the
rectangle completely enclosing the shape of Plane Top.
11
CA 02483361 2011-01-24
Similarly the value ZZ in Fig. 138 is the other axis dimension which is half
the difference between
T and the width of the rectangle completely enclosing the shape of Plane Top.
The length of Plane Top PT is analyzed in Fig. 139 where it is equal to P + R
+ P = 2Z, which is
also used to do an independent verification of R.
Fig. 143 reviews the relationships of the panels J, K, and L in the
calculations in Fig. 140-149, for:
a) the Angle V in Fig. 140 & 144, b) the Angle X in Fig. 141 & 145, c) that
Panel L in Fig. 142
& 143 is made up of exactly 3 Panel J's in Fig. 140, d) the Angle Q in Fig.
140 & 147, e) the
Angle W in Fig. 141 & 148, f) the bottom corner angles of Panel L in Fig. 142
is equal to Q + V
in Fig. 149.
In Fig. 150 is a representation looking down on the overall structure with PT
and PB overlapping.
The dimension S at the bottom if the figure is mirrored in symmetry at the top
of the figure with
the apex of the triangle with base S touching the midpoint of the upper
dimension S.
The dimension SW, Structure Width, is the width of the rectangle which fully
encloses Plane Top
PT (or similarly PB) with a large edge of both sides of the long side of the
rectangle adjacent to
the S dimension of PB for a portion of that length and the short edge of the
rectangle adjacent to a
length of T of the edge of PT.
The rectangle which fully encloses Plane Bottom PB has the same width as for
PT except for the
extension YY as seen at the extreme left center of the figure which is
mirrored symmetrically on the
right side.and is calculated in Fig. 151. The extension of these two
dimensions is used to calculate
the length of the enclosing rectangle by summing various previously calculated
dimensions P and
R as in Fig. 152.
The triangle in Fig. 157 is a bisected half of the isosceles triangle in Fig.
150 with it's base at the
bottom dimension S and apex at the top of the figure. Fig. 153 is an alternate
derivation of R by
using other derived values as a verification of the value, using ZZ and T.
Fig. 155 is a review of
the relationship between S and R.
The length PP in Fig. 150 and 156 is not relevant to the native Icosahedron or
this structure,
except in the context of looking down on either structure from the top, and
measuring the distance
laterally. In other words the true distance of the strut is T, but as viewed 2-
dimensionally as in the
figure is PP. This is a useful dimension for purposes of using the structure
in practical
12
. ,
CA 02483361 2011-01-24
space applications, for example if a support post were to be employed
vertically at Val or VTX2,
the distance to the nearest wall corner at the connection between ZZ and T.
In Fig. 158 the dimension UU is calculated in order to arrive at an alternate
value of the total
length of the rectangle enclosing PT by summing with the line segment S.
Finally, a major discovery in the invention is that the relationship between
the enclosing structure
width, SW in Fig. 154, and T, the unit length of the base sides of the
subcomponent triangles
making up 20 panels of the structure, is a perfect inverse of PHI, otherwise
known as the
"Fibonacci Number", or "Golden Ratio". Which means that viewed in various
other ways is the
same relation as PHI. I.e., an alternate equivalent relation is that T is
equal to SW * PHI.
In Fig. 159-173 are analyses of horizontal front views of the overall
structure summarized in Fig.
160 and developed as follows. Fig. 159 shows how intriguingly the intersection
of Strut S3 in Fig.
101 with Plane Bottom PB as in Fig. 274, creates a perfect square as also
shown in Fig. 172
element WW with side dimensions of R. A similar square is created in perfect
symmetry in the
front view in the vertical plane from this bottom square where the Strut Si in
Fig. 101 intersects
with Plane Top PT in Fig. 274. In aesthetic terms this is useful in
applications as a macro space
structure for habitation or warehousing in portraying balance ergonomically.
This is proven by the derivation of the value HH in Fig. 159 8c 166 as being
equal to R
If the relation R to T, or other dimensions native to the invention can be
found to match with
atomic relations then new synthesized molecular substances will have been
invented.
Further calculations for practical applications follow from Fig. 163 and 162
where Fig. 163 is an
extraction of the right side of the overall structure in Fig. 159 with one of
the base Equilateral
triangles from the set of 20 making up the invention displayed in a plane
perpendicular to the
viewer in Fig. 162 (hence the Not Front indicator since the plane is not
perpendicalar to front).
The practical dimension TI' is the vertical distance of the base component
triangle calculated in
Fig. 161 which would be relevant in calculations for ceiling height through
the triangle if used as a
passageway for human habitation or other functional uses. TT also gives the
distance of a similar
triangle viewed edge on in Fig. 163 making up what would be a roof panel in a
housing
application, another required dimension. Here it is also used to support the
development of the
various angles in Fig. 163 of BB, angle from ceiling to roof inclination,
angle MM, angle from wall
to vertical, angle QQ which is the 90 degree angle offset of the wall to the
ground, and angle
13
¨ ,õ
CA 02483361 2004-10-26
B which is the angle of prime importance in the entire structure of which
derivation and primary
understanding is required in the process to allow the synthesis of the
Icosahedron into the
invention, as in Fig. 52-60.
The process to derive Angle B begins with derivation of Angle QQ in Fig. 163
and 165, to Angle
1VIIVI in Fig. 163 tic 167, proceeding to Angle BB in Fig. 163 8c, 164,
finally to arrive at Angle B in
Fig. 163 and Fig. 169.
Angle B can be rounded to 138.2 degrees as in Fig. 52-60.
Dimension GG in Fig. 163 is slightly different to 'IT in Fig. 162 because
although the triangular
panels are identical, in Fig. 163 there is a slight outward slope, which is
indicated in the edge on
triangle hidden in Figure 163 of the lower dimension panel denoted by U. So 11
is the panel
height, GG is the vertical height, which are slightly different as shown in
Fig. 171.
The total vertical height of the structure TH shown in Fig. 172 as the
addition of the vertical
dimensions of WW * 2 + AA is derived in Fig. 168 but summing previously known
dimensions
as related to T.
A further intriguing discovery in the invention is the relationship in Fig.
170 showing that the
ratio between the vertical distance between the top (PT) and bottom plane (PB)
as in Fig. 274,
GG, (or the height of AA), to T, is PHI.
Further, it is found in Fig. 170 and summarized in Fig. 173 that the ratio of
the height of the
previously mentioned perfect square WW, to the height of the rectangle AA, is
PHI.
The synthesized 26 sided polyhedron structure thus derived, is known as an
ICOSAHEXABEDRON
from Icosa - 20 + Hexa 6 = 26. An alternate nomenclature for 6 is Hexa,
resulting in
ICOSASEXARBDRON
These are acceptable references in general terms, but to be more precise, the
structure is
symmetrical in 20 panels, then another two more J1 and J2, equal to themselves
but not to the
14
,
CA 02483361 2004-10-26
other 20 panels, as in Fig. 100, then two more are different again K1 and K2
in Fig. 100, and
finally another two more which are the Quadrilaterals Li and L2 in Fig. 100 as
well.
To complete the definition may also be included the 3 internal planes PT, EQ,
and PB as in Fig.
274 as they define the orientation of how to connect the two fused kosahedrons
in Fig. 94-96.
So a more precise reference for the structure is:
20 + 2 + 2 + 2
which under nomenclature would be known as:
ICOSADUODUODUOHEDRON
or under a variation on the reference to two being "Do" rather than "Duo"
ICOSADODODOHEDRON
or two being "Di"
ICOSADIDIDIHEDRON
Finally, there is a whimsical identification which refers to the significance
of a 26 sided structure
identified in literature as being defined as: "A fictitious structure". Also
which of note, having 26
sides coincides in a novel way with the number of letters in the alphabet.
A further connection is in an affinity with J.R.R. Tolkien's description of an
ancient mythical
structure of significance with power of influence due to many factors some of
which were in the
proportion of it's shape and the manner of it's grand making. For which after
being the very root
cause of endless war itself found its final resting place after proving too
much a burden for the
world, in the night sky as a lost star. To dramatically return only at a time
when the world was
deemed ready. In light of this it is considered within the bounds of apt
novelty to further apply to
the invention the name:
SILMARIL.
CA 02483361 2004-10-26
Of lesser note there is an alternate 26 sided polyhedron structure which will
be briefly described,
which is related to the invention in that it also has 26 sides, is similarly
made from the fusion of
two Icosahedrons, has 6 extra sides, and is of novelty interest as a parallel
invention but is not
identified as having the same practical applications in macro building
structures to the degree of
great utility of the primary invention previously described above.
It is shown in Fig. 108-209 in wireframe view and Fig. 210-221 in solid view.
Following is a description of the synthesis of this second structure whereupon
the description will
revert back to the primary invention.
This second 26 sided polygon structure has the characteristics of similarly
being two fused
Icosahedrons, but without the alignment of the 3 internal Planes PT, EQ, and
PB in Fig. 274,
which are completely non existent in this structure
The structure has symmetry in two planes, and the six extra interface panels
which are different
again from the base 20 panels, are in this case, identical to each other
resulting in the detailed
nomenclature
ICOSAHEXAHEDRON (and/or ICOSASEWEEDRON)
is completely accurate since the 6 extra panels are all identical.
To construct this structure is similar to the ICOSADUODUODUOHEDRON in that two
base
ICOSAHEDRONS have various panels removed and then joined at various logically
convenient
vertices.
The difference between the two synthesized structures is in that this one does
not align with the
internal planes intact, but rather depends completely on the joining at 3 co-
planar vertices instead.
Meaning also, that after joining the two together, no extra connection struts
are required.
In Fig. 174 is a slight off-angle front view of an Icosahedron. In Fig. 175 is
a Front view.
Note that an alternate method of making both this structure and the
Icosaduoduoduohedron are
presented in Fig. 176, in that rather than follow the process outline
previously shown in Fig. 91-
16
CA 02483361 2004-10-26
93, & 104-115, an alternate method is to simply take ONE Icosahedron, and
split it along a
natural equatorial that follows it's strut connections.
This results in the two half-kosahedrons in Fig. 176 and also creates the same
resultant structures
in Fig. 94-96, in an alternate method.
In this method, now one of the half-Icosahedrons has to be rotated 180 degrees
as in Fig. 177 &
178 to arrive at the orientation in Fig. 179, which is identical to the result
of the process in Fig.
94.
From this point it would be possible to align the internal planes PT, EQ, and
PB as described and
arrive at the synthesis of the kosaduoduoduohedron.
But to create this alternate structure the two structures STR1 and STR2 are
joined differently.
First are some views of the nature of each half-kosahedron shown in Fig. 180-
185, including an
axis of rotation which is perpendicular to the central panel of the structure,
identified as AX4 in
Fig. 186.
To align the two half-Icosahedrons to make this alternate structure requires
aligning them so that
the Axis AX4 for both halfs, is equal, as in Fig. 186-189, next one half must
be rotated about Axis
AX4 180 degrees as in Fig. 190 & 191, whereupon the two halves can be joined
at 3 native
vertices as in Fig. 192. To finish, the Struts SU1, SU2 and SU3 in Fig. 193 &
194 must be
connected, resulting in the complete structure in Fig. 194, a pure
Icosahexadron.
Further wireframe views are in Fig. 195-197. In Fig. 198-209 are shown the new
resultant
interface panels in grey, which total 6 and which are all identical isosceles
triangles, where the
other 20 native Icosahedron Equilateral triangular panels are in transparent
(white), with solid
views in Fig. 210-221.
It is a novel structure that has geodesic strength, is symmetrical in 2 planes
(facing front, left to
right, and top to bottom, as in Fig. 213, 220).
The structure also exhibits the similar trait in the Icosaduoduoduohedron of
"hybrid-symmetry", as
in Fig. 214, and semi-asymmetry in Fig. 210, 211, 212, 215, 216, 217, 218,
219, and 221.
17
¨ _
CA 02483361 2004-10-26
Continuing on with the primary invention, the Icosaduoduoduohedron, which from
this point
forth will be referred to again with it's general reference the
Icosahexahedron, in Fig. 222-236 is
an analysis of substructures which result from the synthesis of the structure.
There are 6 substructures shown in Fig. 249-273 further described below,
whereas in Fig. 222-
236 the actual placements of these 6 subcomponents are shown.
The overlapping interfaces of the interlocking subcomponents contribute to
great geodesic
strength at the same time due to the diversity of slightly different shapes
contribute to an aesthetic
effect in the structure.
In Fig. 237-248 are addressed external interface interactions between several
structures due to
several innate external planes resulting in the resultant fused structure.
In Fig. 237 two Icosahexahedrons can be stacked and joined at Strut S3 of Fig.
101 of Fig. 237
STR-U, and Strut S1 of Fig. 101 of Fig. 237 STR-L.
This results in the substructure DCUL in Fig. 237, a novel structure which
defines physically the
nature of the interface between two Icosahexahedrons in this plane further
shown as Plane MPT in
Fig. 247 and Fig. 246 with 3 units stacked vertically, and also in Fig. 238,
239, 240, & 241.
Next, there is a natural vertical surface which is Panel K1 and K2 in Fig. 100
which allows the
sharing of the Plane MPF in Fig. 247 among several interfaced Icosahexahedrons
in that plane,
also shown in Fig. 240, 241, 242 & 243.
Finally, in the third orthogonal dimension of 3D space, the common vertices of
joined
kosahedrons create the Plane MPR in Fig. 247, where each corner of the Plane
MPR is the
interface point for two adjacent Icosahexahedrons in that plane, also shown in
Fig. 238, 239,242
8c 243.
A variation on interfaces that flips various units around in various planes is
explored in Fig. 244,
245, and 248.
Such orientations and interfaces will have use in micro structures allowing a
large base unit, the
kosahexahedron, but with many planar connection points, which will tend to
create a novel
material with properties of strength.
18
woesswaw...1110.1.% .11.11" vants-va.
CA 02483361 2004-10-26
At a molecular level the synthesis of two Icosahedrons into one fused one will
create a new
synthesized material that similarly will have benefit of low mass due to large
molecules but many
connection points in 3 dimensions.
The native substructures that result from the synthesis of the Icosahexahedron
are listed in Fig.
249-273.
Fig. 249-252 are views of the HEXADUOCAP (6 + 2), named for being a 6 common
plus 2
extra sided pyramid that is defined as the slice created by Plane Top PT in
Fig. 274 resulting in the
top component in Fig. 275..
Fig. 253-256 are views of the DECADUOSECf (10 + 2), the middle section created
by slicing
the Icosahexahedron at both PT and PB in Fig. 274, which has 10 identical
sides, with two K
panels as in Fig. 100, which appears as an elliptical (or oval) shaped, 12
sided drum-kit also shown
as the middle section in Fig. 275.
Fig. 257-260 are views of the 1ETRADUOCAP (4 + 2), the bottom section defined
by slicing
the Icosahexahedron at PB in Fig. 274 resulting in the 4 common sides and 2 L
Panels in Fig. 100
6 sided pyramid, also shown as the bottom section in Fig. 275.
Fig. 261-264 are views of the PENTACAP (5) sided pyramid which is native to
the Icosahedron
and represents the unchanged parts of the Fused Icosahedrons making up the
invention.
Fig. 265-268 are views of the TETRAUNIUNICAP (4 + 1 + 1) sided pyramid which
are the
substructures resulting from the interface of 4 Equilateral triangles, a J
Panel, and a K Panel from
Fig. 100.
Fig. 269-273 are views of the INTEHEXAPENTACAP (integrated 6 and 5 sided)
pyramid,
which is the result of part of a Pentacap with one L Panel in Fig. 100, the L
panel being a
Quadrilateral can be thought to be be one panel as in the view Fig. 269,
making a non-regular
Pentacap, or, inherently can also simultaneously be considered to be dissected
into 2 triangles as in
Fig. 270, meaning that it is also a non-regular Hexacap (6 sided pyramid)
Note that the 6 identified substructures described above, 5 are completely
unique to the invention,
i.e. the Icosahexahedron. This means that do they do not knowingly exist in
any other currently
19
CA 02483361 2004-10-26
existing polyhedron structures. They result inherently because of the planar
and connection
characteristics in joining two Icosahedrons together along PT and PB at the
vertices described. As
such they are unique substructures of the invention.
However, the Pentacap substructure is inherent to the Icosahedron polyhedron
and as such is not
unique to the invention and is well known as a pentagonal structure.
The kosahexadron has a natural equatorial, EQ, as in Fig. 276,277 and defined
in Fig. 274. EQ
is also one of 3 planes in Fig. 274 that are unique to the invention and are
the result of merging
planes in the two fused Icosashedrons into one on each of the 3 levels.
Each level makes for a convenient and useful application as a floor or ceiling
in various further
configurations of the invention.
Hence follows a further analysis of PT, EQ, and PB in Fig. 278-283. Fig. 278 &
279 show plane
Top PT and some characteristics. First, it is 6 sided, a stretched Hexagon.
Also every dimension is
T, the system base unit. The rectangle enclosing PT is described previously
and reviewed in Fig.
279 where the calculation of the Angles Al and A.2 are in Fig. 282.
In a practical application as a building structure, in a preferred
configuration (rightside-up) PT
serves as a very convenient and useful roof-line, as described further below.
The Plane Bottom PB in Fig. 280 & 281 is also a stretched Hexagon but is
different in shape and
has 4 T dimensions and 2 S dimensions. The rectangle enclosing PB also
completely encloses the
entire structure which is useful for building construction purposes, and SL
and SW are defined in
more detail previously in Fig. 152 & 154. The Angles B1 and B2 are further
described in Fig.
282.
Again in a practical application, PB serves as a very convenient and useful
ground floor-line as
described further below.
The Equatorial EQ in Fig. 283 & 284 is a hybrid of Plane Top PT and Plane
Bottom PB, since
struts interfacing the upper and lower plane pass though the equatorial
definition points. This
results in a plane that is 12 sided, is elliptical (or oval) shaped, and has
dimensions that at half of T
or half of S ( R ). The length of EQ is SL YY as in Fig. 150 and has the same
width as both PT
and PB.
oeve.ueveakmaximorm* =
CA 02483361 2004-10-26
Again EQ serves as a very convenient and useful floor or ceiling line as
described further below.
Note that intriguingly, because PT, EQ, and PR all have the same width, this
means that the
panels K in Fig. 100, are perfectly completely vertical planes.
This is directly useful in building construction applications because a) it
allows a natural door
placement allowing a vertical door and not the slight slope out or in that
occurs in the native
Equilateral panels and b) it allows applications where one or more
Icosahexahedrons can be joined
along this vertical interface side by side as described below, and c)
ergonomically it allows for
some standard wall orientations in a structure that otherwise may be too
overwhelming in it's non-
orthodoxy.
Various combinations of slicing and removing substructures from the
kosahexahedron result in
various novel configurations, some of which are well suited to building
construction applications.
The first variation, considered the least desirable, is in by turning the
kosahexahedron upside-
down (bottom-up), slicing it at PT and removing the HEXADUOCAP in Fig. 249
resulting from
the slice, which results in the structure in Fig. 285-289. This is undesirable
simply because it uses
the TETRADUOCAP in Fig. 257 for a roof, which includes the Quadrilateral panel
L in Fig.
100, whereas for purposes of geodesic strength and simplicity of structure, it
is preferable to use a
configuration made up only of triangular panels, which is what results when
using the preferred
"rightside-up" configuration which puts the triangular-only BEXADUOCAP in the
roof position,
as in Fig. 290-294
This preferred configuration also allows for other features like upward
pointing K Panels which
better allows a doorway or window structure whereas the upside-down triangle
in the inverted
structure would make passage through impossible.
The preferred configuration slices the rightside-up structure along Plane
Bottom PB and removes
the TETRADUOCAP in Fig. 257 resulting in Fig. 290-294.
In this configuration, by sizing T to a practical size that would allow the
structure in Fig. 290-294
to be a two storey structure, would as a benefit allow the EQ plane to serve
as a logical second
floor/first floor ceiling, as described further below.
21
CA 02483361 2004-10-26
However, the same structure can be sliced at the Equatorial EQ to arrive at
the convenient one
storey resulting structure ideal as a bungalow, cottage, garage, or shop, as
in Fig. 295-301 for
which again has a perfectly vertical plan on either side in this case being a
dissected K Panel in Fig.
100, that if sized properly, would allow a standard doorway.
For comparison purposes the upside-down version is shown in Fig. 302-308 which
again is not so
ideal for building construction at least, for the reasons described above.
Developing the preferred configuration further in Fig. 309-313 shows a
preferred window
configuration, which is convenient and useful in building construction
applications because a) it
allows window structures to slope slightly outward eliminating the problem of
windows shipping
water, b) any of these openings could also server as doors allowed to be
vertical with a small
amount of vertical support blocking making a vertical doorway., c) a novel
aesthetic effect results,
d) a continuous roof-line is possible from the roof all the way to the ground
in a triangular wall
configuration, albeit requiring specialized eaves-troughing and roof
ventilation in the design used.
Further views of this preferred configuration shows PT, EQ, and PB, the window
configuration,
floor and ceiling configuraitions in Fig. 314-319.
Note that inherent in using the Icosahexahedron in such applications lend well
to Post-and-Beam
consrucdon techniques that would allow using geometrical mathematical
techniques applied to the
strut configuration to be directly applicable, as opposed to a Frame type
approach.
This allows further applications of open type structures like Pavilions or
Salt Domes where only
the roof needs to be covered.
In Fig. 320-325 is shown a further development where one or more units can be
constructed
connected together sideways with the K Panel in Fig. 100 as the logical
interface where a large
opening between units would be allowed, allowing two or more units to be
connected into one
functional dwelling or other functional application.
This sideways connection is allowable in either a two or one storey
configuration where either PB
or EQ are the floorline as in the figures.
In Fig. 326-331 is shown a further development where one or more units can be
constructed
stacked vertically resulting in a new novel application that as in Fig. 326
would create a 4 storey
22
_
CA 02483361 2004-10-26
structure (with attic space) that is its own unique shape. In this scenario
all panels are repeatable
across levels.
With proper sizing and joining methodologies, this configuration can be
utilized to create a
stacked Highrise building that uses standard, repeatable strut components that
would result in a
very novel oscillating floor type effect where the window effects would allow
for a repeating
diamond effect, as in Fig. 330 on the front and back side views of the
structure, and a contrasting
divergent diffractive window effect from the side views.
This structure has inherent geodesic strength due to the oscillating fold-
effect between adjacent
floors that allows efficient use of materials and contruction labour.
To focus back to aspects of the base invention, to develop the Post-and-Beam
approach, there is a
natural support-strut configuration allowed by the fact the majority of panels
making up the
structure, can be dissected at their mid-points and have support struts
connecte there, adding
strength and also allowing weaker materials to be used since the T struts have
support at all their
midpoints, as in panel QP1,2, &3 in Fig. 332.
The elements TP1, 2, & 3 are known as "Tri-panels", being triangular building
panels. The
elements QP1, 2 &3 are known as "Quadpanels" since they are made up of 4
joined Tr-panels.
Hence a method of building up Quad-panels from Tr-panels allows repeatability,
strength, and
efficiency in building construction, shown in Fig. 332-337.
A further development is a more relevant orthogonal arrangement as in Fig. 338-
343, where the
Element QP1b, 2b, &3b represent a migration toward more efficiency in that
standard building
construction practice tends to be naturally oriented to orthogonal structures,
due to the force of
gravity which is vertical.
This configuration has the beneficial side-effect of allowing a larger,
rectangular entrance way
through the K Panel in Fig. 100, or the QP2b panel in Fig. 338, as further
shown in Fig. 339-
343.
A further development upon analysis shows that a logical mixture of both panel
types is beneficial
since the roof and wail panels do not require openings, hence could make use
of the advanges of
23
CA 02483361 2004-10-26
the QP1, 2, &3 configuration, and then the lower floor window and doorway
panels could make
use of the QP1b, 2b, and 3b configuration, as illustrated in Fig. 344-349
In employing the above method various substructure components arise which are
summarized in
Fig. 350-384, which are similar to the already described components in Fig.
249-273 except for
some additions will arise due to the use of the QP method employed above.
The structures Fig. 350-364 are already described. However in Fig. 365-369 is
the result of a
lower corner in the QPb strategy.
Fig. 370-374 is the similar resulting corner adjacent to a K panel in Fig.
100.
Fig. 375-379 is the substructure resulting from a QPb employment between a
wall and roof
interface at the front Ka' panel Interface in Fig. 100.
Fig. 380-384 is the substructure resulting in the corner QPb employment
between a wall and roff
interace at the Pentacap interface in Fig.! 264.
In Fig. 385-392 are various dimensional values for the different panel
configurations. Fig. 384
shows the dimensions for a QP1a (same as QP1).
Fig. 386 shows the equivalent QPb configuration.
Fig. 387 shows the QP2a panel, which is the same as a K Panel in Fig. 100,
with the equivalent
QPb configuration in Fig. 388.
Fig. 389 Shows the J Panel in Fig. 100 as a QP3a configuration, with the
equivalent QPb
configuration in Fig.390.
Fig. 391 shows the QP configuration for a L Panel from Fig.100, and the
equivalent QPb
configuration in Fig. 392.
Thus the Post-and-Beam strategy is set now the internal stud-works to it has
to be established as
in Fig. 393-397, where all standard building construction configurations are
applied.
24
WI IMPRIAMMIAIIM110109.-
CA 02483361 2004-10-26
This means a way of fitting standard 16" or 24" studs-on-center in between the
strut works
developed in the QP and QPb types decribed above.
In doing so 5 different configurations were arrived at that allow for
convenient and useful sizing
of struts, as shown in Fig. 393-397.
Next the strategy for connecting struts in the QP configuration are shown in
Fig. 398. This
method uniquely allows using standard bolts (or screws as shown) to connect
beams (or struts)
together into Tii-panels as standard, repeatable building units that are easy
to fabricate, are
efficient, strong and sized to allow transport in standard trucks.
These panels are then builtup at the construction site into Quad-panels as in
Fig. 399 by applying
the bolt patterns at the interface connections where a virtual dimension point
(VDP) occurs.
A Virtual Dimension Point is defined as: any point on the inside of the
structural shape of the
Icosahexahedron allowing for a reference that is independent of beam or stud
thickness. In other
words all dimensioning and measurements are relative to all the vertices in
the invention as
previously defined in a zero-thickness structure, that attains thickness in
walls, roof, etc, by
extruding beam and stud thickness OUT from the VDP's, which are simply the
vertice co-
ordinates as identified by the Icosahexahedron shape definition.
In this way co-ordinates of the outer dimensions of building components do not
have to be
mapped but are kept track off at the subcomponent level.
Hence the structure is defined independent of wall and roof thickness. A
structure with a roof and
wall of thickness 12" has all the exact same Virtual Dimension Points as a
same sized structure
with a 18" thick roof and wall.
This is demonstrated in Fig.400-404 an application of a two storey building
construction which is
a residential dwelling where the wall and roof thicknesses are extruded out in
the plane of each
building panel.
This results in a triangular valley between each plane extruding outward, as
in View I, all of which
are identical in size and triangular shape at the interfaces between the 20
Equilateral Triangles as
in View2, but where various different panels interface as in Viewl, 3, & 4,
the valley width (not
CA 02483361 2004-10-26
depth) is different, usually smaller as at the interface between an 0 Panel
and a J Panel, although
at the very top of the structure as in View4 central where two J Panels meet
the valley is bigger.
The nature of this valley is utilized, uniquely, by synthesizing it implicitly
into a substructure
known as a "Virtual-Beam", or V-Beam, which is essentially a hollow triangular
beam.
With some additional support this structure becomes what is known in the
Building Construction
field as probably THE strongest building element possible.
This is born out by the fact that ALL large-capacity construction cranes of
the kind that can be
seen constructing Highrise Buildings, where huge weights have to be maneuvered
about at large
fulcrum swing, utilize exactly this structure of a hollow triangular beam.
In this invention, the effect of the triangular valleys forming at the panel
interface points, by
extruding them out the thickness of the wall and roof, is completely usefully
and elegantly utilized
by simply reinforcing the outward gap of the valley so that a triangular beam
by definition results,
as in Fig. 405-410. Fig 407 shows two possible modes of filling in the gaps
between panels
resulting in a very strong interface between building panels.
In Fig. 406 the method employs a lateral placement of support blocking to
create the V-Beam,
whereas in Fig. 407 a series of inserted blocks achieve a slightly different
version.
Bolt (or screw) patterns for either approach are shown in Fig. 408-410.
This has the elegant side-effect of effectively emplacing strong hollow
triangular beams from each
major vertice in the Icosahexadron structure, implementing a very effectively
strong Post-and-
Beam strategy that also has the extra benefit of being completely geodesic
adding even more
strength.
Added to these two effects is a powerful third: the Shell Effect. It results
from the fact there are
essentially two shapes one inside the other connected by each inner Virtual
Dimension Point to
the corresponding out point at the thickness of the beams or studs, making a
shell of that
thickness that has great strength of integrity.
Which when added to the geodesic nature and triangular beam employment makes
the
Icosahexahedron building construction structure strong enough to be free-
standing without
26
CA 02483361 2004-10-26
internal load-bearing walls or beam span structures, although there is nothing
to prevent an
application that would use these structures anyway for various purposes like
being a basis for walls
or other useful structures in a dwelling.
But this free-standing capability allows the structure to be used judiciously
as an open-concept
structure, where one application is to buildup an internal room system
entirely out of a very
flexible free-standing mezzanine structure which rests entirely on the first
floor (or even feasibly
the basement floor), which itself can be designed out of completely unrelated
thematic modes like
steel tube beam or any other architecturally sound method that would contract
very aesthetically
with the non-orthodoxy of the Icosahexahedron structure.
Also, in free-standing warehouse applications where large objects need to be
stored, or for
example like in salt or other chemical storage domes.
In Fig. 411-416 are shown examples of a two-story free-standing structure with
a door entry at
front and window ways at the 4 corner locations that allow outward sloping
windows eliminating
any moisture entry problems that may occur on inward sloping windows.
A roof ventilation strategy that allows air to flow from the edges of the
walls up into the roof and
out the top allows for the elimination of the necessary for eaves-troughs at
the wall-roof boundary.
This also eliminates the need for down-spouts since the equivalent to an eaves-
trough can be run
along the edge of each triangular wall panel to be exhausted at ground level
by default.
The elimination of the roof-overhang and eaves-trough, geodesic structure,
triangulated beam
system, and shell effect, also all contribute to the structure being
effectively a wind-resilient
structure having applications in hurricane-prone locations where the preferred
doorway/window
configuration provides a natural pre-prepared plywood placement strategy for
quickly and easily
preparing a structure for severe oncoming weather, and is probably very
effective without any
such added measures in that the structure itself is aerodynamic.
Wrmd-flow is very forgiving of shapes that flare away, but destruction to flat
surfaces, as used in
most conventional building structures.
The most aerodynamic shape is the head of a whale, or a sphere, because it
flares away, even
though a fair portion of the front surface can be reasonable considered to be
fairly flat to the wind.
27
CA 02483361 2004-10-26
The Icosahexahedron is similar where from any view angle, all walls flare away
back from the
viewer in an aerodynamic way, allowing high wind to flow around the house
easily rather than
getting caught up in destructive vortices underneath eaves-troughs, roof
overhangs, and flat
surfaces with square flaring back effects which itself causes vortices. And in
most cases, the very
way that conventional roves are fastened to wall structures is often not taken
very seriously as
builders consider the immense weight of a trussed roof structure, the mistake
in not realizing that
once the wind gets underneath the leading overhang of a roof that is not
fastened with extreme
integrity, it becomes a perfect wing, with the expected resultant outcome of
flying away suddenly.
Further, in a frame construction building, the building strategy at play is
that it is the placement of
the plywood sheathing that gives triangulated strength to what is actually a
very week frame
structure.
In any frame structure that does not have the sheathing applied, it can very
easily be knocked over
just by leaning agsinst it, even one that hss all it's own primary fasteners
in place. This is why they
have to be very securely braced until the sheathing is applied.
But the problem is, during extreme weather one of the two things that happens
is first, there I a
sudden drop in barometric pressure as the weather system arrives, second, high-
wind. Both have
the effect of applying hostile forces directly to the sheathing, whereupon all
it takes is for the first
few sheets be torn away, and the forces inside the house then contribute in a
chain reaction to tear
the the rest of them away. The more this happens, the more that skew forces in
the now weakened
frame, actually contribute to pushing off the remaining sheathing
mechanistically.
At this point it is very easy for wind forces to get underneath the overhang
of the roof and carry it
away the wing-shape actually contributing to lift in the structure.
None of this is at issue in the Icosahexadron design, in that it is Pm-and-
Beam: it has great
strength of integrity with NO sheathing in place; there is no roof overhang,
the connection
between the roof and the wall is of high integrity and is the same technique
as every where else in
the structure; the lack of eaves-I:mud-ling eliminates destructive vortex
formation, and the overall
shape is very aerodynamic from any angle of oncoming wind.
In employing the structure as a macro structure, eliminating the eaves-
trough/roof-overhang has
certain advantages and disadvantages. The advantages are: a) no eaves-troughs
to clean out, b) no
28
CA 02483361 2004-10-26
down-spouts required, c) better aerodynamics at the roof-line contributing to
wind-resilience, and
d) improved aesthetic appearance when taken in conjunction with other
necessary design factors.
But the following problems are introduced a) the interface between the roof
and wall becomes
non-standard, b) without an overhang there is no convenient shelter for
walkways, c) the roof
must be extended directly to the ground which makes traditional attic
ventilation through the
underneath of the roof overhang impossible.
Building structures according to municipal building-code requirements must
have adequate
ventilation in the roof. To accomplish this and address the other factors
several design elements
were employed: a) making the roof thick enough to have adequate code
insulation and air gap, b)
making the roof continuous with the walls, c) employ ventilation openings at
the interface
between the roof and wall, resulting in a wall the same thickness as the roof,
but not requiring the
same depth of insulation, resulting d) in the advantage of repeatability in
design and manufacture
of wall panels because they are identical to roof panels, e) the roof is
ventilated through air
openings in the downward angle struts of the walls as in Fig. 400 in the
sample wall panel with
vertices included in Viewl, View2, and View3, where the roof is ventilated
through a series of
internal air openings builtin to the traditional over-hange location at the
interface between roof
and wall, flowing up through similar air gaps inside the wall into the roof,
where the air inlets are
lower down along the downward angles from Viewl to View3, and View2 to View3.
Hence airflow is up through the bottom triangular panels edges through air
openings, through the
wall up into the roof and out traditional roof vents at the top of the roof.
The advantages of all this are a) cathedral ceiling inherent in the design
allowing use of attic space,
b) rain-troughs run at an angle downard and meet at 'View3 where a simple
drain removes rain,
resulting in self-cleaning rain-troughs, c) the rain-troughs double as down-
spouts. d) since there
are two troughs per wall, they can be smaller and less visible, e) the overall
structure becomes very
aerodynamic and hence wind-resilient, f) since the interface between roof and
wall is continuous,
last, and not least, the problem of ice-damming is completely eliminated in
this design, a major
achievement in macro building structure design.
Moving on to one final extraordinary feature of the extremely versatile
kosahexahedron is evident
in viewing it from the bottom, i.e. upside-down, i.e. in viewing the
TETRADUOCAP in Fig.
258, where evident is the hour-glass shape made up from the interface of the L
Panels in Fig. 100.
29
...01,4254 MPOWVISKGE.
CA 02483361 2004-10-26
In looking down upon the TETRADTJOCAP hourglass, the angle between the native
Equilateral
triangles is 72 degrees, i.e. 360/5, as derived in Fig. 135. This means that
the angle of the lines
flaring out from the hourglass in Fig. 419 defined by the angle between the
two line segments
iX1-iX2, and iX2-iX3, is exactly 144 degrees (72 * 2).
This is is also empirically known to be the exact same angle in one side of
the hourglass shape in
the Star Constellation Orion, specifically the left side, where upon
observation the two shapes are
strikingly similar, as in Fig. 417 and Fig. 418.
But when the two are overlayed graphically, the novelty of the alignment of
this angle between the
two structures is astoundingly perfectly identical, as in Fig. 419. Resulting
further in the 3
interface points iX1, iX2, and iX3.
Further, in the novel views of points iX4 to iX8 the following is observed: a)
the quadrilateral
defined by the points iX4, iX5, iX6, and iX7, as viewed off-angle, under
transformation is the
same as the L Panel of Fig. 100 native to the Icosahexaduoduoduohedron, and b)
the triangle
defined by points iX4, iX7, and iX8 which is connected along one edge to the
quadrilateral
previously described, similarly as to that occurring in the
Icosahexaduoduoduohedron, represents
the transformation of the two points of the adjoining quadrilateral line
segment into one single
point thus showing the transformation of the L Panel into an interface panel
in transforming the
Icosahexaduoduoduohedron of Fig. 274 into the pure Icosahexahedron of Fig. 198-
221, in
transforming the structure in Fig. 102 into the structure of Fig. 198 whereby
the j1 panel is
mapped to the a panel, the K1 panel to the KX, and the L1 to the LX
respectively. As in the
process of rotating the two structures STR1 and STR2 in Fig. 95 about the axis
defined by V1-2
and V1-3 in Fig. 94 such that in Fig. 102 the short edge of J1 increases, the
short edge of K1
decreases, and the short edge of Li decreases to zero as the points V1-8 and
V2-8 of Fig. 94 are
transformed together as in the described rotation inFig. 98, resulting in the
pure Icosahexadron.
A further study of the interface at iX1 as in Fig. 420, shows a depiction of
the ancient Universal
Symbol of Peace.
______________ e. __ "WM. _____________________ votanparmas. __