Note: Descriptions are shown in the official language in which they were submitted.
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
METHOD OF FORMING STABLE STATES OF DENSE HIGH-TEMPERATURE
PLASMA
Field of the Art
The present invention relates to a method of forming stable states of a dense
high-
temperature plasma which can be used, for example, for controlled fusion.
State of the Art
The existing state of the art related to the realization of stable states of a
dense high-
temperature plasma applicable for the purposes of nuclear fusion can be
defined as a stage of the
formation and confinement of a plasma by a magnetic field in devices which
make it possible to
realize separate techniques of the claimed method but not the method as such,
i.e., a method of
achieving a stable state of a dense high-temperature plasma. In this respect
the claimed method
has no close analogs.
From the state of the art a heavy-current pulsed discharge is known, which is
shaped with
the aid of a cylindrical discharge chamber (whose end faces function as
electrodes) which is
filled with a working gas (deuterium, hydrogen, a deuterium-tritium mixture at
a pressure of 0.5
tol0 mm Hg, or noble gases at a pressure of 0.01 to0.1 mm Hg). Then a
discharge of a powerful
capacitor battery is effected through the gas, with the voltage of 20 to 40 kV
supplied to the an-
ode and the current in the forming discharge reaching about 1 MA. In
experiments (Lukyanov
S.Yu. "Hot Plasma and Controlled Fusion", Moscow, Atomizdat, 1975 (in
Russian)) first a first
phase of the process was observed - plasma compression to the axis by the
current magnetic
field with decrease of the current channel diameter by approximately a factor
of 10 and forma-
tion a brightly glowing plasma column on the discharge axis (z-pinch). In the
second phase of
the process a rapid development of current channel instabilities (kinks,
helical disturbances, etc.)
were observed.
The buildup of these instabilities occurs very rapidly and leads to the
degradation of the
plasma column (plasma jets outburst, discharge discontinuities, etc.), so that
the discharge life-
time is limited to a value on the order of 10"' s. For this reason in a linear
pinch it turns out to be
unreal to fulfill the conditions of nuclear fusion defined by the Lawson
criterion ni > 1014 cm 3s,
where n is the plasma concentration, i is the discharge lifetime..
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
2
A similar situation takes place in a O- pinch, when to a cylindrical discharge
chamber an
external longitudinal magnetic field inducing an azimuthal current is
impressed.
Magnetic traps are known, which are capable of confining a high-temperature
plasma for
a long time (but not sufficient for nuclear fusion to proceed) within a
limited volume (see Artsi-
movich L.A., "Closed Plasma Configurations", Moscow, Atomizdat, 1969 (in
Russian)). There
exist two main varieties of magnetic traps: closed and open ones.
Magnetic traps are devices which are capable of confining a high-temperature
plasma for
a sufficiently long time within a limited volume and which are described in
Artsimovich L.A.,
"Closed Plasma Configurations", Moscow, Atomizdat, 1969.
To magnetic traps of closed type (on which hopes to realize the conditions of
controlled
nuclear fusion (CNU) were pinned for a long time) there belong devices of the
Tokamak,
Spheromak and Stellarator type in various modifications (Lukyanov S.Yu., "Hot
Plasma and
CNU", Moscow, Atomizdat, 1975 (in Russian)).
In devices of the Tokamak type a ring current creating a rotary transformation
of mag-
netic lines of force is excited in the very plasma. Spheromak represents a
compact torus with a
toroidal magnetic field inside a plasma. Rotary transformation of magnetic
lines of force, ef
fected without exciting a toroidal current in plasma, is realized in
Stellarators (Volkov E.D. et al.,
"Stellarator", Moscow, Nauka, 1983 (in Russian)).
Open-type magnetic traps with a linear geometry are: a magnetic bottle, an
ambipolar
trap, a gas-dynamic type trap (Ryutov D.D., "Open traps", Uspekhi Fizicheskikh
Nauk, 1988,
vol. 154, p. 565).
In spite of all the design differences of the open-type and closed-type traps,
they are
based on one principle: attaining hydrostatic equilibrium states of plasma in
a magnetic field
through the equality of the gas-kinetic plasma pressure and of the magnetic
field pressure at the
external boundary of plasma. The very diversity of these traps stems from the
absence of positive
results.
When using a plasma focus device (PF) (this is how an electric discharge is
called), a
non-stationary bunch of a dense high-temperature (as a rule, deuterium) plasma
is obtained (this
bunch is also called "plasma focus"). PF belongs to the category of pinches
and is formed in the
area of current sheath cumulation on the axis of a discharge chamber having a
special design. As
a result, in contradistinction to a direct pinch, plasma focus acquires a non-
cylindrical shape (Pet-
rov D.P. et al., "Powerful pulsed gas discharge in chambers with conducting
walls" in Collection
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
3
of Papers "Plasma Physics and Problem of Controlled Thermonuclear Reactions",
volume 4,
Moscow, Izdatel'stvo AN SSSR, 1958 (in Russian)).
Unlike linear pinch devices, where the function of electrodes is performed by
the cham-
ber end faces, in the PF the role of the cathode is played by the chamber
body, as a result of
which the plasma bunch acquires the form of a funnel (thence the name of the
device). With the
same working parameters as in the cylindrical pinch, in a PF device a plasma
having higher tem-
perature, density and longer lifetime is obtainable, but the subsequent
development of the insta-
bility destroys the discharge, as is the case in the linear pinch (Burtsev
B.A. et al., "High-
temperature plasma formations" in: hogi Nauki i Tekhniki", "Plasma Physics"
Series, vol. 2,
Moscow, Izdatel'stvo AN SSSR, 1981 (in Russian)), and stable states of plasma
are actually not
attained.
Non-stationary bunches of high-temperature plasma are also obtained in gas-
discharge
chambers with a coaxial arrangement of electrodes (using devices with coaxial
plasma injectors).
The first device of such kind was commissioned in 1961 by J. Mather (Mather
J.W., "Formation
on the high-density deuterium plasma focus", Phys. Fluids, 1965, vol. 8, p.
366). This device
was developed further (in particular, see (J.Brzosko et al., Phys. Let. A.,
192 (1994), p. 250,
Phys. Let. A., 155 (1991), p. 162)). An essential element of this development
was the use of a
working gas doped with multielectron atoms. Injection of plasma in such
devices is attained ow-
ing to the coaxial arrangement of cylindrical chambers, wherein the internal
chamber functioning
as the anode is disposed geometrically lower than the external cylinder - the
cathode. In the
works of J.Brzosko it was pointed out that the efficiency of the generation of
plasma bunches
increases when hydrogen is doped with multielectron atoms. However, in these
devices the de-
velopment of the instability substantially limits the plasma lifetime as well.
As a result, this life-
time is smaller than necessary for attaining the conditions for a stable
course of the nuclear fu-
sion reaction. With definite design features, in particular, with the use of
conical coaxial elec-
trodes (M.P. Kozlov and A.I. Morozov (Eds.), "Plasma Accelerators and Ion
Guns", Moscow,
Nauka, 1984 (in Russian)), such devices are already plasma injection devices.
In the above-
indicated devices (devices with coaxial cylindrical electrodes) plasma in all
the stages up to the
plasma decay, remains in the magnetic field area, though injection of plasma
into the interelec-
trode space takes place. In pure form injection of plasma from the
interelectrode space is ob-
served in devices with conical coaxial electrodes. The field of application of
plasma injectors is
regarded to be auxiliary for plasma injection with subsequent use thereof (for
example,. for addi-
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
4
tional pumping of power in devices of Tokamak type, in laser devices, etc.),
which, in
turn, has limited the use of these devices not in the pulsed mode, but in the
quasi-stationary
mode.
Thus, the existing state of the art, based on plasma confinement by a magnetic
field, does
not solve the problem of confining a dense high-temperature plasma during a
period of time re-
quu-ed for nuclear fusion reactions to proceed, but effectively solves the
problem of heating
plasma to a state in which these reactions can proceed.
Disclosure of the Invention
The author proposes a solution of the above-stated problem, which can be
attained by a
new combination of means (devices) known in the art with the use of their
combination (the pa-
rameters considered earlier), which was not only not used heretofore, but
proposed or supposed
in the state of the art, and which is further described in detail in the
sections dealing with carry-
ing the invention into effect and in the set of claims.
Accordingly, the present invention relates to a method of forming stable
states of a dense
high-temperature plasma, which comprises the following steps:
a) generation of a dense high-temperature plasma from hydrogen and isotopes
thereof
with the aid of pulsed heavy-current discharges;
b) injection of the plasma from the area of a magnetic field with parameters
correspond-
ing to the conditions of gravitational emission of electrons with a banded
energy spectrum;
c) energy transfer along the spectrum.
The energy transfer (step c) is performed by cascade transition into the long
wavelength
region of eV-energy to the state of locking and amplification of the
gravitational emission and
simultaneous compression to the states of hydrostatic equilibrium, arid in the
formation of said
states in the composition of a working gas multielectron atoms are used for
quenching the spon-
taneous gravitational emission from the ground energy levels of the keV-region
electron in the
proper gravitational field.
It is preferable that in one of the embodiment of the invention for obtaining
stable states
of a dense high-temperature plasma use is made of hydrogen and multielectron
atoms, such as
krypton, xenon, and other allied elements (neon, argon).
In another preferable embodiment of the invention in order to realize the
conditions for
the nuclear fusion reaction to proceed use is made of hydrogen and carbon,
wherein carbon is
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
also employed both for quenching the spectra of gravitational emission with
keV energies and
as a fusion reaction catalyst.
The claimed method provides a scheme for forming stable states of a dense high-
temperature plasma, which scheme comprises a device for supplying a working
gas, a discharge
5 chamber, a discharge circuit, a chamber for forming a stable plasma bunch.
If and when necessary, each of the cited blocks of the scheme can be fitted
with appropri-
ate measuring equipment.
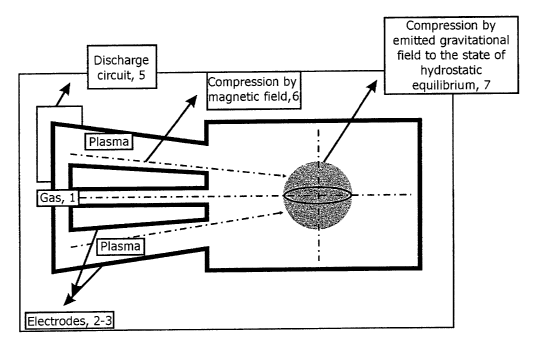
The invention is illustrated by a circuit diagram of a pulsed heavy-current
magnetic-
compression discharge on multiply charged ions with conical coaxial
electrodes, in which
1. a fast-acting valve for supplying a working gas into a gap between an
internal electrode
(2) and an external electrode (3);
2. an external electrode;
3. an internal electrode has a narrowing surface close to conical one;
4. a diverter channel which prevents the entrance of admixtures into the
compression
area;
5. a discharge circuit;
6. an area of compression by a magnetic field;
7. an area of compression due to efflux current in the outgoing plasma jet and
subsequent
compression by the emitted gravitational field.
Carrying out the Invention
Terms and Definitions Used in the Application
The definition "stable states of a dense high-temperature plasma" denotes the
states of
hydrostatic equilibrium of a plasma, when the gas-dynamic pressure is
counterbalanced by the
pressure of a magnetic field or, in the present case, by the pressure of the
emitted gravitational
held.
The definition "a dense high-temperature plasma" denotes a plasma with the
lower values
of densities nC, ni = ( 1023 - 1025) rri 3 and temperatures T~, T; _ ( 10' - 1
O8) K.
The definition "plasma parameters corresponding to gravitational emission of
electrons"
(with a banded emission spectrum) denotes parameters which are in the above-
indicated range of
pressures and temperatures.
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
6
The definition "locking of avitational emission in plasma" denotes the state
of gravita-
tional emission in a plasma ,which takes place when its emission frequency and
electron Lang-
muir frequency are equal. In the present case locking of the emission takes
place for two reasons:
- energy transfer along the spectrum into the long wavelength region as a
result of cas
cade transitions into the long wavelength region with attaining emission
frequency (1013 - 101x)
with plasma Langmuir frequency equal to the electron one, this being the
condition of locking
gravitational emission in plasma;
- quenching spontaneous gravitational emission of electrons from the ground
energy lev-
els by multielectron atoms, when the energy of an excited electron is
transferred to an ion with
corresponding energy levels, leading to its ionization.
The definition "amplification of gravitational emission" denotes amplification
which
takes place when the gravitational emission is locked, because, with the
locking conditions hav-
ing been fulfilled, the gravitational emission remains in plasma with
sequential emission of the
total energy of the gravitational field locked in the plasma.
For a better understanding of the invention, given below is a description of
high-
temperature plasma formations which take place in the proposed method, and a
description of a
method of forming their stable states as hydrostatic equilibrium states. The
conditions of gravita-
tional emission of electrons with a banded spectrum, the conditions of
exciting gravitational
emission in plasma, and locking and amplification owing to cascade transitions
as claimed in the
set of claims presented hereinbelow, are disclosed.
1. Gravitational emission of electrons with a banded spectrum as emission of
the
same level with electromagnetic emission.
For a mathematical model of interest, which describes a banded spectrum of
stationary
states of electrons in the proper gravitational held, two aspects are of
importance. First. In Ein-
stein's field equations x is a constant which relates the space-time
geometrical properties with
the distribution of physical matter, so that the origin of the equations is
not connected with the
numerical limitation of the x value. Only the requirement of conformity with
the Newtonian
Classical Theory of Gravity leads to the small value K = 8~G/c4, where G, c
are, respectively, the
Newtonian gravitational constant and the velocity of light. Such requirement
follows from the
primary concept of the Einstein General Theory of Relativity (GTR) as a
relativistic generaliza-
tion of the Newtonian Theory of Gravity. Second. The most general form of
relativistic gravita-
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
7
tion equations are equations with the A term. The limiting transition to weak
fields leads to the
equation
0~ _ - 4~pG +Ac2~
where ~ is the field scalar potential, p is the source density. This
circumstance, eventually, is
crucial for neglecting the A term, because only in this case the GTR is a
generalization of the
Classical Theory of Gravity. Therefore, the numerical values of K = 8~tG/c4
and A = 0 in the
GTR equations are not associated with the origin of the equations, but follow
only from the con-
fortuity of the GTR with the classical theory.
From the 70's onwards, it became obvious (Siravam C . and Sinha K., Phys. Res.
51
( 1979) 112) that in the quantum region the numerical value of G is not
compatible with the prin-
ciples of quantum mechanics. In a number of papers (Siravam C . and Sinha K.,
Phys. Res. 51
(1979) 112) (including also Fisenko S. et al., Phys. Lett. A, 148"7,9 (1990)
405)) it was shown
that in the quantum region the coupling constant K (K~ 104° G) is
acceptable. The essence of the
problem of the generalization of relativistic equations on the quantum level
was thus outlined:
such generalization must match the numerical values of the gravity constants
in the quantum and
classical regions.
In the development of these results, as a micro-level approximation of
Einstein's field
equations, a model is proposed, based on the following assumption:
"The gravitational field within the region of localization of an elementary
particle having
a mass m0 is characterized by the values of the gravity constant K and of the
constant A that lead
to the stationary states of the particle in its proper gravitational field,
and the particle stationary
states as such are the sources of the gravitational field with the Newtonian
gravity constant G".
The most general approach in the Gravity Theory is the one which takes
twisting into ac-
count and treats the gravitational field as a gage field, acting on equal
terms with other funda-
mental fields (Ivanenko et al., Gage Theory of Gravitation, Moscow, MGU
Publishing House,
1985 (in Russian)). Such approach lacks in apriority gives no restrictions on
the microscopic
level. For an elementary spinor source with a mass rno, the set of equations
describing its states
in the proper gravitational field in accordance with the adopted assumption
will have the form
~iy~'(~~, +tc''Ify~,ys~I'Ys)-moc~~2~'I''0 (1)
R~,v - 2 g~,~R=-x{T~,~(En~-f~g,~~ +(g,,vSasa -s,.s~)}
R(K,A,En,rn) = R(G,En,rn~ (3)
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
8
{lY!'vf~ - mnC~~l}~l - ~ (
1 (
RNv - 2 g~~R =-K~TuvlEn)
The following notations are used throughout the text of the paper: K = 8~K1c4,
K' = 8~tG/c4,
E" is the energy of stationary states in the proper gravitational field with
the constant K, A = K~,,
rn is the value of the coordinate r satisfying the equilibrium n-state in the
proper gravitational
field, x = KpK, Ko is the dimensionality constant, Sa = 'I'ya Ys ~' ~ ~u is
the spinor-coupling co-
variant derivative independent of twisting, E n is the energy state of the
particle having a mass m"
(either free of field or in the external field), described by the wave
function ~' in the proper
gravitational field with the constant G. The rest of the notations are
generally adopted in the
gravitation theory.
Equations (1) through (5) describe the equilibrium states of particles
(stationary states) in
the proper gravitational field and define the localization region of the field
characterized by the
constant K that satisfies the equilibrium state. These stationary states are
sources of the field with
the constant G, and condition (3) provides matching the solution with the
gravitational constants
K and G. The proposed model in the physical aspect is compatible With the
principles of quan-
tum mechanics principles, and the gravitational field with the constants K and
A at a certain,
quite definite distance specified by the equilibrium state transforms into the
filed having the con-
stant G and satisfying, in the weak field limit, the Poisson equation.
The set of equations (1) through (5); first of all, is of interest for the
problem of stationary
states, i.e., the problem of energy spectrum calculations for an elementary
source in the own
gravitational field. In this sense it is reasonable to use an analogy with
electrodynamics, in par-
ticular, with the problem of electron stationary states in the Coulomb field.
Transition from the
Schrodinger equation to the Klein-Gordon relativistic equations allows taking
into account the
fine structure of the electron energy spectrum in the Coulomb field, whereas
transition to the
Dirac equation allows taking into account the relativistic fine strut
ture and the energy level splitting associated with spin-orbital interaction.
Using this analogy and
the form of equation (1), one can conclude that solution of this equation
without the term
x'I'y,, ys'I'y5 gives a spectrum similar to that of the fine structure
(similar in the sense of relativ-
ism and removal of the principal quantum number degeneracy).. Taking the term
x'l;'y~ ys'If ys
into account, as is noted in Siravam C. and Sinha K., Phys. Res. 51 (1979) 112
, is similar to tak-
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
9
ing into account of the term 'Ifo~'~'FF~,v in the Pauli equation. The latter
implies that the
solution of the problem of stationary states with twisting taken into account
will give a total en-
ergy-state spectrum with both the relativistic fine structure and energy state
splitting caused by
spin-twist interaction taken into account. This fact, being in complete accord
with the require-
s menu of the Gauge Theory of Gravity, allows us to believe that the above-
stated assumptions
concern ing the properties of the gravitational field in the quantum region
are relevant, in the
general case, just to the gravitational field with twists.
Complexity of solving this problem compels us to employ a simpler
approximation,
namely,: energy spectrum calculations in a relativistic fine-structure
approximation. In this ap
proximation the problem of the stationary states of an elementary source in
the proper gravita
tional field well be reduced to solving the following equations:
n+~ 2 + ~+e~CK"a v K° z 0
f v, ~' rJf l(lr 1)J''
_ ~ 1 - a~'~ 1 l(l + 1) _
-a ~ z + Z +A=~(2l+1) f2 e-zKn +Ko + 2 + f'Za z
r r r r
- e-~' C ~ + ~ ~ + ~ + A = ~(2l + 1) f 2 Ko - Kn e-v + l( r 2 1~ - a ~ f' 2
1 (v"+v'2)-(v'+~,')Cvl + l~ + z (1+e~) =0
2 4 r r
Y= n
f (0) = const « oo (10)
f(rn) 0 (11)
~.(0) - ~0) = 0 (12)
n
f f Zr2dr =1
° (13)
Equations (6)-{8) follow from equarions (14)--( 15)
S~v ax a'k + g~vr''~ o'~ K° 'h = 0 (14)
v a
1
R,,v - 2 g,.vR =-x'(T,.v - f~g,.v), (15)
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
~_iEtl
after the substitution of 'Y in the from'I~ = fE, (r)Y,", (6, ~p) exp h into
them
and specific computations in the central-symmetry field metric with the
interval defined by the
expression (Landau L.D., Lifshitz E.M., Field Theory, Moscow, Nauka
Publishers, 1976)
dS2 = cze~dt2 -rz(d62 +sinz ~d~p2)-ezdrz. (16)
5 The following notation is used above: f", is the radial wave function that
describes the states
with a definite energy E and the orbital moment l (hereafter the subscripts El
are omitted), YI", (9,
rp) - are spherical functions, Kn = En lhc, Ko = cmo 1h ,~3 = (rcl4~)(t~lmo).
Condition (9) defines rn" whereas equations (10) through (12) are the boundary
condi-
tions and the normalization condition for the function f, respectively.
Condition (9) in the gen-
10 eral case has the form R(K,rn) = R(G,r"). Neglecting the proper
gravitational field with the con-
stant G, we shall write down this condition as R(K,r") = 0, to which equality
(9) actually corre-
sponds.
The right-hand sides of equations (7)-{8) are calculated basing on the general
expression
for the energy-momentum tensor of the complex scalar field:
T~" ='I~~,'I~" +'P;,'If ~ - (~~,'II, ~ _ Ko ~+Ly) . ( 17)
The appropriate components T~" are obtained by summation over the index m with
appli-
cation of characteristic identities for spherical functions (Warshalovich D.A.
et al., Quantum
Theory of Angular Momentum, Leningrad, Nauka Publishers, 1975 (in Russian))
iEtl
after the substitution of 'II = f (r)Ym (9, ~p) exp h into ( 17).
Even in the simplest approximation the problem of the stationary states of an
elementary source
in the proper gravitational field is a complicated mathematical problem. It
becomes simpler if we
confine ourselves to estimating only the energy spectrum. Equation (6) can be
reduced in many
ways to the equations (E. Kamke, Differentialgleichungen, Losungsmethoden and
Losungen,
Leizig, 1959)
f ' = fP(r) + Q(r)z , z' = fF(r) + S(r)z . (18)
This transition implies specific choice of P, Q, F, S, such that the
conditions
P+S+Q'lQ+g=0, FQ+P'+PZ+Pg+h=0, (19)
should be fulfilled, where g and h correspond to equation. (6) written in the
form: f' + gf' + hf =
Q. Conditions (19) are satisfied, in particular, by P, Q" F, S written as
follows:
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
11
Q=1, p=S=-g~2, F=2g'+4gz-h. (20)
Solutions of set (18) will be the functions: (E. Kamke,
Differentialgleichungen,
Losungsmethoden and Losungen, Leizig, 1959)
f = Cp(r) sin 8(r) , z = Cp(r) cos 6(r) , (21)
where C is an arbitrary constant, 6(r) is the solution of the equation:
B' = Q cost 8 + (P - S) sin B cos9 - F sine B, (22)
and p(r) is found from the formula
r
p(Y) = exp J ~P sin2 B + (Q + F) sin 8 cos 8 + S cost 9~dr . (23)
0
In this case, the form of presentation of the solution in polar coordinates
makes it possi-
ble to determine zeros of the functions f(r) at r = rn, with corresponding
values of 8 = n~ (n be-
ing an integer). As one of the simplest approximations for v,~,, we shall
choose the dependence:
e~ = e-~' =1- " + A(r - CZ )Z + C3 r (24)
r+Cl
where
~ - 2Kmn -2KEn -~2K~C~K
n C2 C4 C3 n f
Yn _ rn
C' Ar 2 ' CZ n ' C3 Y r + C'
n n( n 1/ ,
Earlier the estimate for K was adopted to be K~ 1.7 x 1029 Nm2kg-2. If we
assume that
the observed value of the electron rest mass ml is its mass in the ground
stationary state in the
proper gravitational field, then mo = 4mi/3. From dimensionality
considerations it follows that
energy in the bound state is defined by the expression ( Kmo )2 / r1 = 0.17 x
106 x 1.6 x 10-'9 J,
where r1 is the classical electron radius. This leads to the estimate K ~ 5.1
x 1031 Nm2kg'2 which
is later adopted as the starting one. Discrepancies in the estimates K
obtained by different meth-
ods are quite admissible, all the more so since their character is not
catastrophic. From the condi-
tion that ~ is the electron energy density it follows: ~ = 1.1 x 103°
J/m3, A = K~=4.4X 1 O29 m 2.
From (22) (with the equation for f(r) taken into account) it follows:
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
12
2B' _ (1-F)+(1+F)cos2B~ (1-F), (25)
where
1 _ 1 _ _ C2 (v'-~,',~ ~ _ l(l+1)1.
F=2g~+4ga-h~ g=rn ~'+ 2 ~ h= nze~ Kne ~-Ko- Y Jz
The integration of equation (25) and substitution of 8 = gin, r = Yn give the
relation be-
tween Kn and Yn:
2
(Y + a. ) 3
-2~n= ~-rnK" ~ A; " ' -2a;~r" +a;)+ a' +2C,~r" +a;)+
4 A ;_, 2 ~n+a;)
are Cz a; 2 1 2Cla; CZ
+2C, + +B; (r" +a;)+a; + - +
n + a; r" + a; Y" + a; n + a; r" + a;
KZr 3 r l(l + 1) C d
+ AZ n ~ A;'( n + a; ) + " n d, tt - ~ 2 +~ a, ( n + a' ) - (26)
r =1 n r=t
- nn2" ~~2a;ZA; -2a;B; -4C,A;a; +2C,B; +CZA; +KK~'~~a; -C,)-
i=1 n
- YY"2 Al(l + 1)a; (C, - a; )~ 1n( ~ + a, ) - n A-' l(l + 1)(d2 + C1 d, )1n r"
The coefficients entering into equation (26) are coefficients at simple
fractions in the ex-
pansion of polynomials, required for the integration, wherein a; ~ K", d2 ~ Al
~ rn 5, B; ~ r" 4, A';
~ Y" 2, a; "' rn_4, dl = Yn 4. For eliminating Yn from (26), there exists
condition (9) (or the condition
exp v(K,rn) = 1 equivalent to it for the approximation employed), but its
direct use will compli-
cate the already cumbersome expression (26) still further. At the same time,
it easy to note that rn
10-3 r"~, where rn~ is the Compton wavelength of a particle of the mass mn,
and, hence, rn ~ 10-
3 K"'l.The relation (26) per se is rather approximate, but, nevertheless, its
availability, irrespec-
tive of the accuracy of the approximation, implies the existence of an energy
spectrum as a con-
sequence of the particle self interaction with its own gravitational field in
the range r <_ r", where
mutually compensating action of the field and the particle takes place. With l
= 0 the approxi-
mate solution (26), with the relation between r" and K" taken into account,
has the form
E" = Eo (1 + ae-~' ) ~ , (27)
where a = 1.65, (3 = 1.60.
The relation (27) is concretized, proceeding from the assumption that the
observed value
of the electron rest mass is the value of its mass in the grounds stationary
state in the proper
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
13
gravitational field, the values r1 = 2.82 x 10- 15 m, K1 = 0.41 x 1012 m 1
giving exact zero of the
function by the very definition of the numerical values for k and A.
So, the presented numerical estimates for the electron show that within the
range of its lo-
calization, with K 1031N m2 kg 2 and A~ 1 O29m 2, there exists the spectrum of
stationary states
in the proper gravitational field. The numerical value of K is, certainly,
universal for any elemen-
tary source, whereas the value of A is defined by the rest mass of the
elementary source. The dis-
tance at which the gravitational field with the constant K is localized is
less than the Compton
wavelength, and for the electron, for example, this value is of the order of
its classical radius. At
distances larger than this one, the gravitational field is characterized by
the constant G, i.e., cor-
rect transition to Classical GTR holds.
From equation (27) there follow in a rough approximation the numerical values
of the sta-
tionary state energies: E1 =0.511 MeV, E2 =0.638 MeV, ... E~ =0.681 MeV.
Quantum transitions over stationary states must lead to the gravitational
emission charac-
terized by the constant K with transition energies starting from 127 keV to
170 keV Two circum-
stances are essential here.
First. The correspondence between the electromagnetic and gravitational
interaction takes
place on replacement of the electric charge a by the gravitational "charge" m~
, so that the
numerical values K place the electromagnetic and gravitational emission
effects on the same
level (for instance, the electromagnetic and gravitational bremsstrahlung
cross-sections will dif
fer only by the factor 0.16 in the region of coincidence of the emission
spectra).
Second. The natural width of the energy levels in the above-indicated spectrum
of the
electron stationary states will be from 10-9 eV to 10-' eV. The small value of
the energy level
widths, compared to the electron energy spread in real conditions, explains
why the gravitational
emission effects are not observed as a mass phenomenon in epiphenomena, e.g.,
in the processes
of electron beam bremsstrahlung on targets. A direct confirmation of the
presence of the electron
stationary states in the own gravitational field with the constant K may be
the presence of the
lower boundary of nuclear (3-decay. Only starting with this boundary (3-
asymmetry can take
place, which is interpreted as parity non-conservation in weak interactions,
but is actually only a
consequence of the presence of the excited states of electrons in the own
gravitational field in ~3-
decay. Beta-asymmetry was observed experimentally only in (3-decay of heavy
nuclei in mag-
netic field (for example, 2~C6° in the known experiment carried out by
Wu (Wu Ts.S.,
Moshkovskii S.A., Beta-decay, Atomizdat, Moscow, 1970 (in Russian)). On light
nuclei, such
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
14
as 1H3, where the (3-decay asymmetry al- ready must not take place, similar
experiments
were not carried out.
2. Conditions of Gravitational Emission in Plasma (Excitation
of Gravitational Emission in Plasma)
For the above-indicated energies of transitions over stationary states in the
own field and
the energy level widths, the sole object in which gravitational emission can
be realized as a mass
phenomenon will be, as follows from the estimates given below, a dense high-
temperature
plasma.
Using the Born approximation for the bremsstrahlung cross-section, we can
write down
the expression for the electromagnetic bremsstrahlung per unit of volume per
unit of time as
2k T
33 137 - mc2 ne n; ~ a = 0.17 X 1O-39 z2nen, Te, (28)
where Te, k, n;, ne, m, z, ro are the electron temperature, Boltzmann's
constant, the concentration
of the ionic and electronic components, the electron mass, the serial number
of the ionic compo-
nent, the classical electron radius, respectively.
Replacing ro by r~ = 2K m/s2 (which corresponds to replacing the electric
charge a by the
gravitational charge m~ ), we can use for the gravitational bremsstrahlung the
relation
Qg = 0. l6Qe. ' (29)
From (28) it follows that in a dense high-temperature plasma with parameters
ne = ni =
1023 m 3, Te = 10' K, the specific power of the electromagnetic bremsstrahlung
is equal to ~ 0.53
101° J/rri s, and the specific power of the gravitational
bremsstrahlung is 0.86 109 J/m3 s. These
values of the plasma parameters, apparently, can be adopted as guide threshold
values of an ap-
preciable gravitational emission level, because the relative proportion of the
electrons whose en-
ergy on the order of the energy of transitions in the own gravitational field,
diminishes in accor-
dance with the Maxwellian distribution exponent as Te decreases.
3. Locking and Amplification of Gravitational Emission by Cascade
Transitions and Quenching Spontaneous Emission from Ground energy levels
by Ions of Multielectron Atoms in Plasma Injected from Magnetic Field Area
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
For the numerical values of the plasma parameters Te = T1= (!0'-10g)K, ne = n;
_ ( 1 O23-1 O25) m 3 the electromagnetic bremsstrahlung spectrum will not
change essentially with
Compton scattering of electron emission, and the bremsstrahlung itself is a
source of emission
losses of a high-temperature plasma. The frequencies of this continuous
spectrum are on the or-
s der of ( 1018-102°) s 1, while the plasma frequency for the above-
cited plasma parameters is
(1013-10'4) s-1, or 0.1 eV of the energy of emitted quanta.
The fundamental distinction of the gravitational bremsstrahlung from the
electromagnetic
bremsstrahlung is the banded spectrum of the gravitational emission,
corresponding to the spec-
trum of the electron stationary states in the own gravitational field.
10 The presence of cascade transitions from the upper excited levels to the
lower ones will
lead to that the electrons, becoming excited in the energy region above 100
keV, will be emitted,
mainly, in the eV region, i.e., energy transfer along the spectrum to the low-
frequency region
will take place. Such energy transfer mechanism can take place only in
quenching spontaneous
emission from the lower electron energy levels in the own gravitational field,
which rules out
15 emission with quantum energy in the keV region. A detailed description of
the mechanism of
energy transfer along the spectrum will hereafter give its precise numerical
characteristics. Nev-
ertheless, undoubtedly, the very fact of its existence, conditioned by the
banded character of the
spectrum of the gravitational bremsstrahlung, can be asserted. The low-
frequency character of
the gravitational bremsstrahlung spectrum will lead to its ampliftcation in
plasma by virtue of the
locking condition ~K <_ 0.5 103 ne being fulfilled.
From the standpoint of practical realization of the states of a high-
temperature plasma
compressed by the emitted gravitational field, two circumstances are of
importance.
First. Plasma must comprise two components, with multiply charged ions added
to hy-
drogen, these ions being necessary for quenching spontaneous emission of
electrons from the
ground energy levels in the own gravitational field. For this purpose it is
necessary to have ions
with the energy levels of electrons close to the energy levels of free excited
electrons. Quenching
of the lower excited states of the electrons will be particularly effective in
the presence of a reso-
nance between the energy of excited electron and the energy of electron
excitation in the ion (in
the limit, most favorable case - ionization energy). An increase of z
increases also the specific
power of the gravitational bremsstrahlung, so that on the condition cc~g <_
0.5 103 ne being ful-
filled, the equality of the gas-kinetic pressure and the radiation pressure
k(ne Te + n; T;) = 0.16(0.17 1 O-39 Z2 ne n; Te )fit (30)
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
16
will take place at 0t = (10-6 -10-') s for the permissible parameter values of
compressed
plasma ne = ( 1 + a) n; _ ( 1 O25 - 1026) m 3, a > 2, Te ~ Te = 108 K, z > 10.
Second. The necessity of plasma ejection from the region of the magnetic field
with the
tentative parameters ne = ( 1 O23 - 1024) rri 3, Te - ( 10' - 1 Og) K with
subsequent energy pump-
ing from the magnetic field region.
The fulfillment of the above-cited conditions (in principle, irrespective of a
particular
scheme of the apparatus in which these conditions are realized) solves solely
the problem of at
taining hydrostatic equilibrium states of plasma. The use of a multielectron
gas (carbon) as the
additive to hydrogen leads to the realization of nuclear fusion reaction
conditions, since carbon
will simultaneously will act as a catalyst required for the nuclear fusion
reaction.
Another variant of nuclear fusion in compositions with multielectron atoms,
such as kryp
ton, xenon (and allied elements) is the use of a deuterium tritium mixture as
the light component.
An analysis of the processes which take place in the known devices for
generating stable
high-temperature states of a plasma (as well as the absence of encouraging
results) suggests that
the magnetic field can be used only partially, in the first step for the
retention and heating plasma
in the process of forming its high-energy state. Further presence of the
magnetic field no longer
confines the plasma within a limited volume, but destroys this plasma owing to
the specific char
acter of motion of charged particles in the magnetic field. A principal
solution of the problem is
a method of confining of an already heated plasma in an emitted gravitational
field in a second
step, after the plasma has been compressed, heated and retained during this
period by the mag-
netic field. As follows from the above-stated, under any circumstances. Plasma
must be injected
from the magnetic field region, but with subsequent pumping of energy from the
region of the
plasma found in the magnetic field. It is just to these conditions that, among
other things, there
corresponds the original circuit diagram of a magnetoplasma compressor,
presented in the speci-
fication to the Application.
The claimed method is realized in the following manner (see the diagram):
through a
quick-acting valve 1 a two-component gas (hydrogen + a multielectron gas) is
supplied into a
gap between coaxial conical electrodes 2, 3, to which voltage is fed through a
discharge circuit 5.
A discharge creating a magnetic field flows between the electrodes. Under the
pressure of the
arising amperage, plasma is accelerated along the channel. At the outlet in a
region 7 the flow
converges to the axis, where a region of compression with high density and
temperature origi-
nates. The formation of the region of compression 7 is favored by efflux
currents which flow in
the outgoing plasma jet. With the voltage fed to the anode (200) kV and the
starting pressure
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
17
of the working gas (0.5- 0.8) mm Hg, and when the current in the forming
discharge
reaches about 1 MA in the region of compression, the values of the plasma
parameters ne, n; _
(1023-1025) rri3 and of the temperatures Te, T; _ (10'-10g) K, necessary for
the excitation of
the gravitational field of the plasma, will be reached. The presence of the
ions of multielectron
atoms in the composition of the working gas, which lead to quenching the
gravitational emission
from the ground energy levels of the electrons, and cascade transitions along
the levels of the
electron stationary states in the own gravitational field will lead to the
transformation of the
high-frequency emission spectrum into the lows-frequency one with frequencies
corresponding
to locking and amplification of the plasma emission. Simultaneously the
density and temperature
of the plasma will grow owing to its pulsed injection. Therefore, sub sequent
compression of the
plasmas after its injection from the magnetic field region to the state of
hydrostatic equilibrium
(formation of the stable stat of the dense high-temperature plasma) takes
place owing to the exci-
tation, locking and compression of the plasma by the radiated gravitational
field, with the at-
tainment of the plasma parameters ne, n; _ ( 1 O25-1 O26) mi 3 and Te, Ti = 1
Og K
The fundamental difference of such scheme from the known schemes used for
obtaining
plasmodynamic discharges (Kamrukov A.S. et al., "Generators of laser and
powerful thermal
radiation, based on heavy-current plasmodynamic discharges" in the book
"Plasma Accelerators
and Ion Guns", Moscow, Nauka, 1984 (in Russian)), when using this scheme as a
quantum gen
erator of gravitational emission (a quantum generator of gravitational
emission being just the
generator of stable high-energy states of a dense plasma) is as follows:
1. The pulsed character of the discharge circuit with the volt-ampere
characteristics corre-
sponding to the plasmodynamic discharge;
2. The definite ratio of the hydrogen component and of the multielectron gas
component
(approximately 80% and 20%, respectively), including the purposed of attaining
the required
temperature parameters of the plasma.
3. The close correspondence of the electron energy levels in the employed
multielectron
gas with the lower electron energy level in the own gravitational field, which
requires using such
gases as krypton and xenon as the multielectron gas. Here both the percentage
of the multielec-
tron atoms, limited from below by the requirement of quenching the excited
lower energy states
of the electron (in the own gravitational field) and from above by the
requirement of attaining the
necessary plasma temperature should be adjusted.
CA 02538368 2006-03-08
WO 2005/109970 PCT/RU2005/000284
18
One skilled in the art will understand that various modifications and variants
of
embodying the invention are possible, all of them being comprised in the scope
of the Appli-
cant's claims, reflected in the set of claims presented hereinbelow.