Note: Descriptions are shown in the official language in which they were submitted.
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
1
METHOD FOR RECONSTRUCTING GUSTS AND STRUCTURAL LOADS AT
AIRCRAFT, IN PARTICULAR PASSENGER AIRCRAFT
Reference to related applications
This application claims the benefit of the filing date of the German patent
application
DE 10 2005 058 081 filed on December 6, 2005, the disclosure of which is
hereby in-
corporated by reference.
Background of the invention
The invention relates to a method for reconstructing gusts and/or structural
loads at air-
craft, in particular passenger aircraft.
Hitherto, it has only been possible to a limited extent to back-calculate
external influ-
ences such as gusts or turbulence which may result in increased structural
loads at any
locations at an aircraft, in particular at a passenger aircraft. Dynamic loads
could cer-
tainly be measured but it was not possible to infer the perturbation or
disturbance.
Summary of the invention
It is an object of the invention to provide a method whereby structural loads
at an air-
craft can be simulated and their excitation can be reconstructed. In
particular, a method
of this type is to be provided which can be implemented both after the flight
but in par-
ticular, also during a flight.
The object is achieved by a method having the features of claim 1. Exemplary
further
developments and embodiments of the method according to the invention are
specified
in the dependent claims.
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
2
An advantage of the method according to the invention is that it allows rapid
estimates
to be made as to whether particular inspections and/or repairs to a structure
are neces-
sary or not following gusts and/or manoeuvres in the limiting region or other
excita-
tions. This possibility ensures an increased safety standard, minimises ground
times as
well as operating costs and at the same time increases the availability of
aircraft.
Brief description of the drawings
Exemplary embodiments of the method according to the invention are explained
herein-
after with reference to the drawings.
In the figures:
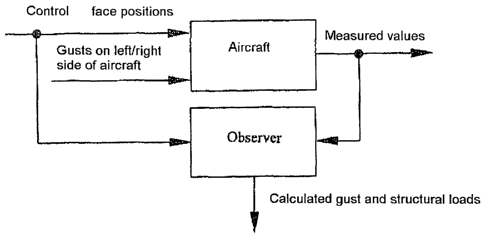
Figure 1 is a schematic diagram of the method according to the invention for
recon-
structing gusts and/or structural loads at an aircraft by an observer
according to one ex-
emplary embodiment of the invention;
Figure 2 is a block diagram of the structure of a nonlinear model of the
aircraft such as
forms the basis of the observer according to the exemplary embodiment of the
invention
from Figure 1;
Figure 3 is a diagram similar to Figure 1 which illustrates how the respective
quantities
used at the observer are allocated to the aircraft distance (plant);
Figure 4 is a diagram of a graphical user interface of a so-called system
optimization
tool (SO tool) used in the method according to the invention;
Figure 5 is a screen shot of a simulink model for the observer test;
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
3
Figures 6, 7 and 8 show the lateral velocity, the vertical velocity on the
left-hand side or
the vertical velocity on the right-hand side of a discrete gust as a
disturbance input
quantity (thin line) and observer calculation (thick line);
Figures 9, 10 and 11 each show a diagram of the lateral velocity, the vertical
velocity on
the left-hand side or the vertical velocity on the right-hand side plotted as
a function of
time for continuous turbulence as a disturbance input quantity (thin line) and
calculated
by the observer (thick line);
Figures 12, 13 and 14 are diagrams of the wing shear forces, the shear forces
on the
horizontal tail fins or the vertical tail fin plotted as a function of the
span or length nor-
malised to unity for the aircraft model (thin line) and the calculation of the
observer
(thick line);
Figure 15 shows the positions of various control faces as a function of time
from a test
flight;
Figure 16 shows measurements of various output quantities as a function of
time from a
test flight (thin line) and calculations of the observer (thick line);
Figures 17, 18 and 19 show calculations of the lateral gust velocity, the
vertical gust
velocity on the left-hand side or the vertical gust velocity on the right-hand
side for the
test flight described with reference to Figures 15 and 16;
Figure 20, 21, 22 and 23 give the shear force close to the right wing root,
the bending
moment close to the right wing root, the shear force near the inner right
engine or the
bending moment near the inner right engine as a function of time for the test
flight de-
scribed with reference to Figures 15 and 16 as a measured quantity (thin line)
and calcu-
lation by the observer (thick line); and
Figure 24 is a screen shot of an animation of the aircraft movement, the gust
velocities
(light arrows) and the structural loads (dark arrows).
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
4
Detailed description of the embodiments
When operating a modern commercial aircraft, it is important to know the
internal loads
(bending moments and shear forces) acting on the aircraft structure during the
flight.
The loads are induced by manoeuvres ordered by the pilot or by the electronic
flight
control system (EFCS) or by turbulences and discrete gusts through which the
aircraft
flies. However, these loads cannot be monitored by measurements at any
arbitrary de-
sired location of the aircraft. According to the invention, these loads are
rather recon-
structed by calculation from the flight data available for a commercial
aircraft (e.g.
Euler angle, "body rates", accelerations, GPS data), the positions of the
control faces
and using a mathematical model of the aircraft. In addition, the gust
velocities should be
estimated by suitable means to calculate the loads caused by the gusts.
The reconstruction of the loads can be of major benefit for the operator of
the aircraft.
One benefit arises from the reaction to intermediate cases, e.g. when the
aircraft flies
through a severe gust. By knowing the loads at any location of the aircraft
structure, it
can easily be decided whether a load has exceeded permissible limiting values
which
necessitate grounding and an extensive inspection of the structure. If the
information
relating to the loads is already available during the flight and reveals that
no critical
loads have occurred, unnecessary ground time of the aircraft can be avoided.
A reconstruction of the loads running during the flight is also important for
lifetime
monitoring systems which allow the operator to carry out an inspection as
necessary and
to optimise the intervals for structural maintenance of the aircraft. It can
be provided
that a special inspection of parts of the structure is only carried out if
particular loads
have occurred during operation of the aircraft. In this way, inspection
intervals could be
increased and inspections only conducted on special parts of the structure,
thus reducing
the operating costs of the aircraft and increasing its availability.
In addition, the gust velocities acting as unknown input quantities on the
aircraft should
be estimated to reconstruct the internal loads. According to the invention,
this should be
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
carried out with the aid of an observer based on a nonlinear mathematical
model of the
aircraft.
The principle of the observer is shown schematically in Figure 1 for the tasks
described.
5 The observer is a parallel model of the aircraft which is controlled by the
pilot and
EFCS commands and corrected by measurements which reflects the resulting
aircraft
motion. By suitably extending the modelling of the aircraft used to design the
observer,
the velocities of gusts and/or turbulences acting as unknown input quantities
at the air-
craft can be incorporated in the observation process. The output quantities of
the ob-
server are estimates or calculations of the gust velocities (hereinafter, only
"gust veloci-
ties " is used for short but this should be understood as the velocities of
gusts, turbu-
lences and other perturbations in steady-state air flows and the structural
loads which
result from the gusts (and turbulences etc.) as well as from the control face
commands.
The estimated gust velocities are advantageous by-products during the
reconstruction of
the structural loads at any desired location of the aircraft.
The basis of the observer design is a nonlinear model of the aircraft. In this
context, the
flexibility or the elastic properties of the aircraft structure is taken into
account in the
model to allow the reconstruction of the internal loads at any desired
location of the
structure. Unknown lateral and asymmetric vertical gust velocities are jointly
taken into
account as input quantities of the observer by extending the model of the
aircraft by so-
called disturbance models.
In the exemplary model described here, the nonlinear observer is designed as a
station-
ary Kalman filter with noise processes at the input and output quantities of
the aircraft.
The observer design is made in a nonlinear parameter optimisation by
minimising a
quadratic quality functional for the errors of estimation of the observer.
The structure of the nonlinear aircraft model according to the present
exemplary em-
bodiment is shown in Figure 2. A set of sub-models reflects the individual
disciplines
used to generate the aircraft model. In the exemplary embodiment, the aircraft
model
was coded in the module-oriented real-time simulation environment VarLoads
(Variable
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
6
Loads analysis environment) which is based on MATLAB/Simulink. A detailed de-
scription of the model and simulation environment is given in [1], J. Hofstee,
Th. Kier,
Ch. Cerulli, G. Looye: A variable, full flexible dynamic response analysis
tool for spe-
cial investigations (VarLOADS), IFASD 2003, Amsterdam, The Netherlands, June
2003.
The sub-model "mechanical structure" shown in Figure 2 represents the model of
the
flexible structure of the aircraft. It combines the nonlinear equations of
motion (EQM)
of the rigid body with all six degrees of freedom (DoF) in order to simulate a
wide
range of flight manoeuvres and a set of linear equations of motion (EQM) for
the elastic
movement of the aircraft structure. This model is derived from a complete
finite element
model in which the degrees of freedom are reduced by static condensation
whereby the
grid points have been allocated corresponding point masses. An additional
modal reduc-
tion can further reduce the elastic degrees of freedom to the number of
elastic modes
which are substantial for the application observed. For an Airbus A340-300
which is to
be considered subsequently as an example, the first forty elastic modes with
the lowest
frequencies are included in the model in order to calculate the loads at the
observation
locations between the grid points of the flexible structure with sufficient
accuracy. The
external forces Põe71 which drive the equations of motion result from air flow
and drive
thrust.
The aerodynamic forces Pa"" from the air flow are modelled in the sub-model
"aerody-
namics". These forces are calculated using so-called aerodynamic strips which
are
placed over the aircraft structure (fuselage, wings, tail assembly etc.). The
strips acting
on the forces are functions of the true air velocity Vt as and the air density
p, the control
face positions u, the movement of the rigid body and the elastic movement
(angle of
attack) of the aircraft, as well as the gust velocities _vgõSt,i and v_gõ5t,r
on the left- or right-
hand side of the aircraft. For slow control face adjustments and aircraft
movements,
these are modelled using steady-state aerodynamic theory. The corresponding
aerody-
namic influential coefficients are derived from wind tunnel measurements. A
discon-
tinuous (delayed) development of aerodynamic forces results from rapid
variations of
the control face positions and rapid variations of the angle of attack for the
individual
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
7
strips caused by the elastic movement of the aircraft structure and the
excitation by
gusts, turbulences etc. These discontinuous or non-steady-state forces are
calculated
separately by using Wagner and Kiissner functions and are superposed. In
addition, the
effects of downwash on the tail in the horizontal direction and sidewash
(caused by
variations in the sideslip angle) on the tail in the vertical direction are
included in the
aerodynamic model. Furthermore, the time delays at each individual strip are
taken into
account for gusts, "downwash" and sidewash".
The aerodynamic forces at the force application points of the individual
strips are allo-
cated to the next grid points of the mechanical structure.
The propulsion forces Pap"'P are calculated in a"drive" sub-model. In the
exemplary
model described here the engine forces are compensated by the resistance
forces on the
aircraft for the angle of attack valid for a steady-state 1 g-level flight and
for constant
forward thrust.
Another sub-model shown in Figure 2 is the "signal selection" sub-system which
deliv-
ers the measured quantities ym required for the observer design.
The internal loads p,, ' ' (bending moments and shear forces) at the
observation locations
of the aircraft structure are calculated in a sub-system "structural loads".
These signals
are the target quantities for the load calculation process. The loads are
calculated by a
force summation method, as is specified for example in [2] H. Henrichfreise,
J. Hofstee,
L. Bensch, D. Pohl, L. Merz: Gust load alleviation of a commercial transport
aircraft,
IFASD 2003, Amsterdam, The Netherlands, June 2003.
The model of the aircraft described above is used as a distance model for
designing the
observer. It is analysed hereinafter in a first formulation in state space
using the first-
order nonlinear differential equation
X =f ~,u,~;Y il.?
t~ -~ ~ n~ },~~~
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
8
and the initial state vector xp (t=0) = xpo. The state vector of the distance
model, i.e. of
the aircraft (index p)
Xp,rigid
?Cp = (2)
Xp,elastic
can be divided into a sub-state vector xp,,;gid for the movement of the rigid
body and a
vector xp,eiastic with the states describing the elastic movement of the
aircraft. The com-
mands at the control faces are combined in a control input vector (index c)
up, of the
distance model
uX,t
uPC uX = uX,2 t3}
U x,20
wherein u,,,t, uX,2 ... uX,n (here with n= 20) are the settings or adjustment
values of rud-
ders, elevators, ailerons, spoilers, stabilisers etc.
The gust velocities , i.e. the velocities of gusts, turbulences and similar
flows on the left-
and on the right-hand side of the aircraft are unknown disturbance quantities
for the
system. These quantities are combined in a disturbance input vector (index d)
for the
distance model
u gust t
Vgust,l
V Wgus~t'I
-gust,I
u pd = _
Vgust,r ('1 )
ugust,r
V gust;r
w gust,r
wherein ugõSt, vgõSt, Wgust describe the corresponding. longitudinal, lateral
and vertical
velocity components in a coordinate system assigned to the aircraft.
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
9
The gust velocities on the left- and on the right-hand side combined in the
disturbance
input vector upd (index d) may contain further velocity components as unknown
distur-
bance quantities
vgust,frant
Vgust;fn
-aa
'h!:~ust, vsring;I. .
W:gust~ng f
wherein vgnst,front, vgust,fin, wgnsc,wing,b Wgust,wing,r describe the
corresponding frontal or lat-
eral velocity components in the coordinate system of the aircraft.
Measurement signals for standard measured values such as those available in a
com-
mercial aircraft are the Euler angles ((D, O, 'I') and "body rates" (PB, qB,
rB) in the coor-
dinate system of the aircraft. In addition, the lateral and vertical
velocities (yE, ZE) of the
centre of gravity in the reference system of the environment and the lateral
and vertical
accelerations (yB, ZB) of the aircraft body close to the centre of gravity in
the coordinate
system of the aircraft are available for the observer. All these signals are
modelled using
the measurement output equation (index m)
(D
O
W
PB
y U
Pm = qB gp rx, UPd)
m
B
YE
ZE
yB
ZB
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
The aim of the observer design is to reconstruct the internal loads. In order
to achieve
this, the unknown gust velocities are to be estimated or calculated, as will
be seen sub-
sequently. These variables are provided by the target output equation (index
o)
Pint
-C { (] }
yPo = ugõst i -gPO(XP,U"UPa)
Vgwt,r
5
In the equations of the aircraft model given above, the gust velocities appear
as input
quantities and as output quantities. As will be described hereinafter, these
gust veloci-
ties can be included in the observer design by a suitable extension of the
distance
model.
The aim is to reconstruct the internal loads at the aircraft structure caused
by flight ma-
noeuvres and excitations through gusts, turbulences etc. at any desired
location of the
aircraft structure. For a normal flight without gusts the loads on the
aircraft structure are
merely caused by the commands of the pilot or the EFCS. These so-called
manoeuvre
loads can be reconstructed using the model of the aircraft described using
figure 2 and
using the measured control face settings as input quantities. However, if the
aircraft flies
through gusts or turbulences, additional gust loads are superposed on the
manoeuvre
loads. In order that these loads can also be reconstructed, the unknown gust
velocities at
the disturbance inputs of the aircraft are also required. Direct measurements
of gust ve-
locities by sensors installed on the aircraft are either not available or not
adequate, there
being two reasons for this. Firstly, the sensors are subject to the movement
of the air-
craft so that they not only measure the gust but also the movement. Secondly,
the sen-
sors available today are only capable of measuring the gust at one location
usually situ-
ated at the nose of the aircraft. Hence, two-dimensional gusts such as
isolated eddies
which result in rolling of the aircraft are not detected.
A nonlinear observer for calculating multi-dimensional gusts, turbulences etc.
and the
structural loads resulting therefrom and from manoeuvres is described
hereinafter. This
approach focuses only on the lateral and vertical velocity components of the
gusts vgõSt
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
11
and wgõS, from Equation (4). At the present time, longitudinal gusts are not
taken into
account. The gust velocities are modelled by the disturbance model
x d - - fd l ~/"-xdIudI-vd)I x d(t=0)-0
--
yd =gdlxd)
in order to include them in the observation process. They are generated by the
output
vector yd and by suitable disturbance input quantities of the model in the
vector upd.
Substituting the disturbance input quantity at the distance model by the
output quantity
of the disturbance model, i.e. upd -- yd in Equation (1) yields the nonlinear
differential
equation
?~p ~ _ fp(Xp'upI'gd(Xd)'up~)
Xd fd(2~6Ud,ud)
xa a(2ia,Upc,Ud,v)
of the extended distance model. The state vector xa contains the states xp of
the aircraft
model and the states xd of the disturbance model. The vector processes v_p,
and vd with
the process noise at the control and disturbance inputs have been added to the
extended
distance model to allow an observer design similar to a Kalman filter design
as de-
scribed in [3] B. Friedland: Control System Design - An introduction to state-
space
methods, McGraw-Hill, 1986. The process noise is combined in the vector v.
From Equation (5), the measurement output equation of the extended distance
model
becomes
ypm = gpm(xp,uN,gd(Xd))_W {~~l
= gam ~a) upc)+w
wherein the vector process w adds the measurement noise at the distance
outputs to the
design of the observer similarly to a Kalman filter. As is usual in the theory
of the Kal-
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
12
man filter, the individual noise processes in the vectors v and w are assumed
to be un-
correlated Gaussian white noise with known constant intensities.
Substantial values for the intensities of the measurement noise can be deduced
from the
specifications of the sensors used, see [4] H. Henrichfreise: Prototyping of a
LQG
Compensator for a Compliant Positioning System with Friction. TRANSMECHA-
TRONICS - Development and Transfer of development systems of mechatronics, HNI-
Verlagsschriftreihe, Vol. 23, 1S' Edition, Paderbom 1997. The paper is
available on the
CLM website www.clm-online.de. The intensities of the process noise, on the
other
hand, are used as design parameters, as is shown subsequently.
Finally, substituting the disturbance input in the target output equation (6)
leads to the
target output equation of the extended distance model
= g
~ POd(?~d))
- gao(Xa' upe
to calculate the structural loads and the gust velocities from the states of
the extended
model and the control input quantities.
The nonlinear extended distance model from Equations (8) to (10) forms the
basis for
the observer design.
With the vector functions from the extended distance model, the structure of
the ob-
server is given by the following equations, see [5] B. Friedland: Advanced
control sys-
tem design. Prentice Hall, 1996.
tll)
Xa = f a(Xa~upc)+L' (yPm - YPm), Xa(t = 0) = Xa0
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
13
(.l'')
ypm am
ypo -~ac5'Xa~UpC)
The solution of the differential equation of state (11) provides an estimate x
a of the
state vector of the extended distance model. Equation (11) is driven by the
control input
vector up, and the measurement output vector yP,,, of the distance model which
are also
the input quantities into the observer (see Figure 3).
The measurement input is used to form the observer measurement error, the
different
between the true measured values in the vector yP,,, and the calculated
measured values
in the vector yp,,, from Equation (12). These are fed back to the derivative
of the state
vector of the observer by the amplification matrix L. If this is correctly
designed, this
feedback has the effect that the calculated measured values follow the true
measured
values, i.e. the observer measurement errors are almost reduced to zero. For
this pur-
pose, the calculated distance model state vector x d in the observer state
vector x a
should closely follow the distance state vector xP. With unknown disturbance
quantities
at the disturbance inputs of the aircraft or the distance model in the vector
uPd the distur-
bance model sub-state x d should generate the disturbance model output
quantities in ya
from Equation (7) which are close to the true disturbance input quantities.
Conse-
quently, the disturbance model output quantities in the observer provides
estimates for
the unknown gust velocities. Together with the internal structural loads at
the measuring
stations, these are available as observer output quantities in the vector
yp,,, calculated
from Equation (13).
With the observer structure given by Equations (11) to (13), the only
remaining task is
to determine the observer amplification matrix L. This is accomplished using
an ob-
server design similar to a Kalman filter which is already prepared by adding
the noise
process to the extended distance model. Since the basic distance model is not
linear, the
observer amplification matrix is determined by a nonlinear parameter
optimisation
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
14
which is based on a simulation of a system consisting of the extended distance
model of
the aircraft and the observer (similar to Figure 3). The extended distance
model is
excited in this case by discrete white noise processes in the vectors v and w.
The simu-
lated time responses are used to calculate the quadratic cost function
N-1
J ( I - ) - ~', ( ? ~ a (k) - Xa (k))T ' (xa (k) - Xa (k))
N k_o
which contains the sum of the autocovariances of the observer estimation error
for the N
simulation steps which are performed. With this design environment which is
the same
as in a linear Kalman filter design, the obseiver amplification L is found by
numerical
minimisation of the cost function J in relation to the elements of the
observer ainplifica-
tion matrix L. As explained in [4], the intensities of the process noise in
the subvector
v. at_the control inputs of the aircraft or the distance model are used to
calculate the
observer amplification matrix in order to tune the observer in relation to
velocity and
robustness towards indeterminacies in the control input path of the distance
model.
Since the disturbance model input ud into the extended distance model is not
known, the
intensities of the corresponding noise processes in vd are set as higll as
possible in order
to make the observer robust towards the fact that the signal is lacking as an
observer
input quantity.
For the following discussion the observer amplification matrix is partitioned
by analogy
with the state vector of the extended distance model
I'p,rigid
L = Lp = LP,elastic (15)
- Ld ----
Ld
wherein the sub-matrices Lp and Ld are used to feed back the observer
measurement
errors to the derivative of the distance states or the disturbance model
states in the ob-
server. As is clear from Equation (2) for the state vector of the distance
model, the sub-
matrix LP can be further divided into feedback amplification matrices Lp,;gid
and L.p elastic.
If the number of distance states is now counted, e.g. np,,;gid = 12, np
elastic = 80, and four
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
disturbance model states nd = 4 are assumed, for npR, = 10 measured quantities
from
Equation (5) a total of 960 elements is obtained for the observer
amplification matrix.
It is obviously not logical to design an observer with so many amplification
elements,
5 not only with regard to the computing expenditure but also with regard to
the conver-
gence of the optimisation problem described above. Therefore, only a few
selected ele-
ments will be used for the observer amplification matrix in the design
process, these
being selected for reasons such as stability and response speed. All other
elements will
be set to zero. The studies conducted in connection with the present exemplary
em-
10 bodiment relating to the observer amplification matrix have revealed that
twelve se-
lected elements are already sufficient to ensure good observer behaviour as
will be seen
subsequently. In addition, this simplification also dramatically reduces the
computing
expenditure for the observer design and the real time implementation.
15 As has already been mentioned further above, the observer design was
carried out by a
nonlinear parameter optimisation based on time responses obtained by
simulation. This
was carried out using a so-called System Optimization Tool (SO Tool), see [6].
S.
Klotzbach, S. Oedekoven, O. Grassmann: Optimisation in the mechatronic
development
process. VDI Mechatronics Conference 2003, Fulda, Germany, 2003, available at
DMecS-website www.dmecs.de which was developed on the basis of algorithms from
the MATLAB Optimization Toolbox. The system to be optimised should be made
available as a Simulink model. The SO tool contains a graphical user interface
under
which the user can conveniently load the simulation model of the system,
define the
target quantities and interactively select the optimisation parameters for an
optimisation
run. Figure 4 shows the graphical user interface of the SO tool.
Test and simulation results for an Airbus 340-300 will be presented
hereinafter.
The tests were carried out using the Simulink model shown in Figure 5 which
imple-
ments the block diagram from Figure 3 in which the nonlinear observer is
linked to the
aircraft model. An additional subsystem was included to generate gust
velocities for
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
16
cosinusoidal discrete gusts and continuous turbulences as excitations. The
subsystem
provides velocities acting on the left and right side of the modelled
aircraft.
By setting the control inputs uPc = u, of the aircraft model and the observer
to zero, ma-
noeuvres and manoeuvre loads are not taken into account hereinafter. This was
carried
out because the observer was designed on the basis of a nominal modelling of
the air-
craft (the distance model for the observer design agrees with the aircraft
model) so that
the manoeuvre loads are correctly reconstructed by the observer. Only the
disturbance
excitation of the system by gusts is relevant with regard to the assessment of
the per-
formance of the observer.
Figures 6 to 8 show the lateral and vertical gust velocities acting on the
aircraft and the
corresponding estimates by the observer. The gust velocities were scaled to
the true air
speed at the aircraft.
Whereas the lateral gust velocities are identical on both sides of the
aircraft, the vertical
gust velocities were assumed to be different for the left and the right side
of the aircraft.
They affect the aircraft at different times and with different amplitudes.
The figures in which the disturbance input quantities are reproduced by thin
lines and
the estimates made by the observer are given by thick lines show that the
lateral and
asymmetric vertical gust velocities are reproduced highly accurately.
Figures 9 to 11 show an excitation by multi-dimensional continuous turbulence
which
comes closer to reality where the lateral and vertical gust velocities acting
on the aircraft
and the estimates by the observer are respectively reproduced by thin or thick
lines. The
time profile shows that the turbulence is reconstructed with the same high
accuracy as
the discrete gust velocities . Using the reconstruction of the gust velocities
, the observer
is able to calculate reliable estimates for the loads caused thereby. This is
shown by so-
called envelope curves which include the maximum and minimum values of the
indi-
vidual loads from the available monitoring locations over the corresponding
parts of the
aircraft structure. These envelope curves allow a quick glance at the maximum
loads
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
17
over the entire aircraft structure which arise in a particular incident or
during an entire
flight. This is very useful for estimating whether the loads on a part of the
aircraft have
exceeded particular predefined values.
Figures 12 to 14 show the envelope curves for the shear forces over the wing
and the
horizontal and vertical tail fins caused by the continuous excitation of
turbulences
shown in Figures 9 to 11. Since the loads for both sides of the aircraft are
equally well
reconstructed, only the left side of the aircraft is taken into account in the
figures. The
forces are scaled to the maximum positive value within the figure and plotted
over the
spans of wings and tail fins normalised to unity. If desired, the bending
moments or the
loads at other aircraft components, e.g. on the fuselage, can also be plotted.
There is almost no difference between the envelope curves in Figures 12 to 14
for the
shear forces of the aircraft model and the observer. The structural loads are
very well
reconstructed by the observer for all measuring stations (these positions are
marked by
crosses). The various measuring positions are available by modelling the
aircraft as a
flexible system, as described further above. This makes it possible to
calculate the loads
at any desired location of the aircraft structure.
In Figure 12 the steps in the shear forces along the aircraft wing are caused
by the
weight of the engines in the basic A340-3000 aircraft model.
The results described here were obtained for an observer which was designed on
a
nominal aircraft model (the distance model for the observer design agrees with
the air-
craft model). With a real aircraft, however, deviations from the aircraft
model occur
both for the model structure and for the model parameters (e.g. weight
distribution,
Mach number, altitude). Studies have shown that the effect on the estimated
loads is
tolerable for deviations which are not too large. The errors are partially
compensated by
greater deviations in the estimate of the gusts or turbulences.
Results obtained in a test flight with a real aircraft are presented
hereinafter. The time
profile of all control face positions (control input quantities) and the
measured quanti-
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
18
ties was recorded during the flight. The data thus collected were evaluated in
a simula-
tion carried out after the flight, using only the observer of the Simulink
model shown in
Figure 5.
Figures 15 and 16 show the control face positions and the measured quantities
which
were recorded during a test flight with an Airbus A340 FT aircraft. The
aircraft was
subjected to manoeuvres of the pilot and also turbulences. The observer worked
very
well in relation to the observer measurement error. The estimates by the
observer in
Figure 16 follow the measured quantities from the test flight with a very
small error so
that the differences are barely discernible in the figures.
Figures 17 to 19 shows the estimates on the left and right side of the
aircraft which
likewise provide good results with regard to the observer measurement error.
Whereas
the estimate for the lateral gust velocity is the same for both sides of the
aircraft, the
estimates for the vertical gust velocities on the left and the right side of
the aircraft dif-
fer.
The estimates for the gust velocities and the control face positions were
input to the
aerodynamic sub-model contained in the observer. The internal structural loads
at the
measuring stations were constructed by allocating the resulting aerodynamic
forces to
the grid points of the mechanical aircraft structure. The test aircraft was
fitted with
stress sensors at some of these measuring stations which made it possible to
detect the
actual loads on the aircraft structure. Figures 20 to 23 compare these loads
at different
positions on the right wing with the corresponding estimates of the observer.
Figure 20
and Figure 21 show the results for the shear force and the bending moment at a
location
near the right wing root. A comparison for the actual and the calculated loads
at a dif-
ferent location near the inner right engine is given in Figure 22 and Figure
23.
The results in Figures 20 to 23 demonstrate that the observer gives very good
estimates
of the loads of a real aircraft. The slight deviations are the consequence of
the differ-
ences between the aircraft model used for the observer design and the real
aircraft. Such
deviations occur in the aircraft structure (e.g. number of elastic modes) and
in the pa-
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
19
rameters (e.g. weight distribution, Mach number, altitude) and can never be
completely
avoided in the real world. It is shown however that the observer is
sufficiently robust in
regard to such influences.
Since the observer measurement errors are small and the structural loads are
well recon-
structed, it can be assumed with a high degree of certainty that the estimates
of the gust
velocities in Figures 17 to 19 are reliable.
An important tool for understanding the aircraft movement corresponding to the
time
profiles shown previously is a three-dimensional animation of the aircraft.
This can
show the control face adjustments, the complete three-dimensional movement of
the
aircraft and the elastic movement of the aircraft structure. Additional
quantities can be
indicated by arrows which vary in their length according to the magnitude of
the respec-
tive quantity. Figure 24 shows an image of the Airbus 340-300 aircraft
considered in the
exemplary embodiment described hereinbefore. The animation is driven with the
ob-
server input quantities (i.e. the control face positions and the measured
quantities) and
the estimated values of the observer (i.e. the elastic deformation of the
aircraft structure,
gust velocities and internal structural loads). The gust velocities and the
loads at differ-
ent locations of the aircraft structure are shown by light or dark arrows.
The method according to the invention can be used to reconstruct loads
occurring at any
positions of the structure of an aircraft caused by flight manoeuvres and
other influences
such as gusts and turbulences during or after the flight. Quick estimates can
therefore be
made as to whether inspections of the structure are optionally necessary after
particular
events. The standard of safety can be increased, ground times and operating
costs can be
minimised and at the same time, the availability of aircrafts can be improved.
It should be noted that the term 'comprising' does not exclude other elements
or steps
and the 'a' or 'an' does exclude a plurality. Also elements described in
association with
different embodiments may be combined.
CA 02627631 2008-04-28
WO 2007/065659 PCT/EP2006/011717
It should be noted that the reference signs in the claims shall not be
construed as limit-
ing the scope of the claims.