Note: Descriptions are shown in the official language in which they were submitted.
CA 02639710 2008-09-22
- 1 -
METHOD TO EXTRACT TARGET SIGNALS OF A KNOWN TYPE FROM RAW
DATA CONTAINING AN UNKNOWN NUMBER OF TARGET SIGNALS,
INTERFERENCE, AND NOISE
FIELD OF THE TECHNIQUE
[0001] The technique generally relates to data processing
and more particularly, to the improvement of in-line oil
debris sensor capability.
BACKGROUND OF THE TECHNIQUE
[0002] Early detection of mechanical damage by
continuously monitoring the metallic debris in lubrication
oil of various mechanical systems such as aircraft engines,
is extremely important for fault diagnosis, maintenance
decision-making, and accident prevention. In-line oil
debris detection sensors have attracted attention recently
because of the advantage of monitoring machine conditions
continuously and eliminating some of the laboratory work
required in off-line oil sample analysis. However, most oil
debris sensors are not only sensitive to metal particles
but also susceptible to various noises and vibrations.
Therefore, there are two major issues to be addressed in
real time oil debris detection. The first issue is how to
use an existing sensor to detect the weakest possible
debris or particle signals that are concealed in noise,
such that quick responses to incipient failures can be
achieved. The second is how to eliminate spurious signals
caused by vibrations in the sensor working environment such
that reliable maintenance decisions can be made.
[0003] The size of a particle that can be detected is
mainly limited by background noise, while the challenge of
eliminating spurious signals lies in their similarity to
CA 02639710 2008-09-22
- 2 -
particle signals. This calls for an effective de-noising
approach to address the two issues simultaneously.
[0004] Many de-noising techniques have been reported in
the literature. Though de-noising has been studied by many
researchers in various fields, work on purification of oil
debris signal from the collected noisy data with the
effects of vibration has not yet been reported in the
accessible literature.
[0005] A collected oil debris signal is a mixture of
several components including intrinsic noise, interfering
vibration signals, and possible target oil-debris signals.
However, most of the existing de-noising methods focus on
the reduction of background Gaussian noise only, and thus
cannot be directly applied to purify the collected oil
debris signals.
[0006] Therefore there is a need for an improved data
processing technique, particularly for enhancing in-line
oil debris sensor capability.
SUMMARY OF THE DISCLOSURE
[0007] In one aspect of the technique, there is provided a
method for extracting intermittent, randomly occurring
transient target signals of known type from a raw data
source signal containing an unknown number of the target
signals in addition to interfering signals and/or intrinsic
noise signals which comprises (a) defining quantifiable
signatures or characteristics that respectively and
independently represent the target signals, the interfering
signals or the intrinsic noise signals; (b) transforming
the raw data source signal with a mathematical transform
that effects a decomposition of the source signal into
CA 02639710 2008-09-22
- 3 -
distinct data sets; (c) processing said data sets to
identify a first group of data sets which display the
signatures or characteristics representing the interfering
signals or intrinsic noise signals and a second group of
data sets which display the signatures or characteristics
representing the target signals, (d) setting the data sets
of the first group to zero; and (e) applying an inverse
transform to the processed data sets in order to
reconstruct a processed output signal.
[0008] In another aspect of the technique, there is
provided a method of enhancing the capability of a sensor
for sensing a particle or bubble in a fluid flow, the
sensor being adapted for generating transient target
signals when particles or bubbles in the fluid pass through
the sensor, which comprises the steps of (a) defining
quantifiable signatures of the target signals, having a
known frequency range of the target signals and a known
kurtosis value range of wavelet coefficients of respective
wavelet scales of interest that reflect a transient nature
of the target signals; (b) defining quantifiable signatures
of interfering signals and intrinsic noise signals, having
two known kurtosis value ranges of wavelet coefficients of
each of wavelet scales that correspond to the interfering
signals and correspond to the intrinsic noise signals
respectively; (c) obtaining a raw data sample signal in a
time domain from the sensor in use for monitoring the fluid
flow; (d) applying a Time-Invariant Wavelet Transform
(TIWT) to said raw data sample signal to effect a
decomposition of said raw data sample signal into a
plurality of data sets in a form of wavelet coefficients of
respective wavelet scales; (e) processing the data sets to
calculate a kurtosis value for each data set to compare the
kurtosis value for each data set with the kurtosis value
CA 02639710 2008-09-22
- 4 -
range defined in step (a) or the kurtosis value ranges
defined in step (b) , in order to identify a first group of
data sets which display the signatures representing the
interfering signals and the intrinsic noise signals and a
second group of data sets which display the signatures
representing the target signals, and then setting the data
sets of the first group to zero; (f) applying a
thresholding rule to process the data sets of the second
group in order to reduce any intrinsic noise signals which
remain in the data sets of the second group; and
(g)constructing a processed output signal by applying an
inverse transform to the data sets processed in step (e)
and (f).
[0009] Other features and advantages of the technique
will be better understood with reference to the preferred
embodiments described hereinafter.
BRIEF DESCRIPTION OF THE DRAWINGS
[0010] Reference will now be made to the accompanying
drawings showing by way of illustration the preferred
embodiments of the technique, in which:
[0011] Figure 1 is a cross-sectional view of an oil debris
sensor according to one embodiment employing the
technology;
[0012] Figure 2 illustrates shapes of ferrous and non-
ferrous particle signatures generated by the sensor shown
in Figure 1;
[0013] Figure 3 is a block diagram showing the length of
each approximation and detail of signal x(n) after a
Discrete Wavelet Transform (DWT) process;
CA 02639710 2008-09-22
- 5 -
[0014] Figure 4 is a block diagram showing a comparison of
the algorithms of DWT and Time-Invariant Wavelet Transform
(TIWT);
[0015] Figure 5 is a graphical illustration of signals for
example with different sinusoidal compositions having
different kurtosis values;
[0016] Figure 6 is a block diagram showing one embodiment
for de-noising a collected sample signal and recovering a
desired signature;
[0017] Figure 7 is a graphical illustration of extraction
of a non-ferrous particle signature from a collected sample
signal without vibration components;
[0018] Figure 8 is a graphical illustration of extraction
of a non-ferrous particle signature from a mixture of the
collected sample signal and simulated vibration signal
components;
[0019] Figure 9 is a graphical illustration of extraction
of a non-ferrous particle signature from a mixture of a
collected sample signal and a periodically modulated
vibration;
[0020] Figure 10 is a graphical illustration of extraction
of a ferrous particle signature from a sample signal
collected from an in-line oil debris sensor mounted on a
shaker; and
[0021] Figure 11 is a block diagram showing another
embodiment for de-noising a collected sample signal and
recovering a desired signature, which is preferred if
memory capacity is limited.
CA 02639710 2008-09-22
- 6 -
DETAILED DESCRIPTION OF THE PREFERRED EMBODIMENTS
[0022] The definition of the following terms are
applicable throughout the specification and the claims of
this application.
[0023] A target signal is a signal which is sought.
According to the described technique, target signals must
be of finite duration, and must possess a known
characteristic profile. Target signals may however occur
at random intervals. In the case of an oil-debris sensor,
a target signal is a transient signal created by the oil-
debris sensor in response to the passage of a suspended
particle passing through the sensor.
[0024] An intrinsic noise signal refers to a minimum,
unavoidable noise of a sensor and measurement system. The
intrinsic noise signal is the signal obtained from the
sensor in controlled conditions. These conditions are
contrived so as to possess no target signals and no
significant interfering signals. In the case of an oil-
debris sensor, the intrinsic noise signal is obtained from
the sensor when operating in quiet laboratory conditions,
without the passage of carrier medium (i.e. no metal
particles) through the sensor.
[0025] An interference signal is any signal other than the
target signal and intrinsic noise signal as defined above.
In the case of an oil-debris sensor, interference signals
may be caused by vibration of the structure where the
sensor is mounted. Such interference is called vibration
interference hereafter.
[0026] A raw data signal is the data collected in full
operating conditions of a sensor system. Raw data signals
may include intrinsic noise, possible interference signals,
CA 02639710 2008-09-22
- 7 -
and possible target signals. In the case of an oil-debris
sensor, raw data is collected over a time window when the
carrier medium (e.g., fluid) that may possess suspended
particles, passes through the sensor and when the sensor is
subjected to interfering signals arising from vibration.
[0027] As illustrated in Figure 1, an oil debris
sensor 20, as an example of sensors used in detecting
particles in a fluid flow, generally includes a tubular
body 22 connected in a pipeline (not shown) , such as a
lubricant oil line, to allow the oil flow to pass through
the tubular body 22 as shown by arrows F. A coil assembly
including one sensing coil 24 and two field coils 26, is
mounted around the tubular body 22. The sensing coil 24 is
located equidistant between the upstream and downstream
field coils 26. When ferromagnetic particles or non-
ferromagnetic particles including bubbles in the oil flow,
pass the sensor 20, the sensing coil 24 generates a target
signal of known characteristics. In real operating
conditions, this target signal is usually mixed with
interfering and/or noise signals and can be definitively
identified only after the raw data output signal from the
sensing coil 24 is properly processed. The sensor 20 is
known and similar to that described in US Patent 5,315,243
granted to Kempster et al. on May 4, 1994, which is
incorporated herein by reference.
[0028] Figure 2 illustrates ferrous and non-ferrous target
particle signals 28 and 30 of characteristics of the
intermittent, randomly occurring and non-periodical
transient signal components generated by the sensor 20 in
Figure 1, representing a detected ferrous particle and non-
ferrous particle passing through the sensor 20. The
ferrous particle signature 28 and non-ferrous particle
CA 02639710 2008-09-22
- 8 -
signals 30 are similar but are 180 out of phase relative
to each other. The shapes of the target signals 28 and 30
may be similar to one full period of a sine wave, depending
on conditions under which the sensor 20 operates.
[0029] In a practical working environment, the particle
target signals 28, 30 in a sample signal obtained from the
sensor 20, are mixed with other unwanted signal components
caused by background noise, vibration interference, etc.
The responsiveness level of the sensor 20 depends on the
size of the particles to be detected in the oil flow. The
detectable particle size is mainly limited by background
noise. Spurious signatures such as vibration-like signals
may cause false alarms. The challenge of improving the
responsiveness and reducing false alarms lies in the very
weak particle signals and their similarity to spurious
signals.
[0030] Therefore, a method of enhancing the capabilities of a
sensor for sensing particles or bubbles in a fluid flow
such as an oil flow is developed, generally based on the
definition of a target signatures or characteristics of the
known target signals generated by sensor 20. The target
characteristic or signature is defined to enable the data
analysis, as described below.
[0031] To provide better de-noising results, target signal
signatures or characteristics can be defined using general
information relating to the target signal. For example,
the target particle signal frequency range may be estimated
and this frequency can be used as a target signal
signature. At the early stage of a fault developed in a
machine, the metal debris is very small and it can be
assumed that the particle and oil speeds are identical.
Hence the particle signal frequency can be estimated based
CA 02639710 2008-09-22
- 9 -
on oil speed. The flow speed of lubricating oil is assumed
to be in range [Vmin,Vmax] = Vnin and Vmax represent the minimum
speed and the maximum speed, respectively. As shown in
Figure 1, the distance l, between the ends of the two field
coils 26 in the sensor 20, can be measured and therefore,
the time required for a particle to pass through the two
field coils 26 can be calculated. A corresponding
frequency component can be obtained as a reciprocal of said
time period. Therefore, a target particle signal
characteristic is a frequency in range 1Vmin /lc" Vmax / lc1 =
Obviously, any signal with a frequency outside the ranges
should be treated as interfering signals and should be
filtered out. However, in practice, not all interfering
signals and noises can be removed in this way. Filtered
signals may still contain noise and vibration-like signals
in the particle frequency range. Therefore, the invention
provides for a more complete digital filtering process
using the above target signal signature.
[0032]In a machine monitoring process, for example, the
sensor 20 of Figure 1 is connected to an oil circuit of the
machine for detecting particles in the oil flow passing
through the oil circuit. A raw data sample signal in a
time domain, as the raw data source signal, can thereby be
obtained from the sensor 20. The raw data sample signal
obtained from the sensor 20 is then processed in a digital
filtering process using defined signatures or
characteristics of the target signal and of the noise
and/or interfering signals. These are used to separate any
target signals from the other raw data signal components.
[0033] According to the invention, this process is conducted
by processing the data, using a mathematical transform that
deconstructs the raw data source signal into distinct,
CA 02639710 2008-09-22
- 10 -
transformed data sets. Each data set is analyzed for
signatures of the target signal and of the background noise
and interferences. Depending on the specific noise, data
sets displaying unwanted signal components are either
nullified (set to zero) as in the case of data sets
containing interference type signatures or, in the case of
data sets containing signatures of the target signal, the
intrinsic noise can be removed from the data sets which can
then be said to be `de-noised' or purified. The processed
data sets are then reconstructed to create a processed
purified signal.
[0034] In a preferred embodiment, several signal
signatures are used, including the frequency range of the
target particle signal as described above, and a
statistical-type signature that distinguishes target
particle signal from vibration interference as described
later.
[0035] The digitally processed sample signal is re-
constructed in the time domain. The re-constructed,
processed sample signal contains the target signal
component in greater proportion with respect to the
unwanted noise and vibration-like components, compared to
that found in the original, pre-processed raw data sample
signal. The capability and responsiveness of sensors such
as sensor 20 is therefore enhanced.
[0036] According to one embodiment, the mathematical
transform utilized is the joint Time-Invariant Wavelet
Transform (referred to as a TIWT hereinafter). In this
case, each data set that results from the transform is
called wavelet coefficients of a scale.
CA 02639710 2008-09-22
- 11 -
[0037] The specific mother wavelets used in the TIWT are
pre-selected so as to possess similar morphology
(signature) to the particle target signal.
[0038] According to one embodiment, signal signatures are
determined by a statistical approach such as a kurtosis
analysis. The statistical analysis is used to
differentiate the target signals from the interference and
noise components. Kurtosis analysis is used to: a) remove
background noise by setting the wavelet coefficients that
are in the scales with kurtosis value between [3-A2, 3+p2]
to zero; b) identify and remove vibration-like signal
components by setting the wavelet coefficients that are in
the scales with kurtosis value between [1.5-01rl.5+p1] to
zero; and c) identify and extract the non-periodic,
intermittent, randomly occurring and transient signal
component of known form by retaining wavelet coefficients,
and hence the associated signal components, in the scales
having sufficiently high kurtosis value.
[0039] Wavelet transform is used to: a) decompose the raw
signal into frequency bands so that some signal components
are de-coupled and each can be more easily handled; b)
remove any signal component with frequency that is out of
range lvmi / lc 'vInaX I 1c 1 by setting the associated wavelet
coefficients to zero (where Vmin and Vmax are the minimum and
maximum particle passage speeds respectively); and c)
remove the Gaussian noise from the high-kurtosis scales
(where the kurtosis is high and so these scales contain the
particle signal, thus the kurtosis cannot be used for
removing noise from these scales and instead a thresholding
rule is used).
CA 02639710 2008-09-22
- 12 -
[0040] In summary, both wavelet transform and kurtosis
analysis contribute to both noise reduction and spurious
signal removal. Such tasks cannot be properly done by
separately applying wavelet transform and kurtosis
analysis. To be effective, the kurtosis analysis has to be
embedded and applied to each wavelet transform scale of
interest.
[0041] In contrast to many existing de-noising algorithms
where discrete wavelet transform (referred to as DWT
hereinafter) is employed, TIWT is adopted in this technique
because compared with DWT, TIWT has the advantage of
translation invariance. In most de-noising methods based
on DWT, the size of a signal shrinks in the process of
wavelet decomposition, with different shrinkage rates in
different frequency bands (or scales) . This leads to two
problems: reduced time resolution and deteriorated
statistical accuracy when a statistical method is jointly
applied. With the TIWT, a signal is never down-sampled and
the filters are different on each decomposition level. The
signal can be decomposed into different scales (frequency
bands) without any size shrinkage in any scales (frequency
bands). Therefore, adopting TIWT can effectively avoid the
two problems. As a result, the same good time resolution
can be preserved in all scales (frequency bands) and a
statistical method can be applied.
[0042] Based on the experimental observation of oil
debris and spurious, particularly vibration-like signals,
it may be suggested that kurtosis, a statistical indicator,
be used to distinguish the two. Machine vibration can be
characterized by a series of consecutive waves with
specific frequency components while the signals generated
by particles appear intermittently but not periodically, it
CA 02639710 2008-09-22
- 13 -
is therefore possible to distinguish vibration signal and
particle signal through the analysis of signal statistical
characteristics. Kurtosis as a statistical indicator is
sensitive to the shape of a signal. Therefore, it will be
adopted for in-line oil debris detection. A joint TIWT and
kurtosis analysis method may be used to de-noise the
collected sample signal data and eliminate spurious
signals.
[0043] Wavelet transform, if properly applied, is able to
reveal useful information of a signal in a time-frequency
domain. A wavelet yi(t) is a function of zero average with
limited duration on(-oo,oo). The continuous wavelet transform
(CWT) of a finite energy signal x(t) can be defined by
a[' 12 fx(t)V ( t - b )dt (1)
a
where a and b are the dilation and time parameters of the
wavelet respectively ( a> 0, b E R), Wah denotes wavelet
transform coefficients, yrph represents a wavelet formed
from a mother wavelet function yr(t) through rescaling and
shifting, yr stands for complex conjugate. A different
scale a corresponds to a specific frequency component
range.
[0044] Scale-time parameters (a,b) can be discretized by
a= 2' and b= k2' for fast computing in practical
implementation. Accordingly, the discrete wavelet
transform (DWT) is given by
WJ,k = 2-'12 f x(t)yr(2-'t - k)dt (2)
where j and k are arbitrary integers.
[0045] A fast discrete wavelet transform called
multi-resolution pyramidal algorithm is known in the art.
CA 02639710 2008-09-22
- 14 -
With this algorithm, the original signal x(t) passes through
two complementary filters and emerges as a signal in a low
frequency band and a signal in a high frequency band,
respectively. Hence, the original signal can be decomposed
into different frequency bands through an iteration
process. The pyramidal algorithm is implemented using
G x(t),Y j,k >- y < x(t), Y j-I,k >g(k - 2n) ( 3)
k
< x(t), y/j,k >= I < x(t), Oj-I,k >h(k - 2n) (4)
k
where 0jk is a scaling function, g(k) and h(k) are
respectively the impulse responses of low and high pass
filters, and <=,=> denotes the inner product operation. For
a signal x(n) , con =x(n) and n is an arbitrary integer.
According to equations (3) and (4), the DWT of signal x(n)
can be written as
Cj,n Y Cj-I,kg(k-2n) (5)
k
wj n=Y Cj-I kh(k - 2n) (6)
k
where cjn and wln are discrete scaling coefficients and
wavelet coefficients, respectively. They represent the
approximations and details of x(n) at resolution 2',
respectively.
[0046] In equations (5) and (6), a down-sampling
algorithm which keeps one point out of two, is used to
perform the transform. The length of signal x(n) will
reduce by half after each transform. If original
signal x(n) has N samples, discrete coefficients cjn and Wjn
have N/2! samples, respectively, j=1,2,===,J . J is the maximum
number of discrete wavelet transform iterations as
illustrated in Figure 3. Therefore, the length of each
CA 02639710 2008-09-22
- 15 -
approximation and detail of x(n) becomes shorter after each
transform iteration. With the decrease in sample length,
the statistical characteristics of the approximation and
detail located in specific frequency bands may no longer be
accurate.
[0047] To alleviate the above difficulty, TIWT is
proposed by introducing an up-sampling algorithm into the
DWT in an attempt to keep the time-invariance property of
signals, which is preferred in statistical signal
processing implementation. For function f(n), the up-
sampling algorithm can be defined as f(2n) = f(n)
and f(2n+1)=0. The basic idea of TIWT is to modify the
quadrature mirror filters through an up-sampling algorithm
by
J g(2n) = g(n)
g(2n-1)=0 (~)
h(2n) = h(n) (10)
h(2n -1) = 0
before performing a convolution between the filters and the
original signal or previous discrete scaling coefficients
obtained by wavelet transform, in order to keep the
redundancy of wavelet transforms. The key is to modify
filters by inserting zeros in them. Consequently,
equations (5) and (6) can be revised as
Cj'" -~cJ ~,,1+z1 ~~g(") (11)
wj,n - ~ Cj-I,n+2j-'i h(l) (12)
respectively, where l is an arbitrary integer. Therefore,
the nature of time-invariant wavelet transform of the
original signal is maintained. All the TIWT coefficients at
CA 02639710 2008-09-22
- 16 -
the Jt'' decomposition level can be written
as {W~ ~ j=1,2,===,J+1} consisting of c,,, w,-,,, ,..., and w,,, .
[0048] The algorithms of DWT as indicated by numeral 32
and TIWT as indicated by numeral 34, are illustrated in
Figure 4, wherein g, and h, represent the filters used at
resolution Z. In the algorithm of TIWT 34, when high-pass
and low-pass filters are applied to a signal, the two new
sequences will have the same size as the original one.
This effectively preserves the time-invariance property of
wavelet coefficients, thereby maintaining the time
resolution of the original signal and the statistical
properties of the wavelet coefficients. Based on the above
analysis, the main differences between algorithms DWT 32
and TIWT 34 can be summarized in Table I.
TABLE I THE DIFFERENCES BETWEEN THE DWT AND THE TIWT
DWT T I WT
Size of filters No changes before Doubled before
g and h each DWT each DWT
Size of wavelet Half of the prior Same as the original
transform of signal size signal size
signals
Translation No Yes
invariance
Time resolution Low High
Statistical Low accuracy High accuracy
properties
Required size The size should be The size should be
of original large enough to large enough to
signal capture signatures capture signatures and
the size should be
CA 02639710 2008-09-22
- 17 -
divisible by 2
Frequency Same
resolution
[0049] As mentioned above, the oil debris sensors are not
only sensitive to metal particles but also susceptible to
noise signals, interferences such as vibration signals.
Some of these effects may generate signals similar to the
particle signals. The similarity between the two types of
signals makes their separation a very challenging issue and
improper removal of noise or vibration signals can spoil
the outcome in later steps. Therefore, the removal of
vibration signal should be handled very carefully. In
practice, a mechanical vibration signal is periodic,
similar to a sinusoidal wave or a combination of several
sinusoidal waves with relatively stable frequencies. On
the other hand, particle target signals are of finite
duration and they occur randomly and intermittently i.e.
neither the target signals nor their rate of occurrence is
periodic. Therefore, the collective pattern of a vibration
signal is different from that of a particle, though their
individual waveforms may look very much alike. It should
also be noted that the signal of an individual particle is
similar to one full period sine wave in the time domain.
As kurtosis is well suited to the detection of such
transient signals, it should also be effective in detecting
particle signals.
[0050] Given a time series x=(x,,xZ,===,x,), the kurtosis
value can be easily computed on line by
Y (x, -x)4 /N
kurlosis = ' (13 )
(Y (x _x)2 IN)2
1
CA 02639710 2008-09-22
- 18 -
where i=1,2,===,N, and x is the mean value of x, N is the
size of x .
[0051] More specifically, the kurtosis of a signal
consisting of successive but non-periodic individual wave
segments is different from that of a periodic signal of the
same wave form. This can be demonstrated by simulated
signals. Consider the following four signals as indicated
by numerals 36, 38, 40 and 42 in Figure 5:
xl(t) = sin(27u100t) , x2(t) = sin(27T15t) , x(t) = x1(t) + x2(t) ,
and
x3(t)_ sin(276t) 0.432 < t < 0.5
0 else
The signals between 0 and 1 second time duration and their
kurtosis are shown in Figure S. It can be seen that 1) the
kurtosis is 1.5 for sinusoidal signals 36 and 38 regardless
of their frequencies; 2) the kurtosis of signal 40 formed
by a combination of multiple sinusoidal functions is 2.25,
higher than that of a single sinusoid function such as
signals 36, 38; and 3) a signal 42 containing only one
segment of a sine wave leads to a much higher kurtosis
value, 22.4999.
[0052] The above observation gives rise to the use of
kurtosis value as a classification criterion for separating
vibration and particle signals. However, the collected
vibration interference signal may be a mixture of several
periodic signals of different frequencies such as
signal 40. The kurtosis value of such a data mixture is
dependent on the mixture contents and hence cannot be
directly used for signal classification. For this reason,
the collected data mixture has to be decomposed into
several frequency bands. A frequency band may be
associated with a unique signal, with or without
CA 02639710 2008-09-22
- 19 -
periodicity. Kurtosis for each frequency band should be
calculated separately to make meaningful classification
decisions.
[0053] As illustrated in Figure 5, the kurtosis of a
sinusoidal signal is 1.5 which can be used as a criterion
to remove such signals from the collected data. Given
signal x(t), all TIWT coefficients at the Jl'' decomposition
level, {W,,, I j=1,2,===,J+1} can be obtained. For each j
corresponding to a specific frequency band, the associated
kurtosis value can be calculated. However, considering the
fact that the actual vibration signals are unlikely to be
truly sinusoidal, a tolerance range is used and the
criterion is relaxed to 1.5 A1 (n1=l in this embodiment).
[0054]In addition to its aforementioned ability to separate
periodic and non-periodic individual wave segments signals,
kurtosis is also a good indicator of background noise. The
background noise is generally Gaussian noise with a zero
mean, the kurtosis of which is three. However, the noise
may not be truly Gaussian noise, therefore the criterion is
relaxed to 3 4Z (\2 is set to 0.5 in this embodiment).
This kurtosis range will be used as a criterion to remove
background noise. Then wavelet coefficients in different
scales are either set to zero or kept based on their
relevance to the transient particle signal. Such decision
may be based on the following rules:
Rule 1: If the frequency range of a scale is not in
the range of interest, i . e . , [Viõin /lc ,VmaX /l, ] ,
set the wavelet coefficients in the frequency
range to zero; and
CA 02639710 2008-09-22
- 20 -
Rule 2: If the kurtosis of the wavelet coefficients
of a scale is between 1.5 01 or 3 A2, set the
wavelet coefficients of this scale to zero.
[0055] The remaining coefficients on a certain scale
should contain the information of particles. It should be
noted that the remaining coefficients also contain the
information of noise as well. For this reason, threshold
6 21og(N) is used to shrink the remaining wavelet transform
coefficients wherein N is the number of samples and 6 is
the standard deviation of the noise. Though the background
noise can be reasonably assumed to be Gaussian noise with a
zero mean, its strength, reflected by its standard
deviation 6, is unknown. In the prior art, 6 is usually
estimated by MAD/0.675. MAD is the Median Absolute
Deviation value of the appropriately normalized fine-scale
wavelet coefficients. To provide more accurate results, it
may be suggested to calculate the true strength of
noise, 6~, corresponding to each scale j directly from the
raw data collected without the presence of any particles or
vibration signals. Since such raw data contains only
background noise, the directly calculated 6/ represents the
true noise level. In practice, the raw data collected for
calculation of 6i values may be obtained from a reference
sample signal obtained from the same sensor 20 of Figure 1
without fluid passing therethrough and in the absence of
structural vibration. The intrinsic noise sample signal is
decomposed into the same number of scales as the number of
scales of the raw data source signal using TIWT.
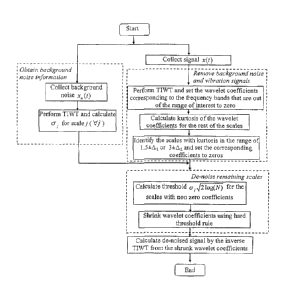
[0056] The main steps of the proposed embodiment are
illustrated in Figure 6. First, as shown in the left two
blocks, the background noise is collected and decomposed
CA 02639710 2008-09-22
- 21 -
by TIWT. Then, the standard deviation 6J of the
coefficients on each scale (j =1,2,..., J) is calculated.
The 61 values will be saved in the computer and used to
calculate the thresholds for de-noising. Next, as
represented on the right part of Figure 6, the raw data
that represents a mixture of particle signal, vibration
signal, and background noise, is for example, the sample
signal obtained from the sensor 20 of Figure 1 during the
monitoring operation of the sensor 20 connected in the oil
circuit of a machine, and is decomposed by TIWT. The
obtained coefficients will be processed based on rules 1
and 2 described above. Once the two rules are implemented,
the undesirable frequency components are filtered out. The
signal components in the remaining scales are then de-
noised using the hard thresholding rule of 6j Dlog(N).
Finally, the particle signal is reconstructed from the
processed coefficients. The reconstructed signal can then
be used for particle identification.
[0057] It should be noted that the kurtosis value
ranges 1.5 1 or 3 0.5 used in the above embodiment are
estimated based on experiments for description and
demonstration of this embodiment. In practice, the
kurtosis value ranges to be used in this process may be
different.
[0058] It should also be noted that since a wavelet basis
is not unique, selecting an appropriate wavelet for a
specific problem is usually desirable. For example,
Daubechies wavelets are orthogonal and compactly supported
so as to provide an ideal mathematical tool for
constructing conjugate quadrature filters in signal
analysis, and are therefore selected for use in this
CA 02639710 2008-09-22
- 22 -
embodiment in order to avoid information leakage in wavelet
transform. It may also be preferable that the mother
wavelets match the shape of the particle signatures, such
as signatures 28 and 30 shown in Figure 2. For this
reason, db4 wavelet function is selected. In other
applications, the wavelet basis to be used in this process
may be different.
[0059] The number of decomposition levels which
determines the number of scales, affects the analysis
results. Increasing the number of decomposition levels
will reduce the band width of the frequency component of
each scale and hence the interfering signal components may
be better distinguished from the transient particle
signature. However, too many decomposition levels
inevitably increase computing time which is undesirable for
on line applications. To specify appropriate decomposition
levels, it may be useful to know the transient particle
signal frequency range. The frequency resolution of the
highest scale may preferably be high enough to identify the
lowest frequency of interest. In other words, the
frequency band width of the highest scale may preferably be
smaller than the lowest frequency of interest. Denoting f,,
as the frequency band width of the highest scale and L as
the number of decomposition levels, f, should satisfy the
following condition
L+1
f,=fl2 <f (12)
where f = Vmin /l, is the lowest frequency of interest, and f.
denotes the sampling frequency. Then,
L>lnf -lnf -l
ln2 (13)
For example, if the sampling frequency is 8000Hz, the
CA 02639710 2008-09-22
- 23 -
decomposition level should satisfy
L> ln 8000 - ln(Vmin / l") (14)
1n 2
[0060] Figure 7 illustrates a sample signal 44 including
a particle target signal generated by a non-ferrous
particle of size 211,u m mixed with a background noise
signal and shows the de-noising result in accordance with
the described method, in which the noise signal components
are removed and the non-ferrous particle signal 46 is
identified.
[0061] Figures 8 and 9 illustrate sample signals 48
and 52 including particle target signals 50 and 54
generated by a non-ferrous particle of size 211,u m. As
seen in the figures the target signals are essentially
hidden in the noise and simulated vibration signals.
Therefore the signatures 50 and 54 in signals 48 and 52 are
not visually observable. It is impossible to successfully
process the signals obtained from the oil debris sensors in
a conventional manner such as described in US
Patent 5,315,243. However, the target signals 50 and 54 of
the non-ferrous particles are recovered by removing the
noise and vibration signal components in accordance with
the above-described technique.
[0062] Figure 10 illustrates a further example of the
digital filtering result using the method developed in this
technique. A target signal 58 of a ferrous particle of
size 125pm is submerged in the original signal sample 56
and as a result of the filtering according to the
invention, is recovered.
[0063] Figure 11 illustrates another de-noising algorithm
in accordance with another embodiment. Modification has
CA 02639710 2008-09-22
- 24 -
been made to the de-noising algorithm illustrated by the
flow chart of Figure 6, in order to reduce the
microprocessor memory required to accommodate many data
samples during the decomposition process for on-line
applications. The embodiment shown in Figure 6 provides
better enhancement performance than the embodiment of
Figure 11, if memory capacity permits. However, if the
memory capacity is limited, the embodiment of Figure 11 is
preferred.
[0064] In the version of TIWT analysis as shown in
Figure 11, following the calculation of kurtosis value, the
wavelet coefficients resulting from every decomposition
step are down-sampled. Down-sampling is performed according
to the level number. For example if the kurtosis value is
in the accepted range and it is decided to use the nth
decomposition level for the reconstruction purpose, such
coefficients will then be down-sampled with the factor
of 2 . With this approach the same memory space as the
number of acquired samples is needed. The reconstruction
would be performed in a way similar to the inverse discrete
wavelet transform (IDWT). In comparison to the algorithm
shown in Figure 6, the memory space saving is (L-1)S,
where L = the number of decomposition levels and S = the
number of samples. The aspects of Figure 11 similar to
those of Figure 6 will not be redundantly described.
[0065] The enhanced ability of oil debris sensors in
detecting very small particles provides better
responsiveness to machinery fault signals and makes it
possible to issue warnings at a much earlier stage. The
added capacity in eliminating vibration or vibration-like
spurious signals can improve the quality of maintenance
decisions and thus reduce false alarms in fault detection.
CA 02639710 2008-09-22
- 25 -
[0066] In the described method, the accuracy of the
analysis results depends, to a certain extent, on the
calculation of kurtosis. If the size of wavelet
coefficients decreases, the accuracy of kurtosis will
decrease accordingly. This weakness can be compensated for
by jointly using TIWT in the algorithm because the TIWT can
effectively maintain constant wavelet coefficient size and
hence the accuracy of kurtosis can be preserved.
[0067] Modifications and improvements brought about by
above-described embodiments may become apparent to those
skilled in the art. For example, the general principles of
the above-described embodiments are not limited to the
processing of transient signals generated by sensors for
the detection of particles in fluid flow. The principles
of the above-described embodiments may be applicable to
data processing in other situations where finite-duration
target signals of known characteristics must be identified
from raw data input source signal in a time domain
containing an unknown number of the target signals and
unwanted interfering or noise signals. The invention in
this broader form could, in principle, be applied to:
acoustic data analysis for detection of finite duration
target signals such as animal calls, mechanical acoustic
signals relating to machine fatigue or failure, gunshots;
optical signals for detection of emboli (gas bubbles) in
blood transfusion lines; acoustic or electronic signals for
the detection of switching noise in communication lines;
electronic signals associated with radar or sonar; cleaning
of `pop' noise in musical recordings, and other
applications. The foregoing description is intended to be
exemplary rather than limiting.