Note: Descriptions are shown in the official language in which they were submitted.
CA 02661753 2011-04-15
METHOD OF LOADFLOW COMPUTATION FOR ELECTRICAL POWER
SYSTEM
TECHNICAL FIELD
[001] The present invention relates to methods of loadflow computation in
power flow control
and voltage control in an electrical power system.
BACKGROUND OF THE INVENTION
[002] The present invention relates to power-flow/voltage control in
utility/industrial power
networks of the types including many power plants/generators interconnected
through
transmission/distribution lines to other loads and motors. Each of these
components of the power
network is protected against unhealthy or alternatively faulty, over/under
voltage, and/or over
loaded damaging operating conditions. Such a protection is automatic and
operates without the
consent of power network operator, and takes an unhealthy component out of
service by
disconnecting it from the network. The time domain of operation of the
protection is of the order of
milliseconds.
[003] The purpose of a utility/industrial power network is to meet the
electricity demands of its
various consumers 24-hours a day, 7-days a week while maintaining the quality
of electricity
supply. The quality of electricity supply means the consumer demands be met at
specified voltage
and frequency levels without over loaded, under/over voltage operation of any
of the power
network components. The operation of a power network is different at different
times due to
changing consumer demands and development of any faulty/contingency situation.
In other words
healthy operating power network is constantly subjected to small and large
disturbances. These
disturbances could be consumer/operator initiated, or initiated by overload
and under/over voltage
alleviating functions collectively referred to as security control functions
and various optimization
functions such as economic operation and minimization of losses, or caused by
a fault/contingency
incident.
[004] For example, a power network is operating healthy and meeting quality
electricity needs of
its consumers. A fault occurs on a line or a transformer or a generator which
faulty component gets
isolated from the rest of the healthy network by virtue of the automatic
operation of its protection.
1
CA 02661753 2011-04-15
Such a disturbance would cause a change in the pattern of power flows in the
network, which can
cause over loading of one or more of the other components and/or over/under
voltage at one or
more nodes in the rest of the network. This in turn can isolate one or more
other components out of
service by virtue of the operation of associated protection, which disturbance
can trigger chain
reaction disintegrating the power network.
[005] Therefore, the most basic and integral part of all other functions
including optimizations in
power network operation and control is security control. Security control
means controlling power
flows so that no component of the network is over loaded and controlling
voltages such that there
is no over voltage or under voltage at any of the nodes in the network
following a disturbance small
or large. As is well known, controlling electric power flows include both
controlling real power
flows which is given in MWs, and controlling reactive power flows which is
given in MVARs.
Security control functions or alternatively overloads alleviation and
over/under voltage alleviation
functions can be realized through one or combination of more controls in the
network. These
involve control of power flow over tie line connecting other utility network,
turbine
steam/water/gas input control to control real power generated by each
generator, load shedding
function curtails load demands of consumers, excitation controls reactive
power generated by
individual generator which essentially controls generator terminal voltage,
transformer taps
control connected node voltage, switching in/out in capacitor/reactor banks
controls reactive
power at the connected node.
[006] Control of an electrical power system involving power-flow control and
voltage control
commonly is performed according to a process shown in Fig. 5, which is a
method of
forming/defining and solving a loadflow computation model of a power network
to affect control
of voltages and power flows in a power system comprising the steps of:
Step- 10: obtaining on-line/simulated data of open/close status of all
switches and circuit breakers
in the power network, and reading data of operating limits of components of
the power
network including maximum power carrying capability limits of transmission
lines,
transformers, and PV-node, a generator-node where Real-Power-P and
Voltage-Magnitude-V are given/assigned/specified/set, maximum and minimum
reactive power generation capability limits of generators, and transformers
tap position
2
I I
CA 02661753 2011-04-15
limits, or stated alternatively in a single statement as reading operating
limits of
components of the power network,
Step-20: obtaining on-line readings of given/assigned/specified/set Real-Power-
P and
Reactive-Power-Q at PQ-nodes, Real-Power-P and voltage-magnitude-V at PV-
nodes,
voltage magnitude and angle at a reference/slack node, and transformer turns
ratios,
wherein said on-line readings are the controlled variables/parameters,
Step-30: performing loadflow computation to calculate, depending on loadflow
computation model
used, complex voltages or their real and imaginary components or voltage
magnitude
corrections and voltage angle corrections at nodes of the power network
providing for
calculation of power flow through different components of the power network,
and to
calculate reactive power generation and transformer tap-position indications,
Step-40: evaluating the results of Loadflow Computation of step-30 for any
over loaded power
network components like transmission lines and transformers, and over/under
voltages at
different nodes in the power system,
Step-50: if the system state is acceptable implying no over loaded
transmission lines and
transformers and no over/under voltages, the process branches to step-70, and
if
otherwise, then to step-60,
Step-60: correcting one or more controlled variables/parameters set in step-20
or at later set by the
previous process cycle step-60 and returns to step-30,
Step-70: affecting a change in power flow through components of the power
network and voltage
magnitudes and angles at the nodes of the power network by actually
implementing the
finally obtained values of controlled variables/parameters after evaluating
step finds a
good power system or stated alternatively as the power network without any
overloaded
components and under/over voltages, which finally obtained controlled
variables/parameters however are stored for acting upon fast in case a
simulated event
actually occurs or stated alternatively as actually implementing the corrected
controlled
variables/parameters to obtain secure/correct/acceptable operation of power
system.
[007] Overload and under/over voltage alleviation functions produce changes in
controlled
variables/parameters in step-60 of Fig. 3. In other words controlled
variables/parameters are
assigned or changed to the new values in step-60. This correction in
controlled
variables/parameters could be even optimized in case of simulation of all
possible imaginable
3
CA 02661753 2011-04-15
disturbances including outage of a line and loss of generation for corrective
action stored and made
readily available for acting upon in case the simulated disturbance actually
occurs in the power
network. In fact simulation of all possible imaginable disturbances is the
modern practice because
corrective actions need be taken before the operation of individual protection
of the power-network
components.
[008] It is obvious that loadflow computation consequently is performed many
times in real-time
operation and control environment and, therefore, efficient and high-speed
loadflow computation
is necessary to provide corrective control in the changing power system
conditions including an
outage or failure of any of the power network components. Moreover, the
loadflow computation
must be highly reliable to yield converged solution under a wide range of
system operating
conditions and network parameters. Failure to yield converged loadflow
solution creates blind spot
as to what exactly could be happening in the network leading to potentially
damaging operational
and control decisions/actions in capital-intensive power utilities.
[009] The power system control process shown in Fig. 3 is very general and
elaborate. It includes
control of power-flows through network components and voltage control at
network nodes.
However, the control of voltage magnitude at connected nodes within reactive
power generation
capabilities of electrical machines including generators, synchronous motors,
and
capacitor/inductor banks, and within operating ranges of transformer taps is
normally integral part
of load flow calculation as described in "LTC Transformers and MVAR violations
in the Fast
Decoupled Load Flow, IEEE Trans., PAS-101, No.9, PP. 3328-3332, September
1982." If
under/over voltage still exists in the results of load flow calculation, other
control actions, manual
or automatic, may be taken in step-60 in the above and in Fig. 3. For example,
under voltage can be
alleviated by shedding some of the load connected.
[010] The prior art and present invention are described using the following
symbols and terms:
Ypq = Gpq + jBpq : (p-q) th element of nodal admittance matrix without shunts
Ypp = Gpp + jBpp : p-th diagonal element of nodal admittance matrix without
shunts
yp = gp + jbp : total shunt admittance at any node-p
VP = ep + jfp = VpL6p : complex voltage of any node-p
AO P7 AVp : voltage angle, magnitude corrections
4
CA 02661753 2011-04-15
Aep, Afp : real, imaginary components of voltage corrections
Pp + jQp : net nodal injected power calculated
PSHp + jQSHp : net nodal injected power scheduled/specified/set/given/assigned
APP + jAQp : nodal power residue/mismatch (PSHp+jQSHp)-(Pp+jQp)
RPp + jRQp : modified nodal power residue/mismatch
VSHp : scheduled/specified/set/given/assigned voltage magnitude at node-p
(DP nodal rotation/transformation angle
[RP] : vector of modified real power residue/mismatch
[RQ] : vector of modified reactive power residue/mismatch
[Y8] : gain matrix of the P-8 loadflow sub-problem defined by eqn. (1)
[YV] : gain matrix of the Q-V loadflow sub-problem defined by eqn. (2)
[GB] : gain/coefficient matrix defined by eqns. (51) & (52)
m : number of PQ-nodes
k : number of PV-nodes
n=m+k+l : total number of nodes
q>p : q is the node adjacent to node-p excluding the case of q=p
[ ] indicates enclosed variable symbol to be a vector or a matrix
PQ-node: load-node, where, Real-Power-P and Reactive-Power-Q are specified
PV-node: generator-node, where, Real-Power-P and Voltage-Magnitude-V are
specified
Bold lettered symbols represent complex quantities in description, and the
word "nodal" refers to
any node-p.
Loadflow Computation: Each node in a power network is associated with four
electrical quantities,
which are voltage magnitude, voltage angle, real power, and reactive power.
The loadflow computation involves calculation/determination of two
unknown electrical quantities for other two
given/specified/scheduled/set/known electrical quantities for each node. In
other words the loadflow computation involves determination of unknown
quantities in dependence on the given/specified/scheduled/ set/known
electrical quantities.
Loadflow Model : a set of equations describing the physical power network and
its operation for
the purpose of loadflow computation. The term `loadflow model' can be
CA 02661753 2011-04-15
alternatively referred to as `model of the power network for loadflow
computation'. The process of writing Mathematical equations that describe
physical power network and its operation is called Mathematical Modeling. If
the equations do not describe/represent the power network and its operation
accurately the model is inaccurate, and the iterative loadflow computation
method could be slow and unreliable in yielding converged loadflow
computation. There could be variety of Loadflow Models depending on
organization of set of equations describing the physical power network and its
operation, including Decoupled Loadflow Models, Fast Super Decoupled
Loadflow (FSDL) Model, and Super Super Decoupled Loadflow (SSDL)
Model.
Loadflow Method: sequence of steps used to solve a set of equations describing
the physical power
network and its operation for the purpose of loadflow computation is called
Loadflow Method, which term can alternatively be referred to as `loadflow
computation method' or `method of loadflow computation'. One word for a set
of equations describing the physical power network and its operation is:
Model. In other words, sequence of steps used to solve a Loadflow Model is a
Loadflow Method. The loadflow method involves steps of
definition/formation of a loadflow model and its solution. There could be
variety of Loadflow Methods depending on a loadflow model and iterative
scheme used to solve the model including Decoupled Loadflow Methods, Fast
Super Decoupled Loadflow (FSDL) Method, and Super Super Decoupled
Loadflow (SSDL) Method. Most decoupled loadflow methods described in
this application use either successive (10, 1V), successive (If, le),
successive
(le, If) iteration schemes or simultaneous (If, le) iteration scheme. The
different iteration schemes are defined in the following description at
appropriate points.
[011] Prior art methods of loadflow computation of the kind carried out as
step-30 in Fig. 3, are
Gauss-Seidel-Patel Loadflow (GSPL) and Super Super Decoupled Loadflow (SSDL)
methods.
The Gauss-Seidel Loadflow method is well known to be not able to converge to
high accuracy
solution because of its iteration scheme that lacks self iterations. This
realization led to the
6
I l
CA 02661753 2011-04-15
invention of the prior art Gauss-Seidel-Patel Loadflow (GSPL) method, and
invention of
Decoupled Gauss-Seidel-Patel Loadflow (DGSPL) method, which is claimed in this
application.
The prior art methods will now the described.
GAUSS-SEIDEL-PATEL LOADFLOW (GSPL)
[012] The complex power injected into the node-p of a power network is given
by the following
equation,
n
Pp- jQp = Vp* Y_ YpqVq = Vp* YppVp + Vp* E YpqVq (1)
q=1 q >p
Where,
n
Pp = Re {V* Y YpqVq } (2)
q=1
n
Qp = - Im{ Vp* Y_ YpgVq } (3)
q=1
Where, Re means "real part of' and Im means "imaginary part of'.
[013] The Gauss-Seidel-Patel (GSP) numerical method is used to solve a set of
simultaneous
nonlinear algebraic equations iteratively. The GSPL-method calculates complex
node voltage
from any node-p equation (1) as given in equation (4).
Vp { (PSHp -jQSHp )/ Vp* } - Y_ YpgVq ] /Ypp (4)
q>p
Iteration Process
[014] Iterations start with the experienced/reasonable/logical guess for the
solution. The reference
node also referred to as the slack-node voltage being specified, starting
voltage guess is made for
the remaining (n-1)-nodes in n-node network. Node voltage value is immediately
updated with its
newly calculated value in the iteration process in which one node voltage is
calculated at a time
using latest updated other node voltage values. A node voltage value
calculation at a time process
is iterated over (n-1)-nodes in an n-node network, the reference node voltage
being specified not
required to be calculated. For the iteration-(r+1), the complex voltage at
node-p equation (4) and
reactive power at node-p equation (3), becomes
1 n
Vp(r+1) _ [{(PSHp- jQSHp )/ (Vp* )r} - Y_ YpgVq(r+1) - 1 Ypq Vqr] / Ypp (5)
q=1 q=p+1
7
CA 02661753 2011-04-15
P-1 n
QP(r+1) Im { (Vp* )r Z YpgVg(r+1) + (Vp* )r y Ypq Vq r } (6)
q=1 q=P
[015] The well-known limitation of the Gauss-seidel numerical method to be not
able to converge
to the high accuracy solution, was resolved in the Gauss-Seidel-Patel (GSP)
numerical method by
the introduction of the concept of self-iteration of each calculated variable
until convergence
before proceeding to calculate the next. This is achieved by replacing
equation (5) by equation (7)
stated in the following where self-iteration-(sr+1) over a node variable
itself within the global
iteration-(r+l) over (n-1) nodes in the n-node network is depicted. During the
self-iteration process
only V, changes without affecting any of the terms involving Vq. At the start
of the self-iteration
VPsr = V P r, and at the convergence of the self-iteration Vp(r+1) = VP(sr+1)
P-1 n
(VP(sr+l))(r+1) = [{(PSHp- jQSHp )/ ((Vp* )sr)r } - > YpgVq(r+l) - Y_ Ypq Vqr]
/ YPP (7)
q=1 q=p+1
Self-convergence
[016] The self-iteration process for a node is carried out until changes in
the real and imaginary
parts of the node-p voltage calculated in two consecutive self-iterations are
less than the specified
tolerance. It has been possible to establish a relationship between the
tolerance specification for
self-convergence and the tolerance specification for global-convergence. It is
found sufficient for
the self-convergence tolerance specification to be ten times the global-
convergence tolerance
specification.
Aff(sr+1) I = I fp(sr+1) - fpsrl < We (8)
Aep(sr+l) = I ep(sr+1) - epsrl < 10E (9)
[017] For the global-convergence tolerance specification of 0.000001, it has
been found sufficient
to have the self-convergence tolerance specification of 0.00001 in order to
have the maximum real
and reactive power mismatches of 0.0001 in the converged solution. However,
for small networks
under not difficult to solve conditions they respectively could be 0.00001 and
0.0001 or 0.000001
and 0.0001, and for large networks under difficult to solve conditions they
sometimes need to be
respectively 0.0000001 and 0.000001.
8
CA 02661753 2011-04-15
Convergence
[018] The iteration process is carried out until changes in the real and
imaginary parts of the set of
(n-1)-node voltages calculated in two consecutive iterations are all less than
the specified tolerance
- E, as shown in equations (10) and (11). The lower the value of the specified
tolerance for
convergence check, the greater the solution accuracy.
Ofp(r+1) _ fp(r+1) - fpr < E (10)
Dep(r+l) I _ ep(r+1) - epr < E (11)
Accelerated Convergence
[019] The GSP-method being inherently slow to converge, it is characterized by
the use of an
acceleration factor applied to the difference in calculated node voltage
between two consecutive
iterations to speed-up the iterative solution process. The accelerated value
of node-p voltage at
iteration-(r+1) is given by
Vp(r+1) (accelerated) = Vpr + R (Vp(r+l) - Vpr) (12)
Where, (3 is the real number called acceleration factor, the value of which
for the best possible
convergence for any given network can be determined by trial solutions. The
GSP-method is very
sensitive to the choice of (3, causing very slow convergence and even
divergence for the wrong
choice.
Scheduled or specified voltage at a PV-node
[020] Of the four variables, real power PSHp and voltage magnitude VSHp are
scheduled/specified/set at a PV-node. If the reactive power calculated using
VSHp at the PV-node
is within the upper and lower generation capability limits of a PV-node
generator, it is capable of
holding the specified voltage at its terminal. Therefore the complex voltage
calculated by equation
(5) or (7) by using actually calculated reactive power Qp in place of QSHp is
adjusted to specified
voltage magnitude by equation (13). However, in case of violation of upper or
lower generation
capability limits of a PV-node generator, a violated limit value is used for
QSHp in (5) and (7),
meaning a PV-node generator is no longer capable of holding its terminal
voltage at its scheduled
voltage VSHp, and the PV-node is switched to a PQ-node type.
9
CA 02661753 2011-04-15
VP(r+1) _ (VSHP VP(r+1))/ I VP (r+1) I (13)
Calculation steps of Gauss-Seidel Loadflow (GSL) method
[021] The steps of loadflow computation by GSPL method are shown in the
flowchart of Fig. I a.
Referring to the flowchart of Fig.1a, different steps are elaborated in steps
marked with similar
numbers in the following. The words "Read system data" in Step-1 correspond to
step-10 and
step-20 in Fig. 3, and step-14, step-20, step-32, step-44, step-50 in Fig. 4.
All other steps in the
following correspond to step-30 in Fig. 3, and step-60, step-62, and step-64
in Fig. 4.
1. Read system data and assign an initial approximate solution. If better
solution estimate is not
available, set specified voltage magnitude at PV-nodes, 1.0 p.u. voltage
magnitude at
PQ-nodes, and all the node angles equal to that of the slack-node angle, which
is referred to
as the flat-start.
2. Form nodal admittance matrix, and Initialize iteration count r= 1
3. Scan all the node of a network, except the slack-node whose voltage having
been specified
need not be calculated. Initialize node count p=1, and initialize maximum
change in real and
imaginary parts of node voltage variables DEMX=0.0 and DFMX=0.0
4. Test for the type of a node at a time. For the slack-node go to step- 12,
for a PQ-node go to the
step-9, and for a PV-node follow the next step.
5. Compute Qp(r+1) for use as an imaginary part in determining complex
schedule power at a
PV-node from equation (6) after adjusting its complex voltage for specified
value by
equation (13)
6. If Qp(r+'' is greater than the upper reactive power generation capability
limit of the PV-node
generator, set QSHp = the upper limit QPma" for use in equation (7), and go to
step-9. If not,
follow the next step.
7. If Qp(r+1) is less than the lower reactive power generation capability
limit of the PV-node
generator, set QSHP = the lower limit Qpmn for use in equation (7), and go to
step-9. If not,
follow the next step.
8. Compute V p(+1) by equations (7), (8), (9) involving self iteration using
QSHp = Qp(r+' ), and
adjust its value for specified voltage at the PV-node by equation (13), and go
to step-10
9. Compute V P('+1) by equations (7), (8), (9) involving self iteration
10. Compute changes in the imaginary and real parts of the node-p voltage by
using equations
CA 02661753 2011-04-15
(10) and (11), and replace current value of DFMX and DEMX respectively in case
any of
them is larger.
11. Calculate accelerated value of V P('+') by using equation (12), and update
voltage by V Pr= V
P(r+') for immediate use in the next node voltage calculation.
12. Check for if the total numbers of nodes - n are scanned. That is if p< n ,
increment p=p+1,
and go to step-4. Otherwise follow the next step.
13. If DEMX and DFMX both are not less than the convergence tolerance (E)
specified for the
purpose of the accuracy of the solution, advance iteration count r--r+1 and go
to step-3,
otherwise follow the next step
14. From calculated and known values of complex voltage at different power
network nodes,
and tap position of tap changing transformers, calculate power flows through
power network
components, and reactive power generation at PV-nodes.
Decoupled Loadflow
[022] In a class of decoupled loadflow methods, each decoupled method
comprises a system of
equations (14) and (15) differing in the definition of elements of [RP], [RQ],
and [YO] and [YV]. It
is a system of equations for the separate calculation of voltage angle and
voltage magnitude
corrections.
[RP] _ [YO] [A0] (14)
[RQ] _ [YV] [AV] (15)
Successive (10, 1V) Iteration Scheme
[023] In this scheme (14) and (15) are solved alternately with intermediate
updating. Each iteration
involves one calculation of [RP] and [AO] to update [0] and then one
calculation of [RQ] and [AV]
to update [V]. The sequence of equations (16) to (19) depicts the scheme.
[A0] = [Y0] -1 [RP] (16)
[0] _ [0] + [DO] (17)
[AV] = [YV] -' [RQ] (18)
[V]_[V]+[AV] (19)
11
CA 02661753 2011-04-15
[024] The scheme involves solution of system of equations (14) and (15) in an
iterative manner
depicted in the sequence of equations (16) to (19). This scheme requires
mismatch calculation for
each half-iteration; because [RP] and [RQ] are calculated always using the
most recent voltage
values and it is block Gauss-Seidal approach. The scheme is block successive,
which imparts
increased stability to the solution process. This in turn improves convergence
and increases the
reliability of obtaining solution.
Super Super Decoupled Loadflow: SSDL
[025] This method is not very sensitive to the restriction applied to nodal
transformation angles;
SSDL restricts transformation angles to the maximum of -48 degrees determined
experimentally for the best possible convergence from non linearity
considerations, which is
depicted by equations (22) and (23). However, it gives closely similar
performance over wide
range of restriction applied to the transformation angles say, from -36 to -90
degrees.
RPp = (APpCos(Dp + AQpSin(Dp)/ Vp2 -for PQ-nodes (20)
RQp = (AQpCos(Dp - APpSin(Dp )/Vp -for PQ-nodes (21)
Cos(Dp = Absolute (BPp / SQRT (Gpp2 + BPP2)) Cos (-48 ) (22)
Sinop = -Absolute (GPP / SQRT (Gpp2 + BPP2)) ? Sin (-48 ) (23)
RPp = AP P / (KPVP2) -for PV-nodes (24)
KP = Absolute (BPP/YOPP) (25)
YApq = -Ypq -for branch r/x ratio <_ 3.0
- (Bpq + 0.9(Ypq Bpq)) -for branch r/x ratio > 3.0
-Bpq -for branches connected between two PV-nodes or a
PV-node and the slack-node (26)
YVpq = Ypq -for branch r/x ratio <_ 3.0
L (Bpq + 0.9(Ypq-Bpq)) -for branch r/x ratio > 3.0 (27)
Y6pp = Y--YOpq and YVPP = bp + Y--YVpq (28)
q>p q>p
12
CA 02661753 2011-04-15
by = (QSHpCos(Dp - PSHpSin(Dp / V,2) - bpCos(Dp or
bpi = 2(QSHPCos(Dp - PSHPSin(Dp )/ Vs2 (29)
where, the words SQRT means take square root of the expression enclosed in
parenthesis
immediately following words SQRT, and Kp as defined in equation (25) is
initially restricted to
the minimum value of 0.75 determined experimentally; however its restriction
is lowered to
the minimum value of 0.6 when its average over all less than 1.0 values at PV
nodes is less
than 0.6. Restrictions to the factor Kp as stated in the above is system
independent. However it can
be tuned for the best possible convergence for any given system. In case of
systems of only
PQ-nodes and without any PV-nodes, equations (26) and (27) simply be taken as
YOpq =
YVpq = -Ypq .
[026] Branch admittance magnitude in (26) and (27) is of the same algebraic
sign as its
susceptance. Elements of the two gain matrices differ in that diagonal
elements of [YV]
additionally contain the b' values given. by equations (28) and (29) and in
respect of elements
corresponding to branches connected between two PV-nodes or a PV-node and the
slack-node.
Equations (22) and (23) with inequality sign implies that transformation
angles are restricted to
maximum of -48 degrees for SSDL. The model consists of equations (16) to (29).
In two simple
variations of the SSDL model, one is to make YVpq=Y6pq and the other is to
make Y6pq=YVpq.
Calculation steps of Super Super Decoupled Loadflow (SSDL) method
[027] The steps of loadflow computation by SSDL method are shown in the
flowchart of Fig. lb.
Referring to the flowchart of Fig.lb, different steps are elaborated in steps
marked with similar
letters in the following. The words "Read system data" in Step-1 correspond to
step-10 and step-20
in Fig. 3, and step-14, step-20, step-32, step-44, step-50 in Fig. 4. All
other steps in the following
correspond to step-30 in Fig. 3, and step-60, step-62, and step-64 in Fig. 4.
a. Read system data and assign an initial approximate solution. If better
solution estimate is
not available, set voltage magnitude and angle of all nodes equal to those of
the slack-node.
This is referred to as the slack-start.
b. Form nodal admittance matrix, calculate CosOp and SinOp using equations
(22) and (23),
and store them. Initialize iteration count ITRP = ITRQ= r = 0
13
I I
CA 02661753 2011-04-15
c. Check Cos(DP and Sinb,, If they, respectively, are less than the Cosine and
Sine of -48
degrees, equate them, respectively, to those of -48 degrees.
d. Form (m+k) x (m+k) size matrices [Y0] and [YV] of (14) and (15)
respectively each in a
compact storage exploiting sparsity. The matrices are formed using equations
(26), (27),
(28), and (29). In [YV] matrix, replace diagonal elements corresponding to PV-
nodes by
very large value (say, 10.0** 10). In case [YV] is of dimension (m x m), this
is not required
to be performed. Factorize [Y0] and [YV] using the same ordering of nodes
regardless of
node-types and store them using the same indexing and addressing information.
In
case [YV] is of dimension (m x m), it is factorized using different ordering
than that of
[Y0].
e. Compute residues [AP] at PQ- and PV-nodes and [AQ] at only PQ-nodes. If all
are less
than the tolerance (s), proceed to step-n. Otherwise follow the next step.
f. Compute the vector of modified residues [RP] using (20) for PQ-nodes, and
using (24) and
(25) for PV-nodes.
g. Solve (16) for [A0] and update voltage angles using, [0] = [0] + [00].
h. Set voltage magnitudes of PV-nodes equal to the specified values, and
Increment the
iteration count ITRP=ITRP+1 and r=(ITRP+ITRQ)/2.
i. Compute residues [AP] at PQ- and PV-nodes and [AQ] at PQ-nodes only. If all
are less
than the tolerance (c), proceed to step-n. Otherwise follow the next step.
j. Compute the vector of modified residues [RQ] using (21) for only PQ-nodes.
k. Solve (18) for [AV] and update PQ-node magnitudes using [V] = [V] + [AV].
While
solving equation (18), skip all the rows and columns corresponding to PV-
nodes.
1. Calculate reactive power generation at PV-nodes and tap positions of tap
changing
transformers. If the maximum and minimum reactive power generation capability
and
transformer tap position limits are violated, implement the violated physical
limits and
adjust the loadflow solution by the method of reference: "LTC Transformers and
MVAR
violations in the Fast Decoupled Load Flow, IEEE Trans., PAS-101, No.9, PP.
3328-3332,
September 1982."
M. Increment the iteration count ITRQ=ITRQ+1 and r=(ITRP+ITRQ)/2, and go to
step-e.
n. From calculated and known values of voltage magnitude and voltage angle at
different
power network nodes, and tap position of tap changing transformers, calculate
power flows
14
CA 02661753 2011-04-15
through power network components, and reactive power generation at PV-nodes.
SUMMARY OF THE INVENTION
[028] It is a primary object of the present invention to improve convergence
and efficiency of the
prior art GSPL and SSDL calculation methods under wide range of system
operating conditions
and network parameters for use in power flow control and voltage control in
the power system.
[029] The above and other objects are achieved, according to the present
invention, with
Decoupled Gauss-Seidel-Patel Loadflow (DGSPL) and Patel Decoupled Loadflow
(PDL)
calculation methods for Electrical Power System. In context of voltage
control, the inventive
system of loadflow computation for Electrical Power system consisting of
plurality of
electromechanical rotating machines, transformers and electrical loads
connected in a network,
each machine having a reactive power characteristic and an excitation element
which is
controllable for adjusting the reactive power generated or absorbed by the
machine, and some of
the transformers each having a tap changing element, which is controllable for
adjusting turns ratio
or alternatively terminal voltage of the transformer, said system comprising:
means defining and solving loadflow model of the power network characterized
by
inventive DGSPL and PDL models for providing an indication of the quantity of
reactive power to be supplied by each generator including the reference/slack
node
generator, and for providing an indication of turns ratio of each tap-changing
transformer in dependence on the obtained-online or given/specified/set/known
controlled network variables/parameters, and physical limits of operation of
the
power network components,
machine control means connected to the said means defining and solving
loadflow model
and to the excitation elements of the rotating machines for controlling the
operation
of the excitation elements of machines to produce or absorb the amount of
reactive
power indicated by said means defining and solving loadflow model in
dependence
on the set of obtained-online or given/specified/set/known controlled network
variables/parameters, and physical limits of excitation elements,
transformer tap position control means connected to the said means defining
and solving
loadflow model and to the tap changing elements of the controllable
transformers
CA 02661753 2011-04-15
for controlling the operation of the tap changing elements to adjust the turns
ratios
of transformers indicated by the said means defining and solving loadflow
model in
dependence on the set of obtained-online or given/specified/set/known
controlled
network variables/parameters, and operating limits of the tap-changing
elements.
[030] The method and system of voltage control according to the preferred
embodiment of the
present invention provide voltage control for the nodes connected to PV-node
generators and tap
changing transformers for a network in which real power assignments have
already been fixed.
The said voltage control is realized by controlling reactive power generation
and transformer tap
positions.
[031] The inventive system of decoupled loadflow computation can be used to
solve a model of
the Electrical Power System for voltage control. For this purpose real and
reactive power
assignments or settings at PQ-nodes, real power and voltage magnitude
assignments or settings at
PV-nodes and transformer turns ratios, open/close status of all circuit
breaker, the reactive
capability characteristic or curve for each machine, maximum and minimum tap
positions limits of
tap changing transformers, operating limits of all other network components,
and the impedance or
admittance of all lines are supplied. DGSPL or PDL model is solved by an
iterative process until
convergence. During this solution the quantities which can vary are the real
and reactive power at
the reference/slack node, the reactive power set points for each 'PV-node
generator, the
transformation ratios of tap-changing transformers, and voltages on all PQ-
nodes nodes, all being
held within the specified ranges. When the iterative process converges to a
solution, indications of
reactive power generation at PV-nodes and transformer turns-ratios or tap-
settings are provided.
Based on the known reactive power capability characteristics of each PV-node
generator, the
determined reactive power values are used to adjust the excitation current to
each generator to
establish the reactive power set points. The transformer taps are set in
accordance with the turns
ratio indication provided by the system of loadflow computation.
[032] For voltage control, system of DGSPL or PDL calculation can be employed
either on-line
or off-line. In off-line studies, the user can simulate and experiment with
various sets of operating
conditions and determine reactive power generation and transformer tap
settings requirements. For
on-line operation, the load flow calculation system is provided with data
identifying the current
real and reactive power assignments and transformer transformation ratios, the
present status of all
16
CA 02661753 2011-04-15
switches and circuit breakers in the network and machine characteristic curves
in steps- 10 and -20
in Fig. 3, and steps 12, 20, 32, 44, and 50 in Fig 4 described below. Based on
this information or
alternately in dependence on this information, a model of the system provide
the values for the
corresponding node voltages, reactive power.set points for each machine and
the transformation
ratio and tap changer position for each tap-changing transformer.
[033] Inventions include Decoupled Gauss-Seidel-Patel Loadflow (DGSPL) and
Patel Decoupled
Loadflow (PDL) methods for the solution of complex simultaneous algebraic
power injection
equations or any set of complex simultaneous algebraic equations arising in
any other subject
areas. The invented DGSPL and PDL methods introduces block successive
iteration scheme (Jf,
Je) or (Je, Jf), where J can take any number decided by the user or determined
experimentally in
addition to the original successive displacement scheme of the well known
Gauss-Seidel method
used in loadflow computations. In other words, in calculation of imaginary
part `f' of the complex
voltage at all of the nodes in the network using formal successive
displacement Gauss-Seidel-Patel
method, the real part `e' of the complex voltage at all nodes is held constant
and vice versa.
BRIEF DESCRIPTION OF DRAWINGS
[034] Fig. 1 is a flow-charts of the prior art GSPL and SSDL methods
[035] Fig. 2 is a flow-charts embodiment of the invented DGSPL, PDL methods
[036] Fig. 3 is a flow-chart of the overall controlling method for an
electrical power system
involving load-flow calculation as a step which can be executed using one of
the invented
load-flow calculation method of Fig. 2.
[037] Fig. 4 is a flow-chart of the simple special case of voltage control
system in overall
controlling system of Fig. 3 for an electrical power system
[038] Fig. 5 is a one-line diagram of an exemplary 6-node power network having
a
slack/swing/reference node, two PV-nodes, and three PQ-nodes
DESCRIPTION OF A PREFERED EMBODYMENT
[039] A loadflow computation is involved as a step in power flow control
and/or voltage control
in accordance with Fig. 3 or Fig. 4. A preferred embodiment of the present
invention is described
with reference to Fig. 5 as directed to achieving voltage control.
17
CA 02661753 2011-04-15
[040] Fig. 5 is a simplified one-line diagram of an exemplary utility power
network to which the
present invention may be applied. The fundamentals of one-line diagrams are
described in section
6.11 of the text ELEMENTS OF POWER SYSTEM ANALYSIS, forth edition, by William
D.
Stevenson, Jr., McGrow-Hill Company, 1982. In Fig. 5, each thick vertical line
is a network node.
The nodes are interconnected in a desired manner by transmission lines and
transformers each
having its impedance, which appears in the loadflow models. Two transformers
in Fig. 5 are
equipped with tap changers to control their turns ratios in order to control
terminal voltage of
node-1 and node-2 where large loads are connected.
[041] Node-6 is a reference-node alternatively referred to as the slack or
swing -node,
representing the biggest power plant in a power network. Nodes-4 and -5 are PV-
nodes where
generators are connected, and nodes-l, -2, and -3 are PQ-nodes where loads are
connected. It
should be noted that the nodes-4, -5, and -6 each represents a power plant
that contains many
generators in parallel operation. The single generator symbol at each of the
nodes-4, -5, and -6 is
equivalent of all generators in each plant. The power network further includes
controllable circuit
breakers located at each end of the transmission lines and transformers, and
depicted by cross
markings in one-line diagram of Fig. 5. The circuit breakers can be operated
or in other words
opened or closed manually by the power system operator or relevant circuit
breakers operate
automatically consequent of unhealthy or faulty operating conditions. The
operation of one or
more circuit breakers modify the configuration of the network. The arrows
extending certain nodes
represent loads.
[042] A goal of the present invention is to provide a reliable and
computationally efficient
loadflow computation that appears as a step in power flow control and/or
voltage control systems
of Fig. 3 and Fig. 4. However, the preferred embodiment of loadflow
computation as a step in
control of terminal node voltages of PV-node generators and tap-changing
transformers is
illustrated in the flow diagram of Fig. 4 in which present invention resides
in function steps 60 and
62.
[043] Short description of other possible embodiment of the present invention
is also provided
herein. The present invention relates to control of utility/industrial power
networks of the types
including plurality of power plants/generators and one or more motors/loads,
and connected to
other external utility. In the utility/industrial systems of this type, it is
the usual practice to adjust
18
CA 02661753 2011-04-15
the real and reactive power produced by each generator and each of the other
sources including
synchronous condensers and capacitor/inductor banks, in order to optimize the
real and reactive
power generation assignments of the system. Healthy or secure operation of the
network can be
shifted to optimized operation through corrective control produced by
optimization functions
without violation of security constraints. This is referred to as security
constrained optimization of
operation. Such an optimization is described in the United States Patent
Number: 5,081,591 dated
Jan. 13, 1992: "Optimizing Reactive Power Distribution in an Industrial Power
Network", where
the present invention can be embodied by replacing the step nos. 56 and 66
each by a step of
constant gain matrix [GB] and replacing steps of "Exercise Newton-Raphson
Algorithm" by steps
of "Exercise Patel Decoupled Loadflow Computation" in places of steps 58 and
68. This is just to
indicate the possible embodiment of the present invention in optimization
functions like in many
others including state estimation function. However, invention is being
claimed through a
simplified embodiment without optimization function as in Fig. 4 in this
application. The inventive
steps-60 and -62 in Fig.4 are different than those corresponding steps-56, and
-58, which
constitute a well known Newton-Raphson loadflow method, and were not inventive
even in United
States Patent Number: 5,081,591.
[044] In Fig. 4, function step 10 provides stored impedance values of each
network component in
the system. This data is modified in a function step 12, which contains stored
information about the
open or close status of each circuit breaker. For each breaker that is open,
the function step 12
assigns very high impedance to the associated line or transformer. The
resulting data is than
employed in a function step 14 to establish an admittance matrix for the power
network. The data
provided by function step 10 can be input by the computer operator from
calculations based on
measured values of impedance of each line and transformer, or on the basis of
impedance
measurements after the power network has been assembled.
[045] Each of the transformers Ti and T2 in Fig. 5 is a tap changing
transformer having a
plurality of tap positions each representing a given transformation ratio. An
indication of initially
assigned transformation ratio for each transformer is provided by function
step 20.
[046] The indications provided by function steps 14, and 20 are supplied to a
function step 60 in
which constant gain matrix [GB] of the invented Patel Decoupled Loadflow model
is constructed,
19
CA 02661753 2011-04-15
factorized and stored. The gain matrix [GB] is conventional tool employed for
solving Patel
Decoupled Loadflow model defined by equations (51) and (52) for a power
system.
[047] Indications of initial reactive power, or Q on each node, based on
initial calculations or
measurements, are provided by a function step 30 and these indications are
used in function step
32, to assign a Q level to each generator and motor. Initially, the Q assigned
to each machine can
be the same as the indicated Q value for the node to which that machine is
connected.
[048] An indication of measured real power, P, on each node is supplied by
function'step 40.
Indications of assigned/specified/scheduled/set generating plant loads that
are constituted by
known program are provided by function step 42, which assigns the real power,
P, load for each
generating plant on the basis of the total P, which must be generated within
the power system. The
value of P assigned to each power plant represents an economic optimum, and
these values
represent fixed constraints on the variations, which can be made by the system
according to the
present invention. The indications provided by function steps 40 and 42 are
supplied to function
step 44 which adjusts the P distribution on the various plant nodes
accordingly. Function step 50
assigns initial approximate or guess solution to begin iterative method of
loadflow computation,
and reads data file of operating limits on power network components, such as
maximum and
minimum reactive power generation capability limits of PV-nodes generators.
[049] The indications provided by function steps 32, 44, 50 and 60 are
supplied to function step
62 where inventive Decoupled Gauss-Seidel-Patel Loadflow computation or Patel
Decoupled
Loadflow computation is carried out, the results of which appear in function
step 64. The loadflow
computation yields voltage magnitudes and voltage angles at PQ-nodes, real and
reactive power
generation by the slack/swing/reference node generator, voltage angles and
reactive power
generation indications at PV-nodes, and transformer turns ratio or tap
position indications for tap
changing transformers. The system stores in step 62 a representation of the
reactive capability
characteristic of each PV-node generator and these characteristics act as
constraints on the reactive
power that can be calculated for each PV-node generator for indication in step
64. The indications
provided in step 64 actuate machine excitation control and transformer tap
position control. All the
loadflow computation methods using Decoupled models can be used to effect
efficient and reliable
voltage control in power systems as in the process flow diagram of Fig. 4.
CA 02661753 2011-04-15
[050] Inventions include Decoupled Gauss-Seidel-Patel Loadflow (DGSPL) and PDL
methods for
the solution of complex simultaneous algebraic power injection equations or
any set of complex
simultaneous algebraic equations arising in any other subject areas. The
invented DGSPL method
introduces block successive iteration scheme (Jf, Je) or (Je, Jf), where J can
take any number
decided by the user or determined experimentally in addition to the original
successive
displacement scheme of the well known Gauss-Seidel method used in loadflow
computations. In
other words, in calculation of imaginary part `f' of the complex voltage at
all of the nodes in the
network using formal successive displacement Gauss-Seidel-Patel method, the
real part `e' of the
complex voltage at all nodes is held constant and vice versa.
Decoupled Gauss-Seidel-Patel Loadflow (DGSPL)
[051] Gauss-seidel-Patel numerical method is further developed by de-coupling
the complex
power injection into two quadratic equations and solving them simultaneously
or preferably
successively as described in the following.
Real and reactive power injection equation at any node-p in rectangular
coordinates can be written
as,
PSHp = (Gpp + gp) (ep2 + fp2) + [ep(egGpq - fqBpq) + fp(fqGpq + eqBpq)] (30)
q >p
QSHp = -(Bpp + bp) (ep2 + fp2) - Y_ [ep(fgGpq + eqBpq) - fp(eqGpq - fgBpq)]
(31)
q >p
[052] PSHp and QSHp can be added as (I1pPSHp + I2pQSHp), where lip & I2p can
take any values
from -oc, ..., -2, -1, 0, 1, 2, ..., oo. Normally, lip & I2p both take value
of 1Ø However, they can
take any other value, both the same or different, to be determined
experimentally for the best
possible convergence. This technique of adding real and imaginary parts of the
complex
equation is applicable in all other subject areas requiring solution of
complex simultaneous
equations. Therefore,
I]pPSHp+I2pQSHp = Ap(ep2+fp2) + epY,(I1pBB 1 I2pBB2p) + fpY.(12pBB lp+I1pBB2p)
(32)
q>p q>p
Where,
Ap = lip (Gpp + gp) - 12p (Bpp + bp) (33)
BB lp = (egGpq - fqBpq) (34)
21
CA 02661753 2011-04-15
BB213 = (fqGpq + eqBpq) (35)
Now, equation (32) can be decoupled into two quadratic equations as,
Alpep2+Blpep+Cip=0 (36)
A2pfp2 + B2pfp + C2p = 0 (37)
Where,
Alp = Alp = Ap (38)
Blp = F. (I1pBB lp - I2pBB2p) (39)
q >p
B2p = E (I2pBB1p + I1pBB2p) (40)
q >p
Clp = A2pfp2 + B2pfp - (I1pPSHp + I2pQSHp) (41)
C2p = Alpep2 + Blpep - (I1pPSHp + I2pQSHp) (42)
Where, PSHp and QSHp are scheduled or specified values. However, QSHp at a PV-
node is
calculated value using specified voltage magnitude constrained by upper and
lower reactive power
generation capability limits of a PV-node generator, and the same description
under the heading of
Scheduled/specified/set voltage at a PV-node on page-9 of this application is
applicable at this
point. Equations (36) and (37) can be iterated incorporating self-iteration
for solution as depicted
in equations (43) and (44).
(ep(sr+1))(r+1) = [{-Clp / ((ep)s`)r } -(B P)r] / Alp (43)
(f p(sr+l))(r+l) = [ { -C2p / ((f p)sr) r } - (B2)r1 / Alp (44)
[053] Equations (36) and (37), which are quadratic in ep and fp, can also be
iterated without
incorporating self-iteration for solution as depicted in equations (45) and
(46).
ep(r+]) _ (-Blpr + SQRT ((BIpr)2 - 4A1pCip)) / 2A1 (45)
fp(r+l) _ (-B2pr + SQRT ((B2pr)2 - 4A2pC2p)) / 2A2 (46)
[054] Equations (36), (43) or (45) and (37), (44) or (46) can be solved
simultaneously or
successively. There are three possible successive iteration schemes in which
equations (36), (43)
22
CA 02661753 2011-04-15
or (45) and (37), (44) or (46) can be solved. It is possible to solve either
first (36), (43) or (45).and,
then (37), (44) or (46) or first (37), (44) or (46) and, then (36), (43) or
(45).
Scheme-1
[055] Solve (36), (43) or (45) and (37), (44) or (46) successively for each
node, always using latest
available ep and fp, until calculations converge to a solution. In other
words, for the known
(available) values of ep at a node, solve (37), (44) or (46) for fp and then,
for the known (available)
values of fp at the same node, solve (36), (43) or (45) for ep. This
calculation for the single node is
carried out for certain number of iterations, before proceeding to the next
node. Repeat
calculations over all nodes always using latest available ep and fp, until
calculations converge to a
solution.
Scheme-2
[056] Solve (36), (43) or (45) and (37), (44) or (46) successively for each
group of nodes in a
network, always using latest available ep and fp, until calculations converge
to a solution. A group
of nodes could be directly connected nodes to a given node, creating n-groups
in a n-node network.
In other words, for the known (available) values of ep at nodes in a group,
solve (37), (44) or (46)
for fp at the same nodes of the group using latest available fp. Then, for the
known (available)
values of fp at the same group of nodes, solve (36), (43) or (45) for for ep
at the same nodes of the
group using latest available ep. This calculation for a group of nodes is
carried out for certain
number of iterations, before proceeding to the next group of nodes. Repeat
calculations over all
group of nodes always using latest available ep and fp, until calculations
converge to a solution.
Scheme-3
[057] For the known (available) values of ep at all nodes, solve (37), (44) or
(46) for fp for all the
nodes in the network always using latest available fp in subsequent
calculations. Then, for the
known (available) values of fp at all nodes, solve (36), (43) or (45) for ep
for all the nodes in the
network always using latest available ep in subsequent calculations. Repeat
until calculations
converge to a solution.
[058] The basic scheme described in the above three schemes is referred to as
(if, le) block
successive iteration scheme. The calculations can also be organized as (2f,
2e), (3f, 3e), (le, lf),
23
1". H
CA 02661753 2011-04-15
(2e, 2f), (3e, 3f), and so on, block successive iteration schemes. The size of
block is of one node in
scheme-1, a given group of nodes in scheme-2, and all nodes of the network in
scheme-3.
ep(r+1) and ff(r+l) values calculated by (43) or (45) and (44) or (46) are
modified as,
ep(r+1) = ePr + R DeP(r+1) (47)
fP(r+1) = fPr + R ,&fP(r+l) (48)
Where AeP = (r+l) _ eP(r+l) - epr (49)
OfP(r+1) = fP(r+t) - ffr (50)
and (3 is an acceleration factor used to speed-up the convergence, and
De7(r+l) and AfP (r+) are the
corrections in the real and imaginary parts of the voltage at node-p in the
(r+l)th iteration.
Calculation steps of Decoupled Gauss-Seidel-Patel Loadflow (DGSPL) method
[059] The steps of loadflow computation method, DGSPL method are shown in the
flowchart of
Fig. 2a, which is given for block successive (Jf, Je) iteration scheme, where
number J is given as
input data. Referring to the flowchart of Fig.2a, different steps are
elaborated in steps marked with
similar numbers in the following. The words "Read system data" in Step-1
correspond to step-10
and step-20 in Fig. 3, and step-14, step-20, step-32, step-44, step-50 in Fig.
4. All other steps in the
following correspond to step-30 in Fig. 3, and step-60, step-62, and step-64
in Fig. 4.
21. Read system data and assign an initial approximate solution. If better
solution estimate is not
available, set specified voltage magnitude at PV-nodes, 1.0 p.u. voltage
magnitude at
PQ-nodes, and all the node angles equal to that of the slack-node angle, which
is referred to
as the flat-start.
22. Read number J for the iteration scheme (Jf, Je), and form nodal admittance
matrix, and
Initialize iteration count r=ITRF=ITRE=O, and DEMX=DFMX=0Ø
23. Scan all the node of a network J number of times, except the slack-node
whose voltage
having been specified need not be calculated. Initialize node count p=1, and
initialize
maximum change in imaginary parts of node voltage variables DFMX=0Ø
24. Test for the type of a node at a time. For the slack-node go to step-32,
for a PQ-node go to the
step-29, and for a PV-node follow the next step.
25. Compute QP(r+l) at a PV-node from equation (31) after adjusting its
complex voltage for
specified value by equation (13)
24
j, I
CA 02661753 2011-04-15
26. If Qp'r+i> is greater than the upper reactive power generation capability
limit of the PV-node
generator, set QSHP = the upper limit Qpmax for use in equation (42), and go
to step-29. If not,
follow the next step.
27. If Qp(r+i> is less than the lower reactive power generation capability
limit of the PV-node
generator, set QSHp = the lower limit Qp' for use in equation (42), and go to
step-29. If not,
follow the next step.
28. Compute f p(r+l) from equation (44) or (46) using QSHp = Qp(r+'l in
equation (42), and adjust
its value for specified voltage at the PV-node by equation (13), and go to
step-30
29. Compute f p(") from equation (44) or (46).
30. Compute change in the imaginary part of the node-p voltage Afp(r+l) by
using equations (50),
and replace current value of DFMX by Afp(r+i) in case it is larger.
31. Calculate accelerated value of f p(r+l) by using equation (48), and update
voltage by f pr = f p(r+l)
for immediate use in the next node voltage calculation.
32. Check for if the total numbers of nodes - n are scanned. That is if p< n ,
increment p=p+ 1,
and go to step-24. Otherwise follow the next step.
33. Advance iteration count ITRF=ITRF+1. If DEMX and DFMX both are less than
the
convergence tolerance (E) specified for the purpose of the accuracy of the
solution, go to
step-45. If not check if ITRF equals J. If not go to step-23, otherwise go to
next step.
34. Scan all the node of a network, except the slack-node whose voltage having
been specified
need not be calculated. Initialize node count p=1, and initialize maximum
change in real
parts of node voltage variables DEMX=0Ø
35. Test for the type of a node at a time. For the slack-node go to step-43,
for a PQ-node go to the
step-40, and for a PV-node follow the next step.
36. Compute Qp(r+l) at a PV-node from equation (31) after adjusting its
complex voltage for
specified value by equation (13)
37. If Qp(r+i) is greater than the upper reactive power generation capability
limit of the PV-node
generator, set QSHp = the upper limit Q1, for use in equation (41), and go to
step-40. If not,
follow the next step.
38. If Qp(r+l) is less than the lower reactive power generation capability
limit of the PV-node
generator, set QSHp = the lower limit Qpmm for use in equation (41), and go to
step-40. If not,
follow the next step.
CA 02661753 2011-04-15
39. Compute e P(r+') from equation (43) or (45) using QSHP = QP(r+l) in
equation (41), and adjust
its value for specified voltage at the PV-node by equation (13), and go to
step-41
40. Compute e P(r+i) from equation (43) or (45)
41. Compute change in the real part of the node-p voltage DeP(r+i) by using
equation (49), and
replace current value of DEMX by iep(r+l) in case it is larger.
42. Calculate accelerated value of ep(") by using equation (47), and update
voltage by epr=ep (r+>)
for immediate use in the next node voltage calculation.
43. Check for if the total numbers of nodes - n are scanned. That is if p< n ,
increment p=p+ 1,
and go to step-35.. Otherwise follow the next step.
44. Advance iteration count ITRE=ITRE+1. If DFMX and DEMX both are less than
the
convergence tolerance (c) specified for the purpose of the accuracy of the
solution, go to
step-45 If not check if ITRE equals J. If yes go to step-23, otherwise go to
step-34.
45. From calculated and known values of complex voltage at different power
network nodes,
and tap position of tap changing transformers, calculate power flows through
power network
components, and reactive power generation at PV-nodes.
Successive (le, If) Iteration Scheme
[060] In this scheme (36), (43) or (45) and (37), (44) or (46) are solved
alternately with
intermediate updating. Each iteration involves one calculation of [e] and [De]
to update [e] and
then one calculation of [f] and [Of] to update [f]. The sequence of equations
(36), (43) or (45), (47),
and then (37), (44) or (46), (48) depicts the scheme. The scheme involves
solution of system of
equations (36) and (37) in an iterative manner. This scheme is block Gauss-
Seidal approach. The
scheme is block successive in addition to the original successive displacement
scheme of the
Gauss-Seidel approach, which imparts increased stability to the solution
process. This in turn
improves convergence and increases the reliability of obtaining solution.
Similarly, there could be
others like (2e, 2f), (3e, 3f), ...block successive iteration schemes.
Successive (if, le) Iteration Scheme
[061] In this scheme (37), (44) or (46) and (36), (43) or (45) are solved
alternately with
intermediate updating. Each iteration involves one calculation of [f] and [Of]
to update [f] and then
one calculation of [e] and [Ae] to update [e]. The sequence of equations (37),
(44) or (46), (48), and
then (36), (43) or (45), (47) depicts the scheme. The scheme involves solution
of system of
26
CA 02661753 2011-04-15
equations (37) and (36) in an iterative manner. This scheme is block Gauss-
Seidal approach. The
scheme is block successive in addition to the original successive displacement
scheme of the
Gauss-Seidel approach., which imparts increased stability to the solution
process. This in turn
improves convergence and increases the reliability of obtaining solution.
Similarly, there could be
others like (2f, 2e), (3f, 3e), ...block successive iteration schemes.
[062] Inventions include Patel Numerical Method (PNM) for the solution of
simultaneous
nonlinear.algebraic equations. The PNM involves organizing a set of nonlinear
algebraic equations,
in linear form as a product of coefficient matrix and unknown vector on one
side of the matrix
equation and all other terms on the other side as known vector. Then solving
the linear matrix
equation for unknown vector in an iterative fashion. In case of simultaneous
nonlinear complex
algebraic equations such as complex nodal power injection equations of power
network, the
method can best be realized by expressing the equations in rectangular
coordinates leading to
invented what is referred to as Patel Decoupled Loadflow (PDL) method, which
is applicable to
any set of simultaneous nonlinear complex algebraic equations arising in any
other subject areas.
Patel Decoupled Loadflow (PDL)
[063] Patel Decoupled Loadflow model comprises a system of equations (51) and
(52) It is a
system of equations for the separate calculation of imaginary and real parts
of the complex node
voltages.
[RP] _ [GB] [f] (51)
[RQ] _ [GB] [e] (52)
Wherein, each component of [RP], [RQ], and [GB] are defined by following
equations.
RPP = [(I1pPSHP + I2pQSHp)/fp] - [Ilp(GPp+gp) - 12p(Bpp+bp)]ep2/fp
- (e1/fp) E (I1pGpq - I2pBpq)eq + (ep/f f) E (I2pGpq + I1pBpq)fq - E (I2pGpq +
IipBpq)eq (53)
9>p pp q>p
RQp = [(I1pPSHp + I2PQSHp)/ep] - [Ilp(GPp+gp) - I2p(Bpp+bp)]fP2/ep
- (fp/ep) Y_ (I1pGpq - I2pBpq)fq - (fp/ep) E (I2pGpq + I1pBpq)eq + I (I2pGpq +
I1pBpq)fq (54)
pp pp pp
GBPq = I1pGpq- I2pBpq (55)
27
CA 02661753 2011-04-15
GBpp = [Ilp(GPp + gp) - 12p(Bpp + bp)] (56)
Equations (51) and (52), which represent decoupled sub-problems of the
loadflow problem, can be
written for solving each linearized sub-problem by Guass-Seidel method as
equations (57) and
(58) respectively.
P-1 n
fp(r+l) _ [RPp - EGBpgfq(r+1) - Y-GBpgfq(r)] / GBpp (57)
q=1 q=p+1
P-1 n
ep(r+l) _ [RQp - EGBpgeq(r+1) - Y-GBpgeq(r)] / GBpp (58)
q=1 q=p+1
At the start of the solution of (51) by Gauss-Seidel method represented by
(57), [RP] is calculated
using latest available estimate of fp and ep, and fp at all nodes is stored as
[f0], and during iterations
only fp changes until the process is stopped by pre-determined number of
iterations or changes in fp
at all nodes in consecutive iterations of (57) are less than or equal to
specified tolerance value.
When iterations of (57) are stopped, the available values of fp at all nodes
is vector [f]. Similarly,
At the start of the solution of (52) by Gauss-Seidel method represented by
(58), [RQ] is calculated
using latest available estimate of fp and ep, and ep at all nodes is stored as
[e0], and during iterations
only ep changes until the process is stopped by pre-determined number of
iterations or changes in
ep at all nodes in consecutive iterations of (58) are less than or equal to
specified tolerance value.
When iterations of (58) are stopped, the available values of ep at all nodes
is vector [e].
Where, PSHp and QSHp are real and reactive power injections
scheduled/specified/set values, and
lip and I2p can take any values from - oo, ..., -2, -1, 0, +1, +2, ..., + oo.
Normally they take the value
of + 1, however, their best possible values can be determined experimentally.
In case of PV-nodes,
QSHp takes the value of calculated Qp if it is within the upper and lower
reactive power generation
capability limits. It tales the value of upper reactive power generation
capability limit, if calculated
Qp is greater than or equal the upper limit, and it tales the value of lower
reactive power generation
capability limit, if calculated Qp is less than equal the lower limit.
[064] The PDL model comprises equations (51) to (56), (10), (11), and (13).
and turns out to be
the simplest possible Loadflow computation model. The PDL method is expected
to be two times
more efficient than the current state-of-the-art and the prior art SSDL
method.
28
CA 02661753 2011-04-15
Convergence
[065] The iteration process is carried out until changes in the real and
imaginary parts of the set of
(n-1)-node voltages calculated in two consecutive iterations are all less than
the specified tolerance
- e, as shown in equations (10) and (11). The lower the value of the specified
tolerance for
convergence check, the greater the solution accuracy.
Scheduled or specified voltage at a PV-node
[066] Of the four variables, real power PSHp and voltage magnitude VSHp are
scheduled/specified/set at a PV-node. If the reactive power Qp calculated
using VSHp at the
PV-node is within the upper and lower generation capability limits of a PV-
node generator, it is
capable of holding the specified voltage at its terminal. Therefore the
imaginary component fp of
complex voltage calculated by equation (51) by using actually calculated
reactive power Qp in
place of QSHp in (53), along with the latest available real component estimate
of ep is adjusted to
specified voltage magnitude by equation (13). Similarly, the real component ep
of complex voltage
calculated by equation (52) by using actually calculated reactive power Qp in
place of QSHp, along
with the latest available imaginary component estimate of fp is adjusted to
specified voltage
magnitude by equation (13). However, in case of violation of upper or lower
generation capability
limits of a PV-node generator, a violated limit value is used for QSHp in (53)
and (54), meaning a
PV-node generator is no longer capable of holding its terminal voltage at.its
scheduled voltage
VSHp, and the PV-node is switched to a PQ-node type.
Schems for the solution of PDL Model
[067] Solving first (51) for [f] and then (52) for [e] repeatedly constitutes
an iteration scheme
referred to as successive (If, le) iteration scheme. Similarly, first solving
(52) for [e] and then (51)
for [f] repeatedly constitutes an iteration scheme referred to as successive
(1 e, 1 f) iteration scheme.
These schemes involve calculation of [RP] and [RQ] always using the most
recent real and
imaginary components of voltage values, and it is the block Gauss-Seidal
approach. The schemes
are block successive, which imparts increased stability to the solution
process. This in turn
improves convergence and increases the reliability of obtaining solution.
Also, solving
simultaneously (51) for [f] and (52) for [e] repeatedly constitutes an
iteration scheme referred to as
simultaneous (If, le) iteration scheme. However, calculation steps for the
solution of PDL model,
29
CA 02661753 2011-04-15
constituting PDL method, are given in the following only for successive (If,
le) iteration scheme,
from which calculation steps for other schemes become obvious.
Calculation steps of Patel Decoupled Loadflow (PDL) method
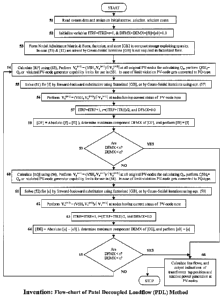
[068] The steps of loadflow computation by PDL method are shown in the
flowchart of Fig. 2b.
Referring to the flowchart of Fig.2b, different steps are elaborated in steps
marked with similar
numbers in the following. The words "Read system data" in Step-1 correspond to
step-10 and
step-20 in Fig. 3, and step-14, step-20, step-32, step-44, step-50 in Fig. 4.
All other steps in the
following correspond to step-30 in Fig. 3, and step-60, step-62, and step-64
in Fig. 4.
51. Read system data and assign an initial approximate solution. If better
solution estimate is not
available, set the real component of voltage at pv-nodes equal to specified
voltage magnitudes
and at PQ-nodes equal to 1.o p.u., and imaginary component at all nodes not
equal to that of the
slack-node, which is zero, but very low value close to zero.
52. Initialize iteration count ITRF = ITRE= r = 0, maximum change in the
imaginary and the real
components of voltage over an iteration variables DFMX=DEMX=0.0, and storage
vectors
for the imaginary and real components of voltage of the previous iteration
[f0]=[e0]=0.0
53. Form nodal admittance matrix. Form (m+k) x (m+k) size matrix [GB] using
(55) and (56),
factorize and store it in a compact storage exploiting sparsity. Storing
factorized matrix is
required if (51) & (52) are to be solved by forward-backward substitution. In
case (51) & (52)
are solved by Gauss-Seidel iteration scheme [GB] is not required to be stored
in
factorized form.
54. Compute the vector of modified residues [RP] using (53). Compute Qp for
use as QSHp in
calculating RPp using (53) at a PV-node after adjusting its latest available
estimate of complex
voltage for specified value by equation (13). If Qp is greater than the upper
or less than the
lower generation capability limits, the violated limit is used as QSHp in (53)
and the node
status is changed to PQ-node type.
55. Solve (51) for [f] by forward-backward substitution using stored
factorized form of matrix
[GB], or by Gauss-Seidel iteration using equation (57) for specified/set
number of iterations or
until local convergence of this sub-problem.
56. Adjust voltage magnitudes at all nodes having current status of PV-node
types equal to the
respective scheduled/specified/set voltage magnitude values using equation
(13).
57. Increment iteration count ITRF=ITRF+1 and r=(ITRF+ITRE)/2, and perform
DFMX=0.0
CA 02661753 2011-04-15
58. Calculate I AfP~r+l~ I for all the nodes using (10), or calculate vector
[Df]= absolute value of each
component of the difference [f]-[f0] and determine maximum value component of
[Df] as
DFMX., and perform [f0]=[f]
59. If both DFMX and DEMX are less than or equal to specified convergence
tolerance, go to
step-66, otherwise follow the next step.
60. Compute the vector of modified residues [RQ] using (54). Compute QP for
use as QSHP in
calculating RQP using (54) at a PV-node after adjusting its latest available
estimate of complex
voltage for specified value by equation (13). If QP is greater than the upper
or less than the
lower generation capability limits, the violated limit is used as QSHP in (54)
and the node
status is changed to PQ-node type.
61. Solve (52) for [e] by forward-backward substitution using stored
factorized form of matrix
[GB], or by Gauss-Seidel iteration using equation (58) for specified/set
number of iterations or
until local convergence of this sub-problem.
62. Adjust voltage magnitudes at all nodes having current status of PV-node
types equal to the
respective scheduled/specified/set voltage magnitude values using equation
(13).
63. Increment iteration count. ITRE=ITRE+l and r=(ITRF+ITRE)/2, and perform
DEMX=0.0
64. Calculate I &ep(r+l) I for all the nodes using (11), or calculate vector
[De]= absolute value of
each component of the difference [e]-[e0] and determine maximum value
component of [De]
as DEMX., and perform [e0]=[e]
65. If both DFMX and DEMX are not less than or equal to specified convergence
tolerance, go to
step-5, otherwise follow the next step.
66. From calculated values of the real and imaginary components of complex
voltage at different
power network nodes, and tap position of tap changing transformers, calculate
power flows
through power network components, and reactive power generation at PV-nodes.
General Statements
[069] The system stores a representation of the reactive capability
characteristic of each machine
and these characteristics act as constraints on the reactive power, which can
be calculated for each
machine.
[070] While the description above refers to particular embodiments of the
present invention, it will
be understood that many modifications may be made without departing from the
spirit thereof. The
31
CA 02661753 2011-04-15
accompanying claims are intended to cover such modifications as would fall
within the true scope
and spirit of the present invention.
[071] The presently disclosed embodiments are therefore to be considered in
all respect as
illustrative and not restrictive, the scope of the invention being indicated
by the appended claims in
addition to the foregoing description, and all changes which come within the
meaning and range of
equivalency of the claims are therefore intended to be embraced therein.
REFERENCES
Foreign Patent Document
1. US Patent Number: 4868410 dated September 19, 1989: "System of Load Flow
Calculation
for Electric Power System"
2. US Patent Number: 5081591 dated January 14, 1992: "Optimizing Reactive
Power
Distribution in an Industrial Power Network"
Published Patent Documents
3. Canadian Patent Number: CA2107388 dated 9 November, 1993: "Method of Fast
Super
Decoupled Loadflow Computation for Electrical Power System"
4. International Patent Application Number: PCT/CA2003/001312 dated 29 August,
2003:
"System of Super Super Decoupled Loadflow Calcutation for Electrical Power
System"
5. International Patent Application Number: PCT/CA2005/001537 dated 01
October, 2005:
"System and Method of Parallel Loadflow Calcutation for Electrical Power
System"
Other Publications
6. Stagg G.W. and El-Abiad A.H., "Computer methods in Power System Analysis",
McGrow-Hill, New York, 1968
7. S.B.Patel, "Fast Super Decoupled Loadflow", IEE proceedings Part-C,
Vol.139, No.1, pp.
13-20, January 1992
8. Suresh.B.Patel, "Supert Super Decoupled Loadflow", Proceedings IEEE Toronto
International Conference (TIC-STH-2009), pp. 652-659, September, 2009
32