Note: Descriptions are shown in the official language in which they were submitted.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
1
MULTIMODAL FUSION DECISION LOGIC SYSTEM USING COPULA MODEL
Cross-Reference to Related Application
[0001] This application also claims the benefit of U.S. provisional patent
application
serial number 60/970,791 (filed on September 7, 2007).
Field of the Invention
[0002] The present invention relates to the use of multiple biometric
modalities and
multiple biometric matching methods in a biometric identification system.
Biometric
modalities may include (but are not limited to) such methods as fingerprint
identification, iris
recognition, voice recognition, facial recognition, hand geometry, signature
recognition,
signature gait recognition, vascular patterns, lip shape, ear shape and palm
print recognition.
Background of the Invention
[0003] Algorithms may be used to combine information from two or more
biometric
modalities. The combined information may allow for more reliable and more
accurate
identification of an individual than is possible with systems based on a
single biometric
modality. The combination of information from more than one biometric modality
is
sometimes referred to herein as "biometric fusion".
[0004] Reliable personal authentication is becoming increasingly important.
The
ability to accurately and quickly identify an individual is important to
immigration, law
enforcement, computer use, and financial transactions. Traditional security
measures rely on
knowledge-based approaches, such as passwords and personal identification
numbers
("PINs"), or on token-based approaches, such as swipe cards and photo
identification, to
establish the identity of an individual. Despite being widely used, these are
not very secure
forms of identification. For example, it is estimated that hundreds of
millions of dollars are
lost annually in credit card fraud in the United States due to consumer
misidentification.
[0005] Biometrics offers a reliable alternative for identifying an individual.
Biometrics is the method of identifying an individual based on his or her
physiological and
behavioral characteristics. Common biometric modalities include fingerprint,
face
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
2
recognition, hand geometry, voice, iris and signature verification. The
Federal government
will be a leading consumer of biometric applications deployed primarily for
immigration,
airport, border, and homeland security. Wide scale deployments of biometric
applications
such as the US-VISIT program are already being done in the United States and
else where in
the world.
[0006] Despite advances in biometric identification systems, several obstacles
have
hindered their deployment. Every biometric modality has some users who have
illegible
biometrics. For example a recent NIST (National Institute of Standards and
Technology)
study indicates that nearly 2 to 5% of the population does not have legible
fingerprints. Such
users would be rejected by a biometric fingerprint identification system
during enrollment
and verification. Handling such exceptions is time consuming and costly,
especially in high
volume scenarios such as an airport. Using multiple biometrics to authenticate
an individual
may alleviate this problem.
[0007] Furthermore, unlike password or PIN based systems, biometric systems
inherently yield probabilistic results and are therefore not fully accurate.
In effect, a certain
percentage of the genuine users will be rejected (false non-match) and a
certain percentage of
impostors will be accepted (false match) by existing biometric systems. High
security
applications require very low probability of false matches. For example, while
authenticating
immigrants and international passengers at airports, even a few false
acceptances can pose a
severe breach of national security. On the other hand false non matches lead
to user
inconvenience and congestion.
[0008] Existing systems achieve low false acceptance probabilities (also known
as
False Acceptance Rate or "FAR") only at the expense of higher false non-
matching
probabilities (also known as False-Rejection-Rate or "FRR"). It has been shown
that
multiple modalities can reduce FAR and FRR simultaneously. Furthermore,
threats to
biometric systems such as replay attacks, spoofing and other subversive
methods are difficult
to achieve simultaneously for multiple biometrics, thereby making multimodal
biometric
systems more secure than single modal biometric systems.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
3
[0009] Systematic research in the area of combining biometric modalities is
nascent
and sparse. Over the years there have been many attempts at combining
modalities and many
methods have been investigated, including "Logical And", "Logical Or",
"Product Rule",
"Sum Rule", "Max Rule", "Min Rule", "Median Rule", "Majority Vote", "Bayes'
Decision",
and "Neyman-Pearson Test". None of these methods has proved to provide low FAR
and
FRR that is needed for modern security applications.
[0010] The need to address the challenges posed by applications using large
biometric
databases is urgent. The US-VISIT program uses biometric systems to enforce
border and
homeland security. Governments around the world are adopting biometric
authentication to
implement National identification and voter registration systems. The Federal
Bureau of
Investigation maintains national criminal and civilian biometric databases for
law
enforcement.
[0011] Although large-scale databases are increasingly being used, the
research
community's focus is on the accuracy of small databases, while neglecting the
scalability and
speed issues important to large database applications. Each of the example
applications
mentioned above require databases with a potential size in the tens of
millions of biometric
records. In such applications, response time, search and retrieval efficiency
also become
important in addition to accuracy.
Summary of the Invention
[0012] The present invention includes a method of deciding whether a data set
is
acceptable for making a decision. For example, the present invention may be
used to
determine whether a set of biometrics is acceptable for making a decision
about whether a
person should be allowed access to a facility. The data set may be comprised
of information
pieces about objects, such as people. Each object may have at least two types
of information
pieces, that is to say the data set may have at least two modalities. For
example, each object
represented in the database may by represented by two or more biometric
samples, for
example, a fingerprint sample and an iris scan sample. A first probability
partition array
("Pm(i,j)") may be provided. The Pm(i,j) may be comprised of probability
values for
information pieces in the data set, each probability value in the Pm(i,j)
corresponding to the
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
4
probability of an authentic match. Pm(i,j) may be similar to a Neyman-Pearson
Lemma
probability partition array. A second probability partition array
("Pfin(i,j)") may be provided,
the Pfm(i,j) being comprised of probability values for information pieces in
the data set, each
probability value in the Pfin(i,j) corresponding to the probability of a false
match. Pfin(i,j)
may be similar to a Neyman-Pearson Lemma probability partition array. The
Pm(i,j) and/or
the Pfin(i,j) may be Copula models.
[0013] A method according to the invention may identify a no-match zone. For
example, the no-match zone may be identified by identifying a first index set
("A"), the
indices in set A being the (i,j) indices that have values in both Pfin(i,j)
and Pm(i,j). A second
index set ("Zoo") may be identified, the indices of Zoo being the (i,j)
indices in set A where
both Pfin(i,j) is larger than zero and Pm(i,j) is equal to zero. FAR za may be
determined,
where FAR Z. = 1 - J(tj)EZx Psn (1, J) . FAR z~ may be compared to a desired
false-
acceptance-rate ("FAR"), and if FAR z. is greater than the desired false-
acceptance-rate, than
the data set may be rejected for failing to provide an acceptable false-
acceptance-rate. If
FAR z~, is less than or equal to the desired false-acceptance-rate, then the
data set may be
accepted, if false-rejection-rate is not important.
[0014] If false-rejection-rate is important, further steps may be executed to
determine
whether the data set should be rejected. The method may further include
identifying a third
index set ZMoo, the indices of ZMoo being the (i,j) indices in Zoo plus those
indices where
both Pfm(i,j) and Pm(i,j) are equal to zero. A fourth index set ("C") may be
identified, the
indices of C being the (i,j) indices that are in A but not ZMoo. The indices
of C may be
Pfin(l~J)k Pfin(l~J)k+1
arranged such that >= to provide an arranged C index. A fifth index
Pm (l,J)k Pm(l,J)k+l
set ("Cn") may be identified. The indices of Cn may be the first N (i,j)
indices of the
arranged C index, where N is a number for which the following is true:
FARZ U)CA, =1- 1(t, j)EZ,, Prm (i) J) - Y(;,j)ECN Pt;n (i, j) 5 FAR . The FRR
may be
determined, where FRR = Y (l P,n U, j) , and compared to a desired false-
rejection-rate.
,f)ECN
If FRR is greater than the desired false-rejection-rate, then the data set may
be rejected, even
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
though FAR z. is less than or equal to the desired false-acceptance-rate.
Otherwise, the data
set may be accepted.
[0015] In another method according to the invention, the false-rejection-rate
calculations and comparisons may be executed before the false-acceptance-rate
calculations
5 and comparisons. In such a method, a first index set ("A") may be
identified, the indices in A
being the (i,j) indices that have values in both Pfm(i,j) and Pm(i,j). A
second index set
("Zoo") may be identified, the indices of Zoo being the (i,j) indices of A
where Pm(i,j) is equal
to zero. A third index set ("C") may be identified, the indices of C being the
(i,j) indices that
are in A but not Zoo. The indices of C may be arranged such that Pfin (t' J)k
>= Pfm(i~ J)k+i
Pm(i,J)k Pm(i,J)k+i
to provide an arranged C index, and a fourth index set ("Cn") may be
identified. The indices
of Cn may be the first N (i,j) indices of the arranged C index, where N is a
number for which
the following is true: FARz, "CN =1- 1(i,J)EZ,. Psn (i, j) - 10> =)ECN Pfin
(i, j) <_ FAR .
The FRR may be determined, where FRR = P11, 0, j) , and compared to a desired
~1,)~ECN
false-rejection-rate. If the FRR is greater than the desired false-rejection-
rate, then the data
set maybe rejected. If the FRR is less than or equal to the desired false-
rejection-rate, then
the data set may be accepted, if false-acceptance-rate is not important. If
false-acceptance-
rate is important, then the FAR z. may be determined, where
FARzx =1- Y_UI )EZx Pt,n (i, J) . The FAR z,,,, may be compared to a desired
false-
acceptance-rate, and if FAR z,,,, is greater than the desired false-acceptance-
rate, then the data
set may be rejected even though FRR is less than or equal to the desired false-
rejection-rate.
Otherwise, the data set may be accepted.
[0016] The invention may also be embodied as a computer readable memory device
for executing any of the methods described above.
Brief Description Of The Drawings
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
6
[0017] For a fuller understanding of the nature and objects of the invention,
reference
should be made to the accompanying drawings and the subsequent description.
Briefly, the
drawings are:
Figure 1, which represents example PDFs for three biometrics data sets;
Figure 2, which represents a joint PDF for two systems;
Figure 3, which is a plot of the receiver operating curves (ROC) for three
biometrics;
Figure 4, which is a plot of the two-dimensional fusions of the three
biometrics taken two at a time versus the single systems;
Figure 5, which is a plot the fusion of all three biometric systems;
Figure 6, which is a plot of the scores versus fingerprint densities;
Figure 7, which is a plot of the scores versus signature densities;
Figure 8, which is a plot of the scores versus facial recognition densities;
Figure 9, which is the ROC for the three individual biometric systems;
Figure 10, which is the two-dimensional ROC - Histogram interpolations
for the three biometrics singly and taken two at a time;
Figure 11, which is the two-dimensional ROC similar to Figure 10 but
using the Parzen Window method;
Figure 12, which is the three-dimensional ROC similar to Figure 10 and
interpolation;
Figure 13, which is the three-dimensional ROC similar to Figure 12 but
using the Parzen Window method;
Figure 14, which is a cost function for determining the minimum cost
given a desired FAR and FRR;
Figure 15, which depicts a method according to the invention;
Figure 16, which depicts another method according to the invention;
Figure 17, which depicts a memory device according to the invention; and
Figure 18, which is an exemplary embodiment flow diagram
demonstrating a security system typical of and in accordance with
the methods presented by this invention.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
7
Figure 19, which shows probability density functions (pdfs) of mismatch
(impostor) and match (genuine) scores. The shaded areas denote
FRR and FAR.
Figure 20, which depicts empirical distribution of genuine scores of CUBS
data generated on DB1 of FVC 2004 fingerprint images.
Figure 21, which depicts a histogram of the CUBS genuine scores
(flipped). Sample size is 2800.
Figure 22, which depicts a histogram of the CUBS genuine scores after
removing repeated entries.
Figure 23, which is the QQ-plot of CUBS data against the exponential
distribution.
Figure 24, which depicts a sample mean excess plot of the CUBS genuine
scores.
Figure 25, which depicts the distribution of estimates F(to).
Figure 26, which depicts the bootstrap estimates ordered in ascending
order.
Figures 27A and 27B, which show GPD fit to tails of imposter data and
authentic data.
Figures 28A and 28B, which depict the test CDFs (in black color) are
matching or close to the estimates of training CDFs.
Figure 29, which depicts an ROC with an example of confidence box.
Note that the box is narrow in the direction of imposter score due
to ample availability of data.
Figure 30, which shows a red curve that is the frequency histogram of raw
data for 390,198 impostor match scores from a fingerprint
identification system, and shows a blue curve that is the histogram
for 3052 authentic match scores from the same system.
Figure 31, which depicts the QQ-plot for the data depicted in Figure 30.
Figure 32A and 32B, which depict probability density functions showing
the Parzen window fit and the GPD (Gaussian Probability
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
8
Distribution) fit. Figure 32A shows a subset fit and Figure 32B
shows the fit for the full set of data.
Figure 33A and 33B, which are enlarged views of the right-side tail
sections of Figures 32A and 32B respectively.
Further Description of the Invention
[0018] Preliminary Considerations: To facilitate discussion of the invention
it may be
beneficial to establish some terminology and a mathematical framework.
Biometric fusion
may be viewed as an endeavor in statistical decision theory [1] [2]; namely,
the testing of
simple hypotheses. This disclosure uses the term simple hypothesis as used in
standard
statistical theory: the parameter of the hypothesis is stated exactly. The
hypotheses that a
biometric score "is authentic" or "is from an impostor" are both simple
hypotheses.
[0019] In a match attempt, the N-scores reported from N<oo biometrics is
called the
test observation. The test observation, x c S, where S c R N (Euclidean N-
space) is the score
sample space, is a vector function of a random variable X from which is
observed a random
sample(XõX2,...,XN ). The distribution of scores is provided by the joint
class-conditional
probability density function ("pdf'):
.f(xI0)= f(xõx2,...,XN 10) (1)
where 0 equals either Au to denote the distribution of authentic scores or Im
to denote the
distribution of impostor scores. So, if 0 = Au, Equation (1) is the pdf for
authentic
distribution of scores and if 0 = Im it is the pdf for the impostor
distribution. It is assumed
that P X 10) = P XI x2 , ... , xN 10) >0 on S.
[0020] Given a test observation, the following two simple statistical
hypotheses are
observed: The null hypothesis, HO, states that a test observation is an
impostor; the alternate
hypothesis, HI, states that a test observation is an authentic match. Because
there are only
two choices, the fusion logic will partition S into two disjoint sets: RAU c S
and R 11 c S ,
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
9
where RAu n R,u, = 0 and R Au u R,,,, = S. Denoting the compliment of a set A
by AC, so
that RAu = R,u, and R in = R au
[0021] The decision logic is to accept HI (declare a match) if a test
observation, x,
belongs to RAu or to accept Ho (declare no match and hence reject HI) if x
belongs to R,u, .
Each hypothesis is associated with an error type: A Type I error occurs when
Ho is rejected
(accept HI) when Ho is true; this is a false accept (FA); and a Type II error
occurs when HI is
rejected (accept Ho) when HI is true; this is a false reject (FR). Thus
denoted, respectively,
the probability of making a Type I or a Type II error follows:
FAR = PTyPe, = P(x E R Au I Im) = f f (x I Im)dx (2)
RAõ
FRR = Type 11 = P(x E R i,u 1 Au) = f f (x I Au)dx (3)
R,
So, to compute the false-acceptance-rate (FAR), the impostor score's pdf is
integrated over
the region which would declare a match (Equation 2). The false-rejection-rate
(FRR) is
computed by integrating the pdf for the authentic scores over the region in
which an impostor
(Equation 3) is declared. The correct-acceptance-rate (CAR) is 1-FRR.
[0022] The class-conditional pdf for each individual biometric, the marginal
pdf, is
assumed to have finite support; that is, the match scores produced by the i"'
biometric belong
to a closed interval of the real line, y; = [a; , w; ], where - 00 < a; < w; <
+oo. Two
observations are made. First, the sample space, S, is the Cartesian product of
these intervals,
i.e., S =)/I x 72 X = = = x IN . Secondly, the marginal pdf, which we will
often reference, for any
of the individual biometrics can be written in terms of the joint pdf:
.E(xile)= f f.. ff(xlOx (4)
y; Vj#i
For the purposes of simplicity the following definitions are stated:
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
= Definition 1: In a test of simple hypothesis, the correct-acceptance-rate,
CAR=1-
FRR is known as the power of the test.
= Definition 2: For a fixed FAR, the test of simple H0 versus simple HI that
has the
largest CAR is called most powerful.
5 = Definition 3: Verification is a one-to-one template comparison to
authenticate a
person's identity (the person claims their identity).
= Definition 4: Identification is a one-to-many template comparison to
recognize
an individual (identification attempts to establish a person's identity
without the
person having to claim an identity).
The receiver operation characteristics (ROC) curve is a plot of CAR versus
FAR, an example
of which is shown in Figure 3. Because the ROC shows performance for all
possible
specifications of FAR, as can be seen in the Figure 3, it is an excellent tool
for comparing
performance of competing systems, and we use it throughout our analyses.
[0023] Fusion and Decision Methods: Because different applications have
different
requirements for error rates, there is an interest in having a fusion scheme
that has the
flexibility to allow for the specification of a Type-I error yet have a
theoretical basis for
providing the most powerful test, as defined in Definition 2. Furthermore, it
would be
beneficial if the fusion scheme could handle the general problem, so there are
no restrictions
on the underlying statistics. That is to say that:
= Biometrics may or may not be statistically independent of each other.
= The class conditional pdf can be multi-modal (have local maximums) or have
no
modes.
= The underlying pdf is assumed to be nonparametric (no set of parameters
define its
shape, such as the mean and standard deviation for a Gaussian distribution).
[0024] A number of combination strategies were examined, all of which are
listed by
Jain [4] on page 243. Most of the schemes, such as "Demptster-Shafer" and
"fuzzy integrals"
involve training. These were rejected mostly because of the difficulty in
analyzing and
controlling their performance mechanisms in order to obtain optimal
performance.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
11
Additionally, there was an interest in not basing the fusion logic on
empirical results.
Strategies such as SUM, MEAN, MEDIAN, PRODUCT, MIN, MAX were likewise rejected
because they assume independence between biometric features.
[0025] When combining two biometrics using a Boolean "AND" or "OR" it is
easily
shown to be suboptimal when the decision to accept or reject H1 is based on
fixed score
thresholds. However, the "AND" and the "OR" are the basic building blocks of
verification
(OR) and identification (AND). Since we are focused on fixed score thresholds,
making an
optimal decision to accept or reject H1 depends on the structure of. R Au c S
and R,,,, C S,
and simple thresholds almost always form suboptimal partitions.
[0026] If one accepts that accuracy dominates the decision making process and
cost
dominates the combination strategy, certain conclusions may be drawn. Consider
a two-
biometric verification system for which a fixed FAR has been specified. In
that system, a
person's identity is authenticated if H1 is accepted by the first biometric OR
if accepted by
the second biometric. If H1 is rejected by the first biometric AND the second
biometric, then
manual intervention is required. If a cost is associated with each stage of
the verification
process, a cost function can be formulated. It is a reasonable assumption to
assume that the
fewer people that filter down from the first biometric sensor to the second to
the manual
check, the cheaper the system.
[0027] Suppose a fixed threshold is used as the decision making process to
accept or
reject H1 at each sensor and solve for thresholds that minimize the cost
function. It will
obtain settings that minimize cost, but it will not necessarily be the
cheapest cost. Given a
more accurate way to make decisions, the cost will drop. And if the decision
method
guarantees the most powerful test at each decision point it will have the
optimal cost.
[0028] It is clear to us that the decision making process is crucial. A survey
of
methods based on statistical decision theory reveals many powerful tests such
as the
Maximum-Likelihood Test and Bayes' Test. Each requires the class conditional
probability
density function, as given by Equation 1. Some, such as the Bayes' Test, also
require the a
priori probabilities P(Ho) and P(H1), which are the frequencies at which we
would expect an
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
12
impostor and authentic match attempt. Generally, these tests do not allow the
flexibility of
specifying a FAR - they minimize making a classification error.
[0029] In their seminal paper of 1933 [3], Neyman and Pearson presented a
lemma
that guarantees the most powerful test for a fixed FAR requiring only the
joint class
conditional pdf for Ho and H1. This test may be used as the centerpiece of the
biometric
fusion logic employed in the invention. The Neyman-Pearson Lemma guarantees
the validity
of the test. The proof of the Lemma is slightly different than those found in
other sources,
but the reason for presenting it is because it is immediately amenable to
proving the Corollary
to the Neuman Pearson Lemma. The corollary states that fusing two biometric
scores with
Neyman-Pearson, always provides a more powerful test than either of the
component
biometrics by themselves. The corollary is extended to state that fusing N
biometric scores is
better than fusing N-1 scores
[0030] Deriving the Neyman-Pearson Test: Let FAR=a be fixed. It is desired to
find
R Au c S such that a = f f (x I Im)dx and f f (x I Au)dx is most powerful. To
do this the
RA,, RAit
objective set function is formed that is analogous to Lagrange's Method:
u(RAu) = f f (x I Au)dx -,I f f (x I Im)dx - a
R e,. IR,,,,
where A >- 0 is an undetermined Lagrange multiplier and the external value of
u is subject to
the constraint a = f f (x I Im)dx. Rewriting the above equation as
u(R Au) = f [ f (x I Au) - f (x I Im)Px + 2a
R,o,
which ensures that the integrand in the above equation is positive for all x e
RA11 Let A >- 0,
and, recalling that the class conditional pdf is positive on S is assumed,
define
RAu ={x:[f(xIAu)-,1f(xJIm)]>0}= {x: f(x I Au)>
f (x I Im)
Then u is a maximum if 2 is chosen such that a = f f (x I Im)dx is satisfied.
R Aõ
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
13
[0031] The Neyman-Pearson Lemma: Proofs of the Neyman-Pearson Lemma can be
found in their paper [4] or in many texts [1] [2]. The proof presented here is
somewhat
different. An "in-common" region, R,C is established between two partitions
that have the
same FAR. It is possible this region is empty. Having Ric makes it easier to
prove the
corollary presented.
[0032] Neyman-Pearson Lemma: Given the joint class conditional probability
density functions for a system of order N in making a decision with a
specified FAR=a, let ?
be a positive real number, and let
RAI, = xES~.f(x~Au)>2 (5)
f (x Im)
RA!I =R1 = xESI f(xIAu)< (6)
f (X I Im)
such that
a = f f (x I Im)dx. (7)
RA,,
then R Aõ is the best critical region for declaring a match - it gives the
largest correct-
acceptance-rate (CAR), hence R c gives the smallest FRR.
[0033] Proo : The lemma is trivially true if R An is the only region for which
Equation
(7) holds. Suppose R0 # RAõ with m(R0 n RA.) > 0 (this excludes sets that are
the same as
R Are except on a set of measure zero that contribute nothing to the
integration), is any other
region such that
a = f f (x I Im)dx. (8)
RO
Let Ric = R 0 n R An , which is the "in common" region of the two sets and may
be empty.
The following is observed:
f f (x I O)dx = f f (x I O)dx + f f (x I O)dx (9)
RAu Reu-Ric RIc
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
14
f f (x ( 9)dx = f f (x 18)dx + f f (x 19)dx (10)
Rq R0-RIC RIc
If R Au has a better CAR than R O then it is sufficient to prove that
f f (x I Au)dx - f f (x I Au)dx > 0 (11)
RAu RO
From Equations (7), (8), (9), and (10) it is seen that (11) holds if
f f (x I Au)dx - f f (x I Au)dx > 0 (12)
RAuRIc R4-Ric
Equations (7), (8), (9), and (10) also gives
aRO-R C= f f (x I Im)dx = f f (x I Im)dx (13)
R,iuRic RO-Ric
When x E R Aõ - R IC c R All it is observed from (5) that
f f (x I Au)dx > f Af (x I Im)dx = 2aRO-R c (14)
R,,,,-R1c RAC,-RIC
and when x E R 0 - R,C c R A,1 it is observed from (6) that
f f (x Au)dx < f Af (x I Im)dx = /'aR.-R C (15)
Ry-R1c RO-Ric
Equations (14) and (15) give
f f (x I Au)dx > 2aRm-R c >- f f (x l Au)dx (16)
RAu-RIc Rv^-Ric
This establishes (12) and hence (11), which proves the lemma. II In this
disclosure, the end
of a proof is indicated by double slashes "H."
[00341 Corollary: Neyman-Pearson Test Accuracy Improves with Additional
Biometrics: The fact that accuracy improves with additional biometrics is an
extremely
important result of the Neyman-Pearson Lemma. Under the assumed class
conditional
densities for each biometric, the Neyman-Pearson Test provides the most
powerful test over
any other test that considers less than all the biometrics available. Even if
a biometric has
relatively poor performance and is highly correlated to one or more of the
other biometrics,
the fused CAR is optimal. The corollary for N-biometrics versus a single
component
biometric follows.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
[0035] Corollary to the Neuman Pearson Lemma: Given the joint class
conditional
probability density functions for an N-biometric system, choose a=FAR and use
the Neyman-
Pearson Test to find the critical region R Au that gives the most powerful
test for the N-
biometric system
5 CARRA = f f(x I Au)dx. (17)
RAõ
Consider the ith biometric. For the same a=FAR, use the Neyman-Pearson Test to
find the
critical collection of disjoint intervals IAõ c R' that gives the most
powerful test for the
single biometric, that is,
10 CARRA = f f (x; I Au)dx (18)
RAu
then
CARRA CARRA . (19)
Proo : Let R; = IAõ x yR X 72 x = = = x yN c RN , where the Cartesian products
are taken over all
the yk except for k=i. From (4) the marginal pdf can be recast in terms of the
joint pdf
f f (x I O)dx = f f (x,. 19)dx (20)
Ri 'Au
First, it will be shown that equality holds in (19) if and only if R A =R i .
Given that
R Au = R; except on a set of measure zero, i.e., m(R A,, n R;) = 0, then
clearly
CAR RA = CAR R . On the other hand, assume CAR RA = CAR Rn and m(R nu n R;) >
0 ,
that is, the two sets are measurably different. But this is exactly the same
condition
previously set forth in the proof of the Neyman-Pearson Lemma from which from
which it
was concluded that CARRA > CAR, , which is a contradiction. Hence equality
holds if and
only ifRA,, =R i . Examining the inequality situation in equation (19), given
that RAõ # R;
such that m(R n,, n R;) > 0, then it is shown again that the exact conditions
as in the proof of
the Neyman-Pearson Lemma have been obtained from which we conclude
that CARRA > CARRA , which proves the corollary. II
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
16
[0036] Examples have been built such that CARRAu = CAR 1 A but it is hard to
do and
it is unlikely that such densities would be seen in a real world application.
Thus, it is safe to
assume that CARRA > CAR1 is almost always true.
[0037] The corollary can be extended to the general case. The fusion of N
biometrics
using Neyman-Pearson theory always results in a test that is as powerful as or
more powerful
than a test that uses any combination of M<N biometrics. Without any loss to
generality,
arrange the labels so that the first M biometrics are the ones used in the M<N
fusion. Choose
a=FAR and use the Neyman-Pearson Test to find the critical region R M c R M
that gives the
most powerful test for the M-biometric system. Let RN =R M X 7M+, X 7M+2 X ...
X 7N c R N,
where the Cartesian products are taken over all the y-intervals not used in
the M biometrics
combination. Then writing
J f (X I B)dX = f J (.xl , .x2 ... , XM I e)dX (21)
RN RM
gives the same construction as in (20) and the proof flows as it did for the
corollary.
[0038] We now state and prove the following five mathematical propositions.
The
first four propositions are necessary to proving the fifth proposition, which
will be cited in the
section that details the invention. For each of the propositions we will use
the following: Let
r = }r,, r2 , ... , rõ } be a sequence of real valued ratios such that r, >_
r2 >_ = = = >_ r, . For each ri we
know the numerator and denominator of the ratio, so that ri = n` , n; , d; > 0
Vi.
d;
[0039] Proposition #1: For ri, ri+, e r and r; = i!-, ri+1 then
; d,+,
n; + n;+, < n; = r Proof Because r,., r+, E r we have
d; + d;+1 d;
n; L < n;
d;+1 d;
= drn;+1 <1
n; d;+,
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
17
= 4q, + ni+1) <_ d; + d;+1
ni
n;+ni+1 <n=r
d; + d,+1 d; `
//
[0040] Proposition #2: For r,, ri+1 E r and ri = ni , ri+, then
di di+I
r+I = ; , < ni + nProof The proof is the same as for proposition #1 except the
order is
di+1 d; + di+1
reversed.
M
[0041] Proposition #3: Forr; = ni , i = (1,..., n), then 11 ni <_ n771 , 1 < m
<M <_ n.
di d d 7
1=111 1
Proof The proof is by induction. We know from proposition #1 that the result
holds for
N=1, that is n; + ni+1 < Now assume it holds for any N>1, we need to show that
it holds
di + d;+1 d;
for N+1. Let m = 2 and M = N + 1 (note that this is the N`h case and not the
N+1 case), then
we assume
N+I
< nz < n]
N+1
';=2 d, d2 d,
N+1
d1 Ji=2 n; <
1
N+1 d.
n ~i-2
d, N+l N+I
n <_ d.
nI i=2 i=2
N+l N+1 N+1
J n. + d 5 y
. d + d
I = ~ di
n 1=2 1 I _2 1
1
N+1
d, l + ~N+1 ..7
Ll
n, 1=I i
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
18
n + N+1
n= d N+I N+1
7=1 ,=t
n, n1
N+1
~i=1 n; < n7
N+1
di di
which is the N+1 case as was to be shown.
//
M
[0042] Proposition #4: Forri = ni , i = ~1,...,n), then M"' 1< t n<_ M<_ n.
di dM d.
=777 i
Proof As with proposition #3, the proof is by induction. We know from
proposition #2 that
the result holds for N=1, that is < ni +n i+1 The rest of the proof follows
the same
d i+1 d; + d i+1
format as for proposition #3 with the order reversed.
//
[0043] Proposition #5: Recall that the r is an ordered sequence of decreasing
ratios
with known numerators and denominators. We sum the first N numerators to get
Sn and sum
the first N denominators to get Sd. We will show that for the value Sn, there
is no other
collection of ratios in r that gives the same Sn and a smaller Sd. For r = i =
(1,..., n), let S
d;
be the sequence of the first N terms of r, with the sum of numerators given by
Sõ _ YN 1 n;
and the sum of denominators by Sd = yN d; , 1<_ N<_ n. Let S' be any other
sequence of
ratios in r, with numerator sum Sõ = Y n; and denominator sum Sd = Y di such
that Sõ = Sõ , then we have Sd <_ Sd S. Proof The proof is by contradiction.
Suppose the
proposition is not true, that is, assume another sequence, S', exists such
that Sd < Sd . For this
sequence, define the indexing sets A={indices that can be between 1 and N
inclusive} and
B={indices that can be between N+1 and n inclusive}. We also define the
indexing set
A`= {indices between 1 and N inclusive and not in A}, which means A n A` = 0
and
A u A` = {all indices between 1 and N inclusive}. Then our assumption states:
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
19
S/7 !I J.EA [ n( .+J.EBn[ .=S
/(
and
Sd _ IiEA di + YiEB di < Sd.
This implies that
N
Y d'. + d[ . < I di . _ d[ . +Yd.
IEA lEB iEA lEA~ [
i=1
~
~ d' . <Y(.EA rd.
IEB
'
1 < 1 (22)
. ~. d.
IEA, d! [EB !
Because the numerators of both sequences are equal, we can write
~_ n' +YI.E B n[ . _ EEAUA ` n.
(EA
'
= EEB n' . iEAL A ` n' . - llEA n ' - n. (23)
LEA, Combining (22) and (23), and from propositions #3 and #4, we have
~iEBni < nN+1 _
_ nN < <
rN dN JiEA` di EEB di dN+1 - rN+]
which contradicts the fact that rN rN+l , hence the validity of the
proposition follows.
//
[0044] Cost Functions for Optimal Verification and Identification: In the
discussion
above, it is assumed that all N biometric scores are simultaneously available
for fusion. The
Neyman-Pearson Lemma guarantees that this provides the most powerful test for
a fixed
FAR. In practice, however, this could be an expensive way of doing business.
If it is
assumed that all aspects of using a biometric system, time, risk, etc., can be
equated to a cost,
then a cost function can be constructed. The inventive process described below
constructs
the cost function and shows how it can be minimized using the Neyman-Pearson
test. Hence,
the Neyman-Pearson theory is not limited to "all-at-once" fusion; it can be
used for serial,
parallel, and hierarchal systems.
[0045] Having laid a basis for the invention, a description of two cost
functions is
now provided as a mechanism for illustrating an embodiment of the invention. A
first cost
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
function for a verification system and a second cost function for an
identification system are
described. For each system, an algorithm is presented that uses the Neyman-
Pearson test to
minimize the cost function for a second order biometric system, that is a
biometric system
that has two modalities. The cost functions are presented for the general case
of N-
5 biometrics. Because minimizing the cost function is recursive, the
computational load grows
exponentially with added dimensions. Hence, an efficient algorithm is needed
to handle the
general case.
[0046] First Cost Function - Verification System. A cost function for a 2-
stage
biometric verification (one-to-one) system will be described, and then an
algorithm for
10 minimizing the cost function will be provided. In a 2-stage verification
system, a subject
may attempt to be verified by a first biometric device. If the subject's
identity cannot be
authenticated, the subject may attempt to be authenticated by a second
biometric. If that fails,
the subject may resort to manual authentication. For example, manual
authentication may be
carried out by interviewing the subject and determining their identity from
other means.
15 [0047] The cost for attempting to be authenticated using a first biometric,
a second
biometric, and a manual check are c, , c2 , and c3 , respectively. The
specified FAR Sys is a
system false-acceptance-rate, i.e. the rate of falsely authenticating an
impostor includes the
case of it happening at the first biometric or the second biometric. This
implies that the first-
biometric station test cannot have a false-acceptance-rate, FAR, , that
exceeds FAR Sys
20 Given a test with a specified FAR, , there is an associated false-rejection-
rate, FRR, , which is
the fraction of subjects that, on average, are required to move on to the
second biometric
station. The FAR required at the second station is FAR2 = FARSys -FAR I. It is
known
that P(A u B) = P(A) + P(B) - P(A)P(B), so the computation of FAR2 appears
imperfect.
However, if FAR Sys = P(A u B) and FAR, = P(A), in the construction of the
decision space,
it is intended that FAR2 = P(B) - P(A)P(B).
[0048] Note that FAR2 is a function of the specified FARSys and the freely
chosen FAR, ; FAR2 is not a free parameter. Given a biometric test with the
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
21
computed FAR2 , there is an associated false-rejection-rate, FRR2 by the
second biometric
test, which is the fraction of subjects that are required to move on to a
manual check. This is
all captured by the following cost function:
Cost = el + FRR, (c2 + c3FRR2) (30)
[0049] There is a cost for every choice ofFAR, FAR,Ys, so the Cost in Equation
30
is a function of FAR,. For a given test method, there exists a value of FAR,
that yields the
smallest cost and we present an algorithm to find that value. In a novel
approach to the
minimization of Equation 30, a modified version of the Neyman-Pearson decision
test has
been developed so that the smallest cost is optimally small.
[0050] An algorithm is outlined below. The algorithm seeks to optimally
minimize
Equation 30. To do so, we (a) set the initial cost estimate to infinity and,
(b) for a
specified FARSYS, loop over all possible values ofFAR, < FAR,Ys. In practice,
the algorithm
may use a uniformly spaced finite sample of the infinite possible values. The
algorithm may
proceed as follows: (c) set FAR, = FARSYS , (d) set Cost = oo, and (e) loop
over possible
FAR1 values. For the first biometric at the current FAR1 value, the algorithm
may proceed to
(f) find the optimal Match-Zzone, R, , and (g) compute the correct-acceptance-
rate over R,
by:
CAR, = f f (x I Au)dx (31)
Ri
and (h) determine FRR1 using FRR, =1- CAR,.
[0051] Next, the algorithm may test against the second biometric. Note that
the
region R, of the score space is no longer available since the first biometric
test used it up.
The Neyman-Pearson test may be applied to the reduced decision space, which is
the
compliment ofR, . So, at this time, (h) the algorithm may compute FAR2 =
FARsys - FAR, ,
and FAR2 may be (i) used in the Neyman-Pearson test to determine the most
powerful
test, CAR 2, for the second biometric fused with the first biometric over the
reduced decision
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
22
space R; . The critical region for CAR 2 is R 2 , which is disjoint from R1 by
our
construction. Score pairs that result in the failure to be authenticated at
either biometric
station must fall within the region R 3 = (R, u R 2 )C , from which it is
shown that
f f (x I Au)dx
FRR2 = R3
FRR,
[0052] The final steps in the algorithm are (j) to compute the cost using
Equation 30
at the current setting of FAR, using FRR, and FRR2 , and (k) to reset the
minimum cost if
cheaper, and keep track of the FAR, responsible for the minimum cost.
[0053] To illustrate the algorithm, an example is provided. Problems arising
from
practical applications are not to be confused with the validity of the Neyman-
Pearson theory.
Jain states in [5]: "In case of a larger number of classifiers and relatively
small training data,
a classifier my actually degrade the performance when combined with other
classifiers ..."
This would seem to contradict the corollary and its extension. However, the
addition of
classifiers does not degrade performance because the underlying statistics are
always true and
the corollary assumes the underlying statistics. Instead, degradation is a
result of inexact
estimates of sampled densities. In practice, a user may be forced to construct
the decision test
from the estimates, and it is errors in the estimates that cause a mismatch
between predicted
performance and actual performance.
[0054] Given the true underlying class conditional pdf for, H0 and HI, the
corollary is
true. This is demonstrated with a challenging example using up to three
biometric sensors.
The marginal densities are assumed to be Gaussian distributed. This allows a
closed form
expression for the densities that easily incorporates correlation. The general
n`'' order form is
well known and is given by
.f (x 10) exp(- 2 [(x -,u)T C-' (x -,u)]) (32)
(2Tr)2 C ,/ 2
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
23
where is the mean and C is the covariance matrix. The mean ( ) and the
standard deviation
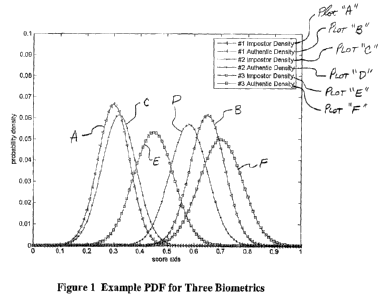
((Y) for the marginal densities are given in Table 1. Plots of the three
impostor and three
authentic densities are shown in Figure 1.
Biometric Impostors Authentics
Number a
#1 0.3 0.06 0.65 0.065
#2 0.32 0.065 0.58 0.07
#3 0.45 0.075 0.7 0.08
Table 1
Correlation Coefficient Impostors Authentics
P12 0,03 0.83
P13 0.02 0.80
P23 0.025 0.82
Table 2
[0055] To stress the system, the authentic distributions for the three
biometric systems
may be forced to be highly correlated and the impostor distributions to be
lightly correlated.
The correlation coefficients (p) are shown in Table 2. The subscripts denote
the connection.
A plot of the joint pdf for the fusion of system #1 with system #2 is shown in
Figure 2, where
the correlation between the authentic distributions is quite evident.
[0056] The single biometric ROC curves are shown in Figure 3. As could be
predicted from the pdf curves plotted in Figure 1, System #1 performs much
better than the
other two systems, with System #3 having the worst performance.
[0057] Fusing 2 systems at a time; there are three possibilities: #1+#2,
#1+#3, and
#2+#3. The resulting ROC curves are shown in Figure 4. As predicted by the
corollary, each
2-system pair outperforms their individual components. Although the fusion of
system #2
with system #3 has worse performance than system #1 alone, it is still better
than the single
system performance of either system #2 or system #3.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
24
[0058] Finally, Figure 5 depicts the results when fusing all three systems and
comparing its performance with the performance of the 2-system pairs. The
addition of the
third biometric system gives substantial improvement over the best performing
pair of
biometrics.
[0059] Tests were conducted on individual and fused biometric systems in order
to
determine whether the theory presented above accurately predicts what will
happen in a real-
world situation. The performance of three biometric systems were considered.
The numbers
of score samples available are listed in Table 3. The scores for each modality
were collected
independently from essentially disjoint subsets of the general population.
Biometric Number of Impostor Scores Number of Authentic
Scores
Fingerprint 8,500,000 21,563
Signature 325,710 990
Facial Recognition 4,441,659 1,347
Table 3
[0060] To simulate the situation of an individual obtaining a score from each
biometric, the initial thought was to build a "virtual" match from the data of
Table 3.
Assuming independence between the biometrics, a 3-tuple set of data was
constructed. The
3-tuple set was an ordered set of three score values, by arbitrarily assigning
a fingerprint
score and a facial recognition score to each signature score for a total of
990 authentic score
3-tuples and 325,710 impostor score 3-tuples.
[0061] By assuming independence, it is well known that the joint pdf is the
product of
the marginal density functions, hence the joint class conditional pdf for the
three biometric
systems, f (x 10) = f (xt , x2 , x3 10) can be written as
.f (x 10) = / /inge,pr int (x I e).fsignatõre (x I e).fffieiar (x 19) (33)
[0062] So it is not necessary to dilute the available data. It is sufficient
to
approximate the appropriate marginal density functions for each modality using
all the data
available, and compute the joint pdf using Equation 33.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
[0063] The class condition density functions for each of the three modalities,
/ finge,pr int (x 10) , fsig,:at ire (x 10) and fiac;ar (x 10), were estimated
using the available sampled
data. The authentic score densities were approximated using two methods: (1)
the
histogram-interpolation technique and (2) the Parzen-window method. The
impostor
5 densities were approximated using the histogram-interpolation method.
Although each of
these estimation methods are guaranteed to converge in probability to the true
underlying
density as the number of samples goes to infinity, they are still
approximations and can
introduce error into the decision making process, as will be seen in the next
section. The
densities for fingerprint, signature, and facial recognition are shown in
Figure 6, Figure 7 and
10 Figure 8 respectively. Note that the authentic pdf for facial recognition
is bimodal. The
Neyman-Pearson test was used to determine the optimal ROC for each of the
modalities. The
ROC curves for fingerprint, signature, and facial recognition are plotted in
Figure 9.
[0064] There are three possible unique pairings of the three biometric
systems: (1)
fingerprints with signature, (2) fingerprints with facial recognition, and (3)
signatures with
15 facial recognition. Using the marginal densities (above) to create the
required 2-D joint class
conditional density functions, two sets of 2-D joint density functions were
computed - one in
which the authentic marginal densities were approximated using the histogram
method, and
one in which the densities were approximated using the Parzen window method.
Using the
Neyman-Pearson test, an optimal ROC was computed for each fused pairing and
each
20 approximation method. The ROC curves for the histogram method are shown in
Figure 10
and the ROC curves for the Parzen window method are shown in Figure 11.
[0065] As predicted by the corollary, the fused performance is better than the
individual performance for each pair under each approximation method. But, as
we
cautioned in the example, error due to small sample sizes can cause pdf
distortion. This is
25 apparent when fusing fingerprints with signature data (see Figure 10 and
Figure 11). Notice
that the Parzen-window ROC curve (Figure 11) crosses over the curve for
fingerprint-facial-
recognition fusion, but does not cross over when using the histogram
interpolation method
(Figure 10). Small differences between the two sets of marginal densities are
magnified
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
26
when using their product to compute the 2-dimensional joint densities, which
is reflected in
the ROC.
[00661 As a final step, all three modalities were fused. The resulting ROC
using
histogram interpolating is shown in Figure 12, and the ROC using the Parzen
window is
shown Figure 13. As might be expected, the Parzen window pdf distortion with
the 2-
dimensional fingerprint-signature case has carried through to the 3-
dimensional case. The
overall performance, however, is dramatically better than any of the 2-
dimensional
configurations as predicted by the corollary.
[0067] In the material presented above, it was assumed that all N biometric
scores
would be available for fusion. Indeed, the Neyman-Pearson Lemma guarantees
that this
provides the most powerful test for a fixed FAR. In practice, however, this
could be an
expensive way of doing business. If it is assumed that all aspects of using a
biometric
system, time, risk, etc., can be equated to a cost, then a cost function can
be constructed.
Below, we construct the cost function and show how it can be minimized using
the Neyman-
Pearson test. Hence, the Neyman-Pearson theory is not limited to "all-at-once"
fusion - it can
be used for serial, parallel, and hierarchal systems.
[00681 In the following section, a review of the development of the cost
function for a
verification system is provided, and then a cost function for an
identification system is
developed. For each system, an algorithm is presented that uses the Neyman-
Pearson test to
minimize the cost function for a second order modality biometric system. The
cost function
is presented for the general case of N-biometrics. Because minimizing the cost
function is
recursive, the computational load grows exponentially with added dimensions.
Hence, an
efficient algorithm is needed to handle the general case.
[0069] From the prior discussion of the cost function for a 2-station system,
the costs
for using the first biometric, the second biometri c, and the manual check are
c, , c2 , and c3 ,
respectively, and FARSYS is specified. The first-station test cannot have a
false-acceptance-
rate, FAR, , that exceeds FARSYS . Given a test with a specified FAR, , there
is an associated
false-rejection-rate, FRRõ which is the fraction of subjects that, on average,
are required to
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
27
move on to the second station. The FAR required at the second station
is FAR2 =FARSYS - FAR, . It is known that P(A u B) = P(A) + P(B) - P(A)P(B),
so the
computation of FAR2 appears imperfect. However, if FARSYS = P(A u B) and FAR,
= P(A),
in the construction of the decision space, it is intended that FAR2 = P(B) -
P(A)P(B).
[0070] Given a test with the computed FAR2 , there is an associated false-
rejection-
rate, FRR2 by the second station, which is the fraction of subjects that are
required to move
on to a manual checkout station. This is all captured by the following cost
function
Cost = C, + FRR1(c2 + c3FRR2) (30)
[0071] There is a cost for every choice of FAR, FARSYS, so the Cost in
Equation 30
is a function of FAR1. For a given test method, there exists a value of FAR1
that yields the
smallest cost and we develop an algorithm to find that value.
[0072] Using a modified Neyman-Pearson test to optimally minimize Equation 30,
an
algorithm can be derived. Step 1: set the initial cost estimate to infinity
and, for a
specified FARSYS, loop over all possible values of FAR, < FARSYS. To be
practical, in the
algorithm a finite sample of the infinite possible values may be used. The
first step in the
loop is to use the Neyman-Pearson test at FAR, to determine the most powerful
test, CAR,,
for the first biometric, and FRR1 =1- CAR1 is computed. Since it is one
dimensional, the
critical region is a collection of disjoint intervals IAu . As in the proof to
the corollary, the 1-
dimensional IAu is recast as a 2-dimensional region, R 1 = 1.4u x 72 c R2 , so
that
CAR1 = f f (x I Au)dx = f f (x, I Au)dx (34)
R, rAu
[0073] When it is necessary to test against the second biometric, the region
R1 of the
decision space is no longer available since the first test used it up. The
Neyman-Pearson test
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
28
can be applied to the reduced decision space, which is the compliment of R, .
Step 2:
FAR2 = FARSYS -FAR, is computed. Step 3: FAR2 is used in the Neyman-Pearson
test to
determine the most powerful test, CAR 2 , for the second biometric fused with
the first
biometric over the reduced decision space R; . The critical region for CAR2 is
R 2 , which
is disjoint from R, by the construction. Score pairs that result in the
failure to be
authenticated at either biometric station must fall within the region R 3 =
(R, u R2 )C , from
which it is shown that
f f (x I Au)dx
FRR2 = R'
FRR 1
[0074] Step 4: compute the cost at the current setting of FAR1 using FRR1
and FRR 2 . Step 5: reset the minimum cost if cheaper, and keep track of the
FAR,
responsible for the minimum cost. A typical cost function is shown in Figure
14.
[0075] Two special cases should be noted. In the first case, if c1 > 0, c2 >
0, and
c3 =0, the algorithm shows that the minimum cost is to use only the first
biometric - that is,
FAR, = FARSYS . This makes sense because there is no cost penalty for
authentication
failures to bypass the second station and go directly to the manual check.
[0076] In the second case, c, = c2 =0 and c3 > 0, the algorithm shows that
scores
should be collected from both stations and fused all at once; that is, FAR, =
1Ø Again, this
makes sense because there is no cost penalty for collecting scores at both
stations, and
because the Neyman-Pearson test gives the most powerful CAR (smallest FRR)
when it can
fuse both scores at once.
[0077] To extend the cost function to higher dimensions, the logic discussed
above is
simply repeated to arrive at
2 N
Cost = c, + c2FRR1 +41 FRR; +... +cN+,1 1 FRR; (35)
i=1 i=1
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
29
In minimizing Equation 35, there is 1 degree of freedom, namely FAR, .
Equation 35 has N-1
degrees of freedom. When FAR, <_ FARSYS are set, then FAR2 5 FAR, can bet set,
then
FAR3 <_ FAR2 , and so on - and to minimize thus, N-1 levels of recursion.
[00781 Identification System: Identification (one-to-many) systems are
discussed.
With this construction, each station attempts to discard impostors. Candidates
that cannot be
discarded are passed on to the next station. Candidates that cannot be
discarded by the
biometric systems arrive at the manual checkout. The goal, of course, is to
prune the number
of impostor templates thus limiting the number that move on to subsequent
steps. This is a
logical AND process - for an authentic match to be accepted, a candidate must
pass the test at
station 1 and station 2 and station 3 and so forth. In contrast to a
verification system, the
system administrator must specify a system false-rejection-rate, FRRSYS
instead of a FARSYS .
But just like the verification system problem the sum of the component FRR
values at each
decision point cannot exceed FRRSYS . If FRR with FAR are replaced in
Equations 34 or 35
the following cost equations are arrived at for 2-biometric and an N-biometric
identification
system
Cost = C, + FAR, (c2 + c3FAR2) (36)
2 N
Cost = C, + C2FAR, + c3 fl FAR; +... +CN+, fl FAR; (37)
i=1 i=1
Alternately, equation 37 may be written as:
N
Cost = Y (cj+, fJ FAR;) , (37A)
j=0 i=1
These equations are a mathematical dual of Equations 34 and 35 are thus
minimized using the
logic of the algorithm that minimizes the verification system.
[00791 Algorithm: Generating Matching and Non-Matching PDF Surfaces. The
optimal fusion algorithm uses the probability of an authentic match and the
probability of a
false match for each p, c P. These probabilities may be arrived at by
numerical integration
of the sampled surface of the joint pdf. A sufficient number of samples may be
generated to
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
get a "smooth" surface by simulation. Given a sequence of matching score pairs
and non-
matching score pairs, it is possible to construct a numerical model of the
marginal cumulative
distribution functions (cdf). The distribution functions may be used to
generate pseudo
random score pairs. If the marginal densities are independent, then it is
straightforward to
5 generate sample score pairs independently from each cdf. If the densities
are correlated, we
generate the covariance matrix and then use Cholesky factorization to obtain a
matrix that
transforms independent random deviates into samples that are appropriately
correlated.
[0080] Assume a given partition P. The joint pdf for both the authentic and
impostor
cases may be built by mapping simulated score pairs to the appropriate p, E P
and
10 incrementing a counter for that sub-square. That is, it is possible to
build a 2-dimensional
histogram, which is stored in a 2-dimensional array of appropriate dimensions
for the
partition. If we divide each array element by the total number of samples, we
have an
approximation to the probability of a score pair falling within the associated
sub-square. We
call this type of an array the probability partition array (PPA). Let Pf,,, be
the PPA for the
15 joint false match distribution and let P,,, be the PPA for the authentic
match distribution.
Then, the probability of an impostor's score pair, (s, , s2) E p,, resulting
in a match is
P0 ,, (i, j) . Likewise, the probability of a score pair resulting in a match
when it should be a
match is P1 ,, (i, j) . The PPA for a false reject (does not match when it
should) is Pfr =1- P,,, .
20 [0081] Consider the partition arrays, Pf,,, and P,,,, defined in Section
#5. Consider the
ratio
Pfi" (i, .I) A. > 0
P1n(i,I)
The larger this ratio the more the sub-square indexed by (i j) favors a false
match over a false
reject. Based on the propositions presented in Section 4, it is optimal to tag
the sub-square
25 with the largest ratio as part of the no-match zone, and then tag the next
largest, and so on.
[0082] Therefore, an algorithm that is in keeping with the above may proceed
as:
Step 1. Assume a required FAR has been given.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
31
Step 2. Allocate the array P,,,Z to have the same dimensions as P,,, and
Pf,,,. This is the match zone array. Initialize all of its elements as
belonging to the match zone.
Step 3. Let the index set A={all the (i,j) indices for the probability
partition arrays}.
Step 4. Identify all indices in A such that P,,, (i, i) = Pf,,, (i, j) = 0 and
store those indices in the indexing set Z={(i,j):
P. (i, j) = P,,, (i, j) = 0 } . Tag each element in P111z indexed by Z as
part of the no-match zone.
Step S. Let B=A-Z={(i j): P,,,(i, j) #0 and Pf(i, j) # 0 }. We process
only those indices in B. This does not affect optimality because there
is most likely zero probability that either a false match score pair or a
false reject score pair falls into any sub-square indexed by elements of
Z.
Step 6. Identify all indices in B such that
Pf;,,(i, j) > 0 and P,,,(i, j) = 0 and store those indices in Z-= {(i,j)k:
P,,, (i, j) > 0, P,,, (i, j) = 0 } . Simply put, this index set includes the
indexes to all the sub-squares that have zero probability of a match but
non-zero probability of false match.
Step 7. Tag all the sub-squares in P,,,Z indexed by Z. as belonging to the
no-match zone. At this point, the probability of a matching score pair
falling into the no-match zone is zero. The probability of a non-
matching score pair falling into the match zone is:
FAR Z. =1- Yci,./)EZ Pf,,,(i, j)
Furthermore, if FARZ <= FAR then we are done and can exit the
algorithm.
Step 8. Otherwise, we construct a new index set
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
32
C=A-Z-Zc {(i,j)k:
Pfin(l,J)k > 0, P.(l,.l)k > 0, Pfm(z,.l)k >= Pfin(1,J)k+l 11
P. (l, .1)k Pm (z, A+1 We see that C holds the indices of the non-zero
probabilities in a sorted
order - the ratios of false-match to match probabilities occur in
descending order.
Step 9. Let CN be the index set that contains the first N indices in C. We
determine N so that:
FARZ L,CN =1-_ (j,I )EZx Pfin(i, j) - 0,J)ECN Pfin(i,j)<FAR
Step 10. Label elements of P,,Z indexed by members of CN as belonging to
the no-match zone. This results in a FRR given by
FRR = 1 P (i, I) _CN and furthermore this FRR is optimal.
[0083] It will be recognized that other variations of these steps may be made,
and still
be within the scope of the invention. For clarity, the notation "(i,j)" is
used to identify arrays
that have at least two modalities. Therefore, the notation "(i,j)" includes
more than two
modalities, for example (i,j,k), (i,j,k,l), (i,j,k,l,m), etc.
[0084] For example, Figure 15 illustrates one method according to the
invention in
which Pm(i,j) is provided 10 and Pfin(i,j) 13 is provided. As part of
identifying 16 indices
(i,j) corresponding to a no-match zone, a first index set ("A") may be
identified. The indices
in set A may be the (i,j) indices that have values in both Pfin(i,j) and
Pm(i,j). A second index
set ("Zoo") may be identified, the indices of Zoo being the (i,j) indices in
set A where both
Pfin(i,j) is larger than zero and Pm(i,j) is equal to zero. Then determine FAR
zc, 19, where
FARZx = 1 - Y(i /)EZr Pfin (i, j) . It should be noted that the indices of Zoo
may be the
indices in set A where Pm(i,j) is equal to zero, since the indices where both
Pfin(i,j)=Pm(i,j)=0 will not affect FAR z., and since there will be no
negative values in the
probability partition arrays. However, since defining the indices of Zoo to be
the (i,j) indices
in set A where both Pfin(i,j) is larger than zero and Pm(i,j) is equal to zero
yields the smallest
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
33
number of indices for Zoo, we will use that definition for illustration
purposes since it is the
least that must be done for the mathematics of FAR z. to work correctly. It
will be
understood that larger no-match zones may be defined, but they will include
Zoo, so we
illustrate the method using the smaller Zoo definition believing that
definitions of no-match
zones that include Zoo will fall within the scope of the method described.
[00851 FAR z,,~ may be compared 22 to a desired false-acceptance-rate ("FAR"),
and
if FAR z~ is less than or equal to the desired false-acceptance-rate, then the
data set may be
accepted, if false-rejection-rate is not important. If FAR zoo is greater than
the desired false-
acceptance-rate, then the data set may be rejected 25.
[0086] If false-rejection-rate is important to determining whether a data set
is
acceptable, then indices in a match zone may be selected, ordered, and some of
the indices
may be selected for further calculations 28. Toward that end, the following
steps may be
carried out. The method may further include identifying a third index set
ZMoo, which may
be thought of as a modified Zoo, that is to say a modified no-match zone. Here
we modify Zoo
so that ZMoo includes indices that would not affect the calculation for FAR
z., but which
might affect calculations related to the false-rejection-rate. The indices of
ZMoo may be the
(i,j) indices in Zoo plus those indices where both Pfin(i,j) and Pm(i,j) are
equal to zero. The
indices where Pfin(i,j)=Pm(i,j)=0 are added to the no-match zone because in
the calculation
of a fourth index set ("C"), these indices should be removed from
consideration. The indices
of C may be the (i,j) indices that are in A but not ZMoo. The indices of C may
be arranged
Pfm(1'Ak Pfm(1'A k+l
such that >= to provide an arranged C index. A fifth index set
Pni G1 )k Pm (" All
("Cn") may be identified. The indices of Cn may be the first N (i,j) indices
of the arranged C
index, where N is a number for which the following is true:
FAR zx RCN =1- 1(i,~ )Ez, Pr~n (i, I) - -c~,~)ECN Pan (i , I) < FAR .
[00871 The FRR may be determined 31, where FRR = (t,f)ECN P1n (i, and
compared 34 to a desired false-rejection-rate. If FRR is greater than the
desired false-
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
34
rejection-rate, then the data set may be rejected 37, even though FAR z. is
less than or equal
to the desired false-acceptance-rate. Otherwise, the data set may be accepted.
[0088] Figure 16 illustrates another method according to the invention in
which the
FRR may be calculated first. In Figure 16, the reference numbers from Figure
15 are used,
but some of the steps in Figure 16 may vary somewhat from those described
above. In such a
method, a first index set ("A") may be identified, the indices in A being the
(i,j) indices that
have values in both Pfin(i,j) and Pm(i,j). A second index set ("Zoo"), which
is the no match
zone, may be identified 16. The indices of Zoo may be the (i,j) indices of A
where Pm(i,j) is
equal to zero. Here we use the more inclusive definition for the no-match zone
because the
calculation of set C comes earlier in the process. A third index set ("C") may
be identified,
the indices of C being the (i,j) indices that are in A but not Zoo. The
indices of C may be
Pfm(1,A k Pfin(1,A+1
arranged such that >= to provide an arranged C index, and a fourth
Pm(l,J)k Pm(l,J)k+1
index set ("Cn") may be identified. The indices of Cn may be the first N (i,j)
indices of the
arranged C index, where N is a number for which the following is true:
FARZ JC,y =1- Y_([,.%)Ezy Pfin (i, J) 1(i,i)ECN Pfn (i, j) <_ FAR . The FRR
may be
determined, where FRR = (1,j)ECN Pln(i, j) , and compared to a desired false-
rejection-rate.
If the FRR is greater than the desired false-rejection-rate, then the data set
may be rejected. If
the FRR is less than or equal to the desired false-rejection-rate, then the
data set may be
accepted, if false-acceptance-rate is not important. If false-acceptance-rate
is important, the
FAR z., may be determined, where FARZ = 1 - Y(, j)EZ Pfn(i, A. Since the more
inclusive definition is used for Zoo in this method, and that more inclusive
definition does not
affect the value of FAR z,,, we need not add back the indices where both
Pfm(i,j)=Pm(i,j)=0.
The FAR z. may be compared to a desired false-acceptance-rate, and if FAR z.~)
is greater
than the desired false-acceptance-rate, then the data set may be rejected.
Otherwise, the data
set may be accepted.
[0089] It may now be recognized that a simplified form of a method according
to the
invention may be executed as follows:
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
step 1: provide a first probability partition array ("Pm(i,j)"), the Pm(i,j)
being
comprised of probability values for information pieces in the data set, each
probability value in the Pm(i,j) corresponding to the probability of an
authentic match;
5 step 2: provide a second probability partition array ("Pfin(i,j)"), the
Pfin(i,j) being
comprised of probability values for information pieces in the data set, each
probability value in the Pfin(i,j) corresponding to the probability of a false
match;
step 3: identify a first index set ("A"), the indices in set A being the (i,j)
indices that
10 have values in both Pfin(i,j) and Pm(i,j);
step 4: execute at least one of the following:
(a) identify a first no-match zone ("Zloo") that includes at least
the indices of set A for which both Pfin(i,j) is larger than zero
and Pm(i,j) is equal to zero, and use Zloo to determine FAR
15 z, where FAR Z. =1- Y(i,j)EZ. Pf,n(a, J) , and compare
FAR z~ to a desired false-acceptance-rate, and if FAR z", is
greater than the desired false-acceptance-rate, then reject the
data set;
(b) identify a second no-match zone ("Z2oo") that includes the
20 indices of set A for which Pm(i,j) is equal to zero, and use
Z2oo to identify a second index set ("C"), the indices of C
being the (i,j) indices that are in A but not Z2oo, and arrange
the (i,j) indices of C such that Pfin (l, J) k >= Pfin(l,J)k+I to
P,n(l,J)k P.(" J)k+1
provide an arranged C index, and identify a third index set
25 ("Cn"), the indices of Cn being the first N (i,j) indices of the
arranged C index, where N is a number for which the
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
36
following is true:
FARZx LJcN =1- (i,j)EZPfin (i, J) - (1,J)ECN Pfin 0, J) <_ FAR
,x,
and determine FRR, where FRR = ([,j)ECN Pin (i, J) , and
compare FRR to a desired false-rejection-rate, and if FRR is
greater than the desired false-rejection-rate, then reject the
data set.
If FAR z,,, is less than or equal to the desired false-acceptance-rate, and
FRR is less than or
equal to the desired false-rejection-rate, then the data set may be accepted.
Zlco may be
expanded to include additional indices of set A by including in Z100 the
indices of A for
which Pm(i,j) is equal to zero. In this manner, a single no-match zone may be
defined and
used for the entire step 4.
[0090] The invention may also be embodied as a computer readable memory device
for executing a method according to the invention, including those described
above. See
Figure 17. For example, in a system 100 according to the invention, a memory
device 103
may be a compact disc having computer readable instructions 106 for causing a
computer
processor 109 to execute steps of a method according to the invention. A
processor 109 may
be in communication with a data base 112 in which the data set may be stored,
and the
processor 109 may be able to cause a monitor 115 to display whether the data
set, is
acceptable. Additional detail regarding a system according to the invention is
provided in
Figure 18. For brevity, the steps of such a method will not be outlined here,
but it should
suffice to say that any of the methods outlined above may be translated into
computer
readable code which will cause a computer to determine and compare FAR z~
and/or FRR as
part of a system designed to determine whether a data set is acceptable for
making a decision.
Algorithm For Estimating A Joint PDF Using A Gaussian Copula Model
[0091] If all the score producing recognition systems that comprise a
biometric
identification system were statistically independent, then it is well known
that the joint pdf is
a product of its marginal probability density functions (the "marginal
densities"). It is almost
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
37
certain that when we use multiple methods within one modality (multiple
fingerprint
matchers and one finger) or multiple biometric features of a modality within
one method
(multiple fingers and one fingerprint matcher or multiple images of the same
finger and one
fingerprint matcher) that the scores will be correlated. It is possible that
different modalities
are not statistically independent. For example, we may not be sure that
fingerprint
identification scores are independent of palm print identification scores, and
we may not be
sure these are different modalities.
[0092] Correlation leads to the "curse of dimensionality." If we cannot rule
out
correlation in an n-dimensional biometric system of "n" recognition systems,
then to have an
accurate representation of the joint pdf, we would need to store an n-
dimensional array.
Because each dimension can require a partition of 1000 bins or more, an "n" of
four or more
could easily swamp storage capacity.
[0093] Fortunately, an area of mathematical statistics known as copulas
provides an
accurate estimate of the joint pdf by weighting a product of the marginal
densities with a n-
dimensional normal distribution that has the covariance of the correlated
marginals. This
Gaussian copula model is derived in [ 1: Nelsen, Roger B., An Introduction to
Copulas, 2nd
Edition, Springer 2006, ISBN 10-387-28659-4]. Copulas are a relatively new
area of
statistics; as is stated in [1], the word "copula" did not appear in the
Encyclopedia of
Statistical Sciences until 1997 and [1] is essentially the first text on the
subject. The theory
allows us to defeat the "curse" by storing the one-dimensional marginal
densities and an n-
by-n covariance matrix, which transforms storage requirements from products of
dimensions
to sums of dimensions - or in other words, from billions to thousands.
[0094] A biometric system with "n" recognitions systems that produce "n"
scores
s = [s , , s2 , ... sõ ] for each identification event has both an authentic
and an impostor cdf of the
f o r m F(s1, s2 , ... sõ) with an n-dimensional joint density f (s1 , s2 ,
... sõ). According to Sklar's
Theorem (see [1] and [2: Duss, Sarat C., Nandakumar, Karthik, Jain, Anil K., A
Principled
Approach to Score Level Fusion in Multimodal Biometric Systems, Proceedings of
AVBPA,
2005]), we can represent the density f as the product of its associated
marginals, f,. (s;) , for
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
38
i =1, ..., n, and an n-dimensional Gaussian copula function with correlation
matrix R is given
by
CR,.n (x1 , x2 ... xn 1 (DRnxn ((D-1 (xi ), (D-1 (X2) ... (D -' (xn (74)(1)
[0095] In Equation 74, x; E [0,1] for i =1,..., n, D is the cdf of the
standard normal
distribution and -' is its inverse, and (DR is an n-dimensional Gaussian cdf
whose
arguments are the random deviates of standard normal distributions, that is
they have a mean
of zero and a standard deviation of unity. (DR is assumed to have covariance
given by R
and a mean of zero. Hence the diagonal entries of R are unity, and, in
general, the off
diagonal entries are non-zero and measure the correlation between components.
[0096] The density of CR is obtained by taking its nth order mixed partial of
Equation 74:
CR,irn (x1 , x2 ... xõ) - a((DR,,.,, ((D-1(x1 ), (D-' (x2 )... (D-' (x,,))) _
~Rarn (~ ' (x1 ), (D-' (x2 )... (D-' (xn )) (75) (2)
axlax2 ... axõ 1 1,-1 ~(( (x1))
where 0 is the pdf of the standard normal distribution and OR is the joint pdf
of (DR and
is n-dimensional normal distribution with mean zero and covariance matrix R.
Hence, the
Gaussian copula function can be written in terms of the exponential function:
1
exp 1
--zTR 'z (3)
I 2 1 2 = 1 exp - 1 zTR-' z + f ;l 1 Zz (76)
CR,,.,õ (x) -- (27cR
(_2
R 2 2
where IRI is the determinant of the matrix R, x = [x1 , x2 , ... xõ f is an n-
dimensional column
vector (the superscript T indicates transpose), and z = [z1, z2 , ... zõ f is
an n-dimensional
column vector with z; = -' (Xi).
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
39
The score tuple s = [s1, s2 , ... sõ ] of an n-dimensional biometric
identification system is
distributed according to the joint pdf f (s1, S2,... s,,). The pdff can be
either the authentic pdf,
fAa , or the impostor pdf, f1in . The associated marginals are f,. (s;) , for
i =1, ..., n, which
have cumulative distribution functions F (s).
[0097] Sklar's Theorem guarantees the existence of a copula function that
constructs
multidimensional joint distributions by coupling them with the one-dimensional
marginals
[1],[2]. In general, the Gaussian copula function in Equation 74 is not that
function, but it
serves as a good approximation. So, if we set zi = -1(F,. (s;)) for i =1,...,
n, then we can
use Equation 76 to estimate the joint density as
2
I zTR-1z + fill 1 Zi (4)
11 I f (Si ) exp 1
-
f(s;,s2,...s,,) 2 2 R (77)
[0098] Equation 77 is the copula model that we use to compute the densities
for the
Neyman-Pearson ratio. That is,
.f (s )eXp - - zT R Ail z + z;
f1''_, 2
iAtl r 2 -1 2
{' (5)
k _ / All = RAu 2 (78)
I zTRnz+nili?i
/Im l m;(s )exp 1
1f f
2 2
R Im
The densities fAõ and f,,n are assumed to have been computed in another
section using
non-parametric techniques and extreme value theory, an example of which
appears below.
To compute RAI, and R1in we need two sets of scores. Let SAMI be a simple
random sample
1 2 11 1,, ;
of nAõ authentic score tuples. That is, SAõ = A I , I I I I... IS All where
sA,, is a column vector
of scores from the "n" recognition systems. Likewise, let Sin = kin SI n = =,
s 11i n" a simple
random sample of n11,, impostor scores. We compute the covariance matrices for
SAõ and
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
n
SIm with CAll = (SAn - SAn)(s It -'SAu )T and CIi (SIM - 'SL)(SIm - Slm)T
where A,, and
i=1 i=1
sl,n are the sample means of SAõ and SI,n respectively. As mentioned above,
the diagonal
entries of the associated R matrices are unity because the copula components
are standard
normal distributions, and the off diagonal entries are the correlation
coefficients in the C
5 matrices just computed. Recall that the correlation coefficient between the
it" and j"
element of C, i # j, is given by pii = 6'' C(i, j) . So, an algorithm to
compute
~icj C i,i C j, j
RAõ is:
= For i=1: nAõ -1
= For j=i+1: nAu
0, 10 = RAI, (" A = CA" j)
(( l CAõ a, a CAn J , J
= RAn( ,1)-RA,, (,i)
= For i=1: nAn
= RAõ(i,i)=1
15 We compute R,,n in a similar manner.
[0099] The only remaining values to compute in Equation 78 are zi = 0-' (F,.
(si)) for
each i. There are two values to compute: x, = F,. (s) and then zi = 0-'(xi).
We compute
Si
x; = F. (s) by numerically computing the integral: xi = f fi (x)dx. Note that
xi = F,. (si) is
Smini
the probability of obtaining a score less than si , hence xi E [0,11. The
value zi = -' (xi) is
20 the random deviate of the standard normal distribution for which there is
probability xi of
drawing a value less than zi , hence xi E (- oo, oo). We numerically solve
zi = -' (xi) = J erf -' (2xi -1), where erf -'(x) is the inverse error
function.
Use Of Extreme Values
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
41
[00100] Statistical modeling of biometric systems at score level may be
extremely
important. It can be the foundation for biometric systems performance
assessment, including
determination of confidence intervals, test sample size of a simulation and
prediction of real
world system performances. Statistical modeling used in multimodal biometric
systems
integrates information from multiple biometric sources to compensate for the
limitations in
performance of each individual biometric system. We propose a new approach for
estimating
marginal biometric matching score distributions by using a combination of non-
parametric
methods and extreme value theory. Often the tail parts of the score
distributions are
problematic and difficult to estimate due to lack of testing samples. Below,
we describe
procedures for fitting a score distribution curve. A general non-parametric
method is used for
fitting the center body part of a distribution curve. A parametric model, the
general Pareto
distribution, is used for fitting the tail parts of the curve, which is
theoretically supported by
extreme value theory. A biometric fusion scheme using Gaussian copula may be
adapted to
incorporate a set of marginal distributions estimated by the proposed
procedures.
[00101] Biometric systems authenticate or identify subjects based on their
physiological or behavioral characteristics such as fingerprints, face, voice
and signature. In
an authentication system, one is interested in confirming whether the
presented biometric is
in some sense the same as or close to the enrolled biometrics of the same
person. Generally
biometric systems compute and store a compact representation (template) of a
biometric
sample rather than the sample of a biometric (a biometric signal). Taking the
biometric
samples or their representations (templates) as patterns, an authentication of
a person with a
biometric sample is then an exercise in pattern recognition.
[00102] Let the stored biometric template be pattern P and the newly acquired
pattern
be P'. In terms of hypothesis testing,
Ho : P = P, the claimed identity is correct;
(38)
H, : P # P, the claimed identity is not correct,
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
42
Often some similarity measure s = Sim(P, P') determines how similar patterns P
and P'
are. Decisions are made based on a decision threshold t. In most applications
this threshold
is fixed, i.e., t = to and Ho is decided if s >_ to and H, is decided if s <
to .
[00103] The similarity measure s is often referred to as a score. If s is the
score of a
matched pair P = P, we refer to s as a match (genuine) score; if s is the
score of a
mismatched pair P # P', we refer to s as a non-match or mismatch (impostor)
score.
Deciding Ho when H, is true gives a false accept (FA), erroneously accepting
an individual
(false positive). Deciding H, when Ho is true, on the other hand, results in a
false reject
(FR), incorrectly rejecting an individual (false negative). The False Accept
Rate (FAR) and
False Reject Rate (FRR) together characterize the accuracy of a recognition
system, which
can be expressed in terms of cumulative probability distributions of scores.
The FAR and
FRR are two interrelated variables and depend very much on decision threshold
to (see
Figure 19).
[00104] Biometric applications can be divided into two types: verification
tasks and
identification tasks. For verification tasks a single matching score is
produced, and an
application accepts or rejects a matching attempt by thresholding the matching
score. Based
on the threshold value, performance characteristics of FAR and FRR can be
estimated. For
identification tasks a set of N matching scores {s, , s2 ,..., sN } , S1 > s2
> ... > SN is produced
for N enrolled persons. The person can be identified as an enrollee
corresponding to the
best ranked score s, , or the identification attempt can be rejected. Based on
the decision
algorithm FAR and FRR can be estimated. The usual decision algorithm for
verification and
identification involves setting some threshold to and accepting a matching
score s if this
score is greater than threshold: s > to .
[00105] The objective of this work is to model the behavior of a biometric
system
statistically in terms of Probability Density Functions (PDFs). The data we
present for
purposes of illustrating the invention are basically two types, the biometric
matching scores
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
43
of genuine and impostor. In a biometric verification system, we are mostly
concerned with
the distribution of genuine matching scores. For an identification system, we
also need to
know the behavior of the impostor matching scores as well as the relation
between genuine
score distribution and impostor score distribution.
[00106] Applications of statistic modeling also include the following [I]:
1. Evaluation of a biometric technique:
a) Distinctiveness evaluation, statistical modeling of the biometric
modalities to study how well they distinguish persons absolutely.
b) Understanding of error probabilities and correlations between different
biometric modalities.
2. Performance prediction:
a) Statistical prediction of operational performance from laboratory
testing.
b) Prediction of large database identification performance from small-
scale performance.
3. Data quality evaluation:
a) Quality evaluation of biometric data, relating biometric sampling
quality to performance improvement.
b) Standardization of data collection to ensure quality; determine
meaningful metrics for quality.
4. System performance:
a) Modeling the matching process as a parameterized system accounting
for all the variables (joint probabilities).
b) Determine the best payoff for system performance improvement.
[00107] The behavior of distributions can be modeled by straightforward
parametric
methods, for example, a Gaussian distribution can be assumed and a priori
training data can
be used to estimate parameters, such as the mean and the variance of the
model. Such a
model is then taken as a normal base condition for signaling error or being
used in
classification, such as a Bayesian based classifiers. More sophisticated
approaches use
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
44
Gaussian mixture models [2] or kernel density estimates [3]. The main
limitation of all of
these methods is that they make an unwarranted assumption about the nature of
the
distribution. For instance, the statistical modeling based on these methods
weigh on central
statistics such as the mean and the variance, and the analysis is largely
insensitive to the tails
of the distribution. Therefore, using these models to verify biometrics can be
problematic in
the tail part of the distribution. An incorrect estimation of a distribution
especially at tails or
making an unwarranted assumption about the nature of the PDFs can lead to a
false positive
or a false negative matching.
[00108] There is a large body of statistical theory based on extreme value
theory
(EVT) that is explicitly concerned with modeling the tails of distributions.
We believe that
these statistical theories can be applied to produce more accurate biometric
matching scores.
Most of the existing works that we consider as related to our work using
extreme value theory
are for novelty detections in medical image processing [2], [4], [5],
financial risk
management [6], [7], structure damage control [8], etc. Extreme values can be
considered as
outliers or as a particular cluster. The methods used for the detection of
extreme values are
based on the analysis of residuals.
[00109] This document describes a general statistical procedure for modeling
probability density functions (PDFs) which can be used for a biometric system.
The design
of the algorithm will follow a combination of non-parametric approach and
application of
extreme value theory for accurate estimation of the PDFs.
Previous Works
[00110] A. Distribution Estimations for Biometric Systems. Statistical
modeling has
long been used in pattern recognition. It provides robust and efficient
pattern recognition
techniques for applications such as data mining, web searching, multimedia
data retrieval,
face recognition, and handwriting recognition. Statistical decision making and
estimation are
regarded as fundamental to the study of pattern recognition [7]. Generally,
pattern
recognition systems make decisions based on measurements. Most of the
evaluation and
theoretical error analysis are based on assumptions about the probability
density functions
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
(PDFs) of the measurements. There are several works which have been done for
estimating
error characteristics specifically for biometric systems [9]-[11].
[00111] Assume a set of matching (genuine) scores X = {X, . . ., XM} and a set
of
mismatching (impostor) scores Y = {Yl, . . ., YN} to be available. Here M < N
because
5 collecting biometrics always results in more mismatching than matching
pairs. (From this it
immediately follows that the FAR can be estimated more accurately than the FRR
[10]). For
the set of matching scores, X assume that it is a sample of M numbers drawn
from a
population with distribution F(x) = Prob(X < x). Similarly, let the mismatch
scores Y be a
sample of N numbers drawn from a population with distribution G(y) = Prob(Y
<y). The
10 functions F and G are the probability distributions or cumulative
distribution functions of
match scores X and Y. They represent the characteristic behaviors of the
biometric system.
Since the random variables X and Y are matching scores, the distribution
functions at any
particular value x = to can be estimated by F(t0) and F(t0) using data X and
Y. In [ 10], [ 11 ] a
simple naive estimator that is also called empirical distribution function is
used:
M
15 F(t0)= 1 l1{xt<t0} = 1 (#X; <_ t0)
M ,_, M
(39)
where the estimation is simply done by counting the X; E X that are smaller
than to and
dividing by M.
20 [00112] In general, there are many other choices for estimating data such
as matching
scores. For example, among the parametric models and non-parametric models,
the kernel-
based methods are generally considered to be a superior non-parametric model
than the naive
formula in (2).
[00113] B. Another Similar Approach. In [13], another similar approach is
proposed,
25 which uses an estimate (2) for constructing the marginal distribution
functions F from the
observed vector of similarity scores, {X,: i = 1, 2,..., N}. The same
empirical distribution
function for the marginal distribution is written as
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
46
N
E(t)= 1 YI(X; <-t)
N i=1
(40)
where I(A) is the indicator function of the set A; I(A) = 1 if A is true, and
0 otherwise. Note
that E(t) = 0 for all t < t,,!õ and E(t) = 1 for all t > tmax, where tm171 and
tmax, respectively, are
the minimum and maximum of the observations {Xj : i = 1,..., N}. Next, they
define
H(t) = - log(1- E(t))
, and note that discontinuity points of E(t) will also be points of
discontinuity of H(t). In
order to obtain a continuous estimate of H(t), the following procedure is
adopted: For an M-
partition [ ], the value of H(t) at a point t E [t.111 , tmax J is redefined
via the linear
interpolation formula
H(t) = H(t ,) + (h(t ,+1) - H(t,, )) t - t ,
tm+l - tn,
(41)
whenever t,,, 5 t<- t,,,+1 and subsequently, the estimated distribution
function, F(t), of F(t) is
obtained as
F(t) =1- e-H(`)
(42)
[00114] It follows that F(t) is a continuous distribution function. Next they
generate
B* = 1,000 samples from F :
(1) Generate a uniform random variable U in X0,1 J;
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
47
(2) Define V = -log(l - U), and
(3) Find the value V* such that H(V*) = V.
It follows that V* is a random variable with distribution function P. To
generate 1,000
independent realizations from F , the steps (1-3) are repeated 1,000 times.
Finally, a non-
parametric density estimate of F is obtained based on the simulated samples
using a Gaussian
kernel.
[00115] Although they did not explain why the simulation or estimation
procedure is
so designed, we can see the underlying assumption is basically that the data
follows the
exponential distribution. This can be roughly seen from the following
explanation. Firstly,
we define an exponential distribution function by G(t) =1- e-'. Then the above
H(t) = - log(1- E(t)) = G-' (E(t)) is actually exponential quantile of the
empirical
distribution, which is a random variable hopefully following exponential
distribution. The
linear interpolation H(t) of H(t) is then an approximation of the random
variable. Also
F(t) is
F(t) = G(H(t)).
[00116] To generate simulation data, as usual, start from uniform random
variable U
in [0,1], data following distribution F is then generated as
V* = F-' (U) = H-1 G-1 (U).
[00117] C. The Problems. When attempting to fit a tail of a pdf using other
techniques, certain problems arise or are created. They include:
* Unwarranted assumption about the nature of the distribution.
* Types of data used in estimation (most data are regular, the problematic
data such as
outliers and clusters which contribute most of the system errors are not
addressed or not
address enough).
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
48
*Forgotten error analysis/estimation (decision boundaries are usually
heuristic without
enough understanding, which may end up with higher than lab estimated errors).
Data Analysis
[00118] For biometric matching scores, we usually adopt that a higher score
means a
better match. The genuine scores are generally distributed in a range higher
than the
corresponding impostor scores are. For most biometric
verification/identification systems, an
equal error rate (EER) of 5% or lower is expected. Among such systems, those
for
fingerprint verification can normally get even 2% EER. For setting an optimal
threshold
level for a new biometric system as well as assessing the claimed performance
for a vendor
system, estimations of the tail distributions of both genuine and impostor
scores are critical
(See Figure 19).
[00119] Most statistical methods weigh on central statistics such as the mean
and the
variance, and the analysis is largely insensitive to the tails of the
distribution. Verification of
biometrics is problematic mostly in the tail part of the distribution, and
less problematic in the
main body of the PDF. An incorrect estimation of a distribution especially at
the tails can
lead to false positive and false negative responses.
[00120] In fact, there is a large body of statistical theory based on extreme
value theory
(EVT) that is explicitly concerned with modeling the tails of distributions.
We believe that
these statistical theories can be applied to produce fewer false positives and
fewer false
negatives.
[00121] Although we are interested in the lower end of the genuine score
distribution,
we usually reverse the genuine scores so that the lower end of the
distribution is flipped to the
higher end when we work on finding the estimation of the distribution. Let us
first
concentrate on this reversed genuine matching scores and consider our analysis
for estimation
of right tail distributions.
[00122] To use Extreme Value Statistic Theory to estimate the right tail
behaviors, we
treat the tail part of the data as being realizations of random variables
truncated at a
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
49
displacement a. We only observe realizations of the reversed genuine scores
which exceed
6.
[00123] The distribution function (d.f.) of the truncated scores can be
defined as in
Hogg & Klugman (1984) by
Fxd(x)=P}X <_xx/X>5}= 0 if x<8,
F(x)-Fz(8) if x__<8,
L 1- Fx(8)
and it is, in fact, the d.f. that we shall attempt to estimate. Figure 20
depicts the empirical
distribution of genuine scores of CUBS data generated on DB1 of FVC2004
fingerprint
images. The vertical line indicates the 95% level.
[00124] With adjusted (reversed) genuine score data, which we assume to be
realizations of independent, identically distributed, truncated random
variables, we attempt to
find an estimate Fx,, (x), of the truncated score distribution Fx,, (x). One
way of doing this is
by fitting parametric models to data and obtaining parameter estimates which
optimize some
fitting criterion - such as maximum likelihood. But problems arise when we
have data as in
Figure 20 and we are interested in a high-excess layer, that is to say the
extremes of the tail
where we want to estimate, but for which we have little or no data.
[00125] Figure 20 shows the empirical distribution function of the CUBS
genuine
fingerprint matching data evaluated at each of the data points. The empirical
d.f. for a sample
of size n is defined by
1 "
Fõ (x) = - ~ 1 {x <<}
n i=1
i.e. the number of observations less than or equal to x divided by n. The
empirical d.f.
forms an approximation to the true d.f. which may be quite good in the body of
the
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
distribution; however, it is not an estimate which can be successfully
extrapolated beyond the
data.
[00126] The CUBS data comprise 2800 genuine matching scores that is generated
using DB1 of FVC 2004 fingerprint images (database #1 of a set of images
available from the
5 National Bureau Of Standards, fingerprint verification collection).
[00127] Suppose we are required to threshold a high-excess layer to cover the
tail part
5% of the scores. In this interval we have only 139 scores. A realistic ERR
level of 2% tail
will leave us only 56 scores. If we fit some overall parametric distribution
to the whole
dataset it may not be a particularly good fit in this tail area where the data
are sparse. We
10 must obtain a good estimate of the excess distribution in the tail. Even
with a good tail
estimate we cannot be sure that the future does not hold some unexpected error
cases. The
extreme value methods which we explain in the next section do not predict the
future with
certainty, but they do offer good models for explaining the extreme events we
have seen in
the past. These models are not arbitrary but based on rigorous mathematical
theory
15 concerning the behavior of extrema.
Extreme Value Theory
[00128] In the following we summarize the results from Extreme Value Theory
(EVT)
which underlie our modeling. General texts on the subject of extreme values
include Falk,
Husler & Reiss (1994), Embrechts, Kluppelberg & Mikosch (1997) and Reiss &
Thomas
20 (1996).
[00129] A. The Generalized Extreme Value Distribution. Just as the normal
distribution proves to be the important limiting distribution for sample sums
or averages, as is
made explicit in the central limit theorem, another family of distributions
proves important in
the study of the limiting behavior of sample extrema. This is the family of
extreme value
25 distributions. This family can be subsumed under a single parametrization
known as the
generalized extreme value distribution (GEV). We define the d.f. of the
standard GEV by
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
51
H~ (x) = e if ~ #0,
L e_e if ~=0,
where x is such that 1 + 4x > 0 and is known as the shape parameter. Three
well known
distributions are special cases: if ~ > 0 we have the Frechet distribution
with shape parameter
a = l / ; if ~ = 0 we have the Weibull distribution with shape a = -l /; if =
0 we have
the Gumbel distribution.
[00130] If we introduce location and scale parameters and 8 > 0 respectively
we can
extend the family of distributions. We define the GEV H11 a (x) to be H, ((x -
,u) / a) and
we say that H ,, 6 is of the type H, H.
[00131] B. The Fisher-Tippett Theorem. The Fisher-Tippett theorem is the
fundamental result in EVT and can be considered to have the same status in EVT
as the
central limit theorem has in the study of sums. The theorem describes the
limiting behavior
of appropriately normalized sample maxima.
[00132] If we have a sequence of i.i.d. ("independently and identically
distributed")
random variables X, , X2 ... from an unknown distribution F. We denote the
maximum of the
first n observations by M,, = max{X, ...Xõ }. Suppose further that we can find
sequences of
real numbers a,, > 0 and b,, such that (M,, - b,, )/a, , the sequence of
normalized maxima,
converges in distribution. That is
P{(Mõ -b,,)l a,, 5 x}= F"(aõx+ bõ)-> H(x),
as n - oo,
(43)
for some non-degenerate d.f. H(X) . If this condition holds we say that F is
in the maximum
domain of attraction of F and we write F E MDA(H).
[00133] It was shown by Fisher & Tippett (1928) that
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
52
F E MDA(H) H is of the type H, for some
Thus, if we know that suitably normalized maxima converge in distribution,
then the limit
distribution must be an extreme value distribution for some value of the
parameters ~, P,
and 6.
[00134] The class of distributions F for which the condition (6) holds is
large. A
variety of equivalent conditions may be derived (see Falk et at. (1994)).
[00135] Gnedenko (1943) showed that for ~ > 0, F E MDA(H,) if and only if
1-F(x)-" IL(x) for some slowly varying function L(x) . This result essentially
says that if
the tail of the d.f. F(x) decays like a power function, then the distribution
is in the domain
of attraction of the Frechet. The class of distributions where the tail decays
like a power
function is quite large and includes the Pareto, Burr, loggamma, Cauchy and t-
distributions as
well as various mixture models. These are all so-called heavy tailed
distributions.
[00136] Distributions in the maximum domain of attraction of the Gumbel
(MDA(Ho )) include the normal, exponential, gamma and lognormal distributions.
The
lognormal distribution has a moderately heavy tail and has historically been a
popular model
for loss severity distributions; however it is not as heavy-tailed as the
distributions in
MDA(H,) for ~ < 0. Distributions in the domain of attraction of the Weibull
(H, for
~ < 0) are short tailed distributions such as the uniform and beta
distributions.
[00137] The Fisher-Tippett theorem suggests the fitting of the GEV to data on
sample
maxima, when such data can be collected. There is much literature on this
topic (see
Embrechts et al. (1997)), particularly in hydrology where the so-called annual
maxima
method has a long history. A well-known reference is Gumbel (1958).
[00138] C. The Generalized Pareto Distribution (GPD). Further results in EVT
describe the behavior of large observations which exceed high thresholds, and
these are the
results which lend themselves most readily to the modeling of biometric
matching scores.
They address the question: given an observation is extreme, how extreme might
it be? The
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
53
distribution which comes to the fore in these results is the generalized
Pareto distribution
(OPD). The GPD is usually expressed as a two parameter distribution with d.f.
1-(1+x) if 0,
G Q (x) = a-
1-e' if 4= 0,
where a > 0, and the support is x >- 0 when 0 and 0<- x<_ -a / when ~ < 0. The
GPD again subsumes other distributions under its parametrization. When ~ > 0
we have a
re-parameterized version of the usual Pareto distribution with shape a =1 / ;
if ~ < 0 we
have a type II Pareto distribution; ~ = 0 gives the exponential distribution.
[00139] Again we can extend the family by adding a location parameter 'U. The
GPD
G, F Q (x) is defined to be G 0. (x -,u) .
[00140] D. The Pickands-Balkema-de Haan Theorem. Consider a certain high
threshold u which might, for instance, be the general acceptable (low) level
threshold for an
ERR. At any event u will be greater than any possible displacement 8
associated with the
data. We are interested in excesses above this threshold, that is, the amount
by which
observations overshoot this level.
[00141] Let xo be the finite or infinite right endpoint of the distribution F.
That is to
say, xo = sup{x E R : F(x) < 1} < co . We define the distribution function of
the excesses over
the high threshold u by
(y) = P{X -u <- y/X > u} = F(y+u)-F(u) ,
1- F(u)
(44)
where Xis a random variable and y = x - u are the excesses. Thus 0<- y < xo -
u .
[00142] The theorem (Balkema & de Haan 1974, Pickands 1975) shows that under
MDA ("Maximum Domain of Attraction") conditions (6) the generalized Pareto
distribution
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
54
(7) is the limiting distribution for the distribution of the excesses, as the
threshold tends to the
right endpoint. That is, we can find a positive measurable function a(u) such
that
lim sup Fõ(y)-GG,C.(,,)(y) = 0,
u-+xo o<_y<z0-1e
if and only if F E MDA(H,).
[00143] This theorem suggests that, for sufficiently high thresholds u, the
distribution
function of the excesses may be approximated by G (y) for some values of ~ and
u .
Equivalently, for x - u >- 0 , the distribution function of the ground-up
exceedances Fõ (x - u)
(the excesses plus u) may be approximated by G 0 (x - u) = G,,,,,, (x) .
[00144] The statistical relevance of the result is that we may attempt to fit
the GPD to
data which exceed high thresholds. The theorem gives us theoretical grounds to
expect that if
we choose a high enough threshold, the data above will show generalized Pareto
behavior.
This has been the approach developed in Davison (1984) and Davison & Smith
(1990).
[00145] E. Fitting Tails Using GPD. If we can fit the GPD to the conditional
distribution (8) of the excesses above a high threshold, we may also fit it to
the tail of the
original distribution above the high threshold For x >- u, i.e. points in the
tail of the
distribution, from (8),
F(x) = F(y + u) = (1- F(u))F, (y) + F(u)
= (1- F(u))Fõ (x - u) + F(u)
(45)
[00146] We now know that we can estimate Fõ (x - u) by G a (x - u) for u
large. We
can also estimate F(u) = P}X < u } from the data by Fõ (u), the empirical
distribution
function evaluated at u .
[00147] This means that for x >- u we can use the tail estimate
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
F(x) = 1 - F,(u))G.1 (x)+Fõ (u)
(46)
to approximate the distribution function F(x). It is easy to show that F(x) is
also a
5 generalized Pareto distribution, with the same shape parameter ~, but with
scale parameter
6 = o(1 - Fõ (u))~ and location parameter ,u = u - 6:((1 - Fõ (u))-~ -1 / 4 .
[00148] F. Statistical Aspects. The theory makes explicit which models we
should
attempt to fit to biometric matching data. However, as a first step before
model fitting is
undertaken, a number of exploratory graphical methods provide useful
preliminary
10 information about the data and in particular their tail. We explain these
methods in the next
section in the context of an analysis of the CUBS data. The generalized Pareto
distribution
can be fitted to data on excesses of high thresholds by a variety of methods
including the
maximum likelihood method (ML) and the method of probability weighted moments
(PWM).
We choose to use the ML-method. For a comparison of the relative merits of the
methods we
15 refer the reader to Hosking & Wallis (1987) and Rootzen & Tajvidi (1996).
Analysis Using Extreme Value Techniques
[00149] The CUBS Fingerprint Matching Data consist of 2800 genuine matching
scores and 4950 impostor matching scores that are generated by CUBS
fingerprint
verification/identification system using DB1 of FVC 2004 fingerprint images.
Results
20 described in this section are from using the genuine matching scores for
clarity, although the
same results can be generated using the impostor scores. For convenience of
applying EVS,
we first flip (i.e. reverse the scores so that the tail is to the right) the
genuine scores so that the
higher values represent better matching. The histogram of the scores gives us
an intuitive
view of the distribution. The CUBS data values are re-scaled into range of
[0,1]. See Figure
25 21.
[00150] A. Quantile-Quantile Plot. The quantile-quantile plot (QQ-plot) is a
graphical
technique for determining if two data sets come from populations with a common
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
56
distribution. A QQ-plot is a plot of the quantiles of the first data set
against the quantiles of
the second data set. By a quantile, we mean the fraction (or percent) of
points below the
given value. A 45-degree reference line is also plotted. If the two sets come
from a
population with the same distribution, the points should fall approximately
along this
reference line. The greater the departure from this reference line, the
greater the evidence for
the conclusion that the two data sets have come from populations with
different distributions.
The QQ-plot against the exponential distribution is a very useful guide. It
examines visually
the hypothesis that the data come from an exponential distribution, i.e. from
a distribution
with a mediumsized tail. The quantiles of the empirical distribution function
on the x -axis
are plotted against the quantiles of the exponential distribution function on
the y -axis. The
plot is
{(Xk:flGO(fl_k 1)),k=1,...,fl}
where Xk:,, denotes the kth order statistic, and Go; is the inverse of the
d.f. of the exponential
distribution (a special case of the GPD). The points should lie approximately
along a straight
line if the data are an i.i.d. sample from an exponential distribution.
[00151] The closeness of the curve to the diagonal straight line indicates
that the
distribution of our data show an exponential behaviour.
[00152] The usual caveats about the QQ-plot should be mentioned. Even data
generated from an exponential distribution may sometimes show departures from
typical
exponential behaviour. In general, the more data we have, the clearer the
message of the QQ-
plot.
[00153] B. Sample Mean Excess Plot. Selecting an appropriate threshold is a
critical
problem with the EVS using threshold methods. Too low a threshold is likely to
violate the
asymptotic basis of the model; leading to bias; and too high a threshold will
generate too few
excesses; leading to high variance. The idea is to pick as low a threshold as
possible subject
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
57
to the limit model providing a reasonable approximation. Two methods are
available for this:
the first method is an exploratory technique carried out prior to model
estimation and the
second method is an assessment of the stability of parameter estimates based
on the fitting of
models across a range of different thresholds (Coles (2001) (b)).
[00154] The first method is a useful graphical tool which is the plot of the
sample
mean excess function of the distribution. If X has a GPD with parameters ~ and
a, the
excess over the threshold u has also a GPD and its mean excess function over
this threshold
is given by
e(u) =E[X -u/X >u]= a-+~u, for <l
1-~
(47)
[00155] We notice that for the GPD the mean excess function is a linear
function of the
threshold u. Hence, if the empirical mean excess of scores has a linear shape
then a
generalized Pareto might be a good statistical model for the overall
distribution. However, if
the mean excess plot does not have a linear shape for all the sample but is
roughly linear from
a certain point, then it suggests that a GPD might be used as a model for the
excesses above
the point where the plot becomes linear.
[00156] The sample mean plot is the plot of the points:
(u, e,, (u)),X1:,, <u <Xaar}
where X,:,, and X,,:,, are the first and nth order statistics and eõ (u) is
the sample mean excess
function defined by
i=1 (X, _u)+
e,, (u) _
E_11{.~ >a}
that is the sum of the excesses over the threshold u divided by the number of
data points
which exceed the threshold u.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
58
[00157] The sample mean excess function eõ (u) is an empirical estimate of the
mean
excess function which is defined in (11) as e(u) = E[X -u/X > u]. The mean
excess
function describes the expected overshoot of a threshold given that exceedance
occurs.
[00158] Figure 24 shows the sample mean excess plot of the CUBS data. The plot
shows a general linear pattern. A close inspection of the plot suggests that a
threshold can be
chosen at the value u =0.45 which is located at the beginning of a portion of
the sample mean
excess plot that is roughly linear.
[00159] C. Maximum Likelihood Estimation. According to the theoretical results
presented in the last section, we know that the distribution of the
observations above the
threshold in the tail should be a generalized Pareto distribution (GPD). This
is confirmed by
the QQ-plot in Figure 23 and the sample mean excess plot in Figure 24. These
are different
methods that can be used to estimate the parameters of the GPD. These methods
include the
maximum likelihood estimation, the method of moments, the method of
probability-weighted
moments and the elemental percentile method. For comparisons and detailed
discussions
about their use for fitting the GPD to data, see Hosking and Wallis (1987),
Grimshaw (1993),
Tajvidi (1996a), Tajvidi (1996b) and Castillo and Hadi (1997). We use the
maximum
likelihood estimation method.
[00160] To get the distribution density function of the GPD, we take the first
derivative
of the distribution function in (7)
1 _0+X) 6 (x) a- + 6 x) if ~ 0,
=
dx
1 e if ~=0.
6
(48)
Therefore for a sample x = {x1,..., xõ } the log-likelihood function L(~, 6/x)
for the GPD is
the logarithm of the joint density of the n observations:
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
59
n
-n log a-( +1)ylog(1+-x;) if ~ # 0
L(, 6/x)
1 "
-n log a-6Yx1 if ~=0.
1
[00161] Confidence Band Of CDF: No matter which statistical model we choose to
estimate the biometric matching scores, the fundamental question is how
reliable the
estimation can be. The reliability ranges of the estimates or the error
intervals of the
estimations have to be assessed. A confidence interval is defined as a range
within which a
distribution F(to) is reliably estimated by F(to) . For example a confidence
interval can be
formed as [P(to) - a, F(to) + a, so that the true distribution F at to can be
guaranteed as
F(to) E LF(to)-a,F(to)+a]
[00162] There are several research on confidence interval for error analysis
of
biometric distribution estimations. In [10] there are two approaches given for
obtaining a
confidence interval.
[00163] A. Reliability of a Distribution Estimated by Parametric Models. For
estimating a confidence interval, first we define that
I'(X) = F(to)
(49)
are the estimates of a matching score distribution at specific value to . See
Figure 25. If we
define a random variable Z as the number of successes of X such that X< to is
true with
probability of success F(to) = Prob (X < to) , then in M trials, the random
variable Z has
binomial probability mass distribution
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
M
P(Z = z) = z)F(to) z (1- F(to )) M-Z , z = 0,...,M
(50)
The expectation of Z, E(Z) = MF(to) and the variance of Z, 62 (Z) = MF(to)(1-
F(to )) .
5 Therefore the random variable Z / M has expectation E(Z / M) = F(to) and
variance
62 (t0) = F(to)(1- F(to )) / M. When M is large enough, by the law of large
numbers,
Z / M is distributed according to a norm distribution, i.e., Z / M-N(F(to ),
6(to )) .
[00164] From (2) it can be seen that, with M the number of match scores, the
number
of success Z = (#X; < to) = MF(to ). Hence for large M, F(to) = Z / M is norm
distributed
10 with an estimate of the variance given by
6(to) - F(to 1- F(t0 )
M
(51)
With percentiles of the normal distribution, a confidence interval can be
determined. For
15 example, a 90% interval of confidence is
F(to) E [F(to) -1.6456(t0 ), F(to) + 1.6456-(to)].
Figure 25 depicts F(to).
[00165] B. Reliability of a distribution estimated by bootstrap approach. The
bootstrap uses the available data many times to estimate confidence intervals
or to perform
20 hypothesis testing [10]. A parametric approach, again, makes assumptions
about the shape of
the error in the probability distribution estimates. A non-parametric approach
makes no such
assumption about the errors in F(to) and G(to) .
[00166] If we have the set of match scores X, then we want to have some idea
as to
how much importance should be given to r(X) = F(to ). That is, for the random
variable
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
61
F(to we are interested in a (1- a) 100% confidence region for the true value
of F(to) in
the form of
[q(al2), q(1- a/2)]
where q(a/2) and q(1- a/2) are the a/2 and 1- a/2 quantiles of
HF (z) = Pr ob(F(to) < z), where HF (z) is the probability distribution of the
estimate F(to )
and is a function of the data X.
[00167] The sample population X has empirical distribution F(to) defined in
(2) or
GPD defined in (10). It should be noted that the samples in set X are the only
data we have
and the distribution estimates of F(to) is the only distribution we have. The
bootstrap
proceeds, therefore, by assuming that the distribution F(to) is a good enough
approximation
of the true distribution F(to) . To obtain samples that are distributed as F
one can draw
samples from the set X with replacement, i.e., putting the sample back into
set X each time.
Hence, any statistic, including F(X) = F(to) , for fixed to, can be re-
estimated by simply re-
sampling.
[00168] The bootstrap principle prescribes sampling, with replacement, the set
X a
large number (B) of times, resulting in the bootstrap sets X k, k =1, ..., B.
Using these sets,
* * *
one can calculate the estimates F k(to) = F k(X k), k =1,..., B . Determining
confidence
intervals now essentially amounts to a counting exercise. One can compute
(say) a 90%
*
confidence interval by counting the bottom 5% and top 5% of the estimates F
k(to) and
*
subtracting these estimates from the total set of the estimates F k(to) . The
leftover set
determines the interval of confidence. In Figure 26, the bootstrap estimates
are ordered in
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
62
ascending order and the middle 90% (the samples between and ) determine the
bootstrap
interval.
[00169] In summary, with fixed x = to, what we are interested in is F(to), but
all that
we can possibly do is to make an estimate 17(X) = F(to) . This estimate is
itself a random
variable and has distribution HF (z) = Pr ob (17(X) S z) = Pr ob(F(to) <_ z).
We are able to
determine a bootstrap confidence interval of F(to) by sampling with
replacement from X as
follows:
1) Calculate the estimate F(to) from the sample X using an estimation scheme
such as
(2) of empirical distribution, or (10) of GPD, of X.
2) Resampling. Create a bootstrap sample X* _ ~X 1.... ,X M } by sampling X
with
replacement.
3) Bootstrap estimate. Calculate Fk(to) from X*, again using (2) or (10).
4) Repetition. Repeat steps 2-3 B times (B large), resulting in
F1(to),F2(to),...,FB(to).
[00170] The bootstrap estimate of distribution HF (z) = Pr ob(F(to) <_ z) is
then
I a * 1
H F(z) = Pr ob(F(to) 5 z) = B 11(F k (to) <_ z) = B (# F k(to) <_ z)
(52)
[00171] To construct a confidence interval for F(to), we sort the bootstrap
estimates
in increasing order to obtain
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
63
F (1)(to ), F (2)(to ), ... , F (B)(to ),
And from (16) by construction, it follows that
H F(z) = H F(F(k) (to )) = Pr ob(F(to) F(k) (to )) = B
[00172] A (1- a) 100% bootstrap confidence interval is [P(1)(to),p(k*2)(to)]
with
k, = L(a / 2)B] and k2 = L(1- a / 2)B], the integer parts of (a / 2)B and (1-
a / 2)B (as in
Figure 26).
[00173] Confidence interval using GPD model. In this section we present a
close form
confidence interval for the tail estimation using Generalized Pareto
Distribution. From (7),
for a given percentile p = GE (x), quantile of the generalized Pareto
distribution is given in
terms of the parameters by
x(p)=6((1-p)-E-1), ~0
_-alog(1-p), =0
(53)
[00174] A quantile estimator x(p) is defined by substituting estimated
parameters
and a for the parameters in (17). The variance of x(p) is given asymptotically
by [ 12]
var.x(p) - (s(e))2 var& + 2 * as(s)s'() COV(, 6) + 62 (s'(~))2 var e
(54)
where
s() _ ((1- p)-E -1)/
s'() _ -(s()+ (1- p)_E log(1- p))/ 6
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
64
[00175] The Fisher information matrix gives the asymptotic variance of the MLE
(Smith 1984 [13]):
Nõ var (1+026(1+s)
Ca) 1+k 262(1+
Thus
vary = (1+e)2 /N,,,varo-262(1 +k)/N,,, and cov(s,6)=6(1+e)/N,,.
(55)
Substitute into (18), we have
varz(p) ,., 62 (1 + k) (2(s(k))2 + 2s(k)s'(k) + (s'(k))2 (1 + k))l N,,
(56)
[00176] Above is considering only for the estimation of exceedances using
Generalized Pareto Distribution. When we use GPD to estimate the tail part of
our data,
recall from (10),
F(x) = (1-Fõ(u))GE0. (x-u)+Fõ(u),
for x > u . This formula is a tail estimator of the underlying distribution
F(x) for x > u , and
the only additional element that we require is an estimate of F(u), the
probability of the
underlying distribution at the threshold [6]. Taking the empirical estimator
(n - Nõ) / n with
the maximum likelihood estimates of the parameters of the GPD we arrive at the
tail
estimator
F(x)=1- n" C1+sx6u I E
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
(57)
thus the quantile from inverse of (21) is
x=u+6 N (1-p) -1
N,,
Compare with 17 and 20 we have
5 var z(p) - 62 (1 + s)(2(s(s)) 2 + 2s(s)s(s) + (s'(s))2 (1 + ))l Nõ
(58)
where
s(s) _ (a-E -1)/c
s'(E) _ (S (C) + a-E oga) / E
and a = N (1- p) . Finally, according to Hosking & Wallis 1987 [12], for
quantiles with
10 asymptotic confidence level a, the (1 - a) 100% confidence interval is
z-z a varz<x<-x+z a varz
2 2
(59)
where z, -a is the 1- 2 quantile of the standard normal distribution.
z
[00177] D. Confidence interval for CDF using GPD model. To build a confidence
15 band of a ROC curve, we need the confidence band or interval for the
estimated CDF. To
derive the confidence interval we start from the Taylor expansion of the tail
estimate (21).
As a function of c and u, we name
_ 11E
g=g(s,a)=1 n~ C1+sxu U
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
66
(60)
The Taylor expansion around (s, 6) to linear terms is
g(, 6) + gE (, 6)( - ) + ga. (, 6)(6 - 6)
= gE (, 6) + ga. (, 6)6 + g(, 6) - g, (, 6) - ga. (, 6)6
(61)
Therefore the variance of F(x) is given asymptotically by
varF(x) - a2 vary+b2 var6+2abcov(s,6)
(62)
where
N s 1 E 1 ll x-u
a = gE (, 6) = - 1 + -(x - uJ -logj I+ -(x - u)J -
n 6 6 +s2(x-u)
bg6 (, 6)=-Nõ 1 (XU) x-u
n 6 62 + (x - u)
(63)
[00178] Substitute (19) and (27) into (26), we have the estimate of variance
of the
CDF. For CDF with asymptotic confidence level a , the (1- a) 100% confidence
interval is
F-Z,_a,2 varF <F <F+zl_Q,,2 varF
(64)
where z, - 2 is the 1- 2 quantile of the standard normal distribution.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
67
Experiments - Fitting Tails With GPD
[00179] We apply the above method to fit the tails of biometric data. We have
a set of
fingerprint data from Ultra-scan matching system. The matching scores are
separated into
training sets and testing sets. In each category, there are two sets of
matching scores each
from authentic matchings and imposter matchings. Both training and testing
imposter
matching score sets contain 999000 values, and both training and testing
authentic score sets
contain 1000 values.
[00180] Figures 27A and 27B show GPD fit to tails of imposter data and
authentic
data. From the figure we can see that the tail estimates using GPD represented
by red lines
are well fitted with the real data, which are inside the empirical estimate of
the score data in
blue color. The data are also enclosed safely inside a confidence interval.
The thick red bars
are examples of confidence intervals.
[00181] To test the fit of tail data of testing data with tail estimate of GPD
using the
training data, we plot the CDF of testing data on top of the CDF of training
data with GPD
fits to the tails. Figures 28A and 28B depict the test CDFs (in black color)
are matching or
close to the estimates of training CDFs. In Figures 28A and 28B, we can see
that the test
CDFs (in black color) are matching or close to the estimates of training CDFs.
The red bars
again are examples of confidence intervals. The confidence for imposter data
is too small to
see.
[00182] Finally, with CDF estimates available, we can build a ROC for each
pair of
authentic data and imposter data. Each CDF is estimated using an empirical
method for the
main body and GPD for the tail. At each score level there is a confidence
interval calculated.
For the score falling into a tail part, the confidence interval is estimated
using the method in
the last section for GPD. For a score value in main body part, the confidence
interval is
estimated using the parametric method in A. of the last section. Figure 29
shows an ROC
with an example of confidence box. Note that the box is narrow in the
direction of imposter
score due to ample availability of data.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
68
[00183] Conclusions Regarding Use Of Extreme Value Theory: Extreme Value
Theory (EVT) is a theoretically supported method for problems with interest in
tails of
probability distributions. Methods based around assumptions of normal
distributions are
likely to underestimate the tails. Methods based on simulation can only
provide very
imprecise estimates of tail distributions. EVT is the most scientific approach
to an inherently
difficult problem - predicting the probability of a rare event.
[00184] In this report we have introduced in general the theoretical
foundation of EVT.
With further investigation of biometric data from fingerprint matching of
various sources, we
have done an analysis in terms of feasibility of the method being used for the
data - the
matching scores of biometrics. Among the theoretical works, the derivation of
confidence
interval for GPD estimation and building of confidence band for ROC, are most
important
contribution to the field of research. Further, we have specifically
implemented EVT tools in
Matlab so that we are able to conduct all the experiments, which have
confirmed the success
of the application of EVT on biometric problems.
[00185] The theory, the experiment result and the implemented toolkit are
useful not
only for biometric system performance assessment, they are also the foundation
for biometric
fusion.
Algorithm For Estimating A Joint PDF Using A Gaussian Copula Model
[00186] If all the score producing recognition systems that comprise a
biometric
identification system were statistically independent, then it is well known
that the joint pdf is
a product of its marginal densities. It is almost certain that when we use
multiple methods
within one modality (multiple fingerprint matching algorithms and one finger)
or multiple
biometric features of a modality within one method (multiple fingers and one
fingerprint
matching algorithm, or multiple images of the same finger and one fingerprint
matching
algorithm) that the scores will be correlated. It is possible that different
modalities are not
statistically independent. For example, can we be sure that fingerprint
identification scores
are independent of palm print identification scores? Are they even a different
modality?
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
69
[00187] Correlation leads to the "curse of dimensionality." If we cannot rule
out
correlation in an n-dimensional biometric system of "n" recognition systems,
then to have an
accurate representation of the joint pdf, which is required by our optimal
fusion algorithm, we
would have to store an n-dimensional array. Because each dimension can require
a partition
of 1000 bins or more, an "n" of four or more could easily swamp storage
capacity of most
computers.
[00188] Fortunately, an area of mathematical statistics known as copulas
provides an
accurate estimate of the joint pdf by weighting a product of the marginal
densities with an n-
dimensional normal distribution that has the covariance of the correlated
marginals. This
Gaussian copula model is derived in [ 1: Nelsen, Roger B., An Introduction to
Copulas, 2nd
Edition, Springer 2006, ISBN 10-387-28659-4]. Copulas are a relatively new
area of
statistics; as is stated in [1], the word "copula" did not appear in the
Encyclopedia of
Statistical Sciences until 1997 and [l]is essentially the first text on the
subject. The theory
allows us to defeat the "curse" by storing the one-dimensional marginal
densities and an n-
by-n covariance matrix, which transforms storage requirements from products of
dimensions
to sums of dimensions, from billions to thousands.
[00189] A biometric system with "n" recognition systems that produce "n"
scores
s = [s1, s2,... sõ ] for each identification event has both an authentic and
an impostor cdf
("cumulative distribution function") of the form F(s,, s2 5... sõ) with an n-
dimensional joint
density f (sõ s2 , ... s,, ). According to Sklar's Theorem (see [1] and [2:
Duss, Sarat C.,
Nandakumar, Karthik, Jain, Anil K., A Principled Approach to Score Level
Fusion in
Multimodal Biometric Systems, Proceedings of AVBPA, 2005]), we can represent
the density
f as the product of its associated marginals, f,. (si), for i =1, ... , n, and
an n-dimensional
Gaussian copula function with correlation matrix R is given by
CR,n,(x1,x2...x,,) (DRnsn(D_1(x1), -'(x2)... t '(x, )) (65)(1)
[00190] In Equation 65, x, E [0,1] for i = 1,...,n, D is the cdf of the
standard normal
distribution and (D-' is its inverse, and 'R is an n-dimensional Gaussian cdf
whose
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
arguments are the random deviates of standard normal distributions, that is
they have a mean
of zero and a standard deviation of unity. (DR,,.,,, is assumed to have
covariance given by R
and a mean of zero. Hence the diagonal entries of R are unity, and, in
general, the off
diagonal entries are non-zero and measure the correlation between components.
5 [00191] The density of CR is obtained by taking its nth order mixed partial
of
Equation 65:
CRnm \xl, x2 ... x~i ) - a(t R_, \~-1(x1), ~-1(x2 )... -'(xi, ))) _ ~Rnrn (~-1
(x1 ), c-1(x2 )... -I (x,, )) (66) (2)
ax1 ax2 ... axõ j 1 (V(x)/
where 0 is the pdf of the standard normal distribution and OR is the joint pdf
of ' Rnsn and
10 is n-dimensional normal distribution with mean zero and covariance matrix
R. Hence, the
Gaussian copula function can be written in terms of the exponential function:
1 Y exp 1
--zTR lz (3)
_ ( 2i /' R 2 1 1 T -1 ITI ;
CR,,,õ (x) - Z = I2 exp - 2 z R z+ 11,-1 2 (67)
where JRI is the determinant of the matrix R, x = [x1, x2,... x,, 1 is an n-
dimensional column
15 vector (the superscript T indicates transpose), and z = [z1, z2,... z,, is
an n-dimensional
column vector with z; = (D -I (Xi) -
[00192] The score tuple s = IS]) s2 , 's,, ] of an n-dimensional biometric
identification
system is distributed according to the joint pdf f (s1 , s2 , ... Sõ). The
pdff can be either the
authentic pdf, fAõ , or the impostor pdf, fl,,,. The associated marginals are
f. (s;) , for
20 i =1, ... , n, which have cumulative distribution functions F. (s,) .
Sklar's Theorem guarantees the existence of a copula function that constructs
multidimensional joint distributions by coupling them with the one-dimensional
marginals
[1],[2]. In general, the Gaussian copula function in Equation 65 is not that
function, but it
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
71
serves as a good approximation. So, if we set z; = (D-1(F,. (si )) for i = 1,
... , n, then we can
use Equation 67 to estimate the joint density as
f 1 2
fl" )eXp -- 2 zTR 'z+ 2
Z (4)
f (si,s2,...sn);" R (68)
[00193] Equation 68 is the copula model that we use to compute the densities
for the
Neyman-Pearson ratio. That is,
{ 2
ZTRA,Z+~;J 1 Z
i=1/A,,,(si)exp 1
H2 2
(5)
= fAi = R Au (69)
{{''
fh t,A,(si)eXp --zTRnz+~fl, Z2
1 1 2 2
R Im
[00194] The densities fAõ and f1,, are assumed to have been computed in
another
section using non-parametric techniques and Extreme Value Theory. To compute
RAõ and
R1,n we need two sets of scores. Let SAn be a simple random sample of nAõ
authentic score 11 ,L,
tuples. That is, S Aõ = kSA115 õ , . . , s , , where s',, is a column vector
of scores from the "n"
Im
recognition systems. Likewise, let S1in = I,n,sln,...,s Im be a simple random
sample of n11
impostor scores. We compute the covariance matrices for SAõ and S1in with
CAI, = ~j (SAu - SA,l)(SA It - SAr()T and C.. = ~ (Si,n - S1m)(S1m - SLn )T
,where sAõ and s1in are the
i=1 i=1
sample means of SAõ and S,,n respectively. As mentioned above, the diagonal
entries of the
associated R matrices are unity because the copula components are standard
normal
distributions, and the off diagonal entries are the correlation coefficients
in the C matrices
just computed. Recall that the correlation coefficient between the i `i' and
j' element of C,
i # j, is given by pu = 6' = C(i' j) So, an algorithm to compute RA, is:
6i6j C i,l C j, j
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
72
= For i=1: nAõ -1
= For j=i+l : nAõ CA" 0, j)
CAõ 1, l CAõ
= RAu(J,i)-RAu(i,J)
= For i=1: nAt,
= RA,, (i, i) =1
We compute R,,,, in a similar manner.
[00195] The only remaining values to compute in Equation 69 are z; _ -' (J ,.
(s; )) for
each i. There are two values to compute: x; = F,. (s) and then z; = (V(xi ).
We compute
Si
x; = F,. (s;) by numerically computing the integral: x; = J f,. (x)dx. Note
that x; = F,. (s;) is
S.1mi
the probability of obtaining a score less than s; , hence x; E [0,I]. The
value z; = q)-'(xi) is
the random deviate of the standard normal distribution for which there is
probability x; of
drawing a value less than z; , hence x; E (- oo, oo). We numerically solve
zi = c-' (x,) = F2erf -' (2x; -1) , where erf -'(x) is the inverse error
function.
Algorithm For Tail Fitting Using Extreme Value Theory
[00196] The tails of the marginal probability density function (pdf) for each
biometric
are important to stable, accurate performance of a biometric authentication
system. In
general, we assume that the marginal densities are nonparametric, that is, the
forms of the
underlying densities are unknown. Under the general subject area of density
estimation
[Reference 1: Pattern Classification, 2nd Edition, by Richard O. Duda, Peter
E. Hart, and
David G. Stork, published by John Wiley and Sons, Inc.], there are several
well known
nonparametric techniques, such as the Parzen-window and Nearest-Neighbor, for
fitting a pdf
from sample data and for which there is a rigorous demonstration that these
techniques
converge in probability with unlimited samples. Of course the number of
samples is always
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
73
limited. This problem is negligible in the body of the density function
because there is ample
data there, but it is a substantial problem in the tails where we have a
paucity of data.
Because identification and verification systems are almost always concerned
with small
errors, an accurate representation of the tails of biometric densities drives
performance.
[00197] Our invention uses a two-prong approach to modeling a pdf from a given
set
of representative sample data. For the body of the density, where abundant
data is available,
we use well-known non-parametric techniques such as the Parzen-window. In the
tail data, in
the extreme is always sparse and beyond the maximum sample value it is
missing. So, to
estimate the tail we use results from Extreme Value Theory (EVT) (see [1:
Statistical
Modeling of Biometric Systems Using Extreme Value Theory, A USC STTR Project
Report to
the U .S. Army] and [2: An Introduction to Statistical Modeling of Extreme
Values, Stuart
Coles, Springer, ISBN 1852334592]), which provides techniques for predicting
rare events;
that is, events not included in the observed data. Unlike other methods for
modeling tails,
EVT uses rigorous statistical theory in the analysis of residuals to derive a
family of extreme
value distributions, which is known collectively as the generalized extreme
value (GEV)
distribution. The GEV distribution is the limiting distribution for sample
extrema and is
analogous to the normal distribution as the limiting distribution of sample
means as explained
by the central limit theorem.
[00198] As discussed in [1], the member of the GEV family that lends itself
most
readily to the modeling of biometric matching scores is the Generalized Pareto
Distribution
(GPD), given by the following cumulative distribution function (cdf)
if~0,
G~6~x)- 1- 1+6x (70) 1
1-ei6 if ~ #0
where the parameter a > 0 and are determined from the sample data.
[00199] Given a sample of matching scores for a given biometric, we employ the
algorithmic steps explained below to determine the values for 6 and ~ to be
used in
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
74
Equation 70, which will be used to model the tail that represents the rare
event side of the
pdf. In order to more clearly see what it is we are going to model and how we
are going to
model it, consider the densities shown in Figure 30. The red curve is the
frequency histogram
of the raw data for 390,198 impostor match scores from a fingerprint
identification system.
The blue curve is the histogram for 3052 authentic match scores from the same
system.
These numbers are typical sample sizes seen in practice. In general, each
biometric has two
such marginal densities to be modeled, but only one side of each density will
be
approximated using the GPD. We need consider only the red, impostor curve in
Figure 30
for our discussion because treatment of the authentic blue curve follows in
identically the
same manner.
[00200] Looking at the red curve in Figure 30, we see that the tail decaying
to the right
reflects the fact that it is less and less likely that a high matching score
will be observed. As a
result, as we proceed to the right down the score axis we have fewer and fewer
samples, and
at some point depending on the sample size, we have no more sample scores. The
maximum
impostor score observed in our collection was .5697. This, of course, does not
mean that the
maximum score possible is.5697. So how likely is it that we will get a score
of.6 or.65,
etc.? By fitting the right-side tail with a GPD we can answer this question
with a computable
statistical confidence.
[00201] To find the GPD with the best fit to the tail data we proceed as
follows:
[00202] Step 1: Sort the sample scores in ascending order and store in the
ordered set
S.
[00203] Step 2: Let s1 be an ordered sequence of threshold values that
partition S into
body and tail. Let this sequence of threshold be uniformly spaced between st
and s1 .
The values of s1 and st are chosen by visual inspection of the histogram of S
with s,
set at the score value in S above which there is approximately 7% of the tail
data. The value
for sIni may be chosen so that the tail has at least 100 elements. For each
st, we construct
the set of tail values T; =ISES:s>_s,;}.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
[00204] Step 3: In this step, we estimate the values of (Ti and 4i the
parameters of the
GPD, for a given Ti. To do this, we minimize the negative of the log-
likelihood function for
the GPD, which is the negative of the logarithm of the joint density of the
N,., ; scores in the
tail given by
NTi
N,. ln(6i)+ 1 +1 Y ln(l+ Li Si if ~ 0
5 negL((i,ai s)= i=i N ai (71)
~ (2)
N,._ ln(ai)+-~si
ai j=1
[00205] This is a classic minimization problem and there are well-known and
well-
documented numerical techniques available for solving this equation. We use
the Simplex
Search Method as described in [3: Lagarias, J.C., J. A. Reeds, M. H. Wright,
and P. E.
10 Wright, "Convergence Properties of the Nelder-Mead Simplex Method in Low
Dimensions,"
SIAM Journal of Optimization, Vol. 9 Number 1, pp. 112-147, 1998.]
[00206] Step 4: Having estimated the values of ai and 4i, we may now compute a
linear correlation coefficient that tells us how good the fit is to the values
in Ti. To do this
we may use the concept of a QQ plot. A QQ plot is the plot of the quantiles of
one
15 probability distribution versus the quantiles of another distribution. If
the two distributions
are the same, then the plot will be a straight line. In our case, we would
plot the set of sorted
scores in Ti, which we call Q,. , versus the quantiles of the GPD with ai and
4i, which is the
set
N k+1
`GGPD - {G,_il,6 Ti , k =1,..., N (7: (3)
N,.+1
where GZi'6i is the inverse of the cdf given in Equation 70. If the fit is
good, then a point-by-
point plot Q,. versus QGPD will yield a straight line. From the theory of
linear regression, we
can measure the goodness of fit with the linear correlation coefficient given
by
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
76
NT,,Isq-I sjq
rt = 2, GPD /NTs2
-(I s~ FNT,jq -( qy
[00207] Step 5: The G, with the maximum r, is chosen as the model for the tail
of
the pdf.
[00208] Step 6: The complete modeling of the pdf uses the fit from a non-
parametric
technique for scores up to the associated s,, , and for scores above se, , G,
is used.
[00209] To demonstrate the power of EVT, we applied this algorithm to our
"red"
curve example in Figure 30. First, a rough outline of what we did and what we
observed. As
mentioned earlier, there are 380,198 scores in the sample. We randomly
selected 13,500
scores and used this for S to show that using EVT on approximately only 3.5%
of the data
available resulted in an excellent fit to the tail of all the data. In
addition, we show that while
the Parzen window gives a good fit for the body it is unsuitable for the tail.
[00210] In Steps 1 through 4 above, we have the best fit with, st. = .29, N1,
= 72,
r; =.9978, 6; =.0315, and E; =.0042. The QQ plot is shown in Figure 31
revealing an
excellent linear fit. In Figure 32A and 32B it appears that the Parzen window
and GPD
models provide a good fit to both the subset of scores (left-hand plot) and
the complete set of
scores (right-hand plot). However, a closer look at the tails tells the story.
In the left-side of
Figure 33A and 33B, we have zoomed in on the tail section and show the GPD
tail-fit in the
black line, the Parzen window fit in red, and the normalized histogram of the
raw subset data
in black dots. As can be seen, both the Parzen fit and the GPD fit look good
but they have
remarkably different shapes. Both the Parzen fit and the raw data histogram
vanishes above a
score of approximately .48. The histogram of the raw data vanishes because the
maximum
data value in the subset is .4632, and the Parzen fit vanishes because it does
not have a
mathematical mechanism for extrapolating beyond the observed data. Because
extrapolation
is the basis of the GPD, and as you can see, the GPD fit continues on. We
appeal to the
right-side of Figure 33A and 33B where we repeat the plot on the left but
replace the
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
77
histogram of the subset data with the histogram of the complete data of
380,198 points. The
GPD has clearly predicted the behavior of the complete set of sampled score
data.
[00211] United States provisional patent application number 60/643,853
discloses
additional details about the invention and additional embodiments of the
invention. The
disclosure of that patent application is incorporated by this reference.
[00212] Although the present invention has been described with respect to one
or more
particular embodiments, it will be understood that other embodiments of the
present
invention may be made without departing from the spirit and scope of the
present invention..
Hence, the present invention is deemed limited only by the appended claims and
the
reasonable interpretation thereof.
References:
[ 1 ] Duda RO, Hart PE, Stork DG, Pattern Classification, John Wiley & Sons,
Inc., New
York, New York, 2nd edition, 2001, ISBN 0-471-05669-3.
[2] Lindgren BW, Statistical Theory, Macmillan Publishing Co., Inc., New York,
New York,
3rd edition, 1976, ISBN 0-02-370830-1.
[3] Neyman J and Pearson ES, "On the problem of the most efficient tests of
statistical
hypotheses," Philosophical Transactions of the Royal Society of London, Series
A, Vol. 231,
1933, pp. 289-237.
[4] Jain AK, et al, Handbook of Fingerprint Recognition, Springer-Verlag New
York, Inc.,
New York, New York, 2003, ISBN 0-387-95431-7
[5] Jain AK, Prabhakar S, "Decision-level Fusion in Biometric Verification",
2002.
[6] E. P. Rood and A. K. Jain, "Biometric research agenda," in Report of the
NSF Workshop,
vol. 16, April 30-May 2 2003, Morgantown, West Virginia, pp. 38-47.
[7] S. J. Roberts, "Extreme value statistics for novelty detection in
biomedical signal
processing," in IEEE Proceedings in Science, Technology and Measurement, vol.
147, 2000,
pp. 363-367.
[8] B. W. Silverman, Density Estimation for Statistics and Data Analysis.
Chapman and
Hall, 1986.
[9] S. J. Roberts, "Novelty detection using extreme value statistics, ice
proc. on vision,"
Image and Signal Processing, vol. 146, no. 3, pp. 124-129, 1999.
CA 02701935 2010-03-08
WO 2009/032020 PCT/US2007/082130
78
[10] -, "Extreme value statistics for novelty detection in biomedical signal
processing," in
Proc. 1st International Conference on Advances in Medical Signal and
Information
Processing, 2002, pp. 166-172.
[11] A. J. McNeil, "Extreme value theory for risk managers," in Internal
Modeling and CAD
H. RISK Books, 1999.
[ 12] -, "Estimating the tails of loss severity distributions using extreme
value theory."
ASTIN Bulletin, 1997, vol. 27.
[13] H. Sohn, D. W. Allen, K. Worden, and C. R. Farrar, "Structural damage
classification
using extreme value statistics," in ASME Journal of Dynamic Systems,
Measurement, and
Control, vol. 127, no. 1, pp. 125-132.
[14] M. Golfarelli, D. Maio, and D. Maltoni, "On the error-reject trade-off in
biometric
verification systems," IEEE Trans. Pattern Analysis and Machine Intelligence,
vol. 19, no. 7,
pp. 786-796, 1997.
[15] R. M. Bolle, N. K. Ratha, and S. Pankanti, "Error analysis of pattern
recognition
systems - the subsets bootstrap," Computer Vision and Image Understanding, no.
93, pp. 1-
33, 2004.
[16] S. C. Dass, Y. Zhu, and A. K. Jain, "Validating a biometric
authentication system:
Sample size requirements," Technical Report MSU-CSE-05-23, Computer Science
and
Engineering, Michigan State University, East Lansing, Michigan, 2005.
[ 17] J. R. M. Hosking and J. R. Wallis, "Parameter and quantile estimation
for the
generalized pareto distribution," Technometrics, vol. 29, pp. 339-349, 1987.
[18] R. Smith, "Threshold methods for sample extremes," in Statistical
Extremes and
Applications, T. de Oliveria, Ed. Dordrecht:D. Reidel, 1984, pp. 621-638.