Note: Descriptions are shown in the official language in which they were submitted.
CA 02706673 2010-06-14
-1-
TITLE OF THE INVENTION
Device and System for Practical Entropy Collection from Dice
FIELD OF THE INVENTION
[0001] The invention relates to entropy collection, or secret truly random
data
generation, for digital electronic systems preforming logic functions with
random
characteristics, such as gaming or gambling machines, information security
systems using
locally generated secret random data for cryptographic key material, and the
like. The
invention materializes as a variation of the classical six-faced cubic die,
and enhancements in
digital systems, both suited to this purpose of entropy collection. The
invention is only
remotely related to the direct use of dice for games or gambling.
BACKGROUND OF THE INVENTION
[0002] It is hard to provide trustworthy and reliable means of generating
secret random
binary data with good statistical distribution for use in a computer system.
Generally, a
reliable system has a predictable behavior, and the very notion of randomness
is suggesting
some erratic behavior. Indeed, deterministic pseudo-random sequences are often
preferred
for computer simulations because a simulation run may be reproduced in the
event of a
software bug with a given sequence of pseudo-randomly generated events or
observations.
Other types of systems nonetheless require the closest possible equivalent to
secret truly
random binary data. Two broad categories of systems are relevant to the
present invention:
gaming, gambling, or lottery machines, and digital systems dedicated to IT
security functions
with a high security level. The inventor refers to systems for which the
operational rules might
specify a complete system halt in the case of secret random source malfunction
(instead of a
degraded operational mode that might turn a fair gaming machine into an unfair
one). While
mundane IT security applications in general purpose computer systems are
typically not
operated this way, the present inventor brings the present disclosure within a
larger effort to
use common computer components and the general purpose Linux operating system
for
cryptographic functions traditionally implemented in dedicated hardware
security modules.
[0003] The typical strategy for providing a secret random source is a
combination of
digital sampling of an unpredictable phenomenon, some processing of raw sample
data
usually intended to output binary digits with a 50% probability of either
value, and some
pseudo-random number generation algorithms. Diversified unpredictable
phenomenon has
been used, from fundamental properties of atomic particles to the precise
timing of user
keystrokes on a computer keyboard. Electromagnetic or acoustic noise is
sometimes used.
As an operating system kernel switches the CPU resources among competing
processes,
some observations of non-deterministic event sequences becomes available as a
contribution
to the random source function. To some extent, the unpredictability of the
very sampling
operation (e.g. an instrument sensor precision limit) may contribute to the
variability in the raw
samples. In most cases, the random data acquisition rate is orders of
magnitude slower than
the typical data processing or transmission pace of modern computers.
CA 02706673 2010-06-14
-2-
[0004] In these prior art arrangements, the system is autonomous in truly
random data
acquisition (no operator intervention). This makes it convenient for system
application
designers to rely on the random data acquisition on a regular basis during
system operations.
It is however very difficult to detect malfunctions in the secret random
source, either with a
generic statistical test (notably the acquisition rate is too slow) or with a
specific self-test in the
unpredictable phenomenon sampling process. Sometimes, a gaming system fraud
agent or
an IT security hacker might attempt to freeze or inhibit the unpredictable
phenomenon such
that the system operations quietly turn more deterministic to the fraud agent
or hacker
advantage.
[0005] The prior art makes it difficult for a given unpredictable phenomenon
sampling
arrangements to remain applicable and available within reasonable costs
through the
technological evolution of electronics and digital systems. The system bus
architecture might
become obsolete so that a sampling peripheral is no longer supported.
Electronic
components that are not used in their exact intended function may be modified
by the
component manufacturer in unexpected ways. Some assumptions in a system
operating
environment may no longer apply to new digital system paradigms (e.g. solid
state mass
storage or processor virtualization).
[0006] For critical systems, a need for third party certification and/or audit
arises (i.e.
independent from the vendor and operating entity). In this context,
certification applies to the
system design and manufacturing, and auditing applies to the system
operations. In both
cases, the prior art reliance on diversified unpredictable phenomenon sampling
may make the
certification or audit quite challenging. Without a universally accepted truly
random data
acquisition arrangement, the statistical validity of a custom approach has to
be demonstrated
with a heightened level of scrutiny, often requiring extensive scientific
knowledge. With the
system vendor employees having an intimate understanding of the exclusive
implementation
details, the certification personnel should even watch for a hidden trap-door
in the system.
[0007] There is thus a need for enhanced arrangements to provide a secret
random
source to digital systems for to circumvent the prior art deficiencies
associated with the
autonomous sampling of selected unpredictable phenomenon.
BRIEF DESCRIPTION OF THE INVENTION
[0008] The invention revisits the prior art idea of a permanent autonomous
secret truly
random source in the gaming, gambling, or IT security system. A properly
seeded pseudo-
random number generator (PRNG) can provide the required secret random source,
provided
a) it is indeed initially seeded from a secret truly random source, b) the
PRNG state is kept
secret through the system operational life cycle, and c) the PRNG is
cryptographically strong
and has a large period. A security specialist comfortable with the prior art
may be rebutted by
the criticalness of PRNG state protection, but it comes with the benefit of
hardware system
design simplification.
[0009] The PRNG seeding occurs through deterministic data collection
representative
of the random outcome drawn from a set of dice having been shuffled. The
outcome data
CA 02706673 2010-06-14
-3-
collection is deterministic in the sense that errors in the data collection
are avoided as much
as possible because no statistical properties might be relied upon from data
collection error
patterns. In essence, operations of both a game and the present invention
comprise four
phases: 1) dice shuffling, 2) putting dice to rest in a conventional position,
3) sensing the
outcome, and 4) acting on the outcome. The present invention pertains to the
set of dice and
the system used in these operations. Both the inventive set of dice and the
inventive system
enhancements have characteristics matching the dice handling (phases 1 and 2)
and the
outcome collection (phase 3) rules.
[0010] The invention may be useful for seeding PRNG in systems where PRNG
state
secrecy is not important, e.g. in stochastic computer simulations. The
invention may also be
useful in applications where truly random data can be used without the
randomness
expansion of a PRNG, such as the direct generation of a long-term private key
for discrete
logarithm public key cryptosystems (those types of long-term keys are not
subject to number-
theoretic restrictions).
[0011] Thus, the present invention uses the basic operation of rolling a cubic
die as an
unpredictable phenomenon. Flipping a coin or rolling a die other than a cubic
one would
equally fit. This means that the system is not autonomous in truly random data
collection, i.e.
a human operator intervention is needed. Thus, when a system is initially put
into production,
its PRNG state is virgin and must be initialized. A single occurrence operator
session
happens at this point, during which the operator handles the inventive dice
with the procedure
to be described below, and the secret data drawn from the dice handling is fed
into the
system according to the detailed arrangements described below. The secret PRNG
state is
thereafter initialized and preserved through system shutdowns and reboots
(e.g. like in the
Linux kernel) with the required secrecy protections. As should be obvious to
an expert in
cryptographic systems, some exceptional circumstances may trigger a
requirement for a
rehearsal of the operator session, i.e. if the PRNG state secrecy is
jeopardized following
some security incidents.
[0012] The invention provides many benefits from the fact that the faces of
the
inventive dice are labeled with bar codes instead of the numbers 1 to 6.
Operator efficiency is
one such benefit. But an unusual benefit arising from the bar code technology
in the present
invention preferred mode is data secrecy: the bar code visible on each die
face is devoid of a
human readable counterpart of the bar code contents (i.e. no numbers or
letters appear below
the bar code). This is against the recommended practice for bar code
application design as it
prevents manual keyboard entry when a bar code is dirty or damaged and can not
be input
with a bar code scanner. It also means that special care has to be taken for
bar code
scanning errors. The procedure for inventive dice handling is adapted
accordingly.
[0013] The preferred mode is a set of 36 different dice, giving 216 (216=36*6)
faces
each having a different encoded bar code indication. The system software logic
is based on
the knowledge of these 216 bar code indications applicable to die 1 face 1,
die 1 face 2, and
so on up to die 36 face 6. This allows to cope with errors caused by duplicate
or unintended
scan.
CA 02706673 2010-06-14
-4-
[0014] Duplicate scans occur when the same bar code label is scanned twice in
succession. Bar code scanner devices come with firmware-based duplicate
rejection logic,
but if a single die was used in the invention, this would interfere with the
intentional capture of
two identical random draw outcomes. E.g. with the inventive set of dice, two 5
in a row might
be scanned as die 17 face 5 followed by die 3 face 5, which are not duplicates
for the scanner
firmware logic.
[0015] Unintended scans (for the present invention bar code application) are
those for a
die face other than the drawn outcome: if the scanner is positioned such that
two or three
faces are in the scanner field of view, any of these might be scanned
depending on the
scanner capabilities. It is usually seen beneficial to data entry efficiency
when a scanner
decodes a bar code positioned at various angles or orientation (and distance
as well). When a
die stands free on a flat surface, any of the 4 faced adjacent to the one at
the top might cause
an unintended scan. With the 216 distinct face indications, it is possible to
detect an
unintended scan. E.g. a scan of die 27 face 2 followed by die 27 face 4
suggests an
unintended scan. Other invention characteristics allow better handling of
seemingly
unintended scans in the digital system software logic.
[0016] The preferred mode of the invention uses a simple bidirectional
scanner, using
the CCD linear array technology instead of a more powerful omni-directional
models. For
instance the Opticon OPT-6125 model has been found useful (the Opticon model
number has
been changed to LGP-6125 for this device). This limited scan orientation
matches the bar
code label orientation on the inventive dice: for any two adjacent faces of
any die, the two
respective labels appear perpendicular when looking at the two faces at a 45
degrees angle
of view. The dice handling and outcome collection rules make use of the linear
scanning
property and the orthogonal polarization of bar code labels in adjacent die
faces. If a scanner
device could report by a flag whether the scanned label was read left-to-right
or right-to-left
(such a capability would require a small custom bar code reader firmware
modification), the
present invention could make good use of this additional data. The preferred
mode uses off-
the-shelf bar code reader equipment for ease of procurement.
[0017] If a die stands free on a flat surface, 4 faces may trigger an
unintended scan. If
one of these faces is aligned to a vertical surface (e.g. the side of a box),
it disappears from a
scanner device field of view. Moreover, if two other dice are positioned on
each side of the
first one and also rest aligned to the vertical surface, two other faces of
the first die disappear
from the scanner device field of view. This leaves 2 faces available to the
scanner, and they
are orthogonal.
[0018] With the recommended dice handling procedure, the dice are shuffled and
then
set to rest in a single line along a small vertical wall, next to each other.
With 19 millimeters
dice, what was found convenient is a 30 inches long board with an L shaped
section and
having 6 and 1 inches wide perpendicular surfaces. With such a single
contiguous alignment
of dice in the angle of an L-shaped board, each die offers two faces to the
scanner field of
view, except for two dice at each end of the alignment which offer an extra
face at each end.
[0019] From the above conventions about how the inventive set of dice should
rest
CA 02706673 2010-06-14
-5-
before the outcome collection phase is undertaken, outcome collection rules
may be specified
that allow the digital system software logic to avoid unintended scans or
other errors and
collect all relevant discrete information available in the random outcome. The
details are
disclosed further below. Thus, the inventive digital system enhancements allow
the collection
of truly random data with good statistical properties with a random process
(dice shuffling)
which is easily certifiable or auditable, and immune to technology
obsolescence associated
with custom electronics. This is achieved while protecting the secrecy of the
truly random data
as is needed for PRNG seeding in IT security and gaming, gambling, and lottery
applications.
[0020] A few observations may be made about human factors in the unusual data
entry
assignment implied by the present invention.
[0021] The secrecy of truly random data rests in a normal person's inability
to visually
decode bar code labels and memorize the discrete outcome so observed. It could
be that very
unusual personalities with exceptional attention to details are able to decode
and memorize
the discrete outcomes. If such an individual is allowed at all to work with
security critical
systems, some attention should be paid to their ability to cheat. Still, the
invention may be
implemented such that this person's mental challenge is greater by a fixed
permutation of
dice face labels, so that the visual decoding of labels would not easily
translate into dice and
face numbers.
[0022] The true randomness depends on sufficient shuffling applied to the set
of dice,
but this cannot be readily verified by the system software. Thus, the
shuffling operation
effectiveness may be ascertained only through some form of operator
supervision, auditing,
or dual control (as is known in the field of manual cryptographic key
management).
[0023] It may be noted that the data entry assignment is a dice handling
procedure,
which could be entertaining if it was part of a game. Since the exact outcome
has no
consequence for the operator, the procedure performance becomes simply boring,
devoid of
any meaningful feedback or intrinsic rewards. This suggests to bring back some
operator
feedback which would otherwise be useless. Notably, the detailed software
logic may allow
some trivial data entry error detection and correction, from which an operator
compliance
mark could be established and displayed as operator feedback.
BRIEF DESCRIPTION OF THE DRAWINGS
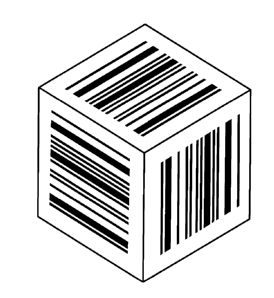
[0024] The Figure 1 is a simple perspective view of a die in the inventive set
of dice.
[0025] The Figure 2 is a flat representation of the 6 faces of an inventive
die where the
bar code labels has been replaced by legible indications of each face number
and the
respective bar code label orientation.
[0026] The Figure 3 shows the inventive set of dice aligned according to the
dice
handling rules that facilitate random shuffling outcome collection by the
inventive digital
system enhancements.
CA 02706673 2010-06-14
-6-
[0027] The Figure 4 shows a complete example of a dice shuffling outcome where
the
bar code labels on each die has been replaced by legible indications of die
face numbers for
two adjacent faces, the two respective bar code label orientations, and the
die number.
[0028] The Figure 5 shows the logical arrangement of an engraving process
proof for
the convenient manufacture of the inventive dice set.
[0029] The Figures 6a) and 6b), when mated along the V indentations at the
bottom of
6a) and the top of 6b), show an actual engraving process proof logically
depicted in figure 5.
DETAILED DESCRIPTION OF THE INVENTION
[0030] Each die in the inventive set looks like the figure 1. Even if the dice
are uniquely
labeled within the set, they are difficult to distinguish without close
examination by someone
trained in the specific bar code symbology. This provides some assurance of
unbiased
handling and secrecy of dice shuffling outcome.
[0031] The Codabar bar code symbology is used in the preferred mode because it
allows short bar code labels made of a single start element (selected among
the 4 defined in
the Codabar symbology), a single data symbol (selected among 16 defined in the
Codabar
symbology), no checksum element, and a single stop element (selected among the
4 defined
in the codabar symbology). No restriction apply to these short bar code
labels, so that 256
different labels would allow up to 42 dice in the set (6 different labels are
required for the 6
faces of each die). Sixteen millimeter dice has been found large enough for
these bar code
labels, but larger dice may be used to ensure improved scanner device
performance with
slightly larger bars (i.e. larger than the 7.5 mils narrow bar thickness that
was used).
[0032] Conventional cubic dice are labeled such that the outcome of opposite
faces
add up to 7. In the preferred mode dice, any two adjacent faces on a die have
their bar code
labels perpendicular to each other. The preferred mode outcome sensing
procedure relies on
this convention. Two further die labeling conventions are specified in here
merely because
they make the design details unambiguous (they are also useful for what seems
the best
mode of manufacturing the inventive set of dice). Firstly, one of the angles
of view showing
three die faces must show the faces 1, 2, and 3 appearing in a clockwise
direction around the
tip closest to the observer (as a consequence of these conventions, the angle
of view
showing the three faces 4, 5, and 6 shows them also in a clockwise direction).
Secondly, the
direction of reading a face indication from left to right must point from face
1 to face 2, from
face 2 to face 3, from face 3 to face 1, from face 6 to face 5, from face 5 to
face 4, and from
face 4 to face 6.
[0033] The resulting die layout is depicted in Figure 2 in which the 6 faces
are flattened
as if the die was made from a foldable cardboard material. Also, the bar code
labels of an
actual die has been replaced by legible indications of each face number and
the respective
bar code label orientation.
[0034] The inventive set of dice is intended to be shuffled and the set to
rest so that the
CA 02706673 2010-06-14
-7-
random draw discrete outcome may be input to the digital system and converted
to useful
secret random data with the inventive programmatic means. The dice handling
procedure
includes a random alignment of the dice such that two adjacent faces of each
die are
available to a bar code scanner. This is shown in figure 3 where an L shaped
board (100)
offers a surface for setting the dice to rest and aligning them in a single
alignment (101). The
two ends of the alignment (102, 103) may be ignored in the outcome collection
rule, or a scan
of their bar code labels might be specified as an additional data validation
step. The discrete
outcome to be collected is fully contained in the row of bar code labels
visible on top of the
alignment (101) plus the row of orthogonal bar code labels visible in front of
the alignment
(101).
[0035] The figure 4 is an example of a complete discrete outcome to be
collected, with
the actual bar code labels replaced by legible indications of each face number
and the
respective bar code label orientation. There are thus two rows of orthogonal
bar codes. Also
shown in figure 4 is the die number for each of the 36 positions in the
alignment rows.
[0036] The characterization of the discrete outcome information available to
the
outcome sensing phase is a simple counting problem in combinational
mathematics. With
every die in a linear sequence having its own number, a permutation of 36
objects is present.
Moreover, each die is aligned, having exactly one ridge positioned at the
intersection of its
two visible faces (there are 12 ridges at the intersection of the 6 die
faces). Finally, there are
two possible orientations for the aligned or winning ridge, e.g. if the ridge
between faces 1
and 5 is the winning one, the outcome may be further characterized from which
of 1-5 (figure
4, 202) or 5-1 (figure 4, 202) is visible from the top-front observation
positions pair. Overall,
each independent die position is selected among 24 possibilities of equal
probability. Another
way to come to this count of 24 positions is that if a given face (among 6) is
visible from the
top observation position, there are exactly 4 independent choices for the
front observation
position. Overall, the available entropy is 303.15 bits (i.e. the base 2
logarithm of 36 factorial
times 24 raised to the power 36) instead of 93.06 bits for the simple outcome
sensing
approach (i.e. the base 2 logarithm of 6 raised to the power 36).
[0037] With these conventions, the preferred outcome sensing procedure using a
bidirectional hand held bar code scanner may be described. In this context,
the scanner
movement may be perpendicular to the dice alignment or parallel to it. Since
the two adjacent
faces visible for any die in the alignment have perpendicular bar code
orientations, one of
them will be scanned with a perpendicular scanner movement and the other one
will be
scanned with a parallel scanner movement.
[0038] The first step in the preferred outcome sensing procedure is a
perpendicular
scanner movement varied laterally (or rolled) (between the top and front
observation
positions) to capture one bar code label (the one easily scanned with a
perpendicular
movement) from each die in the alignment, in sequence. This provides the
system with the
ordering of dice (the permutation outcome) in the alignment, plus a first
indication of the
independent outcome for each die. With the example data in figure 4 and a left
to right
scanner movement along the dice alignment, the following sequence will be
scanned (each
die is indicated with a bracketed pair of integers, respectively the die and
face number).
CA 02706673 2010-06-14
-8-
[0039] This first sequence is [30,2] [21,3] [25,3] [26,2] [16,3] [20,5] [17,4]
[19,6] [24,5]
[8,1] [12,1] [5,2] [23,6] [35,6] [4,3] [2,3] [31,3] [18,4] [36,6] [34,6]
[27,2] [10,2] [28,4] [14,9]
[29,2] [33,3] [6,3] [11,1] [22,4] [3,4] [13,6] [32,1] [9,2] [1,3] [7,3]
[15,1].
[0040] The second step is another perpendicular movement in the same direction
along
the dice alignment, but this time limited to a single observation position for
the scanner field of
view, e.g. the top one. At this step, statistically one half of the dice in
the alignment will be
captured. Again with the example data in figure 4, the following sequence will
be scanned.
[0041] This second sequence is [30,2] [12,1] [4,3] [31,3] [34,6] [28,4] [29,2]
[33,3] [3,4]
[13,6] [32,1] [15,1].
[0042] The third step is a parallel scanner movement still in the same
direction along
the dice alignment, and limited to the same single observation position for
the scanner field of
view (e.g. the top one). Normally, those dice that were not captured in the
previous step will
be captured now, giving a complete indication of dice positions for those.
Again with the
example data in figure 4, the following sequence will be scanned.
[0043] This third sequence is [21,6] [25,1] [26,3] [16,6] [20,4] [17,1] [19,2]
[24,4] [8,5]
[5,3] [23,5] [35,5] [2,6] [18,6] [36,5] [27,3] [10,3] [14,2] [6,1] [11,2]
[22,6] [9,3] [1,6] [7,6].
[0044] The fourth and last step is a second parallel scanner movement still in
the same
direction along the dice alignment, with the other other observation position
for the scanner
field of view. This completes the dice position information for the dice
missing from the third
step (e.g the front one shown as the bottom row in the figure 4). Again with
the example data
in figure 4, the following sequence will be scanned.
[0045] This fourth sequence is [30,4] [12,5] [4,1] [31,6] [34,2] [28,1] [29,4]
[33,1] [3,6]
[13,5] [32,2] [15,2].
[0046] For the parallel scanner movements, because the bar code labels are are
short
and close to each other, it is useful to blind the scanner for a portion of
its field of view. e.g.
with a finger of the hand that holds the scanner device.
[0047] The above outcome sensing procedure implies data validation rules for
the
system software that converts scanned bar code data input through a system
port into
validated truly random data. The sequences indicated above are those expected
in the
absence of errors induced by the scanning process or inadequate operator
compliance. Some
errors may be ignored, like duplicate scans in succession. Other errors may be
fixed, such as
a missing scan from the second sequence for a die number that is present in
both the first
and fourth ones, with coherent values (in fact, the second sequence would not
be useful if the
scanning process and operator compliance were perfect). Other errors may
induce the
system software to obliterate data elements from the discrete outcome. If a
die number is
absent from both the third and fourth sequences, an independent die result
(out of 6
possibilities) may still be used from the first sequence value (instead of an
independent die
result out of 24 possibilities). If a die number is totally absent or reported
incoherently, it may
CA 02706673 2010-06-14
-9-
be obliterated both as an independent result and as an element in the random
permutation.
[0048] The inventive digital system enhancements are functions typically
implemented
in software, or programmatic means. The software has to process the input
stream of bar
code values and reconstruct a validated internal data representation of what
appears in figure
4. For instance, the start of the second sequence may be detected if all (or
nearly all) die
numbers has been scanned (i.e. a complete first sequence) and a die number
detected early
in the first sequence is detected again. Bar code scanned commands (e.g. an
"end of
sequence" indication) could be interspersed in the input stream for an easier
software function
implementation, but too much reliance on such command scans may reduce
operator
efficiency. At a minimum, a "restart sequence" command would be useful because
the
operator is deemed at some point to become conscious of an unrecoverable
error. The
"restart command" may be a short sequence of dice face scans that is
impossible in the
normal outcome collection procedure and very unlikely as an unintentional
error (e.g. coming
back to the same dice face label three times within 5 to 8 consecutive scans
may indicate the
operator willingness to abandon the current outcome collection sequence and
start anew).
[0049] Once a validated internal representation exists for the discrete
outcome as
scanned, the next logical step is to convert it into an index in an implicit
enumeration of the
theoretical set of possible outcomes. Stated differently, a discrete outcome
turns into an
integer from 0 to N-1, where N=2"142*3"53*5"8*7"5*11"3*13"2*17"2*19*23*29*31
is the
exact factorization of 36 factorial times 24 raised to the power 36. From this
random index
expressed in a binary representation, only the least significant 142 bits are
guaranteed to be
perfectly fair. This introduce a difficulty in the system software if a
theoretical reasoning is
required to certify that every truly random bit is fair.
[0050] Here is an explanation of a reasonable solution, using smaller numbers.
If we
take the discrete outcome of a French roulette as a source of true randomness,
we get an
index between 0 and N-1=36 for N=37. The base 2 logarithm of 37 is about 5.21,
so this is the
theoretical maximum average number of fair bits we can collect from repeated
roulette draws.
The simplest fairness assurance heuristic is to collect 5 bits if the outcome
is between 0 and
31 inclusive, and none otherwise. This gives an average of 4.32 bits per draw.
A first
refinement is possible from the fair distribution of outcomes in the range 32
to 36 inclusive
when the draw is rejected: if the draw is between 32 and 35 inclusive, we may
collect two bits
from the drawn number minus 32 in the range from 0 to 3. We gained 0.22 bits
on average,
with an overall efficiency of about 87%. We must collect no bit for an outcome
of 36. A second
refinement is that the random roulette outcomes may be lumped in groups of 5
(with an
efficiency over 99%, it is the most efficient choice with the limitation of 32
bits arithmetic), so
that the grouped outcome is between 0 and N-1 with
N=37A5=69343975=2A26+2A21+2A17+2"12+2"11+2"9+2"7+2"6+2A4+2"2+1 (the latter
reflects the binary expansion of N). From the exponents 26, 21, 17, 12, ... in
the binary
expansion of N and the random index value, we get the following heuristic: if
the index is
below 2"26, take the least significant 26 bits as fair random bits, else if
the index is below
2"26+2"21, take the least significant 21 bits, else if the index is below
2"26+2"21+2"17, take
take the 17 least significant bits, and so on. These indications should allow
a skilled software
designer, engineer, or programmer, to avoid the pitfall of validating a truly
random outcome
and then converting it into a binary stream without assurance of good
statistical properties.
CA 02706673 2010-06-14
-10-
[0051] Turning back to the discrete outcome counting that would be expected
from the
present invention with dice and face identification in the raw data, the
outcome index value
can be expressed as a mixed radix number (reminder: 93784 seconds is zero
weeks 1 day 2
hours 3 minutes and 4 seconds in the everyday radix number base 7,24,60,60
that we use to
count time) with number base elements selected from the factorization
indicated above. This
formulation may remain in the abstract: it merely states that every possible
outcome element
is taken into account in a number representation which is statistically fair
(every possible digit
in each position of the index representation has the same probability). In the
actual software,
the random permutation may be handled as a series of actual outcomes indices
out of
respectively 36, 35, 34, 33, up to 2 possibilities, and the independent dice
adjacent face
indications may be handled as outcome indices out of 24 possibilities. The
preceding heuristic
for the binary fairness in the software conversion would be applied either to
the digits in the
combined index represented as a mixed radix number, or to these elementary
outcome
indices in the actual software suggestion.
[0052] The required software may be developed by a skilled software designer,
engineer, or programmer without further inventive activities. Such software
would be much
influenced by the typical constraints imposed by the operating system,
computer language in
use, bar code input interface details, system or application interface for the
output secret
binary random data, source code conventions, and the like. Once tested and
verified to
perform the intended conversion from bar code scan data to truly random secret
binary data
for system or application use, the software may be included in a system
release to provide the
enhanced inventive system.
[0053] The inventive set of dice may conveniently be manufactured in lots of 6
sets.
With the preferred count of 36 dice per set, a slab of 216 blank dice arranged
in an 18 by 12
rectangle and deposited on a tray may be engraved at once by laser etching or
other process.
As shown in figure 5, the faces 1 to 6 for each die in the set may be engraved
with a single
run of the engraving process. The figure 5 shows the slab divided in 6
sections for the 6
faces. Each die is represented in the figure 5 with the face and die number
(respectively with
the large and small font numbers), and the bar code label orientation. The
logical
arrangement turns into a bar code label arrangement shown in the figures 6a)
and 6b) which,
when mated along the V indentations at the bottom of 6a) and the top of 6b),
show an actual
engraving process proof for the disclosed manufacturing operations.
[0054] Once a slab of 216 blank dice has been engraved on one face, an
employee
rotates the dice sets, from 1 to 2, from 2 to 3, from 3 to 6, from 6 to 5,
from 5 to 4, and from 4
to 1. In doing so, the employee maintains the die number correspondence one-to-
one and
pivots the die 90 degrees such that each die is deposited to receive another
engraved bar
code label for another face. The orientations in figure 5 are such that a die
movement by 1
position (i.e. from 1 to 2, from 2 to 3, from 6 to 5, and from 5 to 4) implies
a pivot indicated by
the arrow (the adjacent blank face pointed to by the arrow is brought on top),
and conversely
a die movement by 3 positions (from 3 to 6 and from 4 to 1) implies a pivot
against the
direction of the arrow (the adjacent blank face in the opposite direction of
the arrow is brought
on top). This can be tried with six mock-up dice made from cut and taped
copies of figure 2.
[0055] After five dice rotation operations each followed by an engraving of
the bar code
CA 02706673 2010-06-14
- 11 -
labels corresponding to figure 5, the 216 dice will be completely engraved on
their 6 faces,
and the 6 sets will be complete.
[0056] Although the invention has been disclosed in the preferred mode, it
should be
obvious that many variations are possible while remaining within the bounds of
the inventive
concept, which is set by the claims. The outcome rules, which includes the
rules for 1) dice
shuffling, 2) putting dice to rest in a conventional position, and 3) sensing
the discrete
outcome, may be as simple as the centuries old usage rule for cubic dice: roll
them so that
they rest on an horizontal surface, and observe which face of each die appears
on top. The
number of dice in the set may be varied from the preferred mode of 36.
Different bar code
symbologies or conventions may be used, e.g. to allow a much larger set of die
face
indications. Dice other than cubic ones may be used. Thoroughly obfuscated bar
codes may
be used with the black-on-black technique where two different black inks are
used for the
background and the bars, respectively a vegetable die black ink for the
background and an
ink based on carbon pigments for the bars, and an infrared bar code scanner is
used (the
former ink type is often transparent to infrared wavelengths).