Note: Descriptions are shown in the official language in which they were submitted.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
IMPLEMENTING A STAND-UP SEQUENCE USING
A LOWER-EXTREMITY PROSTHESIS OR ORTHOSIS
RELATED APPLICATIONS
[001] This application claims the benefit of US Provisional Application
61/238,305,
filed August 31, 2009.
TECHNICAL FIELD
[002] This invention relates generally to lower-extremity prosthetic, orthotic
and
exoskeleton apparatus, components thereof, and methods for controlling the
same.
BACKGROUND
[003] Over 100,000 people in the United States lose their feet through
amputation
every year. Many hundreds of thousands suffer this debilitating loss world-
wide.
Additionally, there are 700,000 individuals that survive a stroke each year in
the United
States often causing a variety of lower limb pathologies that constrain
ambulation. Until
recently, lower-extremity prosthetic and orthotic systems have employed
predominantly
passive or low-power mechanisms incapable of delivering the non-conservative
positive work
on each stride that the body needs to achieve an economical walking motion
even on flat
terrain-let alone on uneven surfaces such as stairs and steps.
[004] It is helpful to understand the normal biomechanics associated with a
gait cycle
of a subject to appreciate the requirements of lower-extremity prosthetic,
orthotic and
exoskeleton apparatus. Specifically, the function of human ankle under
sagittal plane rotation
is described below for different locomotor conditions.
[005] The mechanical characteristics of conventional passive ankle/foot
prostheses
("AFPs") like the Ossur Flex-Foot remain essentially constant throughout the
life of the
device. U. S. Patent Published Application No. US 2006/0249315 ("the `315
application")
represented a significant advance over those conventional AFPs. The `315
application, the
entire contents of which are hereby incorporated by reference in its entirety,
recognized that
performance can be improved by dividing the walking cycle into five phases,
and by
optimizing the mechanical characteristics of the device independently for each
of those five
phases.
[006] FIG. IA is a schematic illustration of the different phases of a
subject's gait
cycle over level ground. The gait cycle is typically defined as beginning with
the heel strike
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
2
of one foot and ending at the next heel strike of the same foot. The gait
cycle is broken down
into two phases: the stance phase (about 60% of the gait cycle) and the
subsequent swing
phase (about 40% of the gait cycle). The swing phase represents the portion of
the gait cycle
when the foot is off the ground. The stance phase begins at heel-strike when
the heel touches
the floor and ends at toe-off when the same foot rises from the ground
surface. The stance
phase is separated into three sub-phases: Controlled Plantarflexion (CP),
Controlled
Dorsiflexion (CD), and Powered Plantarflexion (PP).
[007] CP begins at heel-strike illustrated at 102 and ends at foot-flat at
106. CP
describes the process by which the heel and forefoot initially make contact
with the ground.
Researchers have shown that that CP ankle joint behavior is consistent with a
linear spring
response where joint torque is proportional to the displacement of the joint
in relation to an
equilibrium position of the joint position. The spring behavior is, however,
variable; joint
stiffness is continuously modulated by the body from step to step within the
three sub-phases
of stance and late swing state.
[008] After the CP period, the CD phase continues until the ankle reaches a
state of
maximum dorsiflexion and begins powered plantarflexion PP as illustrated at
110. Ankle
torque versus position during the CD period is described as a nonlinear spring
where stiffness
increases with increasing ankle position. The ankle stores the elastic energy
during CD
which is necessary to propel the body upwards and forwards during the PP
phase.
[009] The PP phase begins after CD and ends at the instant of toe-off
illustrated at
114. During PP, the ankle applies torque in accordance with a reflex response
that catapults
the body upward and forward. The catapult energy is then released along with
the spring
energy stored during the CD phase to achieve the high plantarflexion power
during late
stance. This catapult behavior is necessary because the work generated during
PP is more
than the negative work absorbed during the CP and CD phases for moderate to
fast walking
speeds. The foot is lifted off the ground during the swing phase, from toe-off
at 114 until the
next heel strike at 118.
[0010] Because the kinematic and kinetic patterns at the ankle during stair
ascent/descent are different from that of level-ground walking, a separate
description of the
ankle-foot biomechanics is presented in FIGS. IB and 1C. FIG. IB shows the
human ankle
biomechanics during stair ascent. The first phase of stair ascent is called
Controlled
Dorsiflexion 1 (CD 1), which begins with foot strike in a dorsiflexed position
seen at 130 and
continues to dorsiflex until the heel contacts the step surface at 132. In
this phase, the ankle
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
3
can be modeled as a linear spring. The second phase is Powered Plantar flexion
1 (PP 1),
which begins at the instant of foot flat (when the ankle reaches its maximum
dorsiflexion at
132) and ends when dorsiflexion begins once again at 134. The human ankle
behaves as a
torque actuator to provide extra energy to support the body weight.
[0011] The third phase is Controlled Dorsiflexion 2 (CD 2), in which the ankle
dorsiflexes until heel-off at 136. For the CD 2 phase, the ankle can be
modeled as a linear
spring. The fourth and final phase is Powered Plantar flexion 2 (PP 2) which
begins at heel-
off 136 and continues as the foot pushes off the step, acting as a torque
actuator in parallel
with the CD 2 spring to propel the body upwards and forwards, and ends when
the toe leaves
the surface at 138 to begin the swing phase that ends at 140.
[0012] FIG. 1 C shows the human ankle-foot biomechanics for stair descent. The
stance phase of stair descent is divided into three sub-phases: Controlled
Dorsiflexion 1 (CD
1), Controlled Dorsiflexion 2 (CD2), and Powered Plantar flexion (PP). CD1
begins at foot
strike illustrated at 150 and ends at foot-flat 152. In this phase, the human
ankle can be
modeled as a variable damper. In CD2, the ankle continues to dorsiflex forward
until it
reaches a maximum dorsiflexion posture seen at 154. Here the ankle acts as a
linear spring,
storing energy throughout CD2. During PP, which begins at 154, the ankle
plantar flexes
until the foot lifts from the step at 156. In this final PP phase, the ankle
releases stored CD2
energy, propelling the body upwards and forwards. After toe-off at 156, the
foot is
positioned controlled through the swing phase until the next foot strike at
158.
[0013] For stair ascent depicted in FIG. 1 B, the human ankle-foot can be
effectively
modeled using a combination of an actuator and a variable stiffness mechanism.
However,
for stair descent, depicted in FIG. 1 C, a variable damper needs also to be
included for
modeling the ankle-foot complex; the power absorbed by the human ankle is much
greater
during stair descent than the power released during stair ascent. Hence, it is
reasonable to
model the ankle as a combination of a variable-damper and spring for stair
descent.
[0014] Conventional passive prosthetic, orthotic and exoskeleton apparatus do
not
adequately reproduce the biomechanics of a gait cycle. They are not biomimetic
because
they do not actively modulate impedance and do not apply the reflexive torque
response;
neither on level ground, ascending or descending stairs or ramps, or changing
terrain
conditions. A need therefore exists for improved lower-extremity prosthetic,
orthotic and
exoskeleton apparatus, components thereof, and methods for controlling the
same.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
4
SUMMARY
[0015] The inventions described herein relate generally to lower-extremity
prosthetic,
orthotic and exoskeleton apparatus. Typical use cases for various embodiments
of the
invention include, for example, metabolic augmentation, permanent assistance
for subjects
with a permanent limb pathology, or rehabilitation for wearers with temporary
limb
pathology.
[0016] One aspect of the invention relates to an active orthotic or prosthetic
apparatus
that includes a thigh member, a lower leg member, and a knee joint for
connecting the thigh
member to the lower leg member. The apparatus also includes a rotary motor
with a motor
shaft output, a motor drive transmission assembly coupled to the motor shaft
output, and a
drive transmission assembly coupled to the output of the motor drive
transmission, with an
output of the drive transmission assembly coupled to the lower leg member for
applying
torque to the knee joint to rotate the lower leg member with respect to the
thigh member. The
apparatus also includes at least one sensor having at least one output from
which a position of
the knee joint with respect to an ankle joint can be determined while the
wearer of the
apparatus is in a seated position, and a controller that determines when the
knee joint is
moved to position that is forward of the ankle joint based on the least one
output of the at
least one sensor. In response to that determination, the controller controls
the rotary motor so
as to modulate impedance, position, or torque of the knee joint to help raise
the person from
the seated position to a standing position.
[0017] Another aspect of the invention relates to a method of controlling a
knee
orthosis or prosthesis having at least one actuator. This method includes the
steps of
detecting the position of the person's knee with respect to the person's ankle
while the person
is in a seated position, and determining when the knee is moved to position
that is forward of
the ankle based on a result of the detecting step, and generating an output
indicative thereof.
In response to the output, at least one actuator of the knee orthosis or
prosthesis is actuated to
help raise the person from the seated position to a standing position.
BRIEF DESCRIPTION OF THE DRAWINGS
[0018] FIG. IA is a schematic illustration of the different phases of a
wearer's gait
cycle over level ground.
[0019] FIG. I B is a schematic illustration of the different phases of a
wearer's gait
cycle ascending stairs.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
[0020] FIG. 1 C is a schematic illustration of the different phases of a
wearer's gait
cycle descending stairs.
[0021] FIG. 2A is a schematic illustration of a method for determining ankle
joint,
heel and toe trajectories of a prosthetic, orthotic, or exoskeleton apparatus,
according to an
illustrative embodiment of the invention.
[0022] FIG. 2B is a plot of experimental data showing ankle joint acceleration
during
walking.
[0023] FIG. 3 is a schematic illustration of a method for determining foot
slope (heel
height), according to an illustrative embodiment of the invention.
[0024] FIG. 4 is a schematic illustration of a method for determining the
coordinates
of the heel and toe in relation to the ankle joint in the foot frame of
reference, according to an
illustrative embodiment of the invention.
[0025] FIG 5 is a schematic illustration of a method for estimating a heel
vector,
according to an illustrative embodiment of the invention.
[0026] FIG. 6A illustrates the inertial measurement unit-computed ankle joint
pivot
trajectories in different ambulation contexts.
[0027] FIG. 6B illustrates the 2-D geometry that describes the in-flight
trajectory of
the ankle joint of the prosthetic apparatus.
[0028] FIG. 6C illustrates how a stair-ramp discriminator can be built using
the ankle
angle attack angle as the trajectory feature that discriminates between the
stair and ramp
ambulation context, according to an illustrative embodiment of the invention.
[0029] FIG. 7A illustrates a method for positioning an ankle joint prior to
foot strike,
according to an illustrative embodiment of the invention.
[0030] FIG. 7B illustrates how the method of FIG. 7A can be used to sense the
presence of stairs and overhang of the foot on the landing of the stair,
according to an
illustrative embodiment of the invention.
[0031] FIG. 7C illustrates a method for positioning an ankle joint in a ramp
ambulation context, according to an illustrative embodiment of the invention.
[0032] FIG. 7D illustrates how the method of FIG. 7B is adapted to use the
optimized
impedance, according to an illustrative embodiment of the invention.
[0033] FIG. 8 illustrates a method for determining the inertially-referenced
spring
equilibrium based on the terrain angle at foot-flat.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
6
[0034] FIG. 9 illustrates the effect of walking speed on ankle torque versus
ankle
angle and shows how a push-pull actuator control applies to an appropriately
selected parallel
elastic element.
[0035] FIG. 1 OA illustrates a method for controlling a lower-extremity
apparatus,
according to an illustrative embodiment of the invention.
[0036] FIG. I OB is a schematic illustration of a model-based controller for
implementing impedance and torque control in a lower-extremity prosthetic
apparatus,
according to an illustrative embodiment of the invention.
[0037] FIG. I OC is a schematic illustration of a model-based controller for
implementing torque control in a lower-extremity prosthetic apparatus,
according to an
illustrative embodiment of the invention.
[0038] FIG. I OD is a schematic illustration of the mechanical impedance
relation that
governs the impedance control performed in FIG. 1 OA.
[0039] FIG. I OE is a schematic illustration of the impedance and reflex
relation that
governs the impedance and reflex control performed in FIG. I OB.
[0040] FIG. I OF is a schematic illustration of how zero moment pivot
referenced
ground reaction forces are used to determine the restoring torque necessary to
stabilize
inverted pendulum dynamics of a person wearing a prosthetic apparatus.
[0041] FIG. I IA is a schematic illustration of a lower leg foot member, ankle
joint,
and foot member of an ankle prosthesis showing ground reaction forces and the
zero moment
pivot.
[0042] FIGS. 11 B - I I D are schematic illustrations of the components of an
ankle
prosthesis showing the force and moment relationships among the components
necessary to
determine the ground reaction forces and the zero moment pivot.
[0043] FIGS. 12A-12B illustrate the biomimetic (G? ) behavior of an ankle
prosthesis
on level ground as a function of walking speed during powered plantarflexion.
[0044] FIG. 12C-12D illustrate the effect of foot transitions on ground
contact length.
[0045] FIG. 12E illustrates how velocity-dependent tables of length of contact
attenuation can use normalized ground contact length as a means to achieve
biomimetic
behavior during powered plantarflexion.
[0046] FIG. 12F illustrates how the estimated, y-component of the zero moment
pivot
vector changes during a typical walking motion.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
7
[0047] FIG. 12G illustrates a method for incorporating an attenuation factor
into
performance of an apparatus, according to an illustrative embodiment of the
invention.
[0048] FIG. 13A is a schematic representation of a control system scheme for a
heel
strike case, according to an illustrative embodiment of the invention.
[0049] FIG. 13B is a schematic representation of a control system scheme for a
toe
strike case, according to an illustrative embodiment of the invention.
[0050] FIG. 13C illustrates a method for position control applied to an ankle
prosthesis
(e.g., apparatus 1700 of FIG. 17A), according to an illustrative embodiment of
the invention.
[0051] FIG. 14A illustrates a method for employing step-by-step terrain
adaptation,
according to an illustrative embodiment of the invention.
[0052] FIG. 14B illustrates exemplary impedance that an ankle joint prosthesis
would
apply for three different ambulation contexts.
[0053] FIG. 15 is a schematic representation of a lower-extremity
biomechanical
system, according to an illustrative embodiment of the invention.
[0054] FIG. 16 illustrates a method of pose reconstruction for torso pose,
thigh pose
and torso/body center-of-mass pose, according to an illustrative embodiment of
the invention.
[0055] FIG. 17A is an illustration of a lower-extremity prosthetic apparatus,
according
to an illustrative embodiment of the invention.
[0056] FIG. 17B is an illustration of a portion of the lower extremity
apparatus of FIG.
17A that depicts a passive parallel elastic element.
[0057] FIG. 17C is an illustration of the passive parallel elastic element of
the
apparatus of FIG. 17B.
[0058] FIG. 17D is an illustration of the free-body diagram for the passive
parallel
elastic element of FIG. 17C, according to an illustrative embodiment of the
invention.
[0059] FIG. 17E is an illustration of a perspective view of the structural
element
(pyramid) of the apparatus of FIG. 17A, according to an illustrative
embodiment of the
invention.
[0060] FIG. 17F is an illustration of a cross-sectional view of an alternative
method
for measuring axial force and moment applied to the lower leg member of FIG.
17A,
according to an illustrative embodiment of the invention.
[0061] FIG. 17G is an illustration of a method for computing the in-plane
moment
vector and axial force using a circular array of displacement sensors on a
printed circuit
assembly, according to an illustrative embodiment of the invention.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
8
[0062] FIG. 17H is a schematic illustration of a state and actuator controller
for use
with the apparatus of FIGS. 17A-17G, according to an illustrative embodiment
of the
invention.
[0063] FIG. 171 is a schematic illustration of an electrical circuit
equivalent of a lower
extremity prosthetic apparatus, according to an illustrative embodiment of the
invention.
[0064] FIG. 17J is a schematic illustration of the electrical circuit of FIG.
171
including sensor measurements used in controlling the apparatus.
[0065] FIGS. 18A-18D are illustrations of a passive series-elastic member,
according
to an illustrative embodiment of the invention.
[0066] FIG. 19A is an illustration of a lower-extremity prosthetic apparatus
incorporating a flat series spring, according to an illustrative embodiment of
the invention.
[0067] FIGS. 19B-19C are illustrations of a prosthetic apparatus using an
alternative
series spring, according to an illustrative embodiment of the invention.
[0068] FIG. 20A is an illustration of a perspective view of a linear actuator
capable of
being used in various lower-extremity prosthetic, orthotic, and exoskeleton
apparatus,
according to an illustrative embodiment of the invention.
[0069] FIG. 20B is an illustration of a cross-sectional view of the linear
actuator of
FIG. 20A.
[0070] FIG. 21 is an illustration of a perspective view of a linear actuator
capable of
being used in various lower-extremity prosthetic, orthotic, and exoskeleton
apparatus,
according to an illustrative embodiment of the invention.
[0071] FIG. 22A is a schematic illustration of a top view of a lower-extremity
orthotic
or exoskeleton apparatus (wearable robotic knee brace), according to an
illustrative
embodiment of the invention.
[0072] FIG. 22B is a side view of the apparatus of FIG. 22A.
[0073] FIG. 22C is a schematic illustration of the interior portion of the
knee joint
drive assembly of the apparatus of FIGS. 22A and 22B.
[0074] FIG. 23A is a schematic illustration of the human balance problem on an
inclined slope.
[0075] FIG. 23B is a schematic illustration of acceptable solutions to the
balance
problem based on variable knee flex by a wearer.
[0076] FIG. 23C is a schematic illustration representing the human body and
how
intrinsic sensing can be used to balance the wearer on level ground.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
9
[0077] FIGS. 24A-24C are schematic illustrations for a method for balancing a
wearer
as the wearer stands up from a chair, according to an illustrative embodiment
of the
invention.
[0078] FIG. 25A illustrates a definition of transfer work.
[0079] FIG. 25B illustrates a definition of hip impact forces.
[0080] FIG. 26 depicts the biomechanical features of normal human gait during
ambulation.
[0081] FIG. 27 depicts the biomechanical mechanism by which quadriceps
weakness
affect ambulation on level ground.
[0082] FIG. 28 depicts how a knee apparatus is used to restore normal
ambulation.
[0083] FIGS. 29A-D depicts a stand-up sequence for a healthy person.
[0084] FIGS. 30A-D depicts the problems in implementing the same stand-up
sequence for impaired patients.
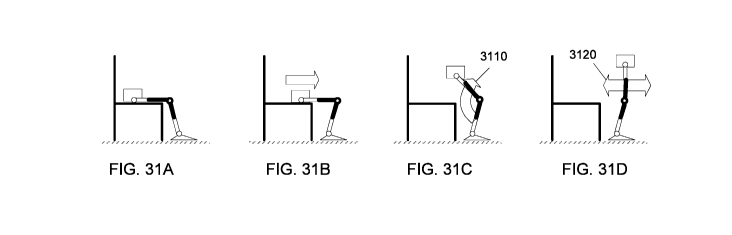
[0085] FIGS. 31A-D depicts how a knee apparatus is used to assist the stand-up
sequence for impaired patients.
DETAILED DESCRIPTION OF THE PREFERRED EMBODIMENTS
[0086] The inventors have recognized that during the course of an ordinary
day, a
person's lower limbs are used to perform and adapt to many different
activities in addition to
ordinary walking, such as ascending and descending stairs, and walking on
inclined ramps.
The ankle-foot components require the most power and must exhibit the most
terrain-
adaptive behavior because these are in the most direct contact with the
underlying terrain.
The inventors have further recognized that the performance of AFPs can be
dramatically
improved by dynamically optimizing the mechanical characteristics of the
device in different
ways and dynamically controlling the device in different ways for each of
those activities.
[0087] For example, when a person is walking on flat ground, it is better to
control the
angle of the foot so that the heel is lower than the toe when the foot touches
down on the
ground. However, when a person is ascending stairs, it is better to control
the angle of the
foot so that the toe is lower than the heel when the foot touches down on the
next step.
[0088] This application describes various embodiments of AFPs that perform
appropriately in each of these different situations by detecting the terrain
that is being
traversed, and automatically adapting to the detected terrain. In some
embodiments, the
ability to control the AFP for each of these situations builds upon five basic
capabilities: (1)
determining the activity being performed; (2) dynamically controlling the
characteristics of
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
the AFP based on the activity that is being performed; (3) dynamically driving
the AFP based
on the activity that is being performed; (4) determining terrain texture
irregularities (e.g., how
sticky is the terrain, how slippery is the terrain, is the terrain coarse or
smooth, does the
terrain have any obstructions, such as rocks) and responding to these with
appropriate traction
control and (5) a mechanical design of the AFP that can respond to the dynamic
control and
dynamic drive.
[0089] The inventors have determined that an exemplary way to figure out what
activity is being performed is to track the trajectory of a spot (typically at
the virtual center of
rotation of the ankle joint) on the lower leg (or shank) between the ankle
joint and knee joint.
FIG. 6A shows the shank trajectories that correspond to five different
activities, with
additional ramp trajectories to distinguish between steep and shallow ramps.
The system can
use this information to figure out what activity is being performed by mapping
the tracked
trajectory onto a set of activities.
[0090] By looking at the trajectory of the lower leg (shank) it is possible to
distinguish
between flat terrain, ascending or descending stairs, or ascending or
descending ramps. For
example, when the system recognizes a trajectory it would switch into an
appropriate mode,
and dynamically control (drive) the AFP as previously established for the
mode. Where a
trajectory does not fall neatly within a classification, the AFP controller
would optimize the
response to minimize an objective function in a stochastic control sense or
would apply fuzzy
logic or ad hoc controls based upon the likelihood the terrain falls into a
classification.
[0091] One suitable way to track the trajectory of the shank is by mounting an
inertial
measurement unit (IMU) at the forward face at the top of the lower leg member
(shank), and
processing the signals that are output by the IMIJ. A suitable way to
distinguish the various
trajectories is to monitor the velocity of the ankle joint angle of attack.
These topics are
described in greater detail below.
[0092] In addition to dynamically optimizing the mechanical characteristics
and
dynamically controlling the device in different ways for each of the different
activities, the
inventors have recognized that the performance of the device can be further
improved by
fine-tuning the characteristics and control of the AFP based on various
parameters.
[0093] For example, when a person is walking slowly (e.g., at a rate of less
than 0.9
meters per second), performance can be improved by increasing the impedance of
the ankle
joint with respect to the impedance used for normal walking. Or when a person
is walking
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
11
quickly (e.g., at a rate of 1.7 meters per second), performance can be
improved by decreasing
the impedance of the ankle joint with to the impedance used for normal
walking.
[0094] In addition, when the controller determines that the ankle joint is not
responding as we would expect it to when traversing normal terrain, the
controller can take
into account (and modify the output of the controller) that there may be
features, texture or
irregularities in the terrain (e.g., how sticky is the terrain, how slippery
is the terrain, is the
terrain coarse or smooth, does the terrain have any obstructions, such as
rocks).
[0095] Each of the five capabilities identified above (i.e., figuring out what
activity is
being performed; figuring out whether there are features, texture or
irregularities of the
terrain; dynamically controlling the characteristics of the AFP; dynamically
driving the AFP;
and the mechanical design of the AFP) is described in greater detail below.
Determining Activity Being Performed
Inertial Pose and Trajectory Estimation
[0096] FIG. 2 is a schematic illustration of a method for determining ankle
joint 200,
heel 212 and toe 216 trajectories of a prosthetic, orthotic, or exoskeleton
apparatus (for
example, apparatus 1700 of FIG. 17A) based on the inertial pose of a lower leg
member 220
coupled to the ankle joint 200, and the angle between the lower leg member 220
and foot
member 208. Pose is the position and orientation of a coordinate system. The
apparatus
1700 includes an inertial measurement unit 204 coupled to the lower leg member
220. The
inertial measurement unit 204 includes a three-axis rate gyro for measuring
angular rate and a
three-axis accelerometer for measuring acceleration. Placing the inertial
measurement unit
on the lower leg member 220 collocates the measurement of angular rate and
acceleration for
all three axes of the lower leg member 220. The inertial measurement unit 204
provides a
six-degree-of-freedom estimate of the lower leg member 220 pose, inertial
(world frame
referenced) orientation and ankle-joint 200 (center of rotation of the ankle-
foot) location.
[0097] In some embodiments, the lower leg member 220 pose is used to compute
the
instantaneous location of the knee joint. By using knowledge of the ankle
joint 200 angle (0)
the instantaneous pose of the bottom of the foot 208 can be computed,
including location of
the heel 212 and toe 216. This information in turn can be used when the foot
member 208 is
flat to measure the terrain angle in the plane defined by the rotational axis
of the ankle
joint/foot member. Mounting the inertial measurement unit 204 on the lower leg
member
220 has advantages over other potential locations. Unlike if it were mounted
on the foot
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
12
member 208, the lower leg member 220 mounting protects against physical abuse
and keeps
it away from water exposure. Further, it eliminates the cable tether that
would otherwise be
needed if it were on the foot member 208-thereby ensuring mechanical and
electrical
integrity. Finally, the lower leg member 220 is centrally located within the
kinematic chain
of the hybrid system (referring to FIG. 15), facilitating the computation of
the thigh and torso
pose with a minimum of additional sensors.
[0098] The inertial measurement unit 204 is used to calculate the orientation,
~~;rakle0
position, r;Y A_,,,p, and velocity, ~raklew, of the lower-extremity prosthetic
apparatus in a ground-
referenced world frame. unkle0 maybe represented by a quaternion or by a 3X3
matrix of
unit vectors that define the orientation of the x, y and z axes of the ankle
joint in relation to
the world frame. The ankle joint 200 coordinate frame is defined to be
positioned at the
center of the ankle joint axis of rotation with its orientation tied to the
lower leg member 220.
From this central point, the position, velocity and acceleration can be
computed. For points
of interest in, for example, the foot (e.g., the heel 212 or toe 216), a foot
member-to-ankle
joint orientation transformation, f'; 0(0) is used to derive the position
using the following
relation:
_ ~~ a ~II ankle0(0) (r foot, .
point-of-interestp - anklep + ankleO(~) foot, point-of-vrterest) EQN. I
where
1 0 0
~faOte0( Y) = 0 cos(y) - i (~) EQN. 2
0 sin,(ry) cos(y)
where y is the inertial lower leg member angle, and
1 0 0
ankle
f oot 0(0) = 0 cos(B) -sin(8) EQN. 3
0 sin(O) cos(O)
where 0 is the ankle joint angle.
[0099] In this embodiment, the inertial measurement unit 204, including the
three-axis
accelerometer and three-axis rate gyro, is located on the forward face at the
top of the lower
leg member 220 (as shown in, for example, FIG. 17A). It is necessary to remove
the effect of
scale, drift and cross-coupling on the world-frame orientation, velocity and
position estimates
introduced by numerical integrations of the accelerometer and rate gyro
signals
Zero-Velocity Update
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
13
[00100] Inertial navigation systems typically employ a zero-velocity update
(ZVUP)
periodically by averaging over an extended period of time, usually seconds to
minutes. This
placement of the inertial measurement unit is almost never stationary in the
lower-extremity
prosthetic apparatus. However, the bottom of the foot is the only stationary
location, and
then only during the controlled dorsiflexion state of the gait cycle. An
exemplary zero-
velocity update method, which is not impacted by this limitation, for use with
various
embodiments of the invention is described further below.
[00101] To solve this problem, orientation, velocity and position integration
of ankle
joint is performed. After digitizing the inertial measurement unit
acceleration, rrr,"a, the
ankle joint acceleration (r ri'aa, ,klp) is derived with the following rigid
body dynamic
equation:
ltirr, r rL a+r li. CZXJ JUWXJ,rJLT'r+cJXr.i'1 EQN.4
ankle "'kle ankle
where r n w and I'llub-IJ are the vectors of angular rate and angular
acceleration,
respectively, in the inertial measurement unit frame and X denotes the cross -
product.
[00102] The relationship is solved õ"n0/e =r_WU 0 similarly as in EQNS. 1-3
using
standard strapdown inertial measurement unit integration methods, in
accordance with the
following relationships known to one skilled in the art:
ankle =W !f(W w)ankie EQN. 5
w V ankle Waankle - [0,0, g]T EQN. 6
W pankle __WY V ankle EQN. 77
foot ankle foot ankle~ROtlltl012x(0" EQN. 8
T
Wheel W% w!f~~ ankle~[~ 0 01 )Wrheel-ankle EQN. 9
T
WV toe W V ankle +W ! ankle ~[~ 0 J JW toe-ankle EQN. 10 r W pheel - pankle +W
heel-ankle EQN. I I
W ptoe - pankle +W rtoe-ankle EQN. 12
_ foot Q
W rheel-ankle foot aeel ankle E N. 13
foot(rtoe - rankle EQN. 14
Wrtoe-ankle=foot w
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
14
In equations 5-14 above, the matrix, 4, will be used interchangeably with the
orientation
matrix, I ti?uo.
[00103] The world frame-referenced ankle joint velocity and position are then
derived
at a point in time after the time of the previous zero-velocity update (ith
zero-velocity update)
based on the following:
u van le (t) _ 7,1'UP(a) (IMU )"1TL' nnkledt EQN. 15
t1(Jnxfe(t) = fzvuP(.) u'1)(na..1edt EQN. 16
where a'Pankle(t = ZV UP(i)) is reset to zero for all i.
[00104] Through experimentation, using logs of inertial measurement unit data
acquired from an exemplary lower-extremity prosthetic apparatus (e.g., lower-
extremity
prosthetic apparatus 1700 of FIG. 17A), we determined that the inertial
measurement unit-
referenced accelerations were sufficiently quiet early (see FIG. 2B at
approximately 50.75
seconds and 50.9 seconds when the z-acceleration is equal to about 1 g
(approximately
9.8m/s2) in the controlled dorsiflexion state and the variance of the z-
acceleration is less than
a predetermined value (<0.005 g2)-indicating a period in time where the lower
leg member
220 is rotating about a stationary ankle joint 200. In another embodiment of
this technique, a
suitable quiet period can be detected on some part of the foot. Knowledge of
the
acceleration, angular rate and angular acceleration of the ankle joint can be
combined with
the knowledge of the sensed ankle angle (angle between the foot member and the
lower leg
member), angle rate and angle acceleration to calculate the acceleration of
any point on the
foot. Some point on the bottom of the foot can often be used to perform a zero
velocity
update on successive gait cycles. Once this velocity is known, the velocity of
the ankle joint
can be computed a posteriori. This velocity (rather than zero) can be used as
a reference from
which the zero velocity update can be performed.
[00105] In the lower-extremity prosthetic apparatus, a quiet period nearly
always exists
in the Controlled Dorsiflexion state, so a zero-velocity update may be
performed for every
step that the wearer takes. During each zero-velocity update, the velocity
error contribution
from each of three terms are preferably evaluated-the tip, 60,; of the world
frame z-axis
about the x-axis (the vector aligned with the ankle joint axis of rotation
during the zero-
velocity update on the previous step); the tilt, 60,, of the world frame z-
axis about the y-axis
(a vector defined as the cross-product of the world-frame vertical (opposing
the gravity
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
vector) and the world frame x-axis); and the inertial measurement unit scaling
along the
vertical axis, Sg. The values of these terms are used to correct the computed
pose, inertial
orientation and previous computed poses and inertial orientations of the
different components
of the apparatus (e.g., the lower leg member 1712 of FIG. 17A).
[00106] While performing the orientation, velocity and position integration, a
sensitivity matrix, M(t) is calculated that relates the velocity error that
would be introduced
by the vector of errors, v= [6O,. S8õ 6g]T. M(t) based on the following
relationship:
M(t)= EQN. 17
ate: ~r.lrt ~~ t~
in which, M(t) is integrated numerically to generate the overall terminal
velocity sensitivity,
M,
111* _ ~~llf(f)t EQN. 18
ZT UP;-i
In some embodiments, the vector of errors is expanded to include accelerometer
bias offsets
if these errors are significant, thereby increasing the number of columns in
M(t) and in M*.
In this case, M*_i takes the form of the Penrose pseudo-inverse or, by an
optimal innovations
gain, K*. K* can be computed using standard optimal linear filtering methods.
To one
skilled in the art, other terms can be included or used without loss of
generality.
[00107] At the zero-velocity update for step i, the value of rv that would
have generated
the estimated non-zero ankle joint velocity, "tVankl, (ZV UP.), is determined
based on:
a = NI *-1W va,aki~ (ZV UPS) EQN. 19
where a, is the innovations correction vector. Since the non-zero velocity
results in part from
noise in the accelerometers and angular rate measurements, not all of the
innovations
correction (a ) is applied. Instead, the correction is scaled by a filtering
constant (fraction),
k, depending on the magnitude of the noise. At this point, the new orientation
matrix (ankle O )
and gravity magnitude (g) are determined based on:
)a (zV(rPz) EQN. 20
azk,e0(ZVUP,+) = O,(-k (l))O,(-k(v(2) O
g(ZVUP+) = g(ZVUP-) - ko(3) EQN. 21
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
16
where O (lip) and O (tilt) denote incremental rotations of tip and tilt about
the x and y axes
respectively, and ZV UP; and ZV UP, denote the times after and before the
ZVUP,
respectively.
[00108] It is possible to extend the zero velocity update to estimate
accelerometer and
rate gyro bias offsets using linear estimators. Consistent angular alignment
errors (e.g., about
a given axis) could be used to estimate the rate gyro bias about that axis. In
one embodiment,
this is performed by creating linear stochastic models of accelerometer and
rate gyro bias and
using the zero-velocity update prediction residuals as inputs to the linear
filter applied to
those models.
[00109] The above method is a method for continually updating the orientation
and
apparent gravity magnitude. An initialization procedure is used in this
embodiment when the
lower-extremity prosthetic apparatus is first powered on. In this method, the
wearer will,
when requested by the apparatus (e.g., by a vibration code transmitted by the
apparatus or an
alternative user interface), take one step forward and stop, then take one
step back to the
original position. In this process, the steps will be taken on the affected
leg (for bilateral
amputees, this calibration will be executed in a serial fashion as selected by
the amputee).
The calibration will invoke two ZVUP's-one to initialize the orientation and
gravity
magnitude, the second to check the result. This will ensure integrity of the
inertial
measurement unit signals, processing and controller communication.
[00110] The above process accomplishes an initialization of the inertial
orientation. It
is, however, of general interest to accomplish a full calibration of the IMIJ,
to account for the
vector (s) of error sources-a vector that includes bias offset, scale and
cross-sensitivity
embodied within the accelerometer and gyro signals. In manufacturing, a robot
or other six
degree-of-freedom machine can carry the IMU and apply reference trajectories
in succession
as a means of measuring the effect of these error sources. The sensitivity
matrix (MO) of
the sensed reference trajectories to each of the error sources can be easily
computed by those
skilled in the art. By measuring the sensed deviations from a rich set of
reference
trajectories-typically the deviation of the end-point of each trajectory
segment-the vector
(. can be estimated using regression or other linear estimation methods-
provided that the
set of reference trajectories is rich enough to excite the influence of each
error source. The
inventors have found that reference trajectories that include closed paths
like polygons and
circles in three orthogonal planes are sufficient to calibrate the full vector
of error sources.
Such reference trajectories can also be conducted by the wearer to recalibrate
key elements of
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
17
the vector (accelerometer bias, scale and cross-sensitivity) by, for example,
walking in a
sequence of closed patterns on a horizontal plane and by rotating in sequence
about a vertical
axis.
[00111] In some embodiments of the invention, these principles of the method
are
similarly applied to correcting or minimizing the effect of accelerometer and
rate gyro drift
error associated with accelerometers and rate gyros located on, for example,
the thigh
member and/or torso of a wearer in which the prosthetic, orthotic, or
exoskeleton apparatus
treats or augments performance of these portions of a wearer's body. In one
embodiment, the
method includes determining offset values for an accelerometer signal and rate
gyro signal
output by an accelerometer and rate gyro coupled to a thigh member of the
prosthesis or
orthosis when the ankle joint is substantially stationary during a walking
cycle of the
prosthesis or orthosis. The method also can include measuring the angle of the
lower leg
member relative to the thigh member. In another embodiment, the method also
includes
determining offset values for an accelerometer signal and rate gyro signal
output by an
accelerometer and rate gyro coupled to a wearer's torso when the ankle joint
is substantially
stationary during a walking cycle of the prosthesis or orthosis. The method
also can include
measuring the angle of the thigh member relative to the wearer's torso. The
methods can
therefore be extended to the thigh member and/or torso of a wearer by
performing these
measurements and relying on the linkage constraint relationships and related
methods, as
shown in Figure 16. At the time of the zero velocity update, the linkage
constraints enable
propagation of the joint velocity references backwards from the ground-
referenced zero
velocity of the lowest link in the kinematic chain (e.g., the linkage that
defines the hybrid
human-robot system). These velocity references can be used as the input to the
pose
realignment and gravity compensation as defined above.
Exemplary Ankle Joint Trajectories and Terrain Context Discrimination
[00112] Once the inertial measurement unit offsets have been calculated and
corrected
(zeroed), the foot-slope (/3) (alternatively referred to as heel height) is
determined as
illustrated in, for example, FIG. 3. From the illustration it is easy to see
that when the wearer
is standing with her foot flat on the ground that /3 = -(0 + -y). By averaging
over a period of
about a tenth of a second an accurate estimate of 13 can be determined.
Thereafter, the
orientation component of the transformation that defines the foot to ankle
coordinate system,
fn te
foot D is computed based on the following:
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
18
1 0 0
ankle
,foot 0( ; Y) = 0 cos(o +'Y) -sin(/ + y) EQN. 22
0 srt,(3 +'y) cos([3 +'y)
As before, the translational component of this transform will remain zero.
[00113] Once the foot-slope is defined, it is then necessary to determine the
heel 212
and toe 216 coordinates in the foot coordinate system. In one exemplary method
for
determining this, f rpneel and f t5 oe are defined as the vector coordinates
of the heel and
toe in the new foot coordinate system. Because the rotational contribution of
~3 has already
been incorporated, the z-component of these vectors is the same. It can be
assumed that the
x-component of these vectors are both zero. So these vectors take the form:
0
fOot9raeel - lie et EQN. 23
zo
0
foot +oe EQN. 24
zo
where z0 defines the z-coordinate of the bottom of the foot (shoe).
[00114] FIG. 4 is a schematic illustration of a method for determining the
coordinates
of the heel 212 and toe 216 in relation to the ankle joint 200 in the foot
frame of reference,
according to an illustrative embodiment of the invention. In the first step of
the foot
calibration method defined in FIG. 4, the y-coordinate of the ankle joint 200
is aligned to a
ground reference (e.g., seam in the pavement, a prominent feature on a rug or
on a linoleum
surface). We arbitrarily define this ground reference to be the origin of the
world coordinate
system. In mathematical notation, this alignment takes the form:
0
0 EQN
.25
' ''l`l Panklet) - -
where world pa kleõ is the starting position for the moves that take place in
steps 2 and 3. In the
second step, the toe 216 is placed onto the ground reference. In mathematical
notation, this
alignment takes the form:
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
19
0 0
0 =World pank iei + 0(y)0(0 + /3) YtOe EQN. 26
0 zo
or
0
f ootp)toe = Yto+ _O_1 ('Y)O-1(8 + /3)WOrld pankle, EQN. 27
zo
[00115] A similar relationship is determined during the alignment in step 3.
When the
equations above are solved independently, two different estimates of zo are
obtained. By
combining the two constraint equations into one, a least-squares estimate of
ghee, ytoe and zo
can be obtained.
[00116] The heel 212 and toe 216 calibration method described above involves a
series
of steps that would be used the first time a new pair of feet/shoes are worn.
Such a
calibration could be performed at, for example, the prosthetist office.
[00117] In another exemplary method, the heel and toe vectors are calculated
on -the-
fly. As shown in FIG. 5, the ankle joint 200 traces an arc 500 in the early
stance phase
between foot-strike and foot-flat. The radius and orientation (midpoint angle)
of the arc 500
fully determine the heel and toe vectors. Mathematically, this is described as
a series of ankle
aorrdp e,,) that are recorded during early stance. Two ankle position
positions
,
(
measurements are needed, corresponding to two statistically distinct lower leg
member 220
(y,,) and ankle joint 200 angle (f3,,) positions, yielding:
vr;orld World oot.
pt,eFl1 = O(yi)0(i) ph.eel EQN. 28
world -world footõ
Phee12 = pas+!rl+ 0(Y2)0(02) heel EQN. 29
Then, by differencing the equations, the vector solution becomes:
foot W,)heel = (0(_Y2)0(02) - ()0(S1))-1(-orldpankde2 -world,) EQN. 30
~1 /arcklel)
The solution requires that (0(72)0(02) - 0(-,1)0(0 1)) is invertible. And from
an optimal linear
filtering standpoint, this "gain matrix" must be large enough so as to yield a
statistically
significant result.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
[00118] Considering the fact that the lower-extremity prosthetic apparatus
undergoes
significant vibration during the early stance phase, the equations above can
be extended to N
sets of ankle joint position/angle measurements. The resulting N-I equations
can be solved
using least-squares techniques to get an optimal estimate of the vector. The
equations above
are similarly adapted to solve for the toe vector when toe-strike initiates
the early stance
phase.
[00119] FIG. 6A illustrates the inertial measurement unit-computed ankle joint
pivot
trajectories in different ambulation contexts for a wearer walking on various
terrain: level
ground (620), up a 5 ramp (624), down a 5 ramp (628), up a 10 ramp (632),
down a 10
ramp (636), up stairs (640), and down stairs (644). Context is the shape of
the terrain and
how the wearer interacts with the terrain.
[00120] FIG. 6B illustrates the 2-D geometry that describes the in-flight
trajectory of
the ankle joint of the prosthetic apparatus. If we treat level-ground walking
as a subset of the
ramp ascent/descent ambulation context (in which level ground is a zero degree
ramp), then
context discrimination devolves into discrimination of stair ascent/descent
from ramp
ascent/descent. This discrimination is important because typically in the
stair context,
plantarflexion (rather than dorsiflexion) of the ankle joint 600 is required
to optimize foot-
strike kinetics whereas in ramp ambulation typically the ankle joint 600 is
dorsiflexed (or
held neutral) to optimize foot-strike kinetics. In the latter context, it is
only in extremely
steep descent that a plantar flexed ankle would be the appropriate
orientation.
[00121] FIG. 6C illustrates how a stair-ramp discriminator can be built using
the ankle
angle attack angle (i) as the trajectory feature that discriminates between
the stair and ramp
ambulation context in a set of recorded data. FIG. 6C is a plot of the
estimated velocity
vector attack angle of the ankle joint 600 of the apparatus throughout a gait
cycle versus each
step taken by the wearer. In this data, an amputee fitted with the prosthetic
apparatus 1700 of
FIG. 17A on his right foot took thirty-one (31) steps (meaning walking cycles
referenced to
the right foot) in the following manner:
1. Steps 1-6: Six (6) steps up the 5 ramp
2. Step 7: One (1) step on the landing
3. Steps 8-9: Three (3) steps down the 10 ramp
4. Recording gap
5. Steps 10-11: Two (2) steps up the stairs
6. Step 12: One (1) step on the landing
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
21
7. Step 14-17: Four (4) steps down the 5 ramp
8. Steps (18-19): Two (2) steps on level-ground
9. Steps (20-21): Two (2) steps up the 10 ramp
10. Step (22): One (1) step from the 10 ramp to the landing
11. Steps (23-24): Two (2) steps down the stairs
12. Steps (25-31): Seven (7) steps on level-ground.
[00122] The steps taken during this recording included both ramp and stair
ascent and
descent. FIG. 6C shows that stairs can be differentiated from ramps while the
ankle is in-
flight prior to foot-strike by monitoring the ankle velocity attack angle
(IV). When I drops
below a small positive value in this recording (and other similar recordings)
the foot 604
always lands on a stair. In all other cases, the foot lands on a ramp,
irrespective of ramp
angle (0 , -5 , +5 , -10 , +10 ). ,If is therefore a suitable ambulation task
context
discriminator that can be used by the processor to determine what activity is
being performed.
[00123] Alternative methods for stair-ramp discrimination can be employed in
other
embodiments of the invention. The attitude (orientation in inertial space)
lower leg member
608 (shank) and the ankle velocity attack angle (T) can be used in one
embodiment of the
invention to distinguish between stairs or a ramp/level ground. The trajectory
of the ankle
joint 600 in the y-z plane (referring to FIG. 6A) could be used in an
alternative embodiment
of the invention for stair-ramp discrimination.
Swing Phase Ankle Positioning
[00124] The stair ramp discriminator provides a real-time prediction of the
terrain slope
angle, c (t). If the discriminator detects a step, including level-ground,
then rb(t)=0.
Otherwise, the slope angle is assumed to be:
E l~teet E) ~s ~ EO)) 1 E' Pt (E) ytoe 0 j z
(Xt) = ma,'rz(ta,n1(( n~ee~Et) P~o~(o1),~),ta,n- (~, (> 1 EQN. 31
This slope angle corresponds to the minimum value possible given that the foot
has not struck
the ground. ca(t) is this the minimum value of two possible slope angles-the
angle that the
heel currently makes relative to the toe position from the last step and the
angle that the toe
makes relative to the toe position from the last step.
[00125] Once c(t) is known, it is possible to apply various different methods
to position
the ankle in a way that adapts to this predicted terrain slope. Two examples
of such methods
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
22
are described below. In one embodiment of the invention, the discriminator
methodology
described above is used to control at least one of joint impedance, position
or torque of a
lower extremity prosthetic, orthotic, or exoskeleton apparatus worn by a
wearer (e.g., the
apparatus 1700 of FIG. 17A). The method involves estimating a velocity vector
attack angle
of the ankle joint of the apparatus throughout a late swing (e.g., the y-axis
values of the data
in FIG. 6C). In one embodiment, the method also involves adjusting the
position of the foot
member of the apparatus to a toe down position when the velocity vector attack
angle has a
predetermined sign (e.g., a negative value in the case of the data in FIG.
6C). In an another
embodiment of the invention, the method involves adjusting the position of the
foot member
of the apparatus to a heel down position when the velocity vector attack angle
has an opposite
sign as the predetermined sign (a positive sign).
[00126] In some embodiments, the method includes adjusting the impedance of
the
apparatus (e.g., the ankle joint impedance) to minimize a cost function based
on projected
force imparted on the lower leg member during a period of time between when a
heel of the
foot member strikes the underlying terrain to when the foot member is
positioned in a flat-
foot position relative to the underlying terrain.
[00127] FIG. 7A illustrates a method for positioning the ankle joint 700 prior
to foot
strike. In this method, the ankle joint angle is optimized so as to minimize a
cost functional
based upon the projected force (f(t)) imparted on the ankle joint 700 from
foot member 708
strike to foot-flat. Both heel-first 716 and toe-first 712 strategies are
evaluated, and a
strategy, including optimal ankle joint 700 angle, which minimizes the cost
functional is
selected. FIG. 7A describes the method used.
[00128] In another embodiment, the method of FIG. 7A is augmented as shown in
FIG.
7B to sense the presence of stairs, and to constrain the angle-of-attack
optimization to toe-
strike only in the event of stairs with short landing areas. For ascending or
descending a
steep, narrow set of stairs, the prosthetic apparatus is programmed to keep
track of the
volume swept by the foot during ascent -a volume for which there has been no
contact
between the foot and the stairs. If in late swing, there is determined to be
no landing area for,
for example, the heel, the optimization is constrained to be the toe-down
solution. In this
embodiment, a z-rotation is a rotation about the longitudinal axis of the
lower leg member
704 (e.g., the z-axis of FIG. 17A) of the apparatus. If one descends stairs
and rotates the foot
member 708 in this way, it is likely that the landing area is limited and the
foot member 708
must be rotated to land squarely on the stair. In this case, the toe 712 down
landing yields the
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
23
only available minimum force solution for the method of FIG. 7A. Such z-
rotation would
signal the system that the landing area is limited, making a toe-down landing
the safest
alternative when compared to heel-down.
[00129] The complex impedance computation employed in the method above can be
applied to any adaptive ankle positioning method as a means of minimizing foot
slap or use
of excessive braking force as the ankle joint 700 rotates to the foot down
state. FIG. 7D
illustrates how the method of FIG. 7A is adapted to use the optimized
impedance. Once the
optimum angle-of-attack (7/?*) is found, an optimal control (F* (t)) is found
that will bring the
linear and angular momentum of the ankle joint to zero without foot-slap. The
corresponding
ankle angle response (9* (t)) is then used as the equilibrium trajectory. A
corresponding
optimal impedance, in relation to this optimal trajectory, can be derived to
accommodate the
uncertainty in the momentum and the local terrain angle.
[00130] A simpler method can also be used as shown in FIG. 7C. FIG. 7C
illustrates a
method for positioning the ankle joint in a ramp ambulation context. In this
method, the
ankle joint 700 angle is articulated so as to be in the foot-flat position on
a sloped-terrain
(with slope angle 0(t)) when the lower leg member 704 is vertical. It is also
useful to
generalize this method to adjust the ankle angle to be linearly related to the
predicted slope
angle by the relation:
0(t) = k, /(t) + 0a EQN. 32
Using this relationship the ankle angle can be adjusted to suit the wearer
preferences.
[00131] In either of the two methods described above, the ankle joint angle
700 prior to
foot-strike will be controlled (steered) continuously to coincide with the
desired ankle joint
700 angle until the foot strikes the ground.
Stance Phase Impedance and Torque Control
[00132] The next step involves restoring the orientation of the lower leg
(shank) to
align with the local vertical during stance phase. FIG. 8 illustrates a method
for determining
the inertially-referenced spring equilibrium based on the terrain angle at
foot-flat of a lower-
limb prosthesis 800, for example, the prosthesis apparatus 1700 of FIG. 17A.
The prosthesis
800 has a foot member 808 with a toe 816 and heel 820. The prosthesis also has
an ankle
joint 804 and lower leg member (shank) 812. The terrain angle (q ) is an input
to the control
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
24
system. The control system shifts the curve (17 - 0) (thereby altering the
impedance of the
ankle joint Keontrolleaplantarfleion) in FIG. 1 OA based on the change in
terrain angle (q$) to
maintain or improve the overall balance (as described an illustrated in FIG. I
OF) of the
wearer during controlled plantarflexion. The control system sets the impedance
of the ankle
joint 804 of the prosthesis such that the ankle equilibrium angle is equal to
the terrain angle
(q$ ); and the control system restores the orientation of the lower leg member
812 (shank) to
align with the local vertical 850.
[00133] FIG. 9 illustrates the effect of walking speed on ankle torque versus
ankle
angle during controlled dorsiflexion. The control system shifts the curve (17 -
O) (thereby
altering the impedance of the ankle joint 804 Keontrolled dorsiexion) in FIG.
1 OA based on the
change in terrain angle (q) to maintain or improve the overall balance of the
wearer during
controlled plantarflexion by commanding the ankle joint 804 to move the lower
leg member
(shank) 812 towards the equilibrium point.
[00134] FIG. 1 OA illustrates a method for controlling a lower-extremity
apparatus,
according to an illustrative embodiment of the invention. As shown in FIG. 1
OA, this is
achieved in the control system by
1) adjusting the late swing impedance (step 1000) (the dynamic stiffness and
ankle-
angle equilibrium angle) so as to soften the impact between the time interval
between
foot-strike and foot-flat, as described herein with respect to FIG. 7A (the
controller
shifts the curve (17 - 0) (thereby altering the impedance of the ankle joint
K powered plantarflexion) based on a minimization of the negative transfer
energy impact and
hip impact forces during powered plantarflexion.
2) introducing a lifting force in the trailing leg-accomplished by asserting a
reflex
response in the ankle (and knee) at or before the time of impact of the
leading leg
(step 1004); and
3) maintaining an inertially-referenced equilibrium angle in the controlled
dorsiflexion phase to maintain balance (equilibrium) (as described an
illustrated in
FIG. 1 OF) on sloping terrain (step 1008).
[00135] FIG. I OB is a schematic illustration of controller for implementing
impedance
and torque control in a lower-extremity prosthetic apparatus (e.g., the
apparatus 1700 of
FIGS. 17A-17E), according to an illustrative embodiment of the invention. FIG.
1OE is a
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
schematic illustration of the impedance and reflex relation that governs the
impedance and
reflex control performed in FIG. I OB.
[001361 As shown, the spring, damping and inertial components of the impedance
are
defined in relation to a trajectory, 90(t). Both the impedance gain matrix and
trajectory
illustrated in FIG. I OB are loaded adaptively and in real-time from the state
controller
processor in accordance with the phase in the gait cycle, the terrain context,
terrain texture
and walking speed as described above.
[001371 Studies have shown that intact limbs exhibit reflex responses that
arise from
non-linear positive torque (force) and non-linear positive joint velocity
feedback. The reflex
relations as illustrated in FIG. I OE employ both types of feedback. Other non-
linear
implementations of these positive feedback relations can be used, including
piece-wise linear
and piece-wise non-linear as would be obvious to those skilled in the art. In
the preferred
embodiment, positive torque feedback is achieved by measuring the torque in
the shank of
the ankle prosthesis and employing this as the non-linear feedback signal, P.
In other
implementations, this reflex torque input can be estimated using a model-based
computation
of ankle dynamics.
[001381 The inventors have observed that the biomimetic impedance and reflex
in
stance are coupled when the effects of walking speed and terrain slope are
taken into account
as shown in FIG. 9. For this reason, in one preferred embodiment, the parallel
elasticity (e.g.,
parallel, or K3 spring) for the prosthesis is picked so as to represent the
stiffness for the slow
walking speed as shown. In biomimetic systems, the stiffness component of the
prosthesis is
attenuated at higher walking speeds and the reflex response is steeper as
shown in FIG. 9.
Through this optimal biomimetic control and mechanical implementation, the
response then
requires the actuator to push on the parallel spring in controlled
dorsiflexion and to pull on it
in powered plantar flexion. We call this bipolar, or push-pull, operation. In
non-optimal
control and mechanical implementations, the reflex is implemented by a
unipolar, pulling-
force-only of twice the magnitude. The preferred embodiment thereby reduces
the peak
actuator force and motor current by a factor of two, thereby extending the
actuator design-life
by 8X and reducing ball-nut speed by nearly a factor of two when an
appropriate bilateral
series spring response is chosen. This has tremendous advantages in increasing
the actuator
durability, reducing actuator weight -the number of ball-bearings and ball-nut
diameter
needed to achieve a design life target are reduced- and reducing acoustic
noise.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
26
[00139] FIG. I OC is a schematic illustration of a controller for implementing
impedance control in a lower-extremity prosthetic apparatus (e.g., the
apparatus 1700 of
FIGS. 17A-17E), according to an illustrative embodiment of the invention. FIG.
1OD is a
schematic illustration of the mechanical impedance relation that governs the
impedance
control performed in FIG. I OC. rM is the torque applied by the linear
actuator to the ankle
joint of a lower extremity prosthetic apparatus. Through suitable "high-gain"
compensation,
G,(z), where z denotes a discrete-time signal transform, it is obvious that
the motor torque
will work to make the sum of the torques applied by 1) the series-elastic
actuator, 2) the "K3"
parallel elasticity and 3) the acceleration torque on the ankle equal to the
torque command,
Q, which is the desired result. The 1`{3 and k, are used to denote model
estimates for these
mechanical parameters, hence the reference to model-based control.
[00140] FIG. I OF is a schematic illustration of how zero moment pivot
referenced
ground reaction forces are used to determine the restoring torque necessary to
stabilize
inverted pendulum dynamics of a person wearing a prosthetic apparatus. The
torque (FCM) is
applied at the center-of-mass of the system (combination of, for example, the
person wearing
the prosthetic and the prosthetic) to maintain the balance of the wearer based
on the
following:
Pc =u' 'r`a.vlP, x fl +u' r'zapt x f EQN. 33
where f and ft are the ground reaction forces acting on the leading and
trailing feet,
respectively. vCM is the velocity vector of the wearer center-of-mass. ZMP7
and ZMP,
denote the zero moment pivot on the leading and trailing feet. urz.,JJp and
u'rz-11p, denote the
world coordinate referenced vectors between the center-of-mass and the zero
moment pivots
on the leading and trailing feet respectively. The term zero moment pivot
refers to the
inertially-referenced point on the foot about which the moment of the ground
reaction force
distribution is zero. We will also refer to this point as the center-of-
pressure (CoP)
interchangeably throughout the remainder of this document.
Ground Reaction Forces and Zero moment pivot
[00141] Ground reaction forces (GRF) are the forces imparted by and underlying
surface onto the foot (or foot member of a lower-extremity apparatus). Ground
reaction
forces are important biomechanical inputs during stance. By knowing the
aggregate ground
reaction force acting at the zero moment pivot (referred to as ZMP and CoP
herein), the
control system (e.g., controller 1712 of FIG. 17A) of a lower-extremity
prosthetic apparatus
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
27
has a direct way of improving balance (of the wearer) and of optimizing power
delivery
during the stance phase. U.S. Patent No. 7,313,463, issued to Herr et al.
further describes
estimating ground reaction forces and the zero moment pivot position as well
as biomimetic
motion and balance controllers for use in prosthetics, orthotics and robotics
and methods (the
entire contents of which are hereby incorporated by reference in its
entirety).
[00142] FIG. 11A is a schematic illustration of a lower leg foot member 1100,
ankle
joint 1104, and foot member 1108 of a prosthesis (e.g., apparatus 1700 of FIG.
17A) that
shows how the GRF components (specifically the vector from the ankle joint
1104 to the
ZMP, wr,,,, and the GRF vector, WFGxr) change during the stance phase in a
typical walking
cycle. The GRF estimation in research settings is often accomplished by
applying sensors on
the sole of the shoe. But, such extrinsic sensing may not be practical in
prosthetic and
orthotic devices because reliable packaging means should preferably survive
the contact
stresses over millions of walking cycles; which the sensors typically used in
a research setting
are unable to do so. Further, such means often require customization of the
shoe which is
often not acceptable to the wearer.
[00143] In another embodiment of the invention, intrinsic sensing of the GRF
is
accomplished in a novel way by combining inertial state and lower leg member
force/torque
inputs 1112 (using, for example, the structural element 1732 of FIGS. 17A and
17E).
[00144] FIGS. 11 B, 11 C, and I I D are schematic illustration of the
components of the
apparatus 1700 of FIG. 17A. The figures also show the force and moment
relationships
among the components (linear series elastic actuator 1116 (e.g., combination
of linear
actuator 1716 plus series elastic member 1724 of FIG. 17A) and parallel spring
1120 (e.g.,
passive elastic member 1724 of FIG. 17A) necessary to determine the ground
reaction forces
and the zero moment pivot. wr,,, and WFGxr are computed based on the following
steps:
1. Update inertial state of the lower leg member 1100 and foot member 1108
using inertial measurement unit and ankle joint 1104 angle inputs. Using
rigid-body assumptions, further calculate the world-referenced acceleration
measured at the center-of-mass (CM) of the lower leg member 1100 and foot
member 1108 and the angular velocity and acceleration of the lower leg
member 1100 and foot member 1108.
2. Solve for F; as a function of the forces acting upon the lower leg member
1100 as these are resolved along the lower leg member 1100 axis.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
28
3. Solve for F- as a function of the moments applied by each of the force and
moment components acting upon the lower leg member 1100.
4. Solve for WFGRF using the values for F; and F- computed in steps 2 and 3
above and then balancing the forces applied on the foot member 1100.
5. Balance the moments about the ankle joint 1104 assuming that WFGRF is
applied at the foot-ground boundary (i.e., wrzMP = 0).
6. Solve for W rzMP
Ankle Joint Behavior Due to Terrain Texture
[00145] FIG. 12A illustrates the biomimetic G? behavior of a prosthetic
apparatus
(e.g., apparatus 1700 of FIG. 17A) on level ground as a function of walking
speed. FIG. 12B
shows that the applied ankle joint torque diminishes rapidly with angle during
powered
plantarflexion, thereby departing from the ideal biomimetic response and
thereby
significantly reducing the net work performed (area under the G? curve),
particularly when
walking at high speed.
[00146] In conventional robotic systems, trajectories or other playback means
are
employed to deliver repeatable and programmable responses. Such means are not
preferable
in prosthetic and orthotic devices because wearer intent may change in the
middle of a
playback segment. For instance, the wearer might be walking fast, then
suddenly stop in
front of a patch of ice for instance. If pre-programmed trajectories or other
are played back,
there is no easy way of aborting them without rapid changes of force and
torque-and
without introducing hazards. Indeed, that is why the intrinsic means are used.
[00147] To extend the application of ankle joint torque during powered
plantarflexion,
walking speed-dependent normalized ground contact length are used as the means
of
attenuating the peak plantarflexion torque, Q. Ground contact length is
estimated by using
an idealized model of the foot derived per the description related to FIGS. 2A-
5 and by
measuring the inertial pose of the foot member during controlled dorsiflexion
and powered
plantarflexion. As shown in FIG. 12C, as the foot transitions from foot flat
to toe-off,
sections of the idealized foot will fall below the terrain, enabling an
estimate of ground
contact length. FIG. 12D shows how Lgro..... oa tcect changes from foot flat
to toe off.
[00148] FIG. 12E illustrates how velocity-dependent tables of Length of
Contact
Attenuation can use normalized ground contact length as a means to achieve
biomimetic
behavior during powered plantarflexion. The tables can be computed by
dynamically
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
29
measuring the ground reaction force and foot member pose of non-amputees in
controlled
environments as a function of walking speed. The functional relationships
between the
attenuation function and ground contact length can be computed for each
walking speed.
These tables can be stored in the controller of the prosthetic apparatus as
reference
relationships. The functions can be shaped to suit specific wearer needs when
the prosthetic
apparatus is fitted to the wearer.
[00149] As described earlier, one of the motivations to use intrinsic feedback
as
opposed to explicit trajectory or playback means is to accommodate changes in
wearer intent
(e.g., decision to stop quickly). Intrinsic sensing using ground contact
length as a means of
attenuating ankle joint torque is not sufficiently general to accommodate
changes in wearer
intent involving stopping and changing direction. Referring to FIG. 12G, in
one embodiment
of the invention implemented on a prosthetic apparatus, a time-dependent
attenuation factor
(e I) is used in series with the ground contact length attenuation. The time
constant for this
attenuation, 7, can be picked so as to extinguish the powered plantarflexion
drive torque so as
to prevent hazards associated with changes in wearer intent. 7 will typically
range from 50-
100 msec.
[00150] Preferably, the prosthetic apparatus enables the wearer to walk faster
with less
effort on all terrain. It is not sufficient to accommodate just changes in
terrain context (stairs,
sloping ascent/descent). Changes in terrain texture as this might introduce
slipping (e.g.,
Ice/snow) or sinking (mud, snow, sand, fine gravel) hazards should preferably
be
accommodated. Intrinsic sensing of the zero moment pivot trajectory can be
used to optimize
walking performance and/or to eliminate hazards while walking on varying
terrain texture.
[00151] FIG. 12F illustrates how the estimated, y-component of the zero moment
pivot
vector, t'v changes during a typical walking motion. As shown, in a no-slip
condition
Cop,
'r (<,P must increase monotonically between the conditions of foot-flat (3)
and toe-off (4).
This is because it is the heel that is lifting off of the terrain surface
during this period
(increasingly as the walking cycle progresses). If the velocity of the zero
moment pivot ever
moves along the negative y-axis, the foot is slipping. In a fashion similar to
how anti-lock
brakes are implemented in vehicles, the prosthetic apparatus can reduce torque
by an
attenuation factor derived from the integral of the negative zero moment pivot
velocity. In
one embodiment, so as to reduce noise sensitivity, only negative velocities
below a noise
threshold are integrated.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
[00152] FIGS. 13A and 13B provide the state control context for an
illustrative
embodiment of the invention applied to, for example, apparatus 1700 of FIGS.
17A-17E.
Normal walking involves the cycling between two phases: the swing phase and
the stance
phase. FIG. 13A depicts a control system scheme involving a walking motion in
which the
stance phase is initiated by the heel striking 1320 the ground. "' V. denotes
the z-component
of the ankle joint velocity in the ground-referenced, world frame. FIG. 13B
shows a walking
motion in which the stance phase is initiated by the toe striking 1324 the
ground.
Exemplary Control System Behavior For Driving Prosthesis or Orthosis Through
Gait Cycle
[00153] FIGS. 13A and 13B illustrate that the control system 1300 changes
ankle
behavior as the ankle transitions between states in the swing 1304 and stance
phases 1308.
The control system 1300 applies position control 1328 in the swing phase-
positioning the
ankle so as to avoid trip hazards in the early swing phase state and so as to
optimize heel-toe
strike attack angle (adaptive ankle positioning) for specific terrain
conditions (slope, stairs,
steps) in the late swing phase state. The control system 1300 applies
impedance and torque
control 1332 in the stance phase-optimizing the inertial, spring and damping
characteristics
of the ankle-as the ankle transitions through the heel/toe strike, foot down,
peak energy
storage (dorsiflexion with exponential hardening), powered plantarflexion and
toe-off events.
[00154] FIG. 13C illustrates a method for position control applied to a lower
limb
apparatus (e.g., apparatus 1700 of FIG. 17A), according to an illustrative
embodiment of the
invention. It is desirable to not move the foot member 1348 forward until the
wearer and/or
the controller of the apparatus are sure the toe 1340 is going to clear the
terrain in front of the
wearer. One exemplary way to accomplish this is to wait until the toe 1340 of
the foot
member 1348 is a sufficient distance above the last known position of the toe
1340 with
respect to the underlying terrain. In this embodiment, the control system 1300
applies
position control 1328 by beginning to rotate the ankle joint 1340 only after
the clearance
distance measured along a normal vector to the terrain surface between the toe
1340 of the
foot member 1348 at time t and at time tk_1 is determined to be greater than
(c o ). This
minimizes the risk that the toe 1340 will encounter a trip hazard. In one
embodiment, the
position of the toe 1344 at the two different times (t and tk_1) are
determined using the
inertial measurement unit measurements, as described previously herein. One
skilled in the
art would understand how to apply other schemes to determine when it is
appropriate to move
the foot member 1348 forward. In some embodiments, the controller may
determine it is
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
31
appropriate to move forward based on, for example, whether the swept volume of
the foot,
when dorsiflexed, achieves the desired clearance relative to the terrain
surface.
[00155] In summary, this embodiment of the invention, the prosthetic apparatus
employs step-by-step terrain adaptation with the intent to achieve true
biomimetic behavior in
all ambulation task contexts; including level-ground walking, stair
ascent/descent and ramp
ascent/descent. FIG. 14A outlines the process by which the step-by-step
adaptation is
accomplished. In the swing phase, the inertial measurement unit supplies the
intrinsic
sensing input (as opposed to say extrinsic neuronal/myoelectric inputs) that
enables the
apparatus to discern terrain context from cues supplied by swing-phase
trajectory features.
Adaptive swing-phase ankle positioning refers to the articulation of the ankle
angle, 0, so as
to achieve a natural heel or toe touchdown that is optimized for the most
likely terrain context
as determined by the terrain context discrimination on the swing phase
trajectory cues.
[00156] FIG. 14B illustrates exemplary impedance that an ankle joint
prosthesis would
apply for three different ambulation contexts. FIG. 14B is a graph of required
ankle torque
1404 (units of Nm/kg) versus ankle joint angle 1408 (units of degrees). The
graph includes
three curves 1412, 1416 and 1420. Curve 1412 illustrates the ankle joint
torque 1404 versus
ankle joint angle 1408 for walking on a ramp incline of 5 degrees. Curve 1416
illustrates the
ankle joint torque 1404 versus ankle joint angle 1408 for walking on a ramp
decline of 5
degrees. Curve 1420 illustrates the ankle joint torque 1404 versus ankle joint
angle 1408 for
walking on a ramp incline of 0 degrees (level ground). The slope of the curves
is equal to the
stiffness (or impedance in general). The area enclosed by the closed F - 0
curve corresponds
to the amount of non-conservative work required for the specific terrain
context (e.g., slope,
stairs) and walking speed. As can be seen in the graphs, an ankle joint
prosthesis would be
required to provide more work to accomplish the ambulation task of walking up
an inclined
ramp versus walking on level ground because the area within the curve 1412 is
greater than
the area within the curve 1416.
Generalization of the Hybrid Lower-Extremity Augmentation System
[00157] FIG. 15 is a schematic representation of a lower-extremity
biomechanical
apparatus 1500, according to an illustrative embodiment of the invention. In
one
embodiment, the apparatus 1500 is an orthotic apparatus that augments the
ambulation
abilities of the wearer. In another embodiment, the apparatus 1500 is an
orthosis apparatus
that attaches to a wearer's body to support and/or correct musculoskeletal
deformities and/or
abnormalities of a wearer's hip, thigh, lower leg and foot. In another
embodiment, the
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
32
apparatus 1500 is an exoskeleton apparatus that attaches to a wearer's body to
assist or
augment the wearer's lower-extremity biomechanical output (e.g., augment the
lower-
extremity strength or mobility of the wearer).
[00158] The apparatus 1500 is a linkage represented by a plurality of links
(or
members) and joints that connect the links. The apparatus 1500 includes a foot
member 1508
(Lo) coupled to a lower leg member 1516 (Li) by an ankle joint 1512. The
apparatus 1500
also includes a thigh member 1524 (L2) coupled to the lower leg member 1516 by
a knee
joint 1520. The apparatus also includes a hip joint 1528 that couples the
thigh member 1524
to the torso 1532 (L3) of the wearer. Center-of-mass 1504 is the center-of-
mass of the
combination of the apparatus 1500 and the wearer.
[00159] The foot member 1508 contacts the terrain 1536 underlying the foot
member
1508 at the zero moment pivot 1540. The foot member 1508 includes a toe
portion 1544 and
a heel portion 1548. Each joint of the apparatus 1500 also includes an
actuator with a
generalized vector of torque (force) F1 , displacement ~, , and impedance K, ,
where i=0
corresponds to the ankle joint 1512, i=1 corresponds to the knee joint, and
i=2 corresponds to
the hip joint. Each joint actuator may include a machine element (e.g., ball-
screw actuator or
rotary harmonic drive), human muscle, or both. Joint displacements typically
take the form
of angular displacement (rotation) but may also include a combination of
linear and angular
displacements as found in, for example, a typical knee joint. The pose of a
link, i, is
represented by a 4x4 matrix that defines the location of the link origin and
the unit vectors of
its coordinate frame in terms of the unit vectors in the world coordinate
frame, W.
[00160] The pose of each link, j, can thereby be determined via linkage
constraint
relationships-specifically by multiplying the pose of link, i-1, by a
transformation defined
by the generalized displacement, 4j, and specific link parameters (link
length, skew and
convergence angles). For example, if the pose of the shank is known, the pose
of the foot,
thigh and torso can be computed provided that the generalized displacements
for those
linkages are known, either by directly sensing these or through the use of
inertial sensors.
The vector of sensor information intrinsic to each link is encapsulated in
what we will call an
intrinsic sensing unit (ISU). Examples of intrinsic sensors include direct or
indirect
measurement of generalized displacements; measurement of the angular rate and
acceleration
of the link (e.g., using, for example, an inertial measurement unit);
measurement or
estimation of the components of force or torque on the link; multi-modal
computer imagery
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
33
(e.g., a range map) or measurement of the outputs of specific neural pathways
on or adjacent
to the link.
[00161] The terrain is modeled as a contour function, z(x,y), with surface
properties,
a(x,y). In this context, the surface properties would include the
elasticity/plasticity, damping
characteristics and coefficient of friction of the surface sufficient to
capture the ability of the
foot to gain traction on the surface and to capture the surface energy as this
would relate to
the work required to touch down on the surface and to push off of it with the
foot member.
[00162] FIG. 16 is a schematic illustration of a method for determining the
pose of the
thigh member, hip member and torso of a wearer, according to an illustrative
embodiment of
the invention. In lower-limb systems employing robotic knee prostheses or
orthosis, the
location of the human hip can also be computed, either by incorporating an
inertial
measurement unit on the thigh or by measuring the relative knee angle as
referenced to the
lower leg member. If an inertial measurement unit is further employed on the
torso, the pose
of the torso can also be instantaneously computed. Alternatively, the pose can
be computed
by measuring the two degree-of-freedom hip joint displacements. Compensation
for the torso
pose prediction errors arising from the rate gyro and accelerometer drift on
the torso inertial
measurement unit can be corrected during the lower leg member zero -velocity
update through
a chaining of velocity constraints through the hybrid system linkages.
[00163] FIG. 16 illustrates a method of pose reconstruction in which j, j -1
velocity
constraints a r e used to correct the prediction of torso pose ( S0T (t
t,,,,,pz )), thigh pose
(thz~ TV t,,,,l~,~)) and torso/body center-of-mass pose t,,,,,r_)). Step 1
(1604)
captures the output of the zero velocity update on the lower leg member 1620
(link 1) to
determine the lower leg member pose, as described above with respect to FIGS.
2A-5. The
solutions (steps 2 and 3) for the thigh member 1624 (link 2) and torso member
1628 (link 3),
respectively, follow the example of step 1 (1604), but in these cases the
velocity constraints
are non-zero and are predicted by the translational and rotational velocity
from the prior link.
Exemplary Mechanical Designs
[00164] FIG. 17A is an illustration of a lower-extremity prosthetic apparatus
1700,
according to an illustrative embodiment of the invention. The apparatus 1700
has a mounting
interface 1704 making it capable of attaching to a complementary lower-
extremity limb
socket member of a wearer. The apparatus 1700 also includes a structural
element 1732 (also
referred to herein as the pyramid) coupled to the mounting interface 1704 and
a first end 1752
of a lower leg member 1712 (also referred to herein as a shank). In some
embodiments, the
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
34
axial force and moment applied to the lower leg member of the apparatus is
determined based
on sensor measurements made using the structural member (pyramid) coupled to
the lower
leg member of the apparatus. The pyramid is an instrumented structure that is
a component
of the prosthesis and which couples to the limb socket of the wearer. In one
embodiment, the
pyramid (structural element) measurements are used by a controller to
determine axial force
and moment applied to the lower leg member. In this embodiment, the structural
element
1732 is coupled to the first end 1752 of the lower leg member 1712 with a set
of pins 1711.
The pins 1711 pass through a set of holes 1713 in the lower leg member 1712
and a set of
holes 1715 (shown in FIG. 17E) in the structural element 1732.
[00165] The structural element 1732 has a top surface 1731 located towards the
mounting interface 1704 and a bottom surface 1733 located towards the lower
leg member
1712. The lower leg member 1712 is also coupled to a foot member 1708 at an
ankle joint
1740 at a second end 1744 of the lower leg member 1712. The ankle joint 1740
(e.g., a
rotary bearing) permits the foot member 1708 to rotate about the x-axis
relative to the lower
leg member 1712. The foot member includes a heel 1772 and a toe 1776.
[00166] The apparatus 1700 also includes a linear actuator 1716 with a first
end 1736
and a second end 1748. The linear actuator 1716 generates a linear motion
1703. The first
end 1736 of the linear actuator 1716 is coupled (with, for example, a rotary
bearing) to the
first end 1752 of the lower leg member 1712. The apparatus 1700 also includes
a first
passive elastic member 1728 in series with the linear actuator 1716. The
passive elastic
member 1728 is coupled to the foot member 1708 and the second end 1748 of the
linear
actuator 1716. The passive elastic member 1728 is coupled to the foot member
1708 (with,
for example, a rotary bearing) at the proximal end 1730 of the passive elastic
member 1728.
A distal end 1726 of the passive elastic member 1728 is coupled between the
second end
1748 of the linear actuator 1716 (with, for example a rotary bearing). The
linear actuator
1716 applies torque about the ankle joint 1740.
[00167] The apparatus 1700 also includes an optional second passive elastic
member
1724 with a first end 1756 and a second end 1760. The second passive elastic
member 1724
provides a unidirectional spring force in parallel (provides parallel
elasticity) with the lower
leg member 1712. The first end 1756 of the second passive elastic member 1724
is coupled
to the first end 1752 of the lower leg member 1712. The second end 1760 of the
second
passive elastic member 1724 is coupled to the foot member 1708. However,
during
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
plantarflexion the spring is not engaged, and therefore only provides a
unidirectional spring
force to the apparatus.
[00168] In some embodiments, the second passive elastic member 1724 is a non-
compliant stop that stores little or no energy and limits further rotation of
the ankle beyond a
predefined angle during powered plantar flexion.
[00169] FIGS. 17B and 17C are illustrations of a portion of the lower
extremity
apparatus of FIG. 17A depicting the second passive elastic element 1724. The
second
passive elastic element 1724 stores energy during dorsiflexion but, not in
plantarflexion. The
elastic element 1724 has a double-cantilever engagement (clamped at a location
1780
between the first end 1756 and the second end 1760). The elastic member 1724
has a
tapered shape 1784 that causes the elastic member 1724 to provide efficient
energy storage
by maximizing bending strain along the entire length (along the y-axis) of the
elastic element
1724. In some embodiments, the normalized spring constant ranges from 0-12
Nm/rad/kg.
At the high end of the range, the energy storage is approximately 0.25 J/kg.
[00170] A cam/ramp arrangement of the elastic member 1724 facilitates
tailoring of the
spring constant to the weight of the wearer. The cam element 1788 is located
at the second
end 1760 of the elastic member 1724. The ramp element 1792 is located on the
foot member
1708. The cam element 1788 engages the ramp element 1792 during dorsiflexion;
however,
the cam element 1788 does not engage the ramp element 1792 or another portion
of the
apparatus 1700 during plantarflexion. Because the cam element 1788 does not
engage the
ramp element 1792 or another portion of the apparatus 1700 during
plantarflexion, the elastic
member 1724 stores energy only during dorsiflexion. In one embodiment, the
position of the
ramp element 1792 is screw-adjustable to allow the wearer or a second party to
tailor the
ramp engagement of the cam element 1788 so as to align the energy storage
characteristics to
the wearer's walking habits. An operator may adjust the position of the ramp
element 1792
relative to the position of the cam element 1788 in order to modify the energy
storage
characteristics of the passive elastic member 1724.
[00171] In alternative embodiments, an actuator is integrated into the ramp to
adjust the
ankle joint angle at which the second passive elastic member 1724 (elastic
member
engagement angle) engages. This would enable the ankle joint 1740 to be
dorsiflexed during
the swing phase without engaging the elastic member 1724 when, for example,
the wearer is
ascending ramps and stairs, and while running.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
36
[00172] The passive elastic element 1724 also functions to increase the
frequency
response of the apparatus 1700 when the elastic element 1724 is engaged in
dorsiflexion.
The apparatus 1700 dynamics in dorsiflexion benefit from a fast response
(bandwidth) series
elastic actuator (i.e., combination of the linear actuator 1716 and first
passive elastic element
1728). The spring constant associated with the second passive elastic element
1724 increases
the bandwidth of the apparatus 1700 by a factor, 0, where:
,3 = K3 (1 + KS/K3 )Y2 /Ks z EQN. 34
where K3 is the spring constant of the second passive elastic member 1724 and
Ks is the
spring constant of the combination of the linear actuator 1716 and first
passive elastic
element 1728. In one embodiment of the invention, the second passive elastic
element
provides a 0 from 1 to 3; thereby increasing the bandwidth of the apparatus
1700 from about
Hz to about 15 Hz.
[00173] The second passive elastic member 1724 employs a dovetail feature 1796
at
both ends to enable clamping at both ends without use of mounting holes. In
one
embodiment, the second passive elastic member 1724 is fabricated from
composite fiber
materials. Mounting holes would form a stress intensity and cause fiber
dislocations in the
passive elastic member 1724 that would compromise the strength of the spring.
The end
clamps 1798 have complementary shapes that hold the passive elastic element
1724 in place.
In one embodiment of the invention, epoxy is employed in the clamps to
permanently secure
the second passive elastic member 1724 in the end clamps. The epoxy joint
would be more
prone to failure in the absence of the dovetail features 1796.
[00174] The passive elastic element 1724 employs a tapered design to maximize
energy
storage in the element 1724 to ensure that energy storage density is constant
over its length
for a given deflection. Referring to FIG. 17D, we illustrate the free-body
diagram for the
passive elastic element 1724, showing how the roller force, FroIler, and the
lower leg member
force, Fshank, combine to create an equal and opposite force by the central
pivot. In this
embodiment, the roller force and the lower leg member force are applied
equidistant from the
center pivot. The forces at the end, F, combine to create a central pivot
force of 17F. Using
standard thin beam relationships, the moment acting at a distance of x from
the central pivot
varies linearly-starting at a value of FL in the center and falling to zero at
x=L, where L is
the length of the passive elastic element 1724 between the locations at which
the forces are
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
37
applied. Energy storage density along x is proportional to the product of
moment (M(x)) and
the strain at the surface (fo (X)), where:
M(x)=F(2 -x) EQN. 35
M (x) - F - X
Fp2.) - EQN. 36
EIw.w . EIw.w
[00175] For a given layup of composite material, the surface strain is kept
below a
critical value, F*. For a given moment, the energy density in the beam will be
maximized
when the surface strain is set to this critical value. To keep the energy
density constant and at
its maximum value, the optimal width of the beam, is defined by the relation:
L * eu* (a;) z a) EQN. 37
[00176] In one embodiment, the taper 1784 varies linearly from the center of
the beam.
By using this design method, we have amplified the energy storage of the
spring by over a
factor of 2 when compared to a beam without a taper 1784. Because the
composite spring
material is not homogeneous and since the thin beam equations are not
applicable,
computational tools are used to estimate the energy storage density in the
passive elastic
member 1724. The shape that is able to store the most energy is highly
dependent upon the
fiber laminate, lamination design, thickness and the exact manner in which the
passive elastic
member 1724 is attached to the apparatus 1700. We have determined, however,
that a linear
taper delivers energy storage within about 10% of the optimal. In a preferred
embodiment,
the linear taper is used because of the relative ease by which a linear taper
pattern maybe cut
from a sheet of laminated ply composite material using a water-jet process. In
alternative,
less preferred embodiments, a non-tapered spring may be used.
[00177] FIG. 17E is an illustration of a perspective view of an embodiment of
the
structural element 1732 (also referred to herein as the pyramid). The
structural element 1732
is coupled between the mounting interface 1704 and the first end 1752 of the
lower leg
member 1712. The structural element 1732 is coupled to the first end 1752 of
the lower leg
member 1712 with a set of pins 1711 (shown in FIG. 17A). The pins 1711 pass
through the
set of holes 1713 in the lower leg member 1712 and a set of holes 1715 in the
structural
element 1732. The pins 1711 allow a rotary degree of freedom for the strain in
structural
element 1732 from being falsely recorded as axial force and moment in the
structural element
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
38
1732. In this embodiment, the structural element 1732 is capable of measuring
the moment
and axial load on the ankle joint 1740, enabling, for example, positive
detection of "foot-
down" for use by the controller 1762 state machine that controls the apparatus
1700
functions; measurement of applied moment for use by the positive-feedback
reflex controls
employed during powered plantarflexion; and positive detection of tripping for
use by a
safety system integrated into the controller 1762.
[00178] In this embodiment, the structural element 1732 is designed as a
flexural
element that amplifies the strain fields induced by the medial-lateral moment
and axial force
applied to the apparatus 1700 during operation. The structural element 1732
creates high
magnitude strain fields of opposite sign (differential strain fields) in the
regions 1738 and
1742 about the center adaptor mounting hole 1734 when a medial-lateral moment
(moment
about the x-axis) is applied. These differential strain fields are not present
when only an axial
force is applied. The structural element 1732 includes one strain gage (1782
and 1786)
bonded to each of the two moment-sensitive regions (1738 and 1742,
respectively) on the
bottom surface 1733 of the structural element 1732. The gages are applied on
opposing sides
of a Wheatstone bridge. The controller 1762 is coupled to the Wheatstone
bridge to measure
the strains. The strain measurements are used to measure moment on the
structural element
1732. In one embodiment, the sensitivity of the measurement is approximately
in the 0.15 N-
m range, where, in this context, sensitivity defines the minimum resolvable
change (signal to
noise=1) when digitally sampled at 500 Hz.
[00179] In contrast to the moment induced strains, high strains are introduced
by axial
forces along the medial-lateral axis in the regions 1746 and 1754 around the
center adaptor
mounting hole 1734. These strains appear in a 0.76 mm thickness region
(regions 1746 and
1754) under the slots (1758 and 1770, respectively) machined along the medial-
lateral axis.
The section above the slot must be thick enough to transfer moment load with
minimum
strain in the thin lower section. The strain magnitude is significantly
diminished in the thin
section when a moment-only load is applied. The structural element 1732
includes one strain
gage (1790 and 1794) bonded to each of the two axial load-sensitive regions
(1746 and 1754,
respectively) on the bottom surface 1733 of the structural element 1732. The
gages are
applied on opposing sides of a Wheatstone bridge. The controller 1762 is
coupled to the
Wheatstone bridge to measure the strains. The strain measurements are used to
measure axial
force on the structural element 1732, and consequently, axial force on the
lower leg member
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
39
1712. The machined slots 1758 and 1770 amplify the axially-induced strains
without
compromising the structural integrity of the structural element 1732.
[00180] Since the structural element 1732 is in the critical chain of
structural support
between the residual limb socket of the wearer (not shown) and the apparatus
1700, in one
embodiment it is preferably designed to withstand more than 60 N/kg of axial
load. In this
embodiment, the sensitivity of the axial measurement is in the range of
approximately 50 N,
which is well below the approximately 100 N threshold normally used in the
apparatus 1700
to sense that the apparatus has been placed firmly on the ground. During
calibration of the
apparatus 1700 a 2X2 sensitivity matrix is determined, enabling true moment
and axial force
to be derived from the pairs of strain measurements.
[00181] FIG. 17F is an illustration of a cross-sectional view of an
alternative method
for measuring axial force and moment applied to a lower leg member, according
to an
illustrative embodiment of the invention. In this embodiment, the structural
element 1732
employs a flexural design that amplifies displacement of its bottom surface
1733 in such a
way that the axial force and in-plane moment (two-degrees of freedom) can be
derived in a
redundant fashion. In this embodiment, the apparatus 1700 includes a
displacement sensing
apparatus 1735 for measuring deflection of the structural element 1732 to
determine the
moment (torque) and axial force applied to the lower leg member 1712.
[00182] In this embodiment, the displacement sensing apparatus 1735 includes a
printed circuit assembly (PCA) employing one or more displacement sensors 1737
(e.g.,
contact or non-contact displacement sensors). The sensors measure, at each
sense coordinate,
the distance between the sensor 1737 and the bottom surface 1733 of the
structural element
1732.
[00183] In one embodiment, changes in mutual inductance of coils printed on
the PCA
with respect to the bottom surface 1733 of the structural element 1732 are
used to measure
the local surface deformation (displacement). In this embodiment, counter-
circulating "eddy"
currents in the structural element 1732 serve to reduce the coil inductance
inversely with the
distance between the coil and the bottom surface 1733 of the structural
element 1732. Other
displacement sensing technologies could be employed, including non-contact
capacitance and
optical sensors or contact-based sensors that employ force-sensitive
resistors, piezo or strain-
gages integral to the PCA. By sampling the array of displacement sensors, the
axial force and
moments can be estimated using a sensitivity matrix that is computed during an
off-line
calibration process.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
[00184] In this embodiment, the structural element 1732 is fastened to the
lower leg
member 1712 with screws, eliminating the need for the pins 1711 employed in
the
embodiment illustrated in FIG. 17E. The screw fastening method reduces weight
and
manufacturing complexity. Furthermore, this fastening method amplifies
displacements
measured in the center of the structural element 1732 where the displacement
sensing
apparatus 1735 is located. FIG. 17G illustrates how the in-plane moment vector
and axial
force may be computed using a circular array of displacement sensors on the
printed circuit
assembly. As shown, demodulation of the bias and sinusoidal-like displacement
function is
used to estimate the moment and force. Other displacement sensor array
configurations could
be used as a means of intrinsic sensing of moment and force.
[00185] Moment and force sensing is useful as a means of signaling walking
state
changes. In addition, measurement of lower leg member 1712 moment serves as a
feedback
means by which reflexive behavior is achieved in powered plantarflexion. When
combined
with inertial and actuator feedback, the intrinsic moment and force
measurements are used to
calculate ground reaction force and zero moment pivot, which are useful for
traction control
and balance. For these reasons, it is beneficial to package the intrinsic
moment and force
sensing with the inertial measurement unit and state control processing
functions. FIG. 17F
shows how these functions could be implemented on a PCA. Such a PCA could be
implemented as a sandwich of FR-4 material with a stable core material (Invar
for instance)
serving as a stiff interposing substrate between the top-side displacement
sensing FR4-based
layer and a bottom FR-4-based layer that incorporates the signal processing
layer. Integrating
the materials and functions in a single assembly eliminates the need for
cabling and other
potentially unreliable means for interconnecting these functions. Such
integration also allows
for a stand-alone tool that can be used by prosthetists to setup a passive
prosthetic and study,
gait parameters, including energy return and walking statistics
[00186] Referring to FIG. 17A, the apparatus 1700 also includes a controller
1762
coupled to the linear actuator 1716 for controlling the linear actuator 1716.
In this
embodiment, the controller is located within a housing 1764 of the apparatus
1700 to protect
it from the environment. A battery 1768 in the housing 1764 provides power to
the apparatus
(e.g., the controller 1762 and various sensors associated with the apparatus
1700).
[00187] The apparatus 1700 includes an inertial measurement unit 1720 to
predict the
inertial pose trajectory of the ankle joint 1740, heel 1772 and toe 1776
relative to the previous
toe-off position. The inertial measurement unit 1720 is electrically coupled
to the controller
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
41
1762 and provides inertial measurement signals to the controller 1762 for
controlling the
linear actuator 1716 of the apparatus 1700. In one embodiment, the inertial
measurement unit
1720 employs a three-axis accelerometer and a three-axis rate gyro. The three-
axis
accelerometer measures local acceleration along three orthogonal axes. The
three-axis rate
gyro measures angular rotation about three orthogonal axes. Through use of
well-established
methods of numerical integration, the position, velocity and pose of any point
on the foot
structure can be computed.
[00188] In some embodiments, the inertial measurement unit 1720 is used to
detect the
terrain slope and the presence of steps and stairs-thereby enabling
optimization of the foot's
"angle-of-attack" relative to the underlying terrain prior to touchdown and
the ankle joint's
spring equilibrium position in the stance phase. In some embodiments, the
inertial
measurement unit 1720 is used to determine ambulation speed of the wearer and
conditions
of the terrain (features, texture or irregularities of the terrain (e.g., how
sticky is the terrain,
how slippery is the terrain, is the terrain coarse or smooth, does the terrain
have any
obstructions, such as rocks)). This enables the wearer to walk confidently on
all terrain types.
The inertial pose comprises the three degree-of-freedom orientation of the
lower leg member
1712 in a fixed ground-referenced (world) coordinate frame-often captured as
the
orientation component of a homogeneous transformation (three unit vectors
defining the x, y
and z axes in the world reference frame) or as a quaternion; the translation
of the ankle joint
1740 in the world frame; and the velocity of the ankle joint 1740 in the world
frame. In this
embodiment, the inertial measurement unit 1720 is physically coupled to the
lower leg
member 1712. In some embodiments, the inertial measurement unit 1720 is
coupled to the
foot member 1708 of the apparatus 1700.
[00189] FIG. 17H is a schematic illustration of a state estimation and
actuator controller
(state and actuator control PCA - SAC) for use with the apparatus of FIGS. 17A-
17G,
according to an illustrative embodiment of the invention. In this embodiment,
the controller
1762 employs dual 40 MHz dsPIC (manufactured by MicrochipTM) processors to
control and
coordinate linear actuator 1716 (e.g., rotary motor 504 of FIGS. 5A and 5B)
and the inertial
measurement unit 1720. In this embodiment, space-vector modulation is employed
to
implement the brushless motor control to create an optimum pulse width
modulated drive that
maximizes motor RPM. Space vector modulation is a PWM control algorithm for
multi-
phase AC generation, in which a reference signal is sampled regularly. PWM of
a signal or
power source involves the modulation of the three-phase motor winding voltage
duty cycles
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
42
(e.g., the rotary motor 504). After each sampling of the reference signal, non-
zero active
switching vectors adjacent to the reference vector and one or more of the zero
switching
vectors are selected for the appropriate fraction of the sampling period in
order to synthesize
the reference signal.
[00190] The controller 1762 receives a variety of input signals, including,
inertial pose
signals 1781 from the inertial measurement unit 1720, torque and axial force
signals 1783
from the structural element 1732 strain measurements, ankle joint angle
signals 1785 from a
hall-effect transducer located in the ankle joint 1740, motor position signals
1787 (quadrature
encoder with index and absolute motor position) from the encoder (e.g.,
encoder 2040 of FIG.
20A), strain signals 1789 from the strain sensor 1704 (referring to FIG. 18A)
of the series
elastic member 1728, and controller parameters 1791 (e.g., apparatus
configuration data,
wearer-specific tuning, firmware updates)). In addition, the controller 1762
outputs a variety
of signals, including, apparatus performance data 1793 (e.g., real-time data,
error log data,
real-time performance data), ankle state updates 1795. In addition, the
controller 1762
outputs commands to the linear actuator 1716 and receives actuator feedback
signals from the
linear actuator 1716 (generally signals 1797), for example, three-phase pulse
width
modulation signals provided to the power electronics for the linear actuator
1716, battery
power to the linear actuator 1716, and current feedback measurements and
temperature
measurements from the linear actuator 1716.
[00191] This embodiment uses the sensor feedback to identify state changes as
the
apparatus 1700 transitions through the stance-phase and swing-phase states. By
using the
redundant and diverse sensor measurements, it also identifies fault conditions
and drives the
apparatus 1700 into an appropriate safe state. Using an on-board real-time
clock, it time-tags
the faults and stores these into an on-board e2PROM (error log). The contents
of the error log
are retrieved wirelessly by the prosthetist and/or manufacturer service
personnel. In this
embodiment, the Motor Driver PCA (MD) takes pulse-width modulation (PWM)
commands
from the SAC PCA to switch current into the motor windings. The MD passes
sensed current
and power information back to the SAC PCA so that it can apply closed-loop
control.
[00192] In this embodiment, the IMU PCA is mounted nominally in the Sagittal
plane
(a local plane parallel to the front of the tibia) and employs a three-axis
accelerometer, a dual-
axis rate gyro (c)z and w) and a single-axis rate gyro (c)y). In this
embodiment, a coordinate
frame definition is used that defines the y-axis as forward, z-axis as up and
x-axis defined as
the cross-product of the y and z axes (y X z). The IMU receives state
information from the
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
43
SAC at the system sampling rate of 500 Hz. It transmits the ankle state vector-
specifically
the position and velocity of the ankle pivot, the position of the heel and the
position of the
toe-all with respect to the foot-flat position from the previous step.
[00193] FIGS. 171 and 17J are schematic illustrations of an exemplary
electrical
equivalent of apparatus 1700 of FIG. 17A. Electrical circuit symbols are used
to describe the
mechanical elements-a resistor denoting a mechanical component with damping
torque that
is linear with velocity; a capacitor denoting a mechanical component with
rotary inertia
properties; and an inductor denoting a mechanical component with linear spring
qualities.
With this circuit notation, current corresponds with torque and voltage
corresponds with
angular velocity.
[00194] The circuit components are defined as follows: J. / a k is the unknown
equivalent inertia of the lower leg member (shank) and residual limb below the
knee (e.g.,
inertia of lower leg member 1712 of FIG. 17A); Jam,,, ,,r is the equivalent
motor and ball-screw
transmission assembly inertia (e.g., inertia of linear actuator 1716 of FIG.
17A); = K QmMss,,"n
9P.i"l.P.S
is the torsional spring constant for the series spring (e.g., passive elastic
element 1728 of FIG.
17A) when in compression; Kt"7L,'"i"'z is the torsional spring constant for
the series spring
~ .4 PT"LE,S
when in tension; K3 is the torsional spring constant for the unidirectional
parallel spring (e.g.,
passive elastic member 1724 of FIG. 17A); and J4.,,k, . is the rotary inertia
of the foot
structure below the ankle (e.g., foot member 1708 of FIG. 17A). The current
(torque) sources
within the model are defined as follows: FHU,n,,,, is the unknown torque
applied by the
wearer's body onto the lower leg member (e.g., lower leg member 1712); Tt,,,.
is the torque
applied by the actuator (e.g., linear actuator 1716); and is the torque
measured using
the structural element (e.g., structural element 1732 of FIG. 17A and 17E).
[00195] FIG. 171 illustrates the importance of the series and parallel springs
as energy
storage elements. Use of the stored energy reduces the power consumption that
would
otherwise be required by the linear actuator. In addition, an additional
purpose of the K3
spring is its function as a shunt across the ankle inertia that increases the
ankle-spring
resonance.
[00196] FIG. 17J illustrates how sensors have been employed in this embodiment
to
provide high-fidelity position and force control, and to achieve the sensor
redundancy and
diversity desirable for delivering an inherently safe design. As shown, the
ankle joint
position, 0, is derived from the following:
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
44
= 0motom EQN. 38
where
IL. 5 if F ? 2r U
7 F 1i it i ../ \ o
EQN. 39
[00197] A redundant measure of 0 is achieved through use of a Hall-effect
angle
transducer, thereby providing a verification that the ankle is being
manipulated properly by
the control system. In one embodiment, the Hall-effect transducer includes a
Hall-effect
device located on the SAC PCA in the housing 1764 of the apparatus 1700. The
transducer
also includes a magnet coupled to the foot member 1708. The field effect
magnitude (signal
output by the transducer) changes in a known way in response to angle joint
rotation (i.e.,
motion of the magnet relative to the Hall-effect device). The Hall-effect
transducer is
calibrated during manufacturing of the apparatus 1700 by, for example,
measuring the output
of the transducer to known displacements of the Hall-effect device relative to
the magnet. In
other ankle angle measurement embodiments, the mutual inductance measured on a
coil on
the lower leg member has a known relationship as a function of ankle angle,
and the
inductance can be calibrated to compute angular displacement in a way that is
not sensitive to
the magnetic fields generated by the motor in the linear actuator or by other
stray fields.
Also, as shown in FIG. 17J, the ankle moment as applied by the wearer is also
measured.
This enables the linear actuator to adapt (e.g., to increase stiffness) to
achieve reflex behavior.
[00198] FIGS. 18A, 18B, 18C and 18D are illustrations of the passive elastic
member
1728 of FIG. 17A, according to an illustrative embodiment of the invention.
The passive
elastic member 1728 provides bidirectional stiffness and is connected in
series with the linear
actuator 1716 and the foot member 1708. The passive elastic member 1728 is
coupled at one
end to the second end 1748 of the linear actuator 1716, and at the other end
to the foot
member (not shown). The passive elastic member 1728 includes a strain sensor
1704
coupled to the passive elastic member 1728 for measuring strains in the
passive elastic
member 1728. In this embodiment, the strain sensor 1704 is a strain gage whose
response is
calibrated to measure the force applied by the linear actuator 1716 - and in
turn, the moment
about the ankle joint 1740 that is applied by the linear actuator 1716. The
strain gage signal
is measured using the controller 1762 of FIG. 17A.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
[00199] In this embodiment, the passive elastic member 1724 is a formed carbon-
fiber
layup that delivers a desired bidirectional (functions in bending in both
directions)
normalized drive stiffness. In one embodiment, the passive elastic member 1724
has a
preferred compression of 14-25 N-m/rad/kg and tension: 4-8 N-m/rad/kg.
Biomechanical
forces and torques strongly scale with body mass of a wearer. When scaling
prosthetic and
orthotic devices, design parameter specifications are typically normalized.
For example,
series and parallel elasticity such devices can be scaled with body mass, or
designed to
provide discrete values that are intended to cover several ranges of body
mass. The ranges of
compression and tension reflect the variation in torque that results from the
difference in the
linear actuator moment arm to the ankle joint across the entire range of
rotation-from
maximum plantarflexion to maximum dorsiflexion. The series spring constant is
optimized
to be relatively non-compliant during swing-phase dorsiflexion position
control (while the
spring is in compression) such as when the ankle is being repositioned
immediately following
toe-off in walking. However, some compliance is maintained to isolate the
linear actuator
from shock loads.
[00200] Referring to FIGS. 18C and 18D, high stiffness is achieved in the
passive
elastic member 1728 in compression by inserting a dorsiflexion rotation bottom
constraint
1708 towards the distal end 1726 of the passive elastic member (spring) 1728.
This restraint
reduces the effective moment arm of the linear actuator 1716 on the bending of
the series
spring 1728 during compression (towards dorsiflexion). In tension, the moment
arm is
effectively increased by placing the plantarflexion top constraint 1716 more
towards the
proximal end 1730 of the spring restraint. With the longer moment arm, the
spring beam will
bend more freely, thereby reducing the spring constant in tension. In addition
to the bilateral
stiffness characteristics, in some embodiments, the spring constant of the
passive elastic
member 1728 is optimized to minimize ball-screw rotational speed. By design,
this
embodiment of the elastic member 1728 has asymmetrical characteristics-
delivering higher
compliance in tension than in compression. The higher compliance in tension
increases the
energy storage in the series spring 1728 for use in powered plantarflexion.
The energy is
released in about the first 100 ms involved in powered plantarflexion, thereby
reducing the
energy contribution required of the linear actuator 1716. In embodiments of
the invention
that use a ball-screw transmission assembly in conjunction with a rotary motor
for the linear
actuator (e.g., ball-screw transmission assembly 2024 of FIGS. 20A-20B), this
has the added
benefit of reducing the required operating speed of the ball-nut assembly
portion of the ball-
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
46
screw transmission assembly and also the motor drive requirements for the
rotary motor. The
spring catapults the foot member without requiring high-speed ball-nut
positioning in this
case. Optimized values for the series elasticity are in the range of 3 -4
Nm/rad/kg.
[00201] FIG. 19A is an illustration of a lower-extremity prosthetic apparatus
1900
incorporating a flat series spring 1928, according to an illustrative
embodiment of the
invention. The apparatus 1900 has a mounting interface 1904 making it capable
of attaching
to a complementary lower-extremity limb socket member of a wearer. The
apparatus 1900
includes a lower leg member 1912 coupled to the mounting interface 1904. The
lower leg
member 1912 is also coupled to a foot member 1908 at an ankle joint 1940 of
the apparatus
1900. The ankle joint 1940 permits the foot member 1908 to rotate about the x-
axis relative
to the lower leg member 1912. The foot member includes a heel 1972 and a toe
1976.
[00202] The apparatus 1900 also includes a linear actuator 1916 with a first
end 1936
and a second end 1948. The first end 1936 of the linear actuator 1916 is
coupled to the lower
leg member 1912. The apparatus 1900 also includes passive elastic member 1928
in series
with the linear actuator 1916. The passive elastic member 1928 is coupled
between the foot
member 1908 and the second end 1948 of the linear actuator 1916. The passive
elastic
member 1928 is coupled to the foot member 1908 at the proximal end 1930 of the
passive
elastic member 1928. The distal end 1926 of the passive elastic member 1928 is
coupled to
the second end 1948 of the linear actuator 1916. The linear actuator 1916
applies torque
about the ankle joint 1940.
[00203] The apparatus 1900 also includes a controller 1960 coupled to the
linear
actuator 1916 for controlling the linear actuator 1916. In this embodiment,
the controller
1960 is located within a housing 1964 of the apparatus 1900 to protect it from
the
environment; however, a portion of the housing is removed in this figure to
expose the
contents within the housing). A battery 1968 coupled to the apparatus 1900
provides power
to the apparatus 1900 (e.g., the controller 1960 and various sensors
associated with the
apparatus 1900).
[00204] The passive elastic member 1928 of FIG. 19A is a flat spring (e.g.,
fabricated
with water-cut equipment). A flat spring reduces the cost of the passive
elastic member 1900
and makes it easier to configure the spring constant to align with the body
mass of the wearer.
In one embodiment, the spring is split longitudinally (along the y-axis) to
reduce the out-of-
plane moment on the components of a ball-nut (see, e.g., FIGS. 20A and 20B) of
the linear
actuator 1916 due to lack of parallelism between the rotation axis of the ball-
nut and the
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
47
series passive elastic member 1928. In this embodiment, no strain sensing is
employed in the
actuator torque feedback loop. Rather, the torque transmitted through the
spring is estimated
by multiplying the known spring constant of the flat spring by the measured
spring deflection
(difference between measured ankle joint 1940 angle, 0 and the angle, ~3,
kinematically
defined as the ankle joint 1940 angle that would result from a specific ball-
nut position along
the screw when the spring deflection is zero.
[00205] FIGS. 19B and 19C are illustrations of an alternative two-piece series-
elastic
spring of a prosthesis apparatus 1900, according to an illustrative embodiment
of the
invention. The apparatus 1900 has a mounting interface 1904 making it capable
of attaching
to a complementary lower-extremity limb socket member of a wearer. The
apparatus 1900
includes a lower leg member 1912 coupled to the mounting interface 1904. The
lower leg
member 1912 is also coupled to a foot member 1908 at an ankle joint 1940 of
the apparatus
1900. The ankle joint 1940 permits the foot member 1908 to rotate about the x-
axis relative
to the lower leg member 1912. The foot member includes a heel 1972 and a toe
1976. The
apparatus 1900 also includes a linear actuator 1916 with a first end (not
shown) and a second
end 1948. The first end of the linear actuator 1916 is coupled to the lower
leg member 1912.
The apparatus 1900 also includes a coupling member 1988 (e.g., bracket) that
couples the
foot member 1908 to the lower leg member 1912 at the ankle joint 1940 with a
bearing that
allows the foot member 1908 to rotate about the x-axis of the ankle joint
1940.
[00206] The apparatus 1900 also includes passive elastic member 1928 in series
with
the linear actuator 1916. Referring to FIG. 19C, the passive elastic member
1928 has two
member sections (e.g., beam-like sections) 1994 and 1996. The elastic member
1928 also has
a first end 1962 on the first member 1994 and a second end 1980 on the second
member
1996. The elastic member 1928 also has an intermediate location 1996 at which
the two
members 1994 and 1996 meet and at which the two members 1994 and 1996 pivot
with
respect to each other around the x-axis. As the second member 1996 pivots
towards the first
member 1994, the elastic member stores energy in compression during
dorsiflexion (shown
by the arrow 1992).
[00207] The first end 1962 of the elastic element 1928 is coupled to the
second end
1948 of the linear actuator 1916 with a bearing that allows for rotation about
the x-axis. The
second end 1980 of the elastic element 1928 couples to a location on the
coupling member
1988 with a bearing that allows for rotation about the x-axis.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
48
Exemplary Linear Actuator
[00208] FIGS. 20A and 20B are illustrations of a linear actuator 2000 for use
in various
lower-extremity prosthetic, orthotic, and exoskeleton apparatus, according to
an illustrative
embodiment of the invention. FIG. 20A is a perspective view of the linear
actuator 2000.
FIG. 20B is a cross-sectional view of the linear actuator 2000. The linear
actuator 2000 can
be used as, for example, the linear actuator 1716 of apparatus 1700 of FIG.
17A or apparatus
400 of FIG. 4. The actuator 2000 includes a motor 2004 and screw transmission
assembly
2024 (in this embodiment, it is a ball-screw transmission assembly, also
referred to as a ball-
screw assembly) for delivering linear power along the A axis. The screw
transmission
assembly 2024 functions as a motor drive transmission to translate rotational
motion of the
motor 2004 to linear motion. In one embodiment, the ball-screw transmission
assembly 2024
is a custom ball-screw transmission assembly manufactured by Nook Industries
(offices in
Cleveland, Ohio). The custom ball-screw transmission assembly has the
following
specifications: 14 mm x 3 mm pitch screw, 4000 N of thrust at 150 mm/s, and an
LI rated life
in the instant application of 5 million cycles. In some embodiments, the screw
transmission
assembly is a lead-screw transmission assembly (also referred to as a lead-
screw assembly).
[00209] The actuator 2000 includes a rotary motor 2004 that has a motor shaft
output
2008. The motor shaft output 2008 has a pulley 2032 coupled (e.g., welded) to
the motor
shaft output 2008. In one embodiment, the rotary motor 2004 is a high-speed
brushless
motor (model EC30 motor manufactured by Maxon Motor AG, Maxon Precision
Motors,
Inc. with offices in Fall River, MA). The motor 2004 includes an inductive
incremental-
absolute angular encoder 2040 that is integrated into the motor 2004 to for
determining
angular alignment between the rotor and stator of the rotary motor 2004. The
encoder 2040
also provides a position feedback signal necessary to control the screw 2060
position of the
linear actuator 2000 and to provide for "instant-on" motor commutation and
redundant
position feedback monitoring.
[00210] The inductively-coupled encoding elements of the encoder 2040 enable
the
system to determine the absolute rotor-stator alignment (with, for example, 10
bits of
resolution per revolution) simultaneously with high-precision incremental
rotor position
feedback. By cross-checking these redundant feedback elements it is possible
to minimize
the possibility that an encoder malfunction can cause ankle control
instability. The
incremental encoder achieves less than 300 rad of run-out so as to eliminate
the sensed
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
49
velocity fluctuations when the ball-screw transmission assembly 2024 (see
below) is
operating at constant-speed. As a result, less torque variation is applied by
the actuator 2000.
[00211] The rotary motor 2004 also includes an integral motor heat-sink 2048.
In one
embodiment, the heat-sink 2048 draws heat out of the windings of the motor
2004, enabling a
wearer to walk at peak levels of non-conservative work without exceeding motor
coil
temperature limits (typically 160 C). Motor heating arises due to resistive
losses (i2R losses)
in the motor 2004 as the linear actuator 2000 delivers thrust force. As the
coil temperature
rises, the coil resistance rises at the rate of 0.39%/ C, thereby further
increasing the coil
temperature. In addition, the motor Kt (a measure of torque as it scales with
motor current)
typically drops by nearly 20% as the coil temperature increases to its limit.
This requires
additional current consumption to perform the same amount of work, further
driving up the
coil temperature. The heat-sink in the linear actuator 2000 reduces coil
temperature rise by
over 40%. Because the wear out phenomenon that drives premature failure of
motor winding
insulation and motor bearing reduces in effect by a factor of 2X for every
coil temperature
reduction of 10 C, the motor life increases significantly if lower motor coil
operating
temperatures are maintained. And, using this intrinsic coil temperature
sensing method, the
motor can be protected from exceeding the absolute maximum rating of 160 C by
simply
reducing powered plantarflexion power (currents) as the maximum rating is
approached, and
ultimately, shutting off battery power when a predefined limit of, for
example, 150 C is
reached.
[00212] Robotic prostheses typically employ compact light-weight motor drives
to
deliver power in bursts to the affected limb. In some scenarios, the power
bursts may be
applied repetitively and at high rate over extended periods of time. The motor
copper and
eddy current losses will cause an excessive accumulated heating effect that
causes the motor
winding temperature to rise. Since the copper winding resistance increases
with temperature
(0.39%/ C), the copper losses will increase thereby amplifying the heating
effect. A critical
winding temperature limit can sometimes be reached in which further
temperature rise will
cause permanent damage to the motor. Sensing when this temperature limit is
reached is
preferably accomplished by the control system.
[00213] Two conventional methods may be used to prevent or detect when the
copper
winding temperature limit is or will be reached. In the first, the copper and
eddy current
losses are computed while the control system operates. These are used to drive
a thermal
model of the windings so that the winding temperature can be estimated.
Sometimes the
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
ambient temperature is measured in order to yield a better winding temperature
measurement.
An advantage of this method is that it is cheap to implement. The disadvantage
is that the
coil temperature model is hard to obtain and to calibrate. Also, it is often
difficult to make a
good measurement of the ambient temperature around the motor, causing the
winding
temperature measurement to be in error.
[00214] In the second method, sometimes combined with the first, the case
temperature
of the motor is measured with a thermistor applied to the outside of the case,
or inside the
motor. The advantage of this is that it provides a direct measurement. The
disadvantage is
that it only measures at one point and the application of the sensor is
expensive and often
unreliable.
[00215] A more preferred approach is to both detect the temperature and to
mitigate the
potential overheating condition. In this, we measure the motor winding
resistance on every
step at a point during the walking cycle when we can briefly hold the ankle at
a fixed position
(this to eliminate back-emf effects on the resistance calculation) to make the
measurement.
In one embodiment, coil temperature is determined by applying a fixed current
(alternatively
fixed voltage) to the motor winding and measuring the corresponding voltage
(alternatively
current) in the winding. To increase the accuracy, we apply the voltage (or
current) in both
the forward and reverse direction and measure the difference in current (or
voltage).
[00216] Since the motor drive electronics employs PWM current control methods,
all
the infrastructure to make this measurement exist. By noting the percentage
difference
between this winding resistance and that when the ankle is at rest (a
calibration constant) we
can estimate the winding resistance in-situ without cost. In a typical servo
system this
measurement cannot be made because the actuator must be continually in closed-
loop
control. But in the ankle prosthesis, there are times (swing phase) when the
ankle position
does not need to sustain the precision control over the 5 milliseconds
typically required to
make the measurement. Once the winding temperature is calculated in this way,
the control
system can detect when the windings are approaching the critical temperature.
During these
times, the drive power available for walking is reduced or eliminated
altogether until the
temperature is reduced to a safe level.
[00217] In some embodiments, the output of the temperature sensor 2052 is
provided to
a controller (e.g., the controller 1762 of FIG. 17A) to control torque output
by the linear
actuator 2000 based on the temperature of the motor 2004.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
51
[00218] A belt 2012 couples the pulley 2032 to the threaded shaft 2060 of a
ball-screw
transmission assembly 2024 such that rotational motion of the motor shaft
output 2008 is
translated to a linear motion of the ball-nut assembly 2036 portion of the
ball-screw
transmission assembly 2024. In some embodiments, two or more belts are applied
in parallel,
each with an ability to drive the linear actuator 2000 ball-screw transmission
assembly 2024
by itself, so as to enable the linear actuator 2000 to survive a single belt
breakage failure. In
such an event, belt break sensor 2056 senses the condition and validates belt
integrity during
operation (e.g., during each gait cycle of a wearer using a prosthesis).
[00219] In one embodiment, an optical sensor (e.g., a thru-beam sensor) is
used as the
belt break sensor and an output signal of the optical sensor changes in a
known manner when
a belt breaks. In another embodiment of the invention, a capacitive sensor is
used as the belt
break sensor and an output of the capacitive sensor changes in a known manner
when a belt
breaks.
[00220] In one embodiment, the pulley 2032 and belt(s) are not used as the
apparatus
for converting rotary motion to a linear motion. Rather, a set of traction
wheels are used as
the transmission apparatus. In this embodiment, the threat of belt failure is
thereby
eliminated.
[00221] In one embodiment, in the event of a belt break, a controller of the
apparatus in
which the linear actuator 2000 is used (e.g., controller 1762 of apparatus
1700 of FIG. 17A),
changes the position of the foot member relative to the lower leg member to a
safe position
that enables the apparatus to operate as a passive ankle prosthesis until the
linear actuator
2000 is repaired. In one embodiment, the controller shorts three electrical
leads of the rotary
motor 2004 in response to the belt breakage sensor detecting a failure of one
or more of the
plurality of belts. Shorting the three-phase electrical input leads to the
motor 2004 introduce
a viscous drag on the motor shaft output 2008. While walking, the viscous drag
holds
roughly fixed the rotor shaft output so that the apparatus operates as a
passive prosthesis.
However, the apparatus can be moved slowly in a way that enables it to move to
a non-fixed
equilibrium position when standing or sitting. Each input lead is shorted to
ground by its
own individual switch.
[00222] In one embodiment, the switches are operated by a rechargeable battery
(a
separate battery from the primary battery used to operate the apparatus). By
using a separate
battery, the switches would short the input leads (and place the apparatus
into a safe mode)
even if a failure occurred (or the primary battery was depleted).
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
52
[00223] In one embodiment, the threaded shaft 2060 includes a hollowed out
portion
that contains a noise damping material to reduce the noise generated by the
actuator 2000 and
the apparatus within which the actuator 2000 is used. In one embodiment, the
threaded shaft
2060 is 14 mm diameter stainless steel shaft 8.7 mm diameter bore that extends
64 mm of the
length of the shaft, filled with ISODAMP C-1002 acoustic damping material
manufactured
by 3M (with offices in St. Paul, MN).
[00224] The actuator 2000 also includes a radial and thrust bearing 2028 that
support
the belt 2024 tension due to the rotary motor 2004 and the thrust force of the
screw 2036.
Loads due to the belt tension and thrust force are present both statically and
during the gait
cycle.
[00225] The ball-nut assembly 2036 includes one or more recirculating ball-
tracks 2042
that retain a plurality of ball bearings; the combination of which support the
linear motion of
the ball-nut assembly 2036. In one embodiment, five ball-tracks are used. The
actuator 2000
includes a coupling element 2020 (e.g., the second end 1748 of the linear
actuator 1716 of
FIG. 17A) that couples the actuator 2000 to, for example, a passive elastic
member of a foot
member of a prosthetic apparatus (e.g., passive elastic member 1724 of FIG.
17A).
[00226] FIG. 21 is an illustration of a perspective view of a linear actuator
2100 for use
in various lower-extremity prosthetic, orthotic, and exoskeleton apparatus,
according to an
illustrative embodiment of the invention. The linear actuator 2100 can be used
as, for
example, the linear actuator 1016 of apparatus 1000 of FIG. 17A or apparatus
400 of FIG. 4.
The linear actuator 2100 is a variation of the actuator 2000 of FIGS. 20A and
20B.
[00227] The actuator 2100 includes a rotary motor 2004 that has a motor shaft
output
2008. The motor shaft output 2008 has a pulley 2032 welded to the motor shaft
output 2008.
The motor 2004 includes an inductive incremental-absolute angular encoder 2040
that is
integrated into the motor 2004 to for determining angular alignment between
the rotary motor
2004 rotor and stator. The rotary motor 2004 also includes an integral motor
heat-sink 2048.
[00228] Two belts 2104a and 2104b are used in parallel, rather than the single
belt 2012
of FIGS. 20A and 20B. Each belt has the ability to drive the linear actuator
transmission by
itself with 1.5x margin on belt breakage, so as to enable the linear actuator
2100 to survive a
single belt breakage failure. In one embodiment, in the event of a belt break,
a controller of
the apparatus in which the linear actuator 500 is used (e.g., controller 1762
of apparatus 1700
of FIG. 17A) moves the ankle to a safe position in a way that would enable the
apparatus to
operate as a passive ankle prosthetic until the linear actuator 500 is
repaired. In one
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
53
embodiment, the controller shorts three electrical leads of the rotary motor
504 in response to
the belt breakage sensor detecting a failure of one or more of the plurality
of belts. In such an
event, one or more belt break sensors would sense the condition and move the
ankle to a safe
position in a way that would enable the system to operate as a passive ankle
prosthesis until
the linear actuator is repaired.
[00229] The two belts 2104a and 2104b couple the pulley 532 to a threaded
shaft of a
ball-screw transmission assembly (e.g., threaded shaft 2060 of FIG. 20B) such
that rotational
motion of the motor shaft output 2008 is translated to a linear motion of the
ball-nut assembly
2036 portion of the ball-screw transmission assembly. The actuator 2100 also
includes a
radial and thrust bearing 2028 that support the tension in belts 2104a and
2104b due to the
rotary motor 2004 and the thrust force of the threaded screw. Loads due to the
belt tension
and thrust force are present both statically and during the gait cycle.
[00230] The ball-nut assembly 2036 includes recirculating ball-tracks that
retain a
plurality of ball bearings; the combination of which support the linear motion
of the ball-nut
assembly 2036. The actuator 2100 includes a coupling element 2020 (e.g., the
second end
1748 of the linear actuator 1716 of FIG. 17A) that couples the actuator 2100
to, for example,
a passive elastic member of a foot member of a prosthetic apparatus (e.g.,
passive elastic
member 1724 of FIG. 17A).
[00231] The actuator 2100 also includes a ball-screw assembly seal 2108. The
ball-
screw assembly seal 2108 protects the screw from, for example, contaminants
(e.g., sand,
dirt, corrosive materials, sticky materials). Such contamination would cause
the design life of
the actuator to become indeterminate.
Exemplary Lower-Extremity Orthotic (Wearable Robotic Knee Brace)
[00232] FIGS. 22A, 22B and 22C are schematic illustrations of a lower-
extremity
orthotic or exoskeleton apparatus 2200 (wearable robotic knee brace),
according to an
illustrative embodiment of the invention. The apparatus 2200 is a knee-brace
that augments
the wearer's lower-extremity function. FIG. 22A is a top view of the apparatus
2200. FIG.
22B is a side view of the apparatus 2200. FIG. 22C is a view of the interior
portion of a knee
joint drive assembly 2204 of the apparatus 2200. Typical use cases for the
apparatus 2200
include, for example, metabolic augmentation, permanent assistance for wearers
with a
permanent limb pathology, or rehabilitation for wearers with temporary limb
pathology.
[00233] An example of a metabolic augmentation use case involves, for example,
wearers (e.g., soldiers or other personnel) that need to traverse heavy
terrain for extended
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
54
periods at high speed while carrying heavy loads. In this use case, the knee
brace apparatus
2200 augments the wearer's own abilities. An example of a permanent assistance
use
involves a wearer that suffers from a permanent limb pathology (e.g., knee
tendon or
meniscus degeneration) with no possibility for rehabilitation. In this use
case, the knee brace
apparatus 2200 provides permanent assistance to the wearer. An example of a
use case
involving rehabilitation for wearers with temporary limb pathology involves a
wearer
recovering from injury or other temporary condition. In this use case, the
knee brace
apparatus 2200 functions as a programmable telerobotic tool deployed by a
physical therapist
to accelerate recovery-through progression of kinesthetic rehabilitation and
gradually
decreasing assistance while the muscle memory and strength recover. In another
embodiment, the method includes specifying a physical therapy protocol
defining a level of
assistance performed by the apparatus on the wearer over a period of time and
reducing the
level of assistance performed by the apparatus on the wearer to assist in
rehabilitation of the
limb pathology. In some embodiments, the level of assistance performed by the
apparatus is
reduced based on impedance and torque contribution of the wearer to the
apparatus.
[00234] Referring to FIGS. 22A and 22B, the apparatus 2200 includes a lower
leg
member 2216 (also referred to as a drive arm), a thigh member 2228, a lower
leg cuff 2208
and an upper leg cuff 2212. The lower leg cuff 2208 is coupled to the lower
leg member
2228. The lower leg cuff 2208 attaches the apparatus 2200 to the lower leg of
the wearer.
The upper leg cuff 2212 is coupled to the thigh member 2228. The upper leg
cuff 2212
attaches the apparatus 2200 to the thigh of the wearer. The apparatus 2200
includes a knee
joint 2232 for connecting the thigh member 2228 to the lower leg member 2216.
The knee
joint 2232 (e.g., a rotary bearing) permits the lower leg member 2216 to
rotate about the x-
axis relative to the thigh member 2228.
[00235] Referring to FIG. 22C, the knee joint drive assembly 2204 includes a
linear
actuator that drives the knee joint drum 2232 through a belt drive
transmission 2236. The
linear actuator is a rotary motor 2240 (e.g., brushless motor) and ball-screw
transmission
assembly 2244 (e.g., the motor 2004 and ball-screw transmission assembly 2024
of FIGS.
20A and 20B). In the apparatus 2200, rotational motion of the motor shaft
output 2256 of the
motor 2240 is translated to a linear motion of the ball-nut assembly 2248
portion of the ball-
screw transmission assembly 2244. The motor shaft output 2256 has a pulley
2260 coupled
(e.g., welded) to the motor shaft output 2256. The motor 2240 includes an
inductive
incremental-absolute angular encoder 2264 that is integrated into the motor
2240 for
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
determining angular alignment between the rotor and stator of the rotary motor
2240. The
encoder also provides a position feedback signal necessary to control the
screw 2252 position
of the ball-screw transmission assembly 2244 and to provide for "instant-on"
motor
commutation and redundant position feedback monitoring.
[00236] A belt 2268 couples the pulley 2260 to the threaded shaft 2252 of the
ball-
screw transmission assembly 2244 such that rotational motion of the motor
shaft output 2256
is translated to a linear motion of the ball-nut assembly 2248 portion of the
ball-screw
transmission assembly 2244.
[00237] In one embodiment, the threaded shaft 2252 includes a hollowed out
portion
that contains a noise damping material to reduce the noise generated by the
knee joint drive
assembly 2204. The knee joint drive assembly 2204 also includes a radial and
thrust bearing
2272 that support the belt 2268 tension due to the rotary motor 2240 and the
thrust force of
the screw 2252. Loads due to the belt tension and thrust force are present
both statically and
during the gait cycle.
[00238] The knee joint drive assembly 2204 also includes a spring 2280 for
series
elasticity, spring cage 2284, drive belt 2236 and a spring cage/belt
connection 2288. In some
embodiments, a drive band (e.g., thin piece of spring steel) is used in place
of the drive belt
2236. In some embodiments, a drive cable (e.g., loop of stranded material) is
used instead of
the drive belt 2236. Spring 2280 is a series passive elastic element,
functioning in the same
manner as the series elastic spring element 1728 of FIG. 17A. The spring cage
2284 provides
a closed volume in which the spring 2280 is located. The ball-nut transmission
assembly
2248 is coupled to the screw 2252. The ball-nut assembly 2248 is also coupled
to the drive
belt 2236. Linear motion of the screw 2252 causes a linear motion in the ball-
nut assembly
2248. The linear motion in the ball-nut assembly 2248 causes a linear motion
in the drive
belt 2236. The linear motion of the drive belt 2236 drives the knee joint
2232.
[00239] The apparatus 2200 includes a controller 2292 (e.g., a printed circuit
assembly
that incorporates the linear actuator 2204, state and inertial measurement
unit 2294 (e.g.,
inertial measurement unit 1720 of FIG. 17A) control and processing functions)
to drive and
control the operation of the apparatus 2200. Referring to FIG. 22B, the
apparatus 2200 also
includes a torque sensor 2220 coupled to the lower leg member 2216 to measure
the torque
applied to the lower leg member 2216 by the knee joint drive assembly 2204.
The sensor
2220 serves as the feedback element in the control loop of the controller 2292
to achieve high
fidelity closed loop position, impedance and torque (for reflex) control of
the knee joint 2232.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
56
In one embodiment, an array of force-sensitive transducers are embedded within
the cuff
structure to provide force measurements used to achieve rapid, biomimetic
response.
[00240] In some embodiments, the motor angle sensor (e.g., encoder 2264)
measures
motor position and the controller controls the rotary motor to modulate
position, impedance
and torque of the knee joint 2232 based on the motor position.
[00241] In some embodiments, the apparatus 2200 includes an angle sensor for
determining position of the drum 2232 of the belt drive transmission relative
to the output of
the motor drive transmission and the controller controls the rotary motor for
modulating
impedance, position or torque based on the position. In some embodiments, the
apparatus
2200 includes a displacement sensor for measuring displacement of a series
spring in the
motor drive transmission for determining force on the series spring and the
controller controls
the rotary motor for modulating impedance, position or torque based on the
force on the
spring. In some embodiments, the inertial measurement unit 2294 is coupled to
the thigh
member or lower leg member for determining an inertial pose of the lower leg
member and
the controller controls the rotary motor for modulating impedance, position or
torque based
on the inertial pose. In some embodiments, the torque sensor 2220 measures the
torque
applied to the lower leg member by the belt drive transmission and the
controller controls the
rotary motor for modulating impedance, position or torque based on the torque
applied to the
lower leg member. In some embodiments, the apparatus 2200 includes an angle
sensor for
determining an angle between the thigh member and lower leg member and wherein
the
controller controls the rotary motor for modulating impedance, position or
torque based on
the angle between the thigh member and lower leg member.
[00242] In some embodiments, the apparatus 2200, instead of a motor drive
transmission, the apparatus includes a screw transmission assembly coupled to
the motor
shaft output for converting the rotary motion of the motor shaft output to a
linear motion
output by the screw transmission assembly. In addition, the drive transmission
assembly
coupled to the output of the motor drive transmission is a redundant belt,
band or cable drive
transmission coupled to the screw transmission assembly to convert a linear
motion output by
the screw transmission assembly to a rotary motion for applying torque to the
knee joint to
rotate the lower leg member with respect to the thigh member.
[00243] Unlike the prosthetic apparatus 2000 of FIG. 20A, the knee brace
apparatus
2200 operates in parallel with human actuation. In metabolic augmentation and
replacement
applications, the knee brace control system will supply all of the impedance
and torque needs
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
57
within the gait cycle. It is desirable for the wearer to be able to walk all
day without getting
tired and without exertion on the augmented side(s) of the body. In
rehabilitation
applications, the knee-brace apparatus 2200 supplies only a programmed
percentage of the
impedance and torque. In such applications, the knee-brace apparatus 2200
serves as a
telerobotic extension of the physical therapist supervising the wearer's
rehabilitation.
[00244] In one embodiment of the knee brace control system, the physical
therapist
creates a protocol to be executed telerobotically by the knee brace over a
period of time
between therapist visits. Using a wireless interface, patient performance can
be fed back to
the physical therapist, thereby achieving telepresence. The protocol specifies
the rate at
which the assistance diminishes over time. As the knee brace apparatus reduces
assistance,
the knee brace apparatus would compute via biomechanical models the impedance
and torque
contribution by the wearer-reducing assistance in accordance with the improved
response to
maintain the desired net biomimetic response. The biomechanical models would
involve
solving the inverse dynamics of the knee-incorporating inertial rotation and
acceleration of
the lower leg member, thigh member and torso. This six degree-of-freedom
information
would be derived from the inertial measurement unit in the thigh member and
knee joint
angular displacement. The zero-velocity update for the inertial measurement
unit would be
accomplished similarly as described herein.
[00245] FIG. 26 depicts the biomechanical features of normal human gait during
ambulation, initiating and ending at the point of heel strike. It is divided
into the stance and
swing phases, and entails all elements of motion at the hip, knee, and ankle.
Myopathic
diseases, such as IBM (inclusion body myositis), are associated with principal
quadriceps
weakness, which adversely impacts the patient's ability to ambulate safely and
efficiently.
Equally as important, patients with IBM are unable to safely transition
between resting
(standing or sitting) and ambulatory states.
[00246] FIG. 27 illustrates the biomechanical mechanism by which quadriceps
weakness affect ambulation on level ground. The overall mechanical sequence is
deficient
with respect to FIG. 26 in two ways. First, the knee may buckle in early
stance if the
stiffness (or mechanical impedance) of the knee joint in early stance is
inadequate to absorb
the shock of foot strike and to apply restorative torque to maintain balance
(indicated by
reference no. 2710). The inability for the quadriceps to actively stiffen the
knee to absorb the
foot-strike constrains walking speed, similar to driving a car without brakes.
Note that
mechanical impedance refers to the stiffness that a joint exerts, and is known
to possess three
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
58
components, a spring component defined by the spring constant and equilibrium
position that
applies a linear or non-linear restoring torque in response to joint
displacement; a damping
component that applies a linear or non-linear viscous restoring torque in
response to joint
velocity; and an inertial component that applies a linear restoring torque in
response to joint
acceleration and second, in late stance and early swing, the quadriceps may be
incapable of
applying the knee braking torque to impede rapid knee flexion (indicated by
reference no.
2720).
[00247] The knee apparatus depicted in FIGS. 22A-C may be used as a robotic-
assisted
solution to deal with the deficiencies identified above in connection with
FIG. 27. FIG. 28
demonstrates using a knee apparatus to restore normal ambulation by employing
intrinsic
sensing of lower limb trajectory, and by applying biomimetic impedance,
augmentative
torque, and position control to the patient's knee joint in accordance with
the phase of the gait
cycle, in order to reconstruct the desired gait trajectory state, terrain,
body pose and stability.
[00248] In early stance (indicated by reference no. 2810), the knee apparatus
provides
an increased stiffness to absorb the foot strike energy and to provide a
stable platform from
which the trailing leg can leave the ground. In late stance as the ankle
plantar flexes
(indicated by reference no. 2820), and the knee apparatus uses intrinsic
measures of thigh and
shank orientation and of the wearer's walking speed to apply a biomimetic,
reflexive
torque-identical to that would be supplied by a fully-functional quadriceps
muscle-that
propels the wearer upward and forward for metabolically-efficient ambulation.
Later, when
the knee apparatus senses that the lower-limb is in the swing-phase (indicated
by reference
no. 2830), the knee is flexed and a high impedance is applied that will absorb
(brake) the
lower-limb as the foot strikes the ground. The result is safe and
metabolically-efficient
ambulation.
Balance Using Ground Reaction Forces and Zero moment pivot
[00249] FIG. 23A illustrates the generic problem of achieving balance on an
incline of
variable (positive or negative) slope. The problem appears to involve a multi-
link, "inverted
pendulum' 'problem, amenable to a non-linear feedback control implementation.
In such
solutions, knowledge of the link angles and the mass properties of the links
(in this case, leg
segments, torso, head and arms) are used to explicitly stabilize the multi-
link system. But
such explicit inputs are not contained within most embodiments of a lower-
extremity
prosthetic, orthotic or exoskeleton apparatus and would therefore be difficult
if not
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
59
impossible to implement and package reliably on the wearer. Further, in some
instances, the
wearer will have one intact leg, so part of the stabilization will be achieved
outside of the
lower-extremity prosthetic, orthotic or exoskeleton apparatus, wherein the
lower-extremity
prosthetic, orthotic or exoskeleton apparatus augments the function of the
intact leg.
[00250] In addition, FIG. 23B shows that there is a continuum of acceptable
solutions
to the balance problem. Specifically, there are an infinite number of bent-
knee solutions that
are entirely acceptable and even desirable depending on human intent (e.g.,
picking up heavy
luggage or boxes or to achieve balance while playing a game). So we see that
the desired
solution will employ intrinsic (to the lower-extremity prosthetic, orthotic or
exoskeleton
apparatus) sensing that complements the intact balance-producing body
components to
achieve equilibrium in alignment with human intent.
[00251] The solution employed in some embodiments of the lower-extremity
prosthetic, orthotic or exoskeleton apparatus uses a simplified representation
of the problem
as modeled in FIG. 23C. In this representation, intrinsic sensing of lower leg
member inertial
state, ankle joint angle and inertially-referenced, ground reaction force, are
used as the
stabilization feedback that drives ankle torque (e.g., torque provided to the
ankle joint by a
linear actuator of a prosthetic apparatus). The body is modeled as a series of
masses (only
one shown in the figure) on a massless, thin, buckling beam with time-variable
stiffness and
moment-of-inertia.
[00252] Balance is achieved based on the following details. A desirable
equilibrium is
achieved when the following conditions are satisfied:
1. WFGRF aligns with World z;
2. The line connecting the zero moment pivot and the ankle joint aligns with
the
World z unit vector; and
3. All time derivatives of the inertial lower leg member angle, y, and ankle
joint angle,
?, are zero.
[00253] A feedback control law is then derived that drives each of these
conditions into
equilibrium based on the following:
0' FcnF Y ]T EQN. 40
T ankle AOcc k (s)[ 'Y LP
where
k (s) _ [kY (s) kF (s) kY (s)] EQN. 41
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
optimizes the quadratic cost index, J, where
j = f (iankle + kT [,,,]T [yyy]T k)dt EQN. 42
0
and
k = [k7 ky kY ] EQN. 43
where the components of k are chosen to emphasize link angle dynamic
contributions to the
cost index. In this embodiment, the control law solution is provided by the
linear-quadratic
regulator (LQR) methodology. In layman's terms this means that the settings of
a
(regulating) controller governing either a machine or process are found by
using the above
mathematical algorithms and minimizing a cost function with weighting factors
supplied by a
human. The "cost" (function) is often defined as a sum of the deviations of
key
measurements from their desired values. In effect this algorithm therefore
finds those
controller settings that minimize the undesired deviations, for example,
deviations from
desired work performed by a prosthesis for the wearer. Often the magnitude of
the control
action itself is included in this sum as to keep the energy expended by the
control action itself
limited. In effect, the LQR algorithm optimizes the controller based on an
engineer's
specification of the weighting factors. The LQR algorithm is, at its core,
just an automated
way of finding an appropriate state-feedback controller.
[00254] Use of the quadratic cost index is not required; however, in one
embodiment,
use of the quadratic cost index as an optimization criterion creates an
objective framework for
analysis and for in-office customization for wearers of the lower-extremity
prosthesis to
achieve an acceptable feel as the system works to maintain the wearer's
equilibrium on
different terrain. It is not uncommon to find that control engineers prefer
alternative
conventional methods like full state feedback (also known as pole placement)
to find a
controller over the use of the LQR algorithm. With these the engineer has a
much clearer
linkage between adjusted parameters and the resulting changes in controller
behavior.
Wearer Assist in Getting Up from a Chair
[00255] FIGS. 24A, 24B and 24C illustrate a method for applying a balancing
control
law to assist a wearer of a lower-extremity prosthetic apparatus in getting up
from a chair,
according an illustrative embodiment of the invention. The Timed Get Up and Go
(TUG) is
often used as an experimental means to evaluate dynamic and functional
balance. Wearers
are given a verbal instruction to stand up from a chair, walk 3 meters, cross
a line marked on
the floor, turn around, walk back, and sit down. To achieve good "TUG"
performance, leg
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
61
prostheses often have a "stand up" and "sit down" button to create the
behavioral context for
the prosthesis' control system. In the lower-extremity prosthetic apparatus
incorporating
principles of the present invention, in one embodiment there is no explicit
requirement to set
behavioral context by, for example, pushing a button. Sitting, standing up and
sitting down
behavioral context is identified by the intrinsic sensors of the prosthetic
apparatus. Control
behavior during standing and sitting is simply part of maintaining the
wearer's equilibrium.
[00256] FIGS. 24A, 24B and 24C illustrate how the intrinsic balance control
algorithm
works to augment the wearer as she stands up from a chair. Referring to FIG.
24A, initiation
of the sitting to standing transition involves three states. In the first, the
foot is off the ground
or only lightly touching it. The prosthetic apparatus (e.g., apparatus 1700 of
FIGS. 17A-17E)
knows the mass of the wearer; the inertial orientation of the lower leg member
and foot
member; and the ground reaction force (as determined, for example, with
respect to FIG.
11A). The apparatus therefore "knows" or senses that the wearer is sitting. As
the wearer
begins to stand up, the increase in ground reaction force is noted and the
state of the foot
(foot flat) is known via the inertial measurement unit measurements and ankle
joint angle
sensor measurements. The intrinsic balance control law execution begins.
During this
second state, the disequilibrium sensed by the imbalance in the ground
reaction force is used
to drive the lower leg member (e.g., driven forward by the controller 1762
commanding the
linear actuator 1716 to increase the torque applied to the ankle joint 1740)
forward as a means
of pulling the torso (center-of-mass) over the ankle joint.
[00257] Referring to FIG. 24B, the intrinsic balance control continues to
drive the
wearer into equilibrium in front of the chair. FIG. 24C shows the wearer in
mid-stance
equilibrium, ready to begin walking if desired. As shown, wearer intent, and
more
specifically the sitting/standing behavioral context can be derived by sensing
that is intrinsic
to the prosthetic apparatus. The implementation cost and complexity of
explicit context
switching (pressing of buttons) is thereby avoided. The prosthetic apparatus
complements
and augments the body function in a natural way.
[00258] The ankle torque induced by the ground reaction force (GRF) is a
preferred
way to achieve exponential hardening during mid-stance. Unlike use of the
torque on the
lower leg (e.g., torque measured using the structural element 1732 of FIG.
17A), the GRF-
computed ankle torque measures the torque applied by the ground on the ankle
joint. The
GRF is often measured by force plates in gait research settings and is thereby
used as a
measure of how an intact ankle interacts with the ground while walking. The
GRF
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
62
establishes what is the biomimetic ankle behavior in different terrain
contexts. A benefit of
using the GRF as the means by which to achieve exponential hardening is the
ease by which
performance can be measured relative to biomimetic references. Further, use of
this measure
ensures that invariance to terrain orientation since it derives from intrinsic
inertial sensing
(e.g., using the inertial measurement unit 1720 of FIG. 17A).
[00259] Stand-up assistance can also be implemented using the knee orthosis
depicted in FIGS. 22A-C or more generally any active knee orthosis or
prosthesis. The
seemingly simple task of elevating oneself from a sitting to a standing
position is actually a
complex task that incorporates the participation of the knee and hip extensors
to apply
lifting torque and restorative balance in a step-wise sequence of actions.
FIGS. 29A-D
depicts the ordinary stand-up sequence for a healthy person, which involves
four phases:
sitting, shown in FIG. 29A; (b) repositioning the knee over the foot in
preparation for
standing up, shown in FIG. 29B; (c) the transition from sitting to standing,
shown in FIG.
29C; and (d) balancing once the body has been lifted, shown in FIG. 29D.
[00260] FIGS. 30A-D depicts the problems in implementing the same stand-up
sequence for a person wearing an active leg orthosis or prosthesis, because
some of those
same four phases cannot be carried out. More specifically, starting at the
seated position,
shown in FIG. 30A, most orthotic or prosthetic wearers maintain sufficient
strength in their
arms to position themselves in a chair, thus allowing them to preposition the
knee and
torso over the ankle and implement phase b, shown in FIG. 30B. However, the
lack of
strength in the quadriceps and/or hip extensors prevents the rotation in phase
c that lifts the
upper leg and torso out of the chair, indicated by the X 3010 in FIG. 30C. In
addition, in
the absence of sufficient extensor torque at the knee and hip, it is virtually
impossible for
the patient with inadequate knee and/or hip muscular strength to decelerate
the torso and to
maintain balance once the upright posture is achieved, indicated by the X 3020
in FIG.
30D.
[00261] FIGS. 31A-D depicts how an active knee apparatus such as an active
orthosis
(depicted in FIGS. 22A-C) or an active knee prosthesis can be used to assist
the stand-up
sequence for a patient suffering from limb pathology. This requires the
ability to
recognize that the user is currently seated, and also an ability to
distinguish between a
user's desire to remain seated and the user's desire to start standing.
[00262] One indicator that the user is currently seated is when the thigh is
substantially horizontal as shown in FIG. 31A. The attitude of the thigh may
be
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
63
determined using inertial sensors mounted in the knee apparatus that measure
the gravity
vector in relation to the thigh coordinate system, because in a seated
position the gravity
vector lies principally in the x-y plane of the thigh (orthogonal to the z-
axis). Another
indicator of being in a seated position is based on the rotation angle of the
shank in
relation to the thigh (which can be obtained using an angular encoder) because
in a relaxed
sitting positions, the ankle joint is typically well-forward of the knee.
These conditions
can be detected and relied on by the system to remain in the seated mode, by,
for example,
maintaining a low joint impedance consistent with a relaxed, sitting position.
[00263] These same sensors can then be used to detect the user's desire to
transition
to a standing position by detecting when the ankle joint has been placed more
nearly under
the knee joint as shown in FIG. 31B. When this situation is detected, the
system preferably
attempts to verify the user's desire to stand by tentatively initiating a
stand-up routine. If
the system received positive feedback from the user, the stand-up routine
proceeds. If,
however, the system does not receive positive feedback from the user, the
stand-up routine
is aborted.
[00264] This tentative initiation of a stand-up routine may be implemented by
having
the knee apparatus apply increasing torque 3110 gradually in accordance with
the estimated
upward and forward velocity of the hip joint, shown in FIG. 31 C. Positive
feedback can be
provided by the user by trying to lift her body with her arms to displace the
hip joint
vertically to assist the knee apparatus in lifting. In this situation, the hip
will displace more
vertically, and the gravity vector will begin to transition towards the z-
axis. The system
interprets those conditions as verification that the user really does want to
stand. In response,
the system applies more torque to continue lifting the user.
[00265] Alternatively, positive feedback from the user could be in the form of
a
measured electromyographic signal from the wearer's thigh and/or hip
musculature using
surface or implanted electrodes. More specifically, once the apparatus has
detected that the
knee joint has moved forward the ankle joint, the standup routine could be
initiated by the
wearer flexing her quadriceps and/or hip extensors. The apparatus would then
measure these
electromyographic signals, amplify and filter each muscle output, and extract
signal features
such as magnitude, variance, and/or frequency using conventional techniques.
These
extracted features could then be used to discern the user's intent to either
remain seated or to
initiate a stand-up routine.
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
64
[00266] Optionally, pressure sensors in the foot may be employed to detect the
ZMP,
and a torso mounted IMU may be used to detect CMP, and the associated ground
reaction
force vector may be used as feedback to balance the wearer over the lower
limb. These
pressure sensors preferably communicate with the controller in the knee
apparatus using a
suitable wireless interface (e.g., Bluetooth). As the patient's approaches the
standing state,
the knee apparatus applies restorative torque 3120 to assist the wearer in
achieving balance
while in the standing state, shown in FIG. 31 D. Application of knee torque
will steer the
force vector fore and aft of the wearer center-of-gravity, thereby nulling ZMP-
CMP over
time. Examples of suitable approaches for implementing this can be found in US
patent
7,313,463 which is incorporated herein by reference.
[00267] Note that the user may occasionally shift positions in her chair while
seated in
ways that will also trigger a tentatively initiation of a stand-up routine.
However, the
applied knee apparatus torque will be relatively small at first and will die
out exponentially
over time (e.g., in 1-2 seconds) if positive feedback is not received from the
user. An
example of no positive feedback in a non-myoelectric system would be when the
user does
not try to lift her body with her arms and the hip joint does not begin to
displace. An
example of no positive feedback in a myoelectric system would be when the user
does not
substantially activate her knee and/or hip extensors to confirm her intent to
the stand-up
intent. If positive feedback is not received, the system will abort the stand-
up routine and
return to a relaxed seated state.
Optimization Methods
[00268] FIGS. 25A and 25B are schematic illustrations for controlling a lower-
extremity apparatus based on a stochastic optimization of 1) the transition
work, Wt,
performed to transfer weight from the trailing leg to the leading leg during
the double-support
phase of the gait cycle 2) minimizing hip impact force and force rate or 3)
minimizing a
combination of both cost (objective) functions. FIG. 25A illustrates the
simplified model
used to calculate transition work. FIG. 25B illustrates the simplified model
used to calculate
hip impact force and force rate.
[00269] The term stochastic denotes that the optimization minimizes the
expected value
of the objective function subject to hip impact force and force rate
constraints, assuming
probability (likelihood) functions for human intent; biomechanical feedback
(including
walking speed); terrain context, and terrain property. The optimization is
achieved through
modification of impedance, torque and position control parameters within the
control
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
algorithms. Practically speaking, the transfer energy is minimized, and the
hip impact force
constraints satisfied, by minimizing the negative impact of foot strike forces
and maximizing
the positive impact of reflex-induced ground forces on the hybrid system
energy.
[00270] The optimization described above can be implemented in real-time by
introducing "evolutionary" perturbations in the key components that contribute
to the
biomimetic behavior and measuring the transfer energy that arises from those
evolutionary
perturbations. The transfer energy can be estimated using biomechanical models
to augment
the inertial measurement unit feedback, or, in special cases, temporary
inertial measurement
unit subsystems (an IMU mounted on the body in the form of a belt around the
torso and/or
upper leg) could be used to facilitate estimate of torso pose and body center-
of-mass velocity.
Using the Fletcher-Powell method (or other suitable optimization method known
to those
skilled in the art), an intelligent evolution of parameters can be introduced
and an optimum
can be calculated. This optimum could, due to the rehabilitative effects of
the augmentation,
change over time. By applying these evolutionary perturbations continually and
slowly over
time, the optimum can be achieved on a continual basis. Or, as would be the
case at the
initial fitting or medical checkup of the prosthesis or orthosis, this
evolutionary optimization
could occur over a much shorter interval, say, in five to ten minutes.
[00271] The following is a description of the different phases of a subject's
gait cycle
and, in one embodiment, the steps performed by an ankle-joint prosthesis
according to
principles of the invention are for sensing the operation of and for
controlling the ankle-joint
prosthesis.
Controlled Plantarflexion
[00272] At impact, check that the ground reaction force and the zero moment
pivot
correspond with the part of the foot that we expect (from the terrain
discrimination model) to
hit the ground first. Confirm that there is a corresponding change in the
ankle angle (or ankle
torque) and that the appropriate end of the foot is stationary. After impact
look for a
condition where the local terrain slope corresponding to the inertial foot-
flat angle is
significantly less than expected. Saturate ankle spring restoring force and
increase damping
when this is detected. For terrain discrimination, based upon the
biomechanical model
feedback confirm that the terrain hypothesis (slope vs. stair) is correct and
that the wearer
hasn't tripped. For example, a tripping event on a stair might be detected as
a large negative
force in the y-direction instead of a large z-force centered on the forward
part of the foot. For
terrain texture, either the heel or the forward part of the foot will impact
first. The non-elastic
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
66
component of the depression associated with this impact will be computed. On
hard ground,
this depression should be negligible--only an elastic deformation (foot
module, linear
actuator) will be observed. In mud or soft ground, terrain plasticity will be
observed by
looking at the trajectory of the impacting foot segment. The terrain
plasticity will be used as
an attenuator on the net work that is performed on this walking cycle.
Slipping can also be
detected by noting the forward velocity of the impacting foot segment after
impact. An
escalator or people mover can be detected by noting that the shank angle is
not rotating in
accordance with the forward velocity of the foot, signaling that the wearer is
well balanced
and is stepping onto a moving surface. For impedance control of the ankle
joint apply
optimal impedance using estimated terrain-referenced velocity attack angle (y)
lower-limb
momentum, estimated terrain slope and terrain property. For reflex control, in
the event that
slipping is detected, a balance-restoring reflex will be generated to move the
knee over the
ankle. For balance control, optimal balance will normally be achieved by
inertially
referencing the spring equilibrium after the local terrain slope estimate is
updated at foot-flat.
In the event that the terrain is slippery, the algorithms that maintain
balance will introduce a
positive torque "reflex" to "pull" the shank forward in order to assist the
wearer as she works
to position the knee over the ankle--thereby getting the body center-of-mass
aligned with the
estimated ground reaction force.
Controlled Dorsiflexion
[00273] Once foot flat is detected, the controller inertially references the
spring
equilibrium angle for this local terrain slope so that when the wearer is
standing in alignment
with gravity on this slope, no restoring torque is applied by the ankle under
static conditions.
At this point, the local terrain context is now known precisely. Foot
reference coordinates at
this "foot flat" position are also defined for use in assessing the impact of
terrain texture. For
terrain texture, the algorithms use integrated measures of slip and
deformation relative to the
"foot flat" reference to update the terrain property model-specifically to
measure plasticity
of the surface and it's slipperiness by measuring how the impacted foot
segment moves
between foot-strike and foot flat. These measures can be used to attenuate
ankle impedance
and net work (reflex torque in late plantar flexion. Also, if "slipping" is
detected between
foot-strike and foot-flat, an algorithm implemented in the controller, also
looks at shank
angular velocity (how the knee is moving in relation to the ankle joint) to
discriminate
between a slippery surface and an escalator/people-mover. In either event, the
zero-velocity
update would not be scheduled since no reliable "ankle joint at zero velocity"
will be
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
67
available on this step. In the event that the terrain is slippery, special
measures will need to
be invoked by the balance function. In the case where the foot lands on a
moving escalator or
people mover, nominal impedance can be used on the new inertial frame. For
impedance
control, the control system can apply optimal impedance that maintains an
inertially-
referenced equilibrium angle; creates a walking speed-dependent stiffness
(lower stiffness for
faster walking speed) to enable a higher level of net work; and reduces the
stiffness in
slippery or highly-plastic surfaces. For reflex control, in the event that
slipping is detected, a
balance-restoring reflex will be generated to move the knee over the ankle.
For balance
control, optimal balance will normally be achieved by inertially referencing
the spring
equilibrium after the local terrain slope estimate is updated at foot-flat. In
the event that the
terrain is slippery, the algorithms that maintain balance will introduce a
positive torque
"reflex" to "pull" the shank forward in order to assist the wearer as she
works to position the
knee over the ankle--thereby getting the body center-of-mass aligned with the
estimated
ground reaction force.
Powered Plantarflexion
[00274] The model monitors slippage and sinking into the surface and
identifies ankle
torque limits that can be used to make ambulation efficient in these
conditions. For terrain
texture, terrain property estimates are refined in this state and are used as
an input to the
impedance, reflex and balance functions. For impedance control, nominal
impedance
parameters will be modified to accommodate changes in walking speed, terrain
surface
characteristics and deformation and foot slippage. A special "force field"-
typically a non-
linear actuator force that exponentially increases as the ball-nut approaches
a predefined end-
stop limit- is applied by the motor controller to make sure that the K3 spring
energy (in the
parallel elastic member) does not exceed the lower bound of its fracture
limit. For reflex
control, reflex amplitude will be adjusted to account for the net work
"setpoint" from the
biomechanical models in combination with the degree to which the terrain can
support
production of this net work. For balance control, optimal balance will
normally be achieved
by inertially referencing the spring equilibrium after the local terrain slope
estimate is
updated at foot-flat. In the event that the terrain is slippery, the
algorithms that maintain
balance will introduce a positive torque "reflex" to "pull" the shank forward
in order to assist
the wearer as she works to position the knee over the ankle--thereby getting
the body center-
of-mass aligned with the estimated ground reaction force.
Early Swing
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
68
[002751 For early swing, shortly after the toe leaves the ground, the model
monitors the
inertial trajectory of the ankle, heel and toe and determines when the ankle
can be dorsiflexed
back to its neutral position without being obstructed by the terrain. The
model computes an
optimal trajectory with suitable impedance gains and feed-forward torque to
move the ankle
to the neutral position (to avoid tripping hazards) in the quickest, efficient
and stable fashion.
For terrain discrimination, the model starts to keep track of the swept ("no
contact" with foot
member) volume through which the foot has moved thereby informing the adaptive
ankle
positioning function in late swing when a toe-down solution is the only viable
solution (e.g.,
to land on a shallow stair or ledge). For impedance control in early swing, a
neutral value of
impedance is applied by the controller. A force-field function is applied to
make sure that the
linear actuator does not impact the hard stop (end of travel)-a condition that
could cause the
actuator to stick there (at the end of travel). For impedance control in early
swing informed
by the hybrid biomechanical model, the controller controls the impedance to
create a
trajectory that exponentially drives the equilibrium position (ankle angle
setpoint) to the
desired neutral position. A feed-forward torque function is applied to reduce
the interaction
between impedance characteristics and the ankle angle following error that
could otherwise
introduce overshoot and ringing, for instance.
Late Swing
[002761 For terrain discrimination, the model keeps track of the "clear"
volume through
which the foot has moved thereby informing the adaptive ankle positioning
function in late
swing when a toe-down solution is the only viable solution, say, to land on a
shallow stair or
ledge. More generally, the ankle trajectory is monitored and pattern
recognition functions are
used to determine the likelihood that the foot will be landing on a
stair/ledge as opposed to a
sloping surface. One simple way that we have found to discriminate between the
two
conditions is to measure the angle that the ankle velocity makes in relation
to vertical; where
in various experiments it was determined that when this angle is less than 10
degrees, the foot
will land on a horizontal step. For impedance control, informed by the terrain
discrimination
model, the ankle trajectory (equilibrium) will be modified by the controller
as needed to
avoid tripping hazards. For example, if the terrain discrimination function
assigns the
maximum likelihood to stair ascent, additional dorsiflexion may be commanded
to make sure
that the toe does not catch on the stair or ledge. As before, the hybrid
biomechanical model
plans a continuously updatable equilibrium trajectory that can be followed
safely and in a
stable fashion with tight tolerances. In the late-stance state, the
biomechanical model
CA 02772620 2012-02-29
WO 2011/026086 PCT/US2010/047279
69
computes the optimum equilibrium angle and ankle impedance that will minimize
an
objective function that includes some combination of transfer energy and knee-
hip impact
forces. This optimization function could be implemented via table lookup in
the State
Machine ROM. Or, in the preferred embodiment, the State Controller function
will perform
the optimization in real-time, using approximations of the rigid-body
dynamics, to compute
and optimize the objective functions.
[002771 Variations, modifications, and other implementations of what is
described
herein will occur to those of ordinary skill in the art without departing from
the spirit and the
scope of the invention as claimed. Accordingly, the invention is to be defined
not by the
preceding illustrative description but instead by the spirit and scope of the
following claims.