Note: Descriptions are shown in the official language in which they were submitted.
CA 02865612 2014-09-30
DC-Bus Controller for an Inverter
Field
This invention relates to methods, circuits, and devices for power inverters.
In particular,
.. this invention relates to controllers for voltage and current source
inverters used in applications
such as distributed power generation, which utilize voltage and current source
inverters to
provide AC power for grid connection.
Background
In voltage and current source inverters, control of the DC-bus voltage or
current is
required to control the balance between AC and DC power. In single phase
systems control
options are limited by ripple in the DC-bus voltage or current that results
from tipple or
harmonics present on the AC side. For example, in utility grid-connected
inverters, such as in
distributed generation (DG) systems, the ripple in the DC-bus voltage or
current is at twice the
grid frequency. The ripple can interact with the DC-bus voltage or current
controller, resulting
in distortion of the current delivered to the utility grid.
Conventional DC-bus voltage and current control methods are limited in terms
of speed
of transient recovery. Furthermore, improvements in speed, achieved by
increasing the
bandwidth of the control method, are not practical due to the presence the
ripple across the DC-
bus voltage or current. The bandwidth provided by conventional DC-bus voltage
control
methods is usually limited in order to prevent the double frequency ripple
from propagating to
the current control loop, which can cause the current delivered to the utility
grid to become
distorted. Furthermore, many commonly used control methods are proportional-
integral (PI)-
based, which introduces the additional difficulty of integration. Fast
integration can lead to
saturation and instability, because large DC values are being integrated. This
necessitates that all
PI-based controllers are designed to provide slow integration, which again
limits the speed of the
control method with respect to transient recovery. However, PI-based control
methods are well-
known, easy to design, and provide simplicity, and accordingly they are often
used for regulating
the DC-bus voltage.
-1-
CA 02865612 2014-09-30
The limitations of prior DC-bus voltage control methods are twofold: (1) speed
is limited
by the bandwidth, which in turn is limited by the double frequency ripple
across the DC-bus
voltage, and (2) the simplicity provided by using conventional PI-based
controllers comes at the
price of further limiting speed due to the slow integrative action of the
controller. Fast
integration by PI-based controllers causes saturation when dealing with large
DC values, so a PI-
based control method necessarily provides slow integration. Both limitations
affect the speed of
the control method. Nonlinear controllers can provide better bandwidth than
linear controllers,
however they are generally not preferred because they tend to be more complex,
and their
stability is hard to deteimine.
Summary
Described herein is a DC-bus voltage or current controller for a voltage or
current source
inverter, comprising: a mean value calculator that provides an output signal
comprising the mean
value of the DC-bus voltage or current; wherein the mean value of the DC-bus
voltage or current
is used as a feedback signal in a closed loop of the voltage or current source
inverter controller,
such that a ripple in the DC-bus voltage or current is substantially prevented
from entering the
closed-loop.
In one embodiment the mean value calculator calculates the mean value of the
DC-bus
voltage from the maximum and minimum of the DC-bus voltage. In another
embodiment the
mean value calculator calculates the mean value of the DC-bus current from the
maximum and
minimum of the DC-bus current.
Embodiments may include a droop controller; wherein the droop controller
operates in
the closed loop with reverse proportional gain; and wherein the output signal
of the mean value
calculator is used as an input of the droop controller.
The droop controller may be an adaptive droop controller; wherein the adaptive
droop
controller provides a constant DC-bus voltage or current. In another
embodiment the droop
controller is an adaptive droop controller; wherein the adaptive droop
controller provides a
variable DC-bus voltage or current; wherein the DC-bus voltage or current is
regulated to an
optimized value such that power losses for load and grid conditions are
minimized or reduced.
- 2 -
CA 02865612 2014-09-30
In one embodiment, power losses across an output filter inductor for varying
load and/or grid
conditions are minimized or reduced.
Also described herein is a method of controlling DC-bus voltage or current of
a voltage
or current source inverter, comprising: using a mean value calculator to
output a feedback signal
.. comprising a mean value of the DC-bus voltage or current; and using the
feedback signal in a
closed-loop controller of the voltage or current source inverter, such that a
ripple in the DC-bus
voltage or current is substantially prevented from entering the closed-loop.
The method may include calculating the mean value of the DC-bus voltage from
the
maximum and minimum of the DC-bus voltage, or calculating the mean value of
the DC-bus
current from the maximum and minimum of the DC-bus current.
Embodiments may further comprise operating a droop controller in the closed
loop with
reverse proportional gain; and using the feedback signal as an input of the
droop controller.
The droop controller may be an adaptive droop controller; the method further
comprising
using the adaptive droop controller to provide a constant DC-bus voltage or
current, or using the
adaptive droop controller to provide a variable DC-bus voltage or current; and
regulating the
DC-bus voltage or current to an optimized value such that power losses for
load and grid
conditions are minimized or reduced. In one embodiment, power losses across an
output filter
inductor for varying load and/or grid conditions are minimized or reduced.
Embodiments may be configured for use in a voltage source inverter (VSI) or a
current
source inverter (CSI) of a power generator in a DG system, such as a renewable
energy power
conditioning system, which may be connected to a power distribution grid. In
one embodiment
the power generator is a photovoltaic cell, wind turbine, or fuel cell.
Brief Description of the Drawings
For a greater understanding of the invention, and to show more clearly how it
may be
carried into effect, embodiments will be described, by way of example, with
reference to the
accompanying drawings, wherein:
- 3 -
CA 02865612 2014-09-30
Figs. 1(a) and 1(b) are generalized schematic drawings of systems with which
embodiments described herein may be used, based on a voltage source inverter
(VS I) and a
current source inverter (CSI) , respectively;
Fig. 2 is a diagram showing where a DC-bus voltage sensing technique employing
a
mean value calculator may be placed in a closed-loop DC-bus voltage control
system, according
to one embodiment;
Fig. 3(a) is a diagram of a mean value calculator, according to an embodiment
for use
with a VSI;
Fig. 3(b) is a diagram of a mean value calculator, according to an embodiment
for use
with a CSI;
Fig. 4(a) is a diagram showing a closed-loop DC-bus voltage control system
with droop
controller, according to one embodiment;
Fig. 4(b) is a diagram showing a closed-loop DC-bus current control system
with droop
controller, according to one embodiment;
Fig. 4(c) is a plot showing how the steady-state operating point of the DC-bus
voltage
control system shown in Fig. 4(a) is determined using droop control;
Fig. 5(a) is a diagram showing a closed-loop DC-bus voltage control system
with
adaptive droop controller, according to one embodiment;
Fig. 5(b) is a plot showing how the steady-state operating point of the DC-bus
voltage
control system is determined with adaptive droop control;
Fig. 6 is a diagram showing that bringing the mean DC-bus voltage closer to
the peak of
the grid voltage reduces output inductor current ripple;
Fig. 7 is a diagram showing a closed-loop DC-bus voltage control system with
optimized
adaptive droop controller, according to one embodiment;
Fig. 8 is a plot showing how the steady-state operating point of a DC-bus
voltage control
system may be determined with optimized adaptive droop control, according to
one embodiment;
Fig. 9(a) is a plot showing optimal trajectories of an optimized adaptive
droop control
method for different grid voltages;
- 4 -
CA 02865612 2014-09-30
Fig. 9(b) is a plot showing how the DC-bus voltage may be determined by an
optimized
adaptive droop control method for different grid voltages and loads;
Fig. 10 is a plot of experimental data showing transient response of a DC-bus
voltage
adaptive droop controller embodiment during a positive step change;
Fig. 11 is a plot of experimental data showing transient response of a DC-bus
voltage
adaptive droop controller embodiment during a negative step change;
Fig. 12(a) is a plot of experimental data showing current ripple of a DC-bus
voltage
adaptive droop controller embodiment;
Fig. 12(b) is an enlargement of part of Fig. 12(a);
Fig. 13 is a plot of experimental data showing transient response of a DC-bus
voltage
optimized adaptive droop controller embodiment during a positive step change;
Fig. 14 is a plot of experimental data showing transient response of a DC-bus
voltage
optimized adaptive droop controller embodiment during a negative step change;
Fig. 15 is a plot of experimental data showing inverter current transient
response of a DC-
bus voltage optimized adaptive droop controller embodiment during a positive
step change;
Fig. 16 is a plot of experimental data showing inverter current transient
response a DC-
bus voltage optimized adaptive droop controller embodiment during a negative
step change;
Fig. 17 is a plot of experimental data showing current ripple of a DC-bus
voltage
optimized adaptive droop controller embodiment; and
Fig. 18 is a plot showing efficiency curves of a DC-bus voltage optimized
adaptive droop
controller embodiment and a DC-bus voltage adaptive droop controller
embodiment.
Detailed Description of Embodiments
DC-bus voltage control methods and circuits described herein regulate the
voltage across
the input of a voltage source inverter (VSI). DC-bus current control methods
and circuits
described herein regulate the current through the input of a current source
inverter (CSI).
Embodiments may be used in, for example, renewable energy power conditioning
systems, such
- 5 -
CA 02865612 2014-09-30
as distributed generation (DG) power systems (e.g., photovoltaic, wind
turbine, full cell), and
may be connected to the power distribution grid. Embodiments are described
herein primarily
with respect to single-phase grid-connected inverters; however, other
applications will be readily
apparent to those of ordinary skill in the art.
Embodiments may be used in substantially any single-phase application where
there is a
two-stage power conditioning system. For example, such a system may include a
first stage
having either an AC-DC rectifier or a DC-DC converter, and the second stage
may a VSI or CSI.
In systems including a VSI there may be an energy storage capacitor between
the two stages. In
systems including a CSI there may be an energy storage inductor between the
two stages. In VSI
embodiments, the DC-bus voltage is the parameter that is regulated; whereas
for CSI
embodiments the DC-bus current is regulated. That is, in the case of a VSI, it
is the DC-bus
voltage that carries the double frequency ripple; whereas in the case of a
CSI, it is the DC-bus
current that carries the double frequency ripple. The DC-bus voltage and
current control
embodiments address two challenges: speed (i.e., transient recovery), and
reduction or
elimination of the ripple in the voltage across the energy storage capacitor,
or in the current
through the energy storage inductor. The embodiments provide a fast transient
response for a
closed-loop system, and ensure optimal operation of the VSI or CSI during
steady-state
conditions.
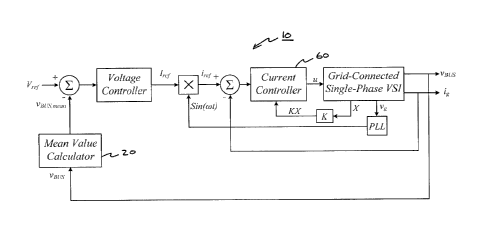
Figs. 1(a) and 1(b) show a generalized VSI and CSI, respectively, to which the
embodiments described herein may be applied. Fig. 2 shows a controller 10
based on a closed-
loop control system. The controller employs a sensing technique, including a
mean value
calculator 20, according to one embodiment. Embodiments of the mean value
calculator are
shown in detail in Figs. 3(a) and 3(b), for a VSI and a CSI, respectively. One
function of the
mean value calculator is to substantially reduce or eliminate the voltage or
current ripple (e.g., a
second harmonic ripple, as may be present in grid-connected inverters); that
is, to effectively
prevent the ripple from entering the closed-loop control system.
In one embodiment, the mean value calculator calculates the mean value of the
DC-bus
voltage or current, and feeds this value into the control system, such as the
DC-bus voltage or
current controller 60, thereby substantially reducing or effectively
eliminating the second
harmonic ripple from entering the closed-loop control system. The embodiments
advantageously
- 6 -
CA 02865612 2014-09-30
avoid the need to reduce the bandwidth in order to inhibit the second harmonic
ripple.
Consequently, the speed of the DC-bus voltage or current controller is not
compromised, and
may be substantially increased.
In Figs. 4(a) and 4(b), further embodiments of a DC-bus voltage controller and
a DC-bus
.. current controller, respectively, are shown. The embodiments include a mean
value calculator
20, and a DC-bus droop controller 30, which operates with a fast response time
to regulate the
DC-bus voltage or current while (1) fixing the DC-bus voltage or current to a
constant value,
and/or (2) reducing overall power losses of the system.
In VSI embodiments, regulating the DC-bus voltage across the energy storage
capacitor
allows the power to flow from the input-side converter to the VSI, as the
capacitor does not store
energy when its voltage is held constant. In the case of CSI embodiments, the
same holds true
for the energy storage inductor. By regulating the DC-bus current, it is
ensured that the power
may flow from the input-side converter to the CSI, as the inductor does not
store energy when its
current is held constant.
In some embodiments, such as the embodiment of Fig. 5(a), an adaptive droop
controller
40 is employed. This technique provides a fast transient response for a closed-
loop system, and
ensures optimal operation of the VSI or CSI during steady-state conditions. In
some
applications, like hybrid renewable energy systems, a constant DC-bus voltage
or current may be
preferred; whereas in other applications, a variable DC-bus voltage or current
that adaptively
changes to optimize efficiency by reducing power losses may be preferred. The
adaptive droop
controller may be configured to produce either: (a) a constant DC-bus voltage
or current,
regulated to a value determined by the requirements of a particular
application, or (b) a variable
DC-bus voltage or current, which is regulated to an optimized value that
reduces power losses
for load and grid conditions. An adaptive droop controller, such as
embodiments described
herein, is also very fast compared to a conventional PI controller because it
does not use any
integration.
Embodiments may be implemented in whole or in part using discrete components,
using
digital technology (e.g., in a digital signal processor (DSP), field
programmable gate array
(FPGA), or application specific integrated circuit (ASIC) device), or using a
combination thereof.
For example, one or more components may be implemented in an algorithm using a
suitable
- 7 -
CA 02865612 2014-09-30
hardware language such as, for example, very high speed integrated circuit
(VHSIC) hardware
descriptive language (VHDL), register transfer language (RTL), or Verilog.
Such an algorithm
may be implemented in, for example, a FPGA or ASIC device.
Embodiments will be further described by way of the following non-limiting
examples.
Example 1. Application to Voltage Source Inverter
As noted above, DC-bus voltage and current control embodiments described
herein may
be used in substantially any single-phase application. Such an application is
a grid-connected
renewable energy power conditioning system, which usually includes a two-stage
power
conditioning system comprised of a first-stage AC-DC rectifier or a DC-DC
converter, a second-
stage grid-connected VSI or CSI, and an energy storage element between the two
stages. This
example employs a VSI in such an application, as may be implemented for a grid-
connected
photovoltaic (PV) panel. However, a CSI could also be employed.
The embodiment of Fig. 2 shows a mean value calculator 20 inserted into a
closed-loop
control system 10 of a VSI. The output of the mean value calculator, the mean
value of the DC-
bus voltage, vBus,,õ,õ,, is used as a feedback signal instead of the DC-bus
voltage itself, vBus.
This effectively removes the second harmonic ripple from entering the closed-
loop control
system, as the mean value is substantially the DC component of the DC-bus
voltage. This allows
the DC-bus voltage controller to have a much higher bandwidth than a
controller using the DC-
bus voltage as the feedback signal.
Fig. 3(a) shows an example of how the mean value calculator 20 finds the mean
value of
the DC-bus voltage. In this example, the mean value of the DC-bus voltage is
calculated using
the following equation:
vB ,max + vBLS,min
v B LIS ,mean
2 Equation 1
wherein the mean value calculator deteimines the maximum and minimum of the DC-
bus
voltage.
- 8 -
CA 02865612 2014-09-30
=
According to Fig. 3(a), the discrete value of the DC-bus voltage is used to
calculate its
mean value. The discrete value of the DC-bus voltage is fed into a discrete
differentiator 22 to
extract the ripple of the DC-bus voltage. The discrete differentiator produces
a noise-free signal.
This may be accomplished by removing the high frequency switching noise from
the DC-bus
voltage by sampling the signal every switching cycle. The signal at the output
of the discrete
differentiator is 900 out of phase with the double frequency ripple of the DC-
bus voltage. The
zero crossings of this signal are then detected through a comparator 24. Two
mono-stable multi-
vibrators 26a, 26b then create the sampling instants of the DC-bus voltage
sample/holds 28a, 28b
based on the rising and falling edge of the comparator. These values
correspond to the minimum
and maximum of the DC-bus voltage. Finally, the mean value is calculated 29
using the
minimum and maximum values. The mean value calculator may be implemented using
a
technology as may be suitable or convenient, such as, for example, a FPGA.
Fig. 1(a) shows a generalized schematic of the system model, from which the
average
model may be derived as the following:
diõ, , -R1 \ 1
d; =iiõ, + 1,Bus (2d 1)
L VC
L
1 1 -1 Equation 2
di, ¨R, 1 1
- = - i + --v
dt L2 g L2 L2 g
Equation 3
dvc 1 1
=
mv
dt C C g Equation 4
dyBus _ I
'de if0,(2d -1)
dt CBUS CBLS Equation 5
The DC-bus voltage control embodiment described herein is based on droop
control
using reverse proportional gain. Thus, the controller output decreases as
positive error increases,
and the controller output increases as the negative error increases.
A block diagram of the embodiment is shown in Fig. 4(a), wherein the droop
controller
is inserted into the closed loop 10. According to this figure, the amplitude
of the reference
value for the grid current is calculated based on the droop controller as
follows:
- 9 -
CA 02865612 2014-09-30
'ref = kImax ¨ kdroopev Equation 6
where ki is used to scale /o., kdroop is the droop gain and e,. is given by:
e =V ¨v
v max. BUS,mean Equation 7
The droop controller provides substantially instant action during transients,
which
considerably increases the speed of the control system. Also, it improves the
steady-state
behavior of the grid-connected VSI, as described below.
In this embodiment, the controller does not try to track a reference signal
applied to the
control loop. Instead, the maximum value of the DC-bus voltage is applied as
the external signal
to the voltage control loop and the equilibrium point of the system is
determined based on the
intersection of the droop controller profile and the load profile (e.g., Fig.
4(c)).
During steady-state, the profile of the droop controller is given by:
droop profile: I. = kI ¨k e
ref i max droop v Equation 8
The load profile during steady-state is detennined by the DC power balance
between the
input and the output of the grid-connected VSI. The input and output powers
are given by:
P = V- I
m,avg mean dr Equation 9
P
2 ref g Equation 10
where Lk is the DC component of ide, and Vg is the amplitude of the grid
voltage. Thus, the load
profile is derived as:
21 Load profile: l"rq = V ( ¨ e)
a
Equation 11
The plot of Fig. 4(c) shows the intersection of the load profile and the droop
profile for a
typical load. According to this figure, one line represents the load profile
and the other shows
the droop profile. The intersection of these lines determines the steady-state
operating point of
the closed-loop control system. This plot is infomiative in designing the gain
of the droop
controller. The closed-loop system potentially has a stable equilibrium if the
two lines intersect;
- 10-
CA 02865612 2014-09-30
otherwise there is no equilibrium point for the closed-loop control system. If
there is an
intersection point, it is derived as follows:
ss 2/dcVmax ¨ k,1"max Vg
e, ¨
2 I k droop V,
Equation 12
This point corresponds to the steady-state DC-bus voltage given by:
k ina,Vg ¨ k drooP V
max
mean k
2/dc ¨ droop Vg Equation 13
According to Equation 13, the final value of the steady-state DC-bus voltage
depends on
different parameters, such as the droop controller characteristic (kiimax, and
kdroop) as well as the
input current and output voltage.
The coefficients of the droop controller may be designed such that the two
lines have an
intersection. Therefore, two conditions are considered:
(1) If (kiImu> 21d,VmalVg), the droop controller must satisfy the following
condition in order
to guarantee an intersection:
k I
V
k i max
,1 max droop
> 21 dc max k > v
max Equation 14
(2) If (kiiniax < 2/dJimalVd, the droop controller must satisfy the following
condition in order
to guarantee an intersection:
21 õV k I
kImax < "" kd < n"
V roop v
iflax Equation 15
Either of the aforementioned conditions can guarantee an intersection to
create a
potentially stable equilibrium. However, the first condition may be selected
to design the droop
profile, since the input power and id, can be zero, whereas the assumption of
the second
.. condition may not be satisfied. The droop gains may be designed such that
all operating
conditions are taken into consideration. In this case, kiln= is designed as
follows:
2/m" V
k I > dc max
i max mm
g Equation 16
-11-
CA 02865612 2014-09-30
Where Equation 16 ensures that the assumption of the first condition is
satisfied for the entire
range of operation. Thus, the droop controller gain is found as:
k2Idc
droop v ruin
Equation 17
where Equation 16 and Equation 17 guarantee an equilibrium point for the
closed-loop system
with the droop controller.
In some applications, it may be preferable to have a constant DC-bus voltage.
An
example of such an application is when the DC-bus feeds other converters, such
as in hybrid
renewable energy power conditioning systems. Thus, the droop control method
may be made
adaptive, such that it will regulate the DC-bus voltage to a constant value.
Changing the droop
gain provides such a control approach with the capability of regulating the DC-
bus voltage.
An adaptive droop controller is illustrated in the embodiment of Fig. 5(a).
According to
this figure, the intersection point between the load profile and droop profile
determines the error
between the mean voltage and the maximum voltage. Furthermore, since the
maximum voltage
is a fixed value, the error actually deteiiiiines the mean voltage. The DC-bus
voltage can be
made constant by placing the intersection point between the load profile and
droop profile at a
fixed error value, which is shown in Fig. 5(b) as a vertical line. In order to
place the intersection
points along the vertical line, the droop gain must be varied adaptively. This
may be achieved by
equating the load profile and droop profile equations with a fixed voltage
error. This deteintines
the droop gain, which is given by:
kiI,õ, 2 /Dricax 2 _________________ õ
k droop ¨ e V TT
Y
e' Equation 18
where ID(' and V; represent the DC-bus current (DC value) and grid voltage
amplitude,
respectively. Equation 18 describes the droop controller gain as a function of
'DC and Vg.
Other applications, such as some renewable energy power conditioning systems,
do not
require that the DC-bus voltage be regulated to a specific value. For such
applications, it may be
more beneficial to generate a variable DC-bus voltage that reduces the overall
power losses of
the system. Thus, an optimized adaptive droop controller can achieve a very
high efficiency by
varying the DC-bus voltage to decrease overall system power losses. For
example, in a grid-
- 12 -
CA 02865612 2014-09-30
connected VSI, the inductor(s) in the output filter account for most of the
power loss. This loss
is usually higher than switching/conduction losses. Therefore, an optimized
adaptive droop
controller embodiment identifies the operating point for a particular droop
and load profile that is
most able to reduce power losses across the output filter inductor.
Power losses that occur across the output filter inductor can be divided into
two main
categories: ohmic losses and core losses. Both types of losses are
proportional to the output
inductor current ripple. The overall losses related to the output inductor
current ripple are given
by:
Posses Pohmi, + Pcore ¨ Rulif2 Rhlr f h2f K fe (AB)13 Alrn
l
Ohmic Core
Losses Losses Equation 19
R 12. R .
where u u represents low frequency ohmic losses, 41 represents high
frequency ohmic
losses, fe is a constant of proportionality that depends on the operating
frequency, AB is the
peak ac flux density, fi represents an exponent determined by the core
manufacturer's published
data, 4 represents the core cross-sectional area, and
represents the core mean magnetic path
length. The low frequency ohmic losses cannot be reduced due to the fact that
the load
determines the low frequency current. However, both the high frequency ohmic
losses and core
losses may be greatly reduced by decreasing the output inductor current
ripple. Both the high
frequency ohmic losses and the core losses are functions of the output
inductor current ripple,
where the current ripple may be defined as follows:
(1, , ¨ vg )dT
AI = __________________
Equation 20
where Vgbs represents the DC-bus voltage, vg represents the grid voltage, d
represents the duty
ratio. T represents the switching period, and L represents the output filter
inductance. The duty
ratio, d, is determined by the controller; the grid voltage, vg, is determined
by a utility grid
operator, while the switching period T and the output filter inductance L are
constant. Thus, the
only variable that can be used to decrease the output inductor current ripple
is the DC-bus
voltage, vBus. Since the output current ripple is a function of the difference
between the grid
-13-
CA 02865612 2014-09-30
=
voltage and the DC-bus voltage, reducing this difference through control of
the mean DC-bus
voltage would result in reducing the output inductor current ripple and its
resulting power losses.
According to Equation 20, the voltage across the output inductor deteimines
the output
inductor current ripple. This voltage can be found through the difference
between the voltage
across the DC-bus capacitor and the grid voltage. However, since an LCL filter
contains two
inductors, and the first inductor is larger than the second inductor (due to
the fact that when there
is a large difference between the two inductors, the resonant frequency is
higher than when they
are the same), the majority of the output current ripple occurs across the
first inductor. The
voltage across the first filter inductor is directly determined by the
difference between the DC-
bus voltage and the grid voltage. Since the grid voltage cannot be controlled,
the mean DC-bus
voltage may be controlled such that it is as close to the grid voltage as
possible. However, it is
important to consider that the mean DC-bus voltage must always be greater than
the grid voltage
so that the direction of power flow is from the VSI into the utility grid. To
minimize the
difference between the DC-bus voltage and the grid voltage while preserving
the direction of
power flow, the optimized adaptive droop controller sets the mean DC-bus
voltage as close as
possible to the peak value of the grid voltage, without preventing the flow of
power from the VSI
into the grid, as shown in Fig. 6. From Fig. 6 it can be seen that bringing
the mean DC-bus
voltage as close as possible to the peak of the grid voltage reduces the
output current ripple.
A generalized block diagram of an optimized adaptive droop controller
embodiment is
illustrated in Fig. 7, which includes a mean value calculator 20, a droop
controller 30, and an
adaptive law implementation 50. By adaptively changing the droop gain, the
operating point can
be placed where it will decrease the mean DC-bus voltage as the grid voltage
decreases. By
decreasing the mean DC-bus voltage, the error between the mean DC-bus voltage
and maximum
DC-bus voltage increases. Thus, operation of the optimized adaptive droop
controller includes
increasing the error when the grid voltage decreases such that the mean DC-bus
voltage is set
very close to the peak of the grid voltage. The result is a lower output
inductor current ripple and
reduced power losses.
To calculate the optimized adaptive law, the rms value of the output current
ripple must
be found. The iiiis value of the output current ripple may be found according
to the following:
-14-
CA 02865612 2014-09-30
AI
AI =
Equation 21
Using Equation 21, the high frequency ohmic losses can be found using the
following:
R
D = D T2 no A = __
ohmic,bighji-eq ilht."- hi- -"hi LA/ rms
3 Equation 22
By substituting Equation 20 into Equation 22, the high frequency ohmic losses
may be rewritten
as follows:
R, ; V g.max ".,ax \ 2 _J 27,2
= pp. r2 pp. A r2 q/ BLS ¨
ohmic,highfreq hf (V
rnis
3 L2
- Equation 23
where the maximum duty ratio is given by:
d max = VBUS + Vg,max
2 I7Bus Equation 24
Therefore, the high frequency ohmic losses are given by:
-
RI (Vius ¨V2 )2
= R 12 = R . A/2 = g ma.
,
Mimic,highfreg rims2 2 2
4vEbsLf,õ,
Equation 25
The core losses are defined as follows:
T The
v (VB ¨ Vg.max)dmax`
Pcore = fi Ac.1õ,
nA,
Equation 26
Thus, the core losses can be rewritten as:
(VB2 ¨ V2 lax)
Pcore K g'n AC1 TO
f
Equation 27
The power losses may be minimized by finding their partial derivative with
respect to the
DC-bus voltage and setting it to zero. This results in the following optimal
operating point:
= Vg,max Equation 28
-15-
CA 02865612 2014-09-30
However, this operating point is practical only if there is no voltage drop
across the output filter,
the inverter gain is unity, and the low frequency ripple on the DC-bus voltage
is negligible.
Therefore, for a grid-connected VSI with an output filter, these factors
should be taken into
account. Thus, the voltage drop across the output filter, the SPWM gain, and
the low frequency
ripple are added to the DC-bus voltage in order to find the closest point to
the optimal operating
point. The SPWM inverter has a gain of unity (for linear modulation region)
and the voltage
drop across the inductor is given by:
V-L XLI = jo/L/,
Equation 29
where L=L1+L2 and co/ is the line frequency.
Also, the low frequency ripple of the output voltage is given by:
AVE.¨
Po V I
g
691%.,r, Bus V pc 269 B SV- DC Equation 30
where Vnc is the DC value of vBtis=
Thus, to counteract these voltage drops, the mean DC-bus voltage is determined
to be the
following:
V I
VBL'S ,niean Vv2g: L2c0124 g g Equation 31
4C0 C BE SV-BUS ,mean
Solving this equation for VBus,õ,õ, results in the following equation, which
represents the optimal
DC-bus voltage:
11- 2 2 2 il , r T/2 ,,
BLS'Tr, g g ,max -7 g,max t-u/ 2 2 9 ,2
V lit* US .nzean vI,L- co, +L
2 \ CBUS1 g,max
Equation 32
The plot of Fig. 8 shows the trajectory of the optimal operating point along
with the
droop profile. According to this figure, the DC-bus voltage is at its maximum
(and e, is at its
minimum) at full-load, where the inductor voltage drop and the low frequency
ripple are at their
maximum values. As the load decreases, the DC-bus voltage is reduced (and e,
increases) in
order to keep the inductor ripple and in turn the losses as small possible.
-16-
CA 02865612 2014-09-30
=
The adaptive law for the droop gain may be derived using Equation 32 and
Equation 18
as follows:
KifmaxDC Vmax
( + 2 IDC
looP v max ¨ D' C,Ineati vE)C,mean V
Equation 33
As shown in Fig. 8, the adaptive law 50 (see Fig. 7) minimizes current ripple
by
adaptively changing the droop gain according to the droop and load profiles.
The plot of Fig. 9(a) illustrates different optimal trajectories for different
grid voltages.
The intersection of these trajectories and the load profile determines the
optimal operating point
of the DC-bus voltage. The plot of Fig. 9(b) shows the optimal value of the DC-
bus voltage for
different load conditions and different grid voltages.
Example 2. Experimental Results with Voltage Source Inverter
DC-bus voltage adaptive droop controllers based on the embodiments shown in
Figs. 5(a)
and 7 were implemented. Simulations were conducted using PS1M, and a 1 kW
experimental
prototype was constructed and tested. The parameters are shown in Table 1, and
the results are
shown in Figs. 10, 11, 12(a)-12(b), and 13-17.
Table 1. VSI Specifications for DC Bus Voltage Control
Symbol Parameter Value
Po Output Power 1 kW
vdc Input Voltage 400-450 VDC
Vg Grid Voltage 85-264 VAC
fsw Switching Frequency 20 kHz
Io,max Maximum Output Current 10 A
L Inverter Side Inductance 2.56 mH
R1 Inverter Side Resistance 35 mS2
-17-
CA 02865612 2014-09-30
L2 Grid Side Inductance 0.307 mH
R7 Grid Side Resistance 15 ml
LCL-Filter Capacitance 10 !IF
CBUS DC-BUS Capacitance 270 uF
Fig. 10 shows the transient response of the DC-bus voltage adaptive droop
controller,
which produced a constant DC-bus voltage under a positive step change of 50%.
The figure
shows that the controller responded immediately to the step change and also
maintained the DC-
bus voltage constant.
Fig. 11 shows the transient response of the DC-bus voltage adaptive droop
controller,
which produced a constant DC-bus voltage under a negative step change of 50%.
These results for the adaptive droop controller demonstrated a very fast and
stable
transient perfol __ mance. However, the controller is responsible for
maintaining a constant DC-bus
voltage. The current ripple across the inverter-side inductor is shown in
Figs. 12(a) and 12(b).
This ripple contributes to the system power losses.
Accordingly, a DC-bus voltage adaptive droop controller, based on the
embodiment
shown in Fig. 7, was implemented. The optimized controller reduced the ripple
and, in turn,
reduced power losses of the VSI. Fig. 13 shows the transient response of the
DC-bus voltage
optimized adaptive droop controller under a positive step change of 50%.
According to this
figure, the optimized controller determined the optimal value of the DC-bus
voltage, such that
the current ripple of the inverter-side filter inductor was minimized. Also,
the figure shows a
very fast transient response due to the immediate action of the controller.
Fig. 14 shows the
transient response of the optimized controller under a negative step change of
50%.
Fig. 15 shows the transient response of the DC-bus voltage optimized adaptive
droop
controller, including the inverter current, under a positive step change of
50%, and Fig. 16 shows
the transient response, including the inverter current, under a negative step
change of 50%.
These results confirm that the current delivered to the utility grid is of
very high quality and that
the closed-loop system remains stable under severe transients.
- 18-
Fig. 17 shows the current ripple of the inverter-side inductor. Comparing this
figure with
Fig. 12(b) shows that the optimized adaptive droop controller significantly
reduces current ripple
across the inverter-side inductor. As a result, losses resulting from current
ripple are greatly
reduced. This is confirmed in Fig. 18 which shows an efficiency curve of the
DC-bus voltage
optimized adaptive droop controller, and an efficiency curve of the DC-bus
voltage adaptive
droop controller with constant DC-bus voltage. It is shown that the DC-bus
voltage optimized
adaptive droop controller increases efficiency by minimizing the power losses
in the system,
particularly for light loads.
15 Equivalents
While the invention has been described with respect to illustrative
embodiments thereof,
it will be understood that various changes may be made to the embodiments
without departing
from the scope of the invention. Accordingly, the described embodiments are to
be considered
merely exemplary and the invention is not to be limited thereby.
- 19 -
CA 2865612 2019-09-23