Note: Descriptions are shown in the official language in which they were submitted.
SYSTEMS AND METHODS FOR HYDRAULIC FRACTURE AND RESERVOIR
SIMULATION
BACKGROUND
[0001] Reservoir simulation is used in subsurface engineering to predict fluid
flow during
injection of fluid into the reservoir and extraction of fluid from the
reservoir. Reservoir simulation
is used to in the petroleum industry to predict future production of a
reservoir and to optimize
hydrocarbon recovery.
[0002] Related fields use reservoir simulation to model geothermal energy,
carbon dioxide
sequestration, and groundwater hydrology. Hydraulic fracture simulation is
also used in
subsurface engineering to describe and predict the propagation of fractures
through rock during
injection of fracturing fluids. Hydraulic fracture simulators generally focus
on the geomechanics
of crack propagation and transport of proppant through the fracture.
Integration of reservoir and
hydraulic fracture simulation may be challenging due to the difference in
timescales of the changes
that occur within the respective simulation models.
SUMMARY
[0003] Recognized herein is the need for computer-implemented systems and
methods for
integrated three-dimensional simulation of reservoir flow, wellbore flow, and
hydraulic fracturing.
The systems and methods may couple fluid flow in the wellbore and reservoir
during injection and
extraction with propagation of fractures through subsurface materials during
fluid injection.
Integrated three-dimensional reservoir, wellbore, and hydraulic fracture
simulation may be useful
for the design of hydraulic fracture treatments and prediction of future
reservoir production.
[0004] In an aspect, the present disclosure provides a system for determining
hydraulic fracture
treatment of a production well, comprising: one or more processors; a
graphical user interface
communicatively coupled to the one or more processors; and a memory,
communicatively coupled
to the one or more processors and the graphical user interface, including
instructions executable
by the one or more processors, individually or collectively, to implement and
to present on the
graphical user interface a method for determining hydraulic fracture
treatment, the method
comprising: receiving, from a user via the graphical user interface, one or
more input parameters
comprising (i) hydraulic fracture treatment conditions of a calibration well,
(ii) geological data
from an area containing the calibration well, (iii) data from one or more
sensors disposed at the
1
CA 3037543 2019-03-20
calibration well, or (iv) production data of oil or gas from the calibration
well; providing, to the
user on the graphical user interface, an integrated three-dimensional (3-D)
model of hydraulic
fracturing and fluid flow in a wellbore and reservoir of the calibration well;
receiving, from the
user via the graphical user interface, one or more hydraulic fracture
treatment conditions for the
production well; inputting the one or more hydraulic fracture treatment
conditions for the
production well into the integrated 3-D model to generate an integrated 3-D
simulation of
hydraulic fracturing and fluid flow in a wellbore and reservoir of the
production well; and
displaying, to the user on the graphical user interface, the integrated 3-D
simulation of hydraulic
fracturing and fluid flow in the wellbore and reservoir of the production
well.
[0005] In some embodiments, the one or more hydraulic fracture treatment
conditions of the
production well include (i) spacing of perforation clusters, (ii) spacing
between wells, (iii) amount
of proppant injected into a perforation cluster, (iv) injection rate, (v)
injection volume, (vi) length
of each stage along the production well, (vii) type of proppant injected,
(viii) type of fluid injected,
(ix) sequencing of fluid and proppant injection during a stage, or (x)
sequencing of injection stages.
In some embodiments, the calibration well is disposed adjacent to or in the
same geological
formation as the production well.
[0006] In some embodiments, the one or more input parameters are provided to
the one or more
processors as an input file. In some embodiments, the integrated 3-D
simulation simulates fracture
growth and the transport of water, oil, gas, and proppant through the wellbore
and reservoir of the
production well. In some embodiments, the one or more processors compares
model predictions
from the 3-D model of the calibration well to production data from the
calibration well. In some
embodiments, the production data includes production rate, production
pressure, injection pressure
during fracturing, or fracture length. In some embodiments, the integrated 3-D
model provides a
sensitivity analysis for the geological data. In some embodiments, the
geological data includes
permeability or fracture conductivity. In some embodiments, the integrated 3-D
model assesses
which of the one or more input parameters have the largest impact on
performance of the integrated
3-D simulation.
[0007] In some embodiments, the system displays to a user via the graphical
user interface one or
more output properties representing the response and state of the production
well at a given time.
In some embodiments, the one or more output properties are selected from the
group consisting of
2
CA 3037543 2019-03-20
fluid pressure, temperature, fluid saturation, molar composition, fluid phase
density, fluid phase
viscosity, proppant volume fraction, and fracture aperture. In some
embodiments, wherein the
system displays to a user via the graphical user interface one or more output
properties representing
the response and state of the production well at a given time. In some
embodiments, the one or
more inputs further comprise production boundary conditions. In some
embodiments, the one or
more hydraulic fracture treatment conditions for the production well are
provided to the processor
as an input file. In some embodiments, the input file is generated by a user
with the assistance of
the graphical user interface.
100081 In another aspect, the present disclosure provides a system for
determining hydraulic
fracture treatment of a production well, comprising: a server in communication
with a user device
configured to permit a user to simulate, in three-dimensions (3-D), a wellbore
and reservoir of a
production well, wherein the server comprises: (i) a memory for storing a set
of software
instructions, and (ii) one or more processors configured to execute the set of
software instructions
to: receive one or more input parameters comprising (1) hydraulic fracture
treatment conditions of
a calibration well, (2) geological data from an area containing the
calibration well, (3) data from
one or more sensors disposed at the calibration well, or (4) production data
of oil or gas from the
calibration well; provide to the user device an integrated 3-D model of
hydraulic fracturing and
fluid flow in a wellbore and reservoir of the calibration well; receive from
the user device one or
more hydraulic fracture treatment conditions for the production well; input
the one or more
hydraulic fracture treatment conditions for the production well into the
integrated 3-D model to
generate an integrated 3-D simulation of hydraulic fracturing and fluid flow
in a wellbore and
reservoir of the production well; and display, on the user device, an
integrated 3-D simulation of
hydraulic fracturing and fluid flow in the wellbore and reservoir of the
production well.
100091 In some embodiments, the one or more hydraulic fracture treatment
conditions of the
production well include (i) spacing of perforation clusters, (ii) spacing
between wells, (iii) amount
of proppant injected into a perforation cluster, (iv) injection rate, (v)
injection volume, (vi) length
of each stage along the production well, (vii) type of proppant injected,
(viii) type of fluid injected,
(ix) sequencing of fluid and proppant injection during a stage, or (x)
sequencing of injection stages.
In some embodiments, the calibration well is disposed adjacent to or in the
same geological
formation as the production well.
3
CA 3037543 2019-03-20
[0010] In some embodiments, the one or more input parameters are provided to
the one or more
processors as an input file. In some embodiments, the integrated 3-D
simulation simulates fracture
growth and the transport of water, oil, gas, and proppant through the wellbore
and reservoir of the
production well. In some embodiments, the one or more processors compares
model predictions
from the 3-D model of the calibration well to production data from the
calibration well. In some
embodiments, the production data includes production rate, production
pressure, injection pressure
during fracturing, or fracture length. In some embodiments, the integrated 3-D
model provides a
sensitivity analysis for the geological data. In some embodiments, the
geological data includes
permeability or fracture conductivity. In some embodiments, the integrated 3-D
model assesses
which of the one or more input parameters have the largest impact on
performance of the integrated
3-D simulation.
[0011] In some embodiments, the system displays to a user, via the graphical
user interface, one
or more output properties representing the response and state of the
production well at a given
time. In some embodiments, the one or more output properties are selected from
the group
consisting of fluid pressure, temperature, fluid saturation, molar
composition, fluid phase density,
fluid phase viscosity, proppant volume fraction, and fracture aperture. In
some embodiments, the
system displays to a user via the graphical user interface one or more output
properties representing
the response and state of the production well at a given time. In some
embodiments, the one or
more inputs further comprise production boundary conditions. In some
embodiments, the one or
more hydraulic fracture treatment conditions for the production well are
provided to the processor
as an input file. In some embodiments, the input file is generated by a user
with the assistance of
the graphical user interface.
100121 In another aspect, the present disclosure provides a method for
determining hydraulic
fracture treatment of a production well, comprising: providing one or more
input parameters
comprising (i) hydraulic fracture treatment conditions of a calibration well,
(ii) geological data
from an area containing the calibration well, (iii) data from one or more
sensors disposed at the
calibration well, or (iv) production data of oil or gas from the calibration
well to one or more
processors, wherein the one or more processors are communicatively coupled to
a graphical user
interface and a memory including instructions executable by the one or more
processors;
generating an integrated three-dimensional (3-D) model representative of
hydraulic fracturing and
4
CA 3037543 2019-03-20
fluid flow in a wellbore and reservoir of the calibration well; providing one
or more hydraulic
fracture treatment conditions for the production well to the one or more
processors; inputting the
one or more hydraulic fracture treatment conditions for the production well
into the integrated 3-
D model to generate an integrated 3-D simulation of hydraulic fracturing and
fluid flow in a
wellbore and reservoir of the production well; and displaying, on the
graphical user interface, an
integrated 3-D simulation of hydraulic fracturing and fluid flow in the
wellbore and reservoir of
the production well.
[0013] In some embodiments, the method further comprises collecting data from
the calibration
well, wherein the one or more input parameters comprises the data collected
from the calibration
well. In some embodiments, the data is measured, derived, or estimated from
well logs, core data,
or seismic data. In some embodiments, the integrated 3-D simulation simulates
fracture growth
and the transport of water, oil, gas, and proppant through the wellbore and
reservoir of the
production well.
[0014] In some embodiments, the method further comprises using the integrated
3-D simulation
of hydraulic fracturing and fluid flow in the wellbore and reservoir of the
production well to
determine the hydraulic fracturing treatment conditions and/or to predict
future reservoir
production of the production well. In some embodiments, the method further
comprises comparing
data generate by the 3-D model of the calibration well to production data from
the calibration well.
In some embodiments, the method further comprises modifying the one or more
input parameters
to generate data from the 3-D model of the calibration well that is within
about 10 to 20 percent of
the production data. In some embodiments, the production data includes
production rate and
pressure, injection pressure during fracturing, or fracture length. In some
embodiments, the one
or more input parameters that are modified include formation permeability,
fracture conductivity,
relative permeability curves, effective fracture toughness, in-situ stress
state, porosity, Young's
modulus, Poisson's ratio, fluid saturation, and tables of pressure dependent
permeability
multipliers.
[0015] In some embodiments, the reservoir of the calibration well and
production well comprises
a matrix and fractures, and wherein the integrated 3-D model and the
integrated 3-D simulation
comprises matrix elements, fracture elements, and wellbore elements for
modeling and/or
simulating multiphase flow and energy transfer in the matrix, fractures, and
wellbore. In some
5
CA 3037543 2019-03-20
embodiments, the matrix elements, fracture elements, and wellbore elements
each comprise one
or more components. In some embodiments, the one or more components are
explicit components
or implicit components, and wherein explicit components and implicit
components are treated with
explicit or implicit time stepping, respectively. In some embodiments, the
method further
comprises using the one or more processors to solve the explicit components to
obtain explicit
variables and using the explicit components and explicit variables to solve
the implicit components
to obtain implicit variables. In some embodiments, the method further
comprises coupling the
explicit components and implicit component of the matrix elements, fracture
elements, and
wellbore elements and using the one or more processors to simultaneously solve
the matrix
.. elements, fracture elements, and wellbore elements to obtain the integrated
3-D model and/or the
integrated 3-D simulation of hydraulic fracture and fluid flow in the wellbore
and reservoir of the
calibration well and/or the production well. In some embodiments, the method
further comprises
using numerical differentiation to approximate derivatives of the implicit
components with respect
to the implicit variables, and wherein the implicit components are evaluated
after substitution of
.. the explicit variables into the implicit components.
[0016] In some embodiments, the one or more hydraulic fracture treatment
conditions of the
production well include (i) spacing of perforation clusters, (ii) spacing
between wells, (iii) amount
of proppant injected into a perforation cluster, (iv) injection rate, (v)
injection volume, (vi) length
of each stage along the production well, (vii) type of proppant injected,
(viii) type of fluid injected,
(ix) sequencing of fluid or proppant injection during a stage, or (x)
sequencing of injection stages.
In some embodiments, the calibration well is disposed adjacent to or in the
same geological
formation as the production well. In some embodiments, the method further
comprises generating
a sensitivity analysis for the geological data. In some embodiments, the
method further comprises
assessing which of the one or more input parameters have the largest impact on
performance of
the integrated 3-D simulation. In some embodiments, the method further
comprises using the 3-
D simulation to generate one or more output properties representing the
response and state of the
production well at a given time. In some embodiments, the one or more output
properties are
selected from the group consisting of fluid pressure, temperature, fluid
saturation, molar
composition, fluid phase density, fluid phase viscosity, proppant volume
fraction, and fracture
aperture. In some embodiments, the one or more inputs further comprise
production boundary
6
CA 3037543 2019-03-20
i
1
conditions. In some embodiments, the method further comprises treating the
production well with
the one or more hydraulic fracture treatment conditions to produce oil and/or
gas.
[0017] Additional aspects and advantages of the present disclosure will become
readily apparent
to those skilled in this art from the following detailed description, wherein
only illustrative
embodiments of the present disclosure are shown and described. As will be
realized, the present
disclosure is capable of other and different embodiments, and its several
details are capable of
modifications in various obvious respects, all without departing from the
disclosure. Accordingly,
the drawings and description are to be regarded as illustrative in nature, and
not as restrictive.
CITED REFERENCES
[0018] To the extent that any patents, patent applications or other
publications cited herein
contradict the disclosure contained in the specification, the specification is
intended to supersede
and/or take precedence over any such contradictory citations.
BRIEF DESCRIPTION OF THE DRAWINGS
[0019] The novel features of the invention are set forth with particularity in
the appended claims.
A better understanding of the features and advantages of the present invention
will be obtained by
reference to the following detailed description that sets forth illustrative
embodiments, in which
the principles of the invention are utilized, and the accompanying drawings
(also "figure" and
"FIG." herein), of which:
[0020] FIG. 1 shows a schematic illustration of a wellbore and reservoir for
hydraulic fracture
treatment and monitoring;
[0021] FIG. 2 shows a schematic illustration of a system for hydraulic
fracture and simulation of
a wellbore and reservoir during hydraulic fracture;
[0022] FIGs. 3A-3B show example structures of Jacobian matrices for systems
with two elements
and two residuals per component; FIG. 3A shows an example structure of a
Jacobian matrix that
is fully implicit; FIG. 3B shows an example structure of a Jacobian matrix
that uses an adaptive
implicit method; FIG. 3C shows an example structure of a Jacobian matrix that
uses an adaptive
implicit method with variable substitution;
[0023] FIG. 4 shows an example process flow diagram for hydraulic fracture and
reservoir
simulation;
7
CA 3037543 2019-03-20
[0024] FIG. 5 shows an example simulation of the distribution of proppant
volume fraction in the
fracture at shut-in displayed on a graphical user interface;
[0025] FIG. 6 shows an example simulation of the distribution of temperature
in the fracture at
shut-in displayed on a graphical user interface;
[0026] FIG. 7 shows an example simulation of the distribution of water
saturation in the fracture
after 215 days of production displayed on a graphical user interface;
[0027] FIG. 8 shows an example simulation of the distribution of pressure in
the fracture after 215
days of production displayed on a graphical user interface;
[0028] FIG. 9 shows an example simulation of the distribution of normal stress
in the fracture
after 215 days of production displayed on a graphical user interface;
[0029] FIG. 10 shows an example simulation of the distribution of fluid
pressure in the matrix
after 215 days of production displayed on a graphical user interface;
[0030] FIG. 11 shows an example simulation of the production rate of water,
oil, and gas as a
function of time displayed on a graphical user interface; and
.. [0031] FIG. 12 shows a computer system that is programmed or otherwise
configured to
implement methods provided herein.
DETAILED DESCRIPTION
[0032] While various embodiments of the invention have been shown and
described herein, it will
be obvious to those skilled in the art that such embodiments are provided by
way of example only.
Numerous variations, changes, and substitutions may occur to those skilled in
the art without
departing from the invention. It should be understood that various
alternatives to the embodiments
of the invention described herein may be employed.
[0033] Design considerations applied to the production of oil and gas aided by
hydraulic fracturing
may include: (i) spacing of perforation clusters along a well, (ii) spacing
between production wells,
(iii) pounds of proppant pumped into each perforation cluster, (iv) injection
rate, (v) injection
volume, (vi) length of each stage along the well, (vii) type of proppant used,
(viii) type of fluid
used, (ix) sequencing of fluid and proppant injection during a stage (e.g.,
changes in rate, proppant
concentration, and parameters over the course of injection), and/or (x)
sequencing of injections
between adjacent stages (e.g., zipperfrac or simulfrac). These design
considerations may drive
production costs and revenue, but are often made through trial and error.
8
CA 3037543 2019-03-20
[0034] Trial and error determination of design considerations may be both
expensive and time
consuming. For example, geological spatial variability may create randomness
in well
performance, which in turn may make it more difficult to achieve statistically
significant
comparisons between well. Additionally, multiple parameters may be changed
simultaneously
and, as such, it may be challenging to differentiate causes and effects.
Computational simulation
may be a tool to manage these difficulties. For example, computational models
may simulate the
physics of fracturing, including fracture growth and the transport of water,
oil, gas, and proppant.
Computational models may be used to investigate the physical processes and
causal relationships
during hydraulic fracturing, computationally test ideas prior to field
testing, quantitatively
optimize design variables, and identify key uncertainties in the fracturing
process.
[0035] Reservoir simulation and hydraulic fracture simulation may be used to
predict fluid flow
during fluid injection and fluid extraction and to predict crack propagation
and transport of
proppant through the cracks, respectively. A variety of differential equations
may be used to
describe the behavior of the physical systems and may include governing
principles such as
conservation of mass, energy, and/or momentum. These differential equations
may be solved
analytically (e.g., using mathematical manipulations to determine closed-form
solutions) or
numerically (e.g., transforming the differential equations into algebraic
equations that may be
solved using a computer). Various numerical methods may be used to solve the
differential
equations and may be tailored to the specific application. Reservoir
simulation may be performed
by numerically solving the governing equations of the system (e.g.,
conservation of mass for
different fluid components) and the constitutive equations that relate
measured variables (e.g.,
pressure) to the governing equations. Hydraulic fracture simulation may be
performed using
governing equations related to the geomechanics of crack propagation and
transport of proppant
through the crack and may not describe flow in the matrix or multiphase flow.
[0036] Modeling hydraulic fracturing and reservoir and wellbore simulation
together may be
challenging because changes in the systems may occur on different timescales.
For example,
hydraulic fracture evolves rapidly during injection and fluid flow in the
matrix may occur
relatively slowly. Another challenge to modeling hydraulic fracturing and
reservoir simulation
together may be the complexity and diversity of the governing equations that
form the model. The
physical laws described by the governing equations may be nonlinear and,
therefore, difficult to
9
CA 3037543 2019-03-20
solve. However, integrating or coupling hydraulic fracturing simulation with
reservoir and
wellbore simulation may provide for a tool to aid in the design of hydraulic
fracturing treatments
and predicting future production of the reservoir. For example, the combined
reservoir, wellbore,
and fracture simulation may enable comparison of proposed fracture designs on
the basis of the
predicted production, realistic simulation of pressure drawdown in the
fracture during production,
description of the processes involving tight coupling of production and
stimulation (e.g.,
refracturing processes), and increase the efficiency of simulation.
[0037] Methods for integrated reservoir, wellbore, and fracture simulation are
described in Mark
W. McClure and Charles A. Kang, Society of Petroleum Engineers, Paper SPE
182593-MS, 20-
22 Feb 2017 and Mark W. McClure and Charles A. Kang, ResFrac Technical
Writeup,
Geophysics, arXiv:1804.02092 [physics.geo-ph]. Additionally, combining
reservoir simulation
and hydraulic fracturing simulation may enable evaluation of proposed
fracturing designs on the
basis of predicted ultimate recovery rather than imperfect proxies such as the
size of the stimulated
rock volume, quantification of depletion effect on refractured wells or wells
near previously
.. depleted wells, and resolution between complex interactions between flow
and fracture processes
that may not be possible to resolve by separate reservoir and hydraulic
fracture simulations.
[0038] Simulation of the wellbore and reservoir may be done with a fully
implicit method or
adaptive implicit method. A fully implicit method of simulating the wellbore
and reservoir may
be computationally inefficient for wellbore and hydraulic fracture simulation
as it expends a large
.. amount of computational effort in calculating values that are changing
slowly with respect to the
time step duration. For example, during fracturing, properties may change
rapidly in fracture
elements near the well, while properties may change slowly in matric elements
that are distant
from the well. The adaptive implicit method (AIM) may increase computational
efficiency by
spending computational effort when needed, which may yield an order of
magnitude reduction in
runtime. Computational efficiency may be important for both simulation cost
and convenience.
For example, each portion of the simulation (e.g., calibrating the model and
running each
simulation with various treatment conditions) may take hours or days to reach
a solution. If each
portion of the simulation takes a large amount of time, the cost and time
required to perform the
simulation may become prohibitive. Simulation runtime may be reduced by
simplifying the
physics of the model or computation detail. For example, separate codes may be
used for hydraulic
CA 3037543 2019-03-20
fracturing and reservoir simulation. The separation of physics into different
models greatly
simplifies the implementation and reduces runtime. However, simplifying the
physics and
separating the models may result in the loss of important physical processes,
which may lead to
worse design optimization and suboptimal decision making. Thus, the use of
computationally
efficient methods that integrate hydraulic fracturing and reservoir
simulation, as described herein,
may be critical.
Systems and methods for determining hydraulic fracture treatment conditions
100391 In an aspect, the present disclosure may provide a system for
determining hydraulic
fracture treatment of a production well. The system may comprise one or more
processors, a
graphical user interface communicatively coupled to the one or more
processors, and a memory
communicatively coupled to the one or more processors and the graphical user
interface. The
memory may include instructions executable by the one or more processors,
individually or
collectively, to implement and to present on the graphical user interface a
method for determining
hydraulic fracture treatment of a production well. The method may include
receiving, from a user
via the graphical user interface, one or more input parameters. Alternatively,
or in addition to, the
one or more input parameters may be uploaded directly and accessible to the
processor without
user input. The input parameters may include hydraulic fracture treatment
conditions of a
calibration well, geological data from an area containing the calibration
well, data from one or
more sensors disposed at the calibration well, production data of oil or gas
(e.g., natural gas) from
the calibration well, or any combination thereof The system may provide, to
the user on the
graphical user interface, an integrated three-dimensional (3-D) model of
hydraulic fracturing and
fluid flow in a wellbore and reservoir of the calibration well. The system may
receiving, from the
user via the graphical user interface, one or more hydraulic fracture
treatment conditions for the
production well, which the one or more processors may input into the
integrated 3-D model to
generate an integrated 3-D simulation of hydraulic fracturing and fluid flow
in a wellbore and
reservoir of the production well. Alternatively, or in addition to, the one or
more hydraulic fracture
treatment conditions may be stored in a memory of the system and may be
uploaded directly and
accessible to the processor without user input. For example, the system may
include a set of
treatment conditions that it automatically employs to optimize production of
oil and/or gas from
the production well. The system may display, to the user on the graphical user
interface, the
11
CA 3037543 2019-03-20
integrated 3-D simulation of hydraulic fracturing and fluid flow in a wellbore
and reservoir of the
production well.
[0040] In another aspect, the present disclosure may provide a system for
determining hydraulic
fracture treatment of a production well. The system may comprise a server in
communication with
a user device configured to permit a user to simulate, in three-dimensions (3-
D), a wellbore and
reservoir of a production well. The server may comprise a memory for storing a
set of software
instructions and one or more processors configured to execute the set of
software instructions. The
software instructions may receive one or more input parameters. The input
parameters may
include hydraulic fracture treatment conditions of a calibration well,
geological data from an area
containing the calibration well, data from one or more sensors disposed at the
calibration well,
production data of oil or gas (e.g., natural gas) from the calibration well,
or any combination
thereof The system may provide to the user device an integrated 3-D model of
hydraulic
fracturing and fluid flow in a wellbore and reservoir of the calibration well.
The user device may
provide to the system one or more hydraulic fracture treatment conditions for
the production well
which may be input into the integrated 3-D model to generate an integrated 3-D
simulation of
hydraulic fracturing and fluid flow in a wellbore and reservoir of the
production well. The system
may display, on the user device, the integrated 3-D simulation of hydraulic
fracturing and fluid
flow in a wellbore and reservoir of the production well.
[0041] In another aspect, the present disclosure may provide a method for
determining hydraulic
fracture treatment of a production well. The method may comprise providing one
or more input
parameters. The input parameters may include hydraulic fracture treatment
conditions of a
calibration well, geological data from an area containing the calibration
well, data from one or
more sensors disposed at the calibration well, production data of oil or gas
from the calibration
well to one or more processors, or any combination thereof The one or more
processors may be
communicatively coupled to a graphical user interface and a memory including
instructions
executable by the one or more processors. The one or more processors may
generate an integrated
3-D model representative of hydraulic fracturing and fluid flow in a wellbore
and reservoir of the
calibration well. One or more hydraulic fracture treatment conditions for the
production well may
be provided to the one or more processors. The one or more hydraulic fracture
treatment
conditions may be input into the integrated 3-D model to generate an
integrated 3-D simulation of
12
CA 3037543 2019-03-20
hydraulic fracturing and fluid flow in a wellbore and reservoir of the
production well. The
simulation results (e.g., graphical representations of production and physical
conditions) may be
displayed to a user on a graphical user interface. The graphical user
interface may be on a display
local to the user that initiated calibration of the model and simulation of
the product well.
100421 The method may include selecting one or more wells to use as a
calibration well(s). The
calibration well may be a well that has been completed and produced. The
method may further
comprise collecting data from the calibration well to be used to calibrate the
model prior to
simulation of the production well. The calibration well may be disposed
adjacent to or in the same
geological formation as the production well. The calibration well may be used
to calibrate the
model. Data from the calibration well may be used as one or more inputs to
generate a 3-D model
of the calibration well. The inputs may include hydraulic fracture treatment
conditions, geological
data from the area containing the calibration well, data from sensors disposed
at or near the
calibration well, and/or production data. The data may be used to generate a
geological model of
the formation containing the calibration well. A geological model may be a 3-D
representation of
the properties of the subsurface in a region of interest (e.g., a region of
interest for hydraulic
fracturing). The properties modeled may include, but are not limited to,
porosity, permeability,
stress, Young's modulus, fluid saturation, fracture toughness, Biot's
coefficient, and porosity
compressibility. The properties may be measured, derived, or estimated from a
variety of sources,
including well logs, core data, and seismic data. The porosity may range from
about zero to thirty
percent. The permeability may range from about 10,000,000 millidarcy (mD) to
lx1 0-6 mD. The
stress may be on the order of hundreds or thousands of pounds per square inch
(psi). The Young's
modulus may range from about 2x105 psi to 7x106 psi. The fluid saturation may
range from zero
to one hundred percent. The fracture toughness may range from about 1000
pounds per square
inch per inch square (psi-in") to 10,000 psi-in". The porosity compressibility
may range from
about 3x10-6 inverse pounds per square inch (psi-') to 104 psi-I. Prior to
operation, the simulator
may perform validation checks on all user inputs. For example, if the inputs
are physically
impossible (e.g., such as a negative value for fluid saturation), the
simulator may print an error
message and terminate. In another example, if the inputs are not physically
impossible, but outside
typical bounds (e.g., such as a permeability equal to 109 mD), the simulator
may print a warning
message and continue. The properties may be isotropic or anisotropic. For
example, permeability
13
CA 3037543 2019-03-20
and stress are usually assumed anisotropic and the lastic moduli, toughness,
and Biot's coefficient
are usually assumed isotropic. Some properties may not be directional and so
categorize them as
isotropic or anisotropic has no physical meaning. These properties include
fluid saturation,
porosity, and porosity compressibility. The properties may be defined in a
'layer cake' model that
assumes lateral homogeneity or may be defined in a general 3-D model that does
not assume lateral
homogeneity. The geological model may also be defined by the relative
permeability and capillary
pressure curves, distributions of dual porosity fracture parameters, and table
of reversible or
irreversible pressure dependent permeability multipliers. The pressure
dependent permeability
multipliers may be inputted as tables of 'permeability multiplier' versus
'change from initial
pressure.' For example, the user may specify that the permeability is constant
until the pressure
increases by 1000 psi, and then increases gradually to 5x the initial
permeability once the pressure
has increased by 3000 psi. These multipliers may be based on the pressure at
the current time step
(e.g., reversible multiplier) or based on the highest pressure reached in the
element (e.g.,
irreversible multiplier). The relative permeability and pressure curve may be
spatially variable or
may not be spatially variable. In an example, the relative permeability and
pressure curve are
spatially variable. The dual porosity fracture parameters may include fracture
spacing, matrix
permeability, and a geometric shape factor.
[0043] FIG. 1 shows a schematic illustration of a wellbore and reservoir for
hydraulic fracture
treatment and data and/or property monitoring. The hydraulic fracturing fluid
105 may be injected
into the wellbore 120 and reservoir 125 through the wellhead 115 using one or
more pumps (e.g.,
high-pressure and/or high-volume pumps). The wellbore 120 may extend from the
wellhead 115
to a gas reservoir in which the reservoir 125 is disposed in. The hydraulic
fracturing fluid 105
may cause fractures within the reservoir 125 to generate free gas and oil 110.
The gas and oil may
be driven out of the reservoir 125 and wellbore 120 through the wellhead 115
using one or more
pumps (e.g., high-pressure and/or high-volume pumps) to be collected for
further processing and
use. The pumps used for injection of the hydraulic fracturing fluid and
collection of gas and/or oil
may be three or four cylinder pumps configured for high-pressure and/or high
volume fluid flow.
The produced gas and/or oil may be separated from the hydraulic fracturing
fluid using one or
more gas processing units. The gas processing units may include one or more
heaters or separators.
14
CA 3037543 2019-03-20
[0044] The well may be monitored throughout the life cycle of the well (e.g.,
drilling, fracturing,
and production) and the monitored data may be used to design 3-D model of the
calibration well
and for simulation of the production well. Monitoring may include generation
of data logs (e.g.,
injection schedule information), measuring physical properties of the well and
surrounding area
during the life cycle, and measuring production rates. For example, well
monitoring may include
generating data logs including amount of fracturing fluid used and oil/gas
produced via monitoring
injection and production at the wellhead 115. Additionally, well monitoring
may include
measuring and monitoring the temperature, pressure, and flow rate at the
wellhead 115 and along
the wellbore 120. Temperature, pressure, and flow rate along the wellbore may
be measure by a
variety of sensors, including fiber-optic cables disposed outside the wellbore
casing, gauges
conveyed by wireline or coiled tubing, or permanently installed downhole
gauges. Fracture
monitoring may include monitoring the injection profile, fracture propagation,
fracture locations,
and flow rates within the reservoir 125. Fracture monitoring may be permitted
using tracers within
the reservoir 125 and microseismic monitoring of the region surrounding the
well 130. Further
monitoring may include monitoring stress via stress monitors and monitoring
seismic activity, for
example, with a geophone. Tiltmeters and electromagnetic imaging may also be
used to monitor
seismic activity. Pressure observations in offset wells and stages may be used
to infer fracture
growth and geometry. Produced fluid samples may be analyzed to infer their
formation of origin.
One or more different types of sensors may be utilized in collecting data when
monitoring the well.
Data from the sensors may be obtained and stored in the data logs. Data from
the sensors may be
automatically transmitted to one or more memory storage units, which may
include the data logs.
Data logs may collect data from a combination of sensors. Sensors may comprise
temperature
sensors, pressure sensors, stress sensors, motion sensors, valve
configurations, and/or optical
sensors.
[0045] The injection schedule used to fracture the calibration well may be
input into the model
and production boundary conditions may be set. The injection schedule may
include the injection
rate, proppant concentration, proppant type, and fluid additive concentration
as a function of time.
The injection rate may range from about 1 barrel oil per minute (bbl/min) to
150 bbl/min. The
proppant concentration may range from zero pounds per gallon (ppg) to 6 ppg.
Proppant types
may include silica sand, walnut hulls, natural sand glass, resin coated sand,
sintered bauxite,
CA 3037543 2019-03-20
sintered kaolin, and fused zirconia. Fluid additives may include linear
polymer molecules (e.g.,
guar, hydroxypropyl guar, hydroxyethyl cellulose, carboxymethyl hydroxypropyl
guar, etc.),
polymer cross-linkers (e.g., borage or metallic-based cross-linkers),
surfactants, acids (e.g.,
hydrochloric acid, hydrofluoric acid, acetic acid, formic acid, etc.),
biocides, scale inhibitors, clay
stabilizers, pH buffers, cross-link breakers, diverting agents, friction
reducers, and fluid loss
additives. Proppants and fluid additives may be stored separately (e.g., in
one or more proppant,
chemical additive, or fracturing fluid storage tanks) from the hydraulic
fracturing fluid. The
proppants and/or fluid additives may be mixed and/or combined (e.g., using a
slurry blender or
sand mixers) with the hydraulic fracturing fluid prior to injection. Fluid
additives may be injected
on the order of parts per million (ppm). Injection may be performed with water
as the base fluid.
Alternatively, or in addition to, injection may be performed with a
hydrocarbon base fluid or with
gas such as CO2 or nitrogen. If the base fluid is liquid, gas such as CO2 or
nitrogen may be added,
with or without foaming agents. In example injection schedule, proppant may be
injected at a low
concentration (e.g., from about 0.25 to about 0.5 pounds per gallon (ppg)) and
increased over time.
For example, within lOs of minutes, proppant concentration may be increased to
about 3.0 ppg to
6.0 ppg. Fluid and proppant type may be constant or may vary over time. For
example, small
diameter proppant (e.g., a 100 mesh proppant) may be injected initially
followed by a larger
diameter proppant (e.g., a 40 or 70 mesh proppant).
[0046] The production boundary conditions may specify the bottomhole pressure
to calculate the
production rate or specify the production rate and calculate the bottomhole
pressure. The model
predictions may be compared to available date from the calibration well (e.g.,
production rate and
pressure, injection pressure during fracturing, and fracture length). If the
model parameters are
not consistent within approximately 10-20% of the production data, the model
inputs may be
modified. Error between the production data and the model data may be
quantified by taking the
root-mean squared difference between the modeled and actual production data.
For example, the
formation permeability, fracture conductivity, relative permeability curves,
effective fracture
toughness, in-situ stress state, porosity, Young's modulus, Poisson's ration,
fluid saturation, and
tables of pressure dependent permeability multipliers may be modified.
Comparison and
modification of the model input parameters may be repeated at least 1, 2, 3,
4, 5, 6, 8, 10, 12, 14,
16, 18, 20, 30, 40, 50, 60, 80, 100, or more times. Comparison and
modification of the input
16
CA 3037543 2019-03-20
parameters may be repeated until the model data is within about 30%, 20%, 15%,
10%, 8%, 6%,
5%, 4%, 3%, 2%, 1%, or less of the production data. Comparison and
modification of the input
data may be repeated until the model data is from about 1% to 2%, 1% to 3%, 1%
to 4%, 1% to
6%, 1% to 8%, 1% to 10%, 1% to 15%, 1% to 20%, 1% to 30%, 2% to 3%, 2% to 4%,
2% to 6%,
2% to 8%, 2% to 10%, 2% to 15%, 2% to 20%, 2% to 30%, 3% to 4%, 3% to 6%, 3%
to 8%, 3%
to 10%, 3% to 15%, 3% to 20%, 3% to 30%, 4% to 6%, 4% to 8%, 4% to 10%, 4% to
15%, 4% to
20%, 4% to 30%, 6% to 8%, 6% to 10%, 6% to 15%, 6% to 20%, 6% to 30%, 8% to
10%, 8% to
15%, 8% to 20%, 8% to 30%, 10% to 15%, 10% to 20%, 10% to 30%, 15% to 20%, 15%
to 30%,
or 20% to 30% of the production data. In an example, comparison and
modification of the input
data is repeated until the model data is from about 10% to 20% of the
production data.
[0047] The calibrated model may be used to conduct a sensitivity analysis of
the system. For
example, geologic parameters may be varied to assess the impact of the
parameter on well
performance. Geologic parameters may include permeability, fracture
conductivity, relative
permeability curves, effective fracture toughness, in-situ stress state,
porosity, Young's modulus,
Poisson's ratio, fluid saturation, and tables of pressure dependent
permeability multipliers. The
sensitivity analysis may be used to prioritize subsequent data collection from
the calibration
well(s).
[0048] The calibrated model may be used to simulate a variety of alternative
fracture designs by
varying parameters such as cluster spacing, stage length, well spacing,
perforation diameter,
perforation shots per cluster, proppant type, proppant mass, proppant
diameter, injection fluid
viscosity, injection rate, and sequencing of stages between adjacent wells
(e.g., zipperfrac versus
simulfrac). Strategies may be evaluated for mitigating interference between
adjacent wells (e.g.,
parent/child wells in which a 'child' well is fracturing after a nearby
'parent' well has been
produced for an extended period of time. Strategies may include refracturing
the parent well,
injecting into the parent well, injecting far-field diverters into the child
well, and shutting in the
parent well. The designs (e.g., hydraulic fracturing treatment conditions) may
be compared to
determine the conditions that provide the highest production or net present
value in a production
well. The hydraulic fracturing treatment conditions that provide the highest
production or net
present value may be applied to the production well to produce oil and gas.
For example, the 3-D
hydraulic fracture simulation may be used to test a variety of hydraulic
fracture treatment
17
CA 3037543 2019-03-20
conditions and the treatment conditions that provide the highest production of
oil and/or gas or net
present value of the production well may be applied to the production well to
produce the oil and/or
gas. Additionally the production data from the production well may be
monitored during hydraulic
fracturing (e.g., using one or more sensors or monitors described elsewhere
herein) and the
simulation may be used to generate additional hydraulic fracturing treatment
conditions to improve
the production or net present value. The simulation may output a variety of
properties. The outputs
may be displayed to a user on a graphical user interface in the form of
discreet data points, charts,
graphs, and/or 3-D renderings of the wellbore and reservoir. The outputs may
be displayed in
color and/or greyscale. The color and/or greyscale may indicate the magnitude
of the output
.. parameters (e.g., pressure, stress, molar composition, temperature,
proppant fraction, etc.) at a
given time and location within the reservoir or wellbore. The outputs may
represent the response
and state of the system at a given time. For example, the outputs may
represent fracture growth
and the transport of water, oil, gas, and proppant through the wellbore and
reservoir of the
production well. The properties may be calculated at every location throughout
the model domain
.. in a series of time steps. Each time step may represent one snapshot in
time. The output properties
may include, but are not limited to, fluid pressure, temperature, fluid
saturation, molar composition
of the water and hydrocarbon mixture, fluid phases density, fluid phase
viscosity, proppant volume
fraction, and fracture aperture. The fluid pressure may range from zero to
about 20,000 psi. The
temperature may range from about 80 F to about 450 F. The fluid saturation
may range from
zero to one hundred percent. The molar composition may range from zero to one
hundred percent.
The fluid phase density may range from 1 kilogram per cubic meter (kg/m3) to
1200 kg/m3. The
fluid phase viscosity may range from 0.01 centipoise (cp) to millions or
centipoise or more. The
proppant volume fraction may range from zero to one hundred percent. The
fracture aperture may
range from micrometers to centimeters. Alternatively, or in addition to, the
simulation may output
.. summary values for each wellbore. Summary values may include the production
rate of oil, gas,
and water, injection rate of water, wellhead pressure, bottomhole pressure,
and temperature of the
produced fluid. Alternatively, or in addition to, the simulation may output
summary statistics for
each fracture, such as the average aperture, approximate height and length of
the fracture, and the
average net pressure.
18
CA 3037543 2019-03-20
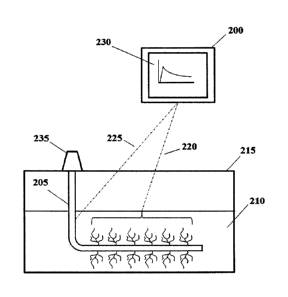
[0049] FIG. 2 shows a schematic illustration of a system for hydraulic
fracture and reservoir
simulation. The system may include a computer system 200 that is programmed or
otherwise
configured to simulate hydraulic fracture and fluid flow in a wellbore 205 and
reservoir 210. The
computer system (e.g., user device) 200 may include one or more processors,
computer memory,
and electronic storage. The hydraulic fracturing at a site 215 may be
simulated by solving a variety
of balance equations (e.g., components) in three types of elements, using
variables defined by the
fracturing site 215 and variables determined by the simulation. The elements
may include fracture
and matrix elements 220 and wellbore elements 225. The fracture and matrix
elements 220 and
wellbore elements 225 may include a variety of balance components (e.g.,
balance equations),
such as proppant mass balance, component molar balance, etc. The simulation
results 230 may be
used to design the hydraulic fracturing treatments delivered to the wellbore
205 and reservoir 210
by the well head 235. For example, the hydraulic fracture treatment conditions
used in the
simulation (e.g., to generate the highest production rate and/or net
production value) may be
physically applied to a production well (e.g., the production well may be
produced using the same
treatment conditions as used in the simulation). For example, the results of
the simulation may be
used to determine the spacing between wells, the amount of proppant injected
into a perforation
cluster, the injection rate of the hydraulic fracturing fluid, the volume of
injected hydraulic
fracturing fluid, the length of each stage along the well, the type of
proppant injected, the type of
fluid injected, the sequencing of fluid an proppant injected during a stage,
and/or the sequencing
of the injection stages..
[0050] The inputs (e.g., properties from the calibration well and/or treatment
conditions of the
production well) may be specified in input filed and provided to the
processor. The inputs may be
manually input into the system by the user through a user interface (e.g., a
graphical user interface).
The processor may then generate the input file that is input into the model.
Alternatively, or in
addition to, the user may generate the input file to be input into the model.
Alternatively, or in
addition to, the inputs may be uploaded to the processor and memory without
input from the user.
For example, the hydraulic fracture treatment conditions of the calibration
well, geological data
from an area containing the calibration well, data from one or more sensors
disposed at the
calibration well, production data of oil or gas (e.g., natural gas) from the
calibration well, or any
combination thereof may uploaded and directly accessible to the system. For
example, geographic
19
CA 3037543 2019-03-20
data may be accessed from one or more sources (e.g., public survey
information, etc) and uploaded
for model calibration and simulation. Additionally, the system memory may
include a listing of
hydraulic fracture treatment conditions that it may input into the simulation
without input from the
user to optimize the treatment conditions. The input file may be an ASCII text
file or a non-human-
readable binary format. The simulation outputs may be exported to ASCII text
files. Alternatively,
or in addition to, the outputs may be exported as binary/hybrid files that are
specialized to be read
by a 3-D visualization tool. The binary/hybrid files may include a VTK format
or other specialized
visualization format.
[0051] The systems for simulating hydraulic fracturing may include one or more
computer
processors, computer memory, and one or more display units. The computer
processors may be
operatively coupled to the computer memory and/or the one or more display
units. The method
may include creating an integrated three-dimensional model representative of
hydraulic fracturing
and fluid flow in the wellbore and the reservoir. The reservoir may include a
matrix and fractures.
The three-dimensional model may include implicit components (e.g., equations),
explicit
components (e.g., equations), or both implicit and explicit equations. In this
context, and in
accordance with the nomenclature used in the field of reservoir simulation,
implicit and explicit
may refer to the treatment of variables and/or equations in the flow terms
with respect to time.
Explicit variables may be treated using values from the previous time step and
implicit variables
may be treated using values from the current time step. Matrix elements,
fracture elements, and
wellbore elements may be obtained (e.g., derived or selected) to model
multiphase flow, energy
transfer, and fracture formation in the wellbore and/or the reservoir. The
matrix elements, fracture
elements, and wellbore elements may each comprise one or more components
(e.g., governing
equations). Secondary element properties (e.g., density, viscosity, etc.) may
be assigned for the
matrix elements, fracture elements, and wellbore elements and stored in the
computer memory.
Each component (e.g., governing equation) for the matrix elements, fracture
elements, and
wellbore elements may be assigned as either explicit components or implicit
and stored in the
computer memory. The one or more computer processors may be used to solve the
explicit
components to obtain explicit variables. The explicit variables may be used to
update the at least
a portion of the stored secondary element properties. The explicit components
and explicit
variables may be used to solve the implicit components to obtain implicit
variables. The implicit
CA 3037543 2019-03-20
variables may be used to update at least another portion of the secondary
element properties stored
in the computer memory. The explicit and implicit components of the matrix
elements, fracture
elements, and wellbore elements may be coupled and the computer processors may
be used to
simultaneously solve the matrix elements, fracture elements, and wellbore
elements to simulate
hydraulic fracturing and fluid flow in the wellbore and reservoir. The
simulation may be used to
design hydraulic fracturing treatments and/or to predict future reservoir
production.
[0052] The systems and methods may represent flow in the fracture with
constitutive equations
designed for fracture flow. When a fracture is mechanically opened, aperture
distribution may be
calculated using appropriate boundary conditions (e.g., fluid pressure equal
to normal stress).
Fracture propagation may be predicted using fracture mechanics. The wellbore
may be included
in, and integrated with, the simulation. The wellbore may be closely coupled
to the reservoir such
that wellbore transport affects reservoir processes. For example, during
fracturing, fluid and
proppant may flow out of the well from multiple perforation clusters and/or
different fracture
initiation points along an openhole interval. The relative amount of fluid and
proppant distributed
into each may depend on the perforation and friction pressure loss along the
well. Additionally,
proppant injection scheduling may depend upon the time to sweep injected
proppant and fluid
through the wellbore. The wellbore temperature may evolve rapidly during
hydraulic fracturing
as relatively cool fluid is injected into a relatively hot wellbore. Fluid
temperature may affect
viscosity and polymer cross-linking. Therefore, cooling in the near-wellbore
region may induce
thermoelestic stress changes.
[0053] The method may include modeling non-Newtonian fluid behavior. The non-
Newtonian
fluid behavior may be modeled with a modified power law (MPL) or power law
fluid model.
Alternatively, or in addition to, alternative rheological models may be used,
such as the Herschel-
Bulkley fluid model. In an example, the MPL may be because it models fluid
using power law at
high shear rates, as a Newtonian at low shear rates, and smoothly handles the
transition between
the two. Constitutive laws that depend on gel concentration and temperature
may be used to define
the rheological properties of the fluid. Using MPL and constitutive laws to
model fluid behavior
may enable simulation of fracturing treatments in which different fluid types
are injected
sequentially. The formation of filtercake on the fracture walls and the
resulting obstruction flow
may also be modeled. Filtercakes may be formed by large-molecules gels that
are unable to
21
CA 3037543 2019-03-20
penetrate the pores of the surrounding rock. A comprehensive model of proppant
transport may
be used. The model may include the effect of viscous drag, bulk gravitational
convection of the
slurry, gravitational settling, hindered settling, clustered settling, and
effects of proppant slurry
viscosity.
[0054] The model may include defining secondary variables. Secondary variables
in each element
of the system may be defined implicitly (e.g., residuals are evaluated by
numerically solving
nonlinear equations) or explicitly (e.g., using mathematical manipulations to
determine closed-
form solutions). In this context, the terms implicit and explicit may refer to
whether a closed-form
solution may be written to calculate the variable and may not indicate whether
variables are
calculated using values from the previous time step or current time step. As
an example of a
variable that is implicitly defined (e.g., a closed-form solution is not
available), the viscosity of a
non-Newtonian slurry containing proppant is a complex nonlinear function of
flow velocity, but
the flow velocity can be calculated from information related to the slurry
viscosity. In this case, a
closed-form solution cannot be obtained in which the flow velocity is isolated
on one side of an
equation. The flow velocity may be calculated using a numerical technique.
Numerical techniques
applied for reservoir simulation may involve calculation of derivatives of the
residual equation,
which may include numerous secondary variables. However, for a coupled or
integrated reservoir
and hydraulic fracturing simulation derivative calculation may be challenging
due to the
complexity and length of the analytical form of the component. The implicitly
defined secondary
variables in the residuals may further increase the difficulty of analytically
deriving the derivatives.
[0055] Reservoir simulation may be performed using the finite difference or
finite volume method
to discretize space and the implicit Euler method to discretize time. The
implicit Euler method
may be unconditionally stable. Other methods (e.g., explicit Euler) may be
more efficient, but
may be numerically unstable and cause unphysical oscillations in the
calculation results.
Numerical instability may be avoided by using small time steps (e.g., a fine
temporal
discretization), however, this approach may reduce the computational
efficiency of the simulation.
Other methods may also be used to discretize time. One method may be the fully
implicit method
(Fl) which used the implicit Euler method for all components of the elements.
Another method
for solving the reservoir simulation equations may be the implicit pressure,
explicit saturation
method (IMPES). In the IMPES, the pressure variables are solved implicitly in
time and the
22
CA 3037543 2019-03-20
saturation variables, and associated equations, in the flow terms are solved
explicitly in time. The
pressure equations may be vulnerable to numerical instability and the
saturation equations may be
less vulnerable to instability. Therefore, in some cases, the IMPES method may
perform more
efficiently than the fully implicit method, but the IMPES method may be
vulnerable to numerical
instability and the time step restrictions used to avoid instability may lead
to lower simulation
efficiency.
100561 The model may include using adaptive implicit methods (AIM) to
calibrate the model and
simulate the production well. The AIM may include techniques used in both the
FT and IMPES
methods. For example, using AIM, some of the spatial distribution are
discretized using the
IMPES method and others are discretized with the FT methods. Various
techniques may be used
to predict which elements, variables, components, and/or properties may be
prone to numerical
instability. Elements, variables, components, and/or properties that are prone
to numerical
instability may be discretized using FT methods. The IMPES methods may be used
with elements,
variables, components, and/or properties that are not prone to numerical
instability. As the
simulation evolves through time and as the time step duration is varied, the
assignment of each
element, variable, component, and/or property may change from IMPES to FT or
from FT to IMPES.
AIM may increase the performance (e.g., efficiency, robustness, and accuracy)
of the simulation.
When a component is treated explicitly (e.g., saturation in the IMPES method),
flow terms between
elements may be evaluated using the value of the corresponding independent
variable at the
previous time step. When a component is treated implicitly (e.g., pressure in
the IMPES method),
flow terms between elements may be evaluated using the value of the
corresponding independent
variable at the current time step. For either explicit or implicit, the
accumulation terms within each
balance equation may be evaluated using the values from the current time step.
The AIM method
adaptively selects whether to treat variables in the flow terms with values
from either the previous
or current time step.
[0057] In each of the Fl, IMPES, and AIM methods, N equations (or N
components) may be
represented by a residual vector, R, and N unknowns (or N variables) may be
represented by a
vector, x. In the AIM method, a subset of the equations or unknowns may be
assigned and treated
with the Fl method and the remaining equations or unknowns may be treated with
the IMPES
method. The system may be solved by finding the values of x such that the
values in R approximate
23
CA 3037543 2019-03-20
to zero (e.g., within a pre-defined specific error tolerance). Other mixtures
of implicit and explicit
assignments may be used. For example, thermal components may include a mixture
of implicit
and explicit assignments and the remaining components and variables may be
treated with the
IMPES method. Alternatively, or in addition to, components may be used that is
implicit with
respect to pressure and saturation and explicit with respect to composition.
[0058] In an Fl method, the system may, in some cases, be solved iteratively
(e.g., using Newton-
Raphson). A Jacobian matrix, J, may be assembled such that each term Jjj is
defined as:
lijaRi
=
(1)
The system of equations may be solved to find an updated vector dx. The
updated vector dx may
be used to update the unknowns as follows:
Jdx = ¨R,
(2)
x(1+1) = x(1) + dx(/),
(3)
where the superscripts (1) and (/+/) may denote the previous and new
iterations, respectively. The
nonlinear iterations may converge to the solution. For example, the solution
may be reached when
each value in R is close to (e.g., within a pre-defined error tolerance) zero
or equal to zero.
Alternatively, the nonlinear iteration may not converge to the solution. In a
system that the
iteration does not converge the value of the time step, At, may be decreased
(e.g., the duration of
the time step may be decreased). In a system that does not contain
discontinuities in the residual
equations, the system may converge if the time step is sufficiently small. The
matrix J may be
sparse because it may contain nonzero values for hydraulically connected
elements and not
elements that are not hydraulically connected. Each hydraulically connected
element may be
adjacent to a small subset of the total elements of the problem. The term
'hydraulically connected
elements' may be used to refer to elements that are adjacent so that the
pressure in one element
directly affects the calculation of the residual equations (e.g., mass balance
equations) in the other
element.
aRi
[0059] In an AIM method, a Jacobian matrix, J, may be assembled and the
derivatives, , of the
axj
equations (e.g., components) that are treated explicitly may be set to zero.
Accumulation terms
relating xj to the other residual equations within the same element may not be
set to zero. Linear
algebraic manipulations may be performed such that the explicit variables and
equations RI and dxj
24
CA 3037543 2019-03-20
are decoupled from the system. For example, the rows of each IMPES element may
be left-
multiplied by the inverse of the block diagonal matrix corresponding to that
element. The explicit
rows and column may be removed from the matrix. The implicit variables, dx,
may be calculated
by solving the system of equations using the implicit equations and the
explicit variables may be
updated by back substitution into the rows of the matrix corresponding to the
explicit equations.
AIM may use the iterative process of equations (2) and (3) to update all of
the unknowns in x,
irrespective of whether they are implicit or explicit variables. This type of
AIM implementation
may have enhanced efficiency due to the explicit treatment of a portion of the
variables in the flow
terms which may allow many of the columns and rows in the Jacobian matrix to
be removed from
.. the matrix solution and updated after solving with back-substitution.
[0060] A computer-implemented method may be employed to handle the challenges
of
analytically deriving the derivatives. The computer-implemented method may
solve the full set of
governing equations (e.g., components) in a way that is efficient, numerically
stable, accurate, and
robust. The computer-implemented method may use a form of the adaptive
implicit method (AIM)
to solve the model elements (e.g., matrix elements, fracture elements, and
wellbore elements). The
method may apply the AIM in conjunction with a numerical approach to solve the
model element
and simulate hydraulic fracture and flow in the reservoir and wellbore. The
method may include
coupled simulation of hydraulic fracturing and reservoir simulation. Coupled
simulation of
hydraulic fracturing and reservoir simulation may include modeling processes
that operate on
different timescales. Therefore, coupling AIM and a numerical approach to
solve the model
elements may permit coupled flow of fluid components, thermal energy, water
solutes, and
proppant transport to be modeled in a single simulator. The method may include
directly solving
explicit components, using the solved explicit components to constrain the
solutions of the implicit
components, and using numerical differentiation to estimate any nonzero values
in the resulting
Jacobian matrix. The components may be assigned as implicit or explicit based
on an estimate of
which equations may be numerically unstable if treated explicitly. The
numerical differentiation
may simplify the process of calculating the derivatives and facilitate the
solution of complex
multiphysics elements that comprise implicitly defined components and
variables. Additionally,
directly solving the explicit components and using the explicitly defined
components to constrain
CA 3037543 2019-03-20
the implicitly defined components may reduce the number of derivatives that
are explicitly
calculated and improve the efficiency of solving the system.
[0061] The computer-implemented method for simulation of hydraulic fracturing
and fluid flow
in the wellbore and the reservoir may include the use of AIM in conjunction
with variable
.. substitution, numerical differentiation, or both variable substitution and
numerical differentiation.
Using AIM in conjunction with variable substitutions may enable solving a
system of equations
(e.g., the fracture, matrix, or wellbore components) at least in part with
analytical manipulations.
Using variable substitution, the explicit equations may be directly solved
(e.g., analytically) and
substituted into the residual during each iteration. Because of this, back-
substitution may not be
used to determine the updated dx for the explicit variables, unlike with the
previously described
AIM technique. Based on the value of x for the previous iteration, each
explicit component] may
be solved directly to find xj in terms of the other unknown variables. The
expression for xj may
then be directly input into the implicit residual equations for the same
element, which modifies
both the residual equation and the derivative values in the Jacobian matrix.
The system of
equations may then be solved to determine updates dx to the implicit
variables, as in Equations (2)
and (3) of the previously described AIM method. The analytical solution and
updated dx explicit
variables may not represent the final solution during the iteration process as
the terms and variables
may be dependent upon the implicit equations and implicit variables, which may
be considered to
be unknown until the system converges. Nevertheless, substituting the values
of x into an explicit
equation RI in the Jacobian matrix may yield residual of zero at each
iteration.
[0062] In an example, the method may include representing a system of two
equations and two
unknowns by:
R [xz 22 + x ¨ 10]
(4)
R2 Xi + 2X2 ¨ 10,
where (xi,x2) may be initially estimated as (1,2). Using the Newton method and
previously
described Equations (2) and (3) this system may converge within five
iterations to the machine
precision solution of (2.0918, 2.8121). Alternatively, equation R2 may be
solved for x2 in terms of
xi and substituted into equation R./ to form a modified residual equation RI*.
Thus, in this example,
the number of residual equations is reduced to one and the updated xi variable
may be calculated
using Equations (2) and (3) with RI* to obtain:
26
CA 3037543 2019-03-20
aR.)-1
Ax = ¨ (1 --
(5)
axi
The derivative of Equation (5) is:
al?* aR aR ax
1+ 1 2
(6)
axi axi ax2ax1*
Once the xi variable is updated, the value of x2 may be directly calculated by
solving R2 for x2.
Because of this, the value of R2 may go to zero after a single iteration.
However, the calculated
value of x2 may not be the final or correct solution for x2 after a single
iteration because the
calculated value of x2 is dependent upon xi, which may not have reached
convergence. Applying
the updated values from Equations (5) and (6) may yield the same solution to
machine precision
within five iterations, the same as the previously described Newton method.
However, the steps
taken for each iteration may differ from the standard Newton method applied
directly to Equation
(4).
[0063] Though the above described adaptive AIM method includes an algebraic
manipulation of
the original Jacobian, the residual equations are nonlinear and substitution
of x2 into RI may include
that nonlinearity. For example, in this case, the solution for x2 yields:
.X2 = _____________________________________________________________ (7)
2
While this substitution may be performed algebraically, it may not be
accomplished solely from
linear manipulations on the original Jacobian matrix.
[0064] The above described solution strategy may be used to eliminate
equations from the
Jacobian in conjunction with a fully implicit method. An explicit equation Rj
may be solved for
the corresponding variable xj and the variable xj may be substituted into each
other residual
equation dependent upon xj (e.g., the equations corresponding to the nonzero
values in the jth
column of the Jacobian). However, this method may degrade the sparsity of the
Jacobian because
the expression for xj may contain the values of many other unknown variables.
For example,
substituting the expression for xj into a residual equation Rk may introduce a
dependence of Rk on
the value of some other variable (e.g., xm). This may introduce additional
nonzero values into the
Jacobian matrix. Degrading the sparsity of the matrix may increase the overall
computational cost
and, consequently, this approach may not be useful.
[0065] Alternatively, if the substitution is performed on an explicit variable
in a Jacobian arising
from the AIM strategy, the sparsity of the matrix may be unaffected. For
example, a variable may
27
CA 3037543 2019-03-20
be treated explicitly in the flow related terms and, consequently, the values
in the jth column of J
may be zero. An exception may be values in the block diagonal corresponding to
the other
equations in the same element, which may already be nonzero. Therefore, in
this case, the
substitution may add no additional nonzero values to the Jacobian matrix.
FIGs. 3A-3B show an
example structures of Jacobian matrices for systems of equations with two
elements and two
residuals per element. FIG. 3A shows an example structure of a Jacobian matrix
using a fully
implicit methodology. FIG. 3B shows an example structure of a Jacobian matrix
that uses an
adaptive implicit method with the "Residual 2" in both elements treated
explicitly. FIG. 3C shows
an example structure of a Jacobian matrix that uses an adaptive implicit
method in conjunction
with variable substitution. Due to the variable substitution, the "Residual 2"
equation has been
eliminated and the "Residual 1" equation has been transformed into "Residual
1*" by substitution
of "Residual 2" into "Residual 1."
[0066] In practice, the AIM strategy with variable substitution may be complex
to implement as
compared to the standard AIM strategy due to the complex nature of the
elements used to describe
hydraulic fracturing and flow in the reservoir and wellbore. Furthermore, it
may not be possible
to solve each explicitly assigned equation analytically to a closed-form
solution in terms of the
other system variables. Therefore, direct substitution may not be possible.
Alternatively, the AIM
strategy may be used with direct substitution and numerical differentiation to
estimate the values
of the Jacobian. This method may follow the same approach as described with
variable substitution,
but may avoid the algebraic strategy described in of Equations (6) and (7).
100671 In the previously described variable substitution method, the nonzero
values in the Jacobian
Matrix .4 may be calculated using analytical derivatives of the residual
equations. In standard
reservoir simulations (e.g., simulations that do not couple reservoir
simulations with hydraulic
fracturing simulations) these analytical derivatives may be lengthy and
complex to manipulate.
.. As additional physics are introduced to the system (e.g., by incorporating
hydraulic fracturing
simulation and wellbore simulation), the complexity of the analytical
derivatives may increase. In
a combined hydraulic fracturing and reservoir simulation, the system may be
solved for mass
balance on fluid components in a reservoir along with mass balance on
viscosifying water solute
components, proppants, and energy in the reservoir and wellbore. The balance
equations may be
.. solved for flow through a fracture, including multiphase flow with
gravitational buoyancy and
28
CA 3037543 2019-03-20
non-Newtonian and non-Darcy effects. Evaluating the residual equations for the
flow equation
may be performed with numerical iteration because it may not be possible to
write a closed-form
equation that isolates the value of the residual on one side of the equation.
For example, due to
non-Darcy effect, the equations for flow velocity may include a nonlinear
squared velocity term.
Additionally, due to non-Newtonian effects, fluid viscosity may be a nonlinear
function of flow
velocity. Consequently, determining the flow velocity may not be possible with
an analytical
solution, but may be determined using a numerical solution. Equations for
proppant settling
velocity in a non-Newtonian fluid may also be determined using a numerical
solution. Though
analytically evaluating these lengthy derivatives may be possible, determining
the residual values
may require the use of implicit differentiation, which, in turn, may require a
numerical solution.
[0068] An alternative to analytical differentiation may be the use of a direct
numerical
approximation of the derivative values in the Jacobian. Using direct numerical
approximation of
the derivatives may be less accurate and use more computational effort to
calculate the values in
the Jacobian. However, careful implementation of the method may mitigate
problems from
machine precision roundoff errors and numerical approximation errors. Direct
numerical
approximation may increase the flexibility of the simulation and permit new
physics or new
equations (e.g., components) to be added to the system with minimal effort.
Using numerical
differentiation, the derivative values in the Jacobian may be approximated
with a finite difference
approximation:
Ri(xj-FAx)-mxi)
(8)
ax; Ax
Using numerical differentiation, the residual may be recalculated using an
updated value of xj
evaluated at xj + 4x and the derivative in the Jacobian may be calculated
using Equation 8. This
procedure may avoid the use of analytical derivation to determine the
derivatives.
[0069] The variable, xj may be perturbed by an appropriate amount. There may
be a tradeoff
between the approximation and the roundoff error. Approximation error may
occur because the
underlying equations R, are nonlinear and the finite difference derivative may
be a linear
approximation. Using smaller values of tlx may result in a smaller
approximation error. Roundoff
error may occur because each double precision floating point variable may be
stored by the
computer with sixteen digits of precision. Perturbing xj by an excessively
small amount may cause
29
CA 3037543 2019-03-20
R, to change near the sixteenth digit of precision such that the calculated
difference between the
two residual values may have few digits of precision.
[0070] The numerical calculation of the derivatives may be performed using any
method that is
designed to maximize accuracy by balancing roundoff error and numerical
precision error. For
example, the residual equations may be resealed such that they have the same
units as the
corresponding independent variable. In an example, the total molar balance
residual Rm may have
units of moles per second (moles/s). It may be resealed to have units of
pressure due to reliance
on a corresponding independent pressure variable. Resealing may be
accomplished by dividing
by the derivative of the accumulation term with respect to the primary
variable of the equation
(e.g., pressure in the case of the total molar balance equation). The
accumulation terms may refer
to the calculation of the amount of conserved quantities (e.g., mass or
energy) in an element. For
example, in reservoir simulation fluid density in an element may directly
affect the fluid quantity
of the element. The non-accumulation terms (e.g., flow terms) may affect
calculations of quantities
flowing in or out of the element. The equations may then be made dimensionless
by dividing by
the characteristic value of the independent variable (e.g., pressure). For
example, a characteristic
value of pressure may be around 10 megapascals (MPa), a characteristic value
of temperature may
be 300 Kelvin (K), and a characteristic value of a mole fraction may be 1Ø
The resealed total
molar balance equation may be:
RmAt 1
(9)
vomct
where At is the time step duration, Vp is the pore volume of the element, cr
is the total pore volume
compressibility of the element, P is a characteristic pressure value (e.g., 10
MPa), and lam is the
total molar density of fluid mixture in the element. The values in Equation 9
may be taken from
the previous time step, with the exception of At and Rm, to maintain
consistency within a time step.
[0071] The finite difference approximation may only be accepted if the change
in the resealed
residual equation is within a certain range, such as between 1 x 1 0-3 and
1x10'3. If the scaled change
is too large, then the process may be repeated with a smaller value of /Ix. If
the scaled change is
too small, the process may be repeated with a larger value of Ax. Maintaining
the scaled residual
change within the above range may reduce the risk of roundoff and
approximation error.
[0072] Equation (9) may scale by the magnitude of the accumulation term. The
accumulation
term may be the dominant term in the residual. However, in a system with a
large time step and
CA 3037543 2019-03-20
elements with high transmissivity and small pore volume elements, flow terms
may become
substantially larger than the accumulation term. This method of flow-term
scaling may help to
avoid problems caused by precision error when small pressure changes drive
large amounts of
flow. The flow term scaling factor may be used when the flow term scaling
factor is larger than
the accumulation scaling factor. The system may also be bound by preventing
phase change to
occur in response to the change Ax. For example, when a pressure or molar
composition is changed
such that the hydrocarbon mixture changes from one phase to two phases, the
derivative may be
discontinuous. If a discontinuity occurs, the change Ax may be discarded and
repeated with a step
in the opposite direction (e.g., - Ax). The system may additionally be bound
by natural constraints
imposed on select variables. For example, a mole fraction may be required to
be between zero and
one. Therefore, if a mole fraction is equal to zero, then the step Ax may be
positive. If a mole
fraction is equal to one, then the step Ax may be negative.
100731 A computer-implemented method for numerically calculating the
derivatives (e.g., for
every implicit variable xj in element Ek) may include adding a small number Ax
to the variable
(e.g., implicit variable). A check may be run to determine if the physical
constraints of the system
are violated (e.g., mole fraction greater than one). If the physical
constraints are violated xj may
be reset and the time step Ax may be subtracted rather than added. The
secondary variables (e.g.,
secondary element properties) in Ek that are affected by variable xj may be
updated. If a phase
change occurs in the element, the Ax value may be altered and the above
described process repeated.
The explicit equations in element Ek may be solved for the corresponding
explicit variables. The
secondary variables in element Ek may then be updated. If a phase change has
occurred in the
element, the Ax value may be altered and the above described process repeated.
The derivative for
each element E. that contains an implicit equation affected by variable xj may
be calculated by: (i)
solving the explicit equations in these elements and updating their secondary
variables; (ii)
calculating the residuals of the implicit equations; (iii) nondimensionalizing
the implicit equations;
(iv) calculating the nonzero Jacobian value using Equation 8 if the
nondimensionalized change in
each implicit residual is within a usable range; and (v) reverting the
variables of each element E..
If the nondimensionalized change in each residual is not within a usable
range, the time step the
Ax may be altered. The variables of element Ek may then be reverted. If the
nonzero derivative
values associated with variable xi have been calculated (e.g., corresponding
to all values in the
31
CA 3037543 2019-03-20
column), the method may be halted. If nonzero derivative values remain that
need a smaller or a
larger time step, the iteration may be repeated. If nonzero derivative values
remain that need both
a smaller and a larger time step, the iteration may be repeated twice.
[0074] Calculation of the nonzero values in the Jacobian may be
computationally expensive.
Therefore, it may be beneficial to calculate the values as infrequently as
possible. The
conventional AIM method described herein, may begin by calculating the nonzero
values in the
full Jacobian matrix, including the values associated with explicit rows and
columns. In some
cases, the nonzero values associated with the explicit variables and/or
residuals may outnumber
the nonzero values associated with the implicit variables and/or residuals.
The AIM method using
variable substitution may bypass directly calculating the derivative of the
explicit equations and/or
explicit variables. For example, the update in Equation (5) may use a single
derivative value and
direct application of the Newton method to Equation (4) may involve
calculation of four derivative
values for a 2x2 matrix. Using the substitution method with numerical
derivatives to estimate the
values in the Jacobian matrix may increase the computational efficiency of the
simulation by
reducing the number of nonzero values that must be calculated when assembling
the Jacobian.
Rather than assembling the full Jacobian and manipulating the matrix to reduce
the size of the
coupled system to be solved, the substitution method directly assembles the
reduced system
involving only the implicit equations and/or variables.
[0075] Using the substitution method with numerical differentiation may reduce
or eliminate
analytically solving the explicit equations and analytically substituting
variables. Substitution may
be accomplished within the numerical differentiation. Prior to each residual
calculation, the
explicit equations may be solved for their corresponding unknown and the
unknown values may
be used directly in the residual calculation. FIG. 4 shows an example process
flow diagram for
hydraulic fracture and reservoir simulation implementing AIM with variable
substitution and
numerical differentiation. The explicit equations may be solved for their
corresponding unknowns
using the current iterated guesses for the unknown variables. The secondary
element properties
(e.g., density, viscosity, etc.) may be updated for the elements that contain
at least one explicit
equation. The residuals may be calculated for the implicit unknowns. The
system may be checked
against a convergence criterion. For example, if the residual values are
resealed according to a
procedure such as is shown in Equation (9), and the absolute value is less
than a certain tolerance,
32
CA 3037543 2019-03-20
the values can be considered to be converged. If the system converges (e.g.,
all residual equations
or components have reached the convergence tolerance), the method may be
halted. If the system
does not meet the convergence criterion, the Jacobian matrix may be
calculated. To calculate the
Jacobian, for each column], a small value Ax may be added to the unknown and
the secondary
element properties for the variables in the element may be calculated. The
flow terms may then
be recalculated. The explicit variables in each element that has a nonzero
value in the jth column
may be recalculated by solving the corresponding explicit equations. The
element's residuals
corresponding to the implicit equations may be calculated along with the
corresponding derivatives
using Equation (8). The element variables that were perturbed in the
calculation of the derivatives
.. may then be reset as described elsewhere herein. Once the Jacobian matrix
is calculated, the matrix
may be solved for the updated vector for the implicit variables dx using
Equation (2) followed by
updating the implicit variables. The secondary element properties that depend
on the implicit
variables may be solved using the implicit variables. The explicit variables
may then be updated
and the iterative process repeated until the convergence criterion is reached.
[0076] Using AIM with variable substitution and numerical differentiation may
involve fewer
residual and secondary variable calculations than AIM methods using analytical
derivatives. The
residual and secondary variable calculations may scale linearly with the
number of elements and
may be readily parallelized to multiple computer processors to increase the
efficiency of the
simulation. Solving the Jacobian may scale poorly with system size and may be
difficult to
parallelize. The cost of solving the Jacobian may be reduced by the use of the
AIM method relative
to a fully implicit method and, thus, the overall method may be more efficient
than a fully implicit
method. Additionally, the computational efficiency may be increased using
system optimizations.
For example, the method may recalculate only the secondary variables that
depend on the
perturbed variables rather than recalculating all of the secondary variables.
This may be useful for
systems with a variety of different physics. For example, it may be
unnecessary to recalculate fluid
properties in response to a perturbation in proppant volume fraction because
proppant volume
fraction may not affect the fluid properties. Additionally, the method may
reuse derivative values
associated with rows and column of the matrix that have converged, which may
reduce the total
number of derivative values recalculate in later iterations. Another
efficiency increase may be
found with the boundary element variables used to calculate stress changes due
to fracture aperture
33
CA 3037543 2019-03-20
changes. The derivative of the effective normal stress with respect to
aperture of another element
may be a constant number that does not change during the simulation.
Therefore, these derivatives
may be calculated once and reused instead of being recalculated.
100771 The systems and methods described herein may implement a simulator that
contains four
types of mass and energy balance equation: multiphase fluid flow (e.g., black
oil or compositional),
water solutes that may impart non-Newtonian flow characteristics on the water
phase, proppant
transport, and thermal energy. The balance equations may be solved using three
different types of
elements: fracture elements, wellbore elements, and matrix elements. Wellbore
elements may
represent sections of a wellbore (e.g., pipe that is cemented into the ground
or an openhole section
comprising a cylindrical well that has been bored through rock). Matrix
elements may represent
volumes of rock that contain fluid in the porosity of the rock. Fracture
elements may represent
sections of cracks formed in the rock that contain fluid and proppant. Each
element may comprise
different sets of governing equations. Some of the governing equations may
overlap between the
elements. In each of the elements, each of the four types of balance equations
may be assigned as
either implicit or explicit. Additionally, the system may include momentum
balance equations
(e.g., components) in the wellbore elements, poroelastic stress response
equations (e.g.,
components) in the matrix elements, and mechanical stress interaction
equations in the fracture
elements that may be treated as fully implicit, partially implicit, or
explicit. In an example, these
equations may be treated as fully implicit.
100781 The equations in the explicit update of a particular element may affect
each other. In an
example, explicit updates within an element may involve simultaneous solution
of all of the
equations in the element. In another example, the equations may be structured
such that the
equations may be solved sequentially. The solution order may be dependent up
on the physics of
the system and may be any order that allows for the system to converge. An
example solution
sequence is, (i) the fluid component molar balance, (ii) water solute mass
balance, (iii) proppant
mass balance, (iv) thermal balance, and (v) the pressure equation for total
molar balance. In order
to reach a solution with the sequential method, the solution to an equation
may be dependent upon
the solution of the preceding equations, but may not be dependent upon the
solutions to subsequent
equations. In an example, pressure is treated explicitly. The preceding
equations may depend on
the pressure variable due to the effect on porosity and phase density.
However, because pressure
34
CA 3037543 2019-03-20
is changing very slightly in explicit pressure components, the error may be
second-order and
negligible.
[0079] The compositional model may be implemented by treating the mole
fractions as primary
or secondary variables. In an example, the mole fractions are treated as
primary variables. There
may be one or more total molar balance equation associated with pressure.
There may be 11,-1
molar balance equations associated with the specific molar fractions, where n,
is the total number
of fluid components being tracked by the model. In this context, a fluid
component is a particular
type of molecule being tracked, such as methane or carbon dioxide. Variable
switching may be
used to ensure that the one molar balance equation that is not explicitly
solved is not the molar
balance with the highest molar fraction. All n, of these equations, including
the pressure
components, may be treated implicitly or explicitly. The component balance
equation may be
treated implicitly or explicitly. In an example, the component balance
equation is treated explicitly.
[0080] In reservoir simulation, pressure may not be treated explicitly because
the time set
restrictions on stability of the pressure equation may be limited. However, in
simulations with
hydraulic fractures embedded in a matrix, the time steps may be on the order
of seconds (e.g., due
to the rapidly changing parameters in the fracture). Using small time steps
may enable the pressure
equations (e.g., components) to be treated fully explicitly in the matrix
elements and still maintain
numerical stability. The number of matrix elements may outnumber the fracture
elements in the
simulation and so treating many, or all, of the matrix elements explicitly may
increase
computational efficiency. If a matrix element is handled fully explicitly, the
matrix components
(e.g., equations that make up the matrix element) may be removed from the
coupled nonlinear
solution of equations in the implicit update. When calculating residual
equations in adjacent
elements that have implicit pressure, the flow terms from the explicit
pressure element may be
calculated using the pressure from the previous time step. The flow terms of
the explicit pressure
elements may be calculated after the nonlinear solution is completed using the
explicit pressure
values from adjacent explicit pressure elements and using the implicit
pressure values from
adjacent implicit pressure elements previously calculated. Once the flow terms
are known, the
explicit equations may be solved in a specified order.
[0081] The effective flowing water properties of the system may require
different treatment
because they may depend nonlinearly on variables that are mixed between
implicit and explicit.
CA 3037543 2019-03-20
Using an AIM strategy, effective flowing properties (e.g., density and/or
viscosity) may be
calculated using the parameters from the previous time step and/or the
parameters from a new time
step. Calculating the effective flow properties using parameters from the
previous or current time
step may be difficult if variables are a mixture of implicit and explicit. The
water properties (e.g.,
density, viscosity, and saturation) may depend on water mole fraction, water
solute mass fraction,
temperature, and pressure. These properties may be mixed between implicit and
explicit. For
example, the water properties may include implicit water mole fraction and
explicit temperature
and composition. In this case, a separate 'effective' water phase may be
calculated that may be
evaluated at mixed molar fraction, water solute fraction, pressure and
temperature. This effective
water phase may be used in the flow calculations. These effective phase
calculations may allow
for implicit thermal mixed with explicit composition equations and/or
variables. For flow terms
in explicit composition elements, values such as density and viscosity may be
used directly from
the previous time step and the dependence on the implicit temperature variable
may be ignored.
This method may be used to simulate flow of the non-water phase. For example,
if an element has
an explicit composition, then the phase properties may be used from the
previous time step
regardless of the explicit and/or implicit status of the temperature
component. However, for the
water phase there may be significant nonlinearity arising from the
viscosifying and non-Newtonian
water solutes and the effective flowing properties may be calculated from a
mixture of implicitly
and explicitly treated variables.
[0082] Assignment of equations and variables as implicit and/or explicit may
be made for each
time step and/or equation and variable assignments may be constant across
multiple time steps.
Implicit and/or explicit assignments for equations and variables for pressure,
composition, water
solute fraction, proppant fraction, and temperature may be made for each time
step. Equation
and/or variable assignment may be performed using the Courant-Friedrichs-Lewy
(CFL) number
method by calculating a sum of the absolute value of the flow terms and
dividing that calculated
value by the total pore volume of the element (e.g., matrix or fracture
element). If the ratio is
greater than one, the variable type may be assigned to be implicit. If the
ratio is less than one, the
variable type may be assigned to be explicit. Alternatively, to be
conservative, a ratio cutoff less
than one may be used.
36
1
CA 3037543 2019-03-20
[0083] The explicit updates may fail if they result in negative quantities.
For example, if a
conserved species (e.g., component, water solute, or proppant type disappears
during a time step,
inaccuracy may occur in the explicit update. Therefore, if an explicit update
results in a negative
amount of a species, then the time step may be discarded. To avoid this
problem, the equations
and/or variables that are at risk of disappearing may be handled implicitly.
In this case, when
calculating the CFL number, the sum of the absolute value of the element may
be divided by the
amount of conserved species. For example, for proppant, the total proppant
flow volume of each
proppant type may be divided by the volume of that type in the element. For
water solutes, the
mass of flowing solute may be divided by the total amount of solute present in
the element. For
components, the flowing moles of each type may be divided by the moles of the
type present in
the element. For composition, the total flowing volume in and/or out of the
element may be
divided by the pore volume of the phase that has the smallest nonzero
saturation. Another method
for assigning equations and/or variables that may be at risk of disappearing
if treated explicitly
may be to estimate the derivative of each volumetric flow term and multiply it
by 0.1 MPa. That
value may then be divided by the pore volume of the phase with the smallest
saturation. For
example, composition may be treated implicitly if this ratio is greater than
one. Alternatively, to
be conservative, a value of less than one may be used. This type of assignment
method may select
for elements that may be emptied of an entire phase by a small change is
pressure.
[0084] For example, matrix elements may be considered for explicit treatment
of pressure. The
CFL number method ay be used to assign the pressure variable as either
implicit or explicit for
each phase. The ratio may be determined by:
k krp At 1
(10)
tipCtO AL2'
where AL is the smallest dimension of either the height, width, or length of
the element, kkrp is the
permeability times the relative permeability of the phase, (/) is the element
porosity, and pip is the
viscosity of the phase. If the ratio in Equation (10) exceeds one for any of
the phases, the element
may be assigned implicitly.
[0085] The time step duration may strongly affect the explicit and/or the
implicit assignments.
The time step may be varied such that a select percentage of variables are
assigned as explicit or
implicit. Alternatively, or in addition to, the time step duration may be
adaptively varied by
37
CA 3037543 2019-03-20
limiting the observed change in the independent variables in each time step.
Thus, the percentage
of implicit or explicit equations may vary widely between time steps.
[0086] FIG. 12 shows a computer system that is programmed or otherwise
configured to
implement methods provided herein. The system may include a computer system
1201 that is
.. programmed or otherwise configured to implement modeling and simulating
hydraulic fracturing
and fluid flow in a wellbore and reservoir. The computer system 1201 may be an
electronic device
of a user or a computer system 1201 that is remotely located with respect to
the electronic device.
The electronic device may be a mobile electronic device. The computer system
1201 may include
a central processing unit (CPU, also "processor" and "computer processor"
herein) 1205, which
may be a single core or multi core processor. In an example, the central
processing unit 1205
comprises a plurality of processors for parallel processing. The processor(s)
may receive data
from the calibration well (e.g., either from a user or via an upload from
sensors or data logs), use
the data to generate a model of the calibration well, generate equations to
represent the matrix
elements, fracture elements, and reservoir elements within the model, solve
the model, compare
the model solution to the production data from the calibration well, receive
hydraulic treatment
conditions (e.g., from a user of from a memory of the system), solve the
calibrated model to
generate simulation data, and display the simulation results to a user (e.g.,
via a display). The
computer system 1201 may also include a memory or memory location 1210 (e.g.,
random-access
memory, read-only memory, flash memory, etc.), electronic storage unit 1215
(e.g., hard disk),
.. communication interface 1220 (e.g., network adapter) for communication with
one or more other
systems, and peripheral devices 1225, such as cache, other memory, data
storage and/or electronic
display adapters. The memory 1210, storage unit 1215, interface 1220, and
peripheral devices
1225 may be in communication with the CPU 1205 through a communication bus
(solid lines),
such as a mother board. The storage unit 1215 may be a data storage unit (or
data repository) for
storing variable assigned or updated matrix, fracture, or wellbore elements,
explicit and implicit
variables, and secondary element properties. Additionally, the memory or
storage unit may store
raw data, calculated data, one or more components of the model, one or more
components of the
calibrated model, and/or simulation outputs (e.g., summary tables, graphical
representations of the
results, and/or specific outputs). The computer system 1201 may be operatively
coupled to a
computer network ("network) 1230 with the aid of the communication interface
1220. The
38
CA 3037543 2019-03-20
network 1230 may be the Internet, and internet and/or extranet, or an intranet
and/or extranet that
is in communication with the Internet. The network 1230 may be, in some cases,
a
telecommunication and/or data network. The network 1230 may include one or
more computer
servers, which may enable distributed computing, such as cloud computing. The
network may be
in communication with one or more sensors, data logs, or production logs such
that the computer
system can access data from the sensor, data logs, or production logs. The
network 1230, in some
cases with the aid of the computer system 1201, may implement a peer-to-peer
network, which
may enable devices coupled to the computer system 1201 to behave as a client
or a server. The
network may facilitate mobile electronic devices 1202 to access the simulated
hydraulic fracturing
and reservoir data, including, but not limited to, calculated and stored
variables and parameters,
governing equations (e.g., components), explicit and implicit equation and
variable assignments,
and/or resulting simulation diagrams.
[0087] The CPU 1205 can be part of a circuit, such as an integrated circuit.
One or more other
components of the system 1201 can be included in the circuit. In some cases,
the circuit is an
application specific integrated circuit (ASIC). The storage unit 1215 can
store files, such as
drivers, libraries and saved programs. The storage unit 1215 can store user
data, e.g., user
preferences and user programs. The computer system 1201 in some cases can
include one or more
additional data storage units that are external to the computer system 1201,
such as located on a
remote server that is in communication with the computer system 1201 through
an intranet or the
Internet.
[0088] The computer system 1201 can communicate with one or more remote
computer systems
through the network 1230. For instance, the computer system 1201 can
communicate with a
remote computer system of a user (e.g., a mobile electronic device). Examples
of remote computer
systems include personal computers (e.g., portable PC), slate or tablet PC's
(e.g., Apple iPad,
Samsung Galaxy Tab), telephones, Smart phones (e.g., Apple iPhone, Android-
enabled device,
Blackberry ), or personal digital assistants. The user can access the computer
system 1201 via
the network 1230.
[0089] Methods as described herein can be implemented by way of machine (e.g.,
computer
processor) executable code stored on an electronic storage location of the
computer system 1201,
such as, for example, on the memory 1210 or electronic storage unit 1215. The
machine executable
39
CA 3037543 2019-03-20
or machine readable code can be provided in the form of software. During use,
the code can be
executed by the processor 1205. In some cases, the code can be retrieved from
the storage unit
1215 and stored on the memory 1210 for ready access by the processor 1205. In
some situations,
the electronic storage unit 1215 can be precluded, and machine-executable
instructions are stored
on memory 1210. The code can be pre-compiled and configured for use with a
machine having a
processer adapted to execute the code, or can be compiled during runtime. The
code can be
supplied in a programming language that can be selected to enable the code to
execute in a pre-
compiled or as-compiled fashion.
100901 Aspects of the systems and methods provided herein, such as the
computer system 1201,
can be embodied in programming. Various aspects of the technology may be
thought of as
"products" or "articles of manufacture" typically in the form of machine (or
processor) executable
code and/or associated data that is carried on or embodied in a type of
machine readable medium.
Machine-executable code can be stored on an electronic storage unit, such as
memory (e.g., read-
only memory, random-access memory, flash memory) or a hard disk. "Storage"
type media can
include any or all of the tangible memory of the computers, processors or the
like, or associated
modules thereof, such as various semiconductor memories, tape drives, disk
drives and the like,
which may provide non-transitory storage at any time for the software
programming. All or
portions of the software may at times be communicated through the Internet or
various other
telecommunication networks. Such communications, for example, may enable
loading of the
software from one computer or processor into another, for example, from a
management server or
host computer into the computer platform of an application server. Thus,
another type of media
that may bear the software elements includes optical, electrical and
electromagnetic waves, such
as used across physical interfaces between local devices, through wired and
optical landline
networks and over various air-links. The physical elements that carry such
waves, such as wired
or wireless links, optical links or the like, also may be considered as media
bearing the
software. As used herein, unless restricted to non-transitory, tangible
"storage" media, terms such
as computer or machine "readable medium" refer to any medium that participates
in providing
instructions to a processor for execution.
[0091] Hence, a machine readable medium, such as computer-executable code, may
take many
forms, including but not limited to, a tangible storage medium, a carrier wave
medium or physical
CA 3037543 2019-03-20
transmission medium. Non-volatile storage media include, for example, optical
or magnetic disks,
such as any of the storage devices in any computer(s) or the like, such as may
be used to implement
the databases, etc. shown in the drawings. Volatile storage media include
dynamic memory, such
as main memory of such a computer platform. Tangible transmission media
include coaxial
cables; copper wire and fiber optics, including the wires that comprise a bus
within a computer
system. Carrier-wave transmission media may take the form of electric or
electromagnetic signals,
or acoustic or light waves such as those generated during radio frequency (RF)
and infrared (IR)
data communications. Common forms of computer-readable media therefore include
for example:
a floppy disk, a flexible disk, hard disk, magnetic tape, any other magnetic
medium, a CD-ROM,
DVD or DVD-ROM, any other optical medium, punch cards paper tape, any other
physical storage
medium with patterns of holes, a RAM, a ROM, a PROM and EPROM, a FLASH-EPROM,
any
other memory chip or cartridge, a carrier wave transporting data or
instructions, cables or links
transporting such a carrier wave, or any other medium from which a computer
may read
programming code and/or data. Many of these forms of computer readable media
may be involved
in carrying one or more sequences of one or more instructions to a processor
for execution.
[0092] The computer system 1201 can include or be in communication with an
electronic display
that comprises a user interface (UI) for providing, for example, QR codes,
transaction information,
fund transfer information, and/or other details. Examples of UI's include,
without limitation, a
graphical user interface (GUI) and web-based user interface. The electronic
display can be
.. integrated or in a user device (e.g., 1235, 1240). The electronic display
can be external to a user
device and in communication via wireless or wired connections to the user
device.
[0093] The user device 1235 may be mobile device (e.g., smartphone, tablet,
pager, personal
digital assistant (PDA)), a computer (e.g., laptop computer, desktop computer,
server, or any other
type of device. The user device 1235 may optionally be portable. The user
device 1235 may be
handheld. The user device may be a network device capable of connecting a
network, such as a
local area network (LAN), wide area network (WAN) such as the Internet, a
telecommunications
network, a data network, or any other type of network. The user device 1235
may be capable of
direct or indirect wireless communications. The user device 1235 may be
capable of peer-to-peer
(P2P) communications and/or communications with cloud-based infrastructure.
The user device
41
CA 3037543 2019-03-20
1235 may be used to simulate hydraulic fracture at the site of hydraulic
fracture (e.g., at the well)
or may be used remotely (e.g., away from the well).
[0094] The user device may include a display 1240. The display may show in
real time one or
more static images (e.g., photographs) and/or dynamic images (e.g., video)
generated by the model
of the calibration well or simulation of the production well. The display may
be able to present
information to a user. The display 1240 may visually illustrate information.
The information
shown on the display may be changeable. The display may include a screen, such
as a liquid
crystal display (LCD) screen, light-emitting diode (LED) screen, organic light-
emitting diode
(OLED) screen, plasma screen, electronic ink (e-ink) screen, touchscreen, or
any other type of
screen or display. The display 1240 may or may not accept user input. In an
example, the display
1240 accepts user inputs and the user inputs enable the user to provide and
vary input parameters
and hydraulic fracturing treatment conditions.
[0095] The display 1240 may show a graphical user interface. The graphical
user interface may
be part of a browser, software, or application that may aid in the user
performing a transaction
using the device. The interface may allow the user to self-identify using the
device. The user may
access a user account using the device. The user account may be used during a
modeling and
simulation of a hydraulic fracture well. The user device may be capable of
operating one or more
software applications. One or more applications may or may not be related to
modeling and
simulating hydraulic fracturing. The user device may be capable of accepting
inputs via a user
interactive device. Examples of such user interactive devices may include a
keyboard, button,
mouse, touchscreen, touchpad, joystick, trackball, camera, microphone, motion
sensor, heat
sensor, inertial sensor, or any other type of user interactive device.
[0096] The user device 1235 may comprise one or more memory storage units
which may
comprise non-transitory computer readable medium comprising code, logic, or
instructions for
performing one or more steps. The user device may comprise one or more
processors capable of
executing one or more steps, for instance in accordance with the non-
transitory computer readable
media. The one or more memory storage units may store one or more software
applications or
commands relating to the software applications. The one or more processors
may, individually or
collectively, execute steps of the software application.
42
CA 3037543 2019-03-20
[0097] A communication unit may be provided on the device. The communication
unit may allow
the user device to communicate with an external device. The external device
may be a device of
a server or may be a cloud-based infrastructure. The communications may
include
communications over a network or a direct communication. The communication
unit may permit
wireless or wired communications. Examples of wireless communications may
include, but are
not limited to WiFi, 3G, 4G, LTE, radiofrequency, Bluetooth, infrared, or any
other type of
communications. The communications unit may or may not aid in collecting data
used for
modeling a calibration well.
[0098] In an example, the user device is a computer system 1201 can include or
be in
communication with an electronic display 1235 that comprises a user interface
(UI) 1240 for
providing, for example, diagrams of the simulation results to a user. Examples
of UI' s include,
without limitation, a graphical user interface (GUI) and web-based user
interface.
[0099] Methods and systems of the present disclosure can be implemented by way
of one or more
algorithms. The method can be implemented by way of software upon execution by
the central
processing unit 1205. The method can, for example, direct the computer memory
to store and
update explicit and implicit variables, store and update secondary element
properties, and/or store
and update components of the matrix elements, fracture elements, and wellbore
elements. The
method may solve the matrix components, fracture components, and wellbore
components. The
method may solve the matrix elements, fracture elements, and wellbore elements
to simulate
hydraulic fracture and fluid flow in the wellbore and reservoir. The method
may generate plots
that represent the simulation results and may display the plots on an
electronic display.
EXAMPLE
[0100] An integrated three-dimensional reservoir, wellbore, and hydraulic
fracturing simulator is
used to simulate a single-stage fracture job from a vertical well, followed by
production. The
system includes injection of a pad followed by water with a 60 mesh proppant.
This is followed
by a lower rate injection of water gelled with guar and 20 mesh proppant. The
fracturing treatment
is shown to generate a large, well-propped fracture. The fracture propagates
below the water-
hydrocarbon contact, resulting in significant watercut during production. The
system includes
molar balance equations on fluid components, water solute mass balance
equations, proppant mass
43
CA 3037543 2019-03-20
balance equations, thermal balance, momentum balance in the wellbore, and
mechanical
interaction equations between the fracture elements.
[0101] The simulation involves injection to create a single hydraulic
fracture. The fracture height
is limited by stress layering. Proppant transports through the fracture and
gravitational settling
settles out and screes out of the fracture tip. Water solutes are injected
that impact non-Newtonian
rheological characteristics and fluid is produced from the fracture and the
surrounding formation.
Multiphase flow occurs in the fracture during production, which involves
gravitational segregation.
[0102] FIG. 5 shows simulation results of the distribution of proppant volume
fraction in the
fracture at shut-in, 2.86 hours, at the end of injection 505 displayed on an
example graphical user
interface 510. At this time, proppant is seen to almost entirely fill the
fracture, indicating
successful proppant placement. FIG. 6 shows simulation results of the
distribution of temperature
in the fracture at shut-in 605, 2.86 hours, on an example graphical user
interface 610. A substantial
region of cooling develops near the wellbore region. As the matrix
discretization is fairly course
in the vertical direction, some mesh dependency is evident in the temperature
distribution. FIG.
7 shows simulation results of the distribution of water saturation in the
fracture after 215 days of
production 705 displayed on an example graphical user interface 710. The
initial water-
hydrocarbon contact is located twenty feet below the perforation cluster. A
substantial amount of
fracture growth and proppant placement occurs below the contact, and so a
significant amount of
the fracture is filled with water. As a result, the well produces a
significant water cut. Above the
water-hydrocarbon contact, there is residual water trapped in the fracture,
reducing relative
permeability to the hydrocarbon phase.
[0103] FIG. 8 shows simulation results of the distribution of pressure in the
fracture after 215 days
of production 805 displayed on an example graphical user interface 810. There
is a pressure
gradient across the fracture from the tips to the well, indicating that
despite the successful proppant
placement, there is pressure drawdown along the fracture. The pressure
drawdown occurring in
the fracture demonstrates the importance of maximizing fracture conductivity,
minimizing non-
Darcy effect near the wellbore region, and minimizing fracture damage from
fracturing fluid. FIG.
9 shows simulation results of the distribution of normal stress in the
fracture after 215 days of
production 905 displayed on an example graphical user interface 910. The
minimum principal
stress at is approximately 8,000 pounds per square inch (psi) at approximately
11,000 feet (ft). In
44
CA 3037543 2019-03-20
the near wellbore region, fracture normal stress is elevated up to 500 psi
above the minimum
principal stress because of the stress shadow caused by the propping open of
the aperture by the
proppant. Near the tips of the fracture, where less proppant is placed, the
stress shadow is weaker
and the normal stress is near the in-situ minimum principal stress. In the
region above the
.. perforation cluster, where little proppant is places, the normal stress is
up to 300 psi less than the
in-situ minimum principal stress. This may occur because the normal stress in
this part of the
fracture is reduced by stresses induced by the aperture in the nearby, highly
propped parts of the
fracture. FIG. 10 shows simulation results of the distribution of fluid
pressure in the matrix after
215 days of production 1005 displayed on an example graphical user interface
1010. The pressure
.. distribution is approximately linear, beginning to transition into
elliptical. There is a narrow region
of large pressure decline immediately surrounding the fracture. There is a
much broader region of
mild pressure decline in the surrounding matrix. FIG. 11 shows simulation
results of the predicted
production rate of water, oil, and gas as a function of time 1105 displayed on
an example graphical
user interface 1110. Rates decline approximately with the square root of time,
as expected for
.. linear flow. The water production rate is relatively high because a large
percentage of the fracture
is placed below the water-hydrocarbon contact.
101041 While preferred embodiments of the present invention have been shown
and described
herein, it will be obvious to those skilled in the art that such embodiments
are provided by way of
example only. It is not intended that the invention be limited by the specific
examples provided
within the specification. While the invention has been described with
reference to the
aforementioned specification, the descriptions and illustrations of the
embodiments herein are not
meant to be construed in a limiting sense. Numerous variations, changes, and
substitutions will
now occur to those skilled in the art without departing from the invention.
Furthermore, it shall
be understood that all aspects of the invention are not limited to the
specific depictions,
configurations or relative proportions set forth herein which depend upon a
variety of conditions
and variables. It should be understood that various alternatives to the
embodiments of the
invention described herein may be employed in practicing the invention. It is
therefore
contemplated that the invention shall also cover any such alternatives,
modifications, variations or
equivalents. It is intended that the following claims define the scope of the
invention and that
.. methods and structures within the scope of these claims and their
equivalents be covered thereby.
CA 3037543 2019-03-20