Note: Descriptions are shown in the official language in which they were submitted.
SQUID-BASED ELECTROMAGNETIC DETECTION METHOD FOR
INDUCTION-POLARIZATION SYMBIOTIC EFFECT OF TWO-PHASE
CODUCTING MEDIUM
TECHNICAL F11- LD
[0001] The disclosure relates to a detection method in the geophysical
exploration field,
and more particularly to a superconducting quantum interference device (SQUID)-
based
electromagnetic detection method for an induction-polarization symbiotic
effect of a two-
phase conductive medium, which is suitable for an actual geological two-phase
conductive medium.
BACKGROUND
[0002] In the geophysical exploration field, a single induction or
polarization effect is
usually obtained by measuring electric and magnetic fields. Since the earth is
a rough and
highly-dissipative medium, underground lithologic and physical properties are
highly
rough and non-linear. Actually, polymetallic ore and other media belong to
composite
multiphase conductive media, so it is particularly important to measure
complex physical
properties or parameters at multiple scales. Under the excitation of an
alternating field,
the induction and polarization effects in multiphase conducing media exist
simultaneously and are accompanied by each other. The induction response can
better
distinguish formation lithology, and the polarization response can effectively
identify
favorable oil and gas reservoirs and metal ore anomalies. To realize high-
resolution and
deep detection of complex underground geological structures, it is necessary
to
simultaneously measure the information of multiple physical fields such as
electrical,
magnetic and polarization fields of the complex geological structures and
simultaneously
acquire multiple parameters comprising conductivity and polarizability of the
rock.
[0003] At present, in the electromagnetic detection field of the induction and
polarization effect, by only considering the single effect of electromagnetic
induction or
polarization during measurement and by only interpreting the resistivity or
polarizability,
there may be multiple solutions, resulting in low detection resolution and the
inability to
1
Date Recue/Date Received 2021-06-21
realize deep and fine detection. In the wide field electromagnetic method
proposed by He
Jishan (He, J.S. Theory and technology of wide field electromagnetic method,
The
Chines Journal of Non-ferrous Metals, 2019, 29(9), pp. 1809-1816), apparent
resistivity
was acquired by measuring the components of the electric field or magnetic
field in
frequency domain. However, this method only focused on the inversion of the
resistivity,
and could not fully reflect the multi-scale dispersion characteristics of
underground
complex multi-phase mediums. Yang Zhenwei (2016) (Yang, Z.W. et al., Current
tituation
and review of complex resistivity, Progress in Geopgysics, 2015, 30(2), pp.
899-904)
obtained the complex resistivity by measuring the imaginary and real
components of the
electric field, but it was required to measure two field quantities which are
the changes
rates of the electric field and the magnetic field. He Zhanxiang (He Z.X. et
al.,
Time-frequency electromagnetic (TFEM) method: Data acquisition design, Oil
Geophysical Prospecting, 2019, 54(4), pp. 908-914) obtained the resistivity
and
polarizability by a time-frequency electromagnetic method; however, in the
method both
time domain and frequency domain were required.
[0004] Chinse Patent Application No. CN201510882791.X discloses a multi-
frequency
detection device for detecting complex resistivity. This device can generate
multiple
types of frequency signals. It can analyze and process the waveforms of
voltage signals
and current signals, and accurately measure the complex resistivity spectrum
of the
formation. However, only the spectral information is acquired by this method,
and it is
difficult to analyze geometrical characteristics and physicochemical
characteristics of an
underground medium.
[0005] Chinse Patent Application No. CN202010339342.1 discloses a method and
system for analyzing a time-domain induced polarization spectrum of a porous
medium.
The relaxation time distribution of the porous medium is jointly inversed and
estimated
by using the apparent polarizability data calculated at several different
charging times,
and the distribution of apertures can be reflected. In the existing
electromagnetic
detection methods, polymetallic ore such as copper ore can be detected by
observing the
induction-polarization symbiotic effect, but it is still required to switch
between the time
domain and frequency domain to measure electric and magnetic fields.
Therefore, it is
2
Date Recue/Date Received 2023-01-11
necessary to design a time-domain electromagnetic detection method which can
finely
measure the induction-polarization symbiotic effect in the multi-phase
conductive
medium.
SUMMARY
2A
Date Recue/Date Received 2023-01-11
[0006] In view of the difficulty of realizing detection of a two-phase medium
by the
existing detection methods, an objective of the disclosure is to establish a
generalized
equivalent induced polarization model according to the complex characteristics
of the
actual underground medium and the composition characteristics of polymetallic
mineral
rock, and provide an electromagnetic detection method for an induction-
polarization
symbiotic effect of a two-phase conductive medium.
[0007] The disclosure provides a two-phase conductive medium induction-
polarization
symbiosis electromagnetic detection method based on SQUID, the method
comprising:
[0008] 1) establishing a dual-time-scale fractional conductivity model of an
induction-
polarization symbiotic effect, and substituting the dual-time-scale fractional
conductivity
model into Maxwell equations to obtain dual-time fractional electromagnetic
field
diffusion equations;
[0009] 2) directly solving the fractional term in the dual-time-scale
fractional
conductivity model by a fractional finite-difference time-domain method
according to the
dual-time fractional electromagnetic field diffusion equations established in
1),
performing discrete recursion on a component form containing the fractional
differential
term to realize dual-time-scale three-dimensional electromagnetic response
numerical
simulation of the induction-polarization symbiotic effect, and calculating the
magnetic
field response of the induction-polarization symbiotic effect;
[0010] 3) for the dual-time-scale fractional conductivity model in 1),
performing three-
dimensional numerical simulation of current excitation with different falling
edges by
using 2), determining, according to characteristics of the induction-
polarization symbiotic
effect, emission parameters in the case of maximum induction and polarization
responses,
and constructing a dual-controllable-edge trapezoidal wave transmission
targeted
excitation relationship to realize targeted excitation of transmission of
trapezoidal waves
with two falling edges;
[0011] 4) transmitting, by a transmission for trapezoidal waves with two
controllable
edges according to the dual-controllable-edge trapezoidal wave transmission
targeted
excitation relationship in 3), receiving based on a superconducting quantum
interference
3
Date Recue/Date Received 2021-06-21
device (SQUID), reading data by using a non-modulated flux phase-locked
readout
circuit, removing geomagnetic interference from read data through an external
AC and
internal DC magnetic field compensation method, and removing human noise and
electromagnetic noise through a multilateralism mixed noise shielding
technology, and
then measuring magnetic fields of the induction-polarization symbiotic effect;
[0012] 5) preprocessing the measured data of the induction-polarization
symbiotic effect
measured in 4), performing polarization identification by a data mining
method, and
intelligently extracting and imaging multiple parameters comprising
conductivity,
polarizability, dispersion coefficient and volume fraction by quantum particle
swarm
optimization (QPSO) and image the results;
[0013] 6) calculating a singularity index of the results extracted in 5) by a
local
singularity index algorithm of a rectangular window, and identifying and
predetermining
valuable economic mineral resources and unvalued mineralized zones.
[0014] Further, 2) is implemented as follows:
[0015] 2.1) according to the dual-time fractional electromagnetic field
diffusion
equations in 1), performing piecewise-linear approximation on the complex
frequency
variable fractional power of the dual-time fractional electromagnetic field
diffusion
equation to obtain diffusion equations of an integer power;
[0016] 2.2) transforming the diffusion equations to the time domain,
performing
difference approximation by a finite difference method, directly solving the
fractional
item in the conductivity model of the two-phase conductive medium, and
deriving the
iterative relationship among components of the electric field and magnetic
field;
[0017] 2.3) dividing a calculation region by a non-uniform Yee grid,
calculating
conductivity, polarizability, dispersion coefficient, polarization volume
fraction and
polarization particle radius, loading an initial field under the excitation of
trapezoidal
waves and boundary conditions, and iteratively calculating each component of
the
electromagnetic fields to realize dual-time-scale three-dimensional
electromagnetic
numerical simulation of the induction-polarization symbiotic effect; and
4
Date Recue/Date Received 2021-06-21
[0018] 2.4) calculating the magnetic field response of the induction-
polarization
symbiotic effect according to 2.3), analyzing the influence of the
transmitting parameters
on polarization, and optimizing the transmitting parameters.
[0019] Further, in 3), the specific control idea of the transmission of
trapezoidal waves
with two falling edges is described below. During the turn-off period of a
first set of
trapezoidal waves in one transmission cycle, it is required to switch a
discharge circuit to
a quick break circuit. At this time, a high-voltage transient suppression
diode is broken
down by voltage overshoot. The voltages at two ends of a transmission coil are
clamped
to a high voltage. The turn-off speed can be quickened by increasing the
clamping
voltage threshold. The time on the falling edge is:
/ =LCOIL
f¨off U
HTVS (1).
[0020] In the formula (1), / is the current value of the transmitting ceiling
section,
LCOIL is the induction value of the wire which is obtained by calculation or
measurement,
and limvs is the clamping voltage of the high-voltage transient suppression
diode.
Broadband excitation mainly measures the electromagnetic information after the
transmitting current is turned off.
[0021] During the turn-off period of a second set of trapezoidal waves, it is
required to
switch the discharge circuit to a slow break circuit, a low-voltage transient
suppression
diode is turned on, and the voltages at two ends of the transmitting loop are
clamped to a
low voltage, so that the falling edge discharges slowly. By selecting
appropriate circuit
parameters, the time on the slow break falling edge can be regulated. The time
on the
falling edge is:
/.LCOIL
s¨off
U LTVS ¨U ¨ Decho U MOS (2)
[0022] where iimvs is the clamping voltage of the low-voltage transient
suppression
diode, liDedio is the voltage drop of the freewheeling diode (FWD) for the
switch device,
Date Recue/Date Received 2021-06-21
and Ums is the forward voltage drop when the switch device is turned on. Soft
turn-off
can prolong the polarization discharge time, to realize stronger induced
polarization
response. The main control circuit controls the operation time sequence of the
power
transmitting circuit and the absorption circuit under the synchronization of
high-precision
timing signals, so that quick and soft turn-off time current waveforms can be
realized in
one transmitting cycle.
[0023] Further, in 4), the non-modulated flux phase-locked loop readout
circuit is of a
structure of two relaxation oscillating circuits and two single flux phase-
locked loop
circuits, wherein the two relaxation oscillating circuits are connected by two
matching
resistors and Josephson Junctions connected to the two matching resistors; the
Josephson
Junctions, the matching resistors and a low-noise biased constant-current
source form a
SQUID loop; the matching resistors are used to limit the damping state during
operation;
each Josephson Junction and the matching resistor connected to the Josephson
Junction
form a single flux phase-locked loop circuit in the form of grounding; an
external
magnetic field signal enters the sensor by magnetic coupling with the SQUID
coil, so that
the two relaxation oscillating comparators generate a signal voltage pulse and
a reference
voltage pulse; the voltage pulses are converted into single flux quantum
pulses via the
single flux-quantum flux phase-locked loop circuits; and finally, flux quanta
are counted
by a high-speed single flux quantum logic counting circuit.
[0024] Further, 5) is implemented as follows:
[0025] 5.1) baseline correcting, superimposing and filtering the data of the
induction-
polarization symbiotic effect measured in 4);
[0026] 5.2) extracting polarization response characteristic attribute
parameters of the
data processed in 5.1) by the partial mutual information method, and screening
characteristics to effectively extract main polarization characteristic
parameters;
[0027] 5.3) based on a support vector machine, establishing a polarization
effect
detection model by using the polarization characteristic parameters extracted
in 5.2),
screening out the optimal input variable, and using WHETHER THERE IS A
POLARIZATION EFFECT' as an output;
6
Date Recue/Date Received 2021-06-21
[0028] 5.4) directly calculating the surrounding rock conductivity a-0 for the
early data
in the measured data of the output 'THERE IS A POLARIZATION EFFECT' in 5.3),
setting a constraint range by using this result, and intelligently extracting
multiple
parameters comprising conductivity, polarizability, dispersion coefficient and
volume
fraction by the QPSO algorithm;
[0029] 5.5) for the dual-time-scale fractional conductivity model, re-deriving
a
generalized skin depth formula, and substituting the multiple polarization
parameters
extracted in 5.4) into the generalized skin depth formula for calculation;
[0030] deriving, according to the generalized effective-medium theory of
induced
polarization (GEMTIP) model of the two-phase conductive medium, the expression
of
the number of complex waves is:
ico
k2 = = t + _____ 1+ (i arcl)c1 + 1+ (i an-2)c2 (3)
k2 = (a+ i R)2
[0031] if P) , then:
a= __ VVM2 ________ N2 M (1/M2 + N2 M)
2N (4)
( ________________________ 6.1( cart CIN2 (6111-2 )c2
M=dep+rop +
[0032] where
1+ (cor , 1+ (n_ 2)2c,
0.,l
o-e
N =¨co-
o,u:+ cop e + 2
1+ (tor)2C1 1+ 0)1_2 2C2
; accordi
1 ng to the definition of the skin
depth, the skin depth d is equal to the distance by which is passed when
the
amplitude of the field quantity is attenuated to its surface value, so that e
= e 1, and
the generalized skin depth formula of the porous polarization medium is
obtained,
1 1
d = = n _____
U -v2 __ 2 2
M +N ¨M(VM2+N2+M)
2N
7
Date Recue/Date Received 2023-01-11
[0033] 5.6) imaging the conductivity and polarizability-depth according to the
results in
5.4) and 5.5).
7A
Date Recue/Date Received 2023-01-11
[0034] Further, the QPSO algorithm in 5.4) is implemented as follows:
1 N 1FI(X)¨BtI
= ¨ L. ________________________________________________
[0035] a. establishing a target function: N i=1 Ft (X) , where Xis a
parameter to be extracted, Ft(X) is the magnetic field response of the
induction-
polarization symbiotic effect in 2), Nis the number of effective sampling
points of the
magnetic field data of the induction-polarization symbiotic effect in 4), and
Bt is the
magnetic field data of the induction-polarization symbiotic effect in 4);
[0036] b. initializing the number M of individuals in the population, and
randomly
xi(I)= (x. (I)' (t), x,2 (i), = = = x11,(t)) of
generating, within the constraint range, the position
particles conforming to uniform distribution, where i 1,2, = = = , M , and D
is the spatial
dimensionality;
[0037] c. calculating the fitness fv(i) of each particle, and initializing the
individual
optimal solution p(i)and the global optimal solution g ID (1) ;
[0038] d. solving the local attract factor AiD = C iD(1)13 (1) [1 ¨ (Pip
(1)]g (1), where
C 113(1) is the random number of (0,1);
1
40= - P0(1)
[0039] e. calculating the average best position -11/1 , and
updating the
position of particles according to the following formula:
1
xiD(t +1) = AiD(1) I aic(t)¨ xiD(t)1 ln(
up(t)
[0040] where u(i) is the random number of (0,1); and, it is "2 if ull)(t)
>0.5, or
otherwise, it is "+";
[0041] f. comparing the fitness value of each particle, and updating the
individual
optimal solution P () and the global optimal solution g iD(1) ; and
8
Date Recue/Date Received 2021-06-21
[0042] g. repeating operations c-f until the optimal value is found or the
maximum
number of iterations is reached, and outputting the global optimal solution
[0043] Further, 6) is implemented as follows:
[0044] 6.1) for any given spatial position, defining a series of spatial
overlay boxes
(squares), where the window size of the spatial overlay boxes increases
successively, i.e.,
6 =61<62 <...<6,2=-
[0045] 6.2) calculating the average 1' of multiple physical quantities such as
the
measurement magnetic field, conductivity and polarizability in each window,
and
performing numerical translation during calculation to ensure that it is not
zero;
(g log pfr l) i = ..n
[0046] 6.3) in the log-log coordinates, drawing \ " i/ (where 2.) by
o. I g(c) log p (6) log p(s)
using .
as the horizontal axis and as the vertical
axis, where is
linear along with log (6), and the slope of the linear relationship is the
estimation of the
codimension (a-2); and
[0047] 6.4) sliding the series of windows to other sampling positions, and
repeating the
processing methods in the first three steps to obtain a spatial distribution
map of local
singularity indexes a of magnetic field data, conductivity, polarizability and
other
anomalies.
[0048] The following advantages are associated with the method of the
disclosure.
Compared with the prior art, by the SQUID-based electromagnetic detection
method for
an induction-polarization symbiotic effect of a two-phase conductive medium
provided
by the disclosure, in the disclosure, high-precision detection of the
induction-polarization
symbiotic effect of the two-phase conductive medium can be realized by a
single
magnetic field, multiple parameters comprising conductivity, polarizability,
dispersion
coefficient and volume fraction of the two-phase conductive medium are
intelligently
extracted, and valuable economic mineral resources and unvalued mineralized
zones are
identified and predetermined. This method provides new technical support for
deep
9
Date Recue/Date Received 2021-06-21
electromagnetic exploration of mineral resources such as complex ore,
polymetallic ore,
which is beneficial to the practical application of electromagnetic
exploration methods.
BRIEF DESCRIPTION OF THE DRAWINGS
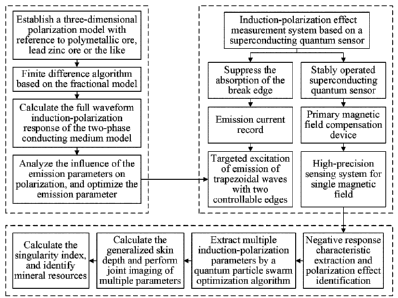
[0049] FIG. 1 is a flowchart of an electromagnetic detection method for an
induction-
polarization symbiotic effect;
[0050] FIG. 2 is a schematic view of a transmitting control module for
trapezoidal
waves with two falling edges;
[0051] FIG. 3 shows a low-noise front adaptive gain amplification and
acquisition
circuit;
[0052] FIG. 4 shows a non-modulated flux phase-locked loop readout circuit;
[0053] FIG. 5 is a schematic view of an automatically controlled constant-
temperature
system;
[0054] FIG. 6 is a flowchart of a QPSO algorithm; and
[0055] FIG. 7 is an effect diagram of resistivity imaging according to an
embodiment of
the disclosure.
DETAILED DESCRIPTION
[0056] To further illustrate, embodiments detailing a superconducting quantum
interference device (SQUID)-based electromagnetic detection method for an
induction-
polarization symbiotic effect of a two-phase conductive medium are described
below. It
should be noted that the following embodiments are intended to describe and
not to limit
the disclosure.
[0057] A two-phase conductive medium is taken as an example.
Date Recue/Date Received 2021-06-21
[0058] As shown in FIG. 1, an electromagnetic detection method for an
induction-
polarization symbiotic effect of an electric source two-phase conductive
medium is
implemented as follows:
[0059] 1) Based on the conductivity model of the two-phase conductive medium,
a
fractional laplace operator is introduced, the multi-capacitance polarization
effect of the
medium is represented by multiple time fractional orders, a dual-time-scale
fractional
conductivity model of the induction-polarization symbiotic effect is
established, and dual-
time fractional electromagnetic field diffusion equations are further
established.
[0060] The conductivity expression of the two-phase conductive effective
medium
model is:
\
0-e = ________________ AM, M2 1
(i1 C9 roc' 1+ (ico )C2
-/ (1)
- Al _______________ a, 2 q -_ 1
Al 1 3 __ '2
2a-0 +a2 2a a a
where 2a-0 +a- 1 - 0 and
(
a2 2 1
T2-.
2a a a01
[006 \ 2 _
[0061] There are total 11 parameters, comprising the surrounding rock
conductivity o-o,
five strong polarization medium parameters and five weak polarization medium
parameters. The strong polarization medium parameters comprise the strong
polarization
medium conductivity at, the strong polarization dispersion coefficient Ci, the
strong
polarization volume fractionfi, the strong polarization particle radius ai and
the strong
surface polarization coefficient ai. The weak polarization medium parameters
comprise
the weak polarization medium conductivity a2, the weak polarization dispersion
coefficient C2, the weak polarization volume fractionf2, the weak polarization
particle
radius a2 and the weak surface polarization coefficient az. to is the angular
frequency.
[0062] According to the fractional conductivity model of the induction-
polarization
symbiotic effect (the formula (1) is substituted into the Maxwell equations to
obtain
11
Date Recue/Date Received 2021-06-21
formulae (2) and (3)), dual-time fractional electromagnetic field diffusion
equations (2)
and (3) are established.
[0063] The formula (1) is substituted into the Maxwell equations to obtain:
v2E, k2E, 0
(2)
v2 fi k2/4 = 0
(3)
i co
k 2 co 2cli -op 1 a: /Wel icori) c' UO2
1 + (
[0064] where 1+(ic'n-2)c,
is the
electromagnetic intensity, I/ is the magnetic field intensity, k is the wave
number, s is
cr' = o- f M
the dielectric constant, ,u is the magnetic conductivity, e 0 + a- 0 1 1 + o-
0f 2M 2
Criel = MI , and ae"2=0-0.f2M2
[0065] 2) The fractional term in the dual-time-scale fractional conductivity
model is
directly solved by a fractional finite-difference time-domain method according
to the
dual-time fractional electromagnetic diffusion equation established in 1),
discrete
recursion is performed on a component folin containing the fractional
differential term to
realize dual-time-scale three-dimensional electromagnetic response numerical
simulation
of the induction-polarization symbiotic effect, and the magnetic field
response of the
induction-polarization symbiotic effect is calculated.
[0066] 2) is implemented as follows:
[0067] 2.1) According to the dual-time fractional electromagnetic field
diffusion
equations in 1), piecewise-linear approximation is performed on the complex
frequency
variable fractional power of the dual-time fractional electromagnetic field
diffusion
equations to obtain a diffusion equation of an integer power, where the
fractional power
in the formulae (2) and (3) is subjected to Laplace transformation, and the
piecewise-
linear approximation is perfoi med on the exponential function s' in the
Laplace
domain.
[0068] 2.2) The diffusion equations are transformed to the time domain,
difference
approximation is performed by a finite difference method, the fractional item
in the
12
Date Recue/Date Received 2021-06-21
conductivity model of the two-phase conductive medium is directly solved, and
the
iterative relationship among components of the electric field and magnetic
field is
derived.
[0069] The control equations are dispersed by a finite difference method to
obtain the
iterative relationship among components of the electric field and magnetic
field:
Ex (x, y, z, tõ,) = A2Ex (x, y, z, In) + A3Ex (x, y, z, tn_,) +
' (x z t ) ,(x,y,z,tr,)
+ .7,2" ) Ex(x,y,z, 0) + A, aH mz 'y " n aH
Ai (ae:
ay az
(4)
A¨ - ¨2AtnAin+,E 4K, E+ AtnK2E ¨ Ain+, K 2E ¨
2K3Aindin+1E
4 1
Atn [4K, +K2E] At?, [4K, +K2E]
[0070] where , , and
- Ain+, [K2-4K1]
A3 __
Ain [4K, +K2E]
'
I-In. (x, y, z+1, ç) = Hmz (x, y, z,t,,)¨
AzHõõ(x+1,y,z,c)¨H,õx(x,y,z,tõ)
[
Ax Ay
(5)
I-I,õ,z,t) = _____________________________
[0071] where /Az PAY , and
E=Ain + At . The iteration equation of EE Ez can be obtained from the formula
(4) by
recursion. The HmY iteration can be obtained from the formula (5) by
recursion.
[0072] Ex, Ey and Ez are three components of the electric field x,y,z; tn is
the nth moment;
= in õ ¨in ; At. = tn ¨in , ; Hõ,= OH lat ;
2 C2 ¨C
, _ ,, 1 , - C2 2 2
Al ¨ _ , ' e nl' 1 ' ' e2 "2 . K2= ¨o-:+ creffirl-ci (1¨ C2) +
Cre"21-2-C2 (1¨ C'; ) .
2 ,
cy: +o-e",T,-`1(1¨Co-
,2)+e"22-2-c2 (1¨C22)
and K2 = .
[0073] 2.3) A calculation region is divided by a non-uniform Yee grid; the
calculated
conductivity, polarizability, dispersion coefficient, polarization volume
fraction and
13
Date Recue/Date Received 2021-06-21
polarization particle radius are set; an initial field under the excitation of
trapezoidal
waves is loaded; boundary conditions are loaded; and components of the
electromagnetic
field are iteratively calculated to realize dual-time-scale three-dimensional
electromagnetic numerical simulation of the induction-polarization symbiotic
effect.
[0074] 2.4) The magnetic field response of the induction-polarization
symbiotic effect is
calculated according to the dual-time-scale three-dimensional electromagnetic
numerical
simulation of the induction-polarization symbiotic effect in 2.3), the
influence of the
transmitting parameters on polarization is analyzed, and the transmitting
parameters are
optimized.
[0075] 3) For the dual-time-scale fractional conductivity model (formula 1) in
1), three-
dimensional numerical simulation of current excitation with different falling
edges is
performed by using 2). Transmitting parameters in the case of maximum
induction and
polarization responses are obtained according to the characteristics of the
induction-
polarization symbiotic effect, to obtain a dual-controllable-edge trapezoidal
wave
emission targeted excitation relationship. The induction and polarization
electromagnetic
responses of different transmitting parameters are analyzed according to the
numerical
simulation results of different falling edge excitations. The emission
parameter in the case
of maximum induction and polarization responses is regarded as the targeted
excitation of
transmission, so that the targeted excitation of transmission of trapezoidal
waves with
two falling edges is realized.
[0076] As shown in FIG. 2, a transmission for trapezoidal waves with two
controllable
edges comprises a synchronization module, a main control circuit, a power
transmitting
bridge and an absorption circuit. An ARM is used as the controller. The
control circuit
generates a time sequence with a variable duty ratio, and controls an H bridge
comprising
IGBTs via a driving circuit to generate alternatively positive and negative
currents. A
current recording unit ensures the capture and recording of transient
waveforms of the
current within a large dynamic range by connecting sampling resistors in
series to the
transmitting cable and using an induction and shunt two-way measurement
technology, so
that the whole process of transmitting the current and the transient
characteristics of the
current can be recorded accurately. The ground resistance is measured in real
time by a
14
Date Recue/Date Received 2021-06-21
built-in precision bridge. The real-time measured data such as the ground
resistance and
transmitting induction are returned to the main control unit. The main control
unit
automatically switches to a reconfigurable impedance matching network built in
the
transmitting system by efficient closed-loop control, performs adaptive
impedance
matching, adjusts the operation state of the transmitting circuit in real time
or performs
abnormity protection, and realizes multi-parameter self-measurement and
monitoring by
the transmitting system. The transmission for trapezoidal waves with two
controllable
edges measures the ground resistance in real time by a built-in precision
bridge. When the
electric source is excited, it is greatly affected by the ground resistance,
which restricts
the magnitude and waveform quality of the transmitting current. When the
ground
resistance is low, current limiting measures are taken to avoid the burning of
the inverter
bridge. When the ground resistance is high, the output voltage and the output
power can
be automatically adjusted to increase the current and improve the excitation
energy of the
field source. The real-time measured data such as the ground resistance and
inductance
are returned to the main control unit. The transmitting system is integrated
with the
ground resistance real-time measurement and feedback unit. The main control
unit
automatically switches to the reconfigurable impedance matching network built
in the
system by efficient closed-loop control, performs adaptive impedance matching,
adjusts
the operation state of the transmitting circuit in real time or performs
abnormity
protection, and realizes the long-term stable operation of the transmitting
system.
[0077] The specific control method for transmission of trapezoidal waves with
two
falling edges is described below. During the turn-off period of a first set of
trapezoidal
waves in one transmitting cycle, it is required to switch a discharge circuit
to a quick
break circuit. At this time, a high-voltage transient suppression diode is
broken down by
voltage overshoot. The voltages at two ends of a transmitting coil are clamped
to a high
voltage. The turn-off speed can be quickened by increasing the clamping
voltage
threshold. The time on the falling edge is:
/.L
t _ COIL
f -off U HT VS (6)
Date Recue/Date Received 2021-06-21
[0078] where I is the current value of the transmitting ceiling sectionõ UHrvs
is the
induction value of the transmitting wire and is calculated or measured, and
LCOIL is the
clamping voltage of the high-voltage transient suppression diode. Broadband
excitation
mainly measures the electromagnetic information after the transmitting current
is turned
off.
[0079] During the turn-off period of a second set of trapezoidal waves, it is
required to
switch the discharge circuit to a slow break circuit. A low-voltage transient
suppression
diode is turned on, and the voltages at two ends of the transmitting loop are
clamped to a
low voltage, so that the falling edge discharges slowly. By selecting
appropriate circuit
parameters, the time on the slow break falling edge can be regulated. The time
on the
falling edge is:
/.LCOIL
is¨off =
uLTVS ¨uDedio¨uMOS (7)
[0080] where LTVS is the clamping voltage of the low-voltage transient
suppression
diode, liDedio is the voltage drop of the FWD for the switch device, and Umos
is the
forward voltage drop when the switch device is turned on. Soft turn-off can
prolong the
polarization discharge time, to realize stronger induced polarization
response. The main
control circuit controls the operation time sequence of the power transmitting
circuit and
the absorption circuit under the synchronization of high-precision timing
signals, so that
quick and soft turn-off time current waveforms can be realized in one
transmitting cycle.
[0081] 4) By the targeted excitation of transmission of trapezoidal waves with
two
falling edges in 3), based on a superconducting quantum interference device
(SQUID),
use a non-modulated flux phase-locked readout technology, an external AC and
internal
DC magnetic field compensation method and a multilateralism mixed noise
shielding
technology, then a high-precision system for sensing a single magnetic field
of the high-
slew rate and low-noise superconducting quantum interference device is
realized, and
magnetic fields of the induction-polarization symbiotic effect are measured.
16
Date Recue/Date Received 2021-06-21
[0082] In the high-precision system for sensing a single magnetic field of the
high-slew
rate and low-noise superconducting quantum interference device, the high-
sensitivity
matching of the acquisition system with the output of the SQUID is realized by
a low-
noise front adaptive gain amplification and acquisition technology; it is
mounted in an
ideal-crosstalk asymmetric manner, and the compensation coil and the
transmitting coil
are synchronously controlled by GPS; flux counting and magnetic field
measurement at a
high slew rate and in a large dynamic range are performed by a non-modulated
flux
phase-locked loop readout circuit; the SQUID can operate continuously and
stable for a
long time by using a constant-temperature control system with an automatic
temperature
control function; by using Cu/Ni or Ag/A1 material, the SQUID is shielded by
selecting
an appropriate thickness of the shielding layer.
[0083] As shown in FIG. 3, low-noise front adaptive gain amplification and
acquisition
circuit suppresses the common-mode interference of signals by differential-
mode
amplification, the dynamic range of the system is improved by adaptive gain
control.
Design the attenuator to avoid signal saturation, filter the out-of-band noise
by the
program-controlled anti-aliasing filtering technology, suppress noise for
different signal
frequencies, and improve the signal-to-noise ratio of the system.
[0084] As shown in FIG. 4, the non-modulated flux phase-locked loop readout
circuit is
of a structure of two relaxation oscillating circuits 6 and two single flux
phase-locked
loop circuits 7. The two relaxation oscillating circuits 6 are connected by
two matching
resistors 4 and Josephson Junctions 5 connected to the two matching resistors
4. The
Josephson Junctions 5, the matching resistors 4 and a low-noise biased
constant-current
source 3 form a SQUID loop 2. The matching resistors 4 are used to limit the
damping
state during operation. Each Josephson Junction 5 and the matching resistor 4
connected
to the Josephson Junction 5 form a single flux phase-locked loop circuit 7 in
the form of
grounding. An external magnetic field signal enters the sensor by magnetic
coupling with
a pickup SQUID coil 1, so that the two relaxation oscillating circuits
generate a signal
voltage pulse and a reference voltage pulse; the voltage pulses are converted
into single
flux quantum pulses via the single flux-quantum flux phase-locked loop
circuits; and
17
Date Recue/Date Received 2021-06-21
finally, flux quanta are counted by a high-speed single flux quantum logic
counting
circuit 8.
[0085] As shown in FIG. 5, the constant-temperature system with an automatic
control
function comprises a low-pass filter, a temperature indicator adjustment
meter, a thyristor
voltage stabilizer, a transformer and a rectifier. The temperature acquired by
the
temperature sensor is transmitted to the low-pass filter, adjusted by the
temperature
indicator adjustment meter, stabilized by the thyristor voltage stabilizer,
passed through
the transformer and the rectifier, and driven by a vacuum pump driven by a DC
motor.
When the Pt/Co temperature sensor senses that the temperature of liquid
nitrogen in
Dewar changes, the temperature signal is transmitted to the temperature
indicator by the
low-pass filter, and the temperature is automatically regulated by a fuzzy
adaptive PD
feedback control algorithm. The temperature of the liquid nitrogen is kept
constant by
changing the pressure in Dewar by the voltage stabilizer, the transformer, the
rectifier and
the vacuum pump driven by the DC motor. The low-pass filter and the current
rectifier
can effectively reduce the noise contribution of the Pt/Co temperature sensor
to the
SQUID.
[0086] 5) The measured data of the induction-polarization symbiotic effect
measured in
4) is preprocessed, polarization identification is performed by a data mining
method, and
multiple parameters comprising conductivity, polarizability, dispersion
coefficient and
volume fraction are intelligently extracted and imaged by QPSO algorithm.
[0087] 5) is implemented as follows:
[0088] 5.1) The measured data of the induction-polarization symbiotic effect
measured
in 4) is baseline corrected, superimposed and filtered.
[0089] 5.2) Polarization response characteristic attribute parameters of the
data
processed in 5.1) are extracted by the partial mutual information method, and
characteristics are screened to effectively extract main polarization
characteristic
parameters.
[0090] 5.3) Based on a support vector machine, a polarization effect detection
model is
established by using the polarization characteristic parameters extracted in
5.2), the
18
Date Recue/Date Received 2021-06-21
optimal input variable is screened out, and 'WHETHER THERE IS A POLARIZATION
EFFECT' is used as an output.
[0091] 5.4) The surrounding rock conductivity ao is directly calculated for
the early data
in the measured data of the output 'THERE IS A POLARIZATION EFFECT' in 5.3), a
constraint range is set by using this result, and multiple parameters
comprising
conductivity, polarizability, dispersion coefficient and volume fraction
intelligently
extracted by the QPSO algorithm.
[0092] The QPSO algorithm is implemented as follows:
1 N IFt(X)¨Btl
mm = _L. _______________________________________________
N 1=1 Ft (X )
[0093] a. A target function is established: ,where Xis a
parameter to be extracted, Ft(X) is the magnetic field response of the
induction-
polarization symbiotic effect in 2), N is the number of effective sampling
points of the
magnetic field data of the induction-polarization symbiotic effect in 4), and
BE is the
magnetic field data of the induction-polarization symbiotic effect in 4).
[0094] b. The number M of individuals in the population is initialized, and
the position
x,(t)= (x11(t),x12(t),= = =,x,D(t))
of particles conforming to uniform distribution is
randomly generated within the constraint range, where i and D is the
spatial
dimensionality.
[0095] c. The fitness fv(i) of each particle is calculated, and the individual
optimal
solution 13 iD (I) and the global optimal solution go(1) are initialized.
[0096] d. The local attract factor AiD = CPiD(t) P (t) +[1. (t)]g i(t) is
solved, where
C 1D(1) is the random number of (0,1).
1
c(t) = DO)
[0097] e. The average best position Mis
calculated, and the position
of particles is updated according to the following formula:
19
Date Recue/Date Received 2021-06-21
1
X iD(t + 1) = ADO XiD(1)1 in(
U0(t)
[0098] where uo(1) is the random number of (0,1); and, it is "-" if uiD(1)>
0.5 , or
otherwise, it is "+".
[0099] f. The fitness value of each particle is compared, and the individual
optimal
solution 13 iD (1) and the global optimal solution giD(1) are updated.
[0100] g. The operations c-f are repeated until the optimal value is found or
the
maximum number of iterations is reached, and the global optimal solution g (1)
is
output.
[0101] 5.5) For the dual-time-scale fractional conductivity model, a
generalized skin
depth formula is re-derived, and the multiple polarization parameters
extracted in 5.4) are
substituted into the generalized skin depth formula for calculation.
[0102] The expression of the number of complex waves is derived according to
the
GEMTIP model of the two-phase conductive medium:
ico la)
k 2 2 = 0.) eiti i cop a re pojeri
1 + (icori)c' I:2 1+ (icor2)c2 (8)
2
k2 (a +=fl) =
[0103] If , then
__________________________ V4m2 ________ N2 A/ (4/2 N2 m)
2N (9)
0,21,02.2)c2
M = co2rp +cop e + e
1+ (a;) 1+(arr2) 2
[0104] where
Crif el e2
N = ¨copc'e
1+ (cori)2 C + 1 (0) 2 \ 2C
. According to the definition of the skin
depth, the skin depth d is equal to the distance by which e is passed when the
amplitude of the field quantity is attenuated to its surface value, so that e-
cxd =e', and
Date Recue/Date Received 2021-06-21
the generalized skin depth formula of the porous polarization medium is
obtained:
1 1
d= =
a 42 .s/m2_1(. JA/2 ___________ +N2 +M)
2N
[0105] 5.6) The conductivity and polarizability-depth are imaged according to
the
results in 5.4) and 5.5).
[0106] 6) The singularity index of the results extracted in 5) is calculated
by a local
singularity index algorithm of a rectangular window, and valuable economic
mineral
resources and unvalued mineralized zones are identified and predetermined.
[0107] Specifically, 6) is implemented as follows:
[0108] 6.1)
For any given spatial position, a series of spatial overlay boxes (squares) is
defined, where the window size of the spatial overlay boxes increases
successively, i.e.,
ginin=81<62<...<6õ=6
[0109] 6.2) The average P of
multiple physical quantities such as the measurement
magnetic field, conductivity and polarizability in each window is calculated,
and
numerical translation is performed during calculation to ensure that it is not
zero.
[0110] 6.3) In the log-log coordinates, (ei, log p (E ))
(where i = 2...n
) is drawn by
log(e) log p (6) log p
(s) .
using as the horizontal axis and as the vertical axis, where is
linear along with log (6), and the slope of the linear relationship is the
estimation of the
codimension (a-2)
[0111] 6.4) The series of windows is slid to other sampling positions, and the
processing methods in the first three steps are repeated to obtain a spatial
distribution
map of local singularity indexes a of magnetic field data, conductivity,
polarizability
and other anomalies.
[0112] FIG. 6 shows the resistivity-depth results of the field experiment in
Luanchuan
in Henan province according to an embodiment of the disclosure. The results
are
21
Date Recue/Date Received 2021-06-21
consistent with the geological data result, so that the effectiveness of this
method is fully
verified.
[0113] It will be obvious to those skilled in the art that changes and
modifications may
be made, and therefore, the aim in the appended claims is to cover all such
changes and
modifications.
22
Date Recue/Date Received 2021-06-21