METHODE, APPAREIL ET ARTICLE D'IDENTIFICATION ET DE SIGNATURE

METHOD, APPARATUS AND ARTICLE FOR IDENTIFICATION AND SIGNATURE

Abrégé anglais

ABSTRACT OF THE DISCLOSURE
A method and apparatus for simple identification and
signature which enable any user to prove his identity and the
authenticity of his messages to any other user. The method and
apparatus are provably secure against any known or chosen
message attack if factoring is difficult, and require only 1%
to 4% of the number of modular multiplications previously
required. The simplicity, security and speed of the method and
apparatus derive from microprocessor-based devices which may be
incorporated into smart cards, personal computers, passports,
and remote control systems.

Revendications

THE EMBODIMENTS OF THE INVENTION IN WHICH AN EXCLUSIVE
PROPERTY OR PRIVILEGE IS CLAIMED ARE DEFINED AS FOLLOWS:
1. A method of creating a unique identifier for
use by an entity which cannot be forged by others
including those capable of verifying the entity,
comprising the steps of:
a) selecting a modulus n which is the product of
at least two secret primes;
b) selecting a pseudo random function f capable
of mapping arbitrary strings to numbers;
c) preparing a string I containing information
unique to an entity;
d) selecting k distinct values of j so that each
vj = f(I,j) is a residue (mod n) having a root sj;
e) computing roots sj of vj-l (mod n);
f) recording on a retrievable medium of an
identifier I, k, sj and related indices j.
2. The method of claim 1 wherein the recording on
the identifier is in binary form.
3. The method of claim 1 wherein the recording is
in a ROM and the identifier includes microprocessing and
input/output features.
4. A method of utilizing the identifier of claim
1 comprising:
a) placing the identifier of claim 1 in
communication with a verifier having recorded therein
modulus n and pseudo random function f;
b) transmitting I and the indices j from the
identifier to the verifier;
c) generating in the verifier vj = f(I,j) for the
indices j;
d) selecting in the identifier a random ri ?
[O,n);
e) computing Xi = ri2 (mod n) in the identifier
and sending Xi to the verifier;
17

f) selecting a random binary vector eil...eik
from a predetermined set of such vectors in the verifier
and sending to the identifier;
g) computing in the identifier
Yi = ri ? sj (mod n)
eij=1
and sending Yi to the verifier;
h) checking in the verifier
Xi = yi2 ? vj (mod n);
eij=1
i) repeating steps (d) through (h) t times,
where t?l.
5. The method of claim 4 wherein the
transmissions between the identifier and verifier are
carried out in binary form.
6. The method of claim 4 wherein all steps are
carried out using binary signals.
7. The method of claim 6 wherein modulus n is
composed of at least 512 bits.
8. The method of claim 6 wherein only a hashed
version of Xi is used.
9. The method of claim 6 wherein steps (d)
through (h) are repeated at least two times.
10. A method of signing a message m exchanged
between an identifier created according to claim 1 and
verifier comprising: -
a) selecting in the identifier random ri...rt ?
[O,n);
b) computing in the identifer xi = ri2 (mod n);
c) computing in the identifier f(m, x1...xt) and
extracting from it kt bits as eij values;
d) computing in the identifier
Yi = ri ? sj (mod n)
eij=1
for i = l...t;
e) sending to the verifier I, the indices j, m,
the eij matrix and all the yi values;
18

f) computing in the verifier vj = f(I,j) for the
indices j;
g) computing in the verifier
Yi = yi2 ? vj (mod n)
eij=1
h) verifying the signature to message m by
determining whether the kt bits extracted from
f(m,zl...zt) are the same as eij.
11. The method of claim 10 wherein the first kt
bits of f(m,zl...zt) are used as eij matrix.
12. The method of claim 10 wherein the exchange is
in binary form.
13. The method of claim 10 wherein the product kt
is at least 72.
14. The method of claim 10 wherein k is at least
18 and t is at least 4.
15. Apparatus for creating a unique identifier for
use by an entity and unforgeable by others including
those capable of verifying the entity, comprising:
a) means for selesting k distinct indices of j so
that each vj = f(I,j) is a quadratic residue (mod n);
b) where f is a pseudo random function f capable
of mapping arbitraxy strings to numbers in the range
[O,n) and n is a modulus which is the product of at
least two secret primes and I is a string containing
information unique to an entity;
c) means for computing roots sj of vj-l (mod n);
and
d) means for recording on a retrievable medium of
an identifier I, sj and related indices.
16. The apparatus of claim 15 wherein the
recording on the identifier is in binary form.
17. The apparatus of claim 15 wherein the
recording is in a ROM and the identifier includes
microprocessing and input/output features.
18. Apparatus for utilizing the identifier of
claim 15 comprising:
19

a) means for placing the identifier of claim 1 in
communication with a verifier having recorded therein
modulus n and pseudo random function f;
b) means for transmitting I and the indices j
from the identifier to the verifier;
c) means for generating in the verifier vj =
f(I,j) for the selected indices j;
d) means for selecting in the identifier a random
ri .epsilon. [O,n);
e) means for computing xi = ri2 (mod n) in the
identifier and sending Xi to the verifier;
f) means for selecting a random vector eil....eik
in the verifier and sending to the identifier;
g) means for computing in the identifier
yi = <IMG>
and sending to the verifier;
h) means for checking in the verifier
xi = <IMG> and
i) means for repeating steps (d) through (h) at
least once.
19. The apparatus of claim 18 wherein the
transmissions between the identifier and verifier are
carried out in binary form.
20. The apparatus of claim 18 wherein all steps
are carried out using binary signals.
21. The apparatus of claim 20 wherein modulus n is
composed of at least 512 bits.
22. The apparatus of claim 20 wherein only a
hashed version of xi is used.
23. The apparatus of claim 20 wherein steps (d)
through (h) are repeated at least two times.
24. Apparatus for signing a message m exchanged
between an identifier created according to claim 1 and a
verifier comprising:

a) means for selecting in the identifier random
ri...rt ? [O,n);
b) means for computing in the identifier xi = ri2
(mod n);
c) means for computing in the identifier
f(m,xi...xt) and extracting from it kt bits as eij
values;
d) means for computing in the identifier
yi = ri ? sj (mod n)
eij =1
for i = l.....t;
e) means for sending to the verifier I, m, the
eij matrix and all the yi values;
f) means for computing in the verifier vj =
f(I,j) for the indices j;
g) means for computing in the verifier
zi = yi ? vj (mod n)
eij=1
for i = l....t; and
h) means for verifying the signature to message m
by determining whether the kt bits extracted from
f(m,zl...zt) are the same as eij.
25. The apparatus of claim 24 wherein the exchange
is in binary form.
26. The apparatus of claim 24 wherein the product
kt is at least 72.
27. An identifier comprising microprocessor means,
memory means and I/O means and having recorded in said
memory means a string I containing information unique to
an entity, a modulus n which is the product of at least
two secret primes, a pseudo random function f capable of
mapping arbitrary strings to numbers, indices j and
values vj which are quadratic residues (mod n), values
sj which are roots of vj-1 (mod n), said microprocessor
means including selection means for selecting a number
ri ? [O,n), and computing means for computing xi=ri2
(mod n) and
21

yi = ri ? sj (mod n)
eij =1
in responsive to receiving a binary vector eil...eik.
28. An identifier according to claim 27, wherein
the microprocessor means includes loop means for
repeating the selection of ri and computing of xi and
yi.
29. An identifier according to claim 27 wherein
the microprocessor means includes selection means for
selecting computing random ri...rt ? [O,n), computing
means for computing xi = ri2 (mod n), computing means
for computing f(m, xi...xt), selection means for
extracting from it kt bits as eij values, and computing
means for computing
yi = ri ? sj (mod n)
eij =1
for i = l.....t.
30. A verification device for use with the
identifier of claim 27, comprising microprocessor means,
memory means and I/0 means and having recorded in said
memory means modulus n and function f, said
microprocessor means including generating means for
generating values of vj = f(I,j) for the indices j;
selection means for selecting a binary vector eil...eik,
and checking means for checking that
xi = yi2 ? vj (mod n)
eij =1
31. A verification device according to claim 30
for use with the identifier of claim 31, wherein the
microprocessor maans includes computing means for
computing
zi = yi2 ? vj (mod n)
eij=1
for i = l...t and comparing means for comparing that the
kt bits extracted from f(m,Zl...Zt) are eij.
32. The method of claim 1 including the step of
placing the numbers vj in a public key directory.
22

33. The method of claim 4 including the steps of
placing the numbers vj in a public key directory, and
retrieving the numbers vj from the public key directory.
34. A method of utilizing the identifier of claim
1 comprising:
a) placing the identifier of claim 1 in
communication with a verifier having recorded therein
modulus n and pseudo random function f;
b) transmitting the numbers vj along with a
signature of a trusted center from the identifier to the
verifier;
c) selecting in the identifier a random ri ?
(O,n);
d) computing xi = ri2 (mod n) in the identifier
and sending xi to the verifier;
e) selecting a random binary vector ei...eik from
a predetermined set of such vectors in the verifier and
sending to the identifier;
f) computing in the identifier
yi = ri ? sj (mod n)
eij=1
and sending yi to the verifier;
g) checking in the verifier
xi = yi2 ? vj (mod n); and
eij=1
h) repeating steps (d) through (h) at least once.
35. The method of claim 4 wherein the repetition
of steps (d) through (h) are carried out in parallel.
36. A method of signing a message m by an
identifier created according to claim 1 comprising:
a) selecting in the identifier random ri ? [O,n);
b) computing in the identifier Xi = ri2 (mod n):
c) computing in the identifier f(m, xi...xt) and
extracting from it kt bits as eij values (l?i?t, l?j?k);
d) computing in the identifier
yi = ri ? sj (mod n)
eij=1
23

for i = l...t; and
e) storing I, indices j, m, the eij matrix and
all the yi values.
37. A method of verifying the stored signature of
a stored message m as defined in claim 36 including the
steps of:
a) retrieving I, the indices j, m, the eij matrix
and all the yi values from storage;
b) computing in the verifier vj = f(I,j) for the
indices j;
c) computing in the verifier
zi = yi2 ? vj (mod n); and
eij =1
d) verifying the signature to message m by
determining whether the kt bits extracted from
f(m,Zl...Zt) are the same as eij.
38. Apparatus as defined in claim 15 further
including means for establishing a public key directory
and means for recording the I, vj and related indices in
said public key directory.
39. Apparatus as defined in claim 38 further
including means for retrieving the I, vj and related
indices from said public key directory.
40. Apparatus for utilizing the identifier of
claim 15 comprising:
a) means for placing the identifier of claim 1 in
communication with a verifier having recorded therein
modulus n and pseudo random function f;
b) means for transmitting the numbers vj along
with a signature of a trusted signature from the
identifier to the verifier;
c) means for selecting in the identifier a random
ri ? [O,n);
d) means for computing xi = ri2 (mod n) in the
identifier and sending xi to the verifier;
e) means for selecting a random vector eil....eik
in the verifier and sending to the identifier;
24

f) means for computing in the identifier
yi = <IMG>
and sending to the verifier;
g) means for checking in the verifier
xi = <IMG>
h) means for repeating steps (d) through (h) at
least once.
41. Apparatus for signing a message m exchanged
between an identifier created according to claim 1 and a
verifier comprising:
a) means for selecting in the identifier random
ri .epsilon. [O,n);
b) means for computing in the identifier xi = ri2
(mod n);
c) means for computing in the identifier
f(m,xi...xt) and extracting from it kt bits as eij
values;
d) means for computing in the identifier
yi = <IMG>
for i = l.....t; and
e) means for storing the verifier I, the indices
j, m, the eij matrix and all the yi values.
42. The apparatus according to claim 41 including
a) means for retrieving the verifier I, the
indices j, m, the eij matrix and all the Yi values from
storage;
b) means for computing in the verifier vj =
f(I,j) for the indices j;
c) means for computing in the verifier
zi = <IMG>
for i = l....t; and
d) means for verifying the signature to message m
by determining whether the kt bits extracted from
f(m,zl...zt) are the same as eij.

Description

`\ ~z~g~
METHOD, APPARATUS AND ARTICLE FOR IDENTIFICATION AND S~GNATURE
Background of the Invention
Field of the Invention
The present invention relates to a method and
apparatus for simple identification and signature.
Creating unorgeable ID cards based on the emerging
technology of smart cards is an important problem with numerous
commercial and military applications. The problem becomes
particularly challenging when two parties (the prover A and the
verifier B) are adversaries, and one wants to make it
impossible for B to misrepresent himself as A even after he
witnesses and verifies arbitrarily many proofs of identity
generated by A. Typical applications includes passports (which
are often inspected and photocopied by hostile governments),
credit cards (whose numbers can be copied to blank cards or
used over the phone), computer passwords (which are vulnerable
to hackers and wire tappers) and military command and control
systems (whose terminals may fall into enemy hands). Three
levels of protection may be distinguished between:
~.

g697
\
1) Authentication: A can prove to B that he is A,
but someone else cannot prove to B that he is A.
2) Identification: A can prove to B that he is A,
but B cannot prove to someone else that he is A.
3) Signature: A can prove to B that he is A, but B
cannot prove even to himself that he is A.
Authentication is useful only against external threats
when A and B cooperate. The distinction between identification
and signature is subtle, and manifests itself mainly when the
proof is interactive and the verifier later wants to prove its
existence to a judge. In identification, B can create a
credible transcript of an imaginary communication by carefully
choosing both the questions and the answers in the dialog,
while in signature only real communication with A could
generate a credible transcript. However, in many commercial
and military applications the main problem is to detect
forgeries in real time and to deny the service, access or
response that the forger wants. In these cases the transcript
and judge are irrelevant, and identification and signature
requirements can be used interchangeably.
-
SummarY of the Invention
The new method and apparatus of the present inventionis predicated upon a combination of zero-knowledge interactive

~L2~9~;g~ ~
proofs ~Goldwasser, Micali and Rackoff (1985), The Knowledge
Complexity of Interactive Proof Systems, 17th ACM Symposium on
Theory of Computations, May 1985) and identity-based schemes
(Shamir (1984~ Identity-Based Cryptosystems and Signature
Schemes, Proceedings of Crypto '84, Lecture Notes in Computer
Science no. 196, Springer Verlag 1985). The theory of the
present invention is based on the difficulty of extracting
modular square roots when the factorization of n is unknown. A
related protocol for proving the quadratic residuosity of
numbers was presented by Fischer Micali and Rackoff at
Eurocrypt, April 1984, A Secure Protocol for the Oblivious
Transfer, but the new protocol of the present invention is
faster and requires less communication, and provides a solution
to practical identification and signature problems.
The method and apparatus utilizes a trusted center (a
government, a credit card company, a computer center, a
military headquarters, etc.) which issues identifiers such as
smart cards, to users after properly checking their physical
identity. No further interaction with the center is required
either to generate or to verify proofs of identity. An
unlimited number of users can join the system without degrading
its performance, and it is not necessary to keep a list of all
the valid users. Interaction with the smart cards will not
enable verifiers to reproduce them, and even complete knowledge
.

t7
of the secret contents of all the cards issued by the
center will not enable adversaries to create new
identities or to modify existing identities. Since no
information whatsoever is leaked during the interaction,
the cards can last a lifetime regardless of how often
they are used.
Various aspects of the invention are as
follows:
A method of creating a unique identifier for use by
an entity which cannot be forged by others including
those capahle of verifying the entity, comprising the
steps of:
a) selecting a modulus n which is the product of
at least two secret primes;
b) selecting a pseudo random function f capable
of mapping arbitrary strings to numbers;
c) preparing a string I containing information
unique to an entity;
d) selecting k distinct values of j so that each0 vj = f(I,j) is a residue (mod n) having a root sj;
e) computing roots sj of vj-l (mod n);
f) recording on a retrievable medium of an
identifier I, k, sj and related indices j.
Apparatus for creating a unique identifier for use
by an entity and unforgeable by others including those
capable of verifying the entity, comprising:
a) means for selecting k distinct indices of j so
that each vj = f(I,j) is a ~uadratic residue (mod n);
b) where f is a pseudo random function f capable
of mapping arbitrary strings to numbers in the range
[O,n) and n is a modulus which is the product of at
least two secret primes and I is a string containing
information unique to an entity;
c) means ~or computing roots sj of vj-l (mod n);5 and
d) means for recording on a retrievable medium of
an identifier I, sj and related indices.

6~7
An identifier comprising microprocessor means,
memory means and I/O means and having recorded in said
memory means a string I containing information unique to
an entity, a modulus n which is the product of at least
two secret primes, a pseudo random function f capable of
mapping arbitrary strings to numbers, indices j and
values vj which are quadratic residues (mod n), values
sj which are roots of vj 1 (mod n), said microprocessor
means including selection means for selecting a number
ri ~ [O,n), and computing means for computing xi=ri2
(mod n) and
Yi = ri ~ sj (mod n)
ei j =l
in responsive to receiving a binary vector eil...eik.
Brief Descri~tion of the Drawings
Figure 1 is a block diagram showing the method
and apparatus of the present invention for issuing an
identifier, such as a smart card;
Figure 2 is a schematic showing the
interaction of an identifier, such as a smart card with
a verifier according to the method and apparatus of the
invention;
Figure 3 is a block diagram showing details of
the interaction in the microprocessors of the identifier
and verifier according to the invention; and
Figure 4 is a block diagram similar to Figure
3 showing the essential interactions to verify
signature~
In the drawings and in the following detailed
description, certain liberties have been taken regarding
the communication, data links between the identifying
apparatus (shown and described as a smart card) of a
party or entity A and the verifying apparatus of a party
or entity B. If the
4a

~96~7 '
communication is to be in binary (described as the preferred
embodiment) then, the actual links are between the I/O oE the
smart card and the I/O of the verifying device. For binary
operations, the apparatuses are microprocessors including
memories, usually ROMs to store information and the required
program to carry out the operations described subsequently and
the usual I/Os. The generation of random numbers can be
accomplished by any known means, such as a noisy diode serving
as a random source of bits with appropriate discrimination to
obtain the random binary output. Usually, 512 bit numbers are
used (correspondiny to about 160 digits). Otherwise, the
following description is rather straight forward and the novel
apparatuses and the various steps of the unique method, as well
as the devices, will be clear and evident.
Description of the Preferred Embodiments
Before a center starts issuing cards, it chooses and
makes pubic a modulus n and a pseudo random function f which
maps arbitrary strings to the range [O,n). The modulus n is
the product of two secret primes p and q. Only the center
knows the factorization of the rnodulus and thus everyone can
use the same n. The function f should appear as a random
function to polynomially bounded computations. Goldreich
--5--

1~ i97
Goldwasser and Micali (1984), How to Construct Random
Functions, 25th Symposium on Foundations of Computer Science,
October 1984, describe a particular function which is provably
strong in this sense, but in practice one can use simpler and
faster functions (e.g., multiple DES, Data Encryption Standard)
without endangering the security of the scheme.
When an eligible user applies for a smart card, the
center (see Fig. 1) prepares a string I which contains all the
relevant information about the user (his name, address, ID
number physical description, security clearance etc.) and about
the card (expiration date, limitations or validity, etc.).
Since this is the information verified by the method and
apparatus of the invention, it is important to make it detailed
(include enough information to make the user unique) and to
double check its correctness. The center then performs the
following steps as shown in Fig. 1. String I from block 10 is
fed to block 12 where the values VJ = f(I,j) for small values
of j are computed using a microprocessor. The modulus n from
block 14 and the output of block 12 are fed to block 16 in
which k distinct values of j are picked for which VJ is a
quadratic residue (mod n). The output of block 16 passes to
block 18 where square roots sJ of VJ~' are computed
using a microprocessor, for example, the smallest square
roots. The output of block 18 passes to block 20 and the
information of I, the k SJ values, and their indices is
recorded in the memory (ROM) of a smart card 30 (see Fig. 2).
--6--
. ~ '

To simplify notation in this specification, the first
k indices j = 1,2...k are used. Also, for non-perfect
functions f, it may be desirable to randomize I by
concatenating it to a long random string R which is chosen by
the center, st~red in the card, and revealed along with I. In
typical implementations, preferably k is between 1 and 18, but
larger values of k can further reduce the time and
communication complexities. Preferably, n should be at least
512 bits long, a number of at least about 160 digits.
Factoring such moduli seems to be beyond reach with today's
computers and algorithms, with adequate margins of safety
against foreseeable developments. However, it should be
appreciated that for simpler, less secure systems, any size
number can be chosen. The center can be eliminated if each
user chooses his own n and publishes it in a public key
directory. However, this variant makes the practice of the
present invention considerably less convenient.
The verification devices 40 are identical standalone
devices which contain a microprocessor, a small memory, and I/O
interface. The only information stored in them are the
universal modulus n and function f. When a smart card 30 is
inserted into a verifier, it proves that it knows s,...s~
without giving away any information about their values. The
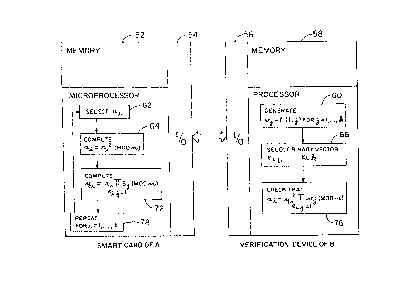
proof is based on the following protocol, see Fig. 3.
,

1%~i97
First, the smart card 30 of party A sends I from
memory 52 via I/0 54, I/0 56 to memor~ 58 of the verification
device 40 of party B. Then device 40 in block 60 generates
VJ = f(I,j) for j = l...k. The following steps are repeated
for i = l...t. Card 30 of A selects a random r,i~[O,n),
preferably a 512 bit number, in block 62, compute x,=r, 2
(mod n) in block 64 and sends xl to device 40 block 66.
Device 40 generates in block 66 a random vector (e "...e~,c)
frolr, a predefined collection of binary vectors (which
preferably contains all such vectors) and sends to card 30. In
response to the vector, card 30 computes in block 72
Yi = r, ~ s~ (mod n)
e,~=l
and sends y, to device 40 which then checks in block 76 that
Xi = Yl ~ VJ (mod n)
e,j=l
The iteration need be repeated only a few times (typically t
ranges from 1 to 4) to make the probability of erroneous
identification sufficiently small, block 78. During each
repeat, a new random number r, is selected. The verifier 40
of B accepts A s proof of identity only if all the t checks are
successful. To decrease the number of communicated bits, x
can be hashed by sending only the first 128 bits of f(x,).
The verifier 40 can check the correctness of this value by
applying f in block 76 and comparing the first 128 bits of the
results.
. ' ' ' ', '

6~
-
A particular message m (e.g., an instruction to a
remote control system or a program sent to a remote computer)
can be authenticated without having to extract new square roots
by sending the first 128 bits of f(m,x,). If m is known to
the verification device 40, this va]ue can be easily checked in
block 76. A is fully protected against modifications and
forgeries of his messages by the pseudo random nature of f, but
this is not a real signature technique. Without participating
in the interaction, a judge cannot later decide if a message is
authentic.
The probability of forgery is an absolute constant,
2-~t, and thus, there is no need to pick large values of k
and t as a safeguard against future technological
developments. In most applications, a security level of 2-2
suffices to deter cheaters. No one will present a forged
passport at an airport, give a forged driver's license to a
policeman, use a forged ID badge to enter a restricted area, or
use a forged credit card at a department store, if he knows
that his probability of success is only one in a million. In
all these applications, the forged ID card (rather than the
transcript of the communication) can be presented to a judge as
evidence in a trial. Even if the onl~ penalty for a failed
attempt is the confiscation of the card, and smart cards cost
only $1 to manufacture, each success will cost about one
million dollars. For national security applications, the
'
,

-
security level can be changed to 2-1. Even a patient
adversary with an unlimited budget, who tries to misrepresent
himself 1000 times each day, is expected to succeed only once
every 3000 years.
To attain a 2-Z level of security, it suffices to
choose k = 5, t = 4 (for 2-30, increase these values by 1).
The average number of modular multiplications required to
generate or verify a proof of identity in this case is t(k +
2)~2 = 14. The number of bytes exchanged by the parties via
the smart card 30 and verification device 40 during the proof
is 323, and the secret SJ values can be stored in a 320 byte
ROM. Even better performance can be obtained by increasing k
to 18 (a 1152 byte ROM). If e,J vectors are used with at
most three l's in them, there are a choice of 988 possible
vectors in each iteration. With t = 2 iterations, the security
level remains about one in a million, but the number of
transmitted bytes drops to 165 and the average number of
modular multiplications drops to 7.6 (which is two orders of
magnitude faster than the 768 multiplications re~uired by the
known prior art of the Rivest, Shamir and Adleman signature
scheme. Note that the 2 x 18 e,J matrix is so sparse that
the verification device 40 of B has to generate at most 6 out
of 18VJ values to verify the proof. This is the preferred
mode of the invention vis-a-vis identification.
--10--
. .
- - : . . .. :
' . ' , .. , .. '
.

12',9g6~7
The time, space, communication and security of the
present invention can be traded off in man~ possible ways, and
the optimal choices of k, t and the e, J matrix depends on the
relative costs of these resources. Further improvements in
speed can be obtained by parallelizing the operations. Unlike
the prior art, the two parties can pipeline their operations
(with A preparing x, + I and y, + , while B is still
checking xl and Yi) and use parallel multipliers to compute
the product of vJ or SJ values in log k depth. Since there
are no gcd or modular division operations, each iteration of
the protocol is in NC, and thus, the invention is suitable for
very high speed applications.
In a further development of the present invention, a
method and apparatus for verifying digital signatures are
provided. B's role in the interactive identification method is
passive but crucial. The random el J matrix sent contains no
information but its unpredictability prevents cheating by A.
To turn the described identification method into a signature
method, B's role is replaced by the pseudo random function f.
To sign a message m, the following method is utilized, see Fig.
4. First, a random rl...rt~ lO,n) is selected, block 80
and then x~=riZ (mod n) is computed, block 82. The
numbers selected in block 80 are random 512 bit numbers and are

~g~i~7
obtained by conventional means such as a noisy diode to provide
a random source of bits which are discriminated to obtain a
random binary number of 512 bits. Next, the function
f(m,xl...xt) is computed, block 84 and a subset of kt bits
are extracted from it in block 86 as e, J values
(l~i<t,l<j<k). The function f is a pseudo random function, as
previously described. The first kt bits can be used as a
random selection, el~, and substitute for the random binary
vector of Fig. 3.
Finally,
Yi = ri ~ SJ (mod n)
e
for i = l....t,
is computed, block 88 and I, m, the ei J matrix and all the
yl values are sent by A (smart card 30) to the verification
device 40 of B.
For B to verify A's signature on m, the following
steps are taken. First, VJ = f(I,j) for j = l...k is
omputed, block lO0. Next,
y 2 ~ V j (mod n)
ei J=
for i=l..... t,
is computed, block 102, using the e, J matrix received from
A. Finally, B verifies that the kt bits extracted from
f(m, zl...z t ) are elj, block 104.
-12-

The sequential version of the interactive
identification method and apparatus according to the present
invention is zero-knowledge and thus B cannot deduce any
information whatsoever about the SJ values from his
interaction with A. The parallel identification method and the
signature method on the other hand, cannot be proven
zero-knowledge for very subtle technical reasons. In both
cases, the difficulties demonstrate the fragility and
inflexibility of the definitions of zero-knowledge rather than
real weaknesses of the present invention. The notion of
zero-knowledge is extremely restrictive, and prevents A from
sending to B even useless information about a secret s. This
difficulty in decision problems tis w a member of the language
L?) becomes almost impossible to solve in computation problems
(generate a member w of the language L), in which A must reveal
w to B. In fact, strong signature schemes cannot be
zero-knowledge by definition. If everyone can recognize valid
signatures but no one can forge them, B cannot generate by
himself A's messages with the same probability distribution.
However, the information about the SJ values that B gets from
signatures generated by A is so implicit that it cannot be used
to forge new signatures, and thus the signature aspect of the
present invention is provably secure (if factoring is
difficult) even though it is not zero-knowledge.
-13-
':
` ~ ' ` '
:
~: ' , ' :

65~7 '
In the proposed signature method of the present
invention, an adversary knows in advance whether his signature
will be accepted as valid, and thus by experimenting with 2k t
random r, values, he is likely to find a signature he can
send to B. Consequently, the product kt must be increased from
20 to at least 72 when the identification technique is replaced
by a signature technique, but smaller values of kt can still be
used for less secure applications.
A choice of k = 9, t = 8 attains the desired 2- 7 2
security level. The private key can be stored in a 576 byte
ROM, and each signature requires 521 bytes. The average number
o~ modular multiplications for this choice is t(k + 2)/2 = 44.
By doubling the key size to 1152 bytes (k = 18), the size of
each signature can be reduced to 265 bytes (t = 9) without
changing the 2- 7 2 security level. By optimizing the order of
the multiplications to compute the t (= 4) subset products
simultaneously, their average number can be reduced to 32.
This is only 4% of the number of multiplications required in
prior known signature techniques. Other points along the
tradeoff curve for the 2- 7 2 security level are summarized in
Table 1.
~ -14-
.. :
~:
. , , . , , , ., i . . . ~ . . . ~ , . . .
` ~ ` ' ' ' ' ~, ' '
: ': : ' .. ' . .
,

6~
-
Tablc 1: Tradeoff- for J; ~nd t t the 2-72 SecuriLy l,eYcl
_
Secret Key Sign~ure Average Averæge Average
~; ~ Size Size # Mult. # Mult. lL v,'~ B
(in byte~) (in by~es)(S~andard)(Op~imi~ed) Benerate~
,
172 64 4608 + 9 108 108 11
236 128 2''04 + 9 72 64 12
324 192 15~6 + ~ 60 49 13
418 256 1152+9 54 ! 46 4
612 384 768 + 9 48 1 41 6
8 9 512_ 576 + 9 45 1 45 8
~ 8 576 512 + 9 ~4 _ 44 9
12 6 768 384 + 9 42 35 12
18 4 1152 256 + 9 40 32 17
24 3 1536 192 + ~ _ 39 28 21
36 2 2304 128 + ~ 38 30 24
72 L~4608 64 + 9 37 37 36
A unique feature of the new identification and
signature method and apparatus of the present invention is that
it is possible to change the level of security after the key
has been chosen. Consider, for example, an access card with k
= 18 s; values. The fast screening procedure at the entrance
to a building will be controlled, e.g., with t=l (2-1~
security level), access to a computer room will be controlled
e.g., by t=2 (2-36 security level), while any usage of the
computer will leave signed audit trails with t=4 (2-72
security level). The only dangerous case is the simultaneous
usage of the same s; values in a parallel identification
- . .

9~i~7
technique with a large t and in a signature technique with a
small t (an unlikely combination), which is susceptible to an
active playback attack.
Since the verification devices store only small
amounts of publicly available information, it is possible to
standardize them. One device can store several values of n and
f and thus check a variety of personal, financial and
occupational ID cards provided by many independent
organizations. This possibility is particularly important in
department stores which have to recognize many types of credit
cards or in check cashing situations which require three ID
cards of many possible types.
The present invention can be generalized in a variety
of ways. For example, the square roots can be replaced by
cubic or higher roots, the e, J matrix can be made non-binary,
and the usage of ri and sJ values can be made more
symmetric in the generation of each yj value.
Although the present invention has been shown and
described with reference to specific embodiments, nevertheless,
changes are possible which will be apparent to those skilled in
the art which do not depart from the spirit and scope of the
invention. Such changes are deemed to come within the purview
of the invention as claimed.
-16-

Dessin représentatif