Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
W O 93/21687 ~ ~. t ~i 2 1 0 P ~ /US92~03024
AN IMPROVED ADAPTIVE RESONATOR VIBRATION CONTROL SYSTEM.
BACKGROUND OF THE INVENTION.
.
Many machines, such as internal combustion engines, generate unwanted
noise and vibration. The vibration typically comprises a fundamental
component whose frequency is, for example, the rotation frequency of
the machine (this is called the first harmonic), plus one or more
additional harmonics at frequencies that are integer multiples of the
first.
Occasionally, the speed of a machine is more-or-less constant and it
is then possible to reduce vibration caused by the machine with a
lS "t u ned damper", or "resonator" (the two terms are used
interchangeably here). A tuned damper is a resonant system that is
attached to a point where vibration is to be reduced, and it is built
to resonate at or close to the frequency of the vibration. Purely
passive tuned dampers have fixed characteristics, and will work only
close to the frequency for which they are designed. At the resonance
frequency, the input impedance of the resonator (defined as the ratio
of a generalized force applied by the resonator at the point of
attachment to a generalized velocity at the same point) will be
exceptionally high (or in some cases, such as a Helmholtz resonator
in a duct, exceptionally low: see the description in L E Kinsler, A R
Frey, A B Coppens, J V Sanders "Fundamentals of Acoustics" 3rd ed.
Wiley and Sons 1982 pp 241-242).
As an example of a tuned damper, a mass suspended on a spring will
resonate at a characteristic resonance frequency. If the spring is
attached to a structure vibrating at this resonance frequency, the
amplitude of vibration of the structure at that point will be reduced
(and as a consequence, the suspended mass will vibrate strongly).
Similar effects can be described for acoustic resonators (eg.
Helmholtz resonators; L E Kinsler, A R Frey, A B Coppens, J V Sanders
"Fundamentals of Acoustics" 3rd ed. Wiley and Sons 1982. pp ZZ5-2Z8)
where sound pressure is the vibration to be reduced.
W O 93/2l687 PCT/US92/03024
2~s2~~
-- 2 --
The disadvantage with passive tuned dampers is that they will work
only close to one frequency, and if the frequency of the vibration
drifts, the damper will cease to be effective. It is obvious that a
damper whose characteristics can be adjusted with the frequency of
S vibration to be reduced would be an advantage. Implicit here is the
concept that the period of the vibration varies only slowly, so that
it takes many cycles of the vibration for the period of the vibration
to change significantly (ie. a "quasi-periodic" system).
There have been many schemes for the adjustment of tuned dampers.
Typically, the resonance frequency of the damper is changed by
mechanically altering a stiffness or mass. The mechanism adjusting
the damper senses the current frequenc~ of the vibration and tries to
adjust the damper resonance frequency to be the same. The main
problem with such systems is that any error in the tuning of the
damper can be extremely detrimental to performance, and there is no
way of detecting this in a simple "open-loop" control system.
In more complicated systems, a "closed-loop" feedback control system
is used to ensure that the damper is always kept close to resonance
at the frequency of the unwanted vibration. These systems require
additional sensors to make them work, but the performance is
improved.
2S There is an important distinction between the systems described here,
with resonators whose properties can be adjusted (called
"adaptive-passive" systems) and so-called "active control systems".
In an active control system, the outputs from the controller change
on a timescale characteristic of the vibration itself, and these
outputs usually drive actuators vibrating at the same frequency as
the vibration (see, for example, P A Nelson and S J Elliott "Active
Control of Sound" A~de ic Press 1992 and G B B Chaplin and R A
Smith, US patent no. 4566118, 1986). In the adaptive-passive system
of the invention, the outputs of the controller vary on the much
slower timescale characteristic of changes in the frequency of
vibration. This reduces the computational requirements of the
controller considerably. Furthermore, the power required to drive the
W 0 93/21687 ~ P ~ /US92/03024
actuators of an active control system is usually considerable,
whereas in an adaptive-passive system, the power used to adjust the
resonator characteristics is usually negligible.
An ideal adaptive-passive system would be able to control components
of vibration at several different frequencies (usually the first and
subsequent harmonics of a quasi-periodic vibration), whilst
maintaining the performance of the system as the frequencies change.
DISCUSSION OF THE SELECTED PRIOR ART.
Sato and Matsuhisa (Internoise '90 proceedings, pp 1305-1308,
"Semi-active noise control by a Resonator with Variable Parameters"
published by the Noise Control Foundation) and Izumi, Takami and
Narikiyo (International Symposium on Active Control of Sound and
Vibration April 91, pp 261-266 "Muffler System Controlling an
Aperture Neck of a Resonator" published by the Acoustical Society of
Japan) describe feedback control systems for a single tuned damper of
variable characteristics.
Both of these papers describe the control of a single tuned damper
only. The damper is a Helmholtz resonator, and the control systems
use the sound pressure level inside the resonator, and just outside
it, as inputs. Both control systems aim to adjust the resonators such
that the phase shift between the two inputs is 90 , when the
resonator will be at resonance.
Sato and Matsuhisa use a two-stage control system that estimates the
frequency of the sound from the inputs and uses an open-loop control
system initially to tune the damper close to that frequency. A second
stage of closed-loop control then iterates to tune the damper
precisely to the correct frequency, although there is no description
of the control algorithm. This system must derive the vibration
~ frequency initially from one of the inputs, which can be difficult if
the fundamental period of vibration is changing and the vibration
comprises several harmonics all of which will be changing
differently. Also, the control system does not allow several tuned
W O 93/21687 '~ 8 2 1 ~ PCT/US92/03024
dampers to be tuned to reduce several different frequencies in the
sound simultaneously.
Izumi, Takami and Narikiyo describe a different control system.
However, if, for example, the vibration comprises several harmonics,
there is no guarantee that the system they describe will work in
general, because their phase-detection system makes the fundamental
assumption that the vibration comprises only the frequency to be
controlled. It also does not allow several tuned dampers to be tuned
simultaneously to different components of the vibration.
SUMMARY OF THE INVENTION.
The invention provides for a noise or vibration control system
comprising the following features
(a) one or more resonators of variable characteristics that can be
tuned by control signals to the same or different resonance
frequencies
(b) sensors attached to parts of the resonators and the structure to
which the resonators are attached in order to monitor the tuning of
the resonators
(c) sensors attached to the source or the structure (or any other
suitable location) that can be used to determine the frequencies of
the noise or vibration
(d) optional additional sensors that are used to monitor other
fac t ors tha t affect the resonators' performances (such as
temperature)
(e) a control system that has as inputs the sensors, and as outputs,
signals to change the resonance frequencies of the resonators wherein
the control system incorporates an algorithm to tune the resonators
close to selected frequencies in the noise or vibration, and to keep
them tuned as those frequencies drift (or as other factors affecting
W O 93/21687 ~ 0 P ~ /US92/03024
resonator performance change).
Accordingly, it is an object of this invention to provide a vibration
control system having one or more resonators of variable
characteristics that can be tuned by control signals to the same or
different resonance frequencies.
It is another object of this invention to provide a vibration control
means having sensors attached to parts of the resonators and the
structure to which the resonators are attached in order to monitor
the tuning of the resonators
A still further object is to have a vibration control system with
sensors attached to the source or the structure (or any other
lS suitable location) that can be used to determine the frequencies of
the noise or vibration
A still further object is the provision of vibration control with
optional additional sensors that are used to monitor other factors
that affect the resonators' performances (such as temperature)
Finally, it is an object to provide a control system that has as
inputs the sensors, and as outputs, signals to change the resonance
frequencies of the resonators wherein the control system incorporates
an algorithm to tune the resonators close to selected frequencies in
the noise or vibration, and to keep them tuned as those frequencies
drift.
Preferably, the control system incorporates mathematical models of
the resonators that are used to enhance the performance of the
control system. Preferably, these models are continuously updated and
refined by the control system as it operates.
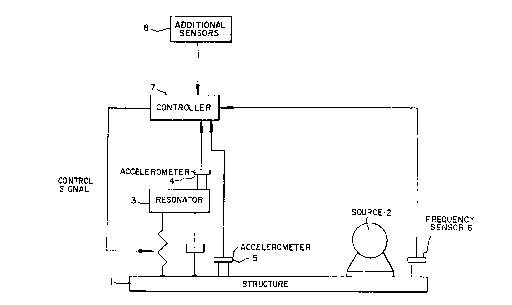
Reference is had to the accompanying drawings in which Figure
illustrates the overall structure of the invention, and Figure 2
illustrates a particular structure of the invention.
W O 93/21687 2~ PCT/US92/03024
DETAILED DESCRIPTION OF THE PREFERRED EMBODIMENTS.
A very simple example of the invention will be used to illustrate the
important features. In figure 2, a structure 1 is excited by a source
S 2 vibrating at a variable fundamental frequency of fl. The spectrum
of the vibration contains harmonics at f1, 2fl, 3fl.... etc. At a
point on the structure where it is desired to reduce the vibration, a
spring-mass-damper resonator 3 is attached. It is assumed in this
example that the nth harmonic of the fnn~ -ntal component of the
vibration is to be reduced by the damper, so that the aim is to tune
the resonator close to nf~, and to keep it tuned as f1 drifts. The
"structure" bears the vibration from the source to the resonator, and
may be a solid, fluid or gas depending on the application.
"Vibration" includes any disturbance in the "structure", including
electromagnetic, as the techniques described here can be equally well
applied to mechanical or electrical systems.
An accelerometer 4 is attached to the mass of the resonator, and
another accelerometer S is attached to the structure close to the
resonator. The displacement of the mass (as monitored via the
accelerometer 4) is denoted x , and the displacement of the structure
m
(as monitored via the accelerometer 5) is denoted x . Obviously other
types of sensor could be used to measure these displacements. It is
immaterial where, in fact, these sensors are mounted provided the
resonator's input impedance could be derived from sensors mounted at
those points. For example, a force guage mounted on the structure
between the structure and the resonator, and an accelerometer also
mounted on the structure would also be an acceptable pair of sensors.
Note that the choice of example here, with linear motions, does not
preclude application of the system to resonators with rotary motion -
the principles of operation are the same.
It is assumed that the frequency responses of the sensors are known
so that x and x can be derived from the sensor outputs. The
frequency response of the sensor can usefully include any other
additional filtering (eg analogue b~n~p~cs filtering and gain
adjustment to improve signal to noise ratios or anti-aliasing). This
.
W O 93/21687 ~ v, 2 f a P ~ /US92/03024
-- 7 --
compensation for the sensor responses can be applied at different
points in the system, but it is most efficient to apply the
compensation to the coefficients X and X described below.
Typically, the control system will store necessary information about
the calibration of the sensors to enable any corrections that are
required to be made. In the description below, these corrections are
not explicitly stated as it will be obvious to anyone skilled in the
art how to compensate for sensor characteristics to derive the
quantities needed by the control system.
The aim is to maximize the modulus of the input impedance of the
resonator at the nth harmonic of the fundamental of vibration, so
that the structure will vibrate less at that frequency at the point
of attachment of the resonator. The input impedance is defined here
to be the ratio of the force applied by the structure to the
resonator and the corresponding velocity of the point of attachment,
and it is a function of frequency.
Elementary mechanics will show that the input impedance of the
Z0 resonator is proportional to the ratio X /X , where Re(X e ) and
Re(X e1 ) are the components in x and x at angular frequency ~.
(Re denotes the real part, X and X are complex numbers, t denotes
time and i=~-l). X and X are themselves functions of ~. For the
m s
simple spring-mass-damper model of the resonator,
X 1 (1)
X 1 - ~ /~
s r
1 ~ /((d Q)
Here, w is the 1In~ d resonance (angular) frequency of the
resonator, and Q is the "quality factor". For the spring-mass-damper
model the relations ~2=k/m and Q~ =k/~ apply, where k is the spring
stiffness, m the mass and ~ the damping rate of the damper.
W O 93/21687 2 ~ ~ ~ 2 ~ ~ PCT/US92/03024
-- 8 --
When Q ~ 1 (which is usually true) the modulus of X /X at an angular
frequency of w=2~nfl will be a maximum if ~ =2nnfl. (This is not
exactly true, but the errors are negligible if Q is large enough).
Also, there will then be a 90 phase difference between X and X at
this frequency.
A frequency sensor 6 in figure 2 is provided to detect the
fundamental frequency of vibration, f1. The location and type of
sensor is preferably chosen to be reasonably immune to the effects of
changing the tuning of the resonator. For example, it could be a
tachometer signal from a part of the source of vibration such that
the output of the tachometer can be used to determine the current
fundamental frequency of the source.~ In some cases, it may be
sufficient to use one or more of the sensors mounted on the structure
and resonators to derive fundamental frequencies, but it is better if
the sensor is insensitive to the effects of tuning the resonators.
The signal from sensor 6 is used by the control system 7 to help to
discriminate those components of x and x at the frequency nf1 in
the presence of components at other harmonics of f1 or any other
"noise". This discrimination is crucial if the control system is to
be able to alter the resonance frequency of the resonator to coincide
with nf1 and to maintain this condition as f1 varies. For example, x
and x will normally contain components at all harmonics of f1 up to
the highest harmonic below the current resonance frequency of the
resonator. Unless the unwanted components can be rejected, there is
no guarantee that the resonator will be adjusted to the correct
frequency.
The signal from sensor 6 can be used in several different ways to
process the inputs from accelerometers 4 and 5. Three examples are
given below.
1. Tracking Filter
It is possible to set up a tracking bandpass filter whose centre
freq~ency is adjusted by the signal from sensor 6 to be close to nf1
W O 93/21687 ~ J 1'~' 2 I ~ PCT/US92/03024
_ g _
(eg. see K Martin and A S Sedra, IEEE Transactions on Acoutics,
Speech and Signal Processing Vol ASSP-29 no. 3 June 1981 pp 736-744).
The bandwidth of the filter is chosen to reject all unwanted
components in the accelerometer signals. Each accelerometer signal is
then filtered through a tracking filter (desirably, these filters
would be identical) to leave only the signals at a frequency of nf1.
One problem with this implementation is that the bandwidth of the
filter (expressed in octaves) will have to vary with the number, n,
of the harmonic to be controlled. This is because harmonics become
more closely spaced (in terms of octaves) as n is increased.
The accuracy with which sensor 6 must detect f depends upon the
required bandwidth of the filter. If~the filter bandwidth must be
narrow to remove an unwanted noise component close to nf1, then the
accuracy with which the filter's centre frequency is set (by the
signal from sensor 6) must clearly be such that the pass-band still
includes the frequency nf1. It is immaterial whether the tracking
filter is implemented digitally or with analogue electronics.
ZO The output of the bandpass filters will be signals that contain
information only at the frequency nf1, as required. In order to
extract the values of the complex coefficients X and X , it is
convenient to process these signals in one of the two ways described
below. Since unwanted components of x and x have already been
removed by filtering, the low-pass filters described for the harmonic
filter can have a bandwidth of up to 2f1. For the same reason, a
single FFT or DFT is all that should be required to calculate X and
X as signal averaging will be unneces~ry.
The outputs of identical b~n~p~cs filters are expected to be
AIX Isin(2nnf t+7 ) and AIX Isin(2~nf t+7 ) where 7 and 7 are phase
m 1 m s 1 s m s
angles and A is the gain of the filter. Therefore, it would also be
possible to estimate IX /X I and/or 7 -7 (which is the phase
m s m s
difference between the original components at frequency nf when the
filters are identical) directly from the filter outputs. For example,
peak value and zero-crossing detection could be used, and such a
scheme might be computationally more efficient than other methods.
W O 93/21687 '~ PCT/US92/03024
-- 10 --
The ratio of peak values gives I X I /I X I directly, and zero-crossings
with a positive slope will occur at times tk = k/nf1+~ /2nnf1 and tk
= k/nf1+~ /2nnf1 (k is an integer). Therefore, the value of 7 -7 can
be deduced from measurement of t -t'.
s
2. Harmonic Filters
From the sensor 6 it is possible to derive auxiliary signals
sin(2nnflt) and cos(2nnf1t). For example, this could be done with
voltage-controlled oscillators whose inputs would be a signal derived
from sensor 6 to generate outputs close to frequency nf1. The signals
x and x are then multiplied by sin(2nnf1t) and cos(2nnf1t) (giving
four signals in total), and each of th~ results is low-pass filtered
by filters whose bandwidths are adjusted to reject all the unwanted
lS components in x and x . For example, if other harmonics in x and x
must be rejected, the bandwidths of the low-pass filters should be
less than fl. Just as with the tracking filter, the low-pass filters
should have bandwidths that are ideally adjusted by the control
system as f1 changes in order to maintain rejection of unwanted
components in the signals (see G P Eatwell, "Control System Using
Harmonic Filters". Copending patent application). Also, the accuracy
with which the frequency of the auxiliary signals must match nf1
depends upon the required bandwidth of the low-pass filters: the
difference between the true value of nf and the frequency of the
auxiliary signals derived from sensor 6 must be less than the
bandwidth of the low-pass filters.
To see how the magnitude and phase of X /X (evaluated at a frequency
of nf1) are calculated from the four demodulated signals, define y
and y to be the outputs from the process of multiplying x by
cos(2nnf t) and sin(2nnf t) respectively and then low-pass filtering
the results. Similarly, define y and y for the results of
sc ss
operating on x . The modulus of X /X can then be calculated as
s m s
/X I 2= (y2 + y2 )/(y2 + y2
m s mc ms sc ss
and the phase difference by 2 1 1 821 0
g m Xs) arctan(ym/ymS) - arctan(y /y )
These results are much easier to compute if the control system is
implemented digitally, and the whole harmonic filtering scheme is
also ldeally lmplemented digitally.
If the bandpass filtering described in (1. Tracking Filter) above has
been performed, it is possible to take some short-cuts to computing
Arg(X /X ). For example, the phase-detection scheme of Izumi, Takami
and Narikiyo (Internatlonal Symposlum on Active Control of Sound and
Vibration April 91, pp 261-266 "Muffler System Controlling an
Aperture Neck of a Resonator" publlshed by the Acoustical Society of
Japan) which uses balanced synchronous demodulation will work because
only one harmonic now appears in the filter outputs, although it is
undesirable that the magnitude of one of the signals appears in the
result.
2a The use of the filtered signals to implement a closed-loop control
system is described below.
3. Fourier Transform
Another method of using the auxiliary signal from sensor 6 to
discriminate against unwanted components in x and x is to use a
Fourler transform (D E Newland "A~ Introduction to Random Vibrations
and Spectral Analysis" Longman 1975 pp 33-40). As this would normally
be implemented digitally, it is described here in those terms. From
the sensor 6 signal, a pulse-train of N pulses per fundamental period
of the vibration is derived. (This would be done directly if, for
example, sensor 6 ~ere a shaft-encoder giving N pulses per revolution
of a shaft in the source rotating at the same frequency as the
fundamental fre~uency of the vibration). This pulse-train is used to
trigger analog-to-digital converters tADC's) sampling x and x
tafter such anti-alias fLltering as is necessary). Alternatively, the
pulse-train can be used to select samples from ADC's triggered by a
: A
. ~
.. . .... . , .. ~ .
W O 93/21687 ~ 0 P ~ /US92/03024
- 12 -
fixed clock running at a frequency considerably higher than Nf
(using interpolation/extrapolation if necessary to get the sample
value at the occurrence of a pulse, which may lie between two
successive samples of the ADC's). In either case, the result of this
process is a sequence of samples of x and x , with N samples per
fundamental period of the vibration.
To discriminate against noise in x and x that is not correlated to
m s
the pulse-train, successive blocks of N samples of can be averaged.
This is synchronous time-domain averaging, and it is only one example
of the standard techniques for removing uncorrelated noise from a
signal that could be used.
To perform the Fourier transform, one of the standard algorithms can
be used if N is a suitable number. (For example, if N is a power of
2, the "Fast Fourier Transform" algorithm can be used; see D E
Newland "An Introduction to Random Vibrations and Spectral Analysis"
Longman 1975 pp 150-166). It is also poss~ble to perform a Discrete
Fourier Transform (see 6. D E Newland "An Introduction to Random
Vibrations and Spectral Analysis" Longman 1975 pp 113-124). The
result of this process is one or more "Fourier Coefficients",
representing the real and imaginary parts of X and X at one or more
of the frequencies fl, 2f1...nfl...Nfl/2. (Clearly, the coefficient
at nf1 will have to be calculated when this is the harmonic of the
vibration that is to be reduced).
Noise in x and x that is not correlated to the pulse-train can also
s
be reduced by averaging corresponding Fourier coefficients from
successive blocks of data (this is frequency-domain averaging,
another example of a standard technique).
The use of the Fourier coefficients to implement a closed-loop
control system is now described.
W O 93/21687 2 ~ ~ ~ '2 1 ~ PCT/US92/03024
The Control System
Once the values of X and X at the frequency nf have been
m s
discriminated from other unwanted components, the control system must
arrange to adjust the tuning of the resonator accordingly. In the
example given above, the modulus of the ratio X /X is to be
maximized, or the phase difference between X and X is to be kept at
as f1 varies. One way of achieving this goal with a model-based
digital control system is described below. In the controller, a
gradient-descent algorithm incorporating a model of the resonator is
used. The purpose of the model is to permit rapid and accurate
estimation of the derivatives of an error function that determines
the current performance of the system. The controller can be
configured continuously to update its model of the resonator, and to
account for additional variables (such as temperature) that affect
the system performance.
Equation 1 is a result based on a simple model of the resonator. In
practice, this model should be a good approximation at least
reasonably close to resonance. If r is defined to be the ratio X /X
evaluated at a frequency of nf , then equation 1 gives
r _ = 1 - w /w (2)
X l+iw/(~ Q)
m r
The aim of the control system is to adjust w to minimize Irl. w
will be a function of a control parameter ~. For example, ~ may be
the position of an actuator that changes the stiffness of the spring
in the spring-mass-damper resonator. From the current value of ~,
denoted ~ , the improved value of ~ to be set by the controller
(~k 1) can be calculated by the following equation
W O 93/216872 ~ i ~ 2 ~ ~ PCT/US92/03024
- 14 -
A = ~ - ~ Re r ar (3)
kll k
k
where ~ is a scalar multiplier determined by the control system, and
an asterisk indicates the complex conjugate. This is the update
equation for a gradient-descent algorithm. As it stands, equation 3
is of limited use because the derivative of r with respect to A is
not measured (whereas r is). It would be possible to determine the
value of this derivative by making small perturbations in A and
observing the results, but it is better to use the model of the
resonator to esti~ate this derivative.
In the current example, equation 2 gives the value of r in terms of
the current values of ~ and Q. Therefore, an estimate of the
derivative is given by
ar ~2 . a~r 2~ + i~ aQ i~wr . (4)
aA w (l+i~/w Q) aA r Q , aA Q2
Now all of the quantities on the right hand side of equation 4 are
either measured, or can be estimated from a model of the resonator.
The current value of ~ can be estimated from the auxiliary sensor 6
signal; w can be estimated from the current value of A and a model
of the function relating ~ to A stored in the controller. Q can be
estimated in a similar fashion. The derivatives with respect to ~ can
also be estimated from the model relationships between w , Q and A.
The important aspect of equation 4 is that errors in the estimates of
the quantities do not become critical around the condition ~ =w. This
is very different from r itself which is sensitive to errors around
the condition w =~: it would be inadvisable to estimate r in the same
way as ar/~, because errors could lead to the wrong sign in the
second term on the right hand side of equation 3, and this would
prevent the control system converging correctly.
15 - 2 1 1 82 1 o
.
As another example, consider a variable Helmholtz resonator mounted
in a duct to prevent transmission of noise at a frequency of nfl.
This system ls very similar to the spring-mass-damper tescribed
above, but here the aim is to minimlze the input impedance (defined
S as the ratio of sound pressure in the duct outside the neck of the
resonator and the particle velocity of the fluid in the nec~) at the
frequency nf1. It is not difficult to show that this amounts to the
minimization of a new error function, Irl, defined by
lo r = 1 - ~Z + i w . (S)
r rQ
r can be derived from measurements of the sound pressure in the duct
~ust outside the neck of the resonator, and inside the cavity of the
resonator. As before, r itself should be meas~red rather than
estimated in view of its sensitivity to errors when ~ ~~. However,
the derivative required in equation 3 can safely be estimated in the
manner described above via the relation
20ar = ah~r w ' 2~ aQ . (6)
a~ a~ W2 ~'Jr Q (d Q2 a~
r - r
It should be noted that ln some circumstances it may be acceptable to
ignore or approximate some of the terms in equations 4 and 6. For
example, the last term in equation 6 would normally be very small,
and it mlght be neglected.
It is most appropriate to apply the gradient-descent algorithm when
the ~esonator is already close to resonance. The step-slze, ~, should
then be sealed approximately as follows
/Q)/I a~ /aAI
where a is a constant independent of w and the resonator performance,
and the derivative is evaluated at the current value of A. The best
value for ~ can be selected by experiment.
A
... .. . . ... . . . . . . . . . .. . .... .
W O 93/21687 2~ P ~ /US92/03024
- 16 -
Initially, it may happen that the resonator is far from resonance.
Two schemes can then be applied to bring the resonator close enough
to resonance to apply the gradient-descent algorithm. First, ~ is
known from the sensor 6 signal, and an estimate of ~ is known from
S the current value of ~ and the relation between A and ~ which is
stored by the controller. Therefore, it is simple to adjust ~ in one
step to bring w much closer to ~. However, the relation between ~
and ~ will in general not be known very accurately since, for
example, the relation may depend upon unobserved variables such as
temperature.
The second scheme, a measurement-based one-step algorithm, estimates
~ directly by solving equation 2 for ~ given the current (measured)
values of ~ and r, and an estimate of Q. This determines the required
change in ~ , and an update of ~ can be computed via
Ak-~ k + ~ ( ~ -- ~ ) /a~
a~
for example. The deri v at iv e is evaluated at a value of
corresponding to a frequency somewhere between ~ and ~ , and ~ is a
positive control parameter that would usually be somewhat less than
l. A value of l tries to converge to the correct value of ~ in one
step. This method relies on the assumption that the gradient a~ /a~
is less sensitive to error than the resonance frequency itself. This
update equation can be applied iteratively, if necessary, to bring
the resonator close enough to resonance for the gradient-descent
algorithm to be applied.
The relationships between ~ , Q and ~ can be continually refined and
updated by the control system as it operates. For example, when the
controller detects that ~ and ~ coincide (through a small value of r
and/or a small value the second term on the RHS of equation 3) it
will be able to update its relationship between ~ and ~, because
will be known from the sensor 6 signal and ~ is a control parameter.
Likewise, the minimum value of Irl, from equation 2 will then be l/Q
(if Q~ l, but it is not difficult to derive an exact relation if
W O 93/21687 ~ ? ~ ~; 2 ~ ~ P ~ /US92/03024
required) so Q at the current value of ~ is also found. As the
frequency w=2nnfl changes, the relationships between w , Q and ~ can
be continuously updated for the range of ~ explored by the change in
w.
It is a fact that w and Q may also be functions of parameters other
than ~. For example, temperature may affect the resonance frequency.
In this case, it may be advantageous to have other inputs (8 in
figure 2) to the control system that monitor such additional
variables. The effect of these variables can then be built into the
model relationships for w and Q to enable better estimates to be
obtained. The control system can still update these relationships as
described above, the only difference being that these relationships
now involve ~ and the additional variables instead of just ~.
In practical implementations of the system, more than one harmonic of
the vibration will usually be controlled. This is easily performed
with the addition of one resonator per harmonic to be controlled,
plus at least one additional sensor on each of the resonators. (The
sensor 5 on the structure can be used to determine the vibration at
all of the harmonics to be controlled, whereas a separate sensor is
needed on each of the resonators). With the processing of the signals
described above, the control of each resonator is largely
independent.
It may be possible to have a single mechanical device that resonates
at two or more independently controllable frequencies. As far as the
control scheme is concerned, no modifications are required provided
each control variable can independently control each frequency.
There is no difficulty in controlling more than one resonator
attached to different points on the structure, tuned to the same or
different frequencies, provided that sensors on the resonators and
structure are provided for each mounting point.
It is also possible that the source generates more than one harmonic
sequence of vibration. In this case, the set of fundamental
W O 93/21687 2 ~ i 8 ~ PCT/US92/03024
- 18 -
frequencies, f1~ f2....f should be resolved either from a single
sensor 6, or preferably from several sensors that measure separately
the different fundamentals. The overall control scheme is unchanged,
as each additional harmonic sequence can be handled independently by
S a separate bank of harmonic filters.
There is sometimes an advantage to combining an active control system
with the adaptive resonator system described here. It often happens
that one or two harmonics of a vibration are particularly strong, or
are at an inconveniently low frequency. Fully active control of these
harmonics may then be costly in terms of actuator size, and power
consumption. It is therefore beneficial to tackle such awkward
vibration components with an adaptive resonator system, and to clear
up the remaining problems actively. It is easy to modify the
performance of an active control algorithm such as those described in
G B B Chaplin and R A Smith, US patent no 4S66118, 1986 and S A
Tretter, US patent no. 50919S3, 1992 to ignore particular harmonics,
if desired, and to combine the two types of control system into a
single controller.