Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
2138~53
"~ 94/00930 PCr/US92/05229
CONTROI, SYSTFM FOR PERIODIC D~TURBANCES
This invention relates to a control system for c~nceling periodic or nearly
periodic di~Lulbances. ~ealuies of this control system include a delayed inverse filter,
s a variable delay and, optionally, a comb filter. Unlike previous systems, little or no
adaption is r~uil~,d and, since the system is based in the time domain rather than the
frequency ~lom~in~ the colllpuL~Lion required does not increase with the number of
harmonics to be controlled.
The control system has many applications including the active control of sound
0 and vibration and the selective removal of periodic noise in co.. ~ ic~tionc signals.
Back.~round
The prin~iple of reducing unwanted di~.Lulbance by g~,nc.atillg a di .Lulballce
with the o~osile phase is well doc!~...e--~e~ The technique is often l~r.~ d to as
15 active control to flictin~lich from passive control where the cle...f .u~ of the system are
ins~r~ble of generating disturbances. Nelson and Elliot, "Active Control of Sound",
Ac~lçmic Press (1992) review some of the work done to date.
The earliest technique in this field was done by P. Lueg who described an
actuator and sensor coupled by a simple negative feedbacl~ loop in U.S. Patent
20 2,043,416.
The main shortcoming of this system is that the disturbance can only be
reduced over a limited range of low frequencies. This is because of the finite response
time of the control system (the time taken for a signal sent to the ~t~l~tor to cause a
response at the sensor). The control loop cannot cOl. .p~ ~c~te for the phase shifts
2s associated with this delay, and so only operates at low frequencies where the phase
shifts are small. The gain of the feedback loop must be low at other frequencies to
m~int~in the stability of the system. This is achieved by incol~ g a low pass filter
into the loop - which introduces additional delay.
WO 94/00930 2 1 3 8 5~ 3 PCI/US92/0522~
The range of applic~bility of ac*ve control systems has been extended by the
use of more mo~ern adap*ve control techniques such as those described by B. Widrow
and S.D. Stearns in "A-l~?tive Si~nal Processing", Prentice Hall (1985). In U.S. Patent
No. 5,105,377, Ziegler achieves fee~lb~cL system stability by use of a compen~*on
5 filter but the digital filter must s*ll try to compensate for the phase characteris*cs of
the system. This is not possible in general, but when the disturbance has a limited
frequency bandwidth the digital filter can be adapted to have al,l,r~ alely the right
phase characteris*c at the frequencies of interest. The filter characteris*c therefore
~epen~l~ on the disturbance as well as the system to be controlled and must be changed
0 as the noise changes.
One class of disturbances for which this approach can be successful is periodic
disturbances. These are characterized by a filn~mtont~l period, a *me over which the
disturbance repeats itself. Disturbances are not often exactly periodic, but anydisturbance where the period changes over a *mesc~le longer than that over which the
15 disturbance itself changes can be incl~l~e~ in this class.
Several approaches have been put forth for controlling periodic disturbances
incl~lfling that desc~ l by C. Ross in U.S. Patent No. 4,480,333. The patent describes
a feedforward control system in which a tachometer signal is fed through an adaptive
digital filter. There is no description of the form of the tachometer signal but it
20 contains no inrol,lla~ion on the amplitude of the disturbance to be controlled and thus
the filter must again be adapted in response to the disturbance. Chaplin et al, in U.S.
Patent 4,153,815, describe the method of wave form synthesis, where a model of one
cycle of the desired control signal is stored and then sent repetitively to the actuator.
Nelson and Elliot, infra, describe the equivalence of these two approaches in the
25 special case where the period remains constant.
In U.S. Patent 4,490,841, Ch~plin et al recognize the benefit of splitting the
stored waveform into its frequency components. The advantage of this step is that
each frequency component can be adapted independently. This can improve the ability
of the system to adapt to rapidly changing disturbances and can reduce the
2-
~ 1 ~ 8:5:5 ~ '
wo 94/00930 PCI /US92/OS229
co~ ulaLional requirements associated with this adaption. Others have recognized this
technique such as Swinb~nkc in U.S. Patent No. 4,423,289 which describes the use of
Frequency Sampling Filters and the equivalence of time or frequency domain weights.
In all of the above systems the filters have to be adjusted to cope with changing
5 disturbances. This requires processing power and so adds costs to the control system.
In addition, all of the systems above become increasingly complicated as the number of
harmonics in the disturbance increase. This is a problem for disturbances which are
impulsive in nature - such as the sound from the exh~mt or inlet of an intern~l
combustion engine.
Accordingly, it is an object of this invention to provide a control system for
periodic disLu~l,ances that requires little or no adaption.
Another object of this invention is to provide a control system based in the time
domain for c~nceling p~rio~lic di~ bances.
A further object of this invention is to provide a unique system for controlling15 the cancellation of periodic di~lulbances whe,c;ill the amount of co~ u~Lion required
does not increase with the number of h~rrnonics to be controlled.
These and other objects of this invention will become appar~ t when reference
is had to the acco~ anying drawings in which
Fig. 1 is a dia~,l~atic view of the basic control system,
Fig. 2 is a dia~,li1.. ~tic view of a recursive comb filter,
Fig. 3 is a diag~all~ atic view of a comb filter configuration,
Fig. 4 is a diagl~",~ ic view of a control system,
Fig. 5 is a dia~ """~ic view of a combined system,
Fig. 6 is a diagr~mm~tic view of the adaption of a delayed inverse filter,
Fig. 7 is a diagr~mm~tic view of the identification of model filter A,
Fig. 8 is a view of an off-line adaption of delayed inverse,
Fig. 9 is a dia ,l~lnlll~tic view of a system with on-line system identification,
Fig. lV is a diagrammatic view of an in-wire noise cancellation system,
Fig. 11 is a diagrammatic view of a multi-channel system, and
- ~ ~1 3 ~ 5 5 3
Fig. 12 is a time analysis of a sampled signal.
Detailed Description
This invention relates to a new type of control system for periodic
disturbances. This control system has the following major advantages:
5 1) The filter is determined by the system to be controlled and so does not have
to be adapted to cope with ch~nging disturbances.
2) The filter operates in the time domain, relying only on the periodicity of the
noise, and so the computational requirements are independent of the number
of harmonic components in the disturbance.
By way of explanation a single channel digital control system will be described
first.
The object of the invention is to control an ullwi~nL~d disturbance. If there
were no output from the controller this unwanted disturbance would produce a signal
y(t) at the controller input at time t. The controller output at time t is defined to be
15 x(t). If the unwanted disturbance is in a physical system rather than an electronic
circuit, the controller output is fed to an actuator which produces a counter
disturbance which mixes with the unwanted disturbance and results in a residual
di~lulbal1ce. The input to the controller is provided by an error sensor which senses
the residual disturbance and produces an error signal e(t) at time t. The relationship
20 between e(t), y(t) and x(t) willnow be described for a digital system. The sampling
period of the digital system is defined to be T, and the nth sample occurs at time nT.
The error signal at time nT, which is denoted by e(nT), is given by
e(nT) = y(nT) + (A * x)(nT), (1)
. .
3 ~ 5 5 3
where A denotes the impulse response of the system between the controller output
and the controller input and where * denotes the convolution operator. (A*x)(nT)
denotes the convolution of A and x evaluated at time nT which is given by the
definition
(A * x) (nT) = ~ A~kT) .x(nT - kT), (2)
and where y(nT) is the signal due to the uncanceled disturbance, A(kT) is the
response at error sensor at time t=kT due to a unit impulse sent to the actuator at
time t=o, and x is the controller output. The system impulse response, A, is known in
control li~ ule as the plant response.
For electrical disturbances the signal y is available, for other applications the
signal y can be estimated by subtracting of the predicted effect of the controller from
the error signal,
y(nT) = e(nT) - (A*x)(nT), (3)
provided that the system impulse response, A, is known. In practice an approximate
15 system model must be used, but we will assume for simplicity of explanation that the
actual impulse response and the system model are equivalent and will denote both of
them by the symbol A. The convolution of x with A in equation (e) is equivalent to
filtering the signal x through a filter with impulse response A. Since the effect of this
term is to compensate for the feedback from the controller output to the controller
20 input, the filter A is referred to as a compensation filter.
The ideal output, x, can be obtained by passing the signal y through a filter F,
and inverting, so that
x(nT) =-(F*y)(nT). (4)
4a
213~553
~v~) 94/00930 PCr/US92/05229
The filter F is the inverse of A, which in digital form is defined by
(A * F)(nT) = 1 if n=0, 0 otherwise. (5)
Unfortunately, the filter F cannot be realized since it must compensate for the delay in
the response A.
s However, it is often possible to realize a filter B which is the delayed inverse of A with
a phase inversion. B is defined by
(A * B)(nT) = -1 if n=rn, 0 otherwise, (6)
where mT is l~f~l~d to as the modeling delay.
We can define a filter D(t) which cc,lfes~onds to a pure delay of time t. Equation (6)
lo can then be written more comp~tly as
A*B=-D(mT). (7)
A periodic disturbance is changed very little by delaying it by one noise cycle, so, for a
disturbance with period ~, we have
y(t-~) _ y(t), (8)
ls or, equivalently,
D(~)*y ~ y. (9)
The control system utilizes this ~ el ~y of the disturbance.
In one form of the control system, the filter is obtained by combining the filter
B and a filter D(~-mT) in series. The ~ct~l~Sor drive signal is obtained by passing the
20 signal y(t), obtained using equation (3), through this combine~ filter. The response at
the sensor is
e = y + A * (B * D(~-mT)) * y. (10)
Using the ~lefinision (7), it can be seen that the comhin~sion A*B*D is equivalent of a
pure delay of time ~, hence the residual disturbance is
=> e(t) = y(t) - y(t-~). (11)
For periodic signals, which satisfy (9), this residual disturbance is small.
If the modeling delay is greater than one period, ~ in equation 10 and the
systems described below must be replaced by an integer multiple of the period, Nl,
such that N~ > mT.
5 - -
~ ~ 3~5 ~ ~
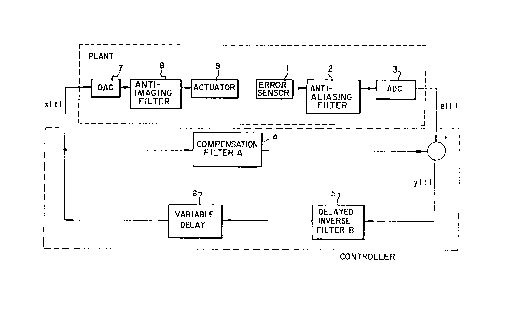
The basic control system, shown in Figure 1, consists of feedback loop
colllplisillg an error sensor (1), anti-aliasing filter (2), analog-to-digital converter
(ADC)(3)(only required if digital filters are to be used), compensation filter (4), a
'delayed inverse' filter, (5), a variable delay (6) with delay ~-mT, digital-to-analog
converter (DAC) (7) (only required if digital filters are to be used), anti-im~ging filter
(8), and actuator (9).
The additional delay introduced by variable delay 6 is chosen so that the
modeling delay and the additional delay is a whole number of noise cycles. If the cycle
length, T, iS not known in advance, or it is subject to variations, the delay must be
varied as the period of the noise varies. The period can be measured from the noise
itself or from a sensor, such as an accelerometer or tachometer, responsive to the
frequency of the source of the noise.
The part of the system from the controller output to the controller input is
referred to as the plant. This includes the elements 7, 8, 9, 1, 2, 3 in Figure 1 as well
as the response of the physical system.
The modelin~ delay is determined by the system to be controlled, and typically
must be greater than the delay through the plant.
The additional delay is determined by the modeling delay and the
fundamental period of the noise (disturbance).
Unlike previous control systems, delayed inverse filter 5 does not need to vary
with the noise.
In another form of the controller, shown in Figure 4, the compensation filter
4(A) can be avoided. In this form, the actuator drive signal from anti-im~ging filter 8
is obtained by passing the error signal e(t) through the delayed inverse filter (B) and
the variable delay 6 D(T-mT) and then through an additional gain K. (Note that the
order of these elements can be interchanged). The response at the sensor is
e = y + A * K.(B * D) * e. (12)
The combination A*B*D is equivalent to a pure delay T, hence
. .
- ~ e(t) = y(t) - K.e(t-~)- (13)
If the error signal is periodic with period ~, (13) can be rearranged to give
e(t) = y(t)/(l + K). (14)
Hence the disturbance is reduced by a factor l+K.
Disturbances with other periods (other frequencies) may not be reduced and
could cause the system to become unstable. This can be avoided by filtering out
disturbances which do not have a fundamental period ~.
One way of doing this is to use a 'comb filter', which can be positioned at any
point in the feedback loop. One example of a comb filter is a positive feedback loop
with a one cycle delay around the loop and a loop gain, _, of less than unity. This is
shown in Figure 2. Another example is a feedforward loop with a delay of 1/2 cycle in
one of the paths as shown in Figure 3.
The full control system is shown in Figure 4. The plant is shown in Figure 1.
The delay and the comb filter have been combined in this example, so that only asingle variable delay is required. The output x from the controller is
x = D(T-mT)(K(l-~)B*e +_D(mT)*x). (15)
In the first form of the control system, shown in Figure 1, the estimate of the
uncanceled signal, y, is obtained using equation (3). This signal is then passed through
the delayed inverse filter 5 (B) to give a signal B*y. This requires the calculation of
two convolutions. However, using the relation
B*y = B*(e-A*x) = B*e - B*A*x = B*e + D(mT)*x, (16)
it can be seen that the signal B*y can be calculated via a single convolution and a
delay. This requires less computation.
The output from the controller is
x = D(~-mT)B*y = D(T-mT)(B*e + D(mT)*x), (17)
which is very similar to equation (15), since the compensation filter 4 appears as a
comb filter 11 in Figure 4. Formally, the two equations are the same in the limit as
loop gain _ tends to one with K(l~
~.,,
If an additional comb filter is added to the controller in equation (17), the
comb filter and the feedback compensation can be combined. The controller output is
then
x = D(T-mT)B*y = D(T-mT)((1-_)B*e + D(mT)*x). (18)
The resulting control system is shown in Figure 5. In this form of the control
system the parameter _ determines the degree of selectivity of the controller, _=0
being the least selective and the selectivity increasing as_ increases.
There are many known ways of implementing the required delays. One
example, which can be used when the sampling frequency is high compared to the
highest frequency of the disturbance, is to use a digital filter with only two non-zero
coefficients. For a delay t = (n + ~)T which is not a whole number of sampling
periods, this is equivalent to writing
D(t) ~ ).D(nT) + ~ .D(nT +T). (19)
This can be implemented as digital filter with n-th coefficient 1-~ and (n+1)-th
coefficient ~.
Other ways of implement the required delays include analog and digital delay
lines and full digital filters.
The inclusion of a comb filter avoids amplification of the disturbance at non-
harmonic frequencies, and also makes the control system selective.
A comb filter can be included in either form of the control system. In the
first form shown in Figure 1 it is only required when selectivity is required, since
stability is obtained by use of the compensation filter. In the second form shown in
Figure 4, the filter is n~cess~ry to stabilize the feedback loop.
There are well-known methods for obtaining the delayed inverse filter B.
25 Some of these are described by Widrow and Stearns. An example is shown in Figure
6. A test signal is supplied to delay mT and the plant (which is shown in Figure 6).
The output signal of the plant is applied to the inverse filter. The difference or error
between the output signal of the inverse filter and delay mT is used to adapt the
~'
- -
- inverse filter. When the filter adaption is complete, the inverse filter will be an
approximation to the required delayed inverse filter B, which is a delayed inverse of
the system with a phase inversion. The delayed inverse filter can be a combination of
finite impulse response filter and a recursive filter.
It is not always possible to obtain a delayed inverse of the system. This
happens, for example, when the system cannot be modeled as minimllm phase systemplus a delay. There are ways of overcoming this problem, one way is to use an extra
filter and actuator. This technique is well known in the field of audio processing,
where compensation for room acoustics is required, see Miyoshi et al. in "Inverse
Filtering of Room Acoustics", IEEE Trans Acoustics Speech and Signal Processing,ASSP-36, 145-152 (1988). For application of active control in aircraft and automobile
cabins for example, where the reverberation of the cabin make a single channel system
difficult to implement, it is likely that multichannel versions of the control system will
be used.
For the first form of the control system, shown in Figure 1, compensation
filter, A, is also required. Again, there are well-known techniques for identifying a
model of A. One example is shown in Figure 7. A test signal is sent to the actuator
shown as part of the plant and through an adaptive filter comprised of Model A and
the adaption unit. The response at the sensor is compared to the output of the
adaptive filter and any difference is used to adapt the filter.
Once the filter A is known, the filter B can be determined as in Figure 8.
This is equivalent to Figure 6 except that the actual system has been replaced by the
model of the system. Alternatively, the filter B can be calculated using Wiener
Filtering Theory. This approach is useful when the frequency bandwidth of the noise
is limited, or when an exact inverse is not achievable (because of finite filter length or
non-minimllm phase effects).
In some applications, the system response may change slowly over time. In
these applications it is n~cess~ry to change the filters A and B.
,~ '
One way of doing this is to turn off the control system and remeasure the
responses. Alternatively, there are some well-known techniques for identifying A 'on-
line', i.e. while the control system is still in operation. For example, a low-level test
signal can be added to the controller output. The difference between the actual
sensor response and the predicted response can be used to adapt the model of A,
provided that the test signal is uncorrelated with the original noise.
The filter B may then be updated 'off-line' using the model of A, as in
Figure 8.
An example of a complete control system, including on-line system
identification, is shown in Figure 9.
The control loop part of the system is the same as shown in Figure 5. The
on-line system identification system is driven by a random test signal. This test signal
is added to the output signal x(t) and the combined signal is sent to the plant. The
difference between the output from the plant (error signal e(t)) and the output from
the filter Model A is used to adapt the filter Model A. The output from the filter
Model A is passed through inverse filter B. The resulting output is then compared
with a delayed test signal, which is obtained by passing the test signal through a
modeling delay, and the error is used to adapt the filter weights of the inverse filter B.
These coefficients are then copied to the inverse filter B in the control loop.
Alternatively, the filter B can itself be treated as an adaptive filter. There are
many methods for performing the adaption as described in the Widrow publication, for
example, one way is the 'filtered-input LMS' algorithm. In this approach the input
to the filter is passed through a model of the response of the rest of the system
(including the variable delay and comb filter if present) and then correlated with the
error signal to determine the required change to the filter. This will only provide
information at frequencies which are harmonic multiples of the fundamental frequency
of the noise. However, in some applications, there are more harmonics in the noise
-
5 ~
- than there are coefficients in the filter. In these cases there is sufficient information
to update all of the coefficients.
In some applications, the disturbance is in an electrical signal, such as a
communication signal. In this case the system response is typically a pure delay (plus
5 some gain factor). The delayed inverse filter, B, is then also a pure delay, and the
whole system consists just of a fixed delay and a variable delay as shown in Figure 10.
The extension of the system to multiple interacting channels willbe obvious to
those skilled in the art. An example of a multi~h~nn~l system with three inputs and
two outputs is shown in Figure 11. One inverse filter, Bjj, is required for each pair of
10 interacting sensor and actuator, whereas only one comb filter (or variable delay unit)
is required for each output channel (CF1 and CF2 in the figure). The comb filters
could be applied to the input channels instead, but often there are more inputs than
outputs in which case this would result in a more complex control system.
The input to the i-th comb filter passed through a gain block and is
ri = ~ Bij*ej (20)
10a
~,~
~ ' ~
2138'553
~ 30 PCI /l lS92/05229
where ej is the signal from the j-th sensor and B~, is the ap~ ufiate inverse filter.
The output from the i-th channel is
Yi = (l-a)D(mT)*ri + D(~)*Yi (21)
- The filters Aij which model the system response can be found in the same way as the
s single channel filters by driving the output channels in turn with a test signal.
Alternatively, all of the ch~nnçl~ can be driven simultaneously with independent(uncorrelated) signals.
Once the filters Aij have been identi~1e~, there are a variety of ways in which
the filters Bij can be obtained. These include time domain approaches, such as
10 Weiner filtering, and frequency domain approaches.
~ lt~rn~tively~ the filters Bij can be obtained directly by adaptive filtering
using the mllltich~nne] Least Mean Square algc.lilhlll, for example.
The other single channel ~y~ s described àbove can also be implemented as
multichannel systems.
Reduction to practir.e
The effectiveness of the control system has been demonstrated on the selective
filtering of a periodic noise from a co,,,,,~ ic~tions signal. In this example the
colllllllll-ic~tions microphone is in the vicinity of a loud periodic noise source and,
20 untreated, the speech cannot be heard above the noise. The time trace of the untreated
signal is shown in the upper plot in Figure 12.
The treated signal is shown in the lower plot, and the speech signal can be
clearly seen (and heard) above the reduced noise level. The noise level decays
exponentially when the system is first turned on since the canceling signal must pass
2s around the control loop several times for the response to build up.
While only one preferred embodiment of the invention has been shown and
described, it will be obvious to those of ordinary skill in the art that many changes and
modifications can be made without departing from the scope of the appended claims.