Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
CA 02259094 1999-O1-15
1
r
A METHOD AND DEVICE FOR DESIGNING AND
SEARCHING LARGE STOCHASTIC CODEBOOKS
IN LOW BIT RATE SPEECH ENCODERS
BACKGROUND OF THE INVENTION
1. Field of the invention:
The present invention relates to an efficient technique
for digitally encoding a sound signal, in particular but not exclusively a
speech signal, in view of transmitting, storing and/or synthesizing this
sound signal.
2. Brief description of the prior art:
The demand for efficient digital speech encoding
techniques with a good subjective quality/bit rate trade-off is increasing
for numerous applications such as voice transmission over land-mobile,
satellite, digital radio, or packed networks, as well as voice storage, voice
response, and wireless telephony.
CA 02259094 1999-O1-15
2
A speech encoder converts a speech signal into a digital
bitstream which is transmitted over a communication channel (or stored
in a storage medium). The speech signal is digitized (sampled and
quantized with usually 16-bits per sample) and the speech encoder has
the role of representing these digital samples with a smaller number of
bits while maintaining a good subjective speech quality. The speech
decoder or synthesizer operates on the transmitted or stored bit stream
and converts it back to a sound signal.
One of the best prior art techniques capable of achieving
a good quality/bit rate trade-off is the so-called Code Excited Linear
Prediction (CELP) technique. According to this technique, the sampled
speech signal is processed in successive blocks of L samples usually
called frames where L is some predetermined number (corresponding to
10-30 ms of speech). In CELP, a linear prediction (LP) filter is computed
and transmitted every frame. The L-sample frame is then divided into
smaller blocks called subframes of size N samples, where L=rN and r is
the number of subframes in a frame (N usually corresponds to 4-10 ms
of speech). An excitation signal is determined in each subframe, which
usually consists of two components: one from the past excitation (also
called pitch contribution or adaptive codebook) and the other from an
innovation codebook (also called fixed codebook). This excitation signal
is transmitted and used at the decoder as the input of the LP synthesis
filter in order to obtain the synthesized speech.
An innovation codebook in the CELP context, is an
indexed set of N-sample-long sequences which will be referred to as N-
dimensional codevectors. Each codebook sequence is indexed by an
CA 02259094 1999-O1-15
3
integer k ranging from 1 to 8 where 8 represents the size of the codebook
often expressed as a number of bits b, where 8=2b.
A codebook can be stored in physical memory (e.g. look-up
table) or can refer to a mechanism for relating the index to a
corresponding codevector (e.g. a formula).
To synthesize speech according to the CELP technique, each
block of N samples is synthesized by filtering an appropriate codevector from
a codebook through time varying filters modelling the spectral characteristics
of the speech signal. At the encoder end, the synthetic output is computed
for all, or a subset, of the codevectors from the codebook (codebook search).
The retained codevector is the one producing the synthetic output closest to
the original speech signal according to a perceptually weighted distortion
measure. This perceptual weighting is performed using a so-called
perceptual weighting filter, which is usually derived from the LP filter.
A first type of codebooks are the so-called "stochastic codebooks".
A drawback of these codebooks is that they involve substantial physical
storage. They are stochastic (i.e., random) in the sense that the path from
index to codeword involves look-up tables which are the result of randomly
generated numbers or statistical techniques applied to large speech training
sets. The size of stochastic codebooks tends to be limited by storage
and/or search complexity.
A second type of the codebooks are the algebraic codebooks. By
contrast of the stochastic codebooks, algebraic codebooks are not random
and require no substantial storage. An algebraic codebook is a set of
CA 02259094 1999-O1-15
4
indexed codevectors of which the amplitudes and positions of the pulses of
the k~" codevector can be derived from a corresponding index k through a
rule requiring no, or minimal, physical storage. Therefore, the sizes of
algebraic codebooks are not limited by storage requirements. Algebraic
codebooks can be designed for efficient search. For these reasons,
algebraic codebooks have known a considerable success in speech coding
standards, where codebooks ranging from 17 bits (e.g. ITU-T
Recommendation 6.729) to 35 bits (ETSI Enhanced Full Rate GSM) were
efficiently used.
As the bit rate is reduced, the number of pulses in the codevectors
of the algebraic codebook are reduced. This results in lower performance
for unvoiced frames and in case of background noise, where codevectors
with stochastic contents are more suitable. This shows the need for
stochastic codebook with efficient storage and search techniques.
OBJECT OF THE INVENTION
An object of the present invention is therefore to provide a method
and device for efficiently designing stochastic codebooks with reduced
storage requirements and fast search procedures for encoding sound
signals.
CA 02259094 1999-O1-15
SUMMARY OF THE INVENTION
More specifically, in accordance with the present invention, there
is provided a method for constructing large stochastic codebooks, and for
5 efficiently searching these codebooks in view of encoding a sound signal.
In this method, an N-dimensional codevector is derived by the
addition of P signed vectors (typically P=2 or 3) from a table containing M
stochastic vectors of dimension N (typically M=32 or 64). Let v; denote the
I-th N-dimensional stochastic vector in the random table, then a codevector
is constructed by
c = s v + s v + ... +
1 Pi 2 Pz SP PP
where the signs s,, s2, ..., sP are signs equal to -1 or 1, and p,, p2, ...,
pP,
are the indices of the random vectors from the random table.
The number of bits needed to encode the index of each vector v;
is log2(M) and the sign information can be encoded with only 1 bit as will
be seen in the detailed description. So the structure described above
corresponds to a codebook of P log2(M)+1 bits.
As an example, with M=32 and P=2, an 11-bit codebook can be
constructed (5 bits for each vector and 1 bit for the signs). Similarly, if
M=32 and P=3, a 16-bit codebook can be obtained using only 32 random
vectors.
CA 02259094 1999-O1-15
6
The present invention further relates to an efficient method for
searching such codebooks, in the context of CELP-type coders. The
goal of the codebook search is to determine the best P vectors in the
stochastic table and their corresponding signs, which maximize the
selection criterion (the maximization of the ratio Qk, which will be described
in detail hereinafter).
In the search method according to the invention, a small subset K
of the vectors in the stochastic table is pre-determined (typically K=6)
using a simplified selection method (testing only the numerator of the
selection criterion Qk). The pre-determination is based on maximizing the
dot products between a vector d and the stored vectors v;, i=0,...,M-1.
The vector d is obtained by computing the correlation between the target
vector x and the impulse response h of a combination of synthesis and
weighting filter (this is also equivalent to backward filtering the target
vector through the synthesis and weighting filters). The dot products
N-1
~'r = ~, yr (h)d (n)
~~=o
are computed, and the K indices k which correspond to the K maxima
of xk are selected.
The search process then proceeds with testing the search criterion
Qk for all the possible combinations of P out of K vectors. For P=2, this
corresponds to testing the selection criterion Kx(K+1 )/2 times (36 times
for K=8). A full search requires testing the criterion Mx(M+1 )l2 times (528
times for M=32). This shows the significant decrease in the search
CA 02259094 1999-O1-15
7
complexity using the search method of the invention (the decrease is
more significant when P=3 and M=64).
Other variation of this new codebook structure can be obtained. In
case of P=3, the third vector can be replaced by a pulse covering the
range 0,..,N-1. The possibility of making the third vector replaced by a
pulse gives the codebook more flexibility to capture special time events
in the signal.
This new stochastic codebook structure can be also used in
conjunction with a sparse codebook (such as an algebraic codebook)
where 1 more bit can be used to denote which codebook is selected.
The objects, advantages and other features of the present invention
will become more apparent upon reading of the following non restrictive
description of a preferred embodiment thereof, given by way of example only
with reference to the accompanying drawings.
BRIEF DESCRIPTION OF THE DRAWINGS
In the appended drawings:
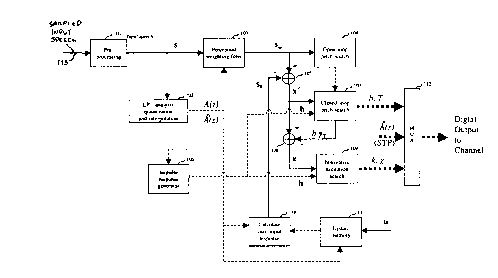
Figure 1 is a schematic block diagram of a preferred embodiment of
encoding device according to the present invention;
CA 02259094 1999-O1-15
Figure 2 is a schematic block diagram of a preferred embodiment of
decoding device according to the present invention;
Figure 3 is a flow chart representing the computation of the index of
the innovation codevector for the case P=2;
Figure 4 is a schematic representation of two nested loops used in
the computation of two optimum indices among the K predetermined random
vectors (for the case P=2);
Figure 5 is a schematic representation of three nested loops used in
the computation of three optimum indices among the K predetermined
random vectors (for the case P=3); and
Figure 6 is a schematic filow chart summarizing the search procedure
of a stochastic codebook in accordance with the present invention.
DETAILED DESCRIPTION OF THE PREFERRED EMBODIMENT
The novel techniques disclosed in the present specification may apply
to different LP-based coding systems. However, a CELP-type coding
system is used in the preferred embodiment of the invention for illustrating
theses novel techniques.
Figure 1 shows the general block diagram of a CELP-type speech
encoding device. The sampled input speech 113 is divided into L-sample
CA 02259094 1999-O1-15
9
blocks called "frames". For each frame, the different parameters
representing the speech signal in the frame are computed, encoded, and
transmitted. These parameters include linear prediction (LP) parameters
representing the LP synthesis filter and excitation parameters. The LP
parameters are usually computed once every frame. Each frame is further
divided into smaller blocks of length N, in which the excitation parameters
(pitch and innovation) are determined. In the CELP literature, these blocks
of length N are called "subframes", and the IV sample signals in a subframe
are referred to as N-dimensional vectors. In the preferred embodiment, the
value of N corresponds to 5 ms and that of L corresponds to 20 ms, which
means that a frame contains four subframes (N=40 at the sampling rate of
8 kHz). Various N-dimensional vectors occur in the encoding procedure. A
list of vectors which appear in Figures 1 and 2 as well as a list of
transmitted
parameters are given herein below:
List of the main N-dimensional vectors
s Input speech vector (after pre-processing);
sW Weighted speech vector;
so Zero-input response of the weighted
synthesis filter;
x' Target vector for pitch search;
h Impulse response of the combination of
synthesis and weighted filters;
fT Adaptive codebook vector at delay T;
yT Filtered adaptive codebook vectpr (f
convolved with h);
x Target vector for innovation codebook
search;
CA 02259094 1999-O1-15
ck Innovation codevector at index k (k th entry
of the innovation codebook);
zk Filtered innovation codeve~tor (c
convolved with h);
v; Random vectors in the random table of size
5 M;
w~ Filtered predetermined random vectors;
a Excitation signal (scaled innovation and
pitch codevectors); and
s' Synthesis signal before postfiltering.
List of transmitted parameters
STP Short term prediction parameters (defining
A(z));
T Pitch lag (or adaptive codebook
index);
b Pitch gain (or adaptive codebook
gain);
k Codevector index (innovation codebook
entry); and
g Innovation codebook gain.
List of other codec
parameters and syrmbols
A(z) Short term prediction filter (LP
filter) in the
subframe;
A(z) Quantized LP filter in the subframe;
W(z) Perceptual weighting filter;
L Frame size;
N Subframe size;
M Size of the random table;
CA 02259094 1999-O1-15
11
P Number of added vectors from the random
table to form the innovative vector;
K Number of predetermined vectors in the
codebook;
Dot product between d and the random
vectors v;;
E Energies of the filtered predetermined
random vectors w;; and
p Dot products between the target vector x
and the filtered predetermined random
vectors w;.
DECODING PRINCIPLE
It is believed preferable to first describe the speech
decoding device of Figure 2 illustrating the various steps carried out between
the digital input (input of the demultiplexer 201) and the output sampled
speech (output of the postfilter 209).
The demultiplexer 201 extracts four types of parameters
from the binary information (input bitstream 210) received from a digital
input
channel. From each received binary frame, the extracted parameters are:
- the short term prediction parameters STP (usually
once per frame);
- the long-term prediction parameters (pitch lag T and
pitch gain b (each subframe);
- the innovation codebook index k; and
the innovation codebook gain g (each subframe).
CA 02259094 1999-O1-15
12
The current speech signal is synthesized on the basis of these parameters
as will be explained below.
The speech decoding device of Figure 2 comprises an
innovative excitation generator 203 to produce an excitation codevector ck
in response to the received index k. The innovation codevector ck is scaled
by the gain factor g through the scaler 207.
The LTP (Long-term prediction) which usually consists of
the past excitation delayed by the pitch lag T is generated by a pitch
codebook unit 202. As illustrated in Figure 2, the pitch codebook unit 202 is
responsive to the pitch lag T and to the past excitation a stored in memory
204 to produce the adaptive codebook vector fT at delay T.
The adaptive codebook vector fT is scaled by the pitch
gain b through the scaler 206 to obtain the signal bfT. The signal bfT
is then added to the scaled innovation codevector gck through the adder
205 to obtain the excitation vector u. The contents of the pitch codebook
(unit 202) is updated through the memory unit 204 which itself receives and
stores the excitation codevector u.
The synthesized output speech s is obtained by filtering
the excitation vector a through the synthesis filter 208, which has a transfer
function 1/A(z), then through the postfilter 209, which is well known to those
of ordinary skill in the art. Both filters 208 and 209 are updated by the
received STP parameters from the demultiplexer 201.
CA 02259094 1999-O1-15
13
It should be pointed out here that the previously described
operations are repeated on a subframe basis, where the subframe size is
equal to the vector dimension N. Although the STP parameters are updated
on a frame basis (2 to 5 subframes), an interpolated filter A(z) is computed
on a subframe basis as it is well known to those of ordinary skill in the art.
ENCODING PRINCIPLE
The sampled input speech signal 113 is encoded on a
block by block (frame by frame) basis by the encoding device of Figure 1.
In Figure 1, the encoding device is broken down into 11 modules numbered
from101to112.
More specifically, the input speech signal 113 is
processed in blocks called frames.
The input frame is first processed through the optional pre-
processing unit 101. This pre-processing unit 101 consists of a high pass
filter with a 140 Hz cut-off frequency. This high pass filter removes the
unwanted sound components below 140 Hz.
The output of the pre-processing unit 101 is denoted s(n).
This signal is used for pertorming linear prediction (LP) analysis, a
technique
well known to those of ordinary skill in the art. The autocorrelation approach
is used, where the signal is first windowed using a Hamming window (usually
of the order of 20-30 ms). The autocorrelations are computed from the
windowed signal, and Levinson-Durbin recursion is used to compute the LP
CA 02259094 1999-O1-15
14
parameters, a,, I=1,...,p, where p is the LP order, which is typically 10. The
parameters a, are the coefficients of the LP filter:
P
Z -i
i=1
Unit 202 performs LP analysis, as well as quantization and
interpolation of the LP parameters. The LP coefficients are transformed into
another equivalent domain more suitable for quantization and interpolation
purposes. Line spectral pairs (LSP) and immitance spectral pairs (ISP)
domains are two domains in which quantization and interpolation can be
efficiently performed. The 10 LP parameters can be quantized in the order
to 18 to 30 bits using split or multi-stage quantization, or a combination
thereof. The purpose of the interpolation is to enable updating of the LP
parameters every subframe while transmitting them once every frame; this
improves the encoder performance without increasing the bit rate.
The following paragraphs will describe the other encoding
operations performed on a subframe basis. In the following description, the
filter A(z) denotes the unquantized interpolated LP filter of the subframe,
and
the filter A(z) denotes the quantized interpolated LP filter of the subframe.
Perceptual weighting
In analysis-by-synthesis encoders, the optimum pitch and
innovation parameters are searched by minimizing the mean squared error
between the input speech and synthesized speech in a perceptually
CA 02259094 1999-O1-15
weighted domain. This is equivalent to minimizing the error between the
weighted input speech and weighted synthesis speech.
The weighted signal sW(n) is computed in the weighted
signal generator 103. This weighting is usually made by means of a filter
5 VI/(z) of the form:
IN(z) = A(zly~) / A(z/y2) where 0 < y2 < y~ < 1
Typical values of y, and y2 are 0.9 and 0.6, respectively.
Other forms of W(z) also exist in the literature and could be used.
Open-loop pitch analysis
In order to simplify the pitch analysis, an open-loop pitch
lag is first estimated in open-loop pitch search unit 104 using the weighted
speech signal s~,(n). Then the closed loop pitch analysis, which is performed
on a subframe basis, is restricted around the open-loop pitch estimate which
significantly reduces the search complexity of the LTP parameters T and b
(pitch lag T and pitch gain b).
In the preferred embodiment, open-loop pitch analysis is
usually performed once every 10 ms (two subframes) using techniques well
known to those of ordinary skill in the art.
Target vector computation
CA 02259094 1999-O1-15
16
The target vector for LTP (Long-Term-Prediction) analysis,
x', is first computed by the adder 105. This is usually done by subtracting
the zero-input response of the weighted synthesis filter Vll(z)lA(z) from the
weighted speech signal. More specifically:
x'-sW -so
where x' is the N~limensional target vector, sW is the weighted speech signal
vector in the subframe, and so is the zero-input response of the filter
W(z)lA(z), which is the output of the combined filter W(z)lA(z) due to its
initial
states. so is computed in the zero-input response calculating unit 110.
Note that alternative, but mathematically equivalent,
approaches can be used to compute the target vector x'.
Pitch codebook search
First, the N~fimensional impulse response vector h of the
weighted synthesis filter is computed in the impulse response generator 106.
The closed-loop pitch or adaptive codebook parameters
are computed in unit 107; this closed-loop pitch search unit 107 is responsive
to the target vector x' and the impulse response vector h to compute these
closed-loop pitch or adaptive codebook parameters b and T.
Traditionally, pitch prediction was represented by a pitch
filter in the form
CA 02259094 1999-O1-15
17
1 / (1 - bz-T)
where b is the pitch gain and T is the pitch delay or lag. In this case, the
pitch contribution to the excitation signal u(n) is given by bu(n-Tj, where
the
total excitation is given by
a (n) = bu (n-T) + gck (n)
with g being the innovative codebook gain and ck(n) the innovation
codevector at index k.
This representation has limitations if the delay T is less
than the subframe length N. In another view point, the pitch contribution can
be seen as an adaptive codebook containing the past excitation signal.
Generally, each vector in the codebook is a shift-by-one version of the
previous vector (discarding one sample and adding a new sample). For
delays T>N, the adaptive codebook is equivalent to the filter structure, and
a codevector fr(n) is given by:
fT(n) - u(n-T), n=0,...,N-1.
For delays less than T, a codevector is built by repeating
the available samples from the past excitation until the codevector is
completed (this is not equivalent to the filter structure).
CA 02259094 1999-O1-15
18
In the recent encoders, a higher pitch resolution is used
which significantly improves the quality of voiced sound segments. This is
achieved by oversampling the past excitation signal using polyphase
interpolation filters. In this case, the codevector f~(n) may correspond to an
interpolated version of the past excitation, with T being a non-integer delay
(e.g.50.25).
The pitch search consists of finding the best delay T and
gain b that minimize the mean squared weighted error between the target
vector and scaled filtered past excitation:
~~X -bYT~~2
where yT is the filtered adaptive codebook vector at delay T:
n
yT(n) =fT(n) *h(n) _~ fT(i)h(n-i), n=0, .. .,N-1
i=0
It can be shown that the error E is minimized by
maximizing the criterion:
Xt Y
C, = T
t
YT YT
where t denotes vector transpose.
CA 02259094 1999-O1-15
19
In this preferred embodiment, a 1/3 subsample pitch
resolution is used, and the pitch search is composed of three stages. In the
first stage, an open-loop pitch lag is estimated in the open-loop pitch search
unit 104. In the second stage, the search criterion C is searched for integer
delays around the estimated open-loop lag (usually t 5), which significantly
simplifies the search procedure. Once an optimum integer delay is found,
the fractions around this integer delay are tested in the third stage of the
search.
Innovative codebook search
Once the pitch, or LTP parameters T and b are
determined, searching for the optimum innovative excitation is conducted by
means of innovative excitation search unit 109. First, subtracfor 108
updates the target vector x' by subtracting the LTP contribution from that
target vector x'
x = x~ - byT
where b is the pitch gain and y,. is the filtered adaptive codebook vector
(the
past excitation at delay T convolved with the impulse response h). The new
target vector x is used for the innovative codebook search and is therefore
supplied to unit 109.
The search procedure in CELP is performed by finding the
optimum excitation codevector ck and gain g which minimize the mean-
squared error between the weighted input speech and weighted synthesis
CA 02259094 1999-O1-15
speech. This is equivalent to minimizing the mean-squared error between
the target vector x and the scaled filtered codevector byT, as it is well
known
to those of ordinary skill in the art. The mean-squared weighted error
(MSWE) is given by:
N-1
(X ~Il~ gZk ~Il~ ~ 2
n=0
where zk(n) is the filtered innovative codevector at index k given by:
5
n
Zk ~I2~ - Ck ~11~ * ~'I ~Il~ - ~, Ck ~ 1~ ~'1 ~111~ , Il=~, . . . , NW .
i=0
It is usually easier to use vector and matrix notations to
represent the MSWE E. That is:
where zk = H~ is the filtered innovative codevector, and H is a lower
10 triangular convolution matrix derived from the impulse response vector h.
The matrix H is given by:
n(o) o o ... o
h(1) h(o) 0 ... 0
15 ~ h(2) h(1) h(0) ... 0
H= ~
CA 02259094 1999-O1-15
21
h(N-1) ... h(2) h(1) h(0)
By differentiating with respect to g, it can be shown that the
MSWE E is minimized by maximizing the search criterion:
(xtzk)2 (xtHck)2
Qk
Zk Zk Ck H tHCk
In an exhaustive codebook search, the search criterion is
evaluated for all possible codevectors ck, k=0,...,8-1, where 8 is the
codebook size. For codebooks exceeding 10 bits (1024 entries), an
exhaustive search procedure becomes impractical. For sparse codebooks
where the codevectors contain few non-zero pulses, it is possible to
construct huge codebooks and efficiently search them. For example,
algebraic codebooks of sizes as large as 35 bits can be easily constructed
and searched using efficient non exhaustive search procedures. Example
of such codebooks are given in the following US patents:
5,444,816 (Adoul et al.) 1995
5,699,482 (Adoul et al.) 1997
5,754,976 (Adoul et al.) 1998
5,701,392 (Adoul et al.) 1997.
For non sparse random codebooks, it is difficult to
construct and search codebooks exceeding 10 bits. The use of sparse
codebooks was efficient at bit rates higher than 6 kbits/s. However, as the
bit rate decreases, multi-mode coding becomes necessary, where the
CA 02259094 1999-O1-15
22
speech signal is divided into different modes (e.g. voiced, unvoiced,
transient, background noise) and a speech frame is encoded according to
the selected mode. In voiced speech mode, algebraic codebooks with small
number of pulses are suitable, while in unvoiced or background noise
modes, non sparse random codebooks are more suitable. Even without the
use of multi-mode coding, it was found that using a codebook which contains
a mixture of algebraic and random codevectors improves the performance
of low bit rate codecs. In this case, 1 bit can be used to denote whether the
algebraic or random part of the codebook is selected.
The present invention relates to a method and device for
constructing and efFciently searching such random codebooks. These
method and device are disclosed in the following description.
Memory update
In update memory 111, the states of the weighted
synthesis filter are updated by filtering the excitation signal
a = gck + bvr
through the weighted synthesis filter. At the end of this filtering, the
states
of the filter are memorized and used in the next subframe as initial states
for
calculating the zero-input response in unit 110.
Similar to the target vector, other alternative, but
mathematically equivalent approaches can be used to update the filter
states.
CA 02259094 1999-O1-15
23
STRUCTURE OF THE RANDOM CODEBOOK
In the method of the present invention, an N dimensional
codevector is derived by the addition of P signed vectors (typically P=2 or 3)
from a table containing M random vectors of dimension N (typically IV~32 or
64). Let v; denote the i-th N-dimensional random vector in the random table,
then a codevector is constructed by:
c = slv + s v + . . . +
Pi 2 Fz sP PP
where the signs s,, s2, ..., sP are signs equal to -1 or 1, and p,, pz,
...,,off,,
are the indices of the random vectors from the random table.
The number of bits needed to encode the index of each
vector v; is log2(M) and the sign information can be encoded with only 1
bit as will be seen below. So the structure described above corresponds
to a codebook of size 8=P log2(M)+1 bits.
As an example, with M=32 and P=2, an 11-bit codebook
can be constructed (5 bits for each vector and 1 bit for the signs).
Similarly, if M=32 and P=3, a 16-bit codebook can be obtained.
This shows the memory efficiency of this new structure,
since random non sparse codebooks with sizes of 2'6 and higher can be
obtained using only a table of M=32 or 64 vectors.
CA 02259094 1999-O1-15
24
The vectors in the random table can be generated using
several approaches. Some suggested approaches for generating the
contents of the random vectors are:
- random generators with uniform distribution;
- random generators with Gaussian distribution;
- band-pass filtered vectors randomly generated as
above;
- vectors generated using training algorithms;
- overlapping vectors obtained from a random sequence
where each vector is a shift-by-k version from the
previous vector, with k = 2 or 3 (this saves memory
requirements since only the first vector is stored as N
samples and other vectors need only k samples each);
- inverse DFT of complex vectors with unit amplitude and
random, uniformly distributed phases; and
- as above but with setting few first and last complex rays
to zero (equivalent to band pass filtering).
Other approaches can be used for generating the contents
of the random vectors without departing from the spirit of this invention.
In this preferred embodiment, the last approach is used,
where: (1) complex vectors are generated with unit amplitudes and randomly
generated phases (uniformly distributed between -~c and ~), (2) the
amplitudes of the few first and last rays are set to zero (to perform a sort
of
band-pass filtering), and (3) inverse DFT is used to obtain the contents of
the
random vectors.
CA 02259094 1999-O1-15
ENCODING THE CODEBOOK INDEX
Let's first consider the case where the table has M random
vectors, and the excitation codevectors are generated by the addition of 2
random vectors from the random table (P=2). That is, the codevectors are
5 given by:
C = S~V; + SZV~
In this case, we have to encode 2 signs, s, and s2, and two indices, i and j.
10 The values of i and j are in the range 0 to M 1, so that encoding thereof
requires log2(Il~ bits for each index, and encoding of the signs requires 1
bit
for each sign. However, 1 bit can be saved since the order of the vectors
v; and v~ is not important. For example, choosing v,s as the first vector and
v25 as the second vector is equivalent to choosing v25 as the first vector and
15 v,s as the second vector. Thus, a total of 2 IQg (11~+1 bits is required to
encode the signs and indices of the two vectors.
A simple approach of implementing the encoding of the
codeword is to use only 1 bit for the sign information and 2 log2(II~ bits for
20 the two indices while ordering the indices in a way such that the other
sign information can be easily deduced. To better explain this, assume
that the two vectors have the indices p, and p2 with sign indices ~, and ~a
respectively (~=0 if the sign is positive and ~=1 if the sign is negative).
The codevector index is given by:
I=~,+2x(p~+p2xM)
CA 02259094 1999-O1-15
26
If p,<p2 then ~z = ~ otherwise g is different from, . Thus, when
constructing the codeword (index of codevector), if the two signs are
equal then the smaller index is assigned to p, and the larger index to p2,
otherwise the larger index is assigned to p, and the smaller index to p2.
Figure 3 shows a flow chart for calculating the index of the
codevector from the vector indices p, and p2 and corresponding sign
indices a, and a~2.
When three random vectors are added to construct the
excitation codevector, each vector requires log2(M) bits and the sign
information needs only 1 bit; a total of 3 log2(M)+1 bits. A simple way of
performing the codeword encoding in this case is as follows. The random
table is divided into two halves with M/2 vectors in each half. The half
which contains at least two chosen vectors is then determined. This
information, denoted by ~, is encoded with 1 bit. The two vector indices
in the same half are encoded according to the algorithm of Figure 3, and
require 2 log2(M/2)+1 bits (which is equal to 2 log (M)-1 bits). The third
vector is encoded separately with log2(Il~ bits for the index and 1 bit for
the sign. The total number of bits is
1 +(21og2(M/2)+1 )+(log2(M)+1 )=31og2(M)+1. The codevector index
(codeword) is given by:
I = ~+2x(Q, +2x(p, +P2xMl2)) +MxMx(~ +2xp3 )
FAST SEARCH PROCEDURE FOR THE STOCHASTIC CODEBOOK
CA 02259094 1999-O1-15
27
The innovative codebook search is performed in
innovative excitation search unit 109.
The codevectors are given by:
C = SI p + S2 p + . . . + Sp P
1 2 p
The goal of the search procedure is to find the indices p,,
p2, ..., pP, of the best P vectors and their corresponding signs s, , s~ ,
..., ~,
which maximize the search criterion:
_ (x/Zk)Z (XrHCk)2 (drCk)2
~k - Zk Zk - Z Zk - Zk Zk
where x is the target vector and zk =Hck is the filtered codevector at index
k. Note that in the numerator of the search criterion, the dot product
between x and zk is equivalent to the dot product between d and,,c ,
where d=Htx is the backward filtered target vector which is also the
correlation between d and the impulse response h. To find the elements
of the vector d, the following relation is used (step 601 of Figure 6):
N-1
d (n) = x(n) * h(-n) _ ~ x(i)h(i - n)
i=n
CA 02259094 1999-O1-15
28
Since d is independent of the codevector index k, it is
computed only once; this simplifies the computation of the numerator for
the different codevectors.
After computing the vector d, a pre-determination process is
used to identify K out of the M random vectors in the random table, so
that the se arch process is then confined to those K vectors.
This pre-determination is performed by testing the numerator
of the search criterion Qk for the K vectors which have the largest
absolute dot product (or squared dot product) between d and v;, i=0,...,M
1. More specifically, the dot products x; given by:
N-1
x; _ ~ d(~)v; (n)
~~=o
are calculated for all the random vectors v; (step 602 of Figure 6) and the
indices of the K vectors which result in the K largest values of I xrl are
retained (step 603 of Figure 6). These indices are stored in the index
vector m;, i=0,...,K 1.
To further simplify the search, the sign information
corresponding to each pre-determined vector is also pre-set. The sign
corresponding to each pre-determined vector is given by the sign of x; for
that vector (step 603 of Figure 6). These pre-set signs are stored in the
sign vector s;, i=0,...,K-1.
CA 02259094 1999-O1-15
29
The codebook search is now confined to the pre-determined K
vectors with their corresponding signs. For typical values of M=64, P=2,
and K=6, the search is reduced to finding the best 2 vectors among 6
random vectors instead finding them among 64 random vectors. This
reduces the number of tested vector combinations from 64x65/2 to 6x7/2.
Once the best promising K vectors and their corresponding
signs are pre-determined, the search proceeds for selecting P vectors
among those K vectors which maximize the search criterion Qk.
The filtered vectors w;, j=1,...,K corresponding to the K pre-
determined vectors, are first calculated (step 604 of Figure 6) and stored.
This can be performed by convolving the pre-determined vectors with the
impulse response of the weighted synthesis filter h. The sign information
is also included in the filtered vectors; i.e.:
n
w.; (n) = s; ~ vn,. (i)h(n -i) , n=0,...,N-1, j=0,...,K 1.
r=o
The energy of each filtered predetermined vector is then computed (step
605 of Figure 6):
N-1
s,; =w~~'v~ =~w.;(n), j=0,...,K 1
n=0
as well as its dot product with the target vector (step 605 of Figure 6):
N-1
P.; = x~w.; _ ~ w; (n)x(n), j=0,...,K 1.
n=o
CA 02259094 1999-O1-15
Note that p.~ and s~ correspond to the numerator and denominator of the
search criterion due to each predetermined vector.
The search then proceeds with the selection of P vectors among
the K predetermined vectors by maximizing the search criterion Qk (step 606
5 of Figure 6).
Let's first start with the case where two vectors are added from the
random table (P=2). The search reduces to finding two vector indices p, and
p2 among the K predetermined vectors. In case of P=2, a codevector is
10 given by:
c=s,vP +szvPz
The filtered codevector z is given by:
z=Hc=s,HvP +sZHvPz =wP +wPz
Note that the predetermined signs are included in the filtered pre-
determined vectors w;.
For two vectors, the search criterion is given by (the codevector
index k is dropped for simplicity)
X Z 2 ~X'wP~ +x/wPz'Z _ ~pP~ +PPz~2
Z Z (WP +wPz~~(WP +WPz~ EP~ +8Pz +2.WP~'VPz
CA 02259094 1999-O1-15
31
The vectors w~ and the values of p~ and s,; are computed before
starting the codebook search. Then Q is evaluated using two nested loops
for all possible positions p, and p2 . Only the dot products between the
different vectors w; need to be computed inside the loop.
The search procedure is shown in Figure 4. The search criterion
is computed as Q=R2/D. However, cross product is used in comparing the
present Q with the optimum one QoP,, in order to avoid the division inside the
loop; more specifically, testing if Q>QoPt is equivalent to testing if
R2DoPt>RZoPtD.
At the end of the two nested loops, the optimum vector indices p,
and p2 will be known. The two indices and the corresponding signs are then
encoded as shown in Figure 3. The gain of the excitation vector is then
found by
pn~ + pn2
g
D oP~
The case where the codevector is found by adding three vectors
from the random codebook (P=3) will now be briefly considered. The K
predetermined vectors and their corresponding signs are found in the same
manner as described above. The filtered pre-determined vectors w; and
their product with x, p;, and their energies, ~, are found also before
starting
the codebook search. The search then proceeds with finding the best three
vectors among the K predetermined vectors, by computing the search
criterion Q=R2/D using three nested loops.
CA 02259094 1999-O1-15
32
Figure 5 shows the structure of the search in three nested loops
in case of adding three vectors to construct the excitation codevector. At the
end of the three nested loops, the optimum vector indices p,, p2, and p3 will
be known. The gain of the excitation vector is then found by:
pn~ + pnZ + Pn3
g=
D oPt
Once the optimum codevector and its gain are chosen, the
codebook index k and gain g are encoded and transmitted.
As evidenced in the foregoing description, the search procedure
described above is summarized in the flow chart of Figure 6.
The stochastic codebook disclosed in the present invention can
be used alone or in conjunction with a sparse codebook such as an
algebraic codebook. In this case, 1 bit can be used to denote whether the
algebraic part or the stochastic part of the innovation codebook is chosen.
Both parts are searched and a candidate from each part is retained. The
two candidates are compared and the one which maximizes the selection
criterion Q is chosen. A modified selection criterion can be used for
choosing the winner among the two codebook sections, by taking into
account the nature of the current speech signal in the subframe. Criteria
such as the pitch gain, the synthesis filter tilt, etc. can be used to modify
the
search criterion such that to favour the algebraic part of the codebook in
case of periodic signals (high pitch gain and strong tilt) or to favor the
stochastic part otherwise.
CA 02259094 1999-O1-15
33
Other variants of the stochastic codebook are also possible. One
such variant is to have the flexibility of replacing the third random vector,
in
case of P=3, with a single pulse. In this case, 1 bit is needed for indicating
that a pulse is chosen to replace the third random vector. This helps in
capturing special time events in the signal.
Although the present invention has been described hereinabove
by way of a preferred embodiment thereof, this embodiment can be modified
at will, within the scope of the appended claims, without departing from the
spirit and nature of the subject invention.