METHODE ET SYSTEME DE CODAGE D'IMAGES PAR REGION AVEC LECTURE DYNAMIQUE EN CONTINU DE BLOCS DE CODES

METHOD AND SYSTEM OF REGION-BASED IMAGE CODING WITH DYNAMIC STREAMING OF CODE BLOCKS

Description

CA 02261833 1999-02-15
METHOD AND SYSTEM OF
REGION-BASED IMAGE CODING
WITH DYNAMIC STREAMING OF
CODE BLOCKS

CA 02261833 1999-02-15
L 1. Region Based Image Coding (RICS) Design Principles
L1.1. Background
With the rapid growth of the Internet and multimedia applications, there is a
great
demand for new image coding tools that that will provide for high quality
processing
capability, an efficient internal architecture, and flexibility in terms of
future
technological advances. This is a challenge that has been put forth before the
JPEG 2000
Committee. Although the main focus should be to provide state-of the-art
compression
performance, JPEG 2000 should also offer unprecedented content based
accessibility of
the compressed format to support applications of various needs. It is highly
preferred and
advantageous that image content be accessed, manipulated, exchanged, and
stored in
compact form.
In order for JPEG 2000 to be the standard coding foundation of new generation
image
processing systems, it must provide for efficiency in coding, different types
of still
images (bi-level, gray-level, color) with different characteristics (natural
images,
scientific, medical imagery, rendered graphics, text, etc.) within a unified
system. In
addition to providing low bit rate operation with quality performance
superiority to
existing standards, this new system should include many modern features as
listed in the
JPEG 2000 requirement document.
The open architecture and the set of algorithms presented in this document are
based on
Digital Accelerator Corporation's (DAC) Region based Image Coding System
(RICS).
RICS has not only achieved a rate distortion performance competitive with best
known
compression techniques, but also demonstrates a high degree of openness and
flexibility
that will accommodate most well known algorithms as well as new yet to be
implemented. The features supported by RICS covers almost all those listed in
JPEG
2000 Requirements document.
Generality
Generality is a primary concern in the architectural design of RICS. The RICS
architecture attempts to be an integrated platform that supports and
facilitates a variety of
applications that may have different characteristics and requirements. For
example,
providing efficient lossless and lossy compression in a single code stream;
efficient
processing of compound documents containing both bi-level (text) and color
imagery;
progressive transmission by pixel accuracy and/or by resolution; random access
of
arbitrary shaped regions; and so on.
Openness
We also understand that the new JPEG 2000 standard is intended to be a
dynamic, rather
than static, suite of coding tools that support the new generation imagery
applications
and, at the same time, keeping abreast with the progress of technology. The
mathematical foundation for those leading candidates of new image coding
methods
(most noticeably the various types of multi-resolution analysis techniques,
such as
wavelet transforms) is relatively young and still under intensive
investigation. If an
architectural design is based on or restricted to one or several particular
existing coding
methods, it may become outdated very quickly.
2

CA 02261833 1999-02-15
In attempting to produce a flexible and open platform, the RICS architecture
organizes
the image coding process into a set of functionally separable modules, such
that each
module can be developed and optimized individually. Furthermore, all modules
in the
system are designed to be functionally orthogonal with each other, in the
sense that a
new algorithm, without affecting the functionality of other modules, can
effectively
replace the base algorithm of any specific module.
This open architecture will not only be able to accommodate future new
algorithms, but
also makes compatibility with other standards an easy and natural extension of
many
concepts, as will be explained later in this document.
Accessibility
Content based accessibility is becoming an important feature in supporting
applications
such as multimedia database query, Internet server-client interaction, content
production,
remote diagnostics, and interactive entertainment. The content-based
accessibility
requires that semantically meaningful visual objects be used as basis for
image data
representation, explanation, manipulation, and exchange. With images being
represented
in compressed format, it is desirable to perform retrieval operations directly
in the code
space without requiring image reconstruction. In fact, any search algorithms
that require
image reconstruction will be infeasible from a practical viewpoint because of
the huge
amount of images in most image databases. The previous JPEG and many existing
coding techniques focus primarily on the issue of compression ratio, paying
minimal
attention to the need of content based image retrieval.
RICS, by its name, has a fundamental consideration to various types of regions
in images.
The regions referred to as ROI (Region of Interest) are usually user-specified
primitive
geometric shapes, such as rectangles or circles. The regions that define the
visual objects
are usually of arbitrary shapes. Regions can also be generated as the result
of certain
mathematical operations or transform properties (e.g. significance of
transformation
coefficients) used to partition the image into disjoint regions of various
(e.g. tiles,
hierarchical blocks, or arbitrary shapes).
In designing the RICS system, DAC considered carefully the distinction between
the
concept of an object and that of a region. RICS is open to very general
definition of
region. A region is a 2D spatial identity with pure syntactic contribution to
a code
stream. In contrast, an object may contain semantic information. Therefore,
the region is
perceived as a more elementary and reliable description than the object. RICS
is region
based, not object based. RICS supports a rich set of region types, from
primitive
geometrical shapes, tiles, hierarchical blocks, to most general arbitrary
shapes.
The region based coding strategy effectively supports the content-based
accessibility of
imagery data. Specifically, this ability enables random access to the code
stream as well
as providing a processing channel for user defined regions of interest or tile
based
techniques. Supporting MPEG-4 object based accessibility is one of the main
objectives
of the RICS design. Furthermore, region-based coding provides a natural bridge
for
'transcodability' with JPEG and JBIG.
3

CA 02261833 1999-02-15
Scalability
Many applications require image data that is available at different
resolutions or qualities
for decoding. For example, in a progressive transmission process, the bit rate
control
mechanism should allow the image data to be transmitted in certain priority
order, and be
able to truncate the remaining data flexibly, either upon request from the
receiving
terminal or upon channel limitation. Scalable image coding involves generating
a coded
representation (code stream) in a manner that facilitates the reconstruction
of the image at
multiple resolutions or quality levels by scalable coding.
Ideally, the control of scalability should be centralized in a single module
as the last stage
on the encoder side right before the code stream is fed to the communication
channel.
Furthermore, it is desirable that the scalability control module can
completely handle the
required processing locally, without any further request propagating back to
any previous
stages in the encoder. In this way the scalability control module avoids the
need for
mufti-pass computation.
The RICS architecture is designed to support three types of scalability:
scalability in
terms of pixel precision, spatial resolution, and regions.
Compactness
There is no doubt that the new image coding standard should offer a higher
compression
performance than the former JPEG, especially at the low bit rate end.
L1.2. The Fundamentals of RICS
Integrating the compactness, scalability, and accessibility into a general
purpose, flexible,
and open architecture represents a challenge for JPEG 2000. The RICS is
designed to
provide a solution. The basic idea of region based coding is as follows:
~ The input image data, after certain transformation, becomes a set of image
primitives. This set of primitives can be wavelet transform coefficients, DCT
coefficients, other transform coefficients, or even raw image data.
~ The image primitives are grouped into regions. Region definition can come
from
user defined ROI, from other application modules, or from certain automatic
segmentation algorithms running in the primitive space.
~ Each region contains one or more independent coding units (ICU). The
primitives
in an ICU are encoded and decoded independently, without reference to
primitives of
any other ICU. This procedure is called the intra-region coding. The outcome
of an
ICU operation is a code block.
~ A multiplexer (MUX) is employed to integrate the code blocks into the final
code
stream.
L2. The System Architecture
The architecture of the RICS system can be described as the scheme of dynamic
streaming of code blocks. In this design, the image primitives of ICUs
generate unit code
blocks. A code block is a logically independent unit of coding and decoding
which does
4

CA 02261833 1999-02-15
not rely on information contained in any other blocks. Compression is achieved
in each
block coder, and the coding efficiency of the block coders determines the
overall
efficiency of a RICS system. The openness of the system is reflected in the
different
coding algorithms that can be used to produce different code blocks. The
system uses a
multiplex structure (a MUX) to assemble the code blocks into the code stream
and realize
the bit rate allocation. In short, the RICS architecture allows for
flexibility in the areas of
compactness and openness to the block coders and, at the same time, allowing
the
multiplexer to handle the various schemes of scalability and random
accessibility to the
code stream.
It should be noted that the block used in RICS is a logical unit rather than a
geometric
concept. A code block may correspond to an 8x8 tile (in the case of JPEG mode
coding),
a pyramid data structure in zero tree like coding schemes, a rectangular area
in block
based coding schemes, or an arbitrary shaped area in the raw image buffer. The
independence of encoding and decoding is the primary requirement of a code
block. A
code block is the outcome of an intra-region coding.
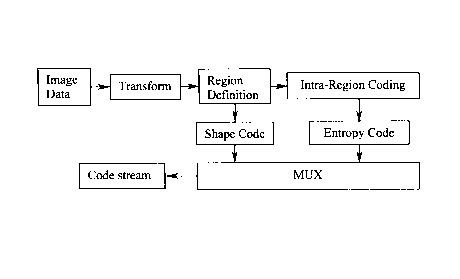
Image Transform Region ~ Intra-Region Coding
Data Definition
Shape Code ~ ~ Entropy Code
Code stream IE--~ MUX
Figure L1. Simplified RICS block diagram.
Figure L I illustrates the simplified RICS coding architecture. A more
detailed diagram is
shown in Figure L2. A detailed description of the function of each module is
given in
this document. Because the RICS is intended to be an open architecture, DAC
does not
limit each module to any specific algorithm. Instead, any individual algorithm
can be
placed into a module as long as it meets the functional requirement of that
module.
Supporting algorithms are included for certain modules, which reflect
preferred operation
of the overall system.
Types of Input Image
As shown in Figure 2, the RICS architecture supports the coding of three types
of image
data: grayscale, color, and bi-level images.
Transformations
In a typical multi-resolution coding scheme, an image is transformed via a
multi-
resolution decomposition process. In the proposed architecture, transforms
such as KL,
wavelet, wavelet package, lifting scheme, etc. can be placed in the
transformation
module. These transforms produce a set of decomposition coefficients {Cij} at
different
resolution levels and in different spatial orientations.

CA 02261833 1999-02-15
The RICS architecture also supports DCT or windowed Fourier transform as a
transformation technique. This is mainly for the transcodability with JPEG. It
should be
noted that the Fourier based transforms have been studied for more than a
century; its
theory is relatively complete and its mathematical and physical properties are
well
understood. Particularly, its translation, scaling, and rotation properties
may be very
useful for content based retrieval computations. On the other hand, wavelet
transforms
are relatively new, and many of its properties require further investigations.
As a result,
the support of DCT may have an impact beyond the sole backward compatibility
consideration.
RICS also allows the NULL transformation (that is, no transformation is
applied at all).
In this case, an identity transformation is applied to the raw image data as
the
transformation step. The NULL transformation is useful in several instances.
For
example, it is usually not beneficial to apply DCT or wavelet transforms to bi-
level
images (text) for compression purpose. Another example is the residual images
in video
coding. The information in a residual image is the difference between video
blocks and
has a high frequency spectral content already. It is highly questionable
whether it is
beneficial at all to apply another mathematical decomposition (DCT or wavelet)
to this
type of data for the purpose of compact coding.
Region Definition
The function of this module is to partition the coefficients produced by the
transformation
module into a number of spatial regions. The RICS supports three region
schemes.
1. Automatic partition based on the preordering of the coefficients.
2. Partition based on user defined ROI or object related shapes.
3. Partition based on tiling.
The first partition scheme is also referred to as the region hierarchy
formation process.
Consider the transformation coefficients as a set. The region hierarchy
formation process
partitions the set into a number of hierarchically disjoint subsets according
to certain
definitions of significance. In providing a very general partitioning
technique captured in
a very general region based control architecture, RICS can perform highly
flexible
progressive transmission modes of operation that depend on data priorities set
up for the
code stream.
Scheme 2 deals with user specified ROI, typically primitive geometrical
shapes, such as
rectangles or circles, as well as object related shapes. Object related shapes
could come
from a variety of sources, such as user input, motion analysis in video
compression, etc.
Scheme 3 is a simple partition and requires minimal for shape coding. This
scheme is
essential in the JPEG mode. Some wavelet based compression techniques utilize
this
scheme to explore coding efficiency. This scheme offers very little support
for content
based accessibility.
6

CA 02261833 1999-02-15
...
t.!
bA a O
~, CI
~
.
G~
~ ~
~ ~
~
~
GY",~ . O
~ U _ ~ _ V _
",
a
' ~f ea
. ~
~ C W
~
~
o
v
s
ev
~
s.
~
~~
~
~,.
~a
~ ~, ~aN~p
i~ V i
~
~
~n
"C
'fl~1 o
a ~~
'~
o
~ i
~ x
8 0~ "~~
~
A~8 '~ ~
' "
~ ~ p40 '
N ~
,=.~
W
W
v
~
a 4 ~o~ c~
' ~
, W i ~ .~ ~ ~~y
i ~ ~
.
~
.
~
.
3 ~ a ~ ~ w ~~ ~ ~ v
~ A
A z o ~ ~a~ o
V . ~ i C~
~ ~
G~ Cat
0
i
G p
~ v ~ ~ W
~
.,.
O
p bA . r.#
w i~ ~ b
~ A a
... .
i
w
~. ~ a o o b
~
~
pA ~ ~ , ~ o
" i
p a U
e~.
~
o
~
e
a
o o G7 ~
~ O W
v
~
. . as
riw' ~ >
~da.

CA 02261833 1999-02-15
Hierarchically disjoint regions can be used in combination with user defined
ROI in still
image processing and objects in video processing. However providing a fair
user
partition for detail information is difficult in still image compression. But
automatic
partitioning or preordering techniques can be performed to control user
selections in both
arbitrary and block based modes of operation. The research presented in this
document
introduces a new multi-level control architecture for advanced multi-level
image
processing. The ability to perform a host of partitioning and preordering
techniques in
both normal and region based modes of operation is encompassed in this
architecture.
Both arbitrary and automatic region formation schemes are handled in the same
manner
at a high level.
Region Shape Coding
Three types of region shape are supported in RICS: tiling, primitive geometric
shapes,
and arbitrary shapes.
1. Tiling requires only a small set of parameters to describe the
configuration especially
in sequence based processing modes. However the sequences can be organized and
presented in many ways in packing them into the final code stream.
2. Primitive geometrical shapes can also be coded efficiently. For example, a
rectangle can be defined by four integers (xm~~, ymin) and (xma~ ymax), or
(xmin5 ymin)
and (width, height) etc.
3. Arbitrary shapes are more difficult and costly to encode. Partitions
produced
automatically by image analysis algorithms may contain many small regions.
Specifically, the auto-region detection routines presented here produces
hierarchically
organized data partitions. This presents a highly challenging problem for
shape
coding. RICS provides two practical solutions to this problem. One is a quad
tree
based hierarchical region description. This mode of operation follows bit
level
ordering at different resolution levels (see embedded quad tree wavelet (EQW)
in Ch.
4.) The other is a DCT coded mufti-level region channel definition followed by
preordering the partition (given the restraints of the code stream in terms of
overhead). Though the coding efficiency of the second solution is currently
slightly
poorer than the first, it does contain a number of attractive features:
~ It provides a single representation for mufti-level bitmaps.
~ From this single representation, region masks can be reproduced at arbitrary
resolution levels, which is useful for subband coding.
~ It generates curved shapes, which potentially (e.g. in case of large number
of
complex curved regions) could outperform quad tree based region descriptions.
~ It has several useful properties, such as translation and rotation
properties, which
the quad tree based description does not offer. In fact, a quad tree
representation
will change dramatically if an object is slightly translated in the image,
making
this type of representation not suitable for content based retrieval
applications.
However, the main advantage of the quad tree representation is its simplicity
and
most noticeably in block based modes.

CA 02261833 1999-02-15
The region shape code is included in the code stream when the region
definition is
determined at the encoder. In the case of decoder specified regions, the
region shape
coding has a whole new meaning.
Intra-Region Coding
The function of the intra-region coding is to arrange the transformation data
in an
arbitrary shaped region into a one dimensional code stream. Regardless of the
region
definition scheme or the region coding technique, this streaming process
requires an
intermediate state where a control architecture can be designed to tailor the
region
channels whether dealing with a bitmap mask, an auto-detection routine or any
other of
numerous classification techniques. At the decoding end, the inverse routine
generates
the same mask to unpack the values from the one dimensional code stream and
place
them back into the correct position in each region.
Intra-region coding is completed in block coders. Different block coders can
be used to
produce the 1D code stream. For JPEG mode, the zigzag scanning/quantization
routine is
called to pack an 8x8 DCT block. For wavelet based coding, both explicit
quantization
and implicit quantization schemes can be used. In particular, embedded zero
tree and
embedded quad tree can be used as implicit quantization schemes. Furthermore
most
implicit quantization schemes are implicitly decodable. In dealing with bi-
level images, a
JBIG routine can be called a block codes. This effect can be staged by calling
an implicit
quantization scheme using one bit plane. Alternatively, efficient JBIG
routines can be
called block coders in an embedded coding scheme at each of the multiple bit
planes.
MUX (The Multiplexes)
The function of the multiplexes is to assemble the code blocks derived from
different
subbands and different regions in proper orders into a single code stream. Due
to the
richness of region definition and block coding schemes, there are plenty of
ways to pack
the code blocks. Different ways to merging the data lead to different
transmission
priorities. For all transmission ordering modes, the final code stream can be
transmitted
progressively, and can be truncated at any desired place.
The notion of using a multiplexes has been adopted in some standardized
processes such
as MPEG. In contrast, the use of a multiplexes in the design of a still image
coding
system is rare. The region based coding strategy opens the opportunity to
systematically
explore the syntactic and semantic richness in code stream ordering and
transmission
medium. With the image segmentation techniques improving in the future, region
shapes
will become more accurate in tracking objects in the image. In that case, the
multiplexes
will not only work as a syntactic composer, but also impose semantic meanings
to the
code stream.
L3. Highlight of Features
The RICS is a true open architecture. It supports not only the algorithms DAC
has
developed, but also can accommodate most existing well known compression
algorithms.
Users may include their own functions that are appropriate to their
application in a
number of modules such as transformation, region definition, region shape
coding, and
9

CA 02261833 1999-02-15
intra-region coding all under the MUX control architecture. It is also
implicitly flexible
to new technological advances.
~ DAC's current implementation offers superior low bit rate performance that
is
competitive with best existing compression techniques.
~ The richness in region definition in the RICS allows great accessibility,
thus
providing a solid foundation for content based image applications.
~ It covers compression for both continuous tone and bi-level images in a
single unified
architecture.
~ It provides lossy and lossless compression in a single, natural, code stream
in the
course of progressive decoding.
~ It provides a variety of progressive transmission modes that allow images to
be
reconstructed with increasing pixel accuracy or spatial resolution using
region priority
modes for user specified ROI or system defined significant areas.
~ It supports both fixed rate and fixed size modes.
~ It supports very flexible random access to and processing for regions with
arbitrary
shape.
~ It provides a graceful backward compatibility (or transcodability) with
JPEG.
~ The generic region definition in RICS is a very suitable interface for
object-based
coding schemes currently under development by MPEG-4. (In fact, as the
arbitrary
region shape begins to fit dynamic objects with more accuracy, motion
estimation is
more definite, and consequently allows for more efficient error compensation
using
region-based coding.)
~ Our general region shape definition provides a solid basis for object based
composition and object based information embedding. Multiple objects with
arbitrary
shape are accepted.
~ Our bit stream is robust to bit errors. Each unit structure used by the MUX
is
independently decodable.
~ Incorporating standardized encryption techniques with the RICS system is
straightforward.
1o

CA 02261833 1999-02-15
II. Transforms
In order to support multiple application needs, provide transcodability, and
accommodate
future growth, the RICS architecture is designed to support three categories
of
transformation: the DCT, wavelet transforms, and a special NULL transform.
IL1. DCT
The RICS architecture supports the DCT transforms as defined in the baseline
JPEG.
IL2. Wavelet Transform
The RICS architecture supports various kinds of subband decomposition schemes,
including the three schemes in Figure IL 1.
IL3. NULL Transform
In dealing with the compound documents with mixed contents, it is sometimes
required
to encode some areas of the image without any transform. In particular,
regions with bi-
level pixels usually do not need to be transformed for coding purpose. In
coding these
regions, the transform stage is bypassed; the effect is simulated by a NULL
transform
stage in the process.
mallat spacl packet
Figure IL1. Subband decomposition schemes.
The present version of RICS uses totally 34 types of wavelet kernels as given
in Table
IL 1. In our experiments, the biorthogonal filters (Bior9-15 of the table)
seemed to give
the best compression. Both low pass filtering and high pass filtering are done
using
convolution. After filtering, the wavelet coefficients are down sampled by 2.
This
process is repeated using the low pass part until the desired decomposition
level is
reached. In inverse wavelet transform, quadtrature mirror filters (QMF) for
low and high
pass are used. Then the coefficients are up-sampled by 2.
11

CA 02261833 1999-02-15
Wavelet Wavelet Typelter h )
~ ( Fi Lengt
Family
Ila<t,=_____-_--~~aar -______-______ -____ T__.___________-__.____T____-_
I I
Daubechies Db4 ~ Uh6 -pb8 Db Db Dh I)b ___
10-._-I 14 I t,
2
_-__ ('t) _ ~O') (g) (t0) (I'?)-_(14j (16)
_ ! _ - _ _ -_
_ -._
_ _ -
Coifle Coifl t C,oif4 - -
C,oif2 C.oit~3
(~) (1') (1~) (~4) _
__ _
_ _
Symmlet Sym? ~;ym3 Sym4 SymS Sym6 Sym7 Sym8 ____
~'~O O~) ( I ( I ( 14) ( 16)
(f') ()) 2)
_-__._~ ____- - _-_ l3ior2.2_ _ _ l3ior5.S
l3ior-thogonal_ E3iorl.5 t3ior3.l__ (3ior4.4
~ t3iorl.l E3ic>r3.3
l3iorl.3
_ _~ (~) _ (6) (I~) _(~) (4) (~) (I~) (I?)
_ ~
E3iortho~onalt3ior9 RiorlOl3iorl __ Riorl3-I3iorl4_
! 1 I l3iorl2_ -3ior15
! (W llascnor)(10)9/7.~(I-~)-(Il)) Lf~__-_W~ (IO) _t(l/l~-._____
~ - __ -_
Table 11.1. Wavelet Filter Library
II.4. Color Transform
In addition to YlIV format, the RIGS system uses the Itarhunen-Loeve
'hransform for
color transformation. Fotlowin~; the notation of statistics we term this
process as the color
stcttzdardi,.atiort. 1'he KL. color transform requires more computation than
YUV
transform. Figure II.I shows the PSNR comparison of the two color transforms.
More
test results are also available from I)nC'.
1M M' 1 Stanc~rcfuired ('nlwr
I?
Figure 11.1. Performance Comparison of YtJV and Standardized Color Systems

CA 02261833 1999-02-15
III. Region Definition and Shape Coding
The notion of region processing plays a fundamental role in the operation of
RICS. The
choice of region based coding is motivated by many application needs such as
content
based retrieval, interactive multimedia application, graphics object and image
composition, and coding of dynamic object in video compression.
There are two fundamental issues in a region based coding strategy: defining
regions and
coding the regions. In the RICS system, region coding is divided into the
shape coding
and the intra-region coding (the content coding). Section 3, describes the
various
schemes for region definition and shape coding. The intra-region coding is
discussed in
Chapter IV.
From the viewpoint of JPEG 2000, the process of region definition does not
have to be
standardized. However, schemes for forming regions that the JPEG 2000 will
need to
support should be defined clearly. The RIGS supports three types of region
definition.
~ Tile based organization
~ primitive geometric representations
~ arbitrary shapes
Region definition is an optional step: an image can be coded without
specifying any
region (the non-region mode). In this case, the entire image area is
considered as a single
region.
IIL1. Tiling: Definitions and Shape Coding
Tiling is perhaps the simplest region definition scheme. In this scheme, the
entire image
area is divided into a number of rectangular blocks. In particular, 8 by 8
tiles are used in
the JPEG coding mode. Most tiling approaches cannot cover the natural shapes,
region
trends or partial objects in a picture.
For coding a tiling scheme, a small set of global parameters will be
sufficient. The
primary parameter is the size of tiling block and the technology is developed
around this
theme. In case of subband decomposition, tiling block size may vary from one
subband
to another. However, the RICS architecture has a sound operational foundation.
It can
be operated in both tile based or arbitrary processing modes of optional
arbitrary region
formation schemes.
13

CA 02261833 1999-02-15
IIL2. Primitive Geometrical Shapes
Primitive geometrical shapes are ideal for supporting user interaction; i.e.
user specified
ROI, and for processing compound documents where the text areas can be well
covered
with one or more rectangular boxes. Geometric shapes currently supported by
RICS are
listed in Table III.1.
Sha a Codin Parameters Availabili
in RICS
Rectangle/Square(,x min, ymin) and (width,present
height) etc.
Circle/Ellipse (XO, ,yo) and i" etc. present
Polygon n ~ (~~ y~) ~ (,x2, _y2)Under development
,.. (Xn, .yn)
Cubic parametricn ~ (~~ ~) ~ ~x2, y2) Under development
curves .. , (Xn, yn)
Table II1.1. Geometric Shapes Supported by RICS
IIL3. Arbitrary Regions and a Generic Binary Partition Hierarchy
Let Co be the set of image primitives. Given an ordering relationship ~- ,
generic
binaries partition of Co into C,o and C" is defined by the following
conditions.
( 1 ) C~ o U C> > = Co
(2) C,o n C" _ ~ , and (Eq.IIL l )
(3) for any a E C,o and b E C~~ , a ~ b holds.
Recursively, each of the new generated subsets can be further partitioned into
two
subsets, resulting in a hierarchical structure to represent the partition (see
Figure III.1.)
............ ........................
Figure IIL1. Hierarchical partitioning
A useful ordering relation popular in the compression community is "more
significant
than": a ~ b whereby a is more significant than b. The definition of
significance can be
very general. One definition may be used to create an ordering, or several
definitions are
combined together to generate an ordering. This can be illustrated by the
following
example shown in Figure IIL2. Suppose the region masks shown in the leftmost
image
are generated by considering the magnitude of wavelet transform coefficients
as the
measure of significance. The region mask in the middle image is an object
shape
14

CA 02261833 1999-02-15
generated by another detinitiron of importance that, for example, can be the
intensive
dynamic region in a video frame. 'l~he rightmost image shows the intersection
of the two
region masks. which is a new region partitioned according to a multiple
definition of
signi f icance.
Rcgiun h9 ask Dy nnmic ()hject Ialracled Dynamic Regions
Figure 111.2. Relationship between regions and objects
As an example, if the significance is measured by magnitude of wavelet
transform
coefficients, then the ordering relation is simply the numeric ">" relation.
ho create a
binary partition, a set ot~thresholds is sufficient. The first threshold. say
7~,, separate the
initial set t'r, itlto two subsets. ('", and ('~~ . subsequent threshold
values can be
specified to recursively partition the new subsets.
~fhe above partition scheme produces accurately a number of disjoint subsets
which
satisfies the strict ordering relationship of ~-. however, it usually produces
many small.
scattered regions. Consequently. the representation of region shapes for these
subsets can
be potentially expensive. f''rom the representation point of view , fewer
numbers of
smoothly shaped regions are desirable. In the following, a less strict
partition scheme is
defined, which takes the ahovc partition scheme as a special case.
Instead of requiring the condition a ~- h to be held for all a E t'", , h E
C'" , it is replaced
by a looser condition
-,h ~ ('~ , h ~ a, for any cx E C'r, . (Ej,d.Ill.2)
Intuitively speaking, this definition defines a partition in which no element
in (',
proceeds any element of ('" . Its other words, some elements belonging to (',
(by
Eq.III.I ) may now be placed i.n ('" , but, no element belonging to ('r, ('~
(by Eq.Ill.l )
can be placed in ('~ (Iq.IlI.2 j. In doing so, the subset ('" will be
enlarged, and the
region shape of ('" will be smoother. At the same time, the enlargement of ('"
is
controlled to such an extent that the loss of classification accuracy is
limited to a
reasonably low level.
Another scheme, which is symmetric to the Eq.IlI.2, can be defined similarly
for the
following condition.
-,cr ~ ( '" , cr -~ h , for any h E C.', . (h;q.I11.3 )
I;

CA 02261833 1999-02-15
In this case, we ensure that no element in Co is proceeded by any element in
C, .
It should be pointed out that there is a tradeoff between the enlargement of
Co and the
space requirement for the region shape representation. It is possible (and
indeed quite
often) that there are some isolated scattered points that belong to Co . But,
in order to
exclude those isolated points from C, , we have to sacrifice many elements
from C, .
This will result in a very large Co , a degraded classification. An
approximation to the
scheme of Eq.IIL2 is introduced to rectify this problem. A small number of
elements in
Co are allowed to be "misclassified" into C~ . Those misclassified elements
can be
separated later in the infra-region coding stage that generally follows
natural processing
orders available for further classification of the partitioned elements.
When such region hierarchy formation schemes are applied to image primitive
planes,
they serve as preordering processes that set up a partial ordering among the
primitives.
Then, the problem of coding this ordering becomes a geometry problem for
coding the
shapes of the partitioned regions. Transformations such as wavelet are known
to use a
joint spatial/frequency domain methodology. The region hierarchy formation
scheme
mentioned above has an intuitive geometric explanation for this class.
Transformations
such as DCT and Fourier transform are purely frequency domain methods. It is
interesting to note that when the above partitioning scheme is applied to a 2D
DCT
transformation plane, the generated regions are roughly circularly shaped
bands. The
popular zigzag sequence used in JPEG turns out to be a simple and reasonable
approximation of these bands. Therefore, the region based coding strategy
accommodates naturally both spatiaUfrequency domains and pure frequency domain
transformations.
IIL4. Automatic Region Formation in the Wavelet Transform Domain
DAC has developed an automatic region formation scheme that is used to
categorize
wavelet coefficients in the transform domain according to magnitude. The
procedure will
be outlined in the following sections. Also included are many of the design
details used
to develop the first version of the general region classification scheme. The
advantages
and disadvantages of the technique as well as performance and overhead issues
will be
discussed. Finally conclusions will be drawn to summarize the results.
IIL4.1. Detecting the Regions
The wavelet transform is used to decompose the original image information into
a multi-
resolution hierarchy of data that is more suitable for compression. The result
of
completing one pass of the 2D wavelet transform is one low pass part (LL i )
and three
high pass parts (HL~, LH1 and HH~.) The transformation procedure is repeated
using the
low pass LL part as the starting point for each succeeding pass. The LL part
is an
approximation of the original image at a lower resolution. At each resolution
level the
HL parts carry the vertical, the LH parts carry the horizontal and the HH
parts carry the
diagonal edge information. The level of detail information contained in any
particular
orientation is specific to the local response generated in the choice of
wavelet kernel.
16

CA 02261833 1999-02-15
The original image is transformed into a unique band pass response hierarchy
of detail
information. In any compression process, it is the highest energy coefficients
that are
considered first for making a contribution to the reconstructed image. It is
this
transformation property that is used to partition the coefficients into
regions of interest
corresponding to high energy locations in the original image space.
The magnitude of the coefficients in a particular subband is related to the
response that
the original image information has to the transform kernel. Sharp edges in the
original
image (or a lower resolution LL part) are indicated by an increased kernel
response in
terms of coefficient magnitude, in the general vicinity of a specified area of
concern.
Other image changes that are not as abrupt will translate into a gradual
response that is
less significant. In those areas where little or no change occurs, the wavelet
transform
will indicate little or no response.
IIL4.1.1. Level 1 Kernel Response Threshold Images
DAC's automatic region formation scheme makes use of coefficient magnitude
information to categorize the data. The starting point for the procedure is at
the highest
resolution level of the wavelet transform hierarchy looking at the three
detail data sets
(HL~, LH,, HH;.) A 2 bit representation of each detail orientation for a 256
by 256 Lena
image is given in Figure IIL3. These images are obtained by using threshold
values to
categorize the coefficients by magnitude. The wavelet kernel used in this case
is the
standard 9-7 filter set implemented in a lifting scheme.
Figure IIL3. Threshold Masks obtained from Level 1 Lena Wavelet Decomposition
A decaying histogram procedure is used to determine the threshold values in
each case.
In this particular analysis the coefficients are partitioned into regions
according to
decreasing levels of magnitude; 10% of coefficients are partitioned into
region 1, 1 S%
into region 2, 25% into region 3 and 50% into region 4. Note that the largest
coefficients
appear darker in the images while the smallest appear lighter. The threshold
values are
calculated automatically for each orientation. The values used to generate the
partition in
each case are given in Eq.IIL4 (assume C; is the magnitude of the coefficient
under
consideration.)
17
HL, LH, HH,

CA 02261833 1999-02-15
HL~:O__<C;<2,2<_C;<4,4<_C;<8andC;>_8
LH~: 0<_C;<3,35C;<5,5<_C;<l4andC;>_14 (Eq.IIL4)
HH~:O<_C;<2,2<_C;<3,3<_C;<SandC;?5
The set of threshold images appearing in Figure IIL3 is motivational in
determining a
region formation scheme based on this approach. It is apparent that wavelet
coefficients
can be classified in this manner to form a mask. However, the large overhead
required to
code each individual mask must be solved in order to make this type of
classification
scheme viable for implementation.
IIL4.1.2. Formation of the Raw Common Mask
The first step taken in the development of a technique designed to reduce the
mask
overhead is to consider a common mask approach that can be used to capture the
most
important coefficients between all three orientations at the lowest resolution
level. Given
that the data range is different in each orientation, the data is normalized
to the largest
range in an absolute value sense. This step is taken in order to compensate
for the range
differences that exist between the data sets, and to ensure that corresponding
pixels from
each orientation can make an equal contribution in the formation of the common
mask.
This step is illustrated in Eq.IILS.
HL', = NewRange(HL,) = ScaleRange(MaxRange(LH,, HL~ , HH,))
LH', = NewRange(LH~) = ScaleRange(MaxRange(LH,, HL~ , HH~)) (Eq.IlLS)
HH', = NewRange(HH,) = ScaleRange(MaxRange(LH,, HL, , HH,))
Once the data ranges for the smallest two sets have been scaled to that of the
largest, the
common mask values can be determined. The next step is to generate a new
normalized
data set by taking the maximum value between scaled orientations at each pixel
location.
Let C'(i) be the new coefficient obtained in this procedure and let C',-IL1 ,
C LH1 ~d C~HH1
be the individual scaled values from each orientation. The new data set is
formed using
the step illustrated in Eq.IIL6.
C'(i) = MAX(ABS(C~HLyi)), ABS(C'HLOI)), ABS(C',iLyi))) (Eq.IIL6)
The final step in forming the common mask is to threshold the new coefficients
based on
the histogram decay and the percentage of the total data amount to encapsulate
in each
region category. The same values mentioned earlier are used in this case (10%,
15%,
25% and 50%.) The raw common mask categorization image appears in Figure IIL4.
The threshold values used to generate the mask are given in Eq.IIL7.
H'1: 0<_C;<5,5_<C;<11,11_<C;<26andC;>_26 (Eq.IIL7)
Note the level of detail contained in this image. High frequency edge
information
representing the most important coefficients appears in the darkest areas. Low
frequency
changes representing areas of the image that are relatively uniform appear in
the lightest
areas. The combined kernel response from each orientation follows the high
energy areas
that exist in the original image.
18

CA 02261833 1999-02-15
Figure IIL4. Level 1 Common Mask Obtained by Thresholding the Combined Data
Set
IIL4.2. Common Mask Conditioning Using the DCT Method
Generally, the raw size overhead of the common mask obtained in the previous
section is
still too large to be included in the final bit stream for most image
processing needs (i.e.
an overhead of 2 Bpp for this particular 4 region mask). This section outlines
the next
step in the automatic region formation scheme. The DCT transform is used to
reduce the
overhead size to an acceptable amount.
The DCT is not applied directly to the common mask data in its mutt-valued
form.
Rather it starts by considering each region contained in the common mask as an
binary
data set such that the sum of the individual data sets is equal to the multi-
valued mask in
functional form. The DCT transform applies the transform of the sum of
functions in the
same manner as taking the transform of each individual function and summing
the
results. Furthermore there are unique spectra in each case that should be
considered
separately for a fully integrated analysis. The individual region masks
obtained by
decomposing the raw common mask for the Lena image appear in Figure IILS.
Notice
that although there are only three images, the fourth region channel (the
background) is
implicit.
Figure ILLS. Individual Region Masks Obtained by Separating Raw the Common
Mask
I9
R1 R2 R3

CA 02261833 1999-02-15
The 2D fast DCT algorithm is used to transform each binary data set into the
frequency
domain for spectral analysis. The spectra for the upper three regions appear
in Figure
IIL6. Please note that a log scaling of the coefficients is used in the images
to exaggerate
the appearance for display purposes. Notice how the low energy content is
dispersed
through the spectrum in each case. Even at such low energy levels, the energy
is
localized in some areas.
Figure IIL6. Individual Region Masks Obtained by Separating Raw Common Mask
It is apparent from the spectral results of Figure IIL6 that the magnitude of
the DCT
coefficients decreases rapidly in moving down each spectrum. The interaction
of the
content retained for each partition is used to guide the classification
procedure. The
interrelationships that exist in each binary spectrum must be investigated
further.
A plot of the overall summed spectra in short integer format appears in Figure
IIL7. The
conventional zigzag ordering is used to re-group the coefficients before
quantization.
Note that only the first half of the data in reflected in the plot. The outer
8K are omitted
since they do not change much from the DC level.
MapHtstde vs. Dia=anal Position
32768
2457 6
16384
8192
0
-8192
-16384
-2457 6
-32768
Diag~al P~ition
Figure IIL~. Spectral Magnitude of Zigzag Spectrum as a Function of Position
R1 R2 R3

CA 02261833 1999-02-15
The first consideration observed in the plot is that the coefficient magnitude
deteriorates
at an alarming rate over a relatively small number of coefficients in the
first portion of the
spectrum. The second observation is that most of the spectral energy is
concentrated in
the first 12% of the data. Together these observations suggest that
implementing a low
pass spectral filtering stage, followed by careful quantization will reduce
the amount of
data that must be retained to capture the region formation concepts at the
lowest level ( in
this common mask partitioning scheme). Note the apparently large do offset.
Part of this
level is introduced by scaling the original wavelet data sets to a unified
range. The rest of
the offset is due to the DCT transform.
IIL4.3. Low Pass Filtering the Common Mask Spectrum
The total mask spectrum must be filtered carefully to reduce the excess
content that has
little contribution to the region trends that exist in the retained
coefficients. The main
concern is to determine how to quantify the filter size such that a dynamic
implementation may be obtained that will work accommodate any arbitrary image
sizes.
The first step taken towards finding a dynamic solution to this problem comes
from
experimentation. In looking at the result of using zigzag ordering,
coefficient magnitude
and significance deteriorate at some exponential rate. Experimental evidence
suggests
that as the size of the original image increases, the number of coefficients
that must be
retained to construct a similar quality mask increase on a logarithmic scale.
This is an
important observation since doubling the original image dimensions translates
into a log
2 increase in the number of retained spectral coefficients.
Assume that (3 is a general log base to begin our discussion. If the filter
size for an N by
N common mask spectrum has been determined experimentally as ~N, then what is
the
size of the filter for a 2N by 2N mask spectrum? If the unknown filter size as
~2N, then
the following simple logarithmic relationship can be used to compute the new
filter size.
128
- l.Ogp (~N ~ ~2N)
256
(Eq.III.B)
»Z
~2N - ~N
A number of experiments were conducted to determine a reasonable filter size
that can be
used as a base for filtering common mask spectra. It has been determined that
for masks
of size 128 by 128, a filter size of 40 to 45 diagonal rows yields reasonable
results. Table
IIL2 give the filter sizes for raw mask sizes using 1.375 for Vii. The
logarithmic base
~i can be used for final calibration in the current design implementation.
Notice the filter size specified for a common mask spectrum of 32 by 32 is
given as 32
diagonal rows. This value is selected to calibrate the filter sizes for the
larger data sets.
The results indicate the filter size required for a first cut of the common
mask coefficients
does not have to be exact since the distribution of the spectral content may
change
slightly from one image to the next. However, it must be large enough to
capture the
majority of the most important spectral content for each region partition.
21

CA 02261833 1999-02-15
Common Mask DimensionS ectral FilterIncluded S ectral
Size Coefficients
32 x 32 32 528
64 x 64 38 741
128 x 128 44 990
256 x 256 52 1378
512 x 512 61 1891
1024 x 1024 71 2556
Table IIL2. Common Mask Spectrum Filter Sizes and Captured Coefficient Numbers
IIL4.4. Spectral Quantization Techniques for Filtered Coefficients
DAC has developed two techniques for quantizing the filtered mask spectrum.
The first
approach is basically a modified uniform quantization procedure that is used
to verify the
concepts. It proved useful in confirming the algorithms and developing the
concepts, but
it lacks robustness and flexibility. The second technique is a general
approach that is
much more robust and elegant. It is dynamic since it tracks the magnitude of
the spectral
content in determining how to quantize the coefficients.
IIL4.4.1. A First Quantization Approach
The first approach combines the filter dimension determination into the
quantization
procedure. A base mask size of 128 by 128 is use as the starting point in this
approach.
Assuming that a logarithmic relationship exists for coefficient importance
along the
diagonal order, a quantization technique can be developed to exploit the
relationship.
The main premise is that there are bands of spectral coefficients that can be
used to guide
the quantization procedure. The importance of the coefficients in each band
decreases
along the spectrum. This concept is illustrated in Figure IILB.
I
and 2
3
Band 4
Note: Coefficients arranged in
zig-zag order from upper left.
Figure II1.8. Coefficient Banding Concept Used to Quantize the Common Mask
Spectrum
The number of diagonal zigzag rows to include in each band is a function of
the filter size
and the original common mask size as well as the spectral content. As a first
approximation, a table look up technique is used to determine the number of
rows to use
in each band. The base band sizes determined experimentally to give reasonable
partition
and reconstruction results for a 128 by 128 mask are given in Table IIL3.
22

CA 02261833 1999-02-15
Band Diagonal Included Spectral
Rows Coefficients
1 3 6
2 6 39
3 12 186
4 24 804
Table II1.3. Quantization Band Sizes for Common Mask Spectrum of size 128 by
128
Notice that the number of diagonal rows doubles in each step. The number of
bits
selected to quantize each band decreases from one band to the next in the
following
fashion.
~ Band 1: 16 bits
~ Band 2: 10 bits
~ Band 3: 8 bits
~ Band 4: 8 bits
A series of band sizes were found experimentally of mask dimensions by powers
of 2
increments. The results are in Table IIL4. These values are used to partition
the spectral
content for quantization. This information together with the number of bits
used in each
band and the filter size measurement determines the common mask overhead of an
image.
Mask S ectrum Band 1 Band 2 Band 3 Band 4
Size Rows Rows Rows Rows
32 x 32 1 2 4 8
64 x 64 2 4 8 16
128 x 128 3 6 12 24
256 x 256 4 8 16 32
512 x S 12 5 10 20 40
Table IIL4. Spectral Quantization Band Sizes for Other Common Mask Sizes
The mask overhead based for this quantization scheme is tabulated in Table
IILS for the
corresponding image sizes. There is an additional overhead header included in
this result
for mask reconstruction on the decoder side. Note that the mask overhead is
the same
size for both grayscale and color images since it is generated from the
intensity
information. However, the percentage overhead in the color case is reduced by
a factor
of 3 since it can be distributed over 3 channels.
Ima a Size Ima a Size Mask Overhead Mask Overhead
ixels b tes b tes
64 x 64 4096 546 13.3
128 x 128 16384 764 4.6
256 x 256 65536 1021 1.6
S 12 x S 12 262144 1420 0.5
1024 x 1024 1048576 1948 0.2
Table IILS. Mask Overhead for Grayscale Images
23

CA 02261833 1999-02-15
After applying the inverse DCT on the quantized coefficients a low pass
approximation
of the original common mask is obtained. It is this result that is used to
guide the region
channels in classifying and processing the wavelet coefficients. The result
indicated in
Figure IIL9 is obtained by applying this technique to the first wavelet
transformed level
for a 256 by 256 Lena image. From Table IIL4, the overhead for this mask is
1021 bytes.
Figure IIL9. Low pass Common Mask Approximation for general coefficient
classification
Notice the high energy changes have been eliminated by low pass filtering
(especially the
changes that occur over small portions of the image). However, the mask does
succeed
in capturing most of the essential parts of the original image. This mask is
common to all
orientation at this level and used to partition the coefficients into region
categories.
IIL4.4.2. A Second Quantization Approach
There are some apparent problems with the underlying procedures used for
quantization
in the first approach. The first of these is that the coefficient band
classification is fairly
rigid and not that flexible. The filtering and quantization stages are tied
together and
fully independent. Affecting one parameter has consequences to the other. It
is true that
a logarithmic relationship exists in the spectrum that can be exploited to
determine a
reasonable filter size, but the quantization step must be tailored from the
filtering stage.
DAC is currently implementing another quantization scheme for mask filtering
that is
much more dynamic and flexible. Quantization is no longer tied to the
filtering stage and
the coefficient banding technique of the previous approach. The current
technique
follows the actual content of the spectrum in forming quantization categories.
In this
way, coefficients are grouped into categories according to the energy gradient
of the
spectral distribution. The concept is illustrated in Figure III.10.
The rate of spectral decent together with position information within the
spectrum can be
used to quantize the number of bits used to categorize the data. This process
can be
controlled precisely. The procedure can be calibrated as required by studying
the effects
of changing image dimension in terms of an optimal quantization change.
24

CA 02261833 1999-02-15
Quanti~tion Intervals
Spectral Peak Magnitude Curve
U
Diagonal Location
Figure IILIO. Mask Quantization following the Spectral Content for Bit
Allocation
The previous quantization technique can be used to estimate the mask overhead
for the
new scheme proposed here. Consider the same base conditions presented for the
banding
approach applied to the 256 by 256 Lena image. The spectral filter size in
this case is 44
diagonal rows. If 4 quantization intervals are used at 16, 12, 8 and 4 bits
each the mask
overhead can be estimated. Let N; be the number of coefficients in each
interval, b; the
number of bits used to quantize this interval, and OM be the total mask
overhead. A
rough estimate of the new packed size is calculated in Eq.IIL9.
OM =~ N;.b;
i -° (Eq.IIL9)
OM =6x16+39x12+186x8+804x4
OM = 5268 bits (~ 659 bytes)
Even though the actual overhead has not yet been determined, from the insight
gained in
using the first quantization approach a saving of 30% is not unreasonable.
This promises
to be a substantial saving in the mask overhead. There are ways to utilize
saved
overhead. The first is to reduce the amount of mask information in the code
stream. This
approach will retain the same mask quality leaving extra space for refinement
information in the code stream. The second way to utilize the saved overhead
is to retain
a better quality mask in keeping the overhead size constant.
IIL4.5. The Common Mask and Multi-resolution Classification
A translation technique is required to apply the region mask at other
resolution levels.
The simplest approach is to look at the significance of the mask coefficients
in a small
block to determine an appropriate value for the next resolution level. This
process is
repeated until a mask for each resolution is obtained. The most logical
approach is to
take the largest coefficient through to the next level.
NIv(L+1)i,j -~x~(L)Zi,2j ~ ~(L~i+1,2j ~ ~(L~i,2j+1 ~ ~(L)Zi+l,Zj+1) ~Eq.IILlO~

CA 02261833 1999-02-15
Some heuristic approaches have been investigated for resolution translation.
One
approach is to make decisions based on the sum of the individual mask
coefficients. The
upper level masks are affected by either enlarging or shrinking the
encompassed coverage
regions. However, there is currently no conclusive evidence confirming the
validity of
this approach and more experimentation is required.
It is worth mentioning at this point, that DAC has begun investigating the
wavelet kernel
ROI mask formation technique of verification model (VM) 3.0 as a method of
resolution
translation for other transformation levels. Preliminary investigations
indicate this
technique introduces a gradient bias for regions of higher classification
level in the
translation. A combined hybrid approach may have some advantages.
The rest of the common mask hierarchy obtained by using the simple 4 to 1
resolution
translation techniques and observing the most important region as key is given
in Figure
III.11. The complete set of region masks is used to classify regions of
importance in the
wavelet transform domain according to coefficient magnitude.
w
I
Figure IIL11. Translated Common Masks for Remaining Resolution Levels
IIL4.6. Misclassification and the Common Region Mask
It should be noted that while it is true that misclassification occurs in this
technique, there
is a tradeoff between code stream overhead and region channel accuracy. The
original
raw common mask size is 32 kBits for a 4 region mask. The basic uniform
quantization
scheme compresses this amount to 8 kBits. The modified scheme suggests that
mask
compression of 5 or 6 to 1 can be achieved with a tradeoff between mask
accuracy and
code stream overhead.
The low pass filtering and spectral quantization steps can be tailored to
deliver similar
quality masks for most images in a dynamic implementation. In addition the
partition
can be studied in regards to how the original grouping is affected by the
filtering step.
For the Lena image example the original partition is 10/15/25/50%. After
filtering the
coverage ratios used for bit budget calculation and the code stream
distribution (see
multiplexer in Ch.V.) changed to approximately 9/31/33/27%. There may be some
advantages in adjusting the original partition such that the data coverage
ratios are
controllable in the final stages.
The question of miscoverage must be addressed in all lossy region formation
techniques.
It is the subsequent modules that are affected by the misclassified
information. Thus the
interaction between the DCT region formation module and the subsequent sorting
and
packing modules must be understood in any attempt to obtain the best region
channel
results for this classification scheme.
26

CA 02261833 1999-02-15
IIL4.7. Handling Misclassification in a Region Formation Scheme
Subsequent stages in the compression algorithm are already tailored to process
information in a descending level of importance. Most wavelet implicit
quantization
procedures process the coefficients in bit plane order of importance. What
this means in
terms of any region formation scheme is that the information encompassed in
each region
is further partitioned by bit level processing. In the common mask approach,
further
processing causes the most important misclassified coefficients to filter to
the top at a
faster rate than misclassified coefficients of lower importance. Effectively
bit level
processing can be considered as a second partitioning stage that deals with
misclassification.
There is a tradeoff between the accuracy of the original region partition and
the additional
bit level processing overhead placed on subsequent sorting stages. It is the
final
processing stages that implicitly accomplish the final coefficient
partitioning. DAC is
currently using two bit plane partitioning core technologies for both
grayscale and color
images, and binary partitioning for bi-level images is now under
implementation.
IIL4.7.1. 1D Bit Plane Sorting for Common Mask Miscoverage
The concept of bit plane sorting is a well know technique used to organize
priority in a
distributed list of data. 1D sorting a list of information generates a map
specific to that
list in an optimal fashion. The largest values are mapped first as the list
transposition
routine progresses. The order of decent is the standard order used to classify
information
if considered from the normal processing standpoint where no regions are
involved at all.
As a result, most of the misclassified information is considered for further
classification
and are thus biased to be included first in the final code stream order. The
only
difference is that now there is a region description overhead as well as the
final mapping
overhead of sorting the region of interest partitions in a hierarchical
fashion.
Currently DAC has not documented the exact overhead introduced by region
processing
in comparison to normal processing modes that do not use regions. But the
final results
obtained by using the common mask approach are encouraging to say the least.
At this
level the underlying routines do not care where the information to be sorted
originated.
The ordering technique will run to completion whether region channels are
involved or
not. The original misclassified coefficients generated in the first cut will
filter through to
the final ordering set by the sorting stage. There is an important tradeoff
here between
the sorting cost and the region overhead that must be considered in the final
design
implementation.
IIL4.7.2. 2D Bit Plane Ordering for Common Mask Miscoverage
DAC has developed a quad tree ordering technique (see EQW Ch.4) to track
coefficient
importance in both normal and region based processing modes of operation. The
normal
quad tree approach is to track the leading one position through each block
under
consideration in a recursive fashion. A map is generated in the process for
each entry
based on importance such that decoding follows the same order. At this basic
level the
quad tree order is an efficient method of processing the mufti-resolution
decomposition
image information in an effective manner.
27

CA 02261833 1999-02-15
The tracking or positioning overhead introduced by mapping the data is
generally smaller
than in the 1D sorting case. Retaining vertical and horizontal positioning
information is
highly advantageous (in most image processing applications) since the
underlying
technology is generally consistent in this medium. The 1 D sorting approach
sacrifices
the natural vertical correlation that may exit (although it can be partially
recovered by bit
level entropy coding in the sorting routine.) However each of the two sorting
techniques
can be used from an operational standpoint to produce a similar net effect.
One may
produce slightly better results than the next, but the control architecture is
consistent.
Each final ordering routine can be tuned to meet specific processing needs.
The 1 D
sorting approach may be a useful candidate for bi-level image processing, and
DAC is
currently investigating this possibility.
The quad tree approach has currently been modified to operate in arbitrary
region
processing modes. The 1D sorting routine tracks the importance in a list of
information
specific to the block under consideration. That is the region partition is
distributed in 1 D
hierarchical lists of information. The original preordering of the
coefficients is captured
in the common mask procedure. Thus the decoder map already exists for the
inverse
ordering.
Initially DAC's region processing quad tree begins by building an information
map for
each region channel to guide the classification. The core engine has been
modified to
drops blocks not contributing to the final ordering in each region category.
Currently the
overhead comparisons for each sorting case have not been documented. The
results will
be available from DAC once the region based quad tree design implementation is
finalized (currently under implementation at DAC.)
In each case, the misclassified coefficients obtained from the original
preorder mask
partition are considered again for ordering in the sorting stages that follow.
Effectively,
the most important misclassified coefficients still have the opportunity to
make important
contributions to the final code stream as well as improving the reconstruction
quality
measurements in the decoded image. The difference between this approach and
most
efficient classification approaches is that the original processing order used
of the
efficient scheme is somewhat distributed through each region channels. However
the
misclassification in each region channel is forgiven to a certain extend the
subsequent bit
level sorting module. One of the prices that must be paid for any automatic
region
classification scheme is that the optimal processing orders that exist in
standard
approaches must be considered in a different context. The original ordering
concepts
used for standard procedures must be extended to include other ordering
techniques
specifically tailored for operation in arbitrary region processing.
IIL4.8. General Region Processing Concerns
There is one important hurdle that must be overcome in the design of any
arbitrary region
processing technology. There are times when rigid tile or block control is the
optimal
way to process image information. However, it is difficult to achieve
arbitrary accuracy
in a strict processing order. DAC's 1 D and 2D sorting techniques address this
issue in
design implementation. In our opinion arbitrary region processing channels can
be
defined in a still image environment. Careful study and analysis suggests that
this is a
viable approach not only for the DCT common mask approach but also for other
arbitrary
28

CA 02261833 1999-02-15
region formations techniques that have not yet been developed. Furthermore
region
classification may have interesting properties that can transferred to video
processing
environment where the region of interest concept and the object motion vectors
can be
considered together in a unified approach to region of interest processing.
DAC's region technology in its original form was designed to include region
processing
capabilities from the start. All internal modules can be operated in both
normal and
region based modes of operation. The MUX architecture (introduced in Chapter
V) is
designed to meet operational requirements in both normal and region processing
modes.
It is possible to extend the notion of block based image processing to a level
where a
block of information is interpreted in an arbitrary way that depends only on
the
underlying core processing technology. In this way, blocks can be considered
as
individual processing units each fully capable of making a contribution to the
final code
stream. Furthermore control architecture can be developed to fully exploit the
region
processing capability. All region formation schemes, whether arbitrarily
defined user
regions of interest, automatic region formation schemes or any other specially
designed
region classification technique, can be processed in a common framework. The
same
overall processing architecture can be tailored to operate in an optimal
fashion for both
normal and region processing modes of operation.
IILS. Additional Processing Concerns
One of the important concerns in the JPEG-2000 community regarding the
development
of a new compression standard is that it must be able to support ROI
processing. There
are a number of techniques that have been tested with some success. Some of
these
techniques are listed below.
Sequence based mode. When this mode of operation is used, each set of data
encapsulated by a specific region is treated as a separate sequence. The
sequences are
coded independently.
~ Scaling based mode. In this mode of operation, the magnitude of each ROI
coefficient is increased using a predetermined shift factor. If multiple ROIs
are used
with increasing levels of importance, multiple shift factors distinguish each
ROI. The
effect of this scaling technique is to force the ROI coefficients to be
encoded first.
~ ROI from the middle. In this mode of operation, a concern of coding an ROI
in the
middle of the bit stream is addressed. This is useful for progressive
transmission of
images where the user is given the opportunity to focus on a specific ROI
before the
complete set of image data arrives at the decoder. This is important for
medical
image processing.
ROI without sending mask information. This mode of operation is a special case
for
scaling based mode. The coefficients for each region are scaled such that the
magnitude of each ROI exceeds that of the ROI of less importance. The decoder
knows which ROI the coefficients belong to based on the magnitude.
29

CA 02261833 1999-02-15
The ROI coding technique that DAC has developed generally falls into the
sequence
based category. But internal modules have been tailored to operate in both
block based
and arbitrary block sized processing units. DAC is currently studying the
different mask
and region formation techniques to determine the effect each ordering and
partitioning
approach has on the overall organizational structure required for region
channel
processing. The current implementation includes a scalable ROI mode of
operation
implemented without actually shifting the ROI coefficients encompassed by the
classification. Data scaling is handled in the MUX control architecture.
Internally, the
scaled version is a special case that can be implemented in MUX control.
Preliminary study has begun for the last of the four categories cited above.
ROI from the
middle implementations can be addressed by using resolution a progressive
processing
order. This type of ordering is supported in the MUX architecture. DAC is
currently
considering a design implementation for client side region of interest
requests in a
resolution progressive architecture for client-server region interaction.
ROI without mask information makes sense in theory. However it places a huge
tax on
the subsequent sorting and classification stages. Generally speaking, the
overhead cost
introduced by additional sorting is comparable to the size of a bitmap mask
that could
have been used to classify the data initially. The shift introduced to each
ROI must be
processed in the sorting stage. Eventually sorting must traverse from top to
bottom.
Coefficient scaling under tight control has some definite benefits in many
cases.
However it would be highly inefficient in a general region processing
architecture
because of the high sorting costs as a result of traversing all region
channels. In a region
formation scheme of 4 or more regions, the total bit level difference between
all ROI is
too large to process entirely. On the other hand, if the resolution of the
overall partition
is reduced (less bit levels), less room is available to form an accurate
region
classification. There is some common ground that must be explored in order to
determine the optimal processing mix.

CA 02261833 1999-02-15
IV. Intra-Region Coding
The segregation of image primitives into regions provides a basis for
accessing the image
contents. Compact representation of image primitives is achieved via intra-
region
coding.
Independent coding units (ICUs) are the building blocks for intra-region
coding. In
RICS, intra-region coding with ICUs is designed with a set of objectives.
( 1 ) Full data independence. From the notion of ICU, the encoding and
decoding of a
region is done without referring to the data of any other regions.
(2) Allowance for multiple coding schemes. Each ICU may be coded using
different
coding schemes. New coding schemes can be added to the system (modular
openness.)
(3) High coding ej~ciency. Depending on the characteristics of the primitives
in a given
ICU, one or more efficient coding schemes can be selected to produce a code
block
with high compactness.
(4) JPEG and JBIG transcodability. It is preferred to have a single JPEG 2000
coding
platform that also accommodates JPEG and JBIG modes of coding.
(5) Scalability of code stream.
(6) Error resilience. The ICUs are natural blocks for bit error localization.
(7) Parallelism. There is no data dependence between ICUs and so the encoding
and
decoding of all ICUs can be performed in parallel.
Intra-region coding in RICS involves the following steps.
( 1 ) Choosing a coding scheme.
(2) Determining ICU structure.
(3) Coding.
(4) Pre-packing.
In the rest of this section the first three steps are described. Pre-packing
is discussed in
Section IV.6.
IV.l. Choosing a Coding Scheme
For coding an ICU, the current RICS design employs six categories of coding
schemes.
~ Zigzag DCT Coefficients Packing (JPEG baseline scheme)
~ Embedded Quad tree (or similar schemes)
~ Embedded Zero tree (or similar schemes)
~ 1 D Progressive Sorting Schemes
Block Based Quantization
~ JBIG Coding Algorithms
31

CA 02261833 1999-02-15
There is no general restriction on what schemes have to be used for coding a
given ICU.
However, certain preferred embodiments may apply. For example, if DCT is used
at the
transform step, then the zigzag DCT coefficient packing might be preferred
(but not
restricted to).
IV.2. Choosing ICU Structures
While being a logic concept, an ICU still has a geometric structure. The ICU
structure is
directly relevant to the coding scheme chosen. Currently, the RICS recognizes
three
types of ICU structures (Figure IV. l ).
Figure IV.1. The three types of ICU structures.
IV.2.1. Type 1 ICU Structure: 8x8 Blocks
This type of ICU is designed exclusively for use in JPEG mode, although it is
not
necessary that DCT transform coefficients be coded this way.
If there is no region defined in the image and the JPEG mode is chosen, the
entire image
is paved with type-1 ICUs.
If a region R is to be coded using JPEG mode, the set of ICUs that covers R
form a
unique, minimal pavement for R, in the following procedure.
Step 1. Let y min be the first row from the top that has at least one pixel in
R, y m~ the
last row, x min the first column from the left, and x m~ the last column.
32

CA 02261833 1999-02-15
Step 2. Let (x min, y min) and (x m~, y m~) be respectively the top-left and
the
bottom-right corners of the bounding rectangle of R.
St_ ep 3. Starting from the top left corner, pave the bounding box completely
with type-1
ICUs.
St, ep 4. Remove those ICUs that cover no pixels in R.
After this procedure, the remaining ICUs form the minimal pavement of R
(Figure IV.2).
ymin
x min
R ~ R
x max
y max
Type-1 ICU
Figure IV.2. Pavement of a region using type-1 ICUs.
IV.2.2. Type 2 ICU Structure: Rectangles
Type-2 ICUs are rectangles. Except for the JPEG and embedded zero tree
schemes, any
other intra-region coding scheme uses type-2 ICUs to pave and code a region.
There is
no general restriction on the dimensions of a type-2 ICU. It is usually
defined by the
selected coding scheme. For example, both embedded quad tree and explicit
block based
quantization can use arbitrary sized rectangles, with some preferred
embodiments (such
as the 64x64 blocks used in EBCOT of VM 3.0 (A)). It should be noted that once
a
region is paved by type-2 ICUs, different coding schemes can be used for each
ICU.
For subband decompositions, no type-2 ICU is allowed to cross subband borders.
Essentially, this means that type-2 ICUs support only various types of intra-
band coding
methods.
IV.2.3. Type-3 ICU Structure: Pyramids
The third type of ICU is the pyramid structure, which is used by various inter-
band
coding methods, such as the embedded zero tree. In the current RICS design,
there is one
limitation on the region definition procedure for type-3 ICUs: a region must
be specified
in the top-down manner, from lower resolution to higher resolution in the
decomposition
pyramid. That is, for a given region definition R in LL, every element in R
defines a set
of type-3 ICUs (i.e. in three spatial orientations, respectively).
33

CA 02261833 1999-02-15
Let C"' (i, j) be a wavelet transform coefficient at spatial location (i, j)
in the LL
subband, C; (m, n) be a wavelet coefficient at spatial location (m, n) in the
subband at
level l (l =l, 2, ...) in orientation r (r=1, 2, 3). Assuming that a 5-level
wavelet -
decomposition is used, the three type-3 ICUs defined by CAL (i, j) can be
represented in
the following fashion.
In orientation 1:
{CS(i,j)} U {C4(2i,2j), C4 (2i+1,2j), C4(2i,2j+1), C4 (2i+1,2j+1)} U ...
In orientation 2:
{CS (i, j)} U {C4 (2i, 2 j), C4 (2i + 1, 2 j), C4 (2i, 2 j + 1), C4 (2i + 1, 2
j + 1)} U ...
In orientation 3:
{CS(i,j)} U {C4(2i,2j), C4 (2i+1,2j), C4(2i,2j+1), C4 (2i+1,2j+1)} U ...
Notice that the primitive CLL (i, j) is not included in any the three ICUs.
Instead, the LL
subband is coded differently, using the type-2 ICUs (see sections IV.S and
IV.6.)
IV.3. Coding Type-1 ICUs
Type-1 ICUs are defined exclusively for coding 8x8 DCT coefficient blocks.
Coding of
type-1 ICUs follows the JPEG baseline algorithms.
IV.4. Coding Type-2 ICUs
Once a region is decomposed into a set of non-overlapping type-2 ICUs, each
ICU is
coded independently, and the collection of codes for all ICUs is the coded
representation
of that region. In this subsection we describe three techniques that may be
used for
coding type-2 ICUs.
IV.4.1. Using Embedded Quad tree
Embedded Quad tree Wavelet (EQW) is an efficient and fast method for type-2
ICU
coding. This technique implements an embedded progressive sorting scheme in a
quad
tree-like structure. In contrast to inter-band coding methods, the EQW
explores the intra-
band self similarity of the wavelet decomposition coefficients. The EQW-
produced
code-stream realizes scalability by pixel-precision (the scalability by
spatial resolution is
realized by the multiplexer.)
IV.4.1.1. Depth-First and Breadth-First Quad trees
The EQW method can be used for both lossless and lossy coding. In lossless
coding, the
primitives to be encoded in the ICUs are coefficients of a reversible wavelet
transform.
In lossy coding, after the wavelet transform, each transform coefficient is
represented in a
fixed-point binary format - typically with less than 16 bits - and is treated
as an integer.
In each ICU, the maximum coefficient magnitude M is determined. Then a value N
is
found which satisfies the condition 2 "' <_ M < 2 "'+' . The EQW works in a
bit-plane
manner: the initial bit-plane is set to 2 "' , followed by 2 "'-' , 2 "'-2 . .
. and so on. A binary
34

CA 02261833 1999-02-15
significance map is produced for every bit-plane by comparing coefficients in
power of 2
increments.
Figure IV.3 illustrates the EQW encoding process on a single bit-plane. Two
working
lists are used. One is called the list of significant primitives (LSP). Each
entry in LSP
corresponds to an individual primitive in the ICU. The LSP is initialized as
an empty list.
Another list is called the list of insignificant blocks (LIB). Each entry in
the LIB is
registered with the coordinates of the top-left corner of the block, together
with the width
and height information. Each LIB entry represents an individual primitive of
width and
height equal to 1. At the highest bit-plane 2" , the ICU to be encoded is put
into the LIB.
A temporary list of insignificant blocks (TLIB) is used for refreshing the LIB
after each
bit-plane coding pass is completed.
There are two methods used to add the four sub-blocks into the LIB that occur
as a result
of the quad tree decomposition. The first method, known as depth-first quad
tree coding,
is to insert the four sub-blocks into LIB at the position of their parent
block. In this case,
the four child blocks are evaluated immediately after the parent block. This
rule is
applied recursively until no more subdivision is possible. This means that
control returns
to the next entry in the LIB only after the present entry is completely
encoded up to the
highest resolution level. The second method, known as breadth-first quad tree
coding, is
to add the four sub-blocks under consideration to the end of LIB. In using the
breadth-
first process, all parent blocks at the same level will be processed first,
followed by their
respective children blocks.
After all entries in the LIB have been processed, the entries in TLIB can be
reordered
according to certain pre-defined set of rules (this is an optional step.)
Experimental
evidence suggests that a higher PSNR can be achieved by using an effective
reordering
scheme. Then the LIB is replaced with the TLIB and the coding resumes at the
next bit-
plane.
The next step is the refinement pass. The Nth bit is output for entries in the
LSP. Then,
the process resumes using the new LIB and a new bit-plane set to 2N-' .

CA 02261833 1999-02-15
Start
LIB emntv? Re-order TLIB ~ Replace LIB with TLIB
Load a block from LIB ~ ~ End
Are all pixels Yes Output 0, and move
in this block the block to TLIB
insignificant?
No
Is there only one Yes
pixel in this Output 1 and its sign
block and is it bit, Move it to LSP.
significant?
No
Output 1, decompose this block into four equal-
sized sub-blocks, and remove it from LLB.
Depth-first Breadth-first
Insert the four sub-blocks Append the four sub-
into LIB at position of the blocks to the end of LIB
orieinal block
Figure IV.3. Embedded quad tree flowchart
IV.4.1.2. EQW with VLC
In order to use variable length coding (VLC), the standard EQW algorithm of
the
previous section is modified as follows.
Step 1. Initialization: output n satisfying the inequality 2" <_ max{ C~ } c
2"+1, set the list
of significant primitives (LSP) as an empty list. Put the ICU to be coded into
the LIB.
Step 2. Bit-Plane Sorting: for each entry of the LIB, perform quad tree
coding.
36

CA 02261833 1999-02-15
If all primitives within the block are insignificant, output a 0 bit and add
this block to the
temporary LIB (TLIB).
Otherwise, look at the significance of the four sub-blocks. Then according to
the VLC
table, output the corresponding VLC sequence (see Table VL1). If significant,
sub-
blocks that are not a single primitive are inserted into the LIB at their
parent position. If
insignificant, they are added to the TLIB. If the sub-blocks are single
primitives, they are
added to the LSP. Sign bits are output only if units are significant. If
insignificant, the
units are added to the TLIB.
Step 3. Reordering (optional).
Step 4. Refinement: for each entry in the LSP, except those included in the
last sorting
pass, (i.e. with same n), output the nth most significant bit of C;~ .
Step 5. Quantization Update: decrement n by 1 and go to step 2.
[Note: Some other researchers have also proposed the embedded coding methods
where
quad tree is used to explore the intra-band similarity ~~»2~. However, some
major
differences exist in how the quad tree operates. The work of [2] has suggested
that
empirically the quad tree decomposition should stop at size 16x16. However (as
a result
of our experience and experimentation) this size may not always be the optimal
choice.
Even without VLC, the efficiency of DAC's EQW is comparable with EZW. In fact,
for
a 2x2 block, if it is insignificant, one zero can represent four zeros.
However, when a
2x2 block is significant, quad tree coding is inefficient.]
For LL For Blocks For Other
Subband of Size Types
nxn (n>2) of Blocks
of Other
Subbands
Se uenceVLC Code Se uence VLC CodeSe uenceVLC Code
1111 000 0001 000 0001 000
1010 001 0010 001 0010 001
0101 010 0100 010 0100 010
0100 011 1111 O11 1000 011
1110 1000 0011 1000 1100 1000
1101 1001 1000 1001 1010 1001
0111 1010 1100 1010 0101 1010
0010 1011 1101 1011 0011 1011
1100 11000 0101 11000 0110 11000
1011 11001 0110 11001 0111 11001
1001 11010 0111 11010 1001 11010
1000 11011 1001 11011 1011 11011
0110 11100 1010 11100 1101 11100
0011 11101 1011 11101 1110 11101
0001 11110 1110 11110 1111 11110
Table IV.1. VLC Codes for EQW
~'~ F. Kossentini et al. "Embedded Quadtree Predictive Codec",
ISO/IEC/JTC1/SC29/WG1/N667.
~2~ Taubman, D. et al. "EBCOT: Embedded Block coding with optimized
truncation", ISO/IEC/
JTC 1 /SC29/ WG 1 / N 10208.
37

CA 02261833 1999-02-15
IV.4.2. Using Block-Based Quantization
The embedded quad tree (EQW, EQPC, etc.) is a special case of the more general
block-
based quantization techniques. Other block-based quantization algorithms, such
as
EBCOT, can also be very efficient for type-2 ICU coding.
IV.4.3. Using JBIG Algorithms
It is noted that in all implicit quantization schemes using progressive bit-
plane coding
methods, including the embedded zero tree and the embedded quad tree
approaches, at
each bit-plane, the ICU coder is actually dealing with a bi-level image (the
significance
map.) Therefore, by adopting those efficient JBIG algorithms as ICU coders in
a JPEG
2000 system, one can realize two modes of interplay with JBIG. In the
following EQW
is used as an example to illustrate this idea.
In the first mode, the transcode mode, the JBIG ICU coder and EQW ICU coder
provide
a two-way transcode between JPEG 2000 and JBIG (Figure IV.4). In this
transcode, the
EQW procedure is called for bi-level type-2 ICUs, with the total number of bit-
planes
being set to one. Note that the sign bit coding in the EQW algorithm should be
skipped.
'traps-in'
'traps-out'
Figure IV.4. The transcode with JBIG.
In the second mode, the embedding mode (Figure IV.S), the proper JBIG routines
are
called as the bit-plane coder in the EQW routine for certain bit-planes and
for certain
decomposition sizes (the quad tree decomposition stops at this particular size
and the
coding is handed over to the JBIG routine). Since the algorithms for bi-level
data coding
are also evolving with the compression technology, having an embedding JBIG
mode
reserved in the JPEG 2000 system can make the Standard evolve with its sister
technologies.
Gray-scale or Embedded bit-plane quantization. At JPEG 2000 code with
color Image ~ certain bit-planes, call JB1G routines ~ embedded JBIG code
segments
Figure IV.S. The 'traps-out' and 'traps-in' modes for transcoding with JB1G.
38

CA 02261833 1999-02-15
IV.S. Coding Type-3 ICUs
Type-3 ICUs are defined to support various inter-band coding methods for
wavelet
transform coefficients. In particular, the methods of EZW, SPIHT, etc., are
known to be
efficient approaches for coding the type-3 ICUs. In testing these approaches,
it is noted
that the standard versions must be modified slightly to make them fit into the
RICS
architecture. Normally, these algorithms implement the ICU coding and
multiplexing
steps into an integrated procedure. A simple modification is required to
bridge the
existing architecture to the RICS architecture. The two steps must be
separated, which is
straightforward. Since the multiplexing stage in RICS can effectively simulate
the
performance of zerotree-based schemes (refer to Ch.V), this particular split
in
functionality has virtually no impact on the attainable coding efficiency for
standard
schemes. Instead it adds more flexibility and openness to the existing
architecture.
IV.6. Intra-Region Coding with Different Types of ICUs
Generally there is a need for using different types of ICUs for a intra-region
coding. For
example, in coding the wavelet transform coefficients, the LL subband is
usually encoded
differently than the other high-pass subbands. Because different sets of
primitives may
possess different statistical characteristics, providing several coding scheme
choices in
the intra-region coding module may offer a higher coding efficiency. In
practice, the
following combinations are useful.
~ In a wavelet decomposition, coding the LL subband with type-2 ICUs whereas
the
other subbands with either type-3 or type-2 ICUs.
~ Tiling an image into several regions, with some of the regions paved with
type-1
ICUs and others with type-2 ICUs.
~ Using different coding schemes in different type-2 ICUs.
IV.6. Intra-Region Coding without Any ICUs
Intra-region coding can be performed without specifying any ICUs in a
particular region.
In this case, the entire region is considered an ICU. If the natural geometric
shape of the
region fits into any of the three ICU categories, the appropriate ICU coder
can be used. If
the region has a very irregular shape, then the 1 D coding method can be an
efficient
approach. Once the data for a particular region is scanned in a certain pre-
defined order
to form a 1 D stream, the following 1 D progressive sorting algorithms can be
used to
produce an embedded code-stream.
IV.6.1. 1D Progressive Sorting Algorithms
The EQW algorithm can be readily extended to 1D cases where a binary partition
is used
instead of a quad tree decomposition:
Let L= {c; } be the 1 D list to be encoded, LSP the list of significant
primitives, LIS the
list of insignificant subsets, TLIS the temporary list of insignificant
subsets.
Step 1. Initialization: Output n satisfying the inequality 2n <_ max{ c; } <
2"+' , set the
LSP as an empty list. Put the set L into LIS.
39

CA 02261833 1999-02-15
Step 2. Bit-Plane Sorting: For each entry in the LIS, perform the binary
partition.
If all primitives within the subset are insignificant, output a 0 bit and add
this subset to
the TLIS.
Otherwise, output the two bits that reflect the significance map. For those
subsets, if they
are not single primitives, insert them into the LIS at their parent position
if they are
significant, or add them to the TLIS if they are not. If the subsets are
single primitives,
add them to the LSP and output the sign bit if they are significant, or add
them to the
TLIS if they are insignificant.
Step 3. Reordering (optional).
Step 4. Refinement: for each entry in the LSP, except those included in the
last sorting
pass, (i.e. with same n), output the nth most significant bit of c; ;
Step 5. Quantization Update: decrement n by 1 and go to step 2.

CA 02261833 1999-02-15
V. Processing with a Multiplexer Architecture
The JPEG-2000 committee has been investigating many emerging compression
technologies in order to define a new still image compression standard. The
emerging
standard will address both present and near future image compression needs.
The task of
selecting what technologies to include in the new standard is not easy given
the rate at
which technological advances occur in this area. The primary focus of DAC has
been to
develop a still image compression engine that addresses the issues set forth
by the
standards committee.
The concept of using a multiplexer (MUX) has been adopted in some standardized
processes of information coding such as MPEG. In contrast, incorporating a MUX
as an
integral part of a still image compression engine is rather unique, and there
has been very
little research conducted in this area. However it will be shown that the MUX
concept is
extremely useful in the development of a general purpose still image
compression engine.
V.1. Background
One of the concerns in developing a new Standard is the layout design of the
encoded bit
stream. A protocol must be developed to guide the new standardized compression
procedures. Some of the important considerations in this area are listed
below.
~ A well defined bit stream. All syntactic and semantic aspects of the encoded
image
format must be defined. The JPEG-2000 standard will encompass a wide variety
of
compression needs. One to one relationships will exist between fields that
exist in the
bit stream and functionality that exists in the core compression /
decompression
engine. The number of fields that exist in the bit stream is directly related
to the
overall functionality encompassed by the new standard.
A highly degree of data accessibility. The bit stream must be organized in
such a
manner that it need not be decoded in its entirety to interpret the physical
meaning of
the compressed data. Highly accessible data requires that the encoded data is
divided
into logical units each corresponding to a specific part of the original
uncompressed
information. The way this was accomplished in the existing JPEG standard was
to
partition the original image into 8x8 blocks. Each block was compressed using
the
DCT. Quantization tables were developed for coding the coefficients such that
the
reconstructed image quality was degraded in a standard fashion. However,
strict
block based data accessibility may not be a suitable medium for many of the
current
image processing needs.
~ Dynamic re-orderability. Dynamic re-orderability is a data access issue
relating to
the degree that encoded information can be reorganized to suite user specific
needs
for an image under consideration. This type of data access is an important
concern
for many applications, especially in the medical field.
~ Built in error resilient. In any transmission medium there is always the
possibility of
incurring bit errors. The encoded bit stream must have a certain degree of
error
resilience to address this concern.
Using a MUX to organize the encoded bit stream can address these issues. The
first step
is to divide the encoded information into logical groups. Organizing the data
in ICUs
41

CA 02261833 1999-02-15
leads naturally into a high degree of accessibility. Each ICU is an
independent unit. The
size and position information is self contained within each ICU. One of the
effects of
using a muliplexed bit stream design is that it is inherently error resilient.
If any logical
unit incurs an error, only that unit needs to be recovered. If the encoded
data is divided
into an array of logical units in preparation for MUX encoding, dynamic re-
ordering is
much easier to achieve.
V.2. MUX Design Overview
There are five important considerations to address in the design of the MUX
for still
image compression systems.
~ Defining a working model.
~ Defining an optimal data processing order.
~ Capturing the data to be compressed in a suitable data structure.
~ Defining a data priority to be used for compression.
~ Packing the compressed data based on data priority and processing order.
V.2.1. A Working Model for the MUX Discussion
In preparation for the MUX discussion, consider that a multi-resolution
decomposition
hierarchy of data has been obtained for an image to be compressed. Also
consider that
there are three channels of data. Assume that the original image has been
transformed
from RGB to YUV for example. In addition to this, assume that the U and V
channels
have been down sampled by a factor of 4:1. This type of approach is common for
lossy
image compression. The data sets appear in Figure V.1. The diagram illustrates
a 4 level
mufti-resolution decomposition for the Y-channel and 3-levels for each of the
U/V-
channels. The wavelet transform MALLAT decomposition is used here for
convenience.
HL, HLz HLz
HLz HLi HL i
LHa H3 LHz Hz LHz HHx
HL~
LHz HHz LHi HH~ LH~ HH~
U-channel V-channel
LH~
Y-channel
Figure V.1. Wavelet Mallot Decomposition for Lossy Color Transform Data.
This is by no means the only model that exists for the MUX design. DAC makes
the
distinction between region and non-region processing modes of operation in
their design
implementation. A hierarchy of list structures is used to control optimal bit
budget
distribution and flow of both non-region and region bit levels through MUX
channels.
The discussion presented in the next Section begins by introducing the
concepts in
42

CA 02261833 1999-02-15
normal processing modes. The normal MUX modes of operation are generalized
later on
to include specialized region and mixed processing modes.
V.2.2. Non-Region Data Processing Orders for the MUX
Generally speaking, given a wavelet mufti-resolution decomposition of data,
coefficients
of a fixed magnitude contained in a lower resolution level are more important
to the
image reconstruction procedure than coefficients of a similar magnitude at a
higher
resolution level. This leads to a natural ordering of the coefficients
beginning at the
lowest resolution level. The natural ordering concept is an important
consideration in the
design of the MUX.
V.2.2.1. General Color Processing Order (Lossy Case)
Given the mufti-resolution data sets of Figure V.1, a natural processing order
exists for
each decomposition channel. This natural order is illustrated in Figure V.2.
This
particular order reflects a level priority inherent to each data set.
Y-channel: LL4-HL4-LH4-HH4-HL3-LH3-HH3-HLZ-LHz-HHZ- HL1-LH,-HH,
U-channel: LL3- HL3-LH3-HH3-HLz-LHZ-HHz- HL,-LH~-HH,
V-channel: LL3- HL3-LH3-HH3-HLz-LHZ-HHz-HL,-LH~-HH,
Figure V.2. Level Priority Processing Order for Each Channel (Lossy Case).
Another two orders are obtained by simply interchanging orientation data sets
in a given
level. The difference lies only in the convention used for ordering the detail
information
(i.e. LH, HL, HH). The 4-1-1 down sampling relationship that exists in the
color
transform domain also exists in the wavelet decomposition data since there is
one less
transform level for the U/V channels. This is one of the keen design
considerations that
can be exploited in many stages of the MUX implementation and encoding /
decoding
procedures. The data is organized into list structures to cover the natural
processing
orders that exist in the data to be compressed.
V.2.2.2. Level Priority Processing Orders (Lossy Case)
The individual orders of Figure V.2 can be combined into a single natural
processing
order for the example under consideration. The new order is obtained by
interleaving the
expressions of Figure V.2 using the inherent decomposition level priority of
the data.
The result is illustrated in Figure V.3.
43

CA 02261833 1999-02-15
YLL4'Y HL4'YLH4'Y HH4'U LL3' V LL3'
YHL3'YLH3'YHH3'UHL3'ULH3'UHH3'uHL3'uLH3'VHH3'
YHL2'YLH2'YHH2'UHL2'ULH2'UHH2'uHL2'uLH2'VHH2'
YHL 1'YLH I-YHH 1'UHLI'U LHl'UHH 1'uHL 1'uLH1'uHH l
Figure V.3. Level Priority Processing Order (Lossy).
Notice that in this particular order, the 4-1-1 color down sampling
relationship is
maintained. In terms of the reconstruction process, the complete level 4 Y-
channel
information (i.e. LL4-HL4-LH4-HH4) is required together with the U and V
channel low
pass information (i.e. LL3 in each case). This is the information the decoder
will need
first to reconstruct the low pass inverse color transform image at the lowest
inverse
wavelet resolution level. A "level split" on the U / V data channels at the
lowest inverse
wavelet resolution level is used to exploit the natural relationships that
exist for both
inverse transform spaces. A similar order exists for the lossless case where
full data sets
are used.
V.2.2.3. Color Interleave Processing Order (Lossy )
Another processing order that exists for color images in the wavelet transform
domain is
obtained by interleaving the color channel detail information. The order is
illustrated in
Figure V.4. This type of ordering may be suitable for certain applications
such as those
that require the data to be encoded for a progressive download. As in the
previous case,
the down sampling relationships that exist are maintained in both color /
wavelet
transform spaces.
yLL4'YHL4'Y LH4'YHH4'ULL3'V LL3'
YHL3'UHL3'uHL3'YLH3'ULH3'uLH3'YHH3'UHH3'uHH3'
YHL2'UHL2'VHL2'YLH2'ULH2'uLH2'YHH2'UHH2'uHH2'
YHL1'UHL1'uHL 1'YLH1'ULH I'uLH 1'YHH 1'UHH I'uHH 1
Figure V.4. Level Priority Color Interleave Processing Order (Lossy).
V.2.2.4. Lossless Color Processing Orders
As in the lossy case, similar processing orders can be designed for lossless
color image
compression where full data sets exist for all color channels. In this case,
corresponding
orientation information from each wavelet channel is related in the original
inverse color
space. These data should be processed and grouped together in the wavelet
transform
domain and eventually the final bit stream.
The natural processing order for lossless color image processing is
illustrated in Figure
V.S. The color interleave order for lossless image processing is illustrated
in Figure V.6.
Note that in each case, the full decomposition data set for each channel is
maintained.
The inherent relationships that exist in the color transform space are
maintained in the
wavelet transform space for ordering and reconstruction of the original image.
44

CA 02261833 1999-02-15
YLL4-ULL4-V LL4-YHL4'YLH4'YHH4'UHL4-ULH4'UHH4-uHL4-uLH4'uHH4-
YHL3'YLH3-YHH4-UHL4'ULH4'UHH4'VHL3-uLH3-uHH3'
YHL2-YLH2-YHH2-UHL2-ULH2-UHH2-uHL2-uLH2-uHH2-
YHL1-YLH1-YHHt'U HL1'ULH l-UHHI-VHL1' V LH l-uHH 1
Figure V.S. Level Priority Color Processing Order (Lossless).
YLL4-ULL4'uLL4-YHL4- UHL4-VHL4-YLH4-ULH4-uLH4'YHH4-UHH4-uHH4
YHL3-U HL3-V HL3'YLH3'U LH3-V LH3'YHH3-UHH3'V HH3
YHL2-UHL2-uHL2-YLH2-ULH2-uLH2'YHH2-UHH2'uHH2
YHLI-UHLI-uHL1-YLHI'ULH1-uLHI'YHHI-UHH1-VHHI
Figure V.6. Level Priority Color Interleave Processing Order (Lossless).
V.2.3. Capturing the Data in a MUX List Structure
There are a number of candidate algorithms under consideration by the JPEG-
2000
committee for optimal quantization of the wavelet coefficients. A common
approach
used to quantize the wavelet coefficients in a progressive manner is to use an
optimal bit
plane ordering technique. DAC has testing a number of bit plane ordering
techniques in
both one and two dimensional schemes. Bit plane ordering techniques are
generally
classified as using implicit quantization for the wavelet data sets.
Coefficients are packed
into the final bit stream based on bit level priority. The bit plane
processing technology
will be used to introduce the data structure used in the MUX design. However,
the MUX
processing discussion that follows is not restricted to bit level processing
algorithms.
The general ordering and processing relationships are useful for introducing
the MUX
control architecture at a basic level. However, the key to the operation and
many benefits
of the MUX technique is in the data structure design used to encompass the
natural
ordering concepts. The first step is to define a list structure for each
level, channel, and
orientation of data that exists in the wavelet transform space. A typical
example of this
type of structure is given in Figure V.7.

CA 02261833 1999-02-15
Data Type:
MUXLIST
Parameters:
liTotBytesPacked- long integer total bytes packed into
the data buffer for this list.
cScheme - character processing scheme used for
data contained in this list.
cHighBit - character highest bit-level where data
processing begins for this list.
*pucMuxBuff - pointer to unsigned character buffer
where data for each
bit-level is packed for this list.
Fields for
MUX: information
for packing
after list
processing
is complete.
pliBitPackInfo[- pointer to long integer number of bits
16] packed into the data buffer
at each bit-level for this list.
liCurBytesCount- long integer current byte count used
for bit budget distribution
when packing this list.
cCurBitLevel- character current bit-level used for
packing this list.
cRemainingBits- character remaining bits to be packed
at a given bit-level when
data to be packed is not evenly divisible
by 8 for this list.
Figure V.7. Typical MUX List Data Structure.
A general list structure for each level data set can be utilized in many ways.
A lossless
"prepack" of multi-resolution hierarchy information is useful for exploiting
the many
relationships that exist in the data taken in MUX list processing context. The
data and
information contained in each list is used to control how the final bit stream
is organized.
All data packed into the final bit stream must conform to this structure. New
fields may
be added, but the basic operation of the structure remains the same. Most
implicit
quantization techniques are implicitly decodable. In other words, minimal
header
information is required for each list. The MUX architecture organizes the
lists or units of
information into a bit stream that is scaleable in terms of bit precision and
resolution and
is controllable by the many MUX modes of operation.
As an example, suppose that EQW (DAC's current two dimensional bit level
processing
design) is used to capture the leading ones and refinement bits at each bit
level in each
data set. Following the order given in Figure V.3, a multi-dimensional
hierarchy of list
structures is defined for use in the ensuing data processing stages. Within
each list (as
EQW progresses), the fields in the corresponding list structure are updated.
The bit
stream at each bit level is appended to the MUX "prepack" buffer as well as
its
corresponding size being added to the total in the bit packing information
field. The bit
level position where processing begins is put in the high bit information
field. The total
packed list size is placed in the total packed field. Finally if more than one
internal
processing scheme is used (e.g. NULL transform mode for bi-level information
or other
internal modes of operation), the scheme used for the list is placed in the
scheme field.
Each MUX list is fully independent, implicitly contains a full set of
statistical information
available for determining the amount of data to pack for each list and is
optimal for
organizing the final compressed bit stream.
46

CA 02261833 1999-02-15
V.2.4. Data Priority and MUX Control
The information contained in each list structure is used to organize the final
bit stream
based on end user compression requirements. DAC has implemented numerous MUX
modes o operation. Two common modes of operation are outlined in this Section.
V.2.4.1. Signal to Noise Ratio (SNR) Progressive Mode
This mode of MUX places priority on the data such that the final ordering
optimizes the
SNR given a user specified image compression size. For the discussion that
follows,
assume that the user has specified the desired compression ratio in some
manner.
Assume that an optimal bit budget distribution scheme is in place. Thus the
number of
bytes that has been allocated to each color channel is known (more will be
said on how to
determine the optimal bit budget distribution for each channel using the MUX
later). The
information fields in the MUX list structures are used to determine the amount
of data to
pack for each list such that the SNR is optimized for the specified bit
budget. A
psuedocode explanation of this technique appears in Figure V.B.
Fields that refer to the MUX list structure appear in italics while other
local variables
appear in normal typeface. Basically the idea is to loop through each list
checking to see
whether the current processing bit level is equal to the bit level of the list
under
consideration. If the two bit levels are equal, the channel bit budget is
decreased by the
amount of data available in this particular list for the bit level in question
(from MUX
field pliPackinglnfo~cCurBitLevelJ. The MUX field liCurBytesCount is
incremented by
the number of bytes available. Additional processing takes care of the
remaining bits.
The remaining bits will be considered in the channel bit budget on the next
visit to this
particular list. The MUX field cCurBitLevel is decreased by one such that it
will again be
enabled when the bit level in the main loop is decreased by one.
This procedure optimizes the SNR since it processes the largest bit levels in
each list first.
Thus information for the largest coefficients throughout individual
decomposition data
sets is sent first according the natural processing order outlined earlier.
Once the channel
loop exits, each MUX list will contain a field indicating the amount of data
to pack into
the final bit stream in each case.
47

CA 02261833 1999-02-15
CALCULATE Channel BitBudget // determine optimal bit-budget for each color
channel.
INITIALIZE Channel CurrentBitPlane // highest bit plane that exists in each
color channel.
INITIALIZE IiCurBytesCount and cRemainingBits FOR each MUX list
FOR Each Color Channel II process each channel separately.
WHILE Channel BitBudget > 0 AND Channel CurrentBitPlane >=0
FOR Each Wavelet Transform level // beginning at lowest resolution level.
FOR Each Orientation Set of Data // according to lossy case natural processing
order.
IF cCurBitLevel NOT_EQUAL to Channel CurrentBitPlane
CONTINUE
ELSE
SET BitLevelBytes to pliBitPacklnfo[Channel CurrentBitPlane] » 3
SET RemBits to pliBitPacklnfo[Channel CurrentBitPlane] & 7
IF Sum(cRemainingBits, RemBits) >= 8
INCREMENT BitLeveIBytes by 1
DECREMENT cRemainingBits by 8 - RemBits
ELSE
INCREMENT cRemainingBits by RemBits
ENDIF
IF Channel BitBudget >= BitLevelBytes
INCREMENT IiCurBytesCount by BitLevelBytes
DECREMENT Channel BitBudget by BitLevelBytes
DECREMENT cCurBitLevel by 1
ELSE
INCREMENT IiCurBytesCou»t by Channel BitBudget
SET Channel BitBudget to 0
ENDIF
ENDIF
IF Channel BitBudget EQUALS 0
BREAK
ENDIF
END FOR
END FOR
DECREMENT Channel CurBitPlane by 1
END WHILE
END FOR
Figure V.B. SNR Progressive Bit Budget Distribution Scheme
V.2.4.2. Resolution Progressive Mode
The resolution progressive mode of bit budget distribution is a simple
extension of the
psuedocode implementation of the SNR mode of the previous Section. In order to
obtain
a resolution progressive mode, the 'Waveket Transform level ' for loop is
taken outside of
the main BitBudget l BitPlane while loop such that resolution level is given
priority. In
this manner, a lower resolution image can be reconstructed in the inverse
wavelet
transform stage. The resolution of the ensuing image depends upon the number
of levels
required in the end user requirements.
48

CA 02261833 1999-02-15
V.2.5. Data Packing Using the MUX Lists
Composing the final bit stream is a simple matter once the bit budget
distribution scheme
has run to completion. The packing technique can follow one of the normal
processing
orders outlined earlier (e.g. color level priority or level priority color
interleave) or
another access technique as required by the end user. The amount of data to
pack for
each list has been determined in the bit budget distribution stage. If the
data to be packed
for a given list is greater than zero, then the total data size, scheme and
high processing
bit level are packed as header information into the final bit stream. If the
data to be
packed for a given list is zero (i.e. not required), then a smaller header is
packed to
indicate a zero length list. Currently a register type approach is being
developed to
handle zero length lists. All lists that have data available will set a bit
position in the list
register so that the decoder can determine which lists have made a
contribution. Empty
list will be flagged with a 0 bit in the list register. The list register is
packed in the final
code-stream. This technique will save the size of the list header overhead of
empty lists.
V.3. Overhead Consideration of the MUX Architecture
There is a small overhead placed the compressed data by the MUX
implementation.
There are three header fields to pack for each MUX list.
~ The total bytes packed.
~ The scheme used to process the list.
~ The highest bit plane for data in list.
Note that if there is only one internal scheme used to process the entire
image, then the
scheme field does not need to be packed for each list.
In order to calculate the cost of using a MUX in terms of header sizes for
each list,
consider that a 24 bit color image of size 2048 by 2048 needs to be processed
in a lossy
fashion (i.e. the working MUX model of Figure V.1 ). Assume that the size of
the
smallest wavelet transform level is 8 by 8. Thus there are 8 decomposition
levels to
consider in forming the MUX list hierarchy. Assume that the wavelet
decomposition
data has been converted to a 16 bit integer representation. Also assume that
there is only
one internal processing scheme for the lists. Given these initial conditions,
a worst case
analysis is conducted to determine the header size for each list. The results
are tabulated
in Table V.1 for the Y-Channel wavelet decomposition.
From Table V.1, the total Y-channel header size for this particular image is
443 bits. A
similar calculation can be conducted on the U/V-Channels (assuming one less
decomposition level for each) to yield 368 bits each. The original raw image
size is 2048
x 2048 x 3 bytes. Thus the MUX packing overhead in this particular example is
about 1
header bit for every 854 bits of compressed data. In the lossless case where
each
channels has the same number of decomposition levels (or correspondingly, in
the 8 bit
grayscale case), the overhead is still very small at 1 header bit for every
757 bits of
compressed data packed.
49

CA 02261833 1999-02-15
OrientationMax. Data Size Req. Req. Bits for
(Bytes) Bits High Bit
LL8 2x8 7 4
HLg 2x8 7 4
LH8 2x8 7 4
HH8 2x8 7 4
HL~ 2x16 9 4
LH~ 2x16 9 4
HH~ 2x16 9 4
HL6 2x32 11 4
LH6 2x32 11 4
HH6 2x32 11 4
HLS 2x64 13 4
LH5 2x64 13 4
HHS 2x64 13 4
HL4 2x l28 15 4
LH4 2x l 28 1 4
S
HH4 2x 128 1 4
S
HL3 2x256 17 4
LH3 2x256 17 4
HH3 2x256 17 4
HLZ 2x512 19 4
LHZ 2x512 19 4
HHZ 2x512 19 4
HL, 2x1024 21 4
LH, 2x1024 21 4
HH, 2x 1024 21 4
Total Header 343 100
Bits
Table V.1. MUX List Overhead for Y-Channel 8-Level Decomposition.
Table V.2 outlines the overhead size for square images with dimensions that
are a power
of 2 beginning at 16 by 16 and ending at 64k by 64k. Note that the overhead
size if 44
bits in both the lossy and gray scale cases. The reason for this is that the
wavelet
transform is not used on the U/V channels when the original image dimensions
are 16 by
16. The Y-channels is decomposed once. A plot of percentage overhead versus
image
dimension is given in Figure V.9. Both lossy and lossless cases appear on the
same plot.
Note that the image size can be quite small while still maintaining a
relatively low
overhead in terms of the total MUX list header sizes.

CA 02261833 1999-02-15
Image DimensionOverhead Overhead Overhead
Rows & ColumnsBits Bits Bits
Loss Lossless Gra Scale
16 44 132 44
32 171 249 83
64 294 384 128
128 435 537 179
256 594 708 236
512 771 897 299
1024 966 1104 368
2048 1179 1329 443
4096 1410 1572 525
8192 1659 1833 611
16384 1926 2112 704
32768 2211 2409 803
65536 2514 2724 908
Table V.2. MUX List Overhead for Square Images of Various Sizes
Percentage List Overhead vs. Image
1.1
0 - - ~-___ ___. _.._._____-__..__._________.
1.0 _.
0
..,
__--_.______ _____._ .__ _ ____ _
0.9 __ _. _ ..
Lossless / Gr scale
Case
0.8
- _ __._._ . __ ..__
._._.
0.7
en
E
0.6
0.5 - _ ~ - _ _. _ _. .. _ _ _
. . _ _ .
-_ __ . _ __ _
_ .._.. _. ___
0.4 _-_.__ _. .__ . _ _
._ _ ._. _ __.
r
0.3 __ _ .____._ . -__... _ _ _ _ ___._....
__ _ _
-___._. ___-~. __._.__.__. _____-.
p _ _-_______
0.2
Lossy Cas~-
_ ___ _. _ _.__ _.
0.1 _ _____ -_.__-
0.0
32
64
128
256
512
1024
Image
Dimension
(Rows
=
Columns)
Figure V.9. Percentage MUX Overhead as a Function of Image Dimensions
51

CA 02261833 1999-02-15
V.4. Bit Budget Control from the MUX Architecture
One of the most difficult tasks that must be addressed in any compression
scheme is
scalability. The internal procedures must be developed such that the image
under
consideration can be compressed to a user specified size in an optimal manner.
The task
is compounded for color images since there are three channels to consider. The
major
problem is how to distribute the user specified bit budget between the three
channels.
Standard color transforms such as YUV or YIQ are normally used to redistribute
the
RGB color information prior to the multi-resolution decomposition stage of the
compression procedure. These transformations concentrate most of the energy
into one
channel making them better suited for compression. Another color transform
that is
gaining popularity is the KL transform. This particular transform technique is
based
upon a principle component analysis (PCA) implemented on the original raw
color
information in order to determine the optimal color redistribution for the
three RGB
channels. Generally speaking, after completing a color transform stage, two of
the three
channels are down sampled by a factor of 4 to 1 for lossy compression. In
doing this, the
amount of data that must be compressed is reduced by a factor of 2 with
minimal loss in
visual quality for the reconstructed image.
The easiest bit budget distribution scheme to implement is one that follows
the color
transform down sampling ratios. If the transform under consideration is YUV-
411, then
4 parts are allocated to the Y-channel for every 1 part allocated to the U I V-
channels
respectively. However, the energy distribution of the wavelet transform data
generally
does not follow this strict down sampling guideline. Instead it varies from
one image to
the next.
DAC has developed a dynamic bit budget control architecture that is based on
the
implicit information contained in each MUX list. In this Section, a bit budget
allocation
procedure will be introduced that can be used for optimal scalability in
normal processing
modes of operation. This technique is based implicitly on the amount of energy
contained in each color channel of the wavelet decomposition data sets. A data
ratio
concept is used together with the prepack information contained in the MUX
list
structures to determine the budget for each channel.
Compression procedures that process wavelet coefficients in a bit plane order
are
implicitly tracking the energy contained in the decomposition. The most
significant bits
(MSBs) of the largest coefficients are packed first followed by refinement
bits and the
MSBs that are significant for coefficients at the next bit level. This process
is repeated in
a recursive fashion until the desired compression size is obtained.
Let y;~ , u;~ and v;~ , be the total data available in a particular
orientation level for the three
color channels. Then the total amount of data available in the Y-channel
decomposition
Yt is obtained by summing the individual totals. A similar procedure can be
followed to
obtain Ui and Vt.
52

CA 02261833 1999-02-15
N 3
Yt - yN4 + ~1 ~~ Y~i
_J
N 3
Ut = aN4 + ~1 ~~ u.; (Eq.V.l)
N 3
Vt - VN4 +
I=1 J=1
The next step is to calculate the pack ratios to be used for each channel of
the wavelet
decomposition hierarchy. The pack ratios are determined by taking the ratio of
the two
largest amounts of data to the smallest amount of data. Let the three pack
ratios be
denoted RY , R" and RY. T'he smallest data size will be in either the U or V
channels
because of the down sampling step. Note that one of the pack ratios will be
unity.
Yt
RY =
MIN(Ut,Vt)
Ut
R~ _ (Eq.V.2)
MIN(Ut,Vt)
Vt
R" MIN(ut,vJ
The pack ratios given in Eq.V.2 are used to determine the optimal amount of
data to
allocate for each color channel based on the user specified compressed file
size.
However, any additional overhead introduced into the final bit stream by the
MUX must
be taken into consideration. Let yh;~, uh;~ and vh;~ be the individual header
sizes in each
wavelet channel for a particular orientation level. Then the total header
sizes for each
wavelet channel are obtained by summing the individual totals.
N 3
1'n = yhNa + ~ ~, Yhu
t=~ J=t
N 3
Uh - uhN4 + ~.i .~'.r~ uh~i (Eq.V.3)
_J
N 3
Vn = vhNa + ~ ~ vh~i
t-
If doing ROI processing, the packing overhead introduced by the mask must be
taken into
consideration in determining the bit budget for each channel. Let the total
pack size for
the ROI mask be denoted as Mt. The logical approach to take is to make an
adjustment in
the bit budget for each channel based upon the pack ratios of Eq.V.2. In this
manner, the
mask overhead is distributed proportionally to each wavelet channel. The unit
adjustment factor Ua is determined from the total mask overhead and the total
pack ratio.
53

CA 02261833 1999-02-15
Mt
U. _ (Eq.V.4)
Rv + Ru + Rv
The adjustment size for each channel is determined by using the result of
Eq.V.4 and the
pack ratios of Eq.V.2.
Ye = Rv . Ue
Ue = Ru ~ Ua (Eq.V.S)
Ve = Rv ~ Ue
A useful set of calculations that comes out of Eq.V.I to Eq.V.S is the minimum
compression bits per pixel (BppM;") and the maximum compression bits per pixel
(BppM~). These values are calculated below (assume that the original raw image
file size
is Ft bits).
8
BppM.~ _- ~ (Y.+Ut+Vt+Yn+Un+Vn+Y8+Ue+Va)
Fr
BppMin = ~ (Eq.V.6)
~ (Yn+Un+Vn+Y8+Ue+Ve)
Ft
These expression represent bounding compression values available for the image
under
consideration. If all data is packed for each of the wavelet data sets, the
result is BppM~.
If just the header information is packed, then the result is BppM;".
Suppose the user specifies a compressed file size of F"Ser. 'The unit bit
budget Ubb is
determined from the pack ratios and the total header sizes.
Ft - (Yn + Un + Vn)
UBB - (Eq.V.7)
Rv+Ru+Rv
Now the optimal bit budget for each channel Ybb, Ubb and Vbb can be determined
using
Ubb, the individual pack ratios and the overhead parameters.
Yse = Uhb . Rv + yn - Y8
UHe = Ubb . Ru + Un- Ue (Eq,V.8)
Vee = Vbb . Rv + Vh- Va
The expressions given in Eq.V.8 will always yield a near optimal bit budget
for each
color decomposition channel. The technique is based implicitly on the energy
distribution map recorded in MUX lists and the total overhead associated with
the
underlying process. Note that if processing with no ROI, then that variable
falls out of
the calculation.
This concept can be extended to form pack ratios for each subband if more
accuracy is
required. A similar data ratio technique can be implemented to control the bit
budget in
54

CA 02261833 1999-02-15
that case. The necessary information is contained in the MUX list structures.
However
for most practical application, the cited distribution technique is
sufficiently accurate.
The user specified file size can be obtained within several bytes in
implementing this
technique. In addition, the maximum and minimum attainable file sizes are
known prior
to the final packing stage.
A simple routine has been developed for distributing the final bit budget in
the level
where it is determined it will expire. The idea is quite simple. Given that
the bit budget
will expire on a particular bit plane in a certain transform level, then the
bit budget is
redistributed such that each orientation gets a proportional amount based on
the amount
of data that each orientation can take. The amount of data each orientation
gets is
determined by using ratios between orientations on the bit level under
consideration.
This is an important consideration since the net effect is approximately a 1
dB
improvement in the PSNR.
V.S. Using the MUX for Region Processing
So far the focus has been on the design of a MUX control architecture for
normal image
processing modes of operation. The main highlights are the data processing
orders, the
MUX list structure, the bit budget control technique, and organizing the final
bit stream.
DAC has extended the MUX concept to include a variety region processing modes
of
operation.
V.5.1. Region Processing Orders
The processing orders introduced in the previous Section are specific to the
normal
processing modes where one or more ROI are not specified. DAC has implemented
a
region processing design based on the natural extension of the MUX concepts
introduced
in the previous Sections. Both lossy and lossless processing orders are again
considered.
V.5.1.1. General Color Region Level Processing Order
The region level processing order places priority on each ROI in a descending
fashion
followed by the normal level priority scheme of the original MUX design.
Inherent in the
MUX scheme is the general assumption that data of similar magnitude in each
succeeding region is less important to the overall image reconstruction. A
secondary
priority key is placed on the wavelet transform level. Data of similar
magnitude
contained in a lower resolution level is more important to the reconstruction
procedure
than data at a higher resolution level. The general processing order for each
color
channel (assuming a 4 region priority scheme) is given in Figure V.10 where R;
is the
region level for i = 1,2,3,4.

CA 02261833 1999-02-15
Y-channel: R,(LL4-HL4-LH4-HH4-HL3-LH3-HH3-HLZ-LHZ-HHZ- HL,-LH,-HH,),
RZ(LL4-HL4-LH4-HH4-HL3-LH3-HH3-HLZ-LHz-HHZ- HL,-LH,-HH,),
R3(LLQ-HL4-LH4-HH4-HL3-LH3-HH3-HLz-LHZ-HHz- HL,-LH,-HH,),
R4(LL4-HL4-LH4-HH4-HL3-LH3-HH3-HLZ-LNZ-HH2- HL,-LH,-HH,).
U-channel: R,(LL3- HL3-LH3-HH3-HLz-LHZ-HHZ- HL,-LH,-HH,),
RZ(LL3- HL3-LH3-HH3-HLZ-LHZ-HHZ- HL,-LH,-HH,),
R3(LL3- HL3-LH3-HH3-HLZ-LHZ-HHz- HL,-LH,-HH,),
R4(LL3- HL3-LH3-HH3-HLz-LHz-HHZ- HL,-LH,-HH,).
V-channel: R,(LL3- HL3-LH3-HH3-HLz-LHZ-HHZ- HL,-LH,-HH,),
RZ(LL3- HL3-LH3-HH3-HLZ-LHZ-HHZ- HL,-LH,-HH,),
R3(LL3- HL3-LH3-HH3-HLz-LHZ-HHZ- HL,-LH,-HH,),
R4(LL3- HL3-LH3-HH3-HLZ-LHZ-HHZ- HL,-LH,-HH,).
Figure V.10. General Region Level Priority Color Processing Order (Lossy).
V.5.1.2. Region Level Color Processing Order (Lossy)
The individual orders of Figure V.10 can be combined into a single processing
order.
The new order is obtained by interleaving the expressions making use of the
inverse color
and wavelet transformation relationship that is presented for the normal MUX
modes of
operation in Section V.2.2.2. The result is illustrated in Figure V.11.
RI(YLL4-YHL4-YLH4-YHH4-ULL3-VLL3-
YHL3-YLH3-YHH3-UHL3-ULH3-UHH3-uHL3-uLH3-uHH3-
YHL2-Y LH2-YHH2-U HL2-U LH2-U HHYV HL2-V LH2-uHH2-
YHLI-YLHI-YHHI-UHLI-ULH1-UHHI-VHL1-VLHI-uHHIO
R2(YLL4-YH L4-Y LH4-YHH4-U LL3-V LL3-
YHL3-YLH3-YHH3-UHL3-ULH3-UHH3-VHL3-uLH3-uHH3-
YHL2-YLH2-YHH2-U HL2-U LH2-UHH2-uH L2-uLH2-V HH2-
YHL1-YLHI-YHH1'UHL1-ULH1-UHH1-uHLI-uLHI-uHHIO
R3(YLL4-YHL4-YLH4-YHH4-ULL3-uLL3-
YHL3-YLH3-YHH3-UHL3-ULH3-UHH3-uHL3-VLH3-VHH3-
YHL2-Y LH2-YHH2-U HL2-ULH2-UHH2-V HL2-V LH2-V H H2-
YHL1-YLH1-YHHI-UHLI-ULHI'UHHt-VHL1-uLHI-uHH1)~
1~(YLL4-YHL4-YLH4-YHH4-ULL3-uLL3-
YHL3-YLH3-YHH3-UHL3-ULH3-UHH3-uHL3-uLH3-uHH3-
YHL2-YLH2-YHH2-UHL2-ULHYUHH2-uHL2-VLH2-VHH2-
YHLI-YLHI-YHH1-UHLI-ULH1-UHHI-uHLI-VLH1-VHHI)~
Figure V.11. Region Level Priority Color Processing Order (Lossy).
The intrinsic 4-1-1 color down sampling relationship is maintained for region
processing
MUX modes. In terms of the reconstruction process, the complete level 4 Y-
channel
information (i.e. LL4-HL4-LH4-HH4) is required together with the U and V
channel low
pass information (i.e. LL3 in each case) for each region under consideration.
56

CA 02261833 1999-02-15
V.5.1.3. Color Interleave Region Level Processing Order (Lossy)
The color interleave processing order extends naturally to the MUX region
processing
modes. The order is illustrated in Figure V.12. This type of ordering may be
more
suitable for certain applications that require the data to be encoded for a
progressive
download based on regions of importance. As in the previous case, the down
sampling
relationships that exist for the inverse color and the wavelet space are
maintained.
RI (YLL4-Y HL4'Y LH4'Y HH4'ULL3-V LL3-
YHL3'UHL3'uHL3'YLH3'ULH3'uLH3'YHH3'UHH3'VHH3'
YHL2'UHL2'VHL2'YLH2'ULH2'uLH2-YHH2'UHH2'VHH2'
YHLI'UHLI'uHLI'YLHI'ULHiWLHI'YHH1'UHHI'uHH1)~
R2(YLL4'YHL4'YLH4'YHH4'ULL3'VLL3'
YHL3'UHL3'uHL3'YLH3'ULH3'VLH3'YHH3'UHH3'uHH3'
YHL2'UHL2'uHL2'YLH2'ULH2'uLH2'YHH2'UHH2'uHH2'
YHLI'UHLI'VHL1'YLHI'ULH1'VLH1'YHH1'UHH1'uHHIO
R3(YLL4'YHL4'YLH4'YHH4'ULL3'uLL3'
yHL3'UHL3'V HL3'YLH3'ULH3'uLH3'YHH3'UHH3'V HH3'
YHL2-UHL2'VHL2'YLH2'U LH2'VLH2'YHH2'UHH2'VHH2'
YHL I'UHL I-uHL1'1'LH I-U LH I'uLH 1'YHH I'UHH 1'V HH 1)~
(YLL4'YHL4'YLH4'YHH4'ULL3'uLL3'
YHL3'UHL3'uHL3'YLH3'ULH3'uLH3'YHH3'UHH3'uHH3'
YHL2'UHL2'uHL2'YLH2'ULH2'uLHYYHH2'UHH2'uHH2'
YHLI'UHLI-VHLI'YLHI'ULH1'VLH1'YHH1'UHHI'uHHI)~
Figure V.12. Color Interleave Region Level Priority Processing Order (Lossy).
V.5.1.4. Region Color Processing Orders (Lossless)
As in the lossy color region processing MUX modes, similar processing orders
can be
outlined for the lossless case where full data sets exist for all color
channels in each
region. In this case, corresponding decomposition level orientation
information in each
channel is related in the original color transform space for each region under
consideration. These data are processed and grouped together in the wavelet
transform
space and are ultimately put in the final bit stream by the MUX control
architecture.
The processing order for lossless color region processing is illustrated in
Figure V.13.
The color interleave order appears in Figure V.14. Note that in each case, the
full
decomposition data set for each channel is maintained. The inherent
relationships that
exist in the inverse color and wavelet space are maintained for each region
channel.
57

CA 02261833 1999-02-15
R1 (YL~,y-ULL4'uLL4'YHL4'YLH4'YHH4'UHL4-ULH4'UHH4'VHL4'uLH4'uHH4'
YHL3'YLH3'YHH4'UHL4-ULH4'UHH4-V HL3'V LH3-V HH3'
YHL2'YLH2'YHH2'UHL2'ULH2'UHH2-VHL2'VLH2'uHH2'
YHLt'YLH1'YHHI'UHLI'ULHI'UHH1'uHL1'uLHI'uHHIO
(YLL4'ULL4'uLL4'YHL4'YLH4'YHH4'UHL4'ULH4'UHH4'uHL4'uLH4'VHH4'
YHL3'YLH3'YHH4'UHL4'ULH4'UHH4'uHL3'uLH3'uHH3'
YHL2'YLH2'YHH2'UHL2'ULH2'UHH2'VHL2'uLH2'uHH2'
YHLI-YLHI'YHH1'UHLt'ULHI'UHHI'uHLI'uLHI'VHHI)~
R3(YLL4'ULL4'VLL4'YHL4'YLH4'YHH4'UHL4'ULH4'UHH4'VHL4'VLH4'uHH4'
YHL3'YLH3'YHH4'UHL4'ULH4'UHH4'uHL3'uLH3'uHH3'
YHL2'YLH2'YHHYUHL2'ULHYUHH2'uHL2'uLH2'uHH2'
YHLI'YLHI'YHH1'UHLI'ULH1'UHHI'uHLI'uLHI'uHHIO
R4(YL~-ULL4'uLL4'YHL4'YLH4'YHH4'UHL4'ULH4'UHH4'uHL4'uLH4'uHH4'
YHL3-YLH3'YHH4'UHL4'ULH4'UHH4'uHL3'uLH3'uHH3'
YHL2'YLH2'YHH2'UHL2'ULH2'UHH2'uHL2'uLH2'VHH2'
YHL1'YLH1'YHHI'UHLI'ULHI'UHH1'VHLI'uLH1'VHHI)~
Figure V.13. Region Level Priority Color Processing Order (Lossless).
DAC has developed both SNR progressive and resolution progressive MUX modes of
operation for region processing. In addition, several specialized MUX modes
were
developed that may be useful in certain applications. The regions can be
defined
automatically by the technique described in Chapter III, or user defined ROI
can be used
to group the data. User defined ROI can have arbitrary shape or can be defined
in terms
of simple geometric elliptical or rectangular region primitives.
One of the specialized MUX region processing modes can be introduced at this
point
since it fits into the context of the ordering discussion.
V.5.1.5. Transparent Region Color Processing Orders (Lossy)
This particular region color processing order is useful for applications that
require
transparent region channels that has little or no influence on the ordering of
the data.
Either of the normal SNR and resolution progressive modes are overlaid with a
complete
region channel description. The technique is implemented simply by taking the
region
index to the inner processing loop in the pseudo code implementation example
of Figure
V.B. This ordering technique may be useful in video processing applications
where a
complete region mask description is required together with a compressed frame
of
information. The region description may be used to process subsequent frames
in the
sequence. One of the processing orders that falls into this MUX mode of
operation is
illustrated in Figure V.15. In this case, the high bit plane of each region
list is processed
first causing the region classification of all coefficients to be transparent
to the
distribution and packing routines.
58

CA 02261833 1999-02-15
YLL4'Y HL4'YLH4'YHH4'U LL3' V LL3'
YHL3'YLH3'YHH3'UHL3'ULH3'UHH3'VHL3'uLH3'uHH3'
YHL2'YLH2'YHH2'UHL2'ULH2'UHH2'VHL2-VLH2'uHH2'
YHLI'YLH1'YHH1-UHL1'ULHI'UHHI'uHLI'VLH1-VHHI (Rl, R2, R3 , R4).
Figure V.15. Transparent Region Level Priority Color Processing Order (Lossy).
V.5.1.6. Transparent Region Color Processing Orders (Lossless)
Corresponding transparent region processing modes exist for the lossless case.
A typical
example is given in Figure V.16. As in the lossy case, the final bit stream is
organized
independent of the constraints of the region channels which may be useful in
certain
cases.
YLL4'ULL4'V LL4'YHL4'YLH4'YHH4'UHL4'ULH4'UHH4-uHL4'V LH4'VHH4'
YHL3'YLH3'YHH4'UHL4'ULH4'UHH4'uHL3-VLH3'VHH3'
YHL2'YLH2-YHH2'UHLYULH2'UHH2'uHL2'VLH2'VHH2'
YHLI-YLH1'YHHI'UHL1'ULHI'UHHI'VHL1'VLHI'uHH1 (Rl, R2, R3, R4)
Figure V.16. Transparent Region Level Priority Color Processing Order
(Lossless).
V.5.2. MUX List Structure for Region Processing
The MUX organizational list structure concepts introduced for normal
processing modes
have been extended to include many region processing modes of operation. In
this case,
the total number of lists is a function of the number of ROI. If there are 4
ROI, then there
are 4 times as many MUX lists. However, the basic operation of the MUX control
architecture is similar in each case.
There are three high level modes used to categorize the MUX architecture.
~ Normal processing mode (ROI disabled).
Region processing mode (ROI only).
~ Mixed processing mode (normal and ROI enabled).
The next Section outlines the operation of the bit budget and MUX controls for
many of
the region processing modes developed at DAC. The mixed processing modes are
briefly
discussed later in the Chapter.
V.5.3. Bit Budget Control for Region Processing MUX Modes
V.5.3.1. Transparent Region Level Color Mode
Transparent region processing is mentioned in Section V.5.1.5 of this Chapter.
In that
particular ordering example, the region index is placed in the inner most loop
in the bit
budget distribution function. The processing index placement is basically a
method of
incorporating a transparent region layer of processing into the normal MUX
modes
59

CA 02261833 1999-02-15
outlined earlier in the Chapter. Processing and packing in this mode gives ROI
a low
priority.
Distributing in this context ensures that the SNR progressive and resolution
progressive
MUX modes operate as they did before. The exception in this case is that there
is a
variable length region mask overhead that must be taken into consideration.
The bit
budget distribution functions are calculated as they were for the normal MUX
processing
modes. Based on the file size (or resolution level) requirements, each color
channel
receives a proportional amount of the bit budget based on the ratio
distribution technique
used in the MUX architecture.
The DCT auto regions and arbitrary or primitives user defined region types can
be
operated in this mode. In DAC's internal processing architecture the user must
select the
region coverage technique used to categorize the wavelet coefficients. DAC has
implemented the wavelet mask down sampling technique of the JPEG-2000 VM, and
it
can be used in any of the region processing MUX modes. In this manner a common
mask can be used in each orientation level or the VM mask down sampling
technique can
be used for individual orientation level mask coverage, for both automatic or
user defined
ROI in lossy and lossless MUX modes of operation. The number of region
categories
can be selected as 2, 3, or 4 channels.
In order to test the transparent mode of operation the YUV-411 color transform
is applied
to a 24 bit 256 x 256 Glacier park mountain scenery image. The 9-7 kernel
implemented
in a lifting scheme is used as the wavelet transform. The DCT region formation
technique of Chapter III is employed to generate the common masks for each
wavelet
transform level. The mean square error (MSE) is measured for a number of
compression
ratios. The result is illustrated in Figure V.17 in a plot of MSE versus Bpp.
The plot
shows the break points in MSE for each automatic ROI used in the example. The
rate of
image degradation (i.e. MSE and PSNR) must be controlled precisely for each
ROI.
MSE vs. Bpp for Glacier Park Image
6.0
5.0
4.0
W
~ 3.0
2.0
I.0
0.0
Bpp
Figure V.17. Transparent region level color mode (4 DCT region channels).
0.0 0.5 1.0 1.5 2.0 2.5

CA 02261833 1999-02-15
The MUX overhead is calculated based on the mask type and process selections.
For
arbitrary user constructed masks, the mask file can be loaded to guide the
MUX. In the 4
ROI common mask case, the overhead is 0.5 Bpp in packing the entire mask. In
the VM
mask case, the overhead is 2.0 Bpp. If simple primitives are used to form the
user mask
instead of an arbitrary shape, the overhead is greatly reduced. The arbitrary
mask
overhead can be reduced with the addition of an entropy coding stage. The
common
DCT mask overhead is cited in Chapter III as approximately 1Kb (0.2 Bpp) for
an 8 bit
256 x 256 image size. These are rough estimates that do not take the header
sizes into
account. However, they do serve as a comparative guideline for the current
discussion.
V.5.3.2. Region Priority Level Color Mode
In this mode of MUX operation, the pack ratios for each wavelet channel are
determined
as in the normal processing mode. However, there is one important difference.
In this
particular mode of operation pack ratios are determined for each region
channel. This
implies that there are 12 pack ratios for a 4 ROI process. The bit budget
distribution is
based on the overall wavelet channel pack ratios and the ROI data totals in
each region
channel. The distribution function also takes the mask and list header size
information
into account in the overall calculation.
This mode of MUX operation is designed to distribute the MSE and the PSNR
image
reconstruction measurements in an approximately uniform manner for all region
channels. A proportional amount of overall bit budget is allocated to each
region channel
based on the region and color channel pack ratios. Figure V.18 illustrates the
result of
using this mode of operation for the Glacier park image. Notice how the
quality of each
region channel degrades in comparison to the others. Auto detected DCT common
masks
are used to generate the result.
MSE vs. Bpp for Glacier Park
16.0
12.0 ~-- _ -. _. - ~~_Reg~on4-~ _._
10.0 - _ . -
8.0 ~ Re ~ on 2 -~ Region 3- ~ -_.- _ -.
6.0 _..,__ r___ ...
2.0 - -. -T-_
0.0 -
0.0 0.5 1.0 1.5 2.0 2.5
Bpp
Figure V.18. Region priority level color mode (4 DCT region channels).
61

CA 02261833 1999-02-15
V.5.3.3. Absolute Region Priority Level Color Mode
In this mode of operation, absolute priority is given to the region channels.
The
distribution function is the same in this case in that the bit budget is
divided into 12
according to total data ratio technique mentioned earlier. However the bit
budget is
distributed in a biased fashion giving the highest priority to the most
important ROI.
Some regions may not receive a budget based on the compression requirements.
The bit
budget is distributed region by region beginning at the most important ROI.
Thus
complete sections of the original image can be eliminated altogether if the
bit budget is
small. If only the important regions of an image need to be saved, this
technique can be
employed to partition the image.
A plot of MSE versus Bpp for the absolute region priority color MUX mode is
given in
Figure V.19 for the Glacier park image. Notice how the regions fade out very
fast and
sharply. This occurs when the region no longer has any budget allocated to it.
At that
point, the region is basically invalidated in terms of any contribution to the
reconstructed
image. That portion of the image basically fades out. Note that the amount of
quality of
the fade out depends on the down sampling technique to translate the masks.
The VM
mask formation technique causes a very gradual fade out to occur. In the
common mask
approach, the effect is much more abrupt.
MSE vs. Bpp for Glacier Park Image
1000 - ---_ T - __- _ _..__ _._.- ___- -__._
800 -_.. _ . .. ___. __. _. __. _. _._.. _ __
gion 4
600 . -__ _._ .. _ __
Region 3
400 .. __. _ l _ ~__ ._ _. _ _. _. _. _ _ _. _
Region
200 -. ____. ~-_.-_-.__._ ____ _ __._
0-
0.0 0.5 1.0 1.5 2.0 2.5
Bpp
Figure V.19. Absolute region priority level color mode (4 DCT region
channels).
V.5.3.4. Scaled Region Priority Level Color Mode
In this mode of MUX operation degradation rate of each ROI can be controlled.
Each
ROI contributes to the final bit stream. However, instead of having each ROI
degrade at
a uniform rate (as Section V.5.3.2.), the quality measurements of each
succeeding can be
controlled. The initial bit budget for each region channel is calculated as
before in that
the specified compressed file size is split into 12 bit budgets to be spread
between each of
the 4 region channels. However after the initial split, the allocation amounts
are changed
heuristically based on a priority factor that is set for each ROI. For
example, suppose it is
decided that ROI 1 is 50% more important than ROI 2, ROI 2 is 30% more
important
62

CA 02261833 1999-02-15
than ROI 3 and ROI 3 is 20% more important than ROI 4 (the background). Using
this
assumption as a starting point, the amount of data allocated to each region
channel is
changed slightly. The net effect is to cause the quality measurements in each
region
channel to degrade at slightly different rates. A plot illustrating this
effect is given in
Figure V.20. Note how the MSE break points for regions 2 and 3 have shifted
slightly
towards the left.
MSE vs. Bpp for Glacier Park Image
24 -
Region .
20 - - ~ . _ ._ Region 4
16 .~ _ _._ _
12 __. -__ __.__~.___._ -.___ _
__- .._~ __~~ Region 2 ~ I -.
_- ___.._ ~_ _ _ _._. ~.-__...
4 t...~~ ..1 __._.t__._r __~ _._~._
0
0.0 0.5 1.0 1.5 2.0 2.5
Bpp
Figure V.20. Scaled region priority level color mode (4 DCT region channels).
The result of using this particular MUX mode illustrates an important property
that
should be available for any ROI processing technique. The problem with many
ROI
processing techniques is that it is difficult to control how much each region
contributes to
the final bit stream. The technique outlined here can be used not only to
implement this
effect, but also to control the degradation for each region channel based
solely on an
importance factor associated with each ROI.
V.5.3.5. Region Percentage Priority Level Color Mode
In this mode of operation the user can specify a data percentage for each
region based on
the total amount available in each region channel. The distribution function
is slightly
different in this case. The data totals are determined for each region channel
along with
the wavelet color channel totals. There are still 3 bit budget for each region
channel. In
this case however, the amount of data to include for each region channel can
be set by the
user as a percentage of the total in each case.
Currently when this mode of operation is invoked in DAC's compression engine,
the user
can cycle through the operation until the desired size for each region is
obtained. The
data totals are displayed after each run. Note also that in using this mode of
operation,
one or more ROI can be eliminated or faded heavily as in the absolute region
priority
MUX mode of Section V.5.3.3.
A plot illustrating the result of using this mode of MUX operation is given in
Figure
V.21. Initially all available data is included for each region followed by
equal
decrements for each region channel.
63

CA 02261833 1999-02-15
MSE vs. Region Data Percentages for Glacier Park Image
16 ~--. _ _ i_._ __. _.__ .. J _.___
R gion 4
12 --. _ .' __ _.. ___ .____ _ _.
Region 3
W
_ ._ -_ . - _._ - _ _
Region 2
_ __-- _____ _ _..____... __.
n-
0.0 0.2 0.4 0.6 0.8 1.0 1.2
Data Percentages
Figure V.21. Region percentage priority level color mode (4 DCT region
channels).
V.6. Using the MUX for Mixed Processing
So far both normal (non-region) and ROI processing modes have been discussed.
In
addition to these modes of MUX operation, DAC has developed mixed mode
processing
capabilities. The modes of operation discussed for both normal and ROI
processing are
extended such that they can be run simultaneously for an image under
consideration. A
wavelet transform level partition is conducted based on the desired number of
region and
the number of non-region levels.
Currently non-region levels can be defined for processing lower resolution
levels and
region levels can be defined for process higher resolution levels. However,
the
implementation is not restricted by this distinction. It can be changed to
regions over
non-regions or to an interlaced combination of the two. The parameter that
controls this
distinction is termed the region start level. It can be set to any valid
wavelet transform
level (it is set internally to -1 to disable region processing.) Thus the MUX
technology
can be used in exclusive non-region mode, exclusive region mode or a
combination
mixed mode of operation.
The ordering techniques outlined for normal and region processing MUX modes
will not
be duplicated in this Section. The same concepts apply for mixed mode
processing. The
bit budget distribution functions work as they did before, but in this case
they exist
simultaneously. In some modes of operation there may be as many as 15 bit
budget
definitions used to organize the final bit stream. The method used to
determine them has
not changes. The same ratio technique that has its basis in the MUX list
structure is used
to determine the appropriate allocation in each case.
There is one additional feature that can be exploited for mixed mode
processing. An
importance factor can be attached to the non-region levels. The net effect of
this
parameter is to taper the amount of data included for the non-region levels.
In the current
implementation, the non-region levels are processed first. Thus they
considered first by
the distribution function. The importance factor allows the user to decrease
the amount
64

CA 02261833 1999-02-15
of data included for the non-region levels by a certain percentage. The delta
amount is
considered in the bit budget distribution for the region levels.
The region processing overhead is slightly smaller in this case. Depending on
the region
start level parameter, there will be less region header information required
in the bit
stream since there are fewer region levels. However, the header overhead for
the lower
resolution levels is quite small anyway.
One example is given here to illustrate the operation of mixed mode processing
(see
Figure V.22). In this particular case SNR progressive mode is used for the
upper 3 levels
and scaled region priority on the bottom 3 levels. Thus the bottom level
degradation rates
have been adjusted to favor the most important region and attenuating in some
fashion
between the other 3 regions. Notice how the MSE is lower in this case with the
same
region overhead as the previous case of Figure V.20.
MSE vs. Bpp for Glacier Park Image
35 _ _ _ _ _ _ ._
30 Re on 4
25 Region 2 _ _ _. _ _ _ ..
~ 20 - _ ___ ___ _ _ ___~ __ _ . _
15 _ __ _.._ __ _______.__-.__ _____ _
_.._ __._ Region 3 - __. _ _ __.- __ . ___ ____ -
5 _..._ ___ ..___ _._____ _ _ _. _
0-
0.0 0.5 1.0 1.5 2.0 2.5
Bpp
Figure V.22. Mixed processing MUX mode of operation (4 DCT region channels).
V.7. DCT Region Formation as a Classification Scheme
In observing this result, it is apparent that for the same region overhead, a
better result is
obtained in mixed mode. There are a number of reasons for this. The first is
that the
region channel coverage is not an exact overlay. All masks used to group or
categorize
data must deal with the down sampling issue at different resolution levels,
and the tight
overhead restraints of the compression channel. As it appears in the results
presented
here the DCT region detection mode can be applied to threshold wavelet
coefficients to
form region channels. The amount of data packed for each channel can be
controlled by
the MUX. In addition the initial data split used to create the partition can
be controlled
before the DCT mask procedure begins.
There is some region migration or intermingling of the coefficients that
occurs at the
boundaries where sharp changes occur in the original image. Some work was
conducted
in developing heuristic techniques to decrease the miscoverage in hot areas.
And there is
a benefit there. Furthermore the DCT low pass filtering stage affects the
original priority

CA 02261833 1999-02-15
bias used to partition the data. There will be a benefit in determining the
optimal data
split. By adjusting the original region partition (e.g. equally spaced
regions), the plot of
MSE versus Bpp can be set to partition the data in other ways. Inter-
resolution coverage
is another problem to consider. The mask generation technique of the JPEG-2000
VM
addresses the miscoverage problem. DAC has completed some initial
investigations of
the VM down sampling technique and further testing is required.
There is a trade off between accuracy of each region channel and mask overhead
required
for region channel operation and generation of the accuracy in the first
place. The DCT
approach shows much promise especially on the highest resolution level where
the masks
are the most accurate. One of the benefits of using this the DCT approach is
that it can be
translated to other transform levels in the frequency domain. Or
alternatively, the new
masks could be generated at a different wavelet level.
V.8. Other Processing Modes
There are many other modes of region processing operation that have not been
presented
in this document. The whole user defined region generation and MUX modes were
not
included. The processing modes introduced in this Chapter can be used in the
same way
to control each region channel. Simple primitives are cheap in terms of
overhead. One
mode of operation supports full mask sets so that arbitrary mask can be loaded
and sent
with the data to form the region channels. The mask coverage technique can be
selected
as common masks (a smaller raw size that is up sampled at the decoder side) or
VM
masks, which retain the original image dimension. More time is required to
study the
effects of both techniques as well as other region formation schemes.
Experimental results for the resolution progressive modes of operation are not
presented
in this document. These modes of operation are not currently available.
However their
implementation is not difficult. These MUX modes are currently under
development.
The experimental results presented in this Chapter were obtained using DACs 1D
bit
level sorting implementation. DAC is currently incorporating the 2D version
based on
EQW into the region processing channel. There may be benefits in retaining
both
techniques. For example, in bi-level image processing. Currently the EQW
sorting is
implemented for normal (non-region) processing MUX modes. Both sorting modes
are
available for lossless compression. There are numerous wavelet kernels and
color
transforms for both lossy and lossless compression. In addition, the number of
region
channels can be set with a current maximum of 4. Primitives can be used as
desired. The
number of primitives is not restricted to 4 with region overlaps given to the
most
important region.
66

CA 02261833 1999-02-15
VI. Bit Stream Syntax
DAC's current bit stream structure is rather dynamic given the different types
of
organizational strategies that exist in the underlying core technology.
Normal, region,
and mixed processing modes in addition to arbitrary wavelet, color, entropy
coding
various sorting stages in both lossy and losses cases.
Currently the core architecture can be divided into 2 categories.
~ Lossless compression
Full data sets lossless color selection, lossless integer lifting scheme
wavelet types,
lossless sorting and packing stages, with additional entropy coding can be
selected for
completely lossless and slightly lossy (some of the color transforms are
slightly lossy)
image compression.
~ Lossy compression
In the lossy case, color selections, more wavelet kernels / lifting schemes,
lossy
sorting and packing stages, with variable length coding can be selected
In both lossy and lossless cases region and mixed modes can be used. Currently
normal
operational modes can be realized in an almost transparent fashion for many
current
compression schemes as well as our own internal EQW / 1D sorting. The general
form
for the lossy and lossless header structures is given in Tables VL1 and VL2.
Lossless Case
Packed Item bitsSelections I Comments
header size 8 Total Header is normall about 6 b es
8 bit scale / 24 1
bit color
Ima a Width 10 64-1024 columns
Entro Codin 2 None, Basic, Ada tive
Ima a Hei ht 10 64-1024 rows
Wavelet Transform 3 Level >= 1
Levels
Re ion Channels 2 1, 2, 3, 4
Mask T a 2 None, User, Auto DCT)
Pack Raw Mask Fla 1 Read in file for mask
Mask Procedure 3 DCT Common Mask, Raw Common Mask with
VM Translation,
Down Sam lin T a 2 Heuristic DCT Down Sam lin
Re ion Start Level 4 No Re ions to # wavelet levels
Loss Fla 1 Lossless
Color Transform 2 2 Internal, YI full data sets
T a
Sort T a 1 1 D, EQW
Wavelet Kernel 2 Liftin Scheme
Table VL1. Lossless Header Structure.
67

CA 02261833 1999-02-15
Lossy Case
Packed Item bits Selections
header size 8 Between 6 to 12 b es
8 bit ra scale 1
/ 24 bit color
Ima a Width 10 64-1024
Ima a Hei ht 10 64-1024
Wavelet Transform 3 L >= 2
Levels
Re ion Channels 2 1, 2, 3, 4
Mask T a 2 None, User, Auto DCT
Pack Raw Mask Fla 1 Read in file for mask
Mask Procedure 3 DCT Common Mask, Raw Common Mask with
VM Resolution
Translation, User primitives Common or
Full Size, User arbitrarily defined
in Common and Full sizes
Down Sam lin T 2 Heuristic DCT Down Sam lin
a
Re ion Start Level4 No Re ions to #wavelet levels
Loss Fla 1 loss
Color Transform 2 2 Internal, KL, YI , YUV down sam led
T a data sets
Post Filter l Under Im lementation
Sort T a 1 1 D, E W
Wavelet Kernel 3 Daubaches, S mlet, Coiflet, Biortho onal,
Liftin Schemes
Filter T a 4 Various common filter eslsizes
KL Color Transform48 (if enabled)
Table VL2. Lossy Header Structure.
The current architecture is very flexible for introducing new technologies.
Many of the
modules are completely interchangeable. The exact bit stream syntax depends
largely on
the mode of operation selected by the user (i.e. regions, no regions, sorting,
lossy/lossless
etc.) Generally normal processing modes can be selected for all transform
levels, or for
any number of lower resolution transform levels. Region levels can be defined
for all
transform levels, or the higher resolution levels used in combination with the
lower
resolution normal levels. At some future date, the region and the normal
levels can be
mixed.
Each unit list organized by the MUX has a header tag. This header tag carries
the list
size and the high bit plane processing level for the list. The current
implementation uses
bytes per list. However bit packing is currently under implementation for tag
headers.
This will reduce this by a significant amount. Only 2 packing schemes are used
at the
global level so that no additional tag header information is currently
required. A diagram
illustrating the structure of the tag header is given in Figure VI.1. As other
core
technologies are added to the core engine or the core technology advances,
other fields
may be required in the tag headers.
68

CA 02261833 1999-02-15
Total Bytes Packed in List
Core Comprssion Scheme Use to
Process List (not currently in use)
Original Uncompressed List Size
(not currently in use)
High Bit-Plane Level Where
Processing Begins for List
Packed Data List
Figure VLI. Basic Header Tag Structure.
The basic structure for normal modes of operation is given in Figure VL2. The
diagram
illustrates a lossy pack arrangement for a color image (YUV down sampled color
transform assumed) according to the packing/processing order given in Figure
V.3 in
Chapter V. In this case the code stream consists of the file header, followed
by the
header tags/data.
File Header
Tag (Y-LL~) Tag (Y-HL~) Tag (Y~LH~) Tag (Y-HH~)
1
Packed Data Packed Data Packed Data Packed Data
Tag (U-LL.,n) Tag (V-LL..,) Tag (Y-HL..i) Tag (Y-LH".i)
Packed Data Packed Data Packed Data Packed Data
Tag (U-HHi) Tag (V-HLi) ~ Tag (V-LHi) Tag (V-HHi)
1 '
Packed Packed Packed Packed
Data Data Data Data
Figure VL2. Basic Bit Stream Syntax for Normal Modes of Operation (Lossy
Case).
69

CA 02261833 1999-02-15
The basic structure for region processing modes of operation is given in
Figure VL3. The
diagram illustrates a lossy pack arrangement for a color image (YUV down
sampled
color transform assumed) according to the packing/processing order given in
Figure V.11
of Chapter V. In this case the code stream consists of the file header, region
header,
regions description and finally the header tagsldata.
File Header Region Header Region Description
Region
i
Tag Tag Tag Teg
(Y-LC,~) (Y-HL~) (Y-LI-1n) (Y-Ht4~)
Packed Packed Packed Packed
Data Data Data Data
Tag(U-LLm) Tag(V-LLm) Tag(Y-HLm) Tag(Y-LHm)
packed Packed Packed
pate Data Data
Tag Tag Tag Tag
(U-HH~) (V-HL~) (V-LH~) (V-HH~)
~
Packed Packed Packed Packed
Data Data Data Data
Region 2
Tag Tag Tag Tag
(Y-LLn) (Y-HL,.) (Y-LH") (Y-HH")
Packed Packed Packed Packed
Data Data Data Data
Tag(U-LLm) Tag(V-LLm) Tag(Y-NLm~) Ta8(Y-LHm)
Packed Packed Packed Packed
Data Data Data Data
Tag (U-HHi) Tag (V-HLi) ~ Teg(V-LHi) Teg(V-HHi)
Packed Data ~ Packed Data ~ ~ Packed Data ~ ~ Packed Data
Figure VL3. Basic Bit Stream Syntax for Region Modes of Operation.
The basic structure for mixed processing modes of operation is given in Figure
VL4. In
this case the first item in the code stream is the file header followed by the
normal
processing mode header tags/data. Next in line is the region header, region
description
followed by the header tags/data. Notice that there is a region start level
parameter 'r' in
this case. Since there is one less transform level for U/V channels in the
lossy case, there
is a processing shift in the U/V channels. This makes reference to the "level
split" notion
discussed in Chapter V whereby the natural 4:1:1 relationship that exists for
inverse
color/wavelet transforms can be maintained for internal processing and the
final code
stream.

CA 02261833 1999-02-15
File Header
Tag Tag Tag Tag
(Y-LL,) (Y-HL.) (Y-LH.) (Y-HFh)
Packed Packed Packed Packed
Data Data Data Data
Tag Tag Tag Tag
(U-LL..n) (V-LL..,) (Y-HL..n) (Y-LFh-n)
Packed Packed Packed Packed
Data Data Data Data
Tag (U-HH..-~) Tag (V-HL,...r) ~ Tag (V-LH....~) Tag (V-HH...-~)
Packed Data Packed Data Packed Data Packed Data
Region Header Region Description
Region 1
Tag (Y-HL.-..n) Tag (Y-LH.-..~) Tag (Y-HH..-n)
Pecked Data Packed Data Packed Data
Tag (U-HL,..-x) Tag (U-LH,...z) Tag (U-HhG-.-x)
Packed Data Packed Data Packed Data
Tag (V-HL,...x) Tag (V-LFG..-z) Tag (V-HHe.r-x)
Packed Dua Packed Data Packed Data
Tag (V-HLn) Tag (V-HLi) ~ Tag (V-HHr)
Packed Date Packed Data Pecked Data
Region 2
Tag
(Y-HLm..~)
Tag
(Y-LH,-..,)
Tag
(Y-HH.-.-~)
Packed Packed Packed
Date Data Data
Tag
(U-HL,.-x)
Tag
(U-LH,...x)
Tag
(U-HH.-r.z)
Packed Packed Packed
Data Data Data
Tag
(V-HL,-.-x)
Tag
(V-LH.-.-x)
Tag
(V-HH.-.-x)
Pecked Packed Packed
Data Data Data
Tag
(V-HLn)
Tag
(V-HLn)
~
Tag
(V-HH~)
Packed Pecked Packed
Date Data Data
Figure VL4. Basic Bit Stream Syntax for Mixed Modes of Operation.
71

CA 02261833 1999-02-15
VII. Transcodability
In order to illustrate the generality and openness of RICS, two examples are
shown to
depict how the 'transcode' with bi-level images (JBIG) and JPEG can be handled
in
RICS.
VIL1. JPEG transcode
Figure VIL1 shows how a DCT-based code can be produced in RICS. With this
transcodability, it will be straightforward to write a small conversion
program to
transcode an old JPEG file into a JPEG 2000 file. Although it is possible to
transcode a
JPEG 2000 file into a JPEG file (losing some scalability), it will probably be
of very little
use.
VIL2. JBIG transcode
Figure VIL2 shows the execution path illustrating how a bi-level image such as
a text
document can be efficiently handled in the RICS system. The NULL transform is
applied (nothing has to be done). Generally binary text documents contain
mostly high
frequency energy. Mufti-resolution decompositions will not necessarily be a
suitable
basis for efficient coding. In fact, current well-known techniques specialized
for binary
images are applied directly in spatial domain. While using a RICS system for
processing
a compound document with mixed grayscale/color/text information, a set of
rectangle
shapes suffice to enclose the text regions. This is roughly equivalent to run-
length coding
in existing binary image compression techniques to skip strings of zeros. The
pixels
within each rectangular region are then coded into a one-dimensional stream
via 1-D
algorithms or JBIG routines, as discussed in Ch. IV.
72

CA 02261833 1999-02-15
a
O
~'~
.
, x
,
,~
a b
0
i, -
L-I
~
CL bA
a
a s~.~ a
W
U
a
a
~~ o
a ~o ~ a
N ~ '~:
w O ~ O
b . ,9 O W
fsi
V
a
~. o
o ~.
U ~ ~ >
o ~o
w
. . .
a
0
U
r", r",
s. ~.
0 8
w ~ o ~ o as
O ~O ,'..,
~
~ ~ ~d0. W'
a U

CA 02261833 1999-02-15
a
...
as
d
"a
~o
z
U
0
a
~,~a
a
W 0..
d
~o a
~O ~ o
'
o a
U U ~ vs
G7 bio 0
a , 's~
~ a
' a H
V
a ~ '""'o '''
a o -'
z
w
x
...
~. a °o
~> ~ ~, it ~, '~ ~ ~ N C~ H
c ~ c ~ ~, ~ W ~ ~O
~ .a ~ o d ~ ~ U

CA 02261833 1999-02-15
VIII. Post Processing
For reconstructed images with wavelet based coding methods at low bit rate, de-
ringing is
usually a useful post processing procedure to improve (mainly) the visual
quality.
Nonadaptive procedures, which apply the de-ringing filtering to all pixels
without
discrimination, have the following problems.
While they can successfully remove ringing artifacts, they may also wash out
details of image.
They usually rely on too many parameters that are to be determined by human
users.
The process is time consuming.
The RICS system employs an adaptive de-ringing algorithm for post processing.
Since
the ringing artifacts usually appear around edges where sharp changes occur,
this
adaptive filtering process is applied only to edge areas. As the result, the
post processing
removes artifacts around edges and prevents fine details from being smoothed
out by the
filter. Compared with non-adaptive methods, the processing time is remarkably
reduced
since the filtering is applied selectively to pixels. The diagram of Figure
VIII.1 shows
the algorithm of the adaptive post processing filter. First of all, the pixels
of reconstructed
image are classified into edge pixels and non-edge pixels. Edge pixels are
enlarged into
edge regions since the ringing artifacts do not occur right at the edges but
around the
edges. Then the artifact removal filter is applied only to the edge areas.
Edge Pixels Ed a De-rin in Final
Reconstructed Edge g ~ g g
Image Detection Thickening Filtering Image
Figure VIIL1. A modified post filtering procedure.
We did some tests on this adaptive de-ringing procedure. For the filtering
stage we used
the filter described in the JPEG 2000 VM 3.0 (B). Figure VIIL2 shows the
result of the
modified post processing. Artifacts are clearly visible in the first picture
especially
behind the cameraman's back and around the tripods. As we can see from the
second
picture, artifacts are removed, however, the details in the grass field and on
the man's
pants are also removed. In the last picture, the modified filter successfully
removes
artifacts and at the same time retains the details. Figure VIIL3 shows the
edge area (in
white color) that was used in producing the third picture.
76

CA 02261833 1999-02-15
Re-constructed Image VM i.0 (L3) Post-Processing Adaptive' t'ost-Processing
Filter
Figure V111.2. Performance comparison.
Figure V111.3. Edge areas where the de-ringing tiltering is selectively
applied.
As the result of using this adaptive filtering, processing time is greatly
reduced since less
pixel are processed. Table VIII.I shows the performance comparison 0f the VM
3.0 (B)
post filtering and the RICS adaptive filtering
77

CA 02261833 1999-02-15
CompressionVM 3.0 RICS CompressionVM 3.0 RICS
ratio (B) Adaptive ratio (B) Adaptive
time time sec time (sec)time sec
(sec)
3.2170 7.310 1.743 3.709 22.392 5.398
9.0140 7.260 1.702 8.889 23.023 8.151
40.210 7.325 1.482 10.000 22.442 5.288
48.763 7.170 1.462 11.428 22.232 5.809
56.492 8.262 1.402 13.333 22.462 5.878
66.550 8.703 1.382 16.000 22.482 5.629
81.143 6.769 1.362 20.001 22.522 5.489
103.716 7.171 1.175 26.666 22.382 5.568
130.168 7.170 1.222 32.000 22.422 5.338
169.019 8.310 1.132 40.002 22.352 3.896
253.337 7.130 1.052 79.987 22.282 3.465
Table VIIL1. Test Image: Camera (256x256 grayscale) Test Image: hk (256x256
color).
VIIL1. Edge Detection
To determine if a pixel is an edge pixel, the average power difference between
the pixel
and its neighboring pixels are measured against a threshold (bottom
threshold). If the
average power difference of a pixel is above this threshold, the pixel is
marked as an edge
pixel. The threshold acts as a high pass filter that filters out the pixels
with low power
levels (Band pass filters can also be used for edge detection by introducing a
proper
ceiling threshold).
Edges are thickened to form edge areas after the edge pixels are detected.
With the right
choice of the threshold, this modified filtering process can be applied to
reconstructed
images with compression ratios as low as 8:1. Since for most wavelet coded
images, no
artifacts can be visually detected for compression ratio lower than 8:1, our
results suggest
that this filter can be applied to most reconstructed pictures regardless of
its compression
ratio.
VIIL2. Parameters Optimization
One of the problems with Shen's filter is that there are many parameters
associated with
the filter, which makes the filter difficult to use. Reducing the number of
parameters will
improve the usability of the post processing filter.
There are three different potential functions implemented in VM 3.0 (B) for
controlling
the post processing: Quadratic Truncation, Huber, and Lorenzian. Our test
results shown
that the potential functions Huber and Lorenzian do not outperform the
Quadratic
Truncation in any of the 62 cases for PSNR measurements. Furthermore, visually
Lorenzian creates many noticeable ghost images and shadows, and Huber does
remove
artifacts successfully however it blurs the image more than Quadratic
Truncation.
78

CA 02261833 1999-02-15
Computation Speed
For evaluating the three potential functions, the following computation needs
to be
calculate n x (n -1) I 2 times for every pixel (where n = filter size x 2 -1
).
Lorenzian: 1 float division, 2 float multiplication, 1 float addition and 1
float
log operation
Huber: 1 comparison, 1 float multiplication or 2 float multiplication with 1
addition
Quadratic Truncation: 1 comparison and 1 float multiplication
In our tests, Quadratic Truncation is the fastest and it performs the best for
artifact
removal with the least degradation to image quality. Therefore, the other two
potential
functions will not be used.
Threshold (y parameter in the potential function)
The y parameter is examined using the quadratic truncation potential function
(default
value is 16), given by:
a = arg min ~ p(X; - Xj )
xi x~eN
Yz ~(xi xj)>Y
where, p = { (Xr - Xl ) z ~ (xl _ x j ) <- Y
We can see from the equations that only pixels with similar neighboring pixels
are
affected when varying y. When y is decreased, there will be more y2 as the
result of p
and the intensity of similar pixels output image will be more uniformed
resulting a more
blocky looking type of image (less gradual) for regions with similar
intensities.
Experiments were performed with 2 images (one grayscale and one color image).
Table
VIIL2 shows the result for the color image.
79

CA 02261833 1999-02-15
CompressionPSNR (~=8)PSNR (~=12)PSNR (0=16)
Ratio
3.709 31.32961131.177579 30.511348
4.000 31.30045231.154471 30.490295
5.333 31.15703130.994670 30.357978
8.000 30.63038330.474574 29.862022
8.889 30.40164930.216825 29.646734
10.000 30.06777829.909074 29.375402
11.428 29.69134729.546710 29.056083
13.333 29.22845429.103298 28.645196
16.000 28.40772428.276664 27.908937
20.001 27.50867027.413509 27.134810
26.666 26.38541926.307257 26.084268
32.000 25.33380825.280108 25.111808
40.002 24.69665524.660851 24.509536
79.987 22.17927422.152787 22.093103
100.004 21.59259521.568550 21.525140
Table VIIL2. Test Image hk.raw results.
We can see from the results that the higher the y, the worst the image
quality. However,
the difference in image quality is not very significant. The pictures look
very similar and
there are no significant changes that can be detected. However as predicted,
the blocky
looking clouds (see Figure VIIL2) are seen when y = 8 or below. Therefore by
setting y
lower we can increase the image quality by some small amounts without changing
the
visual quality of image. Therefore y = 12 was chosen to be the default value
for y
parameter in the potential function.
Filter Length
Filter length (F) determines of the size of samples collected for pixel
estimations. It is
obvious that the larger the filter length the longer the processing time. The
default length
given by VM3.0 (B) is 9 pixels. Experiments are performed with varying filter
lengths to
examine how the length affects the image quality (MSE and PSNR) and the
artifact
removal ability. Two pictures are used in this experiment (one color and one
grayscale).
The results are shown in the following Tables VIIL3 and VIIL4.

CA 02261833 1999-02-15
CompressionPSNR (F=3)PSNR PSNR (F=7)PSNR PSNR (F=11)
Ratio (F=5) (F=9)
1.583 35.51459234.20686733.68744833.40984933.223806
1.600 35.51620434.20180133.67456533.40817833.220934
2.000 35.31459534.08023733.53899833.30123233.090358
2.667 34.95761233.76571933.29127033.01171332.832969
4.000 34.00279732.99773532.56424832.33825732.200522
8.000 31.08973530.55402730.32438130.19646330.106473
8.889 30.57214530.14234829.93520929.79633529.725453
9.999 30.13195229.79563129.60454929.47240129.394763
11.429 29.62934629.39045629.26147129.1313129.064764
13.334 28.85487328.70127128.60214528.52796428.470308
16.000 27.87010127.76047827.67114227.63260927.579655
19.999 27.03180626.91091426.85712326.83549226.794267
26.662 25.96269225.99410025.99975926.01978725.991909
40.010 24.15913424.17876124.17301124.19161824.182049
80.020 21.65434021.68392021.73155921.76167621.774576
Table VIIL3. Test Image camera.raw (grayscale) results.
CompressionPSNR (F=3)PSNR PSNR (F=7)PSNR PSNR (F=1l)
Ratio (F=5) (F=9)
3.709 31.65696030.74042030.80626730.51134830.298514
4.000 31.63476330.73584230.79179130.49029530.278695
5.333 31.43641130.55889830.63512130.35797830.141580
8.000 30.81958730.06578930.12671329.86202229.680912
8.889 30.53757929.83907429.87985429.64673429.474362
10.000 30.17040629.54109929.60352729.37540229.205815
11.428 29.74085829.18672629.25512329.05608328.880456
13.333 29.25522528.75259828.83929428.64519628.494299
16.000 28.39171527.98294328.07586627.90893727.788081
20.001 27.47911727.16236927.27092127.13481027.012976
26.666 26.32900726.07913226.17559026.08426825.999266
32.000 25.27996025.08825525.18138725.11180825.044080
40.002 24.64933424.48689624.56857924.50953624.446939
79.987 22.19535122.09985322.12775722.09310322.066329
100.004 ~ 21.598939~ 21.520845I 21.561808~ 21.525140I 21.501686
Table VII1.4. Test Image hk.raw (color image) results.
As we can see from the experimental results, the small the length, the better
the image
quality and the shorter the processing time. However, artifacts are not
completely
removed for length = 5 (or smaller) at high compression ratios. The default
value for the
filter length is chose to be 7 pixels to increase image quality and to
decrease processing
time without degrading the ability for artifact removal.
s1

CA 02261833 1999-02-15
Constraint
The value of constraint (~Thl ) alfects the filter as described in the
equations below.
v =.e+c(cl.Thl)
cl= ~-x
c(cl,Thl ) = sign(cf) * Max(0, abs(d) - Max(0, 2*(abs(c~ - Thl )))
From the equations above, we can see that as Thl increases, more pixels will
have 'd' as
the output for c(cl,Tlrl). Iherelore, as 'I~hl increases, more estimate value
of x will be
used as the innal estimate and the image quality will decrease while the
smoothness of an
image will increase. In order to keep the image quality as high as possible,
ft~hl should
be kept as low as possible. 1-lowever, artifacts might not be properly removed
if Thl is
set too low. 'three images were tested with different level of constraints in
the
experiment. The test results are given in Tables VIII.S to VII1.7.
(pompMSE PSNR MSE PSNR .VISE PSNR ~'ISI~: I'SNR
~ ('4 ('=t (.'6 ('6 ( ('8 ('IO-__ C'l0-
Ratio 8
1.583:'~.'7654~139.229159]~.~ft~Il436.5883552U;'2.~3~35.(16384524.678U7~134.207
692
: '<
l.6lt(t.:''l.~$32I~339.21922(11~.~'7'1~~23h.5Rti(171120.31259..35.0531142~."~~~
33~34.IS)3714
-
2.o(l(t~:~2'~8~it38.925459t~.~9$59636.37(1297Z'~.,t,23~~~34.883178~~5.~5664-
134.055766
a ' ' .
i
9.~~2i~Qt3R.26t'~66')16;9322535.957748~2.9'9"~$~434.5139292~'.4~$~0~33.737744
2.tib7'. '
4 19.?22U4G36.451 21.984?S34.709662.28.8U8>'~~333.53551433.09'14$832.932853
oou : 122 ;
8.0(104~p~;83~p931.64885249.9(1~~8Ei31.1497125~.~4913330.6R4o31~~.Q"73$3~:3U.-
416851
' I
R.8R952."~~I9.~30.9045315'~.66~~843(1.521456-.fi2.~b74'773o.IR1222~~.3~6~~~I
,' ' .' 2'O')77944
9999 i6(t.63~t11~r30.303783~4.$8T3~4..30.00920468,"1?~~19G3
29_756500'~1,20~bi~C29.ti05845
~
' 6~:2~~'~~$~'~.72768772;'~6~31$29_51 '7~.~131$4
29.35()57('~.~9~488.'29.232327
I -- 1321 >
1.429
13.33.1e~l:~~?8~Z528.962695$5;~46~5$328.813043$~.9d386~ 28.6887-
tR~9:7~1'(~'T~28.602798
I~ IQ~,~"~'s~27.899311~1$.2F~a~0~?7.7R5~r~9.~~3099'. 27.717939.;I ~
27.(59899
I ' t5 1,~~~('~i
-
19.999(~'~:3~$~tH1'26.94655913~.(61~~~526.88683913~#:35~13?
26.84842t>~~~.84~~~2ti.R32~18tt
~ ' i
26.662~1'z612(73~i25 9265741C~.2~I$I25.9490791~4~ia*9~~ti~ 25.98(1794.
7C3.3f3~r7'25.999188
40.010;Z4'~;$$19IU'24.1539772~~.1~4$~~.24.165936~~~;"~t~I~B
24.181593~4?,~~~4k~624.187081
8(1.020~~~.~2~~5031.704967~t3?.6t4~fl21.719818~~~~l~It~~-
21.736217~13~.?x336'21.748404
Table VlII.S. Camera.raw (part a) results-
82

CA 02261833 1999-02-15
Comp MSE PSNR MSf. I'SNR MSIC'161'SNR
Ratio C'12 C'12 C14 C1.~ C'16
1.583 'x2~.~5~1'$3133.40')84935~7~,$5i-32.65652141.~a*$9S731.965423
I
1.600 ~9.6frfs~~4533.408178~~~~5$~#0532.656995' 43.37~42~; I .9(i2959
' ~
x.000 '30.~4~$S~33.30123236.~49fi~~:32.537766' 4~.3~'~~~a31.860463
?.667 32.$Q192333.0117138.26~$G9_i2.30268843.~$"~1231.(i97c)84
' 3 '
4 000 39.95~'7~132.338257'~3~"~~?LI~.~''31.758905:.~$.'~~~~9731.252020
I 8.c)oo~2.148~$"~30.1964636~~~2'7~29.942129b9.U7f2'7129.737452
-
j 8.889= i5$.~4~bt~29.796335'70~5~~$29.626910~3.~'~~~~~29.463474
9.999 '~3.~~~3~'~29.472401?S$$61 29.329176'~$.$~~C~29.160108
; ~~' I.
'
11.429''~9,42~56929.1 81,6~~~1~.29.012885$~<3~~0~3_'28.869385
- 31310
13.3349],~~'~~X8.527964~3.2J~~5~28.436833-- ~5.~~3~a3528.340178
' ' ;
16.000~12.X3~212X7.632609l 1~.~$~~5:127.697400l 1~.~~#56127.54661
> I I
i 19.999134.75U?'4$26.8354921~~:18~$1626.821589' '1~5.'732~I2(i.8()3981
i X6.662.=162:5394126.0197871~~.$33~?~$26.013378I'6~.~I92~26.005148
.
40.010'~~'3.&~~~402:1.191618~4~..~7~i'~92:24.183297249.1~$4$~=24.165350
I
80.020~3~.c(;~3$~3X1.7616764~3.~~3(?~~721.7585784~~.8~31'T1=21.747777
Table V111.6. ('amera.raw (part b) results.
Comp MSE C6 1'SNR MSE PSNR MSE CIO E'SNR
Ratio C6 C8 C8 C10
3.709 $0.$66U4$32.01717748,~2,~~1 31.280383,~3.3,t83'730.858253
'
4.000 ~~:13~"'2~231.9882384.~2$~~5 31.26191853.6~8~7$30.837691
. :'-
6.333 ~~.I$~41931.777734~~,'7~~$$~ 31.077137~.~~$~8~30.684074
' :,
8.000 $Q.f6?9~331.092(149S:T<"~7Q~b2" 30.5137686~.5$~1~30.16791
' 1
s.8s9 5~.322~G~30.781 61.44~U~$ 30.245965,94152829.939214
() 34
17
l0.00os9.zs37$4'30.4o364s~~.~SS6~1 29.92310070:7~~ti~9~29.633349
11.42s65.83Q$S29.9470217~.~896~~; 29.546os6.:7~.~4~~~32.29.296639
13.33 ?3.$$'T9~'729.4.62736$0"~4~7~9 29.086581$~.5~51~'~28.861458
3 - .
16.00()9U.$$1"l'7tt28_646036~~'.1$4U'~~'28.254853~U1.~~$i~~i328.078663
20.001~~~.()806~327.696921~~.$,3$(~'' 27.398874~22.If92'71'27.261184
26.666~~7:8,1~'~~026.4.335971~2,.9~,~'~'~Z 26.285258~Sd:G463~$=26.181599
32.0001$~.~~T~~fx.25.3.628051~~.~93~b~' 25.252939t9'1.4~?~1626.175851
40.0022~9.$l6'73~24. ~9...~I~~~$' 24.626109rZ'~'.~3f?'1~3'4.$6985
7 10196 3
79.9873$$.3'321832?.238546~9.~,~5845I) 22.176299~9'~.$l$',~'9~~~.133956
100.0044~6,~I~S'~9''l.(~34422~$~.8$$4~$ 21.590113~~.3~I78-21.567097
J
'Table V111.7. HK.raw results.
These results show that image quality decreases as constraint increases.
However, some
artifacts (very small, can only be seen when the picture is enlarged) are not
completely
removed when C' is equal to ~~ or less. In order to achieve the best image
quality while
successfully remove artifacts, l:he value 8 is suggested to be the default
value.
83

CA 02261833 1999-02-15
Iteration
It is obvious that processing time is directly proportional to the number of
iterations.
However, artifacts might not be removed successfully if the image is not
processed
enough times. Table VIIL8 below clearly shows that image quality decreases as
the
number of iteration increases. However, when image is enlarged, small
artifacts can be
still visible for Rl. In order to achieve the best image quality while
successfully remove
artifacts, 2 iterations is suggested to be the default setting.
Comp PSNR PSNR PSNR PSNR PSNR
Ratio Rl R2 R3 R4 R5
1.583 36.57457034.64294333.40984932.69751932.241311
1.600 36.56205234.63752633.40817832.69010032.238019
2.000 36.36253734.48670133.30123232.59959732.146102
2.667 35.93246534.13405533.01171332.34781631.926978
4.000 34.72258633.30159832.33825731.77851731.416868
8.000 31.26437930.64044030.19646329.89213129.673122
8.889 30.66043130.18369729.79633529.54711729.365451
9.999 30.20114129.80043929.47240129.24420929.090109
11.42929.70653629.39825529.13131028.94210928.805907
13.33428.94695028.73363728.52796428.37840728.263955
16.00027.92464527.78411927.63260927.51037327.424183
19.99927.01821026.93889126.83549226.74966326.687918
26.66226.02514226.04556426.01978725.97115325.921551
40.01024.20951424.21433824.19161824.15266324.116273
80.02021.7043621.74727621.76167621.76226721.751451
Table VIIL8. Quality versus iterations.
Mask Shape
Different shapes of masks are discussed in Shen's paper, however, only the one
with the
shape of a + sign was implemented in VM3.0 (B). Different masks were
experimented
and the shape of mask is best left unchanged since simplifying the mask
degrades the
performance of the filter and complicating the mask increases processing time
greatly.
VIIL3. Using the Modified Post Processing Filter
The adaptive de-ringing is implemented based on the post processing filter in
VM3.0 (B).
Few parameters have been eliminated and default values have been established
to
increase the usability of the post processing filter.
To use the modified post processing filter:
Usage: post2 -s width height bpp -i infile -o outfile [-1 mask lower
threshold]
[-w mask width] [-t thresh] [-f f length] [-c constraint] [-r iterations]
Default values will be used for the parameters if the parameters are not
specified in the
command line. The default parameters are:
mask lower threshold: lower threshold for edge detection [30]
84

CA 02261833 1999-02-15
mask width: width of mask [12]
thresh: ~y parameter in the potential function (for estimation) [12]
f_length: filter length [7]
constraints: constraints using in the clipping function [8]
iterations: number of iterations [2]
The modified post processing filter performs well with the above default
parameters,
however, these parameters can be changed at the command line if the user
wishes. The
post processing filter can now be applied to pictures with 8:1 compression
ratio with very
small increase in MSE. The modified post processing filter seems to improve
image
quality for compression ratio beyond 1 I :1.
In practice, there are two ways for the user to play with the settings: on the
encoder side
and on the decoder side.
Decoder end
The decoder will have the full control of the post processing and the of the
associate
parameters. The encoder will have no control on how the images will look at
the decoder
end. Accordingly, there will be no addition to file header since no post
processing
parameters will be included.
Encoder end
When necessary, the encoder can also predetermine the post processing filter
parameters.
Post processing filter parameters will be stored in the image header, and the
image will be
restored according to these parameters. In this setting, the user at the
encoding end
knows exactly how the image will look at the decoder end. However, adding
these
parameters in the header will increase the size of the compressed image.
Total of 6 parameters will need to be packed in the header: mask lower
threshold, mask
width, estimation threshold, filter length, constraints and number of
iterations. Table
VIIL9 suggests range limits on the parameters to reduce the header size.
Parameter Number of Value Ran
Bits a
Mask Threshold7 0-127
Mask Width 4 5-20
Estimation 4 5-20
Threshold
Filter Len 3 3-10
h
Constraints 4 3-18
Iteration 2 1-4
Table VIIL9. Quality versus iterations.
In total, three bytes will be needed to include these parameters in the
header.

Dessin représentatif