Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
CA 02273377 1999-OS-31
METHOD AND APPARATUS FOR
CHANNEL ESTIMATION FOR MULTICARRIER SYSTEMS
BACKGROUND OF THE INVENTION
The present invention is directed to a method and apparatus for estimating a
wireless communication channel. More particularly, the present invention is
directed to a method and apparatus for providing robust channel estimation in
a
multicarrier communication system.
As wireless communications demands continue to grow the goal is to be able
to provide effective communication channels capable of transporting a wide
range of
information. As one example it has become desirable to provide wireless
services
capable of transporting multimedia information such as, for example high
definition
television. Multimedia wireless services require high-bit-rate transmission
over
radio channels. Those radio channels can provide mobile communications. One
technique for reducing the effect of intersymbol interferences (ISI) caused by
the
dispersive Rayleigh fading environment is to make the symbol duration much
larger
than the channel delay spread. This can be achieved using a multicarrier
configuration. One example of such a configuration is orthogonal frequency
division multiplexing (OFDM) on which the entire channel is divided into many
narrow subchannels, which are transmitted in parallel, thereby, increasing the
symbol duration and reducing the ISI.
Orthogonality is a property of a set of fimctions such that the integral of
the
product of any two members of the set taken over the appropriate interval is
zero.
(For discrete fimctions summing is done rather than integrating.) For example,
trigonometric functions appearing in Fourier expansions (e.g., sines and
cosines) are
CA 02273377 1999-OS-31
2
orthogonal functions.
Orthogonality ensures that a receiver demodulating a selected carrier
demodulates only that carrier without simultaneously and unintentionally
demodulating the other carriers that are providing parallel data transmission
along
the multiplexed communication channel. Accordingly, there is no cmss talk
between carriers even though the carrier spectra overlap and there is no
requirement
of explicit filtering.
Therefore, OFDM is an effective technique for combating multipath fading
and for providing high-bit-rate transmission over mobile wireless channels.
It is known to use differential demodulation, for example differential phase
shift keying (DPSK) in OFDM systems to avoid system complexities that would
otherwise arise from having to track a time varying channel. This differential
demodulation technique comes at the expense of a 3-4 dB loss in signal-to-
noise
ratio (SNR) compared with coherent demodulation. If there is an accurate
estimate
of the channel characteristics that can be used to adjust the received signal,
then the
channel OFDM system performances can be improved by allowing for coherent
demodulation. Furthermore, for systems with receiver diversity, optimum
combining can be obtained by means of channel estimators.
It is well known that the structure of an OFDM signal allows a channel
estimator to use both time correlation and frequency correlation. An ideal
estimator
would have a two dimensional structure that attempts to estimate the channel
response in time and frequency. FIG. 1 illustrates a two dimensional frequency
(y-
axis) - time (x-axis) matrix. The ideal estimator must estimate the response
over this
grid.
It is suggested in one paper that such a two-dimensional estimator structure
is generally too complex for a practical implementation. See OFDM CHANNEL
ESTIMATION BY SINGULAR VALUE DECOMPOSITION, Edfors, et al. VTC
'96, pp. 923-927. Additionally, it is known in the art to provide an estimator
using
only frequency correlation to avoid the complexities otherwise involved in
utilizing
time and frequency correlation. In one example an estimator considers minimum
mean square error (MMSE) and least squares (LS) estimations.
CA 02273377 1999-OS-31
3
It would be advantageous to provide estimation that takes advantage of both
the time and frequency correlation of the channel while avoiding the
complexities
alluded to in the prior art. It would also be advantageous if that estimation
could be
robust, that is the estimator would provide good transmission characteristics
over a
widely varying channel which can easily arise in a mobile communication
environment.
SUMMARY OF THE INVENTION
The present invention addresses the concerns known in the art by providing a
robust channel estimator that can be employed in a multicarrier wireless
communication system. In accordance with one embodiment of the invention the
estimator is used in an OFDM system and is a minimum mean-square error (MMSE)
estimator, that makes full use of the correlation of the channel frequency
response at
different times and frequencies. In particular, for mobile wireless channels,
the
correlation of channel frequency response at different times and frequencies
can be
separated into the multiplication of the time- and frequency-domain
correlation
functions. Hence, an MMSE channel estimator can be a frequency-domain filter
using a Fast Fourier Transform (FFT), followed by time-domain filters. Since
the
channel statistics, which depend on the particular environment, are usually
unknown, it is advantageous to provide a robust estimator, that is, an
estimator
which is insensitive to the channel statistics.
In addition the present invention provides a unique reference generator with
respect to the estimation process. In particular, the reference signal can be
derived
from a number of different sources. Either decoded information or undecoded
information can form the basis for the reference generation operation.
BRIEF DESCRIPTION OF THE DRAWINGS
FIG. 1 illustrates a block diagram of an example of a system in which the
present invention can be implemented.
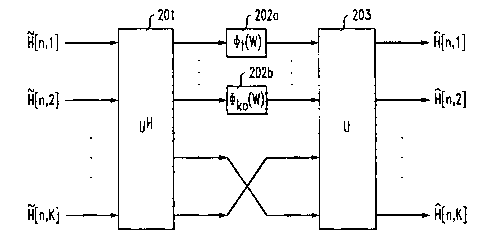
FIG. 2 illustrates a block diagram of components forming part of a channel
estimator in accordance with an embodiment of the present invention.
CA 02273377 1999-OS-31
4
FIG. 3 to 10 are plots which are helpful for understanding the operation and
effectiveness of an embodiment of the present invention.
DETAILED DESCRIPTION
Overview of the Invention
The present invention provides a channel estimator for use in a mufti-carrier
system. In the particular example shown the system is an orthogonal frequency
division multiplexing system. Other mufti-carrier systems may take advantage
of
this system by appropriately modifying the equations set forth in the proofs
that
follow this overview. An example of a system in which the present invention
can be
implemented is shown in FIG. 1. The system includes a transmitter 110 and a
receiver 160. In this example the receiver has a property called diversity,
that is
there are multiple receiver antennas adapted to receive channels that have
traversed
different paths. It is possible in one example that the antennas be arranged
to have
different orientation, but this is not necessary. Furthermore, the invention
need not
employ multiple antennas. Instead, the invention described below can be
adapted to
a single antenna environment.
In the transmitter, encoder 111 receives a data signal, for example b [n, k],
which is a signal constituted by multiple blocks of data, each block having a
number
of tones ("n" refers to the time channels where a plurality of blocks of tones
are
transmitted over time; "k" refers to the tones) in a given block). It is
assumed that a
"b [n, k]" has unit variance and the data symbols are independent. The code
across
tones is utilized in the system to correct burst errors that can result from
frequency-
selective fading. In one embodiment the encoder is a Reed-Solomon (R-S)
encoder,
although other encoders may be employed. The output of the coder, a [n, k], is
the
signal modulating the k-th tone during the n-th block. The output of the coder
is
supplied to modulation module 112 which produces output x [n, k] to be
supplied to
inverse fast fourier transformer (IFFT) 113 whose output is transmitted over
the
radio channel. In one embodiment this module provides QPSK modulation but
other modulation techniques could be used. Note that since the phase of each
sub-
channel can be obtained by the channel estimator in the receiver as described
below,
CA 02273377 1999-OS-31
coherent detection is used to enhance system performance. Thus, the
transmitted
signal comprises the OFDM signals.
At the receiver 160 each receiver antenna, (not shown) provides its received
signal to a corresponding FFT module, e.g., 1621, 1622, 162P where p equals
the
number of receiver antennas and thus channels. The outputs of these FFTs are
shown as x,, [n, k],... xp [n, k]. All of these received signals are supplied
to a
channel estimator 170. They are also supplied to their own corresponding
signal
adjuster, e.g., 1641, 1642,...164P. The outputs of the adjusters are coupled
to a
summing device 166 which yields as an output y [n, k]. This latter signal is
supplied
to a reference generator 175 and a demodulator 167. The output of the
demodulator
a [n, k] is also supplied to the reference generator and is further supplied
to a
decoder 168. Again, the decoder need only complement the encoder, but in the
specific embodiment described the decoder is a R-S decoder. The output of the
R-S
decoder b [n, k], under ideal conditions, would completely match b [n, k] the
input
to the transmitter. The output of the R-S decoder is yet another input to the
reference generator 175. The output of the reference generator 175, ~ [n, k],
provides another input to channel estimator 170. The estimator generates
adjustment parameters I~, [n, k],....I~p [n, k] that adapt the receiver to the
detected
characteristics of the various channels.]
As will be described in the proofs and equations that follow this overview, a
correlation function rH [n, k] of the channel frequency response H [n, k] over
all of
the channels can be separated into the multiplication of a time domain
correlation
r~[n] and a frequency domain correlation r,{k]. The time domain correlation is
dependent upon the speed of relative movement between a receiver and a
transmitter
or equivalently the Doppler frequency. On the other hand, the frequency domain
correlation depends on the multipath delay spread.
Using this separation property, a channel estimator is created using minimum
mean square error estimations.
The estimator provides two dimensional filtering, that is, in both time and
frequency. As shown in FIG. 2 the channel estimator includes two frequency
transformation blocks, 201 and 203, and a plurality of filters, 202x, 202b,
that
CA 02273377 1999-OS-31
6
exploit the time correlation of the channel parameters. The details of the
transform
modules and the filters will be described below. It is believed, however, that
this
unique arrangement of filters, namely placing the time correlation based
filters in the
middle of the estimator, between the frequency transformation operations is
very
beneficial because it achieves good channel matching without need for high
computational complexity. This contrasts with what would be required to
achieve
two-dimensional filtering based on the disclosure by Edfors et al. described
above.
Once the channel statistics, such as the time-domain correlation and
frequency-domain correlation are known, the optimum channel estimator can be
designed. However, in the mobile wireless links, the channel statistics depend
on
the particular environments, for example indoor or outdoor, urban or suburban,
and
change with time. Hence, it may not always be advantageous to design a channel
estimator that tightly matches the channel statistics. Therefore, it may be
beneficial
to use information about performance degradation that can arise from a
mismatch of
the estimator to the channel statistics to provide a more robust estimator
design.
More specifically, in accordance with an embodiment of the present
invention, coefficients for the estimator calculations, e.g., the time
correlated filters,
are set taking into account a maximum delay spread and are chosen to match a
rectangular spectrum rather than attempting to match the doppler spectrum. By
properly choosing the coefficients the estimator is largely insensitive to
particular
changes in the channel characteristics such as might arise where at least one
of the
transmitter and receiver are moving relative to the other. Subsequent
description
will set forth a comparison of performance of the robust filter and exact
matching
filters under both known and unknown conditions.
The present invention also includes the notion of selecting a reference
generator but put for use with the channel estimator. More specifically, as
illustrated in FIG. 1 the reference generator receives y (n, k) from summer
166, a
[r, kJ from demodulator 167, and b [n, k]. If the decoder can successfully
correct
the received signal, then b [n, k] will be used to generate the reference
signals a [n,
k]. If the decoder cannot successfully correct then the output of the
demodulator,
signal a [n, k] is used to generate the reference since otherwise the decoder
would
CA 02273377 2002-05-02
_ 7
create more errors for the system by propagating the uncorrected errors to the
reference generator. Thus this decoded/undecoded dual mode reference generator
further suppresses error propagation in the robust channel estimator of the
present
invention.
Proofs and Calculations Supporting reinvention
Statistics Related to Mobile Radio Channel
It is known that a complex baseband representation of a mobile wireless
channel impulse response can be described by
h(~~~) _~ Yk(t)a(~ _Tk) c
k
(1)
where zk is the delay of the k-th path and yk(t) is the corresponding complex
amplitude. Due to the nature of the environment yk(t) 's are wide-sense
stationary
(WSS), narrow-band complex Gaussian processes, which are independent for
different paths.
It is assumed that yk(t) has the same normalized correlation function r~(nt)
for
all k, and therefore, the same normalized power spectrum p, (S~). Hence,
r~k(nt) ~ E~Yk(~+~t)YkU)}
= akr (~t)~
(2)
where ok2 is the average power of the k-th path.
From Jakes' model as described in Microwave Mobile Communications,
Jakes, published in the U.S. in IEEE Press, 1974, the normalized power
spectrum is
If I~~ < ~d
J~JU~ = f .
~ otherwise
(3)
CA 02273377 1999-OS-31
and therefore,
r~(nt) 2f ' 1 {p~(iZ) } = Jo (Clot),
(4)
where Jo(x) is the zero-order Bessel function of the first kind, ~d = 2afd and
fd is the
Doppler frequency, which is related to the vehicle speed v and the carrier
frequency
f~ by
.fd = y
c
(5)
where c is the speed of light. For example, for a system where the user is
moving at
60 miles/hour and there is a carrier frequency f' = 2GHz, then fd = 184 Hz.
Using ( 1 ), the frequency response of the time-varying radio channel at time
t
is
hl(t~ s f ~h(t,z)e '1"~dT
-~ Y~(t)e ;mhk
(6)
Hence, the correlation function of the frequency response for different times
and
frequencies is
1'H(=~t,~f) -_' E{H(t+_lt,f+.:lf)H'(t,f))
- ~''7k~Vt)e ~'"°IT'.
~.~~,t~(~~ke_~~a~jrk)
Lrk
- ~Ef''~('t)rl(:~f),
. 15
where azH is the total average power of the channel impulse response defined
as
CA 02273377 1999-OS-31
9
a~~ a2
k k'
(g)
and
2
rf (°'~_~, .~k a jlaelck
k
aH
(9)
It is obvious that rt(0)~rf (0)=l . Without loss of generality, we also assume
that a2H
=1, which, therefore, can be omitted from (7).
From (7), the correlation function of H(t,fj can thus be separated into the
multiplication of a time-domain correlation rt(°t) and a frequency-
domain
correlation r~(°f) as described above in the overview section.
r~(°t) is dependent on
the speed, for example, of the receiver relative to the transmitter, or,
equivalently the
Doppler frequency, while r~(°fj depends on the multipath delay
spread. As
described above, this separation property, is useful in simplifying our MMSE
channel estimator as described in the next section.
For an OFDM system with block length T f and tone spacing (subchannel
spacing) °f, the correlation function for different blocks and tones
can be written as
rH[n,k] =rt[nJr~[k],
( 10)
where
CA 02273377 1999-OS-31
- 1~
rt[n]sr~(nT~, and r~[k]sr~(kof).
(11)
Let p~(c.>) represent the Fourier transform (FT) of the discrete sequence
{rJ[n] } .
Then, for Jake's model, from (3), the FT of rJ[n] is
if ~:.y < ;.rd
PJ~W~ Wa 1'l"'~'''a)= ,
0 otherwise
(12)
where c.>d = 2 ~T ffd.
A Channel Estimator
As described in the overview section for a diversity receiver, the signal from
the m-th antenna at the k-th tone and the n-th block can be expressed as a
signal
based on the transmitted signal a [n, k] as influenced by the channel
characteristics
and noise. This can be expressed as
xm[n,k] = H,~[n,k]a[n,k]+W [n,k].
(13)
In the above expression, Wm[n,k] is additive Gaussian noise from the m-th
antenna
at the k-th tone and the n-th block, with zero-mean and variance p. It is also
assumed that Wm[n,k] is independent for different n's, k's, or m's. Hm[n,kj,
the
frequency response at the k-th tone and the n-th block corresponding to the m-
th
antenna, is assumed independent for different m's, but with the same
statistics.
a[n,k] is the signal modulating the k-th tone during n-th block, and is
assumed to
have unit variance and be independent for different k's and n's.
With knowledge of the channel parameters, a[n,k] can be estimated as y[n,k],
by a minimum mean-square-error comb~ner,
CA 02273377 1999-OS-31
m 1Hm[n,kJx,"[n,k]
y[n,k] _
m 1 Hm I [n'k] I 2
(14)
However, the multipath channel parameters are time-varying and are usually
unknown. Hence, a channel estimation algorithm must be derived to obtain
accurate
estimation of the channel parameters.
Since the channel corresponding to each antenna has the same statistics, the
channel estimator for each antenna has the same coefficients. Furthermore, the
estimator for each antenna works independently since the signal from the other
antennas carries no information about the channel parameters corresponding to
this
antenna. Therefore, the subscript m is eliminated from Hm[n,k], in the next
two
subsections.
MMSE Channel Estimation
If the reference generator 175 in FIG. 1 can generate an ideal reference
a[n,k], then a temporal estimation of H[n,kJ can be obtained as
H[n,k] = x[n,k]a'[n,k]
=H[n,k] +W [n,k]a ' [n,k],
(15)
where the superscript * denotes the complex conjugate. H[n,k]'s for different
n's,
and k's are correlated; therefore, a minimum mean square error (MMSE) MMSE
channel estimator can be constructed as follows,
CA 02273377 1999-OS-31
- 12
0 k-1 ...
c[m~hk]fin -m~-1],
m=-~ 1=-(K-k)
(16)
where c[m,l,k]'s are selected to minimize
MSE({c[m,l,k] })=E ~ H[n,k] -H[n,k] ~ 2.
( 17)
K, in the above expression, is the number of tones in each OFDM block.
Denote
c(m,k] s' c[m,k-l,k]~
c[m,0,k]
c[m, -K+kk]
(18)
0
c(c~;k) ~ ~ c[n,k]e '"''',
n=_.
( 19)
and
C(w) °-(c(c~;1 ), c(c.~;2),..., c(c~;ln).
(20)
Then, using the separation property (10), it can be shown that the estimator
CA 02273377 1999-OS-31
- 13
coefficients are given by
C(c.~) -_ U x~(~)U.
(21 )
In the above expression, ~(c.~) is a diagonal matrix with the 1-th diagonal
element
~1(~)=1 _ 1
Mi( _w)Yi[0)
(22)
where M,(c.~) is a stable one-sided Fourier transform
s
Mn~)=~ Y,[n}e '"~
=o
(23 )
which is uniquely determined by
d
M~(~)M,( -~) = P j(~) + 1.
P
(24)
A do component, Y,[0) in M,(c.~) can be found by
n
y1 [0)=exp{ 2~ f In[~ pt(c~)+1]dca}.
_n P
(25)
The d,'s and u,'s are the corresponding eigenvalues and eigenvectors of
frequency-
domain correlation matrix Rf, defined as
tvf0] rJ(1] ... T.I(l; _ 1]
R ~ ''I ( W ] r! (0) ~ r,~ f K - 2]
I
''J (-li + 1] J'l (-Ii. + 2] . ... rJ (~]
(26)
CA 02273377 1999-OS-31
- 14
and U=(u,,....,uk), which is obviously a unitary matrix.
An MMSE channel estimator is shown in Figure 2. The unitary linear
inverse transform UH and transform U in the figure perform the eigen-
decomposition
of the frequency-domain correlation. The estimator turns off the zero or small
d,'s
to reduce the estimator noise. For those large d,'s, linear filters are used
to take
advantage of the time-domain correlation.
As noted above, the MMSE estimator described here exploits the channel
correlations in both the time- and frequency-domains, resulting in better
performance than the estimators in the prior art. More specifically, the time
correlation filter ~(c~) is placed within the frequency transform process, UH
, U and
as a consequence provides better channel estimation without an overwhelming
amount of complex computations.
The average MMSE of the channel estimator is
x n
MMSE s ~ E ~ H[n,kJ H[n,k ( 2
x " d
-KL (1-exp{ 2~ f ~~ pP'(~)+l~dt~})-
(27)
For Jakes' model, p~(ca) = p,(co). Then by direct calculation,
_'-'d c~d(b(a~) + 1 )
~~-1-( 2 ) " exP(-
(28)
and
MMSE~(~ud)= P ~ 1-( a~) ~exp(- ~~b(a~+1))~
Kr_~ 2 n
(29)
CA 02273377 1999-OS-31
where
«l_ 2dt
wdP
(30)
and
n 2 1+~ al
-a~-1 1-~iln if ar<1, and
b(ar)s 2 ar
2 ar-1- a i -1 ( 2 -ercsin a ) ef a~ 1.
r
(31 )
5 If the time-domain correlation is ideal wd- bandlimited, i.e.,
_n
PB(w) ~ ~ ~"> i, f ~ w ~ s w~,
d
0 otherwise
(32)
and then
~t=1 _ 1
~d
(1+lLdt )a
wdP
(33)
and
CA 02273377 1999-OS-31
16
x
MMSEB (~'d) = K~ 1- 1
( 1 + ndr ) n
(34)
For any c.~d-bandlimited function pt(c.~) satisfying
~d
1 f Pr(w)dc,~ -_ 1
2n _
~d
(35)
we have
" d d
1 f 1n[ pB(w) + 1 )dc~u - 1 f ~ 1n[ ~pl(w) + 1 ]dw
2~ ~ p 2n -n p
- 1 ~~[dlp~(~)-~lcad+l~dc.~
2n _~ p n/wd+1
d
1 ~ dl p~(c.~)-nl~ddw
2n _~ p n/c~d+1
d
S
(36)
with equality if and only if p,(ca)=p~,,~(c,~) almost everywhere. In the above
derivation, the inequality ln(x+1 ) s x for all x > -1 has been used. Hence,
CA 02273377 1999-OS-31
17
x
MMSE (~~ = K~ 1'exp{ 2,~ f ~~[dPt+(~)+1]due}
P
x d
K ~ I'exp{ _ 2~~ ~~[ pp~(~) + 1]dw
MMSEB ~~d).
(37)
The above inequality suggests that a channel with an ideal bandlimited time-
domain
correlation gives the worst MSE performance among all channels.
Robust Estimator
Once the channel statistics, such as the time-domain correlation and
frequency-domain correlation, are known, the optimum channel estimator can be
designed. In mobile wireless links, however, where the channel statistics
depend on
the particular environments, for example, indoor or outdoor, urban or
suburban, and
change with time it is not robust to design a channel estimator that tightly
matches
the channel statistics.
In this subsection, the performance degradation due to a mismatch of the
estimator to the channel statistics is analyzed and a robust estimator design
approach
is developed.
If an MMSE channel estimator is designed to match a channel with time- and
frequency-domain correlations r ~ [m] and i f[l], respectively, then its
coefficients
c [m, l, k] are determined from equation (21 ) by
C(ue)=U ~(~)U~
(38)
where the definitions of U and ~ (ca) are similar to those of U and ~(c~)
except that
ri[m] and r~[1] there are respectively substituted by rt[m] and r~{1].
For a channel with time- and frequency-domain correlations r~[m] and r~{1],
CA 02273377 1999-OS-31
- 18
rather than rt[mJ and r~{1], from equation ( 17), the MSE for the designated
channel
estimator is
x o t-~
MSE({~~,l.k]))°~ { ~ ~ (~~~~l,.k)-3[m~,hJr~(mi-m~)
k.i .,~,._.r,h. _~x-~f
o t-~
'~1~-hxZ~~.~~1-a(~zD~;P E E IZm,hkll=)
o _ _
- ~ r,(ms-"i,)r~{(GTrre,l-al~re,7l~~(GTinil-afne~ln")
~,,~,._
o _
+P ~ Tr{~m)c$Iml )
.._.
= 2~ j ~,~pc~)Ti{(C(t~)-1)R~(C(u~)-ly~)dt~
+2~ f_~T~cc(w)cg(~))~.
(39)
where b[m, I] = b[m)8[1) and
b[nJ= 1 if n=0,
0 otherwise.
(40)
Substituting (38) into (39), we obtain a general formula for the MSE of the
channel
estimator that does not match the channel statistics,
MSE({~m~hk)}) = 2n~ ~'(~)Tr{UH~(~)U nR~U ~(t~)U ~x}dt~
~ Tr{Ux~W)U(UH~(~)Ux}dt.~
2n ~-'~
2~ f ~p~(ca)Tr{UR~IIA(~(w)-nH(~(t~)-n}dc.~
+ P/' ~ Tr{~(uu)~(c.~)H}dw
2n.1 'n
(41 )
Assume that the frequency-domain correlation of the channel estimator
matches that of the channel, i.e.,
CA 02273377 1999-OS-31
- 19
rr (kJ =_ rr [k1
(42)
for k=1,...,K, and the time-domain correlation r~[m] is mismatched. Then
UR f U X = D = diag{dl,...,dx}
(43)
and
MSE({~Inr.l,~E] ) ) ' E Zn I ~n p~ ~~) I ~~~) 1 I ~ +~ P ,r n ( ~~~) I idc.~
r. i 2n
=E ~l f ppo~) pc~»n,c~)-~i=~
,., 2a _
x d _ x _
+ 2 ~ 2n ~ ~1~~) p<<~) ~ ~~~)' 1 ~ _~ *~ p ~ ~ ~~C~) I Zdw
,_, 2nI-n
x _
2nJ ic~<<~) P,(~)lI ~,c~)'lI Z~tMMSE~
(44)
The first term in the above expression represents the MSE variation due to the
mismatch. By means of equations (25) and (22), MSE ({ c [m, l, k]}) can be
further
simplified into
MSE({c[m,l,kl }) _ ~ P ~ d~ ~~(~) p~(~)ld~+MMSE
~°~ 2~Y2 0 ~ d~ Pr(c,~)+p
1[ 1
x d (w)+
=P~ 1 ( 1 ~ _~r P du,~_1)+~SE
i_1 Y~ f01 2n d~ p~(~)+P
(45)
If p ,(c.~) = p8(c.>), that is, the time-domain correlation of the designed
estimator is
CA 02273377 1999-OS-31
ideal cod- bandlimited, then, for any channels with pt(co) zero outside [-wd,
c.~d], and
~d
1
- f Pr(c.>)dc.~ = 1,
2n
~d
(46)
we have
1 " dl Pr(u!~) + p
dc~ = 1.
2n ~ d~ pt(~)+P
(47)
5 Therefore,
MSE({c[m,l,k]}} = MMSEB(~d).
(48)
Hence, if an OFDM channel estimator is designed using p$ (w) as the time-
domain
correlation, then the time-domain correlation mismatch of the estimator will
not
degrade its performance. This suggests that a robust channel estimator should
use
10 pB (c.~) as the time-domain correlation.
To analyze a frequency-domain correlation mismatch, it is assumed that the
time-domain correlation of the designed estimator is the same as that of the
channel,
that is p~ (c.>}= p(~}, and the frequency-correlation matrix of the designed
estimator
has the same eigenvectors as that of the channel. That is, Rt. can be eigen-
15 decomposed into
R f = U HDU, or UR~Il ~ = D,
(49}
where D = diag {d,, ..., dK} and ~K dK = K. dK and dK for k=1, ..., K are
generally
CA 02273377 1999-OS-31
21
different.
Although the second assumption seems strange, it is in fact reasonable. As
indicated in one paper, "On Channel Estimation in OFDM Systems," Van de Beek
et al., Proc. of 45th IEEE Veh. Tech. Confd., pp. 815-819, July 1995, with
tolerable
leakage, both matrices U and U can be approximated by the discrete Fourier
transform (DFT) matrix that is defined as
1 1 ...
W ~ 1 a
Iv : ... ... ~ .
~rr~-o s. ~y x-v
1 eJ h ... eyc '
(50)
The leakage of the above approximation depends on the guard interval and the
channel multipath delay profile. If the delay i of a path is an integer
multiple of the
sampling interval TS, that is, t = TTS, then all the energy from the path will
be
mapped to d,. Otherwise, if the delay is a non-integer multiple of the sample
interval, that is, (l-1) TS < z < ITs, then most of its energy will be
contained in d,.,
and dr, although the energy will leak to all dk's. Hence, if the maximum delay
spread is td, then for all l s ICo (Ko = ( Ktd/'I"f ~, d, = 0.
Applying the above two assumptions to (41 ), we get
MSE({c[m,l,Arl}) ' 2~~ ~~~~~Tr{D(~(t~)-Ix~(t~)-I~)dr,~
P ~~ Tr{~(t~)~(t~~'}dt~
2nI-
K K
E 2,~ ~ ,c o
_~ 2nI ndpa~>n~~~-'~n~' P j n ~ ~ =adr~
x _ _
=~.~d,'dO2n~ ?t'°'~~)I~U)-1)IZ~*MMSE
K _ _
'~ Cdr-dyi'~dy'MMSE'
~. i
(S1)
where,
CA 02273377 1999-OS-31
22
r(d~) ~ 2 ~ - pt(~) + dw.
2n'yl [0J -~ dl pr(~) 1
P
(52)
In the above derivation, we have used equations (24) and (22). From its
definition,
r(0) = 1 and r(d)< 1 for any d>0.
If the channel estimator is designed such that
d _ KIKo for 1 s 1 s Ko,
0 for Ko + 1 s 1 s K,
(53)
then, for any channel with d, = 0 for ICa + I s I s K and ~K°~.l d, =
K, we have
MSE({cZrrt,l,k]}) = MMSE
(54)
However, if
xo
dr<K,
l=1
(SS)
then
MSE( { ~m,l,k) } ) > MMSE
(56)
since r (d) < r (0) for any d > 0.
From the above discussion, a robust estimator, which is insensitive to the
channel statistics, should have an ideal bandlimited time-domain correlation
CA 02273377 1999-OS-31
23
rf[n} _F_lp B(~)_ sin(nc~d)
nwd
and a frequency domain correlation matrix
. .
-_ WHDW,
r,~-r. + iJ . . . TUoJ
(57)
where
D = diag{KIKo,...,KIKo,O,...,0},Ko=[oft KJ=[t~IT~J, and wd = 2nTfJ'~.
Ko elements
Note that W is the DFT matrix defined in equation (50). In this case, the
average
MSE of the robust estimator
KoP C 1 _ 1
MMSEB K ~K
+1~ n
KoP~'d
(58)
For any channel with fdsfm~ and tds't""x, the average MSE should be MMSE B,
FIG. 3 shows an MSE of a robust estimator that matches different Doppler
frequencies and delay spreads. As shown, the MSE is almost a constant if
t~"xf",~ is
fixed. In particular, let
CA 02273377 1999-OS-31
24
2pt~ f~
p -_ rail
(59)
For the ODFM systems satisfying
p < < 1 and ~d In 1 > > 1,
n p
the average MSE of the robust channel estimator can be approximately expressed
as
MMSEB = !~ ~
p
(60)
If the channel estimator is designed to match the Doppler spectrum given by
equation ( 12), then from equation (29), we have
MMSE~ _ !~(~ ~ - 0.144'n.
(61 )
Hence, compared with the estimator that tightly matches the Doppler spectrum,
the
performance degradation of the robust channel estimator is negligible.
Having identified a more specific example of a robust estimator, one can
consider that it may be beneficial to provide a finite-tap robust estimator.
Note that
from the previous section for a robust estimator,
R f = W XDW and r~[n] = s~(nc.>d)
' ~d
(62)
CA 02273377 1999-OS-31
Let
''I (l, r1 (k - 1)
k)
- W ''
''J (Ii i J (-Ii + k)
~')
(63)
and
v(m, 1, ~;) c(in; k - 1, k)
c(m,'k, kJ = W c(m,.0, k) ,
c(m, .Ii , ~:) c(m, -Ii + k, kJ
where c(m, l, k] is the coefficient of the designed channel estimator. Then,
from
10 equation (15), for an FIR channel estimator with length L, we have
o _ " _
1) rr[n m]c [m,l,k] rt(n] d l r f [1'k] +Pdl c [n' f k] -0,
(65)
for n=0, -1, ..., -(L-1). Note that
d I = {KalK if lsKo,
and zero otherwise.
.. (66)
From equation (65), it is obvious that c [n,l,k]=0 for hlCo. For 1 sKo,
CA 02273377 1999-OS-31
26
c[-n,l,k] _ ~c
KIKo "'
(67)
where
K
(co,cl,...,cL_1)T = (Rr + ~ I)-lrr
(68)
r=[O] T~[1] ' ' ~ T~[L - 1J
''r[-1J Tt[~J ~ ra[L - ZJ
~ ,
r't[-L + 1] ~'r[-L + 2J . ~'c[~J
(69)
and
r! - (rr[0]~ rr[1]~...,r~[L-1])T
(70)
Using derivations similar to those above, the Fourier transform of the
coefficient
matrix of the designed FIR channel estimator is determined by
CEw) = R' H~(w) R'
(71 )
where ~(w) is a diagonal matrix with
CA 02273377 1999-OS-31
27
~(c~) = diag{c(w),...,c(c~),0,...,0}
Y
Ko elements
(72)
and c(c.~) is the Fourier transform of c~. The estimation error of the FIR
estimator
can be found by
xocoP
MSE
(73)
Hence, for the robust FIR channel estimator, the U in Figure 2 is the DFT
matrix W
and the ~k(c.>)'s for k = 1, ..., K are c(c~).
In FIG. 4, the average MSE of a robust FIR channel estimator is shown as a
function of its length. From the figure, for the estimator matching a 40 Hz
maximum Doppler frequency, a 50-tap FIR estimator is needed to exploit the
time-
domain correlation of the channel parameters, while for one matching a 200 Hz
maximum Doppler frequency, only a 5-tap channel estimator is sufficient.
Reference Generation and Computer Simulation
In this subsection section, the performance improvement of an OFDM
system using a robust channel estimator will be demonstrated.
The simulation uses a two-path Rayleigh fading channel model with delay
from 0 to 40 ~s and Doppler frequency from 10 Hz to 200 Hz. The channels
corresponding to different receivers have the same statistics. Two antennas
are used
for receiver diversity.
To construct an OFDM signal, assume the entire channel bandwidth, 800
kHz, is divided into 128 subchannels. The 4 subchannels on each end are used
as
guard tones, and the rest ( 120 tones) are used to transmit data. To make the
tones
orthogonal to each other, the symbol duration is 160 psec. An additional 40
psec
CA 02273377 1999-OS-31
28
guard interval is used to provide protection from intersymbol interference due
to
channel multipath delay spread. This results in a total block length T f = 200
.sec
and a subchannel symbol rate rb = 5 kbaud.
To compare the performance of the OFDM system with and without the
channel estimation, PSK modulation with coherent demodulation and differential
PSK modulation with differential demodulation are used, respectively. A (40,
20)
R-S code, with each code symbol consisting of 3 QPSK/DQPSK symbols grouped
in frequency, is used in the system. Hence, each OFDM block forms a R-S
codeword. The R-S decoder erases 10 symbols based on the signal strength and
corrects 5 additional random errors. Hence, the simulated system can transmit
data
at 1.2 Mbits/sec before decoding, or 600 kbits/sec after decoding, over an 800
kHz
channel.
An ideal reference is assumed in the derivation of the channel estimator. In
practical systems, a reference can be generated during a training block. In
subsequent blocks, a reference is generated using the received signals.
Possible
reference generating schemes include (but are not limited to):
1. Undecodedldecoded dual mode reference: If the decoder, in one example an
R-S decoder, can successfully correct all errors in a OFDM block, the
reference for
the block can be generated by the decoded data; hence ~[n,k]=a[n,k].
Otherwise,
a[n, k]=a[n, k].
2. Undecoded reference: ~(n, k]=a[n, k], no matter whether the decoder can
successfully correct all errors in a block, or not.
3. DecodedlCMA dual mode reference: Constant modulus algorithm (CMA) is
one of most effective adaptive blind equalization algorithms. It can be also
used to
generate a reference for the OFDM channel estimator. If the R-S decoder can
successfully correct all errors in a block, the reference for the block can be
generated
from the decoded data; hence ~[n, k]=a[n, k]. Otherwise, the reference can use
the
projection of y[n, k] on the unit circle, i.e., ~[n, k]=y[n, k]/y[n, kJ ~ .
4. Error removal reference: If the decoder can successfully correct all errors
in
a block, the reference for the block can be generated by the decoded data.
Otherwise, the I~[n-k]'s are used instead of H [n,kj's for k=1,...,K,
respectively.
CA 02273377 1999-OS-31
29
C. Simulation Results
FIGS. 5, 6, 7 and 8 demonstrate the performance of the channel estimator
using different references under different channel conditions. To get insight
into the
average behavior of the channel estimator, the performance has been averaged
over
10,000 OFDM blocks.
FIG. 5 shows a word error rate (WER) and nom~alized MSE (NMSE) for the
OFDM system with only the first block as a training or synchronizing block and
for
a channel with fd=40 Hz and td = 20 sec. From the figure, when SNR z 8 dB, the
channel estimator using the decoded/undecoded dual mode reference or the
undecoded reference can estimate the channel parameters with NMSE as small as -
22 dB. Hence, the WER of the system is almost the same as the performance
assuming ideal knowledge of the channel parameters, which is about 3 dB better
than using differential detection. However, due to error propagation through
references, there is a noise threshold for the channel estimator. For the
estimators
with the decoded/undecoded dual mode reference and the undecoded reference,
the
noise thresholds are 7 and 8 dB respectively. For the estimators using the
other two
reference schemes, the noise thresholds are 12 and 19 dB, respectively, Once
the
SNR is larger than the noise threshold, the system performance will be
significantly
better than that of the OFDM system using DQPSK.
To suppress the error propagation, training blocks are periodically inserted
in
the data stream. FIG. 6 illustrates the WER and NMSE for the systems with 1
training blocks. In this situation, the noise threshold disappears and hence
the
OFDM system with channel estimation has better performance than the one
without
channel estimation when the SNR ranges from 0 dB to 20 dB.
For a channel with a Doppler frequency as large as 200 Hz, as indicated in
FIG. 7, if 1 % training blocks are used, then the OFDM system with channel
estimation has about a 1.5 dB SNR improvement compared to the one without
channel estimation. If the training blocks are increased from 1 % to 10% of
the data,
then the required SNR for WER= 10 '2 is almost the same as before, as shown in
FIG. 8.
FIGS. 9 and 10 illustrate the robustness of the channel estimator of the
CA 02273377 1999-OS-31
present invention. As indicated in the analysis above, if a channel estimator
is
designed to match the channel with 40 Hz maximum Doppler frequency and 20 sec
maximum delay spread, then for all channels with fd s 40 Hz and td s20 psec,
the
system performance is not worse than the channel with fd = 40 Hz and td psec,
as
5 indicated by FIG. 9. However, for channels with fd > 40 Hz or td > 20 sec,
such as,
fd = 80 Hz and td = 20 psec, or fd = 40 Hz and td = 40 psec, the system
performance
degrades dramatically. On the other hand, as indicated in Figure 10, if the
estimator
is designed to match the Doppler frequency or delay spread larger than the
actual
ones, the system performance degrades only slightly compared with estimation
that
10 exactly matches the channel Doppler frequency and delay spread.
Conclusion
A robust channel estimators for OFDM systems makes full use of the time-
and frequency-correlations of the rapid dispersive fading wireless channel,
and is
insensitive to the channel statistics. Computer simulation demonstrates that
channel
15 estimation gives abo>.;t 2.5 dB improvement when the Doppler frequency is
40 Hz,
and about 1.5 dB improvement when the Doppler frequency is as large as 200 Hz.
This channel estimation used together with antenna arrays has potential to
provide
significant suppression of co-channel interference in OFDM systems.