Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
CA 02374896 2011-07-04
1
METHODE POUR DÉFORMER GRADUELLEMENT UNE RÉPARTITION
INITIALE D'OBJETS DANS UN MILIEU HÉTÉROGENE POUR L'ADAPTER A
DES CONTRAINTES PHYSIQUES IMPOSÉES
La présente invention a pour objet une méthode pour déformer graduellement une
répartition initiale d'objets de nature géologique, formée par simulation d'un
modèle
stochastique de type objet, d'après des mesures ou observations, pour
l'adapter au mieux à
des contraintes physiques imposées, de type hydrodynamique par exemple.
La méthode selon l'invention trouve des applications dans la modélisation de
zones
souterraines où il s'agit de générer des représentations montrant comment est
distribuée
une certaine grandeur physique dans une zone du sous-sol (la perméabilité par
exemple),
qui soient compatibles au mieux avec des données observées ou mesurées :
données
géologiques, enregistrements sismiques, mesures obtenues dans des puits
notamment
mesures des variations au cours du temps de la pression et du débit de fluides
issus d'un
gisement, etc.
ETAT DE LA TECHNIQUE
Par le brevet FR 2 780 798 du demandeur, on connaît une méthode pour déformer
graduellement un modèle stochastique (de type gaussien ou apparenté) d'un
milieu
hétérogène tel qu'une zone souterraine, contraint par un ensemble de
paramètres relatifs à
la structure du milieu. Cette méthode comporte le tirage d'un nombre p de
réalisations (ou
représentations) indépendantes du modèle ou d'une partie au moins du modèle
choisi du
milieu, parmi l'ensemble de toutes les réalisations possibles et une ou
plusieurs étapes
itératives de déformation graduelle du modèle en effectuant une ou plusieurs
combinaisons
linéaires successives de p réalisations initiales indépendantes entre elles
puis des
réalisations composites successivement obtenues éventuellement avec de
nouveaux tirages,
etc., les coefficients de cette combinaison étant tels que la somme de leurs
carrés est égale à
1.
CA 02374896 2011-07-04
la
Par le brevet FR 2 795 841 du demandeur, on connaît une autre méthode pour
déformer graduellement les représentations ou réalisations, générées par
simulation
CA 02374896 2002-03-06
2
séquentielle, d'un modèle stochastique non nécessairement gaussien d'une
grandeur
physique z dans un milieu hétérogène maillé, afin de les ajuster à un ensemble
de données
relatives à la structure ou l'état du milieu qui sont collectées par des
mesures et
observations préalables. La méthode comporte essentiellement l'application
d'un
algorithme de déformation graduelle d'un modèle stochastique à un vecteur
gaussien à N
variables mutuellement indépendantes, qui est relié à un vecteur uniforme à N
variables
uniformes mutuellement indépendantes par la fonction de répartition gaussienne
de façon à
définir des réalisations du vecteur uniforme, et l'utilisation de ces
réalisations pour générer
des représentations de cette grandeur physique z, que l'on cale par rapport
aux données.
Les méthodes précédentes sont applicables aux modèles maillés (modèles de type
pixel) qui conviennent pour modéliser des champs de grandeurs continues et, de
ce fait,
sont mal adaptés à la modélisation de zones traversées par des réseaux de
fractures ou des
systèmes de chenaux, par exemple.
Les modèles basés sur des objets sont des arrangements dans l'espace, d'une
population d'objets définis géométriquement. A la base, un modèle de type
objet est un
modèle booléen que l'on peut définir comme une réunion d'objets identiques par
nature,
distribués au hasard dans l'espace. Les modèles booléens (de type objet)
présentent un
grand intérêt pour la description géométrique des milieux hétérogènes, tels
que les
systèmes de dépôt méandriformes, les réseaux de fractures, les milieux poreux
à l'échelle
granulométrique, les milieux vacuolaires, etc. Les objets géologiques sont
définis par leurs
formes et leurs tailles. Leurs emplacements dans le champ sont définis en
tenant compte de
leurs interactions : attirance-répulsion, tendance au regroupement
(clustering), etc.
Contrairement aux modèles de type pixel, les modèles basés sur des objets
peuvent
fournir par exemple des représentations géologiques réalistes d'un réservoir
souterrain à un
stade précoce où les données obtenues par des mesures in situ sont encore
rares.
L'état de l'art dans le domaine des modèles de type objet, est décrit
notamment
dans les publications suivantes :
Matheron, G., 1967, "Élément pour une théorie des milieux poreux", Masson,
Paris;
Matheron, G., 1975, "Random sets and intégral geometry", Wiley, New York;
CA 02374896 2011-07-04
3
Serra, J., 1982, "Image analysis and mathematical geology", Vol.1, Academic
Press,
London;
- Stoyan, D.S., et al., 1995, "Stochastic geometryy and its applications", 2 d
Edition,
Wiley, Chichester;
Lantuéjoul, C., 1997, Iterative algorithms for conditional simulations, in
Baafi et
others, eds.; Geostatistics Wollongong 96, Vol. 1, Kluwer Acad. Publ.,
Dordrecht, The
Netherlands, p.27-I0.
La position des objets dans un modèle de type objet est distribuée suivant un
processus ponctuel de Poisson bien connu des spécialistes. La forme et la
taille des objets
sont indépendantes de leurs positions. Ce modèle peut être généralisé par une
combinaison
d'objets de nature différente ou/et en utilisant un processus ponctuel de
Poisson de densité
non-stationnaire.
Bien que les modèles booléens aient été largement étudiés dans la littérature,
on ne
dispose pas de méthode cohérente et efficace pour contraindre ces modèles aux
données
physiques, notamment aux données hydrodynamiques, ce qui est pourtant un enjeu
majeur
pour leur application en ingénierie de réservoir. Les méthodes de déformation
graduelle des
modèles stochastiques de réservoir de type pixel telles que décrites par
exemple dans les
deux brevets précités, ne sont pas directement utilisables pour les modèles
booléens.
Contraindre les modèles booléens aux données hydrodynamiques par exemple
requiert le
développement des algorithmes cohérents pour la déformation et le déplacement
des objets.
LA METHODE SELON L'INVENTION
La méthode selon l'invention permet de généraliser la technique de déformation
graduelle décrite dans les deux brevets précités, aux modèles booléens
stationnaires ou
non-stationnaires et ceci avec ou sans contrainte géométrique aux puits. La
méthode
s'avère particulièrement utile notamment pour les ingénieurs de réservoir
soucieux
d'ajuster de façon cohérente et efficace les modèles de réservoir de type
objet.
CA 02374896 2011-07-04
3a
Plus particulièrement, la présente invention vise une méthode pour déformer
graduellement une image formée d'après des mesures ou observations et montrant
une répartition d'un ensemble d'objets dans une zone d'un milieu hétérogène,
constituant une réalisation initiale générée par simulation d'un modèle
stochastique
de type objet, les objets étant répartis dans la zone suivant un processus
ponctuel
de Poisson sous forme de points figuratifs avec une densité de points A(x) qui
varie
en fonction de leur position (x) dans la zone, caractérisée en ce que:
on génère une réalisation d'un vecteur aléatoire uniforme selon lequel la
position (x) de chaque objet est définie tout en respectant la densité de
points A(x);
et
- on modifie graduellement le vecteur aléatoire uniforme selon une procédure
de déformation graduelle, pour obtenir une migration graduelle de chaque objet
et
par conséquent un changement graduel de la répartition des objets dans la
zone,
jusqu'à obtenir une réalisation finale ajustée au mieux à des paramètres
relatifs à la
structure du milieu, donnant une image réaliste de la configuration des objets
dans
le milieu hétérogène modélisé.
De préférence, la méthode selon l'invention permet de déformer
graduellement une réalisation initiale définissant la répartition d'un
ensemble
d'objets dans une zone d'un milieu hétérogène tel qu'une structure géologique,
formée par simulation d'un modèle
CA 02374896 2002-03-06
4
stochastique de type objet, les objets étant répartis dans la zone selon un
processus ponctuel
de Poisson sous forme de points figuratifs avec une densité de points 2(x) qui
varie en
fonction de leur position (x) dans la zone. Elle comporte essentiellement les
deux étapes
suivantes :
- on génère une réalisation d'un vecteur aléatoire uniforme selon lequel la
position de
chaque objet est définie tout en respectant la densité 2(x) ; et
- on modifie graduellement le vecteur aléatoire uniforme selon une procédure
de
déformation graduelle, pour obtenir la migration graduelle de chaque objet et
par
conséquent le changement graduel de la répartition des objets dans la zone,
jusqu'à
obtenir une réalisation finale ajustée au mieux à des paramètres relatifs à la
structure du
milieu tels que des paramètres hydrodynamiques.
Il est possible de limiter la migration des points figuratifs d'objets dans un
sous-
domaine de la zone (un puits traversant la zone par exemple) en imposant une
densité de
points nulle dans la partie complémentaire du sous-domaine.
Suivant un mode de mise en oeuvre, on passe graduellement d'une réalisation
contenant un premier ensemble de N, points à une réalisation contenant un
deuxième
ensemble de N2 points en construisant une chaîne N(t) de nombres de Poisson
entre les
deux nombres N, et N2 en utilisant la procédure de déformation graduelle.
Il est possible aussi de modifier graduellement la taille, la forme et
l'orientation
d'un objet au cours de sa migration en utilisant la procédure de déformation
graduelle.
En cas où elle est entachée d'incertitude, il est possible aussi d'ajuster
graduellement la densité de points 2(x) en utilisant la procédure de
déformation graduelle.
La réalisation finale obtenue par la méthode constitue une représentation
réaliste de
la configuration des objets dans le milieu hétérogène.
PRESENTATION SOMMAIRE DES FIGURES
D'autres caractéristiques et avantages de la méthode selon l'invention,
apparaîtront à
la lecture de la description détaillée ci-après, en se référant aux dessins
annexés où :
CA 02374896 2002-03-06
la Fia.lA, 1B montrent respectivement une fonction de densité d'un processus
ponctuel
de Poisson non-stationnaire et une réalisation du processus ponctuel de
Poisson non-
stationnaire générée par la méthode séquentielle ;
les Fig.2A à 2D montrent différents exemples de trajectoires de migration
graduelle
5 entre deux points d'un processus ponctuel de Poisson non-stationnaire ;
la Fig. 3montre les domaines possibles de migration d'un disque dans le cas de
trois
points conditionnant ;
les Fig. 4A à 4H montrent différentes étapes successives d'une réalisation du
processus
ponctuel de Poisson non-stationnaire lors de la migration graduelle des points
;
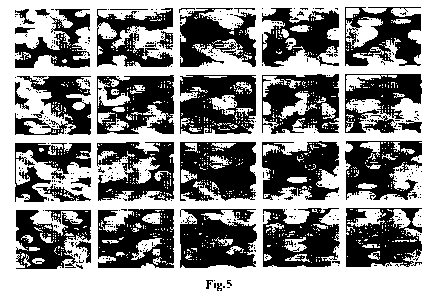
- la Fig.5 montre à titre d'exemple, une chaîne complète de réalisations
successives
d'une simulation booléenne d'objets elliptiques où le paramètre de déformation
t varie
entre - ir et ir par pas At =0.17t ; et
- la Fig.6 montre à titre d'exemple, une chaîne incomplète de réalisations
successives
d'une simulation booléenne d'objets elliptiques où le paramètre de déformation
t varie
entre 0 et 0.2,r par pas At =0.017V .
DESCRIPTION DETAILLEE
Généralités
Les objets géologiques auxquels la méthode s'applique sont par exemple des
fractures à plus ou moins grande échelle, à l'intérieur d'une zone réservoir,
ou bien encore
des chenaux. La méthode peut s'appliquer également à des structures
granulaires ou
vacuolaires de taille beaucoup plus réduite. Tous ces objets sont difficiles à
modéliser par
des modèles de type pixel.
Les opérations de migration progressive qui vont être décrites, s'appliquent à
un
modèle initial où les positions des objets sont représentés par des
configurations de points
(dites processus ponctuels). La répartition de ces points varie en densité en
fonction de
leurs positions dans la zone modélisée. Cette répartition est basée sur
différentes données
connues par mesures ou observations : mesures géomécaniques obtenues dans des
puits par
exemple, données sismiques issues d'opérations sismiques préalables.
CA 02374896 2002-03-06
6
Partant de ce modèle initial, la méthode va permettre de déformer
graduellement la
répartition initiale suivant une série de règles, de manière que dans la
répartition finale, le
modèle soit optimisé pour mieux correspondre à des contraintes que l'on impose
sur un ou
plusieurs paramètres physiques, telle que par exemple une distribution de
valeurs de
perméabilité. Les règles de migration sont telles que l'on peut déplacer
globalement un
grand nombre de points différents du modèle à partir d'un nombre réduit de
paramètres de
contrôle.
En général, on définit une fonction objectif qui mesure la différence entre
les
paramètres physiques issues du milieu hétérogène réel et ceux simulés sur une
réalisation
du modèle stochastique. La valeur de la fonction objectif dépend donc des
paramètres de
contrôle du modèle stochastique. On obtient les valeurs de ces paramètres de
contrôle par
minimisation de la fonction objectif.
Rappel sur le processus ponctuel de Poisson
Le processus ponctuel de Poisson est un ensemble aléatoire dénombrable de
points
répartis dans tout espace 9t" . Cet ensemble de points a les caractéristiques
suivantes:
Soit D un domaine de 91". Si le volume de D, noté IDI, est fini, alors le
nombre
de points tombés dans D, noté N(D), suit une loi de Poisson de paramètre AIDI.
Soit
(2D)"
Vn>_0 (1)
P[N(D)=n]=e-zI I n!
n.
où A est appelée la densité du processus ponctuel; elle mesure le nombre moyen
de points
tombés dans un domaine de volume unitaire de 91'.
Soient Di , D2,..., Dk des domaines de 91" disjoints deux à deux, alors les
nombres
de points tombés dans ces domaines N(D, ), N(D, ),..., N(Dk) sont des
variables aléatoires
mutuellement indépendants.
Conditionnellement à N(D) = n p , ces n,, points sont indépendants et
uniformément répartis dans D .
CA 02374896 2002-03-06
7
Dans ce qui suit, nous nous intéressons au processus ponctuel de Poisson dans
le
domaine borné D.
Migration d'un processus ponctuel de Poisson stationnaire
Considérons le problème de migration d'une réalisation d'un processus ponctuel
de
Poisson stationnaire dans D rectangulaire. Afin d'alléger la présentation, on
admet que D
est un hyper cube unitaire [0,1]" à n dimensions. Soientx1 et x2 deux points
indépendants
uniformément tirés dans [0,1]". Nous définissons une trajectoire entre x1 et
x2 par
x(t) = G[G-' (x1) cos t + G1 (x,) sin t] (2)
où G est la fonction de répartition gaussienne centrée et réduite. Selon
l'algorithme de
lo déformation graduelle décrit dans le brevet FR 2 780 798 précité, pour tout
t, x(t) est un
point uniforme dans [0,1]" . Quand les deux points sont fixés, la trajectoire
de la migration
graduelle entre eux est entièrement déterminée. Le changement d'emplacement
d'un des
deux points changera la trajectoire de migration. On peut montrer que la
trajectoire définie
par l'équation (2), est symétrique par rapport au centre du domaine [0,11", et
ceci quel que
soit le nombre de dimensions n. Cela suggère que même si les deux points sont
isolés dans
un coin/côté du domaine, la trajectoire de la migration graduelle entre eux
peut toujours
atteindre la partie opposée du domaine.
Migration d'un processus ponctuel de Poisson non-stationnaire
On considère maintenant le processus ponctuel de Poisson dans un domaine D de
densité 2(x) de forme générale. Le nombre de points dans D est une variable
aléatoire de
Poisson de moyenne 2(D) = f 2(x)dx. Ces points sont distribués indépendamment
dans
D suivant la fonction de densité de probabilité :
f (x) _ 2(x) / 2(D) x e D (3)
La simulation d'un processus ponctuel de Poisson de densité 2(x) dans D peut
se
réaliser en deux étapes:
générer un nombre n selon la loi de Poisson de moyenne égale à 2(D) , puis
CA 02374896 2002-03-06
8
générer n points dans D indépendamment les uns des autres selon la même
densité de
probabilité f (x).
On peut voir sur l'exemple de la Fig.lA une fonction de densité, et sur celui
de la
Fig.1B, une réalisation de processus ponctuel de Poisson de densité Å(x).
Si on simule la loi f (x) par l'inversion de sa fonction de répartition, le
point x
correspond alors à un vecteur uniforme u. On peut donc appliquer l'algorithme
de
migration graduelle au processus ponctuel de Poisson de densité 2(x) . Par
construction,
cette méthode préserve la densité et le nombre de points du processus initial.
Les Fig.2A à
2D montrent quatre exemples de trajectoire de migration.
Prenons l'exemple du processus ponctuel de Poisson non-stationnaire dans un
domaine en deux dimensions D = [0,1]2 dont la densité est linéairement
croissante dans
l'axe X et constante dans l'axe Y. Soit (x, y) le vecteur des coordonnées d'un
point dans
D de ce processus. Alors (x, y) admet la densité de probabilité bivariable :
f (x, y) = 2x, (x, y) E [0,1]2. (4)
La simulation d'un point selon la loi (4) précédente est simple:
- générer l'abscisse x selon la densité linéaire f (x) = 2x, puis
- générer l'ordonnée y uniformément entre 0 et 1. Soient
x = (5)
yv
où u et v sont deux nombres indépendants et uniformes entre 0 et 1.
Nous pouvons ainsi appliquer l'algorithme de migration graduelle (2) au
vecteur
uniforme (u, v) afin d'établir une trajectoire de migration du point (x, y)
dans D.
En pratique, la fonction de densité 2(x) est souvent sous forme de grille. A
titre
d'exemple, on considère le cas d'une grille en 2 dimensions de M x N noeuds.
Soient xi et
yi les coordonnées du noeud (i, j). La loi marginale de xi est alors :
CA 02374896 2002-03-06
9
N
.f (xi) = 1 f (xi, Y1) (6)
J=1
et la loi conditionnelle de yl sachant x; vaut :
f, (Y 1) = .f (xi, Y j) l .f (xi) (7)
A partir de ces lois de probabilité monovariables, il est aisé de générer les
points du
processus de Poisson de densité 2(x) sur une grille.
Afin d'illustration, nous avons construit une fonction de densité en deux
dimensions à partir d'une simulation gaussienne centrée et réduite. Le
variogramme est
anisotrope et de type gaussien. Les directions principales d'anisotropie sont
diagonales par
rapport au système des coordonnées. Les facteurs d'échelle dans les directions
principales
d'anisotropie sont de 0.3 et 0.1 respectivement. La taille du champ est de lx
l et il est
discrétisé en 1000x1000 pixels. Les nombres gaussiens sont transformés en
nombres
positifs selon l'expression suivante :
2(x) = 400er3-' (8)
où Y(x) est la simulation gaussienne. La Fig. lA montre la fonction de densité
ainsi
construite. La figure 1B montre une réalisation de processus ponctuel de
Poisson admettant
la fonction de densité de la Fi- lA. 2000 points sont générés selon la méthode
séquentielle.
Les Fig. 4A à 4H illustrent l'évolution d'une réalisation du processus de
Poisson
lors de la migration graduelle des points. On peut constater qu'au cours de la
migration, la
densité de points est respectée.
Migration d'objets de simulations booléennes conditionnelles
La méthode ci-dessus peut être immédiatement appliquée à la migration d'un
domaine S de forme quelconque dans D. En fait, la migration d'un point dans S
peut être
réalisée dans D en utilisant la fonction de densité de probabilité tronquée
fs (x) _ 2(x)1.Es /2(S), x É D, S c D . (9)
Par l'algorithme d'itération markovienne décrit dans la référence à
Lantuéjoul,
1997, on peut simuler un modèle booléen dans un domaine D sachant que deux
sous-
CA 02374896 2002-03-06
ensembles C, et CO de D appartiennent respectivement à l'union des objets et à
son
complément. Ensuite, les algorithmes de migration dans un domaine quelconque
peuvent
être utilisés pour la déformation graduelle des simulations booléennes
conditionnées par
des données géométriques des puits. En effet, à partir d'une simulation
booléenne
5 conditionnelle et sans compromettre le conditionnement par C1 et Co , les
objets doivent se
déplacer uniquement dans leurs domaines respectifs définis selon les formes
des objets et
la configuration de CI et CO .
Considérons un objet A d'une réalisation booléenne conditionnelle, qui inclut
un
sous-ensemble CIA de CI et exclut CO . Si lors de la migration de A, il doit
toujours inclut
10 CIA mais exclut CO, le domaine autorisé de migration de l'objet A est:
DA ={x: CO nAx = 0;CIA c Ax} (10)
La Fig. 3 montre un cas avec trois points conditionnant et les huit domaines
possibles de migration d'un disque. Si par exemple le disque doit toujours
couvrir les
points (a) et (b) mais éviter le point (c), alors son centre peut se déplacer
seulement dans le
domaine 3.
Migration avec apparition et disparition de points
Le nombre de points dans D d'un processus ponctuel suit une loi de Poisson de
paramètre A(D). Il est donc nécessaire de faire varier le nombre de points
dans D au
cours de leur migration. Dans cette section, nous présentons d'abord deux
méthodes pour
construire des chaînes de nombres poissonniens, et ensuite nous verrons
comment migrer
entre deux ensembles de points dont les cardinaux ne sont pas identiques.
Nous cherchons à construire une chaîne de nombres poissoniens entre deux
nombres poissoniens Ni et N2, générés indépendamment par l'inversion de la
fonction de
répartition. Soient U1 et U, deux nombres uniformes (entre 0 et 1)
indépendants à partir
desquels sont obtenus les nombres Ni et N2
Ni =F-1(U1) (11)
N, =F-'(U2)
CA 02374896 2002-03-06
11
où F-' désigne la fonction de répartition inverse de la loi de Poisson. Selon
l'algorithme de déformation graduelle, nous pouvons construire une chaîne de
nombres
uniformes entre U, et U2 par
U(t) =G[G-'(U,)cost+G-'(U2)sint]. (12)
En inversant la fonction de répartition de la loi de Poisson, on obtient une
chaîne de
nombres poissonniens
N(t) = F-'[U(t)]. (13)
Le calcul de la fonction de répartition inverse peut s'effectuer par
dichotomie.
Néanmoins, si le paramètre de la loi de Poisson est trop grand, cette méthode
reste quelque
lo peu coûteux.
Pour éviter le calcul de la fonction de répartition inverse de la loi de
Poisson, on
peut envisager une autre façon de générer les nombres poissoniens. On sait que
le nombre
de sauts, d'un processus de Poisson de paramètre unité, dans un segment de
longueur Å,
suit précisément une loi de Poisson de paramètre Å. Simuler un processus de
Poisson est
chose simple. En effet, les intervalles entre deux sauts consécutifs du
processus sont
indépendants et suivent la loi exponentielle de paramètre 1. En déformant
graduellement
les segments exponentiels, on obtient une chaîne de nombres poissoniens. Il
est aisé de
construire une chaîne de nombres exponentiels, car le calcul de la fonction de
répartition
inverse de la loi exponentielle est simple. On rappelle ici que la fonction de
répartition de
la loi exponentielle de paramètre 1 s'écrit
F(s)=1-e-s, s>0 (14)
et sa fonction inverse s'écrit :
F-'(u)=-ln(1-u), 0<u<1. (15)
Toujours est-il que, comme le nombre de sauts dans le segment de longueur A
est
en moyenne égal à Å, le nombre de chaînes de nombres exponentiels est en
moyenne
proche de Å.
CA 02374896 2002-03-06
12
Considérons maintenant la migration d'un ensemble de N, points (ensemble 1) à
un ensemble de N2 points (ensemble 2). Comme N, # N2, la migration de
l'ensemble 1 à
l'ensemble 2 implique nécessairement l'apparition ou la disparition de certain
points. Le
nombre de points à apparaître ou à disparaître est déterminé par la chaîne de
nombres
poissoniens entre N, et N2. L'algorithme de migration est le suivant :
a) Calculer le nombre maximal N. de la chaîne N(t).
b) Compléter l'ensemble 1 de Nmax - NI points et l'ensemble 2 de Nmax - N2
points.
c) Pour chaque ensemble, classer les points de 1 à Nmax . Tous les points
initiaux
sont classés au début.
d) Calculer la trajectoire de migration du point n de l'ensemble 1 au point n
de
l'ensemble 2. (n = 1,2,..., Nmax)
e) A chaque état t de l'ensemble, supprimer les N. - N(t) derniers points.