Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
CA 02378035 2001-12-31
WO 01/02929 PCT/L1S00/18165
1
TITLE OF THE INVENTION
CODED DOMAIN NOISE CONTROL
CROSS-REFERENCE TO RELATED APPLICATIONS
This is a utility application corresponding to provisional application no.
60/142,136 entitled
"CODED DOMAIN ENHANCEMENT OF COMPRESSED SPEECH " filed July 2, 1999.
BACKGROUND OF THE INVENTION
The present invention relates to coded domain enhancement of compressed
speech and in particular to coded domain noise contol.
This specification will refer to the following references:
[1] GSM 06.10, "Digital cellular telecommunication system (Phase 2); Full rate
speech; Part 2:
Transcoding", ETS 300 580-2, March 1998.
[2] GSM 06.60, "Digital cellular telecommunications system (Phase 2); Enhanced
Full Rate (EFR)
speech transcoding", June 1998.
[3] GSM 08.62, "Digital cellular telecommunications system (Phase 2+); Inband
Tandem Free
Operation (TFO) of Speech Codecs", ETSI, March 2000.
[4] J. R. Deller, J. G. Proakis, J. H. L. Hansen, "Discrete-Time Processing of
Speech Signals", Chapter
7, Prentice-Hall Inc, 1987.
[5] S. V. Vaseghi, "Advanced Signal Processing and Digital Noise Reduction",
Chapter 9, Wiley
(ISBN 0471958751), 1996.
The specification may refer to the following abbreviations:
ACELP Al ebraic Code Excited Linear Prediction
AE Audio Enhancer
ALC Ada tive or Automatic Level Control
CD Coded Domain or Com ressed Domain
CDEC Coded Domain Echo Control
CDNR Coded Domain Noise Reduction
EFR Enhanced Full Rate
ETSI Euro can Telecommunications Standards Institute
FR Full Rate
GSM Global S stem for Mobile Communications
ITU International Telecommunications Union
MR-ACELP Multi-Rate ACELP
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
2
PCM Pulse Code Modulation (ITU 6.711)
RPE-LTP Re ular Pulse Excitation - Lon Term Prediction
TFO Tandem Free O eration
VSELP Vector Sum Excitation Linear Prediction
Network enhancement of coded speech would normally require decoding, linear
processing and re-encoding of the processed signal. Such a method is very
expensive.
Moreover, the encoding process is often an order of magnitude more
computationally
intensive than the speech enhancement methods.
Speech compression is increasingly used in telecommunications, especially in
cellular telephony and voice over packet networks. Past network speech
enhancement
techniques which operate in the linear domain have several shortcomings. For
example,
past network sp"ech enhancement techniques which operate in the linear domain
require
decoding of compressed speech, performing the necessary enhancements and re-
encoding of
the speech. This processing can be computationally intensive, is especially
prone to
additional quantization noise, and can cause additional delay.
The maintenance of the speech level at an optimal level is an important
problem in the Public Switched Telephone Network (PSTN). Telephony customers
expect a comfortable listening level to maximize comprehension of their
conversation. The transmitted speech level from a telephone instrument depends
on
the speaker's volume and the position of the speaker relative to the
microphone. If
volume control is available on the telephone instrument, the listener could
manually
adjust it to a desirable level. However, for historical reasons, most
telephone
instruments do not have volume controls. Also, direct volume control by the
listener
does not address the need to maintain appropriate levels for network
equipment.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
3
Furthermore, as technology is progressing towards the era of hands-free
telephony
especially in the case of mobile phones in vehicles, manual adjustment is
considered
cumbersome and potentially hazardous to the vehicle operators.
The responsibility of maintaining speech quality has generally been the role
of
the network service providers, with the telephone instrument manufacturers
playing a
relatively minor role. Traditionally, network service providers have provided
tight
specifications for equipment and networks with regard to speech levels.
However, due
to increased international voice traffic, deregulation, fierce competition and
greater
customer expectations, the network service providers have to ensure the proper
speech
levels with lesser influence over specifications and equipment used in other
networks.
With the widespread introduction of new technology and protocols such as
digital cellular telephony and voice over packet networks, the control of
speech levels
in the network has become more complex. One of the main reasons is the
presence of
speech compression devices known as speech codecs (coder-decoder pairs) in the
transmission path. Automatic level control (ALC) and noise reduction (NR) of
speech signals becomes more difficult when speech codecs are present in the
trans-
mission path, while, in the linear domain, the digital speech samples are
available for
direct processing.
A need has long existed in the industry for a coded domain signal processing
approach that reduces computational costs, reduces delay, and reduces
additional
quantization noise.
CA 02378035 2001-12-31
WO 01/02929 PCT/IJS00/18165
4
The GSM Digital Cellular Network
In the GSM digital cellular network, speech transmission between the mobile
stations (handsets) and the base station is in compressed or coded form.
Speech
coding techniques such as the GSM FR [1] and EFR [2] are used to compress the
speech. The devices used to compress speech are called vocoders. The coded
speech
requires less than 2 bits per sample. This situation is depicted in Figure 1.
Between
the base stations, the speech is transmitted in an uncoded form (using PCM
companding which requires 8 bits per sample).
Note that the terms coded speech and uncoded speech are defined as follows:
Uncoded speech: refers to the digital speech signal samples typically used in
telephony; these samples are either in linear 13-bits per sample form or
companded
form such as the 8-bits per sample ,u -law or A-law PCM form; the typical bit-
rate is
64 kbps.
Coded speech: refers to the compressed speech signal parameters (also
referred to as coded parameters) which use a bit rate typically well below
64kbps such
as 13 kbps in the case of the GSM FR and 12.2 kbps in the case of GSM EFR; the
compression methods are more extensive than the simple PCM companding scheme;
examples of compression methods are linear predictive coding, code-excited
linear
prediction and mufti-band excitation coding.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
Tandem-Free Operation (TFO) in GSM
The Tandem-Free Operation (TFO) standard [3] will be deployed in GSM
digital cellular networks in the near future. The TFO standard applies to
mobile-to-
mobile calls. Under TFO, the speech signal is conveyed between mobiles in a
5 compressed form after a brief negotiation period. This eliminates tandem
voice codecs
during mobile-to-mobile calls. The elimination of tandem codecs is known to
improve
speech quality in the case where the original signal is clean. The key point
to note is
that the speech transmission remains coded between the mobile handsets and is
depicted in Figure 2.
Under TFO, the transmissions between the handsets and base stations are
coded, requiring less than 2 bits per speech sample. However, 8 bits per
speech
sample are still available for transmission between the base stations. At the
base
station, the speech is decoded and then A-law companded so that 8 bits per
sample are
necessary. However, the original coded speech bits are used to replace the 2
least
significant bits (LSBs) in each 8-bit A-law companded sample. Once TFO is
established between the handsets, the base stations only send the 2 LSBs in
each 8-bit
sample to their respective handsets and discard the 6 MSBs. Hence vocoder
tandeming is avoided. The process is illustrated in Figure 3.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
6
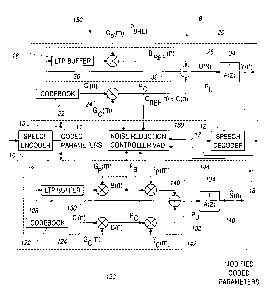
The Background Noise Problem and Traditional Solutions
Environmental background noise is a major impairment that affects telephony
applications. Such additive noise can be especially severe in the case of
cellular
telephones operated in noisy environments. Telephony service providers use
noise
reduction equipment in their networks to improve the quality of speech so as
to
encourage longer talk times and increase customer satisfaction. Although noise
could
be handled at the source in the case of digital cellular handsets, few handset
models
provide such features due to cost and power limitations. Where such features
are
provided, they may still not meet the service provider's requirements. Hence
service
providers consider network speech enhancement equipment to be essential for
their
competitiveness in the face of deregulation and greater customer expectations.
The
explosive increase in the use of cellular telephones, which are often operated
in the
presence of severe background noise conditions, has also increased the use of
noise
reduction equipment in the network.
The traditional method for noise reduction is shown in Figure 4. It is based
on
a well known technique called spectral subtraction [5].
In the spectral subtraction approach, the noisy signal is decomposed into
different frequency bands, e.g. using the discrete Fourier transform. A
silence detector
is used to demarcate gaps in speech. During such silence segments, the noise
spectrum (i.e. the noise power in each frequency band) is estimated. At all
times, the
noisy signal power in each frequency band is also estimated. These power
estimates
provide information such as the signal-to-noise ratio in each frequency band
during
CA 02378035 2001-12-31
WO 01/02929 PCT/ITS00/18165
7
the time of measurement. Based on these power estimates, the magnitude of each
frequency component is attenuated. The phase information is not changed. The
resulting magnitude and phase information are recombined. Using the inverse
discrete
Fourier transform, a noise-reduced signal is reconstructed.
Techniques such as the one described above require the uncoded speech signal
for noise reduction processing. The output of such noise reduction processing
also
results in an uncoded speech signal. Under TFO in GSM networks, if noise
reduction
is implemented in the network, a traditional approach requires decoding the
coded
speech, processing the resulting uncoded speech and then re-encoding it. Such
decoding and re-encoding is necessary because the traditional techniques can
only
operate on the uncoded speech signal. This approach is shown in Figure 5. Some
of
the disadvantages of this approach are as follows.
This approach is computationally expensive due to the need for two decoders
and an encoder. Typically, encoders are at least an order of magnitude more
complex
computationally than decoders. Thus, the presence of an encoder, in
particular, is a
major computational burden.
The delay introduced by the decoding and re-encoding processes is
undesirable.
A vocoder tandem (i.e. two encoder/decoder pairs placed in series) is
introduced in this approach, which is known to degrade speech quality due to
quantization effects.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
8
The proposed techniques are capable of performing noise reduction directly on
the coded speech (i.e. by direct modification of the coded parameters). Low
computational complexity and delay are achieved. Tandeming effects are avoided
or
minimized, resulting in better perceived quality after noise reduction.
Speech Coding
Overview
Speech compression, which falls under the category of lossy source coding, is
commonly referred to as speech coding. Speech coding is performed to minimize
the
bandwidth necessary for speech transmission. This is especially important in
wireless
telephony where bandwidth is scarce. In the relatively bandwidth abundant
packet
networks, speech coding is still important to minimize network delay and
fitter. This
is because speech communication, unlike data, is highly intolerant of delay.
Hence a
smaller packet size eases the transmission through a packet network. The four
ETSI
GSM standards of concern are listed in Table 1.
Table 1: GSM Speech Codecs
Codec Name Codin Method Bit Rate (kbits/sec)
Half Rate (HR) VSELP 5.6
Full Rate (FR) RPE-LTP 13
Enhanced Full Rate ACELP 12.2
(EFR)
Adaptive Multi-Rate MR-ACELP _
(AMR) ~ ~ 5.4-12.2
In speech coding, a set of consecutive digital speech samples is referred to
as a
speech frame. The GSM coders operate on a frame size of 20ms (160 samples at
8kHz
sampling rate). Given a speech frame, a speech encoder determines a small set
of
parameters for a speech synthesis model. With these speech parameters and the
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
9
speech synthesis model, a speech frame can be reconstructed that appears and
sounds
very similar to the original speech frame. The reconstruction is performed by
the
speech decoder. In the GSM vocoders listed above, the encoding process is much
more computationally intensive than the decoding process.
The speech parameters determined by the speech encoder depend on the
speech synthesis model used. The GSM coders in Table 1 utilize linear
predictive
coding (LPC) models. A block diagram of a simplified view of a generic LPC
speech
synthesis model is shown in Figure 6. This model can be used to generate
speech-like
signals by specifying the model parameters appropriately. In this example
speech
synthesis model, the parameters include the time-varying filter coefficients,
pitch
periods, codebook vectors and the gain factors. The synthetic speech is
generated as
follows. An appropriate codebook vector, c(n) , is first scaled by the
codebook gain
factor g~ . Here n denotes sample time. The scaled codebook vector is then
filtered
by a pitch synthesis filter whose parameters include the pitch gain, gp , and
the pitch
period, T . The result is sometimes referred to as the total excitation
vector, u(n) . As
implied by its name, the pitch synthesis filter provides the harmonic quality
of voiced
speech. The total excitation vector is then filtered by the LPC synthesis
filter which
specifies the broad spectral shape of the speech frame.
For each speech frame, the parameters are usually updated more than once.
For instance, in the GSM FR and EFR coders, the codebook vector, codebook gain
and the pitch synthesis filter parameters are determined every subframe (Sms).
The
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
LPC synthesis filter parameters are determined twice per frame (every lOms) in
EFR
and once per frame in FR.
Encoding Steps
Here is a summary of the typical sequence of steps used in a speech encoder:
5 Obtain a frame of speech samples.
Multiply the frame of samples by a window (e.g. Hamming window) and
determine the autocorrelation function up to lag M .
Determine the reflection coefficients and/or LPC coefficients from the
autocorrelation function. (Note that reflection coefficients are an
alternative
10 representation of the LPC coefficients.)
Transform the reflection coefficients or LPC coefficients to a different form
suitable for quantization (e.g. log-area ratios or line spectral frequencies)
Quantize the transformed LPC coefficients using vector quantization
techniques.
The following sequence of operations is typically performed for each
subframe:
Determine the pitch period.
Determine the corresponding pitch gain.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
11
Quantize the pitch period and pitch gain.
Inverse filter the original speech signal through the quantized LPC synthesis
filter to obtain the LPC residual signal.
Inverse filter the LPC residual signal through the pitch synthesis filter to
obtain the pitch residual.
Determine the best codebook vector.
Determine the best codebook gain.
Quantize the codebook gain and codebook vector.
Update the filter memories appropriately.
Add any additional error correction/detection, framing bits etc.
Transmit the coded parameters.
Decoding Steps
Here is the typical sequence of steps used in a speech decoder:
Perform any error correction/detection and framing.
For each subframe:
Dequantize all the received coded parameters (LPC coefficients, pitch period,
pitch gain, codebook vector, codebook gain).
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
12
Scale the codebook vector by the codebook gain and filter it using the pitch
synthesis filter to obtain the LPC excitation signal.
Filter the LPC excitation signal using the LPC synthesis filter to obtain a
preliminary speech signal.
Construct a post-filter (usually based on the LPC coefficients).
Filter the preliminary speech signal to reduce quantization noise to obtain
the
final synthesized speech.
Arrangement of Coded Parameters in the Bit-stream
As an example of the arrangement of coded parameters in the bit-stream
transmitted by the encoder, the GSM FR vocoder is considered. For the GSM FR
vocoder, a frame is defined as 160 samples of speech sampled at 8kHz, i.e. a
frame is
20ms long. With A-law PCM companding, 160 samples would require 1280 bits for
transmission. The encoder compresses the 160 samples into 260 bits. The
arrangement of the various coded parameters in the 260 bits of each frame is
shown in
Figure 7. The first 36 bits of each coded frame consists of the log-area
ratios which
correspond to LPC synthesis filter. The remaining 224 bits can be grouped into
4
subframes of 56 bits each. Within each subframe, the coded parameter bits
contain the
pitch synthesis filter related parameters followed by the codebook vector and
gain
related parameters.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
13
Speech Synthesis Transfer Function and Typical Coded Parameters
Although many non-linearities and heuristics are involved in the speech
synthesis at the decoder, the following approximate transfer function may be
attributed to the synthesis process:
H(z) = g' M (1A)
'1 gPZ T ' \1 ~k=lakZ k
The codebook vector, c(n) , is filtered by H(z) to result in the synthesized
speech. The key point to note about this generic LPC model for speech decoding
is
that the available coded parameters that can be modified to achieve noise
reduction
are:
c(n) : codebook vector
g~ : codebook gain
gP : pitch gain
T : pitch period
{ ak , k = l, ..., M } : LPC coefficients
Most LPC-based vocoders use parameters similar to the above set, parameters
that may be converted to the above forms, or parameters that are related to
the above
forms. For instance, the LPC coefficients in LPC-based vocoders may be
represented
using log-area ratios (e.g. the GSM FR) or line spectral frequencies (e.g. GSM
EFR);
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
14
both of these forms can be converted to LPC coefficients. An example of a case
where
a parameter is related to the above form is the block maximum parameter in the
GSM
FR vocoder; the block maximum can be considered to be directly proportional to
the
codebook gain in the model described by equation (1A).
Thus, although the discussion of coded parameter modification methods is
mostly limited to the generic speech decoder model, it is relatively
straightforward to
tailor these methods for any LPC-based vocoder, and possibly even other
models.
Applicability of Older Speech Processing Techniques to the Coded Domain
It should also be clear that techniques such as spectral subtraction used with
uncoded speech for noise reduction cannot be used on the coded parameters
because
the coded parameter representation of the speech signal is significantly
different.
BRIEF SUMMARY OF THE INVENTION
The invention is useful in a communication system for transmitting digital
signals using a compression code comprising a predetermined plurality of
parameters
including a first parameter. The parameters represent an audio signal having a
plurality of audio characteristics including a noise characteristic. The
compression
code is decodable by a plurality of decoding steps. In such an environment,
according
to one embodiment of the invention, the noise characteristic can be managed by
reading at least the first parameter, and by generating an adjusted first
parameter in
response to the compression code and the first parameter. The first parameter
is
replaced with the adjusted first parameter. The reading, generating and
replacing are
preferably performed by a processor.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
The invention also is useful in a communication system for transmitting
digital
signals comprising code samples further comprising first bits using a
compression
code and second bits using a linear code. The code samples represent an audio
signal
having a plurality of audio characteristics including a noise characteristic.
In such an
5 environment, according to a second embodiment of the invention, the noise
characteristic can be managed without decoding the compression code by
adjusting
the first bits and second bits in response to the second bits.
BRIEF DESCRIPTION OF THE DRAWINGS
Figure 1 is a schematic block diagram of a system for speech transmission in a
10 GSM digital cellular network.
Figure 2 is a schematic block diagram of a system for speech transmission in a
GSM network under tandem-free operation (TFO).
Figure 3 is a graph illustrating transmission of speech under tandem-free
operation (TFO).
15 Figure 4 is a schematic block diagram of a traditional noise reduction
approach using spectral subtraction.
Figure 5 is a schematic block diagram illustrating noise reduction of coded
speech using a traditional approach.
Figure 6 is a schematic block diagram of a generic LPC speech synthesis
model or speech decoder model.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
16
Figure 7 is a schematic block diagram illustrating an arrangement of coded
parameters in a bit-stream for GSM FR.
Figure 8 is a schematic block diagram distinguishing coded domain digital
speech parameters from linear domain digital speech samples.
Figure 9 is a graph illustrating GSM full rate codec quantization levels for
block maxima.
Figure 10a is a schematic block diagram of a backward adaptive standard
deviation based quantizer.
Figure lOb is a schematic block diagram of a backward adaptive differential
based quantizer.
Figure 11 is a schematic block diagram of an adaptive differential quantizer
using a linear predictor.
Figure 12 is a schematic block diagram of a GSM enhanced full rate codebook
gain (speech level related parameter) quantizer.
Figure 13 is a graph illustrating GSM enhanced full rate codec quantization
levels for a gain correction factor.
Figure 14 is a schematic block diagram of one technique for coded domain
ALC.
CA 02378035 2001-12-31
WO 01/02929 PCT1US00/18165
17
Figure 15 is a flow diagram illustrating a technique for overflow/underflow
prevention.
Figure 16 is a schematic block diagram of a preferred form of ALC system
using feedback of the realized gain in ALC algorithms requiring past gain
values.
Figure 17 is a schematic block diagram of one form of a coded domain ALC
device.
Figure 18 is a schematic block diagram of a system for instantaneous scalar
requantization for a GSM FR codec.
Figure 19 is a schematic block diagram of a system for differential scalar
requantization for a GSM EFR codec.
Figure 20a is a graph showing a step in desired gain.
Figure 20b is a graph showing actual realized gain superimposed on the
desired gain with a quantizer in the feedback loop.
Figure 20c is a graph showing actual realized gain superimposed on the
desired gain resulting from placing a quantizer outside the feedback loop
shown in
Figure 19.
Figure 21 is a schematic block diagram of an ALC device showing a quantizer
placed outside the feedback loop.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
18
Figure 22 is a schematic block diagram of a simplified version of the ALC
device shown in Figure 21.
Figure 23a is a schematic block diagram of a coded domain ALC
implementation for ALC algorithms using feedback of past gain values with a
quantizer in the feedback loop.
Figure 23b is a schematic block diagram of a coded domain ALC
implementation for ALC algorithms using feedback of past gain values with a
quantizer outside the feedback loop.
Figure 24 is a graph showing spacing between adjacent R; values in an EFR
codec, and more specifically showing EFR Codec SLRPs: (R; + 1- R; ) against i.
Figure 25a is a diagram of a compressed speech frame of an EFR encoder
illustrating the times at which various bits are received and the earliest
possible
decoding of samples as a buffer is filled from left to right.
Figure 25b is a diagram of a compressed speech frame of an FR encoder
illustrating the times at which various bits are received and the earliest
possible
decoding of samples as a buffer is filled from left to right.
Figure 26 is a schematic block diagram illustrating a single-band linear
domain noise reduction technique.
Figure 27 is a schematic block diagram of a differential scalar quantization
technique.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
19
Figure 28 is a schematic block diagram of a system for differential
requentization of a differentially quantized parameter.
Figure 29 is a graph illustrating reverberations caused by differential
quantizarion.
Figure 30 is a schematic block diagram of a system for reverberation-free
differential requantization.
Figure 31 is a simplified schematic block diagram of a simplified
reverberation-free differential requantization system.
Figure 32 is schematic block diagram of a dual-source view of speech
synthesis.
Figure 33 is a schematic block diagram of a preferred form of network noise
reduction.
Figure 34 is a graph illustrating magnitude frequency response of comb
filters.
Figure 35 is a graph illustrating increase in spectral peakresponse of a comb
filter due to pitch gain control.
Figure 36 is a schematic block diagram of one preferred form of a coded
domain noise reduction system using codebook gain attenuation.
Figure 37 is a flow diagram of a preferred form of coded domain noise
reduction methodology according to the invention.
CA 02378035 2001-12-31
WO 01/02929 PCT/LTS00/18165
Figure 38 is a schematic block diagram of a system for coded domain noise
reduction by modification of the codebook vector parameter.
Figure 39 is a graph illustrating a spectral interpretation of line spectral
frequencies.
5 DETAILED DESCRIPTION OF THE PREFERRED EMBODIMENTS
While the invention will be described in connection with one or more
embodiments,
it will be understood that the invention is not limited to those embodiments.
On the
contrary, the invention includes all alternatives, modifications, and
equivalents as may be
included within the spirit and scope of the appended claims. For example, the
ALC
10 techniques described in this specification also have application to NR
techniques.
In modern networks, speech signals are digitally sampled prior to
transmission. Such digital (i.e. discrete-time discrete-valued) signals are
herein
referred to in this specification as being in the linear domain. The
adjustment of the
speech levels in such linear domain signals is accomplished by multiplying
every
15 sample of the signal by an appropriate gain factor to attain the desired
target speech
level.
Digital speech signals that are typically carried in telephony networks
usually
undergo a basic form of compression such as pulse code modulation (PCM) before
transmission. Such compression schemes are very inexpensive in terms of
20 computations and delay. It is a relatively simple matter for an ALC or NR
device to
convert the compressed digital samples to the linear domain, process the
linear
samples, and then compress the processed samples before transmission. As such,
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
21
these signals can effectively be considered to be in the linear domain. In the
context of
this specification, compressed or coded speech will refer to speech that is
compressed
using advanced compression techniques that require significant computational
complexity.
More specifically, in this specification and claims, linear code and
compression code have the following meanings:
Linear code: By a linear code, we mean a compression technique that results
in one coded parameter or coded sample for each sample of the audio signal.
Examples of linear codes are PCM (A-law and ,u -law) ADPCM (adaptive
differential
pulse code modulation), and delta modulation.
Compression code: By a compression code, we mean a technique that results
in fewer than one coded parameter for each sample of the audio signal.
Typically,
compression codes result in a small set of coded parameters for each block or
frame
of audio signal samples. Examples of compression codes are linear predictive
coding
based vocoders such as the GSM vocoders (HR, FR, EFR).
Speech compression, which falls under the category of lossy source coding, is
commonly referred to as speech coding. Speech coding is performed to minimize
the
bandwidth necessary for speech transmission. This is especially important in
wireless
telephony where bandwidth is a scarce resource. In the relatively bandwidth
abundant
packet networks, speech coding is still important to minimize network delay
and fitter.
This is because speech communication, unlike data, is highly intolerant of
delay.
Hence a smaller packet size eases the transmission through a packet network.
Several
industry standard speech codecs (coder-decoder pairs) were listed in Table 1
for
reference.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
22
In speech coding, a set of consecutive digital speech samples is referred to
as a
speech frame. Given a speech frame, a speech encoder determines a small set of
parameters for a speech synthesis model. With these speech parameters and the
speech synthesis model, a speech frame can be reconstructed that appears and
sounds
very similar to the original speech frame. The reconstruction is performed by
the
speech decoder. It should be noted that, in most speech coders, the encoding
process
is much more computationally intensive than the decoding process. Furthermore,
the
millions of instructions per second (MIPs) required to attain good quality
speech
coding is very high. The processing capabilities of digital signal processing
chipsets
have advanced sufficiently only in recent years to enable the widespread use
of
speech coding in applications such as cellular telephone handsets.
The speech parameters determined by the speech encoder depend on the
speech synthesis model used. For instance, the coders in Table 1 utilize
linear
predictive coding (LPC) models. (To be more specific, these coders belong to
the
class of code-excited linear prediction or CELP coders.) A block diagram of a
simplified view of the LPC speech synthesis model is shown in Figure 6. This
model
can be used to generate speech-like signals by specifying the model parameters
appropriately. In this example speech synthesis model, the parameters include
the
time-varying filter coefficients, pitch periods, excitation vectors and gain
factors.
Basically, the excitation vector, c(n), is first scaled by the gain factor, G.
The result is
then filtered by a pitch synthesis filter whose parameters include the pitch
gain, g p ,
and the pitch period, T, to obtain the total excitation vector, u(n). This is
then filtered
by the LPC synthesis filter. Other models such as the multiband excitation
model are
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
23
also used in speech coding. In this context, it suffices to note that the
speech
parameters together with the assumed model provide a means to remove the
redundancies in the digital speech signal so as to achieve compression.
As shown in Figure 6, the overall DC gain is provided by G and ALC would
primarily involve modifying G. Furthermore, the gain factor g p may be
modified to
obtain a certain degree of noise reduction, if desired, in the case of noisy
speech.
Among the speech parameters that are generated each frame by a typical
speech encoder, some parameters are concerned with the spectral and/or
waveform
shapes of the speech signal for that frame. These parameters typically include
the LPC
coefficients and the pitch information in the case of the LPC speech synthesis
model.
In addition to these parameters that provide spectral information, there are
usually
parameters that are directly related to the power or energy of the speech
frame. These
speech level related parameters (SLRPs) are the key to performing ALC of coded
speech. Several examples of such SLRPs will be provided below.
The first three GSM codecs in Table 1 will now be discussed. All of the first
three coders process speech sampled at 8kHz and assume that the samples are
obtained as 13-bit linear PCM values. The frame length is 160 samples (20ms).
Furthermore, they divide each frame into four subframes of 40 samples each.
The
SLRPs for these codecs are listed in Table 2.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
24
Table 2. Speech Level Related Parameters in GSM Speech Codecs
Codec Name SLRP Descri tion
GSM Half R(0) R(0) is the average signal power of the speech
Rate frame. The signal
ower is computed using an analysis window which
is centered over
he last 100 samples of the frame. The signal
power in decibels is
uantized to 32 levels which are s aced uniforml
in 2dB ste s.
GSM Full x,I,aX xI"a,~ is the maximum absolute value of the
Rate elements in the subframe
xcitation vector. x~X is also termed the block
maximum. All the
ther subframe excitation elements are normalized
and then
uantized with respect to this maximum. The
maximum is quantized
0 64 levels non-uniforml .
GSM EnhancedyR yR~ is the gain correction factor between a
gain factor, g~ , used to
Full Rate scale the subframe excitation vector and a
gain factor, g~ , that is
redicted using a moving average model, i.e.
yR~ = g~ l g~ . The
orrection factor is uantized to 32 levels non-uniforml
.
Depending on coder, the SLRP may be specified each subframe (e.g. the GSM FR
and EFR codecs) or once per frame (e.g. the GSM HR codec).
Throughout this specification, the same variable with and without a caret
above it will be used to denote the unquantized and quantized values that it
holds, e.g.
yR~ and y and are the unquantized and quantized gain correction factors in the
8c
n
GSM EFR standard. Note that only the quantized SLRP, y , will be available at
the
gc
ALC device.
0 The quantized and corresponding unquantized parameters are related through
the quantization function, Q(.), e.g. y =Q(yR~). We use the notation somewhat
Rc
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
liberally to include not just this transformation but, depending on the
context, the
determination of the index of the quantized value using a look-up table or
formula.
The quantization function is a many-to-one transformation and is not
invertible. However, we use the 'inverse' quantization function, Q-' (.), to
denote the
5 conversion of a given index to it corresponding quantized value using the
appropriate
look-up table or formula.
Figure 8 distinguishes the coded domain from the linear domain. In the linear
domain, the digital speech samples are directly available for processing. The
coded
domain refers to the output of speech encoders or the input of the speech
decoders,
10 which should be identical if there are no channel errors. In this context,
the coded
domain includes both the speech parameters and the methods used to quantize or
dequantize these parameters. The speech parameters that are determined by the
encoder undergo a quantization process prior to transmission. This
quantization is
critical to achieving bit rates lower than that required by the original
digital speech
15 signal. The quantization process often involves the use of look-up tables.
Furthermore, different speech parameters may be quantized using different
techniques.
Processing of speech in the coded domain involves directly modifying the
quantized speech parameters to a different set of quantized values allowed by
the
20 quantizer for each of the parameters. In the case of ALC, the parameters
being
modified are the SLRPs. For other applications, such as noise reduction (NR),
other
parameters may be used.
CA 02378035 2001-12-31
WO 01/02929 PCT/LTS00/18165
26
The quantization of a single speech parameter is termed scalar quantization.
When a set of parameters are quantized together, the process is called vector
quantization. Vector quantization is usually applied to a set of parameters
that are
related to each other in some way, such as the LPC coefficients. Scalar
quantization is
generally applied to a parameter that is relatively independent of the other
parameters.
A mixture of both types of quantization methods is also possible. As the SLRPs
are
usually scalar quantized, focus is placed on the most commonly used scalar
quantization techniques.
When a parameter is quantized instantaneously, the quantization process is
independent of the past and future values of the parameter. Only the current
value of
the parameter is used in the quantization process. The parameter to be
quantized is
compared to a set of permitted quantization levels. The quantization level
that best
matches the given parameter in terms of some closeness measure is chosen to
represent that parameter. Usually, the permitted quantization levels are
stored in a
look-up table at both the encoder and the decoder. The index into the table of
the
chosen quantization level is transmitted by the encoder to the decoder.
Alternatively,
given an index, the quantization level may be determined using a mathematical
formula. The quantization levels are usually spaced non-uniformly in the case
of
SLRPs. For instance, the block maxima, x ~X , in the GSM FR codec which has a
range [0,32767] is quantized to the 64 levels shown in Figure 9. In this
quantization
scheme, the level that is closest but higher than x ",ax is chosen. Note that
the vertical
axis which represents the quantization levels is plotted on a logarithmic
scale.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
27
Instantaneous quantization schemes suffer from higher quantization errors due
to the use of a fixed dynamic range. Thus, adaptive quantizers are often used
in
speech coding to minimize the quantization error at the cost of greater
computational
complexity. Adaptive quantizers may utilize forward adaptation or backward
adaptation. In forward adaptation schemes, extra side information regarding
the
dynamic range has to be transmitted periodically to the decoder in addition to
the
quantization table index. Thus, such schemes are usually not used in speech
coders.
Backward adaptive quantizers are preferred because they do not require
transmission
of any side information. Two general types of backward adaptive quantizers are
commonly used: standard deviation based and differential. These are depicted
in
Figure 10.
In the standard deviation based quantization scheme of Figure 10(a), the
standard deviation of previous parameter values are used to determine a
normalization
factor for the current parameter value, ((n). The normalization factor divides
prior to
quantization. This normalization procedure allows the quantization function,
Q(.), to
be designed for unit variance. The look-up table index of the normalized and
quantized value, y (n), is transmitted to the dequantizer where the inverse
process
norm
is performed. In order for the normalization and denormalization processes to
be
compatible, a quantized version of the normalization factor is used at both
the
quantizer and dequantizer. In some variations of this scheme, decisions to
expand or
compress the quantization intervals may be based simply on the previous
parameter
input only.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
28
In the backward adaptive differential quantization scheme of Figure 10(b), the
correlation between current and previous parameter values is used to
advantage.
When the correlation is high, a significant reduction in the quantization
dynamic
range can be achieved by quantizing the prediction error, r(n). The prediction
error is
the difference between the actual and predicted parameter values. The same
predictor
for ((n) must be used at both the quantizer and the dequantizer. A linear
predictor,
P(z), which has the following form is usually used:
P(Z) - ~k_1 171 k Z_k (1)
It can be shown readily that the differential quantization scheme can also be
represented as in Figure 10 when a linear predictor, P(z), is used. Note that
if we
approximate the transfer function P(z)/[1-P(z)] by the linear predictor,
P 1 (z)- ~k=~ bk z k , then a simpler implementation can be achieved. This
simpler
differential technique is used in the GSM EFR codec for the quantization of a
function
of the gain correction factor, yg~ . In this codec, a fourth order linear
predictor with
fixed coefficients, [bl,b2,b3,b4] _ [0.68, 0.58, 0.34, 0.19], is used at both
the encoder
and the decoder.
In the EFR codec, g ~ (n) denotes the gain factor that is used to scale the
excitation vector at subframe n. This gain factor determines the overall
signal level.
The quantization of this parameter utilizes the scheme shown in Figure 11 but
is
rather indirect. The actual 'gain' parameter that is transmitted is actually a
correction
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
29
factor between g ~ (n) and the predicted gain, g ~ ' (n). The correction
factor, yg~ (n),
defined as
Yg~(n) - g~ (n)
g~(n) (2)
is considered the actual SLRP because it is the only parameter related to the
overall speech level that is accessible directly in the coded domain.
At the encoder, once the best g ~ (n) for the current subframe n is
determined, it
is divided by the predicted gain to obtain yg~ (n). The predicted gain is
given by
g~ (n) =10°.os~Ecn~-E, (n)+El (3)
A 32-level non-uniform quantization is performed on y 8~ (n) to obtain y (n).
The
corresponding look-up table index is transmitted to the decoder. In equation
(3), E is a
constant, E, (n) depends only on the subframe excitation vector, and E(n)
depends
only on the previously quantized correction factors. The decoder, thus, can
obtain the
predicted gain in the same manner as the encoder using (3) once the current
subframe
excitation vector is received. On receipt of the correction factor y~ (n) ,
the quantized
gain factor can be computed as g~ (n) = y~ (n)g~ (n) using the definition in
equation
(2).
CA 02378035 2001-12-31
WO 01/02929 PCT/LTS00/18165
The quantization of the SLRP, y~ , is illustrated in Figure 12. In this
Figure,
R(n) denotes the prediction error given by
R(n) = E(n) -E(n) = 20 log yg~ (n) (4)
Note that the actual information transmitted from the encoder to the decoder
5 are the bits representing the look-up table index of the quantized R(n)
parameter,
R(n) . This detail is omitted in Figure 12 for simplicity. Since the preferred
ALC
technique does not affect the channel bit error rate, it is assumed that the
transmitted
and received parameters are identical. This assumption is valid because the
result of
undetected or uncorrected errors will result in noisier decoded speech
regardless of
10 whether ALC is performed.
The quantization of the SLRP at the encoder is performed indirectly by using
the mean-removed excitation vector energy each subframe. E(n) denotes the mean-
removed excitation vector energy (in dB) at subframe n and is given by
E(n) =lOlo Ng~~ o'CZ(i) -E
(5)
= 201oggc+l0 log N ~ ;'o CZ(i) -E
15 Here N = 40 is the subframe length and E is constant. The middle term in
the
second line of equation (5) is the mean excitation vector energy, E, (n) ,
i.e.
E, (n) =10 log N ~ No' Cz (i) (6)
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
31
The excitation vector ~c(i)~ is preferred at the decoder prior to the
determination of the SLRP. Note that the decoding of the excitation vector is
independent of the decoding of the SLRP. It is seen that E(n) is a function of
the gain
factor, g~ . The quantization of y~ (n) to y~~ (n) indirectly causes the
quantization of
g~ to g~ . This quantized gain factor is used to scale the excitation vector,
hence
setting the overall level of the signal synthesized at the decoder. is the
predicted
energy given by
E(n) _ ~ ~ ~ b;R(n - i)
where ~R(n - i)~ are previously quantized values.
The preferred method of decoding the gain factor,-, will now be discussed.
First, the decoder decodes the excitation vector and computes E, (n) using
equation
(6). Second, the predicted energy is computed using previously decoded gain
correction factors using equation (7). Then the predicted gain, g1 (c) , is
computed
using equation (3). Next, the received index of the correction factor for the
current
subframe is used to obtain from the look-up table. Finally, the quantized gain
factor
is obtained as g~ (n) = yg~ (n)g~ (n) . The 32 quantization levels for are
illustrated in
Figure 13. Note that the vertical axis in Figure 13 which represents the
quantization
levels is plotted on a logarithmic scale.
Those skilled in communications recognize that the quantizer techniques
descriged in connection with SLRPs apply equally to NR parameters.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
32
For most codecs, only a partial decoding of the coded speech is necessary to
perform ALC. The speech is decoded to the extent necessary to extract the SLRP
as
well as other parameters essential for obtaining sufficiently accurate speech
level,
voice activity and double-talk measurements. Some examples of situations where
only
partial decoding suffices include:
1) In CELP decoders, a post-filtering process is performed on the signal
decoded using the LPC-based model. This post-filtering helps to reduce
quantization
noise but does not change the overall power level of the signal. Thus, in
partial
decoding of CELP-coded speech, the post-filtering process can be avoided for
economy.
2) Some form of silence suppression scheme is often used in cellular
telephony and voice over packet networks. In these schemes, coded speech
frames are
transmitted only during voice activity and very little transmission is
performed during
silence. The decoders automatically insert some comfort noise during the
silence
periods to mimic the background noise from the other end. One example of such
a
scheme used in GSM cellular networks is called discontinuous transmission
(DTX).
By monitoring the side information that indicates silence suppression, the
decoder in
the ALC device can completely avoid decoding the signal during silence. In
such
cases, the determination of voice and double-talk activities can also be
simplified in
the ALC device.
3) In the proposed Tandem-Free Operation (TFO) standard for speech codecs
in GSM networks, the coded speech bits for each channel will be carried
through the
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
33
wireline network between base stations at 64 kbits/sec. This bitstream can be
divided
into 8-bit samples. The 2 least significant bits of each sample will contain
the coded
speech bits while the upper 6 bits will contain the bits corresponding to the
appropriate PCM samples. The conversion of the PCM information to linear
speech is
very inexpensive and provides a somewhat noisy version of the linear speech
signal. It
is possible to use this noisy linear domain speech signal to perform the
necessary
voice activity, double-talk and speech level measurements as is usually done
in linear
domain ALC algorithms. Thus, in this case, only a minimal amount of
interpretation
of the PCM samples is necessary. The SLRP and any other parameters that are
required for the requantization of the SLRP would have to be interpreted. The
other
parameters would be decoded only to the extent necessary for requantization of
the
SLRP. This will be clear from the examples that will follow in later sections.
Thus, we see that it is possible to implement an ALC device that only
performs partial decoding and re-encoding, hence minimizing complexity and
reducing quantization noise. However, the ALC approach illustrated in Figure
14 can
be improved. The sub-optimality is due to the implicit assumption that the
process of
gain determination is independent of SLRP requantization. In general, this
assumption
may not be valid.
Those skilled in communications recognize that the ALC approach shown in
Figure 14 also is applicable to NR.
There are three main factors which suggest an improvement over the Figure 14
approach. First, note that requantization results in a realized SLRP that
usually differs
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
34
from the desired value. Hence the desired gain that was applied by the Gain
Determination block will differ from the gain that will be realized when the
signal is
decoded. When decoding, overflow or underflow problems may arise due to this
difference because the speech signal may be over-amplified or over-suppressed,
respectively. Second, some ALC algorithms may utilize the past desired gain
values
to determine current and future desired gain values. Since the desired gain
values do
not reflect the actual realized gain values, such algorithms may perform
erroneously
when applied as shown in Figure 14. Third, the requantization process can
sometimes
result in undesirable reverberations in the SLRP. This can cause the speech
level to be
modulated unintentionally, resulting in a distorted speech signal. Such SLRP
reverberations are encountered in feedback quantization schemes such as
differential
quantization.
Turning now to Figure 15, to overcome the overflow/underflow problems, the
iterative techniques of Figure 15 can be incorporated in the Gain
Determination block.
Basically, after deciding on a desired gain value, the realized gain value
after
requantization of the SLRP may be computed. The realized gain is checked to
see if
overflow or underflow problems could occur. This could be accomplished, for
example, by determining what the new speech level would be by multiplying the
realized gain by the original speech level. Alternatively, a speech decoder
could be
used in the ALC device to see whether overflow/underflow actually occurs.
Either
way, if the realized gain value is deemed to be too high or too low, the new
SLRP is
reduced or increased, respectively, until the danger of overflow/underflow is
considered to be no longer present.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
In ALC algorithms where past desired gain values are fed back into the
algorithm to determine current and future gain values, the following
modification may
be made. Basically, the gain that is fed back should be the realized gain
after the
SLRP requantization process, not the desired gain. A preferred approach is
shown in
5 Figure 16. If the desired gain was used in the feedback loop instead of the
realized
gain, the controller would not be tracking the actual decoded speech signal
level,
resulting in erroneous level control.
Note that the iterative scheme for overflow/underflow prevention of Figure 15
may also be incorporated into the Gain Determination block of Figure 16.
10 Finally, the methods to avoid SLRP reverberations in feedback-based
quantization schemes will be discussed in detail below. In general, these
methods
preferably include the integration of the gain determination and SLRP
requantization
techniques.
Hence the joint design and implementation of the Gain Determination block
15 and SLRP Requantization block is preferred to prevent overflow and
underflow
problems during decoding, ensure proper tracking by feedback-based ALC
systems,
and avoid the oscillatory effects introduced by feedback quantization schemes.
Figure
17 illustrates the general configuration of an ALC device that uses joint gain
determination and SLRP requantization. The details will depend on the
particular
20 ALC device.
The techniques for requantization of SLRPs will now be discussed. In most
speech encoders, the quantization of the SLRP is performed using either
instantaneous
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
36
scalar quantization or differential scalar quantization, which were discussed
above.
The requantization of the SLRPs for these particular cases will be described
while
noting that the approaches may be easily extended to any other quantization
scheme.
The joint determination of the gain and SLRP requantization in the ALC device
configuration of Figure 17 may utilize the requantization techniques described
here.
The original value of the quantized SLRP will be denoted by y(n) , where n is
the frame or subframe index. The set of m quantization table values will be
denoted
by ~%I,...ym~. Depending on the speech coder, these values may, instead, be
defined
using a mathematical formula. The desired gain determined by the ALC device
will
be denoted by g(n) . The realized gain after SLRP requantization will be
denoted by
g(n) . In instantaneous scalar requantization, the goal is to minimize the
difference
between g(n) and g(n) . The basic approach involves the selection of the
quantization table index, k, as
k = argmini llg(n)y(n)-yill (8)
The requantized SLRP is then given by ya,~ (n) = Yx
If overflow and underflow prevention are desired, then the iterative scheme
described in Figure 15 may be used. In another approach for overflow/underflow
prevention, the partial decoding of the speech samples using the requantized
SLRP
may be performed to the extent necessary. This, of course, involves additional
complexity in the algorithm. The decoded samples can then be directly
inspected to
ensure that overflow or underflow has not taken place.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
37
Note that for a given received y(n), there are m possible realized gain
values.
For each quantization table value, all the realized gains can be precomputed
and
stored. This would require the storage of m2 realized gain values, which is
often
feasible since m is usually a small power of two, e.g. m = 32 in the GSM EFR
codec
and m = 64 in the GSM FR codec.
If the SLRP quantization table values are uniformly spaced (either linearly or
logarithmically), then it is possible to simplify the scalar requantization
process. This
simplification is achieved by allowing only a discrete set of desired gain
values in the
ALC device. These desired gain values preferably have the same spacing as the
SLRP
quantization values, with OdB being one of the gains. This ensures that the
desired and
realized gain values will always be aligned so that equation (8) would not
have to be
evaluated for each table value. Hence the requantization is greatly
simplified. The
original quantization index of the SLRP is simply increased or decreased by a
value
corresponding to the desired gain value divided by the SLRP quantization table
spacing. For instance, suppose that the SLRP quantization table spacing is
denoted by
0. Then the discrete set of permitted desired gain values would be 1+{..., -2,
-, 0, , 2,
} if the SLRP quantization table values are uniformly spaced linearly, and
0+{..., -2,
-, 0, , 2, ... } if the SLRP quantization table values are uniformly spaced
logarithmically. If the desired gain value was 1+ k,0 (linear case) or k,0
(logarithmic case), then the index of the requantized SLRP is simply obtained
by
adding k, to the original quantization index of the SLRP.
Note that this low complexity instantaneous scalar requantization technique
can be applied even if the SLRP quantization table values are not uniformly
spaced.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
38
In this case, 0 would be the average spacing between adjacent quantization
table
values, where the average is performed appropriately using either linear or
logarithmic distances between the values.
An example of instantaneous scalar requantization is shown for the GSM FR
codec in Figure 18. This codec's SLRP is the block maximum, x~X , which is
transmitted every subframe. The Q and Q-' blocks represent the SLRP
requantization
and dequantization, respectively. The index of the block maximum is first
dequantized using the look-up table to obtain x~X . Then, x~x is multiplied by
the
desired gain to obtain x~,,~~ which is then requantized by using the look-up
table.
The index of the requantized x",aX is then substituted for the original value
in the
bitstream before being sent out. This requantization technique forms the basic
component of all the techniques described in Figures 14-17 when implementing
coded
domain ALC for the GSM FR standard.
Application of the above technique to SLRPs will now be discussed, although
the techniques will be applicable to other parameters just as well, such as NR
related
parameters. The GSM EFR codec will be used as an example for illustrating the
implementation of coded domain ALC using this requantization technique.
Figure 19 shows a general coded domain ALC technique with only the compo-
nents relevant to ALC being shown. Note that (G(n) denotes the original
logarithmic
gain value determined by the encoder. In the case of the EFR codec, G(n) is
equal to
E(n) defined in equation (5) and R(n) is as defined in equation (4). The ALC
device
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
39
determines the desired gain, 0~ (n) . The SLRP, R(n) , is modified by the ALC
device to R A~ (n) based on the desired gain. The realized gain, OR(n) , is
the
difference between original and modified SLRPs, i.e.
OR(n) = Ra,e (n) -R(n) (9)
Note that this is different from the actual gain realized at the decoder
which,
under steady-state conditions, is ~1 + P, (1)~tlR(n) . To make the distinction
clear, we
will refer to the former as the SLRP realized gain and the latter as the
actual realized
gain. The actual realized gain is essentially an amplified version of the SLRP
realized
gain due to the decoding process, under steady-state conditions. By steady-
state, it is
meant that OG(n) is kept constant for a period of time that is sufficiently
long so
that OR(n) is either steady or oscillates in a regular manner about a
particular level.
This method for differential scalar requantization basically attempts to mimic
the operation of the encoder at the ALC device. If the presence of the
quantizers at the
encoder and the ALC device is ignored, then both the encoder and the ALC
device
would be linear systems with the same transfer function, Y~l + P, (3)~ , with
the result
that GALS (n) = G(n) + OG(n) . However, due to the quantizers which make these
systems non-linear, this relationship is only approximate. Hence, the decoded
gain
given by
Ga,~ (n) = G(n) + ~G(n) +quantization error
(10)
CA 02378035 2001-12-31
WO 01/02929 PCT/LTS00/18165
where (OG(n) + quantization error) is the actual realized gain.
The feedback of the SLRP realized gain, OR(n) , in the ALC device can cause
undesirable oscillatory effects. As an example, we will demonstrate these
oscillatory
effects when the GSM EFR codec is used. Recall that, for this codec, Pl (z)
has four
5 delays elements. Each element could contain one of 32 possible values. Hence
the
non-linear system in the ALC device can be in any one of over a million
possible
states at any given time. This is mentioned because the behavior of this non-
linear
system is heavily influenced by its initial conditions.
The reverberations in the actual realized gain in response to a step in the
10 desired gain, OG(n) , will now be illustrated. For simplicity, it is
assumed that the
original SLRP, R(n) , is constant over 100 subframes, and that the memory of
P, (z)
is initially zero. Figure 20(a) shows the step in the desired gain. Figure
20(b) shows
the actual realized gain superimposed on the desired gain. Although the
initial
conditions and the original SLRP will determine the exact behavior, the rever-
15 berations in the actual realized gain shown here are quite typical.
The reverberations in the SLRP realized gain shown in Figure 20(b) cause a
modulation of the speech signal and can result in audible distortions. Thus,
depending
on the ALC specifications, such reverberations may be undesirable. The
reverberations can be eliminated by 'moving' the quantizer outside the
feedback loop
20 as shown in Figure 20. (In this embodiment, the computation of is
unnecessary but is
included for comparison to Figure 19.)
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
41
Placing the quantizer outside the feedback loop results in the actual realized
gain shown in Figure 20(c), superimposed on the desired gain. It should be
noted that,
although reverberations are eliminated, the average error (i.e. the average
difference
between the desired and actual realized gains) is higher than that shown in
Figure
20(b). Specifically, in these examples, the average error during steady state
operation
of the requantizer with and without the quantizer in the feedback loop are
0.39dB and
1.03dB, respectively.
The ALC apparatus of Figure 21 can be simplified as shown in Figure 22,
resulting in savings in computation. This is done by replacing the linear
system
1
Y~1 + P, (z)~ with the constant,
~1 + P, (1)~
For the purposes of ALC, this simpler implementation is often found to be
satisfactory especially when the desired gains are changed relatively
infrequently. By
infrequent changes, it is meant that the average number of subframes between
changes is much greater than the order of Pl (z) .
Some ALC algorithms may utilize past gain values to determine current and
future gain values. In such feedback-based ALC algorithms, the gain that is
fed back
should be the actual realized gain after the SLRP requantization process, not
the
desired gain. This was discussed above in conjunction with Figure 16.
Differential scalar requantization for such feedback-based ALC algorithms can
be implemented as shown in Figure 23. In these implementations, the ALC device
is
mimicking the actions of the decoder to determine the actual realized gain.
CA 02378035 2001-12-31
WO 01/02929 PCT/(TS00/18165
42
If a simplified ALC device implementation similar to Figure 21 is desired in
Figure 23(b), then the linear system 1 may be replaced with the constant
~1 + P, (z)~
1 A further sim lification can be achieved in Fi ure 23 b b
multiplier, ~1 + Pl (1)~ . p g ( ) y
replacing the linear system 1 + P, (z) with the constant multiplier 1 + P, (1)
, although
S accuracy in the calculation of the actual realized gain is somewhat reduced.
In a
similar manner, the implementation shown in Figure 23(a) can be simplified by
replacing the linear system by with the constant multiplier P, (1) .
In applications that are tolerant to reverberations but require higher
accuracy
in matching the desired and actual realized gains, any of the methods
described earlier
that have quantizers within the feedback loop may be used. For applications
that
cannot allow reverberations in the actual realized gains but can tolerate
lower
accuracy in matching the desired and actual realized gains, any of the methods
described earlier that have quantizers outside the feedback loop may be used.
If,
however, both accuracy and avoidance of reverberations are necessary as is
often the
case in ALC, then a different approach is necessary.
The current method avoids reverberations in the actual realized gains by
placing the quantizers outside the feedback loop as in Figures 21, 22, or
23(b).
Additionally, the average error between desired and actual realized gains is
minimized
by restricting the desired gain values to belong to the set of possible actual
realized
gain values, given the current original SLRP value, R(n) .
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
43
Let the set of m possible SLRP values be ~R o , R, , R z ,..., R m_, ~. Given
the
original SLRP, R(n) , that is received from the encoder, the ALC device
computes the
set of m values, ~ ~R ~ - R(n)~ ~l + P, (1)~ ~. This is the set of possible
actual realized
gain values. The ALC algorithm should preferably be designed such that the
desired
gain, , is selected from this set. Such restrictions can be easily imposed on
a large
variety of ALC algorithms since most of them already operate using a finite
set of
possible desired gain values.
If the R i values are uniformly spaced, i.e. R i+1 - R = ~ , the above
restriction
on the desired gain values is further simplified to selecting a desired gain
value that is
a multiple of the constant 0~1 + P, (1)~ . This reduces computations
significantly as the
desired gain value is independent of the current original SLRP value, R(n) .
Even when the values are not uniformly spaced, such simplifications are
usually possible. For instance, the 32 R i values in the EFR codec can be
divided into
three sets, each with approximately uniform spacing. The spacing between
adjacent
R i values is illustrated in Figure 24. Most of the values lie in the middle
region and
have an average spacing of 1.214dB. For this codec, ~HP,(1)~=2.79. Thus the
desired gain values are selected to be multiples of 1.214x2.79 = 3.387 dB when
R(n)
falls in the middle region. A further simplification is possible by always
setting the
desired gain value to be a multiple of 3.387dB regardless of for this codec.
This is
because R(n) will fall into the lower or higher regions only for very short
durations
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
44
such as at the transitions between speech and silence. Hence reverberations
cannot be
sustained in these regions.
Thus, in general, for each uniformly spaced subset of possible SLRP values
with a spacing 0 , the desired gain value can be selected to be a multiple of
0~1 + Pl (1)~ if the corresponding current original SLRP belongs to that
subset.
Large buffering, processing and transmission delays are already incurred by
speech coders. Further processing of the coded speech for speech enhancement
purposes can add additional delay. Such additional delay is undesirable as it
can
potentially make telephone conversations less natural. Furthermore, additional
delay
may reduce the effectiveness of echo cancellation at the handsets, or
alternatively,
increase the necessary complexity of the echo cancellers for a given level of
perfor-
mance. It should be noted that implementation of ALC in the linear domain will
always add at least a frame of delay due to the buffering and processing
requirements
for decoding and re-encoding. For the codecs listed in Table 1, note that each
frame is
20ms long. However, coded domain ALC can be performed with a buffering delay
much less than one frame. Those skilled in communications recognize that the
same
principles apply to NR.
The EFR encoder compresses a 20ms speech frame into 244 bits. At the
decoder in the ALC device, the earliest point at which the first sample can be
decoded
is after the reception of bit 91 as shown in Figure 25(a). This represents a
buffering
delay of approximately 7.46ms. It turns out that sufficient information is
received to
decode not just the first sample but the entire first subframe at this point.
Similarly,
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
the entire first subframe can be decoded after about 7.l lms of buffering
delay in the
FR decoder.
The remaining subframes, for both coders, require shorter waiting times prior
to decoding. Note that each subframe has an associated SLRP in both the EFR
and FR
5 coding schemes. This is generally true for most other codecs where the
encoder
operates at a subframe level.
From the above, it can be realized that ALC and NR in the coded domain can
be performed subframe-by-subframe rather than frame-by-frame. As soon as a
subframe is decoded and the necessary level measurements are updated, the new
10 SLRP computed by the ALC device can replace the original SLRP in the
received
bitstream.
The delay incurred before the SLRP can be decoded is determined by the
position of the bits corresponding to the SLRP in the received bitstream. In
the case of
the FR and EFR codecs, the position of the SLRP bits for the first subframe
15 determines this delay.
Most ALC algorithms determine the gain for a speech sample only after
receiving that sample. This allows the ALC algorithm to ensure that the speech
signal
does not get clipped due to too large a gain, or underflow due to very low
gains.
However, in a robust ALC algorithm, both overflow and underflow are events
that
20 have low likelihoods. As such, one can actually determine gains for samples
based on
information derived only from previous samples. This concept is used to
achieve
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
46
near-zero buffering delay in coded domain ALC for some speech codecs. Those
skilled in communications recognize that the same principles apply to NR
algorithms.
Basically, the ALC algorithm must be designed to determine the gain for the
current subframe based on previous subframes only. In this way, almost no
buffering
delay will be necessary to modify the SLRP. As soon as the bits corresponding
to the
SLRP in a given subframe are received, they will first be decoded. Then the
new
SLRP will be computed based on the original SLRP and information from the
previous subframes only. The original SLRP bits will be replaced with the new
SLRP
bits. There is no need to wait until all the bits necessary to decode the
current
subframe are received. Hence, the buffering delay incurred by the algorithm
will
depend on the processing delay which is small. Information about the speech
level is
derived from the current subframe only after replacement of the SLRP for the
current
subframe. Those skilled in communications recognize that the same principles
apply
to NR algorithms.
Note that most ALC algorithms can be easily converted to operate in this
delayed fashion. Although there is a small risk of overflow or underflow, such
risk
will be isolated to only a subframe (usually about Sms) of speech. For
instance, after
overflow in a subframe due to a large gain being applied, the SLRP computed
for the
next subframe can be appropriately set to minimize the likelihood of continued
overflows. Those skilled in communications recognize that the same principles
apply
to NR algorithms.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
47
This near-zero buffering delay method is especially applicable to the FR codec
since the decoding of the SLRP for this codec does not involve decoding any
other
parameters. In the case of the EFR codec, the subframe excitation vector is
also
needed to decode the SLRP and the more complex differential requantization
techniques have to be used for requantizing the SLRP. Even in this case,
significant
reduction in the delay is attained by performing the speech level update based
on the
current subframe after the SLRP is replaced for the current subframe. Those
skilled
in communications recognize that the same principles apply to NR.
Performing coded domain ALC in conjunction with the proposed TFO
standard in GSM networks was discussed above. According to this standard, the
received bitstream can be divided into 8-bit samples. The 2 least significant
bits of
each sample will contain the coded speech bits while the upper 6 bits will
contain the
bits corresponding to the appropriate PCM samples. Hence a noisy version of
the
linear speech samples is available to the ALC device in this case. It is
possible to use
this noisy linear domain speech signal to perform the necessary voice
activity, double-
talk and speech level measurements as is usually done in linear domain ALC
algorithms. Thus, in this case, only a minimal amount of decoding of the coded
domain speech parameters is necessary. Only parameters that are required for
the
determination and requantization of the SLRP would have to be decoded. Partial
decoding of the speech signal is unnecessary as the noisy linear domain speech
samples can be relied upon to measure the speech level as well as perform
voice
activity and double-talk detection.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
48
An object of the present invention is to derive methods to perform noise
reduction in the coded domain via methods that are less computationally
intensive
than using linear domain techniques of similar quality that require re-
encoding of the
processed signal. The flexibility available in the coded domain to modify
parameters
to effect desired changes in the signal characteristics may be limited due to
quantization. A survey of the different speech parameters and the
corresponding
quantization methods used by industry standard speech coders was performed.
The
modification of the different speech parameters will be considered, in turn,
and
possible methods for utilizing them to achieve noise reduction will be
discussed.
Due to the non-stationary nature of speech, 'short-time' measurements are
preferably used to obtain information about the speech at any given time. For
instance, the short-time power or energy of a speech signal is a useful means
for
inferring the amplitude variations of the signal. A preferred method utilizes
a
recursive averaging technique. In this technique, the short-time power, P(n),
of a
discrete-time signal s(n) is defined as
P(n) = BP(n -1) + a52 (n)
(11)
The transfer function, Hl (z) , of this recursive averaging filter that has 52
(n) as its
input and P(n) as its output is
HP(z)= a ,B~/
1-BZ_,
(12)
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
49
Note that the DC gain of this filter is HP (1) _ (1 aB) . This IIIR filter has
a pole at
which can be thought of as a forgetting factor. The closer /3 is to unity, the
slower the
short-time power changes. Thus, the rate at which the power of newer samples
is
incorporated into the power measure can be controlled through /~ . The DC gain
parameter a is usually set to 1- ~3 for convenience to obtain a unity gain
filter.
In some circumstances, the root-mean-square (RMS) short-time power may be
more desirable. For cost-effective implementations in digital signal
processors, the
square-root operation is avoided by using an approximation to the RMS power by
averaging the magnitude of s(n) rather than its square as follows:
P(n) _ ~3P(n -1) + a s(n)I
(13)
If the resulting infinite length window of recursive averaging is not
desirable,
the power in an analysis window of size N may, for example, be averaged as
follows:
1 rr ' z
P(n) =-~S (n)
N x=o
(14)
VAD algorithms are essential for many speech processing applications. A
wide variety of VAD methods have been developed. Distinguishing speech from
background noise relies on the a few basic assumptions about speech. Most VAD
algorithms make use of some or all of these assumptions in different ways to
distinguish between speech and silence or background noise.
The first assumption is that the speech signal level is usually greater than
the
background noise level. This is often the most important criterion used and
many
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
VAD algorithms are based solely on this assumption. Using this assumption, the
presence of speech can be detected by comparing signal power measurements to
thresholds values.
A second assumption is that speech is non-stationary while noise is relatively
5 stationary. Using this assumption, many schemes can be devised based on
steadiness
of the signal spectrum or the amount of variation in the signal pitch
measurements.
The development of VAD algorithms is outside the scope of this specification.
Many sophisticated and robust algorithms are already available and can be
applied
directly on the decoded speech. As such, we will assume that, where necessary,
that a
10 good knowledge of the demarcations between speech and background noise is
available.
A single-band noise reduction system is the most basic noise reduction system
conceivable. In the method illustrated in Figure 26, two short-time power
measure-
ments, PT (u) and PN (n) , are performed. The former is called the total power
and is
15 the sum of the speech and background noise power. The latter is the noise
power.
Both power measures may be performed using recursive averaging filters as
given in
equation (11). The total power measure is continuously updated. The noise
power
measure is updated only during the absence of speech as determined by the VAD.
Note that the clean speech power, PS (n) , can be estimated at any time as
20 PS (n)=PT(n)-Prr (n)
(15)
Ideally, the noise suppression is effected by a gain, g~°' , given
by
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
51
g(n) = PS (n)
PT (n)
(16)
By using equation (16), the proportion of the noisy signal, y(n), that is
retained after
attenuation has the approximately the same power as the clean speech signal.
If the
signal contained temporarily contained only noise, the gain would be reduced
to zero.
At the other extreme, if no noise is present, then the gain would be unity. In
this
example, an estimate, s(n), of the clean speech signal is obtained.
In practice, note that equation (15) may actually result in a negative value
for
the desired signal power due to estimation errors. To avoid such a result,
additional
heuristics are used to ensure that is always non-negative.
A serious blemish associated with the single-band noise suppression technique
is the problem of noise modulation by the speech signal. When speech is
absent, the
noise may be totally suppressed. However, noise can be heard at every speech
burst.
Hence the effect is that the noise follows the speech and the amount of noise
is
roughly proportional to the loudness of the speech burst. This annoying
artifact can be
overcome to a limited extent (but not eliminated) by limiting the lowest
possible gain
to a small but non-zero value such as 0.1. The modulation of the noise may be
less
annoying with this solution.
Among all the parameters considered, the pitch gain, gr , and codebook gain,
g~ , are perhaps the most amenable to straightforward modification. These gain
parameters are relatively independent of the other parameters and are usually
quantized separately. Furthermore, they usually have a good range of quantized
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
52
values (unlike the codebook excitation). The preferred embodiment uses these
two
parameters to achieve noise reduction.
As discussed above, the computational cost of re-encoding necessary for
coded domain noise reduction can be several orders of magnitude lower than
full
encoding. This is true if only the pitch and codebook gains have to be
requantized.
The requantization process often involves searching through a table of
quantized gain
values and finding the value that minimizes the squared distance. A slightly
more
complex situation arises when a gain parameter (or any other parameter to be
modi-
fied) is quantized using a differential scalar quantization scheme. Even in
this case,
the cost of such re-encoding is still usually several orders of magnitude
lower.
Requantization for a differentially quantized parameter will now be discussed.
The quantization of a single speech parameter is termed scalar quantization.
When a set of parameters are quantized together, the process is called vector
quantization. Vector quantization is usually applied to a set of parameters
that are
related to each other in some way such as the LPC coefficients. Scalar
quantization is
generally applied to a parameter that is relatively independent of the other
parameters
such as gr , g~ and T. A mixture of both types of quantization is also
possible.
When a parameter is quantized instantaneously, the quantization process is
independent of the past and future values of the parameter. Only the current
value of
the parameter is used in the quantization process. The parameter to be
quantized is
compared to a set of permitted quantization levels. The quantization level
that best
matches the given parameter in terms of some closeness measure is chosen to
represent that parameter. Usually, the permitted quantization levels are
stored in a
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
53
look-up table at both the encoder and the decoder. The index into the table of
the
chosen quantization level is transmitted by the encoder to the decoder.
The use of instantaneous quantization schemes suffers from higher
quantization errors due to the fixed dynamic range. Thus, adaptive quantizers
are
often used in speech coding to minimize the quantization error at the cost of
greater
computational complexity. A commonly used adaptive scalar quantization
technique
is differential quantization and a typical implementation in speech coders is
illustrated
in Figure 27. In a system implemented according to Figure 27, the correlation
between current and previous parameter values is used to advantage. When the
correlation is high, a significant reduction in the quantization dynamic range
can be
achieved by quantizing the prediction error, r(n). The quantized prediction
error is
denoted by r(n) . The prediction error is the difference between the actual
(unquantized) parameter, ((n), and the predicted parameter, yPrea (n) . The
prediction
is performed using a linear predictor P(z) _ ~k-, bk~_k . The same predictor
for ((n)
is preferably used at both the quantizer and the dequantizer. Usually, when
coding
speech parameters using this technique, the predictor coefficients are kept
constant to
obviate the need to transmit any changes to the decoder. Parameters that
change
sufficiently slowly such as the pitch period and gain parameters are amenable
to
differential quantization.
Vector quantization involves the joint quantization of a set of parameters. In
its simplest form, the vector is compared to a set of allowed vectors from a
table. As
in scalar quantization, usually a mean squared error measure is used to select
the
closest vector from the quantization table. A weighted mean squared error
measure is
CA 02378035 2001-12-31
WO 01/02929 PCT/C1S00/18165
54
often used to emphasize the components of the vector that are known to be
perceptually more important.
Vector quantization is usually applied to the excitation signal and the LPC
parameters. In the case of LPC coefficients, the range of the coefficients is
unconstrained at least theoretically. This as well as stability problems due
to slight
errors in representation have resulted in first transforming the LPC
coefficients to a
more suitable parameter domain prior to quantization. The transformations
allow the
LPC coefficients to be represented with a set of parameters that have a known
finite
range and prevent instability or at least reduce its likelihood. Available
methods
include log-area ratios and inverse sine functions. A more computationally
complex
representation of the LPC coefficients is the line spectrum pair (LSP)
representation.
The LSPs provide a pseudo-frequency representation of the LPC coefficients and
have been found to be capable of improving coding efficiency by more than
other
transformation techniques as well as having other desirable properties such as
a
simple way to guarantee stability of the LP synthesis filter.
Gain parameters and pitch periods are sometimes quantized this way. For
instance, the GSM EFR coder quantizes the codebook gain differentially. A
general
technique for differential requantization will now be discussed.
Suppose G(n) is the parameter to be requantized and that the linear predictor
used in the quantization scheme is denoted P(z) as shown in Figure 28. The
quantized
difference, R(n), is the actual coded domain parameter normally transmitted
from the
encoder to the decoder. This parameter is preferably intercepted by the
network
speech enhancement device and possibly modified to a new value, P(z) . The
operation of this method will now be explained with reference to Figure 28.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
Suppose the speech enhancement algorithm required G(n) to be modified by
an amount OG(n) . The differential requantization scheme at the network device
basically attempts to mimic the operation of the encoder. The basic idea
behind this
technique can be understood by first ignoring all the quantizers in the figure
as well as
5 the interconnections between the different systems. Then it is seen that the
systems in
the encoder and the network are both identical linear systems. The encoder has
G(n)
as its input while the network device has OG(n) as its input. Since they are
preferably identical linear systems, it is realized that the two systems can
be
conceptualy combined to effectively result in a single system that has (G(n) +
OG(n))
10 as its input. Such a system preferably includes an output, RneW(n), which
is
preferably be given by
RneW (n) = R(n) + OR(n)
(17)
However, due to the quantizers which make these systems non-linear, this
relationship
15 is only approximate. Hence, the actual decoded parameter is preferably
given by
G neH, (n ) = G(n ) + OG (n ) + quantization error
(18)
where OG(n)+ quantization error is the actual realized change in the parameter
achieved by the network speech enhancement device.
20 The feedback of the quantity, OR(n) , in the network requantization device
can cause undesirable oscillatory effects if G(n) is not changing for long
periods of
time. This can have undesirable consequences to the speech signal especially
if G(n)
is a gain parameter. In the case of the GSM EFR codec, the G(n) corresponds to
the
CA 02378035 2001-12-31
WO 01/02929 PCT1US00/18165
56
logarithm of the codebook gain. During silent periods, G(n) may remain at the
same
quantized level for long durations. During such silence, if attenuation of the
signal is
attempted by the network device by modifying G(n) by an appropriate amount
OG(n) , quasi-periodic modulation of the noise could occur resulting in a soft
but
disturbing buzz.
As an example, such oscillatory effects will be demonstrated when the GSM
EFR codec is used. This linear predictor, P(z), preferably has four delay
elements,
each of which could take on one of 32 possible values. Hence the non-linear
system in
the ALC device can be in any one of over a million possible states at any
given time.
This is mentioned because the behavior of this non-linear system is heavily
influenced
by its initial conditions.
The reverberations in the actual realized gain, GneW (n), will now be
demonstrated in response to a step, OG(n) , in the desired gain. For
simplicity, it is
assumed that the original transmitted parameter, R(n), is constant over 100
subframes,
and that the memory of P(z) is initially zero. Figure 29(a) shows the step in
the
desired gain. Figure 29(b) shows the actual realized gain superimposed on the
desired
gain. Although the initial conditions and the value of G(n) will determine the
exact
behavior, the reverberations in the actual realized gain shown here are
typical.
The reverberations can be eliminated by 'moving' the quantizer outside the
feedback loop as shown in Figure 30. (In Figure 30, the computation of is
unneces-
sary but is included for comparison to Figure 28.) Placing the quantizer
outside the
feedback loop results in the actual realized gain shown in Figure 29(c),
superimposed
on the desired gain. It should be noted that, although reverberations are
eliminated,
the average error (i.e. the average difference between the desired and actual
realized
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
57
gains) is higher than that shown in Figure 29(b). Specifically, for this
example, the
average error during steady state operation of the requantizer with and
without the
quantizer in the feedback loop are 0.39dB and 1.03dB, respectively.
Hence a trade-off exists between accurate control of a differentially
quantized
parameter and potential oscillatory effects. However, through the use of a
voice
activity detector, it is possible to switch between the accurate scheme and
the
reverberation-free but less accurate scheme. The reverberation-free scheme
would be
used during silent periods while the more accurate scheme with the quantizer
in the
feedback loop would be used during speech. When switching between the schemes,
the state of the predictor should be appropriately updated as well.
It should also be pointed out that the reverberation-free technique can be
simplified as shown in Figure 31, resulting in some savings in computations.
This is
done by replacing the linear system 1/[1+P(z)] with the constant, 1/[1+P(1)].
This
implementation is often found to be sufficient especially when the parameters
are
changed relatively infrequently. By infrequent changes, we mean that the
average
number of subframes between changes is much greater than the order of P(z).
Even when more sophisticated quantization schemes are used, the cost of re-
encoding these parameters is still relatively small. With an understanding of
how
parameter modification can be practically effected even when the parameter is
differ-
entially quantized, the problems associated with coded domain noise reduction
and
echo suppression may be addressed.
A low complexity, low delay coded domain noise reduction method will now
be discussed. The various coded domain parameters that could be used to effect
noise
reduction were discussed above. Of these parameters, it was determined that
the two
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
58
gain parameters, the pitch gain, gP , and the codebook gain, g~ , are most
amenable to
direct modification. Accordingly, the preferred embodiments will involve these
parameters.
By way of example only, a commonly used subframe period of duration Sms
will be assumed. With the typical sampling rate of 8000Hz used in telephony
applications, a subframe will consist of 40 samples. A sample index will be
denoted
using n, and the subframe index using . Since the coded parameters are updated
at
most once per subframe and apply to all the samples in the subframe, there
will be no
confusion if these coded parameters are simply indexed using m. Other
variables that
are updated or apply to an entire subframe will also be indexed in this
manner. The
individual samples within a subframe will be normally indexed using n.
However, if
more than one subframe is spanned by an equation, then it will make sense to
index a
sample, such as a speech sample, as s(n, m).
The speech synthesis model that is used in hybrid, parametric, time domain
coding techniques can be thought of as time varying system with an overall
transfer
function, Hm (z) , at subframe m given by
H (z) - g~ (m)
I- gP (m)z Tim' m (z)
(19)
with an excitation source provided by the fixed codebook (FCB). Another view
that is
closer to actual implementation is shown in Figure 32. The FCB output is
indicated as
C'(n). In Figure 32, the buffer of the long-term predictor (LTP) or pitch
synthesis
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
59
filter is shown. Recall that the LTP has the transfer function 1 T , where
both
1 _ gpz_
gP and T are usually updated every subframe. According to this transfer
function, the
LP excitation would be computed for each subframe as
u(n) - g~ (m)c' (n) + gP (m)b' (n)
= g~ (m)c' (n) + g p (m)u(n -T ) (20)
n = 0,1,...39
where b'(n) is obtained from the LTP buffer. The most recently computed
subframe
of LP excitation samples, u(n), are preferably shifted into the left end of
the LTP
buffer. These samples are also used to excite the LP synthesis filter to
reconstruct the
coded speech.
Using this viewpoint of the speech synthesis model, the two sources of the LP
synthesis filter excitation, u(n), have been explicitly identified. These two
excitation
sources, denoted as b(n) and c(n), are called the pitch excitation and
codebook
excitation, respectively. Due to this two source viewpoint, the LTP is also
often called
the adaptive codebook, due to its ever-changing buffer contents, in contrast
to the
FCB. Obviously, the LTP output is not independent of the FCB output. Hence
spectral
subtraction concepts preferably are not directly applied to the two sources.
However,
it is noted that, due to the manner in which the encoder optimizes the coded
domain
parameters, the two sources have different characteristics. This difference in
characteristic is taken advantage of to derive a noise reduction technique.
To achieve noise reduction, the gain factors, gp and g~ that are received from
the encoder are modified. This modification will be achieved by multiplying
these
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
gain factors by the noise reduction gain factors, yp and y~ , respectively, to
generate
an adjusted gain value. This will result in a modified time varying filter at
the
decoder given by
Hm (z) = Y~ (m)g~ (m)
1 Yp (m)gp (m)Z T(m) m (Z)
5 (21 )
A preferred network noise reduction device is shown in Figure 33. In this
embodiment, there are two decoders. A decoder 20 is termed the reference
decoder
and performs decoding of the coded speech received from the encoder, such as
the
speech encoder 10 shown in Figure 14. The decoding performed by decoder 20 may
10 be complete or partial, depending on the particular codec. For the current
embodiment, it is assumed that it performs complete decoding, producing the
noisy
speech output y(n). However, as described above, the embodiment also will
operate
with partial decoding. Essentially, decoding which does not substantially
affect, for
example, the power of the noise characteristic, can be avoided, thereby saving
time.
15 The bottom half of Figure 33 shows a destination decoder 120. Using this
decoder, the coded parameters may be optimized. This destination decoder
mimics
the actual decoder at the destination, such as the receiving handset. It
produces the
estimated clean speech output on a conductor 148. Note that, although drawn
separately for clarity, some of the parts of the reference decoder and
destination
20 decoder model can be shared. For instance, the fixed codebook (FCB) signal
is
identical for both decoders.
Those skilled in communications will recognize that decoders 20 and 120 may
be substituted for the following blocks of Figure 14:
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
61
Partial or Complete Decoding block;
Speech Level Measurement block;
Gain Determination block;
Multiply function having inputs SLRP and gain;
SLRP Requantization; and
Modify SLRP.
In addition, the Voice Activity function referred to in Figure 14 is
incorporated into the Figure 33 embodiment. As a result, the speech decoder 12
shown in Figure 33 may be the same type of speech decoder shown in Figure 14.
More specifically, the Figure 33 decoders are useful in a communication
system 8 using various compression code parameters, such as the parameters
described in Figure 7, including codebook gain, pitch gain and codebook RPE
pulses.
Such parameters represent an audio signal having various audio
characteristics,
including a noise characteristic and signal to noise ratio (SNR). The Figure
33
apparatus provides an efficient technique for managing the noise
characteristic.
Decoders 20 and 120 may be implemented by a processor generally indicated by
150
which may include a noise reduction controller 160 which includes a VAD
function.
Processor 150 may comprise a microprocessor, a microcontroller or a digital
signal
processor, as well as other logic units capable of logical and arithmetic
operations.
Decoders 20 and 120 may be implemented by software, hardware or some
combination of software and hardware.
Processor 150 responds to the compression code of the digital signals sent by
encoder 10 on a network 11. Decoders 20 and 120 each read certain compression
code parameters of the type described in Figure 7, such as codebook gain and
pitch
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
62
gain. Processor 150 is responsive to the compression code to perform the
partial
decoding , if any, needed to measure the power of the noise characteristic.
The
decoding results in the decoded signals in the linear domain which simplify
the task
of measuring the noise power.
The reference decoder 20 receives the compression coded digital signals on
terminals 13. Decoder 20 includes a fixed codebook (FCB) function 22 which
generates codebook vectors C' (n) that are multiplied or scaled by codebook
gain g~ in
a multiply function 24. The codebook gain is read by processor 150 from the
compressed code signals received at terminals 13. The multiply function
generates
scaled codebook vectors c(n) which are supplied to a pitch synthesis filter
26.
Processor 150 calculates the power P~ of the scaled codebook vectors as shown
in
equation 31. The power is used to adjust the pitch gain. Processor 150 reduces
the
codebook gain to attenuate the scaled codebook vector contribution to the
noise
characteristic.
Filter 26 includes a long term predictor (LTP) buffer 28 responsive to the
scaled codebook vectors c(n) to generate sample vectors. The samples are
scaled by
the pitch gain gP in a multiply function 30 to generate scaled samples bref
(n) that are
processed by an adder function 32. Processor 150 increases the pitch gain to
increase
the contribution of the scaled samples in order to manage the noise
characteristic as
indicated in equations 30-33. Processor 150 determines the power of the scaled
samples Pbref . A similar power Pb is generated by decoder 120. The two powers
are
used to adjust the pitch gain as indicated by equations 30 and 33.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
63
Filter 26 generates a total codebook excitation vector or LPC excitation
vector
u(n) at its output. Processor calculates the power P" of vector u(n) and uses
the power
to adjust the pitch gain as indicated in equation 32.
The vector u(n) excites an LPC synthesis filter 34 like the one shown in
Figure
6. The output of filter 34 is returned to controller 160.
Decoder 120 includes many functions which are identical to the functions
described in connection with decoder 20. The like functions bear numbers which
are
indexed by 100. For example, codebook 22 is identical to codebook 122. Decoder
120 includes multiplier functions 140 and 142 which are not included in
decoder 20.
Multiplier function 140 receives ~yp as an input which is defined in equation
33. As
shown in equation 30, the value of ~yp depends in part on a ratio of powers
previously
described. Multipler function 142 receives ~y~ as an input which is defined in
equation
28. As a result of multiplier functions 140 and 142, decoder 120 uses a pitch
synthesis filter 144 which is different from pitch synthesis filter 26.
As explained by the equations in general and equations 21-33 in particular,
processor adjusts the codebook gain and/or pitch gain to manage the noise
characteristic of the signals received at terminals 13. The adjusted gain
values are
quantized in the manner previously described and the quantized parameters are
transmitted on an output network 15 through a terminal 16.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
64
The basic single-band noise suppressor discussed above can be implemented
in the coded domain. Since g~ (m) is the DC gain of the time-varying filter
given in
equation (19), this DC gain can be modified by setting y~ (m) as
y~ (m) = ma 1- PW (m) , E
PY (m)
(22)
where PW (m) and Py (m) are the noise power and total power estimate,
respectively,
at subframe m, respectively. Also, E is the maximum loss that can be applied
by the
single-band noise suppressor. It is usually set to a small value such as 0.1.
Such a
DC gain control system will suffer from severe noise modulation because the
noise
power fluctuates in sync with the speech signal. This can be perceptually
annoying
and one way to compensate for this is by trading off the amount of noise
suppression
for the amount of noise modulation.
A coded domain noise reduction method may be derived that is superior to the
that in equation (20). The two parameters, yP and y~ , can be controlled in
the time-
varying system Hm (z) . Due to the recursive nature of the decoder, the joint
optimization of both gain factors to achieve noise reduction is rather
complex. This is
because the modification of the present value of - would have implications on
future values of gP . Hence such optimization would preferably determine y~
(m) and
yP (m + l ) where l depends on the time-varying pitch period, T(m). Even a sub-
optimal optimization would require knowledge of coded parameters at least a
few
subframes into the future. This would require crossing frame boundaries and
has
severe practical implications. First, more buffering would be required. More
CA 02378035 2001-12-31
WO 01/02929 PCT/ITS00/18165
importantly, additional delay would be incurred which may be unacceptable espe-
cially in cellular and packet networks. Thus, the problem is preferably
approached in
a manner that does not require knowledge of future frames.
The basic idea behind the technique will first be stated. During silence as
5 indicated by a voice activity detector, it is safe to perform the maximum
attenuation
on the signal by limiting the DC gain of Hm (z) by controlling y~ . At the
beginning
and trailing ends of speech, the y~ will be allowed to rise and fall
appropriately.
However, during voiced speech, the LTP excitation output contributes to a
large
amount of the resulting signal power and has a better SNR relative to the FCB
10 excitation output. Hence, during voiced speech, we can also perform a
limited amount
of attenuation of the FCB output. To compensate for the eventual loss of power
in the
noise-reduced decoded speech signal, yp will be carefully boosted. yP and y~
will
be optimized in two stages.
First, the optimization of y~ will be considered. To reduce the noise
15 effectively, y~ should preferably be driven close to zero or some maximum
loss,
0(E(/ . The trade-off with using a high loss is that the decoded speech signal
would
also be attenuated. To reflect this tug-of- war between maintaining the
decoded
speech level which requires that y~ =1 and obtaining effective noise reduction
which
requires that y~ = E can be stated in terms of a cost function, F, as follows:
20 F~Y~~~i~~a~=~i~Y~ -E~~ +~z~Y~ -1)z
(23)
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
66
Here ~.1 and ~,2 are suitable weights to be determined. By minimizing this
cost
function, an optimal amount of DC gain reduction may be achieved. In this
context,
one set of suitable weights that have proven to provide consistently good
results will
be considered. Nevertheless, other suitable weights may be formulated that
perform
just as well.
During silence, we would like to achieve the maximum amount of noise
suppression. Hence ~,, should preferably be large during silence gaps and
small
during speech. A suitable continuous measure that can achieve such a weighting
is the
SNR measured using the reference decoder, denoted as SNRref . The first weight
may
be set as
_ 1
.SNIZ ref (m)
(24)
A voice activity detector can be used to demarcate the silence segments from
the speech segments in the reference decoder's output signal, y(n). The
background
noise power, PW , can be estimated during silence gaps in the decoded speech
signal
y(n). The recursive averager of equation (11) with a pole at 15999/16000 and
unity
DC gain is found to be a suitable means for updating the background noise
power
during such silence gaps. This large time constant is suitable since noise can
be
assumed to be relatively stationary. The power, Py , of the signal, y(n), can
also be
measured using a similar recursive average or other means. If a recursive
average is
utilized, an averager with a pole at 127/128 and unity DC gain was found to be
suitable. Then, SNR ref can be estimated as
CA 02378035 2001-12-31
WO 01/02929 PCT/ITS00/18165
67
SNR ref = max O, Py P PW , PW ) O
W
(25)
Here, the maximum function disallows meaningless negative values for the
SNRref
that may occur. It is assumed that the noise power estimation algorithm always
ensures that PW is greater than zero.
If only ~,1 was used and ~2 was set to unity, then the y~ will rise and fall
with
the SNRref . However, during voiced speech which typically also has higher
SNR,
y~ is preferably attenuated to some extent. This would reduce the overall
amount of
noise during voiced speech as the FCB models the majority of the noise signal
during
voiced speech. Hence the noise modulation that typically occurs in single-band
noise
reduction systems will be reduced. An appropriate parameter that reflects the
presence of voiced speech is necessary. The ratio, Pb,ref ~ Pc,ref ~ where Pb
and P~ are
the short-time powers of the reference decoder signals, bref (n) and Cref (n)
, indicated
in Figure 33, reflect the presence of voiced speech. Alternatively, the pitch
gain,
g P (m) , which also reflects the amount of correlation in the speech, may be
used.
Recall that the pitch gain is the result of an optimization procedure at the
encoder that
determines the pitch synthesis filter. In essence, this procedure finds a past
sequence
from the LTP buffer that has the best correlation with the sequence to be
embodied.
Therefore, if the correlation is high, then the pitch gain would also be
correspondingly
high. As such, the remaining weight may be specified to be inversely
proportional to
the pitch gain:
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
68
1
gp (m)
(26)
By specifying ~,2 in this manner, keeping y~ close to one during voiced speech
is
deemphasized.
The parameter ~, is preferably empirically determined. It is quite common to
have parameters that require to be tuned based on perceptual tests in speech
enhancement algorithms.
Thus, the resulting cost function to be minimized is
F~Y~~~~= 1 ~Y~ -E~2 +~ 1 ~Y~ -1)~
S~ref gp
(27)
By taking the derivative of F with respect to y~ and setting it to zero, the
optimum
value of y~ is determined to be
E+~ S~ref
gp
Y
1+~ S~ref
gp
(28)
where ~, will be optimized empirically. Now y~ still generally rises and falls
in sync
with the SNR ref . However, a smaller y~ may result even if SNR ref is large
if, in
addition, gp is also large.
By determining y~ according to equation (28), the overall signal power of the
clean speech estimate, S(n) , may be reduced. This power loss can be
compensated to
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
69
some extent by increasing yP appropriately. First, the characteristics of the
LTP or
pitch synthesis filter used in the coder will be considered.
The pitch synthesis filter is basically a comb filter. The first lkHz range of
the
magnitude frequency response of comb filters obtained when the pitch period of
T =
40 is shown in Figure 34. Two curves are shown, one corresponding to a pitch
gain
of 0.1 and the other 0.9. We note that since only the pitch gain and pitch
period are
used to specify the pitch synthesis filter, there is no DC gain factor
available to
simultaneously control the amount of gain at both the spectral peaks and the
valleys.
Another point to note is that some encoders allow pitch gains greater than
one.
Theoretically, this results will result in an unstable comb filter. However,
due to the
manner in which the optimization procedure attempts to match the synthetic
signal to
the original speech signal, no actual instability results. Another way to look
at this is
to think of the FCB output as being designed in such a manner that never
actually
results in instability.
By multiplying yP with the original pitch gain, gP , it is possible to cause
instability or at least large undesirable fluctuations in power. It is noted
that the
increase, I~~ , in the magnitude frequency response at a spectral peak of the
comb
filter due to applying yP is given by
I~~ =201og1o 1 gP ,YPgp~ and gP~
1_YPgP
(29)
Typical values of I~a~ are illustrated in Figure 35 for two values of gP that
are common during voiced speech in a noisy speech signal. From this figure, it
is
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
seen that large gains can be induced at the spectral peaks. It should be noted
that the
spectral valleys are also attenuated.
Some level of noise reduction is achieved by the attenuation of the spectral
valleys. However, at the same time, the noise present in the spectral peaks of
the LTP
5 gets amplified. Overall, this can result in the noise being shaped to have a
harmonic
character. Such harmonically shaped noise, if present in significant amounts,
can
make the speaker's voice sound somewhat nasal in character. Thus, great care
should
be taken when boosting yp . Amplification to compensate for power loss may be
performed only if gp ~ I and the amplified pitch gain should satisfy ypgp
10 Preferably, one could compensate for the power loss in the LTP excitation
out-
put. To achieve this power compensation accurately, a first possibility for yp
would
be computed as
Pb,ref
Yp,~ - P
b
(30)
15 This could sometimes result in instability in total LP excitation. To
compensate for power loss and ensure stability, yp,, could be compared with
yp,2
computed as yp,2 = Pu,ref /P" . However, this involves a trial and error
process as Pu
depends on Yp . An alternative is to approximate P" as P" = Y~ Pe + Yp Pb .
Then, the
stability condition can be specified as
20 Y~ P~ + Yp Pb ~ Pu,ref
(31)
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
71
which would give the second possible value for yP as
_ z
Pu,ref Yc Pc
yp,z - P
b
(32)
Then, yP should be determined as the minimum of the two quantities in
equations
(30) and (32). A further check to ensure that the resulting filter will be
stable may be
performed. In this case, yP is preferably chosen as
min~yp,, ~ YP,z ~f min~yP,, ~ YP,z ~P~
yp 1 otherwise
(33)
However, as the risk of instability is small, this last check may be avoided.
Furthermore, the criterion in equation (32) ensures that the resulting LTP
output will
be stable.
Two additional embodiments for coded domain noise reduction (CDNR) will
be discussed in connection with Figure 36. In one of the two embodiments, only
the
codebook gain parameter ( g~ ) is modified. In the second embodiment, both the
codebook gain and pitch gain ( gP ) are modified. The first embodiment is
suitable for
low levels of noise while the second embodiment is suitable for higher noise
conditions.
CDNR by Codebook Gain Attenuation
Figure 36 shows a novel implementation of CDNR. Given the coded speech
parameters corresponding to each frame of speech, the uncoded speech is
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
72
reconstructed using the appropriate decoder. A silence detector (also referred
to as a
voice activity detector) is used to determine whether the frame corresponds to
speech
or silence. If the frame is silence, then the background noise power is
estimated. At all
times, the total power of the signal is estimated. Using the total power and
noise
power, it is possible to infer the relative amount of noise in the signal,
such as by
computing the signal-to-noise ratio. Based on these power estimates, the
dequantized
codebook gain parameter is attenuated, and then quantized again. This new
quantized
codebook gain parameter substitutes the original one in the bit-stream.
The careful attenuation of the codebook gain parameter can result in noise
reduction in the case of noisy coded speech. Many attenuation methodologies
can be
formulated. Before describing any methods, the notation used is first
described.
We assume that the noisy uncoded speech, y(n) , is given by
y(n) = s(n)+w(n) (34)
where s(n) is the clean uncoded speech and w(n) is the additive noise. The
power estimates, Py (n) and Pw (n) , are the noisy uncoded speech power and
the noise
power, respectively. In Figure 36, Py (n) is measured in the block labeled
"Total
power estimator" and P"(n) is measured in the block labeled "Noise power
estimator". Power estimates may be performed in a variety of ways. One example
approach is the recursive formula given by Py (n) _ /3PY (n) + (1- /3 ) I y(n)
I , with
/3 = 0.992 , and a similar formula for the noise is given by
P". (n)=~3Pw.(n)+(1-/3)Iw(n) with /3=0.99975.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
73
The codebook gain factor, g~, is multiplied by an attenuation factor, y~, to
obtain an attenuated codebook gain factor. Two alternative methods for
determining
Y~ are as follows:
y~ = max 0,1-,u p"' (35)
Y
y~ = min l, 0.2 +,u p'' P P (36)
w
In most vocoders, the codebook gain parameters are defined every subframe.
If this is the case, the formulae are evaluated using the power estimates
computed
during the last sample of the corresponding subframe. In both the above
approaches,
the attenuation factor depends on the signal-to-noise ratio of the uncoded
speech. In
formula (35), a suitable value for ,u are in the range from 1 to 1.5. In
formula (36), a
suitable value for ,u is 0.8.
CDNR by Optimization of Gain Factors
Partial Decoding
The decoding of signals may be complete or partial depending on the vocoder
being used for the encode and decode operations. Some examples of situations
where
partial decoding suffices are listed below:
In code-excited linear prediction (CELP) vocoders, a post-filtering process is
performed on the signal decoded using the LPC-based model. This post-filtering
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
74
process reduces quantization noise. However, since it does not significantly
affect the
power estimates, the post-filtering stage can be avoided for economy.
Under TFO in GSM networks, the CDNR device may be placed between the
base station and the switch (known as the A-interface) or between the two
switches.
Since the 6 MSBs of each 8-bit sample of the speech signal corresponds to the
PCM
code as shown in Figure 3, it is possible to avoid decoding the coded speech
altogether in this situation. A simple table-lookup is sufficient to convert
the 8-bit
companded samples to 13-bit linear speech samples using A-law companding
tables.
This provides an economical way to obtain a version of the speech signal
without
invoking the appropriate decoder. Note that the speech signal obtained in this
manner
is somewhat noisy, but has been found to be adequate for the measurement of
the
power estimates.
Coded Parameter Modification
Minimal Delay Technique
Large buffering, processing and transmission delays are already present in
cellular networks without any network voice quality enhancement processing.
Further
network processing of the coded speech for speech enhancement purposes will
add
additional delay. Minimizing this delay is important to speech quality. In
this section,
a novel approach for minimizing the delay is discussed. The example used is
the GSM
FR vocoder.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
Figure 7 shows the order in which the coded parameters from the GSM FR
encoder are received. A straightforward approach involves buffering up the
entire 260
bits for each frame and then processing these buffered bits for coded domain
echo
control purposes. However, this introduces a buffering delay of about 20ms
plus the
5 processing delay.
It is possible to minimize the buffering delay as follows. First, note that
the
entire first subframe can be decoded as soon as bit 92 is received. Hence the
first
subframe may be processed after about 7.lms (20ms times 92/260) of buffering
delay.
Hence the buffering delay is reduced by almost lams.
10 When using this novel low delay approach, the coded LPC synthesis filter
parameters are modified based on information available at the end of the first
subframe of the frame. In other words, the entire frame is affected by the
echo
likelihood computed based on the first subframe. In experiments conducted, no
noticeable artifacts were found due to this 'early' decision.
15 Update of Error Correction/Detection Bits and Framing Bits
When applying the novel coded domain processing techiques described in this
report for removing or reducing noise, some are all of the bits corresponding
to the
coded parameters are modified in the bit-stream. This may affect other error-
correction or detection bits that may also be embedded in the bit-stream. For
instance,
20 a speech encoder may embed some checksums in the bit-stream for the decoder
to
verify to ensure that an error-free frame is received. Such checksums as well
as any
CA 02378035 2001-12-31
WO 01/02929 PCT/ITS00/18165
76
parity check bits, error correction or detection bits, and framing bits are
updated in
accordance with the appropriate standard, if necessary.
Figure 38shows a technique for coded domain noise reduction by modification
of the codebook vector parameter. In the preferred mode, noise reduction is
performed
in two stages. The first stage involves modification of the codebook gain as
discussed
earlier.
In the second stage, the codebook vector is optimized to minimize the noise.
In essence, for each subframe, several codebook vector patterns are attempted
that
vary from the original received codebook vector. For each codebook vector
pattern,
the partial decoding is performed and the noise power is estimated. The best
codebook
vector pattern is determined as the one that minimizes the noise power. In
practice, a
fixed number of iterations or trials are performed.
For example, in the GSM FR vocoder (Reference [1]), the codebook vector
pattern for each subframe has 40 positions, of which 13 contain non-zero
pulses. In
our preferred mode, the positions of the 13 non-zero pulses are not modified.
Only
their amplitudes are varied in each trial. The non-zero pulses are denoted by
xM (i), i = 0,1, ...,12 . Note that each pulse may be one of the following
amplitude
values only: ~28672,~20480,~12288,~4096. The codevector optimization is
described by the following steps:
Using the original codebook vector, modified codebook gain parameter, and
the remainder of the original parameters, partially decode the signal.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
77
Estimate the noise power in the decoded signal and save this value.
Set i=0, j=1.
In the original codebook vector, modify the i'" pulse xM (i) to be j levels of
amplitude smaller but of the same sign, so as to obtain a modified codebook
vector. If
already at the lowest level for the given sign, then change the sign.
Using the modified codebook vector, modified codebook gain parameter, and
the remainder of the original parameters, partially decode the signal.
Estimate the noise power in the decoded signal and save this value.
Repeat steps 2 to 4 for i = l, 2, ...,12 .
Set i = 0, j = 2 and repeat steps 2 to 5 for this new value of j .
At this point, the partial decoding would have been performed 27 times. Pick
the codebook vector that resulted in the minimum amount of noise.
It is straightforward to modify the above search technique for the codebook
vector optimization, or implement other codebook vector search techniques such
as
those used in codebook-excited linear prediction (CELP) vocoders.
CDNR by modification of the representation of the LPC parameters
A commonly used technique for the representation of the LPC parameters is
considered as an example. This representation, called the line spectral pairs
(LSPs) or
frequencies (LSFs) has become widely used in many vocoders, e.g. the GSM EFR,
CA 02378035 2001-12-31
WO 01/02929 PCT/L1S00/18165
78
due to its good properties in terms of quantization and stability, as well as
interpretation. The LSFs are a pseudo-frequency representation of the LPC
parameters. This allows the quantization techniques to incorporate information
about
the spectral features that are known to be perceptually important. Another
advantage
of LSFs is that they facilitate smooth frame-to-frame interpolation of the LPC
synthesis filter.
As another example, LPC parameters also are represented by log area ratios in
the GSM FR vocoder.
LSFs may be directly modified for speech enhancement purposes. A technique
that directly adapts the LSFs to attain a desired frequency response for use
in a coded
domain noise reduction system is described in the following. This general
technique
may be applied to modify the LSFs, for example, received from a GSM EFR
encoder.
In a coded domain noise reduction technique, the adaptive technique may be
used to alter the spectral shape of the LPC synthesis filter,
1 / A(z) =1 / [l - ~ p 1 a; z-'' , when represented in terms of LSFs, to
attain a desired
spectrum according to spectral subtraction principles.
If the denominator polynomial, A(z) _ ~°la;z-' , of the LPC synthesis
filter
transfer function has p coefficients, then an anti-symmetric and a symmetric
polynomial can be derived as follows:
CA 02378035 2001-12-31
WO 01/02929 PCT/LJS00/18165
79
p(z) - A(z) _ z-cn+1>A(z-1 )
Q(z) = A(z) + z-cP+uA(z-1 )
1
Note that A(z) can be recovered as A(z) = 2 ~P(z)+Q(z)~ .
S The roots of these auxiliary polynomials are the LSPs and their angular
frequencies are called the LSFs. Basically, each polynomial can be thought of
as the
transfer functions of a (p + 1) th order predictor derived from a lattice
structure. The
first p stages of each of these predictors have the same response as the A(z)
. P(z)
and Q(z) have an additional stage each with reflection coefficients -1 and +1,
respectively.
These auxiliary polynomials have some interesting properties. Given that
A(z) is minimum phase, the two important properties of P(z) and Q(z) can be
proven. First, all the zeros of both these polynomials are on the unit circle.
Second,
the zeros of P(z) and Q(z) are interlaced. Furthermore, if the zeros remain
interlaced through a quantization process, then the resulting A(z) obtained is
guaranteed to be minimum phase.
In addition to these useful properties, the LSFs have a pseudo-frequency
interpretation that is often useful in the design of quantization techniques.
Figure 39
shows a randomly generated set of LSFs and the frequency response of the
corresponding linear predictor which has 10 coefficients. The solid vertical
lines are
the angles of the roots of P(z) while the dashed lines are the angles of the
roots of
Q(z) . Note that the angles completely specify the roots of these polynomials
which
all lie on the unit circle.
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
A loose spectral interpretation of the LSFs comes about from the observation
that the sharp valleys tend to be bracketed by the LSFs. Thus, the sharp peaks
of each
formant region of the LPC synthesis filter, 1/ A(z) , which are perceptually
important
in speech, tend to correspond to a pair of closely spaced LSFs.
5 We now derive a novel technique for the direct adaptation of the LSFs to
achieve a desired spectral response. We constrain our discussion to even
orders of p
only. This is not a major restriction as speech coders usually use even
ordered A(z)
functions. Use of an odd number of coefficients in A(z) would be somewhat of a
waste since DC components are usually removed prior to speech processing and
10 coding.
First, the polynomials, P(z) and Q(z) are factorized as
P(z)=(1-z-')~p12(1+c;z-1+z-Z)
Q(z) _ (1+ z-')~P 1z (1+d;z-' + z-2
15 where c; _ -2 cos 9~.~ and d; _ -2 cos 9d.; . The ~9~.; , 6d.; ~ are the
LSFs
specified in radians. The ~c; , d; ~ are termed the LSFs in the cosine domain.
Note that
if A(z) is minimum phase, then
~ ~ e~.~ < ed.~ < e~.~ < ed.2 < ... < e~.P~z < ed.p~2 < ~
will be true if the LSFs are sorted and labelled appropriately.
20 The power or magnitude squared frequency response of A(z) is
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
81
IA(C.v)Iz = 0.25 P((.~) z +0.25IQ(Ct~)Iz
where it can be shown that P(co) z and Q(a~) z are given by
P(CV)I z = 2(1- COS (.~)~ p 1z [CZ + 4c; cos co + ( 2 + 2 cos 2co )~
Q(co)Iz = 2(1+cosa~)~p izCcz +4c; cosco+(2+2cos 2co)]
Next, we utilize the method of steepest descent to adapt the LSFs in the
cosine
domain, ~c; , d; ~ , to achieve the power frequency response specified at a
set of fre-
quencies {cok } . Suppose the specified power frequency response is given as
{Ak } at
N different frequencies. Then we write the squared error between { Ak } and
the
actual power frequency response {IA(cok )Iz } of A(z) at frequencies {cok } as
a
function of the ~c;, d~ ~ . This error function is
F~~ca'di~~=~x--o[Ak - A(~k)~z
=~x--o[Ak -0.25 P(~k)Iz-0.25IQ(~k)~z~
According to the method of steepest descent, we can update the LSFs in the
cosine domain at the (n + 1) th iteration in terms of the values at the n th
iteration as
follows:
aF
c; (n+1)=c~(n)-,u-
ac;
d; (n+1)=d; (n)-,u ad
CA 02378035 2001-12-31
WO 01/02929 PCT/US00/18165
82
where ,u is an appropriate step-size parameter.
In our preferred mode, the value of ,u is set to 0.00002.
We have described a method for directly modifying the coded parameters,
particularly the line spectral frequencies which are a representation of the
LPC
parameters. Using this method, the frequency response of the LPC synthesis
filter can
be modified to have a desired frequency response. For noise reduction
purposes, the
desired frequency response of the LPC synthesis filter can be computed based
on, for
example, standard noise reduction techniques such as spectral subtraction. In
summary, the compression code parameters are modified to reduce the effects of
noise. More specifically, the LPC coefficients or one of their representations
(e.g.,
line spectral frequencies or log-arc ratios) are modified to atenuate the
noise in
spectral regions affected by noise.
Those skilled in the art of communications will recognize that the preferred
embodiments can be modified and altered without departing from the true spirit
and
scope of the invention as defined in the appended claims. For example, the ALC
techniques described in the specification also apply to NR techniques.