APPAREIL ET METHODE D'ANALYSE POUR DETERMINER LA TENEUR EN HUMIDITE DE MATERIAUX

APPARATUS AND ANALYSIS METHOD FOR DETERMINATION OF MOISTURE IN MATERIALS

Abrégé français

L'invention concerne une méthode pour estimer la teneur en humidité d'un matériau, ladite méthode consistant à diriger un signal d'un première fréquence (f¿1?) et un signal d'une deuxième fréquence (f¿2?) à travers un matériau, à déterminer un premier déphasage absolu (.PHI.¿1?) dudit signal de première fréquence et un deuxième déphasage absolu (.PHI.¿2?) dudit signal de deuxième fréquence, à transformer .PHI.¿1? en un premier déphasage absolu corrigé (.PHI.¿1c?) et .PHI.¿2? en un deuxième déphasage absolu corrigé (.PHI.¿2c?) en fonction d'une relation escomptée entre .PHI.¿1? et .PHI.¿2?, et à estimer la teneur en humidité à partir de .PHI.¿1c? et .PHI.¿2c?.

Abrégé anglais

There is disclosed a method of estimating moisture content in a material
involving directing a first frequency (f1) signal and a second frequency (f2)
signal through a material, determining a first absolute phase shift (.PHI.1)
of said first frequency signal and a second absolute phase shift (.PHI.2) of
said second frequency signal, transforming .PHI.1 to a first corrected
absolute phase shift (.PHI.1c) and .PHI.2 to a second corrected absolute phase
shift (.PHI.2c) in accordance with an expected relationship between .PHI.1 and
.PHI.2, and estimating moisture content from .PHI.1c and .PHI.2c.

Revendications

-18-
CLAIMS:
1. A method of estimating moisture content in a
material involving:
directing a first frequency (f1) signal and a
second frequency (f2) signal through a material;
determining a first absolute phase shift (.PHI.1) of
said first frequency signal and a second absolute phase
shift (.PHI.2) of said second frequency signal;
transforming .PHI.1 to a first corrected absolute
phase shift (.PHI.1c) and .PHI.2 to a second corrected absolute
phase shift (.PHI.2c) in accordance with an expected
relationship between .PHI.1 and .PHI.2; and
estimating moisture content from .PHI.1c and .PHI.2c.
2. A method as claimed in claim 1, wherein said
expected relationship of the transformation step is
.PHI.1= K.PHI.2.function.2 where K is a constant that takes into account
dispersion of the material at the two frequencies.
3. A method as claimed in claim 1, wherein said step
of transforming said first and second absolute phase
shifts is performed using the transformations:
<IMG>
where .gamma. is affixed constant.
4. A method as claimed in claim 3, wherein .gamma. = K.function.1/.function.2.
5. A method as claimed in claim 1, wherein
frequencies f1 and f2 are used in said directing step are
chosen so that K is close to 1Ø

-19-
6. A method as claimed in claim 4, wherein f1 and f2
are both in the range of 0.5 to 2.0 GHz.
7. A method of estimating moisture content in a
material involving:
(a) obtaining measured data including measured phase
data, actual moisture content data, and weighting
data, where the weighting data is representative
of the material mass per unit area of the
material for which moisture content is to be
estimated;
(b) setting up a first modelling function to model
any non-linearity in said weighting data, said
first modelling function having a first set of
coefficients;
(c) setting up a second modelling function relating
estimated moisture content to measured phase and
said first modelling function, said second
modelling function having a second set of
coefficients;
(d) determining values of said first and second sets
of coefficients which minimise error between
estimated moisture content and actual moisture
content for said measured data; and
(e) estimating moisture content using said first and
second modelling functions with said determined
values of said first and second sets of
coefficients.
8. A method as claimed in claim 7, wherein step (d)
involves:
(i) determining a plurality of sets of trial values
for said first set of coefficients;
(ii) performing a regression to determine values of
said second set of coefficients which minimise
error for each set of trial values; and
(iii) determining which set of trial values minimises

-20-
error.
9. A method as claimed in claim 8, wherein step
(d)(i) is performed using a non-linear minimisation
scheme.
10. A method as claimed in claim 9, wherein said non-
linear minimisation scheme is the Nelder-Mead downhill
simplex method.
11. A method as claimed in claim 7, wherein said
first modelling function is in the form w* - G (w, B),
where w* is the modelled weighting, w is the actual
weighting and B represents the first set of coefficients.
12. A method as claimed in claim 11, wherein G(w,B)
is chosen to most closely model non-linearity in w.
13. A method as claimed in claim 11, wherein G(w,B)
- b1 + b2 w + b3 W2, where the first set of coefficients, B =
{ bi, b2. b3}.
14. A method as claimed in claim 7, wherein said
second modelling function is a set of functions, in the
form
<IMG>
where M* is estimated moisture content, Ci
represent a set of n second coefficients and, Fi represents
a set of functions.
15. A method as claimed in claim 14, wherein said set
of function Fi are functions of measured phase (.PHI.) and
said first modelling function w*.
16. A method as claimed in claim 15, wherein n = 3
and F(.PHI., w*)=
<IMG>

21
17. A method as claimed in claim 1, wherein said step of
estimating moisture content is performed using first and second
modelling functions with determined values of first and second
sets coefficients which are obtained by
(a) obtaining measured data including measured phase
data, actual moisture content data, and weighting
data, where the weighting data is representative
of the material mass per unit area of the
material for which moisture content is to be
estimated;
(b) setting up a first modelling function to model
any non-linearity in said weighting data, said
first modelling function having a first set of
coefficients;
(c) setting up a second modelling function relating
estimated moisture content to measured phase and
said first modelling function, said second
modelling function having a second set of
coefficients; and
(d) determining values of said first and second sets
of coefficients which minimise error between
estimated moisture content and actual moisture
content for said measured data.
18. A method as claimed in claim 17, wherein step (d)
involves:
(i) determining a plurality of sets of trial values
for said first set of coefficients;
(ii) performing a regression to determine values of
said second set of coefficients which minimise
error for each set of trial values; and
(iii) determining which set of trial values minimises
error.
19. A method as claimed in claim 18, wherein step
(d)(i) is performed using a non-linear minimisation

22
scheme.
20. A method as claimed in claim 19, wherein said
non-linear minimisation scheme is the Nelder-Mead downhill
simplex method.
21. A method as claimed in claim 17, wherein said
first modelling function is in the form w* - G (w, B),
where w* is the modelled weighting, w is the actual
weighting and B represents the first set of coefficients.
22. A method as claimed in claim 21, wherein G(w,B)
is chosen to most closely model non-linearity in w.
23. A method as claimed in claim 21, wherein G(w,B)
may equal b1 + b2 w + b3 w2 where the first set of
coefficients, B = {b1, b2, b3}.
24. A method as claimed in claim 17, wherein said
second modelling function is a set of functions, in the
form
<IMG>
where M* is estimated moisture content, C1
represent a set of n second coefficients and, F1 represents
a set of functions.
25. A method as claimed in claim 24, wherein said set
of function F1 are functions of measured phase (.PHI.) and
said first modelling function w*.
26. A method as claimed in claim 25, wherein n = 3
and F(.PHI., w*) =
<IMG>
27. Apparatus for estimating moisture content in a
material, including:

23
a transmitter for directing a first frequency
(f1) signal and a second frequency (f2) signal through a
material;
a receiver for receiving said first and second
frequency signals;
determining means for determining a first
absolute phase shift (.PHI.1) of said first frequency signal
and a second absolute phase shift (.PHI.2) of said second
frequency signal;
transformation means for transforming .PHI.1 to a
first corrected absolute phase shift (.PHI.1c) and .PHI.2 to a
second corrected absolute phase shift (.PHI.2c) in accordance
with an expected relationship between .PHI.l and .PHI.2; and
moisture content estimating means for estimating
moisture content from .PHI.1c and .PHI.2c.
28. Apparatus as claimed in claim 27, wherein said
expected relationship is .PHI.1 = K.PHI.2 f1 / f2 , where K is a
constant that takes into account dispersion of the
material at the two frequencies.
29. Apparatus as claimed in claim 27, wherein said
transformation means transforms said first and second
absolute phase shifts is performed using the
transformations:
<IMG>
where y is a fixed constant.
30. Apparatus as claimed in claim 29, y = Kf1/f2.
31. Apparatus as claimed in claim 27, wherein
frequencies f1 and f2 used in said directing step are
chosen so that K is close to 1Ø

24
32. Apparatus as claimed in claim 31, wherein f1 and
f2 are both in the range of 0.5 to 2.0 GHz.
33. Apparatus as claimed in claim 1, wherein said
estimating moisture content means is calibrated by:
(a) obtaining measured data including measured phase
data, actual moisture content data, and weighting
data, where the weighting data is representative
of the material mass per unit area of the
material for which moisture content is to be
estimated;
(b) setting up a first modelling function to model
any non-linearity in said weighting data, said
first modelling function having a first set of
coefficients; and
(c) setting up a second modelling function relating
estimated moisture content to measured phase and
said first modelling function, said second
modelling function having a second set of
coefficients; and
(d) determining values of said first and second sets
of coefficients which minimise error between
estimated moisture content and actual moisture
content for said measured data,
whereby said estimating means can estimate
moisture content using said first and second modelling
functions with said determined values of said first and
second sets of coefficients.

Description

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 1 -
APPARATUS AND ANALYSIS METHOD FOR DETERMINATION OF
MOISTURE IN MATERIALS
Field of the Invention
The present invention relates to a method and
apparatus for determining the moisture content of
materials.
Background to the Invention
Moisture content is a key production parameter in
many processes. Materials of interest are wide ranging and
include food-stuffs, chemicals, mineral ores, mineral
concentrates, coal, oil and gas. For some time it has been
recognised that electromagnetic wave interaction with the
material of interest may provide a method for moisture
determination. Microwave-based methods rely on the
observed high correlation between moisture content and
either one or more of the parameters of wave phase shift,
reflectance or attenuation. This correlation exists for a
wide range of materials. Fundamentally the correlation
occurs because unbounded water exhibits a dielectric
constant with a very large magnitude compared to the
material in which it is entrained. The effective
dielectric constant may be derived from the dielectric
tensor, which is the most general physical quantity that
describes wave dispersion in all types of linear media,
both magnetic and non-magnetic. In general the non-
magnetic material response is dependent on both real and
imaginary parts of the effective dielectric constant.
However, the phase shift and reflectivity is usually
mostly affected by the real part for typical materials of
interest, while attenuation is more dependent on both real
and imaginary parts. Similar considerations apply for
magnetic materials, so long as the magnetic response
remains somewhat weaker than the dielectric response
imparted by the presence of free moisture.

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
_ 2 _
Microwave methods may generally be divided
between different classes of measurement. For example,
measurements may employ the apparatus of tuned microwave
resonant cavities. Another class of measurement involves
free space measurements. In free space measurements
radiating structures (antennas) launch electromagnetic
waves which are transmitted without the use of any guiding
structure towards the material of interest. Free space
methods have the general advantage that the apparatus does
not constrain the flow of material in any way, which may
be important in industrial processes. Free space
measurements themselves may be generally subdivided
between transmission and reflection measurements.
In reflection measurements the wave reflected off
an air-material interface is measured. This wave may be
received by the same structure that is used to transmit
the wave, or with alternative receiving antennas. The
amplitude and phase of the reflected wave is correlated in
some way to the moisture content.
In transmission measurements, the waves are
allowed to propagate through the material of interest from
one side and are measured with a separate receiving
antenna on the other side of the material layer. Either or
both the phase shift and attenuation of the wave through
the material may serve as the basic variable used to
estimate moisture content, although phase shift generally
demonstrates the better correlation to moisture content.
However, phase shift and attenuation are also generally
dependent on both the density and thickness of the
material. Specifically, phase shift varies most linearly
with the quantity defined by material mass per unit area
(MPUA) presented to the transmitted wave. Because of
inevitable variation of this quantity in most
applications, an auxiliary or normalising parameter
approximating MPUA is usually required to compens-ate for

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 3 -
these variations. For example, MPUA may be approximated by
either of the parameters of material height or mass
loading. The auxiliary parameter is used to provide a
weighting parameter to normalise the wave phase shift
before moisture is inferred from the measurement. Where
significant non-linearities exist between the weighting
parameter and MPUA this will increase error in the
estimated moisture content.
An important detail of free space transmission
technology is the magnitude of phase shift imparted by the
material. Often the phase shift is greater then 360
degrees. Since a single measurement of phase can only
define the phase shift in the 0-360 degree range,
measurements that rely on a single transmission frequency
are often limited to materials that do not change markedly
in presentation or moisture content. This fact limits the
utility of single frequency measurements. Presently the
state of the art in transmission measurements is to employ
multi-frequency methods. There are several classes of
multi-frequency method. One class employs two (dual)
discrete frequencies separated by a modest frequency range
(high frequency approximately 1.05 to 2 times the lower
frequency). Another class employs a multitude of discrete
frequencies or a continuum of frequencies within a
frequency band; these may generally be regarded as "swept"
frequency methods. Yet another class may employ
electromagnetic wave pulses (in this case the finite
length of the pulse implicitly defines the frequency band
that is used by the generation of sidebands). In all cases
the information carried in extra frequency components is
used to resolve the absolute phase shift beyond 360
degrees.
Error in transmission measurements may derive
from a number of sources. One source of error is the
reception of spurious waves with phase that may be

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 4 -
unrelated or weakly related to the moisture in the
material. Such spurious waves include waves reaching the
receiver that have not passed through the material (or
only a small section of material), and waves which pass
several times through the material by way of multiple
reflections. These spurious waves act to distort the
measured phase in all types of transmission measurements.
Another source of error may be from limitations in the
receiver itself. For example the receiver may loose
sensitivity at high attenuation, resulting in the
measurement of phase that is not a true representation of
the actual received wave phase.
It would be desirable to provide an improved
technique for estimating moisture content.
Summary of the Invention
Accordingly, the invention provides a method of
estimating moisture content in a material including:
directing a first frequency (f1) signal and a
second frequency (f2) signal through a material;
determining a first absolute phase shift (~1) of
said first frequency signal and a second absolute phase
shift (c~2) of said second frequency signal;
transforming ~1 to a first corrected absolute
phase shift (~1~) and ~~ to a second corrected absolute
phase shift (~2~) in accordance with an expected
relationship between ~1 and ~~; and
estimating moisture content from ~l~ and ~2
Preferably, said expected relationship is
K~2fi/f2, where K is a constant that takes into account
dispersion of the material at the two frequencies.
Preferably, transforming said first and second
absolute phase shifts is performed using the following

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 5 -
transformations, where ~(is a fixed constant:
~2~ _ ~z + Y~l
1+Y2
Y'1 c - YY'2c
Preferably, fl and f2 are chosen so that K is
close to 1Ø
Preferably, fi and f2 are in the range of 0.5 to
2.0 GHz.
The invention also provides a method of
estimating
moisture
content
in a material
involving:
(a) obtaining measured data including measured phase
data, actual moisture content data, and weighting
data, where the weighting data is representative
of the material mass per unit area of the
material for which moisture content is to be
estimated;
(b) setting up a first modelling function to model
any non-linearity in said weighting data, said
first modelling function having a first set of
coefficients;
(c) setting up a second modelling function relating
estimated moisture content to measured phase and
said first modelling function, said second
modelling function having a second set of
coefficients;
(d) determining values of said first and second sets
of coefficients which minimise error between
estimated moisture content and actual moisture
content for said measured data; and
(e) estimating moisture content using said first and
second modelling functions With said determined
values of said first and second sets of
coefficients.

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 6 -
Preferably, step (d) involves (i) determining a
plurality of sets of trial values for said first set of
coefficients, (ii) performing a regression to determine
values of said second set of coefficients which minimise
error for each set of trial values; and (iii) determining
which set of trial values minimises error.
Preferably step (d) (i) a.s performed using a non-
linear minimisation scheme.
Preferably, said non-linear minimisation scheme
is the Nelder-Mead downhill simplex method.
Preferably said first modelling function is in
the form w* = G (w, B), where w* is the modelled
weightings W 1S the actual weighting and B represents the
first set of coefficients.
Preferably, G(w,B) is chosen to most closely
model non-linearity in w.
In one embodiment, G ( w , B) may equal b1 + b2 w +
b3w2 where the first set of coefficients, B = ~ b1, b2,
b3~ .
Preferably, said second modelling function is a
set of functions, in the form
M*=~C;F~
3 0 t=i
where M* is estimated moisture content, Ci represent a set
of n second coefficients and, Fi represents a set of
functions.
Preferably, said set of function Fi are functions
of measured phase (~) and said first modelling function
w*.

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
Preferably, n = 3 and F ( ~ , w * ) - 1~ * ~ 2
~*
It will be apparent that the above methods can be
combined to estimate moisture content of a material.
Brief Description of the Drawings
Figure 1a shows a standard regression;
Figure 1b shows a regression following the
correction technique of the preferred embodiment;
Figure 2a shows a standard regression;
Figure 2b shows how non-linearity in the
weighting can be taken into account;
Figure 2c shows predicted moisture plotted
relative to sample moisture; and
Figure 3 shows typical apparatus for carrying
out the methods of preferred embodiments of the present
invention.
Description of the Preferred Embodiment
The preferred embodiment of the present invention
is a method which employs a dual discrete frequency free
space transmission apparatus that is used to measure
continuously the phase shifts and attenuations of
electromagnetic waves at each frequency that are
propagated through the material of interest. The preferred
embodiment exploits the discovery of an analysis
technique, hereafter referred to as method (I), involving
the use of two measured phases that provides a superior
accuracy of moisture measurement. Specifically, a
transformation involving two measured phases is used to
calculate a correction so as to obtain a more accurate
absolute phase shift by reducing the effect of spurious
waves and receiver errors. Secondly, the preferred
embodiment exploits a compensation technique, henceforth
known as method (II), during device calibration to improve
measurement accuracy. This method (II) method is used to

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
_ g _
reduce distortions in an auxiliary weighting parameter
(described above) required to normalise the measured phase
shift.
A special configuration of apparatus is employed
to facilitate the use of method (I), namely:
(i) the operation of the apparatus at low microwave
frequency (approximately 0.5-2GHz) so as to avoid
dispersion effects imparted by materials;
(ii) at each measurement (carrier) frequency, the
configuration of a quadrature modulator to provide
single side-band (SSB) modulation of a microwave
carrier at a suitably chosen intermediate frequency
CIF)
(iii) for each measurement frequency, the generation of
appropriate phase balanced and stable modulating
signals provided to the modulator in (ii), so as to
provide a suitably high level of suppression of the
unwanted sideband in the SSB modulation;
(a.v) for each measurement frequency, the configuration of
a receiver to demodulate the received signal to a
single analog signal at the IF frequency, with
suitably applied low noise factor; and
(v) at each measurement frequency, the logarithmic
demodulation of the intermediate frequency in signal
(iv), which provides two continuous signals each
proportional to phase and the logarithm of amplitude.
The apparatus in this particular configuration
specifically aids the implementation of method (I) through
the high accuracy of phase measurement provided by this
configuration. With inferior phase accuracy the error in
moisture estimates is generally increased. In turn, the
error reduction afforded by method (I) is reduced. while
method (I) can be used with other apparatus, the value of
method (I) is fully utilised and overall performance of
the apparatus is enhanced if systematic and random phase

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 9 -
errors related to the microwave receive circuitry are
reduced.
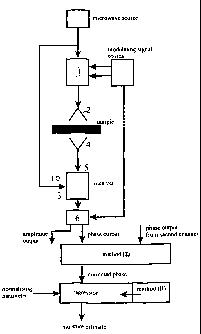
An example of a preferred configuration of the
apparatus used to implement the high accuracy phase
measurement scheme is shown in block diagram form in
Figure 3, where one channel of the transmit-receive system
is shown. The device would normally have two transmit-
receive channels at separate frequencies, each operating
continuously. Modulating signals, together with the
carrier at microwave frequency, are applied to a
quadrature modulator 1. The modulating frequency may lie
anywhere between audio and high frequency radio bands.
Two waves at microwave frequency are therefore available
to the channel; the original carrier and the output of the
quadrature modulator. One of these waves may be
propagated through the material (probe wave) after being
launched from a transmitting antenna 2, while the other
may be used as a local oscillator in a receiver subsystem
3. Upon reception of the probe wave by a receiving
antenna 4, the probe wave is fed to the low-noise
demodulating receiver 5. A component of the receiver
output will be in the same frequency band as the
modulating signals. This output wave may be compared to
one of the modulating signals (either serving as a
possible reference wave) in order to determine phase shift
and attenuation imparted to the microwave probe wave. A
direct reading of the phase and amplitude is provided
using a phase comparator and a logarithmic demodulator 6.
In general, accuracy of the method depends on the amount
of suppression of unwanted sidebands generated by the
modulator. Generally guadrature modulators have
imperfections that produce small but non-zero unwanted
sidebands. However very high sideband suppression
(greater than 50 decibels compared to the carrier) in this
system is afforded through a specific choice and
generation of modulating signals. This in turn leads to

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 10 -
high phase accuracy e.g., less than 0.5 degree phase
accuracy over an entire 360 degree phase range.
In its simplest form method (I) may be described
as follows. Let ~1 and ~2 be the absolute phase shifts
measured at the two respective discrete frequencies fj
andf2. The absolute phases are calculated from the
measured phases using methods known to persons skilled in
the art. The following transformation may then be used to
determine corrected phases ~l~ and
~a~ _ ~z + Yet
1+y
~n = Yea
(1)
The parameter y is a fixed constant with a value
suitably chosen so as to reduce measurement error. Persons
skilled in the art will appreciate that other
transformations linearly related to equation (1) may also
be used to the same effect.
After application of this correction procedure
the corrected phases at each operating frequency are
linearly related, and therefore either corrected phase can
be used to the same effect in a regression that determines
predicted moisture. The reduction in measurement error
afforded by this transformation (and the consequent
improvement in the quality of the regression) depends on
the value of y chosen and the distribution of phase
errors. A particular value of y found to be suitable may
be derived as follows. In the loss-free case the
theoretical relationship between the absolute phase of two
waves is given by:
3 0 ~1 = K ~a fi ~.fa
(~)
where K is a fixed parameter for a given pair of
frequencies that takes into account dispersion of the

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 11 -
material at the two frequencies. A similar but more
complicated equation may be derived in the high-loss case.
In practice the measured phases do not obey this relation
because of the presence of spurious waves or errors due to
the phase detector used. A particular choice of y that
forces the corrected phases to obey equation (2) is
y = Kfl l f2 . This prescription for y therefore yields
corrected phases with ratio most closely related to that
expected from theory, and therefore provides a significant
reduction in the effect of spurious waves. However other
values of y may provide similar error reduction.
The reduction in measurement error afforded by
the transformation defined by equation (1) also depends on
the distribution of phase errors. For example, the
following error distribution may be assumed:
~~T l - Y'1 ~ Y'T 2 - ~2 ~i - ~Ei COS ei , &i Slri ~i ~ ,
(3)
2 0 where ~T1 s ~T2 are the true phase shi f is at fl and f2
respectively, and ~1,~2 are the corresponding measured
phase shifts. The subscript i denotes sample number. The
variables ~ and ~ are used to model an assumed error
distribution. For the purposes of this example y =Kfi l f2
If over a large number of samples ~ is uniformly
distributed and s normally distributed around a mean of
zero, then the transformation yields a revised error that
is 70~ the value of the uncorrected error. This reduction
typically accounts for a similar reduction in the
uncertainty of the moisture estimate, thereby providing a
superior measurement. If the phases have fixed offsets,
due for example to changes in transmission coefficient at
the material-belt interface, then estimates of the offset
obtained by other means may be included in the scheme to
retain the full benefit of uncertainty reduction. It is
noted that this correction procedure does not require
knowledge of the moisture of the material. Method (I) is

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 12 -
important for the operation of the apparatus since it
affords significant error reduction in on-line
applications, and is not merely a post-acquisition method
useful only in off-line laboratory measurements. The
method is aided by operating at low frequency so that the
parameter K is often very near unity for many materials;
this allows application of the method without recourse to
complicated measurements to determine K. Furthermore the
simultaneous measurement of the wave phase and amplitude
at two frequencies and sufficiently high accuracy
delivered by the apparatus is required for proper
application of method (I).
Further to this application of the correction
technique is the technique of compensation (method II)
applied to an external weighting signal w that is usually
provided to normalise measured phase, e.g., conveyer mass
loading cell, mass flow meters in pipes etc. This is
required since to a good approximation the moisture
content is dependent on phase shift normalised to the
material mass per unit area (MPUA). The auxiliary
parameter w is used indirectly to infer relative MPUA. The
technique described here may be used to remove to some
extent the non-linearity that often exists between the
parameter w and the material MPUA. As an example, it is
assumed that calibration data is available where the pair
of variables (~,w~ are the measured phase and weighting
variable respectively, and M the corresponding actual
moisture measured through some means, for example manual
sampling. A conventional method of fitting involves
fitting the set of measurements M to the measured phases
and weightings (~,w~ using a set of basis functions F
involving (~, w~
Ma~A;F; , A-{al'az'a3} , F(~,w)- 1, ~, ~ . (4)
=1 w w2

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 13 -
In the example above it is assumed that the set
A contains three elements and that the form for F is
quadratic in ~~w, where the symbol t~ denotes the least
squares fitting operation for the unknown set of
coefficients A . Here it is assumed that a square or
overdetermined system is established where the number of
measurements equals or exceeds the number of required
coefficients. In turn, a predicted moisture M*may be
calculated from the measured phase ~ using the derived set
of coefficients A:
3
M*~~,w)=~A;F
r=i ( 5 )
A one to one correspondence between M and M
is therefore defined for each value of (~,w). The quality
of this regression may be defined by the standard
deviation of differences between M and M* defined for
each ~~,w). This quantity may be denoted as the standard
error.
An improved scheme described here (method II) may
be employed where there is significant variation in the
parameter w. The parameter w is replaced by w*, where w*
is determined by the dependence w*= G(w,B), where G is a
function involving w and a first coefficient set B. This
function G(w,B) is set up to model any non-linearity in w.
The function G may be quite generally defined and may
depend non-linearly on parameters in B. G should be
chosen so as to most accurately model the supposed
underlying non-linearity. As a simple example a quadratic
functional form for G may be assumed involving three
coefficients, but any number greater than one may be used.
w*=G(w,B)=bl+b2w+b3w2, B={bl,b2,b3~
(6)
As in the usual case, a regression may be
performed but with w* replacing w, and a second set of
coefficients C defining the regression may be obtained

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 14 -
3 2
M*=~GF,. C={~n~z~~3~ F(~,u~)= 1, ,
i-1 W* W* (7)
In this particular case degeneracy between
coefficient set B and C must be removed by setting, for
example, b2 to unity. The first set of coefficients B are
determined by a mufti-dimensional non-linear minimisation
scheme, e.g. the Nelder-Mead downhill simplex method,
although any suitable minimisation scheme will suffice.
For each trial value of first set B in the minimisation,
the second set C and therefore the standard error of the
regression is determined by the usual known least squares
method described above. The standard error is the variable
that is the object of minimisation. The mufti-dimensional
scheme is used to search the parameter space spanned by
the first coefficient set B in order to find the optimal
first set B that minimises the standard error. The second
set C corresponding to the optimum is determined
simultaneously and, if significant non-linearity exists
between W and MPUA, the first and second sets B and C
together describe a regression with a reduced standard
error compared to that which would be obtained without the
introduction of the first set B. Note that in general the
function Cp must be chosen to adequately simulate the non
linearity in w in order to reduce the standard error.
Compensation method (II) provides a fitting
technique that removes non-linearity between the parameter
W and MPUA. This formulation of a non-linear fitting
method is straightforward, avoids strong redundancies
between coefficients and has the advantage of transparency
compared to the usual application of say, neural networks.
The method can be performed off-line during measured
calibration or may be implemented on-line in special
circumstances where calibration data may be available to
the device on-line

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 15 -
EXAMPLES
A. Method (I)
Method (I) has been applied to a set of phase
data measured in the laboratory for semi-bituminous coal
for thickness spanning the range between 200-400mm and
moisture in the range 14.5-21.5wt.~. Figure 1(a) shows the
regression obtained by fitting a quadratic between sampled
moisture data M and ~, where ~ is the phase at high
frequency normalised to the material mass. In this case
the sample mass is a good estimator of mass per unit area,
since in the experiment the material filled a container of
fixed cross sectional dimension. The standard error of the
fit is 0.27wt.~ while the correlation coefficient is
0.990. The regression is defined by
M* _ -41.12 + 7.808 - 0.24252 , where M * is the predicted
moisture. A similar procedure may be separately performed
for the low frequency phase data; in this case the
standard error is 0.31 and correlation coefficient is
0.992. However, figure 1(b) shows the case where the
correction procedure has been implemented, where
y = Kfl 1 f2 , K =1 and fl l f~ = 0.76. That is, the phase has been
modified according to equation (1) before performing the
regression. The subsequent regression using the modified
high frequency phases yields a standard error of 0.19 and
a correlation coefficient of 0.996. The improved
regression is defined byM*_-45.61+8.547-0.27192.
B . Method ( I I ) .
Method (II) was applied to data collected in an
on-line application. A calibration consisting of a set
containing 37 points was available to the method. For each
sampled moisture M a measurement of the pair of variables
~~,w) was available for the fit, where ~ is the absolute
phase and w a normalising parameter, in this case derived
from a beltweigher. The variation in w over the
calibration set was sufficient to merit use of method

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 16 -
(II). The regression resulting without application of
method (II) is shown in figure 2(a). The standard error is
0.33, where the regression has been performed using the
relation
Ma~AiF , A=~at~a2~a3}~ F'~~~u')= h ~ ~ ~2 ~
w w2
t=i
3
M* O~ w) _ ~ Aif''i ,
f=I
whereto * is the predicted moisture and al = 3.690 ,
a2 = 7.468 x 103 and a3 = -$.295 x 105 . Coefficient set A was
obtained using standard least squares analysis, as denoted
by the operator
In the implementation of method (II) the underlying
relation between w and MPUA, denoted by w*, was assumed
to be of the form
w*=bl+w+b2w2, B={bl,ba~~
The Nelder-Mead minimisation of the standard error
returned coefficients b1 =-178.0 and b2 =1.925x10-5 . The
derived relation between w*and w is shown in figure 2(b).
The revised regression equation was simultaneously
provided:
M*=~C1F , C={cl,c~,c3}, F'~~~u'*)= 1~ ~ ~ ~2 ,
w* w*2
i=1

CA 02448904 2003-11-28
WO 03/005008 PCT/AU02/00902
- 17 -
where c~ _ -15.80 , ca =1.680 x 104 and c3 = -1.943 x 106 . Upon
implementation of method (II) the standard error was
reduced to 0.27, with the regression plotted in figure
2 (c) .
It will be apparent to persons skilled in the art
that various modifications can be made to the preferred
embodiment without departing from the scope of the
invention.

Dessin représentatif