Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
PROCÉDÉ DE TRAITEMENT DE DONNÉES SISMIQUES CORRESPONDANTS Ä DES ACQUISITIONS
RÉA
LISÉES SUR üN MILIEU PRÉSENTANT UNE ANISOTROPIE AZIMUTAL
DOMAINE GENERAL
La présente invention est relative au traitement de données
sismiq ues correspondant à des acquisitions réalisées dans un milieu
présentant une anisotropie azimutale.
Elle trouve en particulier avantageusement application comme
traitement de filtrage préalablement à la mise en oeuvre de traitements de
caractérisation d'anisotropie et notamment de caractérisation d'anisotropie
due à la fracture de la roche.
L'anisotropie azimutale ou « Horizontal Transverse Anisotropy »
(anisotropie « HTI ») se produit dans les unités géologiques contenant des
familles de fractures verticales et parallèles de dimension maximimum
décamétrique.
Rüger (1998) a fourni une approximation mathématique du
coefficient de réflexion R de l'onde sismique (onde P) dans un tel milieu
dépendant de l'orientation du couple source-récepteur par rapport à l'axe
principal de l'anisotropie (correspondant à l'orientation des fractures)
R(~ - ~) = Ro + ( Gi + GA cos2( ~ - j3)] sin20
avec Ro = Intercept
GI = Gradient Isotrope
GA = Gradient Anisotrope
~ = Azimut du couple source récepteur par rapport au Nord
(3 = Azimut de l'axe principale de l'anisotropie par rapport au
Nord
8 = angle d'incidence
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
2
PRESENTATION DE L'INVENTION
Un but de l'invention est de proposer un traitement permettant, dans
un jeu de données sismiques, d'isoler des données propres à l'anisotropie
correspondant à 45° de l'axe principal.
Un autre but de l'invention est de filtrer des données d'amplitude
sismiques pour permettre la détermination de paramètres d'anisotropie
aimutale.
II a déjà été proposé par la Demanderesse dans sa demande
FR 02 00397 un procédë de filtrage de données dans lequel, pour filtrer
deux séries de données représentatives d'au moins un même paramètre
physique sur une même zone, on détermine une estimation d'une
composante commune à ces deux séries de données.
L'invention propose quant à elle un procédé de traitement de
données sismiques correspondant à des acquisitions, réalisées dans un
milieu présentant une anisotropie azimutale, caractérisé en ce pue pour
deux jeux de données correspondant, pour une même variable sismique et
pour une méme zone au sol, à au moins deux secteurs de couple source-
récepteur d'azimuts différents, on dëtermine, pour chacun des azimuts
considérés, une moyenne entre les données qui correspondent à l'azimut
considéré et des données qui correspondent, pour la même variable et la
même zone au sol, à un secteur d'azimut perpendiculaire et en ce qu'on
détermine une estimation de la partie commune aux deux jeux de données
moyennées ainsi obtenus.
Comme on le comprendra dans la suite de la description, dans le
cas où cette variable sismique est la réflectivité, les deux jeux de données
obtenus en moyennant des données correspondant à des secteurs
d'azimuts perpendiculaires correspondent tous deux, pour la même variable
et la même none, à un azimut à 45° de l'axe principal.
La détermination d'une estimation de la partie commune - c'est à
dire de la partie qui entre les deux jeux de données est invariante - permet
de disposer, pour l'azimut à 45° de l'axe principal, de données
filtrées dans
lesquelles le bruit non corrélé a été supprimé.
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
3
Et on notera que cette propriété est vraie non seulement lorsque la
vraiable sismique considérée est la réflectivité, mais de façon plus générale
pour toute variable sismique dépendant de la réflectivité ou dont la variâtion
azimutale peut s 'approximer par une combinaison linéaire de cosinus carré
et/ou de sinus carré : amplitudes sismiques, attributs calculés à partir des
amplitudes sismiques, vitesses NMO, etc...
Selon un autre aspect de l'invenfiion également, pour au moins un
azimut
- on soustrait à un jeu de données correspondant à un
secteur selon cet azimut et à un ieu de données
correspondant à un secteur selon un azimut perpendiculaire
le jeu de données qui correspond à une estimation de la
partie commune aux deux jeux de données moyennées,
- on inverse le signe d'un des deux jeux de données
résiduelles ainsi obtenu,
- on détermine une estimation de la partie commune à ce jeu
de données résiduel dont le signe a été inversé et à l'autre
jeu de données résiduel.
II est en effet possible de montrer que les donnëes communes ainsi
obtenues correspondent aux variations liées à l'anisotropie selon les
azimuts considérés.
Connaissant cette anisotropie residuelle, on reconstitue des jeux de
données residuelles filtrées.
Les variations d'anisotropie et/ou les données residuelles filtrées
ainsi obtenues peuvent être utilisées directement pour le calcul des
paramètres d'anisotropie azimutale.
PRESENTATION DES FIGURES
D'autres caractéristiques et avantages de l'invention ressortiront
encore de la description qui suit, laquelle est purement administrative et non
limitative, et doit être lue en regard des dessins annexés, sur lesquels
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
4
les figures 1 et 2 illustrent différentes étrapes d'un traitement
conforme à un mode de mise en oeuvre possible de l'invention ;
- la figu re 3 illustre un mode de mise en oeuvre possible pour la
détermination d'une estimation de la partie commune à deux cubes
correspondant chacun à la sommation de deux azimuts
perpendiculaires;
- la figure 4 illustre un exemple de masque appliqué aux
cartographies 2D ;
- la figure 5 illustre un autre mode de mise en couvre possible avec
plusieurs itérations ;
- la figu re 6 illustre une autre variante de mise en oeuvre encore
possib le.
DESCRIPTION D'UN OU PLUSIEURS MODES DE MISE EN CEUVRE
Exemple de traitement de filtrage
On s'intéresse ici au cas où l'on dispose de données sismiques
correspondant pour une même zone au sol à au moins deux azimuts de
couple source-récepteur différents et à au moins deux azimuts
perpendiculaires à ceux-ci.
Ces données sont par exemple des cubes d'amplitudes sismiques.
Les données peuvent également peuvent être des cubes d'attributs,
dérivés de ces cubes d'amplitudes sismiques : amplitudes RMS, amplitudes
moyennes, vitesses de correction NMO, attributs AVO, impédances, etc...
Par « cu be », on entend ici et dans tout le présent texte, toute
collection de données sismiques (amplitudes, attributs) associant des
positions données sur la zone au sol sur laquelle l'acquisition qui
correspond à ces données sismiques a été réalisée, une succession de
valeurs prises successivement dans le temps par l'amplitude ou l'attribut
considéré.
Les cubes d'amplitudes sismiques utilisés pour obtenir les cubes de
données correspondent pâr exemple à des collections de traces à « point
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
milieu commun » ou « PMC » ayant fait l'objet d'une correction NMO et le
cas échéant de traitements de correction statiques.
Plus précisément, les jeux de données utilisés pour chaque azimut
sont une pluralité de cubes d'un secteur représentatif de l'azimut considéré.
5 Le nombre de secteurs pris en compte et leur ouverture sont choisis de
manière à optimiser la répartition régulière des données en azimut.
Dans l'exemple illustré sur les figures 1 et 2, on dispose de
cartographies d'amplitudes correspondant, pour un temps donné, à des
amplitudes de collections de traces sismiques issues d'acquisitions selon au
moins deux azimuts de couple source-récepteur différents (0° et
20°) et au
moins deux azimuts perpendiculaires à ceux-ci (90° et 110°)
Pour chacun de ces azimuts, on dispose de plusieurs cartographies
correspondant à différents couples source-récepteur dans le secteur
considéré comme représentatif de cet azimut.
Dans l'exemple illustré sur ces figures, le traitement comporte les
différentes étapes suivantes.
Dans une première étape, on détermine, pour chacun des deux
azimuts de couple source-récepteur considérés (respectivement 0° et
20°),
la carte d'amplitude correspondant à la moyenne des cartographies
d'amplitude du secteur représentatif de cet azimut et de celles du secteur
représentatif de l'azimut perpendiculaire (resp. 90° et 110°).
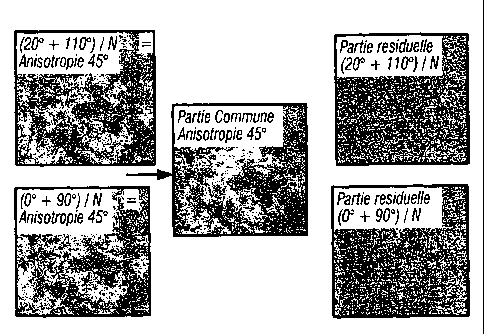
Les cartographies sur la partie gauche de la figure 1 correspondent
dans l'exemple choisi l'u ne à la moyenne des cartes correspondant aux
azimuts 0° et 90°, l'autre à la moyenne des cartes correspondant
aux
azimuts de 20° et 110°.
II est possible de montrer que la moyenne de cartographies
correspondant à des azimuts de couples source-récepteur perpendiculaires
est équivalente à une cartographie correspondant à celle d'un
enregistrement effectué avec un azimut source-récepteur à 45° de l'axe
principal de l'anisotropie.
En effet, d'après la formule d'approximation mathématique citée
précédemment ;
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
6
R(~-,Q)+R(~+~/2-~)=R + G +G °os2(~-/3)+cos2(~+~/2-~) sinzB
a r A
=Ro + G, +G~ cosz(~-,l3)+sinz(~-,l3)
sinz
2
=Ro +CGr +G,r ~~sinZ B
=R(~/4)=R(45°)
Les deux moyennes ainsi obtenues à l'issue de la première étape
illustrée sur la partie gauche de la figure 1 correspondent donc toutes les
deux à un même enregistrement avec un azimut source-récepteur à 45° de
l'axe principal de l'anisotropie.
En calculant la partie commune de ces deux moyennes de couples
d'azimuts perpendiculaires en théorie identiques, on élimine les bruits non
corrélés de chaque moyenne.
Ce calcul de partie commune est réalisé dans une deuxième étape
du traitement, par exemple par co-krigeage factoriel automatique. Sur la
figure 1, le résultat correspond à la cartographie représentée en partie
centrale.
La partie commune ainsi obtenue correspond alors à la référence
non bruitée de la valeur de l'amplitude sismique à 45° de l'axe
principal
d'anisotropie azimutal.
Dans une troisième étape, on peut soustraire cette partie commune
aux deux cartographies moyennes calculées dans la première étape.
Les deux cartographies rësiduelles ainsi obtenues (partie droite de
la figure 1) permettent de mettre en évidence le bruit éliminé.
La cartographie commune déterminée à la deuxième étape peut en
outre être utilisée, ainsi que l'illustre la figure 2, pour en déduire le
bruit
spatialement organisé et le bruit aléatoire dans les cartographies initiales
correspondant à chaque secteur d'azimut.
II est à cet effet possible, dans une quatrième étape du traitement,
de déterminer des cartographies résiduelles qui, pour un azimut donné et
son azimut perpendiculaire, correspondent à la différence entre d'une part
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
7
l'amplitude pour l'azimut considéré et d'autre part l'amplitude de la partie
commune qui est utilisée comme référence et qui correspond théoriquement
à un enregistrement à 45° de l'axe principal d'anisotropie.
Ces cartographies résiduelles sont illustrées sur la partie gauche de
la figure 2 dans le cas de l'azimut correspondant à un angle de 0° et
de
l'azimut perpendiculaire 90°.
Une fois ces deux cartographies résiduelles déterminées, on
inverse les amplitudes de l'une d'entre elles (multiplication par -1) et on
détermine, dans une cinquième étape, la partie commune aux deux
cartographies résiduelles ainsi obtenues.
Cette détermination de partie commune est elle aussi réalisée à titre
d'exemple par co-krigeage factoriel automatique.
La cartographie commune ainsi obtenue (représentëe au centre sur
la figure 2) correspond à la valeur d'amplitude résiduelle correspondant à
l'anisotropie azimutale pour ces deux azimuts perpendiculaires. Le fait de
calculer la partie commune permet de filtrer le bruit aléatoire et le bruit
spatialement corrélé des cartes d'amplitudes résiduelles.
II est possible en effet de montrer que les résidus correspondant à
la différence des amplitudes de deux azimuts perpendiculaires et des
amplitudes correspondant à un azimut à 45° de l'axe principal
d'anisotropie
sont équivalents au signe prés
Rit -~) - Ri~zl4) _ _ ~R(~~.~-l~ ~3) - R(~-14~I
Chaque secteur peut alors être recomposé par la somme des
amplitudes résiduelles (en respectant les polarités (signe) de ces dernières)
et de la composante commune filtrée qui est obtenue à l'issue de la
deuxième étape et qui correspond à un azimut source-récepteur à 45° de
l'axe principal de l'anisotropie. Chaque secteur est alors filtré du bruit
aléatoire et du bruit spatialement corrélé (bruit d'acquisition).
II est alors possible de mettre en oeuvre sur les données filtrées ainsi
obtenues des traitements de détermination de valeurs globales
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
8
d'anisotropie azimutale et notamment des traitements d'inversions
permettant de déterminer les paramètres de la fractures, lesquels sont
fonction de la variation azimutale en cosinus carré ou sinus carré.
A cet effet, on rnet en oeuvre un traitement consistant à adapter les
paramètres d'une ellipse aux variations azimutales du coefficient R. Ceci est
par exemple effectué par une inversion utilisant comme critère d'erreur les
moindres carrés.
Un traitement en ce sens est par exemple du type de ceux décrits
dans les publications suivantes
- Hall et al., « Fractured reservoir characterization using
P-wave AVOA analysis of 3D OBC data, TLE, 2002, Vol. 21,
n° 8, 777-781 ;
- Jennifer, "Azimutal AVO : Methodology and data examples"
- TLE, 2002, Vol. 21, n°8, 782-786 ;
Pour une présentation générale des connaissances théoriques de
base sur ce sujet, on pourra avantageusement se référer à la publication
suivante
- Rüger, A., 1998 - " Variation of P-Wave reflectivity with offset and
azimuth in anisotropie media "- Geophysics, Vol. 63, n°8, 935 - 947.
On notera que dans l'exemple qui vient d'être décrit, les données
sont des amplitudes sismiques.
Le traitement décrit s'applique toutefois de la même façon à des
données correspondant à des attributs dérivés de ces amplitudes : gradient
AVO, amplitudes moyennes, variation elliptique des vitesses NMO dans un
milieu anisotropique déterminée selon la méthode de Tvsankin (1997) ou
Grechka et Tvanskin (1998, 1999), variation d'impédance élastique avec
l'azimut déterminée selon la méthode de Connoly (1998).
II s'applique de façon plus générale pour toute variable sismique
dépendant de la réflectivité ou dont la variation azimutale peut s
'approxirner
par rapport à l'azimut comme une combinaison linéaire de cosinus carré
et/ou de sinus carré.
Par ailleurs, dans l'exemple qui a été décrit, les données traitées sont
des cartographies 2D.
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
9
II est également bien entendu possible de mettre en oeuvre le
traitement proposé sur des cubes de données.
Exemple de calcul de partie commune sur des cubes de données
La figure 3 illustre un exemple de calcul sur des cubes de données
Les données temporelles initiales sont transformées par FFT en
cubes de parties réelles et de parties imaginaires dans le domaine
fréquehtiel.
La partie commune de chaque plan fréquentiel réel et imaginaire est
calculée par la méthode dite « co-krigeage factoriel automatique » avec un
opérateur 2D dans le plan (x, y).
Par le processus de transformée de Fourier inverse du cube commun
des parties réelles et du cube commun des parties imaginaires, on obtient
alors le cube commun temporel des données sismiques.
Un exemple plus dëtaillé de traitement est donnë ci-dessous
1 ) Dans une première étape, on lit les données qui correspondent
aux deux cubes à traiter (cube A, cube B). Ces données sont enregistrées
dans un fichier où chaque trace est identifiée par un numéro de ligne et un
numéro de colonne qui correspondent à une position au sol.
2) Dans une deuxième étape, on sélectionne une fenêtre de temps
pour définir sur les traces sismiques l'intervalle de temps , pris en
considération pour le traitement. On complète le cas échéant les portions de
traces ainsi sélectionnées par des valeurs nulles pour obtenir pour chaque
trace un nombre d'échantillons correspondant à une puissance de deux
pour permettre la transformée de Fourier rapide de l'étape suivante.
3) Dans une troisième étape, on applique à la succession
d'échantillons correspondant à chacune des traces et à la fenétre
temporelle sélectionnée une transformée de Fourier rapide (FFT).
On obtient alors au total quatre cubes en fréquence correspondant à
la partie réelle et la partie imaginaire de chaque sélection des cubes A et B.
4) Pour chaque plan de fréquence, on construit alors, dans le
domaine réel d'une part et dans le domaine imaginaire d'autre part, deux
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
cârtes (2D) correspondant l'une aux données du cube A et l'autre aux
données du cube B.
Puis on applique sur les cartes ainsi obtenues pour les cubes de
données A et B un traitement de co-krigeage factoriel automatique afin d'en
5 déduire une carte commu ne aux deux cartes initiales.
Ce traitement de co-krigeage factoriel est bien entendu réalisé de
façon indépendànte d'une part avec les parties réelles et d'autre part avec
les parties imaginaires.
Le traitement comporte notamment, dans chacun de ces deux
10 domaines, les étapes suivantes
- En fonction d'un rayon de variogramme donné, calcul d'un
variogramme 2D pour la carte correspondant aux données A et, pour la
carte correspondant aux données B, calcul d'un cross-variogramme.
- Construction des matrices de covariances et cross-covariance à
partir des 3 variogrammes ainsi obtenus.
- Résolution du système de co-krigeage factoriel qui correspond à
ces matrices, afin d'en déduire un opérateur spatial, c'est-à-dire fonction de
la position en ligne et en colonne de l'échantillon considéré sur la
cartographie. Pour stabiliser l'inversion de la matrice du système, on ajoute
sur la diagonale des matrices de covariance une constante qui correspond
à un très petit pourcentage 'de la racine carrée du produit des deux
variances.
- On convolue alors l'opérateur spatial ainsi obtenu avec les cartes
initiales pour obtenir la partie commune des deux cartes. En fait, une seule
convolution est suffisante.
5) Le traitement qui vient d'être décrit est répété pour chaque plan
fréquence des parties rëelles et imaginaires. On obtient deux cubes, un
pour les parties réelles communes et l'autre pour les parties imaginaires
communes.
6) Une fois tous les plans fréquences calculés, on met en oeuvre une
transformée de Fourier inverse des cubes complexes communs pour
obtenir un cube en temps de sismique commune.
D'autres variantes de calcul sont bien entendu envisageables.
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
11
Ainsi que l'illustre la figure 4, le calcul de l'opérateur peut être limité â
des régions précises correspondant à des données valides. Les
variogrammes et cross-variogrammes sont ainsi calculés sur les régions
définies par le masque. Le masque peut par exemple cacher une zone sans
données due à une plate-forme de forage ou des données très bruitées par
des effets de bords. L'utilisation d'un masque va améliorer la qualité de
l'opérateur et donc du filtrage de bruit. Le masque est défini avec des
valeurs valides en blanc (1) et des valeurs non valides en noir (0).
II est parfois avantageux de faire le calcul du cube commun en deux
itérations : (Figure 5)
La première itération consiste à calculer un spectre commun
d'amplitude.
A cet effet, pour chaque plan de fréquence, on détermine à partir des
cartes de parties réelles et imaginaires, une cartographie d'amplitude, ainsi
qu'une cartographie de phase. Puis, à partir des cartographies d'amplitude
ainsi déterminées pour les données A et les données B pour chaque
fréquence, on détermine une cartographie commune d'amplitude spectrale.
Cette cartographie est de façon appropriée déterminée par co-krigeage
factoriel automatique.
La partie réelle et imaginaire de A et B est ensuite reformulée avec
l'amplitude commune ainsi obtenue et la phase initiale de A et B. Après un
traitement de FFT inverse des cubes, on obtient deux cubes de sismique A'
et B' ayant le même contenu fréquentiel.
Ces deux cubes sont ensuite traités avec une seconde itération.
La seconde itération calcule la partie commune réelle et imaginaire
de A' et B'. En fait, elle va fixer la phase commune des deux cubes
sismiques A' et B' puisque le spectre d'amplitude est déjà commun après la
première itération.
On détermine ensuite la partie commune, de la même façon que ce
qui a été précédemment décrit en référence à la figure 4.
Une autre variante encore possible de mise en oeuvre est illustrée
sur la figure 6.
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
12
Dans cette variante de mise en oeuvre, on extrait des cubes
d'amplitude associés respectivement au cube A et au cube B.
En parallèle ou dans une deuxième étape, on sort des parties réelles
et imaginaires des cubes A et B, des cubes correspondant au cosinus et au
sinus de la phase des données.
On détermine ensuite des cubes correspondant l'un à la partie
commune des cubes de cosinus, l'autre à la partie commune des cubes de
sinus.
Puis on détermine un cube dont les données sont le ratio des
4
données du cube de sinus et du cube de cosinus ainsi obtenus : on dispose
alors d'un cube donnant la partie commune de la phase.
Ce cu be de phase commune est combiné avec les deux cubes
d'amplitude i nitialement extraits des cubes A et B pour en déduire des
cubes filtrés A' et B'.
Ces deux cubes de données filtrées peuvent eux-mêmes faire l'objet
de la seconde itération décrite en référence à la figure 5.
En variante encore, il est possible de calculer le cube commun aux
cubes de données A et B en combinant d'une part le cube de partie
commune de phase et d'autre part le cube de partie commune d'amplitude.
On notera que dans les exemples qui précèdent, on a calculé la
partie commune de chaque plan fréquentiel par une méthode géostatistique
appelée co-krigeage factoriel automatique (ou analyse krigeante multi-
variables automatique).
D'autres traitements d'estimation de partie commune, et notamment
de traitements mettant en oeuvre un co-krigeage factoriel sont
envisageables.
On peut notamment déterminer une partie commune directement
dans le domaine temps sur une succession de cartes (x,y) d'amplitude
sismique (ou d'autres données).
Pour chaque instant considéré, on détermine alors la partie
commune aux deux cartographies qui correspondent à cet instant en
mettant en oeuvre un traitement de co-krigeage automatique factoriel.
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
13
Egalement, le traitement peut utiliser des opérateurs 3D au lieu
d'opérateurs 2D. Le traitement de co-kriegeage automatique factoriel se
généralise en effet avec une matrice de co-variance à trois dimensions.
II est à noter que l'utilisation d'opérateurs 2D (x,y) (ou 3D le cas
échéant) rend la méthode très performante pour filtrer des bruits
spatialennent organisés.
Annexe I - Rappel sur le co-krigeage factoriel
On décrit ci-dessous un exemple d'obtention d'une cartographie
commune par co-krigeage factoriel. On désigne par Z1 et Z2 les deux
fonctions correspondant à ces deux cartographies.
Dans un premier temps on calcule le variogramme croisé de ces
deuxfonctions, dont les valeurs sont
~y~2 (h)= ~ ~ (Z1 (x) - Z1 (x+h))(Z2(x) - Z2(x+h))
où x et x+h désignent les couples de points pris en considération selon la
direction et pour la distance h pour lesquels on détermine la valeur du
variograrnme, et
où N est le nombre de ces couples de points pour cette direction et cette
distance.
Connaissant ce variogramme croisé, on détermine ensuite une
estimation de la fonction qui lui correspond, laquelle vérifie
Z*12 (x)= ~ ~.~Z~ + ~ 7~aZp
où a et ~3 sont deux indices muets désignant les points considérés autour du
point x pour lequel on cherche à déterminer une estimation de ladite
fonction, ~â et ZR étant la valeur audit point x, N étant le nombre de ces
points et où ~,â et 7~R sont des coefficients de pondération.
Ces coefficients de pondération ~,â et ~,â se déterminent par
inversion de l'équation de co-krigeage
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
14
C" C" N1 C,211. . . ~1," C,Z
11 C,211 1X
.
.
.
C" C" NN C, . . . a,, C,
1N z 11 C,Z NN N Z
. NX
.
.
C2,11 Cz, Nl . . . ~.2, C,Z
. Cz211 Czz Nl 1X
.
.
CZ,1N CZ,NN Cz211... CZZNN~,ZN C,ZNX
...
où les coefficients C12a(3 et C21a~i sont les valeurs de variance
croisée des fonctions Z1 et Z2 aux points correspondants aux indices a et ~i
où les coefficients C11 a(3 et C22a~3 sont les valeurs de covariance
respectivement de la fonction Z1 et de la fonction Z2 auxdits points. L'indice
X correspond au point désigné par x précédemment.
On notera que la matrice qui apparait dans cette équation a
l'avantage d'être inversible sous certaines conditions de calcul.
De cette façon, en utilisant les covariances expërimentales, on
décompose de façon automatique les deux variables correspondant aux
deux séries de données initiales en une composante commune et deux
composantes résiduelles orthogonales. La régularité des données fait que
la covariance expérimentale est connue pour toutes les distances utilisées.
aucune interpolation n'est nécessaire et la matrice est définie positive
La fonction alors obtenue est une estimation de la composante
commune aux deux séries de données que constituent les deux
cartographies.
CA 02523073 2005-10-20
WO 2005/040859 PCT/FR2004/000996
Annexe II - Références
- Coléou, T., 2002, Time-lapse filtering and improved repeatability
with automatic factorial co-kriging (AFACK), 64t" Mtg.: Eur. Assn. Geosci.
5 Eng., Session: A018
- Hall, S.A., Kendall, J-M., and Barkved, O.I. 2002, « Fractured
reservoir characterization using P-wave AVOA analysis of 3D OBC data,
TLE, Vol. 21, n°8, 777-781
- Jenner, E., 2002, "Azimutal AVO : Methodology and data examples"
10 - TLE, Vol. 21, n°8, 782-786
- Rüger, A., 1998, "Variation of P-wave reflectivity with offset and
azimuth in anisotropic media" - Geophysics, Vol. 63, n°8, 935-947
- Tsvankin, I., 1997, "Reflection moveout and parameter estimation
for horizontal transverse isotropy", Geophysics, Vo1.62, n°2, 614-629
15 - Grechka, V. and Tsvankin, I., 1999, "3D moveout velocity analuysis
and pararneter estimation for orthorhombic media", Geophysics, Vol. 64,
n°3, 820-837
- Connolly, P., 1999, "Elastic Impedance", TLE, n°4,448-452