Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
1
Lesion Boundary Detection
Field of the Invention
The present invention relates to a method of detecting" the junction of a
lesion with
a wall, such as a lung nodule attached to the pleura or a polyp attached to
the colon wall, in
an image previously scanned from a human or animal body, particularly but not
exclusively in a computed tomography (CT) image. The invention encompasses
soflware
and apparatus for carrying out the method.
Background of the Invention
Detection of suspicious lesions in the early stages of cancer can be
considered the
most effective way to improve survival. Lung nodule detection and polyp
detection are
some of the more challenging tasks in medical imaging.
Computer-assisted techniques have been proposed to identify regions of
interest
containing a nodule within a CT scan image, to segment the nodule from
surrounding
objects such as blood vessels or the lung wall, to calculate physical
characteristics of the
nodule, and/or to provide an automated diagnosis of the nodule. Fully
automated
techniques perform all of these steps without intervention by a radiologist,
but one or more
of these steps may require input from the radiologist, in which case the
method may be
described as semi-automated.
Detection of the size or extent of a lesion is important for accurate
diagnosis, but it
is difficult to detect the extent of a lung nodule attached to the pleura, or
to separate a
nodule from the pleura, because of their similar intensity in CT scans.
Likewise, it is
difficult to detect the boundary between a polyp and the colon wall.
Patent publications US-A-2003/0099384 and US-A-2003/0099389 disclose
methods of detecting pleural nodules using morphological closing for small
nodules, and a
deformable surface model for nodules larger than the structural element used
for
morphological closing.
Patent publication WO 03/010102 and the article 'Lung Nodule Detection on
Thoracic Computed Tomography Images: Preliminary Evaluation of a Computer-
aided
Diagnostic System', Gurcan M et. al., Med. Phys. 29 (11), November 2002, pp.
2552-
2558, disclose a method of detecting pleural nodules using a local indentation
search next
to the hing pleura by finding a pair of points on a closed contour along the
boundary of the
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
2
lung where the ratio of the distance between the points along the boundary is
greater than
the straight line distance between the two points by more than a predetermined
threshold.
Statement of the Invention
According to the present invention, there is provided a method of detecting
the
junction between a lesion and a wall in a scan image, comprising determining
the boundary
of the wall to an internal space, identifying critical points along the
boundary, and selecting
one critical point at either side of the lesion as a junction point between
the wall and the
lesion. The critical points may be points of maximum local curvature and/or
points of
transition between straight and curved sections of the boundary. The critical
points may be
selected by receiving first and second seed points, at either side of the
lesion; moving the
seed points to the boundary if they are not already located on the boundary;
and fmding the
closest critical points to the seed points. The seed points may be determined
by displacing
the selected junction points from an adjacent slice of the image into the
current slice.
An advantage of this method is that the points of contact between the lesion
and the
pleura can be determined accurately in three dimensions, and the extent of the
lesion can
therefore be determined more precisely.
The location of the junction points may be fine tuned using various
techniques, and
may in some circumstances not coincide precisely with the determined critical
points.
The present invention is preferably implemented using a computer, and extends
to
software for carrying out the method.
Brief Description of the Drawings
Figure 1 is a schematic diagram showing a CT scanner and a remote computer for
processing image data from the scanner;
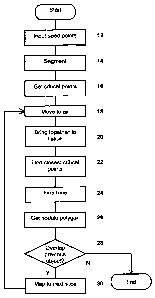
Figure 2 is a flowchart of an algorithm in an embodiment of the invention;
Figures 3a to 3c show respectively a single slice of a CT scan image of a
lung, the
lung area as obtained by segmentation, and the boundary of the lung area;
Figures 4a to 4c show critical points detected on the lung botuldary with
three
different thresholds;
Figure 5 shows seed points at either side of the nodule;
Figure 6 illustrates a method of moving the seed points from the pleura to the
boundary;
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
3
Figure 7 illustrates a method of moving the seed points from the lung space to
the
boundary;
Figure 8 illustrates a method of moving the seed points to the closest
critical points;
Figure 9 illustrates a method of determining the best critical point when they
are
approximately equidistant;
Figure 10 shows an example where the lung is divided into multiple boundaries;
Figure 11 shows where a join between the boundaries is determined;
Figure 12 is a graph of width against distance on a line midway between the
two
boundaries, showing how the join is determined;
Figures 13a to 13d show a method of correcting overshot edges of a nodule;
Figures 14a to 14d show a method of correcting overshot edges of a nodule
where
the detected edges lie beyond the nodule;
Figure 15 shows the detected extent of the nodule;
Figure 16 illustrates an alternative method for detecting the extent of the
nodule;
Figure 17 illustrates mapping of junction points to seed points in the next
slice; and
Figure 18 shows the detected extent of the nodule in a sequential series of
slices.
Detailed Description of the Embodiments
CT Image
Each embodiment is performed on series of CT image slices obtained from a CT
scan of a human or animal patient. Each slice is a 2-dimensional digital grey-
scale image
of the x-ray absorption of the scanned area. The properties of the slice
depend on the CT
scanner used; for example, a high-resolution multi-slice CT scanner may
produce images
with a resolution of 0.5-0.6 mm/pixel in the x and y directions (i.e. in the
plane of the
slice). Each pixel may have 32-bit greyscale resolution. The intensity value
of each pixel is
normally expressed in Hounsfield units (HU). Sequential slices may be
separated by a
constant distance along the z direction (i.e. the scan separation axis); for
example, by a
distance of between 0.75-2.5 mm. Hence, the scan image is a three-dimensional
(3D) grey
scale image, with an overall size depending on the area and number of slices
scanned.
The present invention is not restricted to any specific scanning technique,
and is
applicable to electron beam computed tomography (EBCT), multi-detector or
spiral scans
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
4
or any technique which produces as output a 2D or 3D image representing X-ray
absorption.
As shown in Figure 1, the scan image is created by a computer 4 which receives
scan data from a scanner 2 and constructs the scan image. The scan image is
saved as an
electronic file or a series of files which are stored on a storage medium 6,
such as a fixed or
removable disc. The scan image may be processed by the computer 4 to identify
the extent
of a lung nodule, or the scan image may be transferred to another computer 8
which runs
software for processing the image as described below. The image processing
software may
be stored on a carrier, such as a removable disc, or downloaded over a
network.
Nodules Attached to Lung Wall
A specific embodiment is designed for detection of the boundary between a
nodule
and a lung wall. Peripheral pulmonary nodules often exhibit some degree of
attachment to
the pleural surface (on the periphery of the lung, compressed against the
external boundary
of the thorax). The nodules share a significant amount of their surface with
the pleura. For
this reason, the delineation of the boundary between pleura and nodule is a
difficult task.
This complexity is reduced by taking two seed points as input on the periphery
of the lung
wall at opposite ends of the nodule. The seed points may be selected by a
user, such as a
radiologist, or determined automatically. The theory and implementation of the
boundary
delineation method is described below.
In a first embodiment, the method comprises the following steps described in
outline with reference to Figure 2, each of which is described in detail
below:
1) Input the seed points (step 12)
2) Apply coarse segmentation to separate the lung from the surrounding
tissue and determine the boundary (step 14);
3) Determine critical points on the contour (step 16);
4) For each slice (starting from the starting slice):
a. If not at the starting slice and either of the current points are in
the tissue, move the current points to the boundary (step 18). If
this process fails, then terminate the process.
b. If either point is in the lung space, move it towards the other
point until it hits the boundary (step 20) - terminate if failed;
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
c. Find closest critical points along the contour to the current two
points (step 22);
d. Fine tune the points (step 24)
e. Get outline of nodule (step 26) in the current slice;
5 f. Check the overlap with the nodule in the previous slice (step 28)
- terminate if no overlap.
g. Map the two points to the next slice (step 30)
5) Repeat for consecutive slices in both directions from the starting slice.
Input Seed points (Step 12)
The user inspects one or more slices of a CT scan and visually identifies a
potential
pleural nodule. By means of a user input device, the user selects two seed
points either side
of the potential pleural nodule on one of the slices. The seed points need
only be located
either side of the pleural nodule, and need not be precisely on the boundary.
_
Alternatively, the user may draw a box or other shape around the potential
pleural
nodule, using the input device. The points of intersection between the shape
and the pleura
may be taken as the two seed points.
As another alternative, the scan image may be pre-processed to identify
potential
pleural nodules, and the seed points may be input from this pre-processing
stage.
Segmentation (Step 14)
A sub-image of a plurality (e.g. 30) of slices below and above the slice
containing
the seed points is selected and coarse segmentation is performed so as to
separate the
image into the lung space and the pleura (including any nodule attached to the
pleura). The
segmentation may be perforrned by applying a predetermined threshold to the
image, since
the intensity of the h.ing space is much lower than that of the pleura and
nodules. Objects
above the threshold but not connected to the pleura are not considered by this
algorithm.
Alternatively, in order to make the iinplementation more reproducible, an
optimum
centre slice may be found and the sub-image may be centred on the optimum
centre slice.
A window is chosen, for example of 60 pixels x 60 pixels x 10 slices, centred
on the mid
point between the two seed points. The point with the maximum intensity within
the
window is found and the corresponding slice containing that maximum intensity
point is
chosen as the centre slice for the sub-image.
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
6
The segmentation may be further improved by performing an adaptive
segmentation after the initial coarse segmentation. In the adaptive
segmentation, the lung
space obtained by coarse segmentation is enlarged using a distance transform,
to obtain a
mask containing the lung space and an envelope around the lung space. The
enlargement
factor may be 50%. The adaptive segmentation is performed with a threshold
which is
derived only from the intensity values within the mask.
The result of the segmentation is a binary map of the slice, with pixels
representing
the lung space having one binary value and pixels representing surrounding
tissue having
another binary value. Pixels on the boundary between the lung space and the
surrounding
tissue are labelled as boundary pixels.
As an example, Figure 3a shows the scan image of a slice of a lung, while
Figure
3b shows the result of the segmentation. Figure 3b is a binary image in which
the lung
space is white (binary 1) and the surrounding tissue is black (binary 0).
Figure 3c shows, in
white, the boundary pixels derived from the segmentation.
Determine critical points (Step 16)
As a preliminary step for detecting the junction between a nodule and the
pleura,
critical points on the boundary are determined. Each section of the boundary
is identified
as concave, convex, or straight. A critical point is either a point of maximum
convexity or,
.
concavity, or a transitional point between the states of concave, convex, or
straight; in
other words, between straight and convex or concave, or directly between
convex and
concave. Critical points are of interest because they can indicate a boundary
between the
pleura and a nodule.
A specific method of determining critical points will now be described. The
input is
the map of the boundary contour; this could for example be a binary array in
which the
position within the array represents the x and y coordinates of each pixel,
and boundary
pixels are flagged as binary 1; in other words, a bitmap of the boundary.
Next, a boundary pixel is selected as the starting point. This could be any
boundary
pixel; for example, the first boundary pixel found in a raster scan (left to
right, top to
bottom) of the bitmap.
The algorithm then moves along the boundary, recording the angle between
successive neighbouring boundary pixels. As the pixels of each slice are
arranged in 2D
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
7
Cartesian coordinates, there are only 8 possible angles. For each pixel, the
neighbours can
be represented on a grid:
Pixel (x-l,y-I) Pixel (x,y-l) Pixel (x+l,y-l)
Pixel (x-l,y) Pixel (x,y) Pixel (x+l,y)
Pixel (x-1,y+1) Pixel (x,y+l) Pixel (x+l,y+l)
The angle between each pixel and its neighbours can be encoded as follows:
7 0 1
6 Pixel (x,y) 2
4 3
5
Where the codes correspond to the following angles:
Code 0 1 2 3 4 5 6 7
Angle 180 135 90 45 360 315 270 225
Therefore, the bitmap is converted to a chain code comprising a one-
dimensional
vector of codes representing the angle between successive neighbotiring
boundary pixels in
a loop around the boundary, e.g. (1,1,1,2,1,3,3...). Note that these are
absolute angles
relative to a downwards direction.
Next, the chain code is converted to an angle of curvature of the boundary at
each
boundary pixel. This may be done by taking the chain codes around each
boundary pixel
and applying a weighted filter so that the chain codes for boundary pixels
closer to the
current boundary pixel are more heavily weighted. Note that the angle of
curvatttre is
relative to the boundary rather than an absolute angle, so that chain codes
preceding the
current pixel around the loop are subtracted from those following the current
pixel around
the loop.
In one example, the angle of curvature for boundary pixel i is calculated as
follows:
3l2 j cCi+j
j~
a; _
Y,I
;=-õ
where mj is the weighting factor, which may follow a Gaussian distribution;
cc;+j is the chain code for pixel (i+j), and are negative for negative j;
n represents the number of pixels taken into account in each direction around
the
boundary; for example, n=5.
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
8
The result is a one-dimension vector representing the angle of curvature of
the
boundary at each boundary pixel, taking into account nearby pixels in either
direction
around the boundary. The effect of the weighted filter is to smooth the angles
from the
discrete, granular values of the chain codes.
Next, the local maxima and minima of the angles of curvature are identified.
For
example, a neighbourhood comparison method may be used in which each angle is
compared with a predetermined number (e.g. 3) of preceding and following
angles in the
vector.
To identify the transitional points between straight and concave or convex, a
range
of angles corresponding to 'straight' is defined. For example, all angles of
180 :Lf may be
classified as straight.
Figures 4a to 4c show the critical points for f= 5, 15 and 30 respectively.
Concave
maxima and transitions between straight and concave are labelled with squares,
while
points of maximum convexity or transitions between straight and convex are
labelled with
circles. Figure 4a shows that setting f too low results in a large number of
critical points
representing only slow transitions in the curvature of the boundary. The value
off may be
predefined in the software, and/or adjustable by the user.
Finding the nodule direction
Before the nodule is detected, it is first determined in which direction,
relative to
the two seed points pl and P2, the nodule extends into the lung. In one
embodiment, as
illustrated in Figure 5, a vector v is formed between the two points pi and
P2, and an
orthogonal vector o is constructed from the midpoint of the vector v in both
directions. The
direction of o which falls into the lung space L indicates the direction of
the lung and
therefore the direction in which the pleural nodule N extends into the lung
from the pleura
P:
After the initial slice, the nodule direction is determined from the direction
of the
detected nodule in the previous slice, relative to the seed points pi and P2.
Move to air (Step 18)
For each slice, the seed points p1 and P2 must first be checked to detemiine
whether
they are on the boundary B, and if not, they are moved to a suitable point on
the boundaiy.
In the initial slice, the user is not required to position the seed points pl
and P2 precisely on
the botmdary. After moving the seed points to the boundary, and moving the
seed points to
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
9
the next slice, by changing their z coordinates, the seed points may no longer
be on the
boundary in the new slice.
If either of the seed points pl and P2 is within the pleura P, that point is
moved onto
the boundary B. The direction and distance of movement may be limited to avoid
moving
away from a critical point likely to represent an interface between the nodule
and the
pleura. In particular, the angle of the interface is unlikely to change
greatly from one slice
to the next. One technique for moving seed points from the tissue to the
boundary will now
be described.
First, it is detennined whether there is any lung space L in a window (e.g.
20mm x
20mm) centred on the seed point to be moved. If there is not, then an error
condition may
be indicated. If there is, then the following steps are performed, as shown in
Figure 6:
= Draw two lines ll, b from each of the points pl, P2 which are in the tissue,
at 45 and
135 degrees respectively from the vector v, in the direction o of the nodule
N, each
of 10 units in length.
= Get the minimum size rectangle R from the seed point to be moved to the ends
of
the two lines Z1, Z? (note that there may only be one pair of such lines if
one of the
points pl, P2 is not in the tissue);
= Find the nearest point to the seed point on the boundary B, within the
rectangle R.
= Move the point to that boundary point provided that the distance moved is
less than
10 mm.
This technique applies a suitable restriction on the angle by which the vector
v can
rotate and the distance by which the seed points can move.
Bring two points together (Step 20)
If either of the two seed points pi and P2 are in the lung space L, that point
is moved
towards the other point until it hits the boundary B, as shown in Figure 7. If
the moved
points are within a predetermined distance (e.g. 2 mm) of each other, the
process is
terminated as this indicates that there is only air between the points.
Find closest critical points (Step 22)
The seed points pi and P2 should now both be on the boundary B. Next, they are
moved to the closest critical points along the boundary B, subject to certairi
conditions
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
-
which are designed to avoid a poor choice of critical point,, as explained in
more detail
below.
For each seed point, the closest critical point is determined along the
boundary B in
either direction. If the critical point in one direction along the boundary is
significantly
5 closer than the critical point in the other direction, then the seed point
is moved to the
closer critical point. For example, if the distance between the seed point and
the closest
critical point in one direction is greater than a threshold, the seed point is
moved to the
closest critical point in the other direction. The threshold may be a function
of the distance
between the seed point and the closer of the two closest critical points in
either direction,
10 for example twice that distance.
If the closest critical points in either direction are approximately
equidistant, a
critical point is selected based on the amount of lung space in a straight
line between the
seed point and each critical point. For example, as shown in Figure 9, if the
difference
between the distances between the seed point pl and the two closest critical
points cl, c2
along the boundary B is less than the threshold, a line 13 is constructed from
the seed point
p1 to each of the two closest critical points cl, c2, and the proportion of
the line length
which passes through the lung space L is determined. If the proportion is more
than a
predetermined threshold (e.g. 20%) then the critical point is considered a bad
choice and
the seed point is moved to the closest critical point cZ in the other
direction, if the
proportion for that critical point is less than or equal to the threshold. If
both critical points
have a proportion of greater than the threshold, then the seed point is not
moved to either
critical point.
Moving the points if too close
In some cases, one of the seed points might be relatively far from the best
critical
point and therefore, when finding the closest critical point, both seed points
will be moved
to the same critical point, or to critical points very close to each other.
This may happen
when the seed points are mapped from a previous slice and especially when fine
segmentation movement is applied, as will be described below. If the distance
between the
two seed points along the boundary is less than a threshold distance, such as
5 mm, the
seed point closer to the critical point is moved to that critical point while
the other seed
point is moved along the boundary to the nearest critical point away from the
other seed
point, provided that the distance between the two seed points does not
increase beyond a
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
11
predetermined threshold, such as the original distance between the seed
points. In other
words, the distance between the seed points after moving one away should not
be more
than double the distance before moving away.
No critical point nearby
In some cases there is no critical point near to one of the seed points, which
may
cause that seed point to move to the closest critical point to the other seed
point. This may
be avoided by preventing a seed point from being moved along the boundary by
more than
a predetermined proportion, such as 50%, of the distance between the seed
points before
moving; in that case, the seed point far away from any critical point is not
moved.
Fine Segmentation (Step 24)
After finding the nearest critical points using the coarse segmented boundary,
the
movement of the seed points may be fine tuned by re-evaluating the boundary B
in the
vicinity of the seed points using fine segmentation, dependent on the local
contrast. For
example, the threshold for determining whether each point is foreground or
background
may be determined by the intensities of points within a mask of local points
of
predetermined extent surrounding that point. The threshold may be selected so
that the
mean of the centroids of intensities above and below the threshold is equal to
the threshold,
or offset from the threshold by a predetermined degree.
Next, the critical points are determined on the fine-segmented boundary. The
seed
points may be moved to the closest critical point on the fine segmented
boundary, subject
to certain conditions, as set out below by way of example:
- the movement of the seed points to the fine-segmented boundary is always
away from
the direction of nodule.
- the distance moved must be less than a predetermined threshold. The
threshold is set
according to how much the seed point was moved from its initial point within
the slice to
its final point using coarse segmentation.
- the angle by which the line between the seed points rotates when moving to
the fine
segmented boundary critical points must be less than a predetermined angle,
such as 40
degrees.
The coarse segmented boundary might not be near the fine-segmented boundary of
the nodule where there is a strong partial voh.ime effect. In this case the
nearest critical
point might be away from the nodule; only movement away from the nodule is
allowed, so
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
12
the correct critical points might not be found. This may be solved by, if the
seed points are
in the lung relative to the fine-segmented boundary, moving the seed points
towards each
other until they hit the boundary, and then fmding the closest critical points
on the fine-
segmented boundary.
The effect of fine-segmentation is to remove the effect of material around the
nodule, such as infected tissue, which obscures the junction of the nodule to
the pleura.
Coarse segmentation will normally include the material as part of the
boundary, whereas
fine segmentation will reclassify the material as background.
Multiple Boundaries
In some cases, the lung L is split into two or more parts by the coarse
segmentation,
and the seed points are located in different parts, as illustrated for example
in Figure 10.
This can occur when a blood vessel extends across the lung in the current
slice, and may
cause difficulties in determining the extent of the nodule N by including the
blood vessel
as part of the nodule N.
To overcome this problem, it is determined whether the seed points, when moved
to the boundary B, form part of different, unconnected boundaries. If so, the
variation of
the distance between the two boundaries is calculated, proceeding from between
the two
seed points in the direction o of the nodule, as shown in Figure 11. A sample
graph of the
variation of the distance is shown in Figure 12. The point g of greatest
change in the
gradient of the graph is taken and the boundaries B are joined at that point.
This allows the
nodule N to be separated from the blood vessel.
Contour correction
In some cases the boundary between the detected junction points has overshot
edges, as shown for example in Figure 13a; the critical points might not be at
the exact
location of nodule attachment to the lung wall, for example because of slow
angular
changes at the junction.
To avoid this problem a contour correction function may used to re-adjust the
jtmction points to allow correct region extraction, as shown in Figures 13b to
13d. First, a
line is constructed between the junction points. If the line intersects the
boundary, then one
junction point is moved towards the other along the boundary until there is no
intersection
with the boundary on that side. Then the other junction point is moved towards
the first
junction point until the line no longer intersects the boi.tndary.
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
13
In some cases, particularly when the nodule is small, the line between the
junction
points when the edges are overshot does not intersect the boundary, as shown
in Figure
14a. In this case, the junction points are moved together along the boundary,
as shown in
Figure 14b, alternately by a small increment until the line intersects the
boundary, as
shown in Figure 14c. The contour correction then proceeds as described above,
until the
line no longer intersects the boundary, as shown in Figure 14d.
Get Nodule Boundary
At this stage two junction points have been determined, representing the
points
along the boundary B at which the nodule N joins the pleura P. These junction
points may
be used to estimate the boundary of the nodule N within the slice. As a first
approximation,
a straight line joining the junction points is used to define the junction
between the nodule
N and the pleura P. Alternatively, a curved line may be used, with a curvature
estimated
from that of the pleura surrounding the nodule N.
Next, the extent of the nodule N is determined. In one embodiment, it is
assumed
that the nodule N is not attached to or proximate to any features other than
the pleura P.
The result of the segmentation in step 14 is used to identify all of the
foreground region
beyond the line joining the junction points as forming part of the nodule N,
as shown in
Figure 15.
In an alternative embodiment, a fuzzy contrast region growing scheme is used
to
identify the extent of the nodule N. First, the extent of the nodule N is
estimated by means
of a local threshold-based segmentation process. A local mask is used to
derive a threshold
intensity value for each point. The threshold is therefore sensitive to the
local contrast and
can distinguish low contrast nodules from their background. The nodule area N
acquired
by fine segmentation may include 'holes' i.e. background pixels surrounded by
foreground
pixels. The holes may result from the sensitivity of the fine segmentation to
small local
differences in contrast. A suitable hole-filling algorithm is used to fill
such holes, in other
words to convert them to foreground pixels.
Next, the pixel with the highest intensity within the nodule area N is taken
as a seed
point, and binary region-growing is performed from that seed point to identify
a connected
foreground region F. This region is enlarged using a distance transform method
with an
enlargement factor, to obtain a mask M containing both foreground and
background. The
enlargement factor may be 50%. However, as shown in Figure 16, the mask M does
not
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
14
include any pixels on the other side of the line joining the junction points,
including a
projection of that line beyond the junction points. Next, the foreground
pixels segmented
by the fme segmentation process that are not part of the connected foreground
region F are
removed from the mask M. The background pixels of the mask M are labeled as
the
background region B.
The mean and the standard deviation of the intensity and gradient
distributions of
the foreground and background regions F and B are determined. The mean of the
background intensity,uB , the mean of the foreground intensity uF , the
standard deviation
of the background intensity aB and the standard deviation of the foreground
intensity 6F are
calculated. A parameter s is estimated by counting the number of the
foreground standard
deviations 6F that the seed point is away from the background mean
intensity,uB and this
is taken as the measure of the contrast, which is subsequently used in
constructing a fuzzy
map as described below.
A fuzzy object extraction technique is used to define a 2D map of fuzzy
connectivity of each pixel within the mask M with respect to the seed point. A
fuzzy
affinity function between adjacent pixels is defined and the fuzzy
connectivity between
each pixel and the seed point is derived by finding the affinity along a path
between the
pixel and the seed point.
The fuzzy connectivity between two points (not necessarily adjacent) is
obtained by
considering the path with the strongest affinity between two points. The path
with the
strongest affinity is chosen as the best path and the strength of each path is
equal to that of
the weakest affinity of adjacent points along the path. The strengtli between
two adjacent
points is the affinity between those points.
The affinity between two pixels is a measure of the probability that they
belong to
the same object. This probability is a function of closeness (i.e. Euclidian
distance) and the
similarity of the image features (i.e. intensity) between those pixels.
The general model for fuzzy affinity is given by:
k =(c, d) = h( a(c,d), f(c), f(d), c, d)
where h is a scalar value with range [0,1], c and d are image locations of two
pixels,
and f(i) is the intensity of spel i. a is an adjacency function based on
distance between
two pixels which is given by,
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
1' f ? i~e~ - d; ) Z< 1
,ua(c, d) =
0, otherwise
A simplified shift invariant version is defined as
,uk (e, d ) = ,ua (e, d ) [w; h; (.f (c),.f (d ))+ c)o (1.0 - hok (f (e)j (d
)))]
if c:Ad, and
5 I-Gk (C, C) = 1
where the subscripts 'i' represents the calculations related to intensity and
'gk'
represents the calculations related to gradient values in relevant direction
(which could be
x, y, z) respectively. co; and cog are free parameter weight values whose sum
is 1. The value
of 0.9 for (j); and 0.1 for o)b has been chosen to allow intensity similarity
to have more
10 effect. The fuzzy affinity that was used for the current function is:
[(1 / 2)(.f (c)+f (d))-mt ]2
hi (f(c), f(d)) = e (sd)2
LQ.f (c)-.f (d )I l dx)-rngz]z
h,(.f(c) j(d)) = e (sgr )z
[(I.f (c)--f'(d)Il dy)-m V] 2
h, (f(c), .f (d)) = e (s':5' )2
15 where m;, s;, mo and sD are the Gaussian parameters for the intensity and
gradient.
These can be predefined, or are estimated from a small region around the seed
point as
described below.
The mean and standard deviation 6 of the intensity and gradient are calculated
over
all points within the mask M. The parameters related to the gradients are
computed in three
directions (x, y and z) separately. The corresponding 6 are calculated based
on the
difference between maxilnum and minimum gradient.
The calculation of the statistics is now described in more detail. The
parameter ni;
is taken as the intensity of the seed whereas rne, , rna. are taken as the
means of the
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
16
gradients in x- and y- direction respectively. The parameters S., , S., are
the standard
deviation of the gradients in their respective direction.
The standard deviation ( Sd ) appearing in the affinity expression affects the
formation of the fuzzy map and hence the determination of the boundary of the
nodule. If it
is too big, the affinity curve will be relatively flat. Resultantly, the
background region will
have higher affinity and region growing will result in over-segmentation. On
the other
hand, if it is too small, the shape of the affinity curve will be narrow and
the foreground
will have less affinity with the seed and the result would be under-segmented.
Ideally, the
curve should be spread to such an extent that the background has minimal but
finite
affinity with the seed. The affinity Gaussian curve is therefore limited or
extended by
modifying the standard deviation so as to achieve the ideal spread.
A fuzzy map is then constructed by finding the fuzzy connectivity value for
each
pixel relative to the seed point. The fuzzy map may be considered as an
enhanced image
whose pixels represent how strongly are attached to the seed point.
Next, contrast based region growing is applied to the fuzzy map, starting from
the
seed point. As each pixel is added to the region during region-growing, the
peripheral
contrast is calculated between the internal and extern.al boundaries of the
region. The
peripheral contrast of the region may be defined as the difference between the
average grey
level of the internal boundary and average grey level of the current boundary.
At each iteration of the contrast-based region growing, one pixel is selected
from
the current boundary and added to the current region. The selection priority
of pixels in the
current boundary is determined on the basis of their intensity and the
distance to the centre
of the current region. As each pixel is added to the region during region-
growing, the
peripheral contrast is calculated between the internal and external boundaries
of the region.
The peripheral contrast of the region may be defin.ed as the difference
between the average
grey level of the internal boundary and average grey level of the cturent
boundary. The
peripheral contrast at each stage is recorded, and the region growing
continues until the
region fills the mask M. The highest peripheral contrast value obtained during
region
growing is selected as indicating the optimum region, with a boundary most
likely to
correspond to that of the nodule N.
Map to next slice (Step 28)
After the extent of the nodule N in the current slice has been determined, it
is
detenilined whether the nodule N in the current slice overlaps the determined
extent of the
CA 02571720 2006-12-21
WO 2006/000738 PCT/GB2005/001841
17
nodule N in the previous, adjacent slice. This may be done in a variety of
ways, for
example by determining a circular 'core' of a predetermined radius surrounding
the centre
of the nodule N in each slice, and determining whether the cores overlap in
adjacent slices;
i.e. if there are any pixels having the same x and y coordinates between the
two cores. If
there is no overlap, or no nodule has been detected at all in the current
slice, this may
indicate the limit of the nodule N in the current direction from the starting
slice. If the
algorithm has proceeded in only one direction from the starting slice, it then
proceeds in
the other direction. If nodule boundary detection has been performed in both
directions,
then the algorithm ends, and outputs the detected extent of the nodule in each
of the slices
in which the nodule N has been detected.
If there is overlap with the previous slice, the algorithm proceeds to the
next slice,
using the junction points j1, j2 from the current slice as the two input seed
points.p1, P2 for
the next slice, as shown in Figure 17. For example, the seed points for the
new slice have
the same x and y coordinates as the junction points for the previous slice.
Results
Figure 18 shows the detected extent of the nodule N in a sample scan image.
Applicability to the colon
The embodiment described above can also be applied to the detection of polyps
in a
CT scan image of the colon. Polyps are always attached to the colon wall,
which has a
similar intensity in the CT scan image. Although the shape of polyps is
somewhat different
from that of lung nodules, the junction between the colon wall and the polyp
has similar
geometrical properties, and the embodiinent may be used to detect that
junction.
The present invention may be applied to the detection of other abnormal
growths
attached to walls of internal spaces of the human and/or animal body.
Alternative embodiments
The embodiments above are described by way of example, and are not intended to
limit the scope of the invention. Various alternatives may be envisaged which
nevertheless
fall within the scope of the claims. As will be apparent from the above
discussion, the
method can be performed on a 2D image consisting of a single CT slice, or a 3D
image
consisting of consecutive CT slices.