Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
METHODS AND APPARATUSES FOR NONINVASIVE DETERMINATIONS OF ANALYTES
Technical Field
[0001] This present invention relates generally to determining analyte
concentrations by
analyzing light that has passed through a material sample. More specifically,
the present invention
relates to methods for improving the accuracy of analyte determinations in
material samples that both
scatter and absorb light.
Background Art
[0002] It is well known that absorbance spectra measured in the presence of
scattering media
differ from spectra of the same chemical species measured in the absence of
scattering. It is also well
recognized that the paths that light rays travel through a scattering sample
are more difficult to
characterize than those in non-scattering samples, within which, light rays
generally travel a straight
line. In non-scattering samples, path length can be calculated from the
physical dimensions of the
sample and a basic knowledge of beam and sample geometry. Furthermore, path
length in an ideal
transmission measurement is a common property for all light rays incident on
the sample and thus
path length can be represented with a scalar value common to all rays and all
wavelengths.
[0003] In contrast, light rays traveling through a scattering sample have
multiple potential paths
and are therefore best described by a path length distribution (PLD). In
simple terms, this distribution
will have some fraction of rays that traveled the typical path length, as well
as a fraction of rays that
traveled shorter and longer paths through the sample via the random nature of
scattering interactions.
The properties of this path length distribution can also be further
characterized with statistical
properties, such as the distribution's mean and standard deviation. These
properties are not
necessarily fixed for a measurement system as they depend, in complex ways, on
sample properties
including both the scattering and absorbance.
[0004] There is great interest in measuring analyte concentrations in samples
that both absorb
and scatter light, despite the difficulties described above. This is because
many important biological
systems scatter light due to their heterogeneous composition. One example of
these heterogeneous
structures is coliagen fibers in skin that scatter light because they have a
different refractive index
than the interstitial fluid that surrounds them. This scattering can
complicate noninvasive glucose
measurements such as those described in Patent number 4,975,581, issued
December 4, 1990.
Another important example is measuring the concentration of urea in suspension
of cells, such as
those in whole blood. In this example, the red blood cells have a different
refractive index than the
surrounding serum that causes them to scatter both visible and infrared light.
Another important
example, is measuring lactate concentration in bioreactor cell cultures. This
is an example where
structures inside the cells, such as mitochondria, can be strong scattering
elements. Determining
analyte concentrations in all of these sample types is complicated by
intrinsic biological variability in
their absorbance and scattering properties.
1
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
[0005] Known methods for determining an analyte concentration in a sample from
optical
measurements with variable path length distributions, due to scattering and
absorbance changes,
typically involve simplifying assumptions that limit their measurement
performance in practice or
involve methods that seek to estimate the path length distribution.
[0006] One class of methods uses theoretical approaches to estimate absorbance
and scattering
properties separately by applying Diffusion Theory. For example, Tissue
Optics: light scattering
methods and instruments for medical diagnosis, Tuchin V., ISBN 0-8194-3459-0,
The Society of
Photo-Optical Instrumentation Engineers, 2000 Section 1.1 includes
descriptions of optical properties
of tissue with multiple scattering including blood and skin. The Diffusion
Theory approach requires
simplifying approximations that are not valid for all combinations of
absorbance and scattering
properties. For example, Diffusion Theory is not accurate when the effects of
absorbance are greater
than scattering or when the number of scattering events is small. Noninvasive
tissue measurements
in the near infrared spectral region can have one or both of these conditions.
[0007] Another theoretical approach uses Monte Carlo simulations to estimate
the path length
distribution from explicit knowledge of the system under study, which requires
some, if not all, of the
foilowing optical properties: absorbance coefficient, scattering coefficient,
scattering phase function,
and sample geometry. In practice, it is difficult to accurately estimate the
optical scattering properties
of tissue as the true shapes of collagen fibers or blood cells need to be
simplified to geometric forms
like spheres or cylinders with known analytical solutions.
[0008] Another class of methods makes assumptions about optical properties of
the sample at
specific wavelengths. For example, that non-absorbing wavelengths exists that
can be used to
correct analyte absorbance at wavelengths with similar scattering properties.
Patent number
5,099,123 issued March 24, 1992. This approach is typically limited to
spectral regions where water, a
major constituent in many biological samples, is a weak absorber. A second
example of assumed
optical properties is the use of isobestic points. Patent number6,681,128,
issued January 20, 2004.
An isobestic point occurs at a wavelength where there are only two absorbing
species, typically an
analyte and another major absorber, and both species have the same
absorptivity. Again, these
approaches are applicable in some biological measurements, like pulse
oximeters measurements in
the 500 to 1000 nm region, but not throughout the infrared region where there
are many more
spectrally active biological species.
[0009] Multiplicative Scatter Correction, Multivariate Calibration, Martens
and Naes, Section 7.4
and similar publications, estimates the net effect of scattering on path
length across spectral
wavelength with low-order poiynomials, such as a quadratic function. Such
functions do not
accurately represent scattering over broad spectral range, such as the 4000 to
8000 cm-1 region
commonly used in noninvasive glucose measurements.
[0010] Another approach to determining analyte concentrations in highly
scattering and
absorbing samples is to measure the path length distribution explicitly and
incorporate the path length
2
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
estimate in the measurement algorithm. One such technique is to use photon
time-of-flight
measurements to characterize the sample's optical properties at discrete
wavelength in combination
with absorption measurements, Leonardi, L; Burns, DH Multiwavelength Scatter
Correction in Turbid
Media using Photon Time-of-Flight; Applied Spectroscopy, 50(6), 637-646,1999.
This approach
requires additional measurement apparatus including a pulsatile or frequency-
modulated light source,
which adds cost and complexity. It also assumes that the path length
properties at all wavelengths
can be inferred from one or more discrete measurements.
Brief Description of the Drawings
[0011] FIG. 1 shows an idealized absorbance measurement system.
FIG. 2 shows the difference between a pure analyte signal and a net analyte
signal.
FIG. 3 shows a net analyte signal with selectivity errors
FIG. 4 shows a net analyte signal with proportional errors
FIG. 5 shows pathlength changes that produce proportional errors
FIG. 6 shows a conceptual framework for understanding prediction errors
FIG. 7 shows a spectroscopic framework for understanding prediction errors
FIG. 8 shows spectra from several application areas
FIG 9.shows glucose measurement results in scattering media
FIG 10.shows ethanol measurement results in scattering media
FIG 11.shows urea measurement results in scattering media
FIG 12. shows the dependence of scatter on wavelength
FIG 13. shows the different in predictor functions for two scatter levels
FIG 14. shows the interaction between interfering substances and the predictor
function
FIG 15. a illustration of the fundamental probe of analyte measurement in
scattering media
FIG 16. illustrates a system with multiple observations point
FIG 17. illustrates the relationship between path and scattering media
FIG 18. illustrates the relationship of photon travel to scattering media
FIG 19. illustrates the influence of scattering media on glucose predictions
FIG 20.illustrates a conceptual framework for determining media
characteristics through multiple
observations
FIG 21. shows the ability to classify media based upon the diagnostic metric
FIG 22. illustrates the path characteristics of the calibration samples
FIG 23. illustrates the path characteristics of the validation samples
FIG 24. plots the prediction results for standard single channel processing
FIG. 25 plots the prediction results generated by the sub-model approach
FIG. 26 shows the process of generating predictions results from multi-channel
spectra
FIG. 27 plots the resulting prediction results and error structure
FIG. 28 plots the prediction results generated by the X-Y model approach using
glucose only
FIG. 29 plots the prediction results generated by the X-Y model approach using
multiple analytes
FIG. 30 show different predictor functions developed from different media
3
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
FIG. 31 shows the relationship between different predictor functions
FIG. 32 shows prediction differences as a function of different predictor
functions
FIG. 33 plots the prediction results generated by the adaptive model approach
Disclosure of Invention
[0012] This patent describes a new family of methods to improve the accuracy
of analyte
concentrations measured in samples that both absorb and scatter light. Light
scattering in biological
samples, including blood, skin and bioreactor cell cultures, causes light rays
to travel different paths
through a sample. The paths of these rays violate several assumption of Beer's
law because the
paths are no longer parallel or of equal lengths. As a result, there is no
longer a simple relationship
between absorbance and concentration changes because interactions between
scattering and
absorbance properties across the desired operating spectral range distort the
absorbance features of
the analyte. The consequences of these distortions, in particular their effect
on measurement
precision, are not adequately discussed in prior art except for algorithmic
approaches that generally
compensate for scattering with multiplicative and offset corrections. The
following discussion
describes a novel family of methods for determining analyte concentrations in
a sample from one or
more optical measurements. These methods improve the accuracy of analyte
determinations in
material samples that both scatter and absorb light. One clear benefit of
these methods is their
improved ability to measure new samples with optical properties that are
different from the samples
used to calibrate the method. This overcomes a known limitation for applying
existing methods in
many practical applications where the method appears to perform well on a
calibration set but
performs poorly on new sample types that require extrapolation or
interpolation. These new methods
also overcome limitations in applying linear prediction methods based on
Beer's law to samples that
span a range of optical measurement or sample properties that violates its
inherent assumptions.
Absorbance Spectroscopy
[0013] Spectroscopy measures the interaction of light with a sample. In
general, light intensity
entering and exiting a sample is compared to extract qualitative or
quantitative information. The
following section outlines the assumptions inherent in spectroscopy for ideal
samples before moving
on to more complex systems. For illustrative purposes, this section focuses on
absorbance
spectroscopy in the visible and infrared regions. The visible region includes
wavelengths from 380 to
780 nm. The near infrared region includes wavelengths from 780 to 2500 nm and
the mid-infrared
region includes wavelengths from 2500 nm to 50000 nm. This illustrative
discussion is not restrictive,
as the same fundamental principles apply broadly to absorption measurements
outside these regions,
including absorbers in the ultraviolet region and X-ray region and nuclear
magnetic resonance. In the
visible and infrared .regions, a molecule absorbs light at frequencies
characteristic of its chemical
structure, which is determined by vibrational and electronic energy levels. In
qualitative spectroscopy,
the frequency and relative intensities of these characteristic absorbance
features are used to identify
specific chemical species (such as ethyl alcohol) or a broader class of
chemicals (such as alcohols).
In quantitative spectroscopy, the magnitude of one or more absorbance features
is used to estimate
4
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
the concentration of an individual chemical species in a sample (such as
alcohol levels in blood) or a
family of related compounds (such as total proteins in blood). Thus it is
understood that the analyte
measurement can estimate the concentration of a single species (such as
glucose), a composite
property (such as octane number of gasoline), a physical property (such as
sample temperature), or a
subjective sample property (such as fruit ripeness).
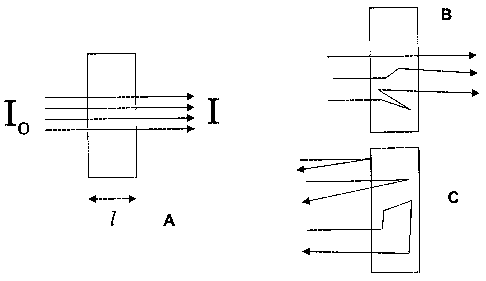
[0014] An idealized system for absorbance measurements is shown in Figure 1a
where the
sample is presented in a cuvette with rectangular cross-section to the
incident beam, which has
parallel rays of monochromatic radiation. The sample transmittance (T) is the
ratio of the intensity of
the exiting light (I) to the incident light (Io),
T = 1/l0
[0015] The sample absorbance (A) is calculated from transmission with a
logarithmic transform
A = -logto (T) = loglo (lJl)
[0016] Absorbance spectra are generally used for quantitative and qualitative
analysis because,
in these ideal systems, their magnitude is linearly related to concentration
through Beer's law
A = eic
[0017] Where e is molar absorptivity, I is path length, and c is concentration
of the absorbing
species. Note that in the measurement example shown in Figure 1 a the path
lengths of the three
illustrated rays are equal and equivalent to the internal dimension of the
cuvette. Thus path length is
completely described with a scalar value of path length, I. In contrast the
scattering systems shown in
both a transmission (Figure 1 b) and a diffuse reflectance (Figure 1c)
measurement modes where
three possible light rays are shown that have different path lengths in the
sample due to scattering
interactions.
[0018] Also note, that the Beer's law notation is easily extend to a spectrum
measured at
multiple wavelengths using a vector notation,
Aõ = eõIc
[0019] where Aõ is a vector containing the absorbance measured at each
wavelength (v), ev is a
vector containing the molar absorptivity at each wavelength (v) and path
length, I, is still a scalar
quantities as it is the same for all wavelengths. For a measurement system
with a fixed pathlength,
the change in absorbance at each wavelength for a unit change in concentration
will be called the
pure component spectrum, Kõ
K, = evl
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
[0020] While this pure component spectrum is often considered to be the
absorbance of the
analyte, such as absorbance features of the glucose molecule, there are also
cases where the signal
includes the influence of the analyte on the solvent or other constituents of
the sample. Examples of
these indirect effects include negative absorbance features of displaced
solvent and changes in the
hydrogen bonding structure of the solvent due to temperature or dissolved
ions, such as the spectral
changes associated with adding salts like sodium chloride.
[0021] The Beer's law equation can be similarly extended to describe a sample
with multiple
absorbing components using a matrix representation,
Av = I Ev,n cn
[0022] where E,,,, is matrix with the absorptivity of species 1 to n at each
wavelength, v, and c, is
a concentration vector of the n constituent concentrations in the sample. Note
again, that path length,
I, is assumed to be a scalar quantity for this sample.
[0023] Also note, while many methods of determining analyte concentration are
described for
absorbance measurements, this choice of units is for mathematical convenience
and compactness
alone, as equivalent computational algorithms can be written by one skilled in
the art to operate on
other inputs forms including transmission spectra, detector intensities, and
interferograms.
A calibration estimates the relationship between measured absorbance and
analyte concentration
[0024] In practice, a calibration step can be required to create an accurate
relationship between
the measured absorbance spectra and analyte concentration for a given
measurement system. In
this discussion, method calibration refers broadly to using a set of spectral
measurements of samples
with known properties to calibrate the relationship between the measured
spectra and the analyte of
interest. Method validation refers to a subsequent step where new samples are
used to test the
validity of the calibrated measurement method. Ideal validation samples have a
distinct composition
(absorber concentrations and scattering properties) from the calibration
samples.
[0025] If a wavelength exists where only the analyte of interest absorbs then
Beer's Law
describes a linear relationship between the absorbance at this selective
wavelength, A,, and the
analyte concentration, c,
A, = cK,
[0026] where K, is the slope of the calibration curve - a plot of measured
absorbance versus
analyte concentration.
[0027] Estimated concentration, Chat, is determined with the predictor
function, b,
chat = Alb and b=1/Kj
6
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
[0028] This calibration approach will be called a single-wavelength single-
component prediction
model, as it requires the one component's (the analyte) spectral properties to
be calibrated at one
wavelength. This concept can also be extended to a multiple-wavelength single-
component
prediction model,
Chat = Avbv
[0029] Note that the predictor function (also called a regression vector) for
a single-component
model, bv, is simply a scaled version of the pure component signal of that
analyte and, as such, the
entire signal is used to predict analyte concentration.
[0030] Biological samples typically contain many constituents, which can
potentially interfere with
the single-component prediction functions described above. The constituents or
conditions that
interfere with analyte measurements will collectively be called interferences
or interfering species. In
some cases, the interference is a chemical component that absorbs at one or
more wavelengths
common to the absorbance of the analyte. In other cases, the interference is a
spectral change
resulting from changes in the sample environment, like temperature or pH. As
discussed above,
scattering can be viewed as an interferent it alters or modifies the measured
spectrum. In other cases,
the interference results from spectral artifacts due to component aging or
alignment changes in the
optical measurement system.
[0031] If uncorrected for, such interfering species degrade the measurement
performance of the
prediction function. Thus, the goal of multi-component calibrations is to
calculate a 'net-analyte'
spectrum that responds proportionally to analyte concentration but is
selective against interfering
species. As the name implies, a multi-component calibration requires both
analyte properties and the
interfering species properties to be adequately represented in the calibration
set in order to produce
an accurate prediction model.
[0032] A simple geometric presentation of a net analyte signal is shown in
Figure 2. In this
example the net analyte signal is the portion of the pure component signal
that is perpendicular (or
orthogonal) to the interfering species' signal. There are two classes of
linear models that estimate
such net analyte signals: forward calibrations and inverse calibrations. One
example of a forward
calibrations the Classical Least Squares (CLS) solution of the multi-component
Beer's law described
previously.
bv = KT(KKT)-'
[0033] where K is a matrix of pure component spectra. Solving this least-
squares solution
requires pure component spectra to be known for all absorbing components in
the calibration set.
[0034] In practice, the knowledge required to solve a CLS model can be
difficult to obtain for
biological samples due to their potentially large number of constituents. As a
result, many biological
measurements systems use another class of multi-component models called
inverse models.
7
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
Inverse models estimate the predictor function b from
b = (ATA)-'ATcõ
where c, is a vector of analyte concentrations.
[0035] Inverse models only require concentration values to be known for the
analyte of interest in
the calibration step. These reference concentrations are often available from
standard clinical
methods. For example, the glucose reference concentrations used in this
disclosure were measured
with an electrochemical method on a Yellow Springs Analyzer.
[0036] The class of inverse methods includes many specific computational
algorithms including
inverse least squares (ILS), multiple linear regression (MLR), partial-least
squares (PLS), principal
components regression (PCR), canonical correlation, ridge regression, and
Tikhonov regression.
Multivariate Calibration, Martens and Naes, Section 7.4 The PLS algorithm is
used to solve the
inverse multi-component models in this work, unless stated otherwise. The goal
of each of these
methods is to produce a regression vector for the multiple-wavelength
prediction model shown above.
While the prediction functions (regression vectors) produced by forward and
inverse models will look
similar for some chemical systems, the two approaches have different
optimization functions.
Forward models, like those defined in the CLS approach, find solutions with
spectral signals that best
represent true spectral shapes, in other words, CLS is an optimal estimator of
pure component
spectra. In contrast, inverse models, like those solved with the PLS approach,
find solutions for the
predictor function so its output best matches the reference concentrations, in
other words, solutions
that minimize prediction error. This is an important distinction, as the
predictor functions in a the
presence of path length changes can be very different from the predictor
function that are optimal for
a fixed pathiength measurement. For details see Brown C., Discordance between
Net Analyte Signal
Theoty and Practical Multivariate Calibration, Analytical Chemistry, Vol. 76,
No. 15, August 1,
2004.....
Sources of prediction error
[0037] The following discussion focuses on three general classes of prediction
errors:
measurement noise errors, selectivity errors, and proportional errors.
[0038] Measurement noise errors result from the propagation of random
instrument noise
through the prediction equation. Random instrument noise arises from a variety
of sources including
photon counting, dark current noise at the detector and Johnson noise across
electronic junctions.
While reduced by good instrument design and signal averaging, instrument noise
is never eliminated.
This noise reduces the precision of the concentration predictions. The
relationship between optical
signal variance and concentration estimate variance depends on the magnitude
of the net analyte
signal and the predictor function derived from it. Specifically, for a given
measurement error
magnitude the concentration variance is proportional to the Euclidean length,
(sqrt(v v)) of the
8
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
regression vector. Accordingly, the effects of measurement error noise are
smallest when the
maximum amount of the pure component signal is retained.
[0039] Selectivity errors as diagramed in Figure 3a result when the prediction
function (drawn as
a regression vector) is not completely selective for the analyte of interest.
In this case, concentration
changes of the interfering signal will influence the analyte prediction. This
influence can bias the
sample prediction away from the true analyte concentration in samples
containing interfering species.
Measuring the same sample repeatedly does not reduce such a bias. Note that
the sample can be
biased to over- or under-report the analyte concentration. The direction and
magnitude of the bias
depends on spectral differences between the analyte and interfering species
and the concentration of
the interfering species in a prediction sample relative to the average value
in the calibration set.
[0040] Although the effect of a selectivity error on individual sample
predictions is a constant
bias, the effect of selectivity errors across muitiple samples with variable
composition can appear
random, especially when plotted as analyte prediction versus true
concentration. A simple example of
this is shown in Figure 3b where variation in an interferent concentration can
cause the analyte
concentration to be over- or under- reported. In a controlled setting, the
effect of a single interfering
species would be clear if the prediction errors (predicted concentration minus
true concentration) were
plotted as a function of the interfering species concentration. In practice
the effect of selectivity error
can appear random, particularly if the model has selectivity errors for
multiple interfering species.
Selectivity errors can occur if the interfering species variation was not well
represented in the
calibration set or if the shape of the interfering species spectrum (and hence
its direction) is different
in a new sample as a result of distortions caused by changes in the path
length distribution.
[0041] Proportional errors occur when the magnitude of the regression vector
is incorrect. The
resulting errors are proportional to the analyte concentration as shown in
Figure 4. Unlike the
prediction error structure observed for selectivity in Figure 3, the predicted
concentrations lie on a line.
The nature of the proportional error is that this line differs from the line
of indentity. Note that the
optimal net analyte signal and estimated net analyte signal in this example
point in the same direction
but differ in magnitude. As such, if the optimal net analyte is orthogonal to
the interfering species then
the estimated net analytical signal will maintain the same selectivity. This
implies that the proportional
errors can be distinct from selectivity errors in their origin and observed
error structure.
Example of path changes that produce proportional errors
[0042] Figure 5 illustrates a hypothetical system where path length changes
are induced by
changing the physical dimensions of the cuvette. The effect of these path
length changes is equal for
all wave lengths of the spectrum. This system was mathematically constructed
with knowledge of the
pure component spectra of water, glucose, urea, and ethanol, which will be
components of tissue
phantoms discussed in the following sections. Figure 5a shows the spectral
effect of this path length
change on one sample. As would be expected from Beer's law, these spectra
differ only by a scalar
factor. For this example, the prediction function was calibrated using only
samples collected at the 1
9
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
mm path length. Figure 5b shows prediction results for the 1 mm prediction
function on a set of
validation samples, also collected with the a 1 mm path length. These
predictions lie along the line of
identity with little variation as the prediction function is optimal for these
data. In contrast, predcitions
from the 1 mm predictor function applied to samples with 0.8 and 1.2 mm path
lengths show clear
proportional errors. It is important to note that the change in path length
for each wavelength is the
same in this measurement system and this is not the behavior generally seen
when scattering and/or
absorbance changes in many of the biological systems where the path length is
a distribution.
[0043] Figure 6 shows a mathematical framework for assessing prediction errors
in a linear
prediction model that can be used to assign the origins of the three classes
of errors discussed in the
previous section: measurement noise errors, selectivity errors, and
proportional errors. The glucose
value estimated by applying the prediction function to a spectrum is equal to
the sum of the glucose
prediction values applied to each constituent of the sample as Beer's law
describes as linear additive
system. This framework is used in Figure 7 for the case of the 1.0 mm model
predicting 500 samples
measured in a 1.2 mm cuvette. Note that the proportional error in glucose
predictions is consistent
with that of a net analyte signal calibrated on a system on samples with a
shorter path length but that
this path length change in a nonscatteing sample does not increase selectivity
errors because
concentration variation in the two potential interferents (urea and ethanol)
have no significant effect on
the glucose prediction. Also note that measurement noise errors are not
significantly increased.
[0044] Given the proportional nature of these errors, it is reasonable to
apply a multiplicative
correction using methods described in the prior art section. In general, such
approaches assume that
path length is constant across small spectral regions or changes smoothly with
wavelength. These
methods are adequate because the correction does not need to adjust the model
to correct for a
selectivity error with respect to the ethanol or urea components.
A major limitation in biological samples is path length changes due to
scattering elements.
[0045] The cuvette example shown in Figure 1a and discussed in the previous
section is not an
accurate representation of path length changes that occur in measurements of
biological samples. In
these systems, the path length distribution results from scattering, which is
defined here to broadly
include interactions that change the direction of a light ray due to
interactions with inhomogeneties in
the sample including scattering structures described previously (such as cell
structures and collagen
fibers) as well as inhomogeneites from concentration gradients, temperature
gradients, and diffuse
reflecting surfaces (such as air-sample boundaries). Figures 1 b and 1 c show
how such scattering
events can change the direction of a light ray and influence its total path
length within the sample.
Many factors can change the scattering of a sample, including changes in the
number, size, and
geometry of scattering elements.
[0046] In blood samples, scattering changes occur due to hematocrit level
differences across a
population or changes within a single patient over time, due to factors like
dehydration or blood loss
during surgery. The shape of red blood cells can also change as a function of
blood pH and tonicity.
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
[0047] Noninvasive tissue measurements can also include significant scattering
variations due,
in part, to physiological variations in collagen-to-water ratios and collagen
fibril diameter changes as a
function of age and disease state. It should also be noted, that the very act
of placing skin on an
optical sampling element can change its scattering properties through
compression, tension,
temperature, and humidity changes.
[0048] Large scattering changes also occur during bioreactors run where cell
density can vary
over the course of a single run as cells multiply or are extracted.
[0049] Figure 8 shows examples of spectral variation observed in noninvasive
tissue
measurements, blood samples, and bioreactor runs. To further understand
problems of this nature, a
set of tissue phantoms was constructed with well-characterized variation in
absorbing and scattering
constituents. This set of tissue phantoms was then studied to test the effects
of changing path length
distributions through several mechanisms, including changes in scatter bead
concentration, absorber
concentration, and optical sampler configuration. These tissue phantoms
contained polystyrene
beads (0.298 m diameter sphere supplied by Bang's Beads) as scattering
elements with a two-fold
variation in concentration (4000 to 8000 mg/dL). These scattering beads were
suspended in 0.9%
saline solutions, phosphate buffered to physiological pH and warmed to a
physiological temperature
range (varied from 36 to 38 C) consistent with noninvasive tissue sampling.
The scattering bead
concentrations were clustered around nine discrete levels with steps of 500
mg/dL between 4000 and
8000 mg/dL of polystyrene. For convenience, these will be referred to a
scatter levels I to 9. Each
scattering level included samples with variable analyte and interference
concentrations. These
scattering samples also contained glucose, urea, and ethanol over a wide, but
physiologically
representative range. For example, the glucose range of 100 to 600 mg/dL
includes values observed
in diabetic subjects. These spectra were obtained by [Extract a description
and figure from the
Noncontact Sampler Patent].
[0050] Figure 9 includes results from a study that essentially repeats the
path length
investigation shown in Figure 5, now using tissue phantoms instead of variable
thickness cuvettes to
induce path changes. Figure 9a shows results of using prediction function
calibrated for glucose with
low-scattering samples (scatter levels 1-3) performs (versus reference glucose
concentration) on a
validation set with similar scattering levels. The slope of the glucose
predictions is close to unity and
the scatter around the line is consistent with the measurement noise errors
for this instrument. Panel
9d shows similar behavior for a prediction function calibrated for glucose
with high scattering samples
(scatter levels 7-9) and validated on samples with similar scattering levels.
[0051] Figures 9b and 9c illustrate prediction errors that occur when these
same prediction
functions are applied to validation samples with scattering characteristics
outside the calibrated range.
Although there are slope errors of about 3 and 7% respectively, the greatest
loss in overall
measurement performance results from prediction errors that scatter around
these lines. Given the
measurement noise and prediction functions are the same as those in Figures 9a
and 9d, errors of
11
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
this magnitude and character are more consistent with a selectivity error such
as those illustrated in
Figure 3b. Figures 10 and 11 illustrate similar behavior for the ethanol and
urea predictor functions
calibrated and validated in the same way. These examples illustrate a loss of
prediction performance
with for all three chemical constituents when a prediction function is used on
samples with different
path length distributions that differ from those used to calibrate the
predictor function. This behavior
was confirmed by measuring validation samples with both high and lower
concentrations of scattering
elements than samples included in the calibration.
[0052] The error structure seen in the scattering samples is in contrast to
that observed with the
non-scattering samples in Figure 5. The differences in the prediction errors
are due to the fact that
the change in path length is different at each wavelength. In fact the
observed pathiength is a function
of both scattering and absorbance. This pathiength change as a function of
wavelength has been
described as a distortion of the glucose signal. Both scattering and
absorbance are wavelength
dependence. The pathiength change between samples is a complicated vector
which changes with
every wavelength versus a simple scalar multiplier. The changes in pathlength
as a function of
wavelength effectively distort the glucose signal. This distortion creates a
slightly different PLD at
every wavelength which results in the observed glucose prediction errors. This
distortion can be
conceptualized as a variable degree of blurring across an image. Figure 12
illustrates the change in
scattering as a function of wavelength.
[0053] Returning to a more rigorous spectroscopic interpretation of the error,
Figure 13 illustrates
key geometric properties of glucose predictor functions (specifically the net
analyte signals calculated
with the PLS algorithm) of glucose estimated from high and low scattering
calibrations with an inverse
model. It is important to note that the optimal model for low scatter samples
is different than the
model for high scatter samples, with respect to the length of the regression
vector but also the
direction of the regression vector. This implies that a single regression
vector will under-perform a
regression vector optimized for a given path length distribution.
[0054] Figure 14 illustrates how scattering changes distorts not only the
analyte signal shape
(through a nontrivial rotation) but also the spectra of potential glucose
interferences, like urea and
ethanol. For example, the glucose model calibrated for low scattering samples
is orthogonal to the
spectral response of urea and ethanol in low scattering measurements, which is
consistent with the
measurement performance for these samples. This performance is not maintained
when these
chemical species are distorted by path length changes in a manner that reduces
the glucose model
selectivity by rotating or distorting the signals in a manner that induce
overlaps with the glucose
model. This is the origin of selectivity error with path length distribution
changes, the behavior of this
error is consistent with discussion of Figure 3. This is a key spectroscopic
insight into why path
variation in scattering media generates both proportional errors and /or
selectivity errors when the
path length distributions change in a complex manner as a function of wave
length. Samples that
exhibit these selectivity errors with path length distribution changes require
a new class of prediction
12
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
methods to maintain acceptable performance across samples that have scattering
and absorbance
changes.
New Approach to Pathlength Determination by Prediction Differences
[0055] As described above, path length distributions can be a complex function
of scatter,
absorbance and wavelength. The process of determining the effective PLD at
each wavelength with
information obtained from a single spectral observation (also called a single-
channel measurement)
on each sample is extremely difficult. In general, the problem is one where
the number of unknown
parameters exceeds the number of independent measurements.
[0056] To accurately determine analyte concentrations in material samples that
both scatter and
absorb light, additional information can be obtained by using an optical
system that acquires multiple
observations of the sample. These observations can differ in the subsets of
light rays they collect
from the sample. These subsets of light rays are collected by what are often
referred to a as multi-
channel samplers, or equivalently a multi-path samplers or equivalently as
multi-depth samplers.
These samplers have the capability of acquiring spectral data that have
differences in their PLDs .
These subsets of light rays are filtered out of the set of all rays exiting
the tissue through the use of
filters. In this discussion, filter has a broad definition that includes
optical filters that attenuate light
rays based on their linear or elliptical or circular polarization state. The
definition of filter also includes
spatial filters (also called masks or apertures) that attenuate rays based on
the physical location they
leave the sample such as described in US patent 5,935,062, Diffuse reflectance
monitoring
apparatus.. The definition of filter also includes and angular filters such as
the intrinsic acceptance
angle of a fiber optic, lens, or set of baffles that attenuate rays based on
the angle they leave the
sample. None, one, or combinations of these filters can be applied to each
measurement channel of
a multi-channel sampler.
[0057] Even with a multiple-channel measurement, determining the effect of
scattering on the
PLD and the prediction function can remain a complex calculation. A simple
approach for
determination of the relative pathlength is needed.
The approach disclosed below is based upon the fact that Beer's law:
A = elc
is unable to distinguish between path length changes and concentration
changes. This fundamental
characteristic of Beer's law can be exploited to characterize the scattering
characteristics of the
tissue. As discussed previous, historical approaches have sought to deduce the
path length properties
directly from the one or more spectral measurement. In contrast the analysis
framework disclosed
herein uses the net effect of the path length distribution changes on the
predicted analyte
concentration to characterize the sample.
[0058] In Figure 15, the problem is described in a pictorial representation.
Samples of scattering
media are represented in Figures 15a and 15b. Both boxes are filled with the
same glucose
13
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
concentration. In Figure 15a the light rays travel a more direct path due to
the fact that less scattering
occurs, resulting in an average path of 5. In Figure 15b the light rays
travels a much less direct path
due to the increase scattering and travels a average pathlength of 8. Thus, if
the same prediction
function is applied to both measurement channels, the glucose prediction for
the box in figure 15A will
be less than the prediction result for the box in figure 15B despite the fact
that both boxes are filled
with solution of the same glucose concentration. As the goal of the system is
to measure glucose, one
has the inability to determine if the boxes have different glucose
concentration or different path
lengths based upon the information and results generated by this single
observation system.
[0059] For description purposes and explanation of the key inventive concept,
consider the
boxes in Figure 16 to contain nails that are perpendicular to the plane of the
paper. If marbles or balls
were dropped in the top of these two boxes, the number of nails and resulting
bounces (which are
considered here to be a type of scattering) would influence the path traveled
and the resulting
distribution of balls in the collection bins. In the case of fewer nails, the
distribution is much more
center focused. As the number of nail bounces increase the distribution
becomes more dispersed
and the relative differences in the number of balls in adjacent bins is
reduced. Thus, by examination of
the number of balls in each bin or an examination of the ball distribution as
a function of bin location, a
relative measure of the effect of nail interactions can be determined. The
observed ball distribution
allows one to assess the density of nails in the box without looking in the
box.
[0060] Figure 17 illustrates the same information as Figure 16, but now
includes information
regarding the pathlength traveled by the balls as they travel from top to
bottom. Those balls that
effectively drop straight through will have the shortest pathlength, while
balls on the outer bins in a
case with lots of nail encounters will have the longest pathlength. Thus, if
one could obtain a measure
of pathlength at each bin location, like counting the number of balls in each
bin, a relative
determination of the number of nails within the box could be made (e.g.
scattering events).
[0061] Figure 18 returns to a spectroscopic illustration. The boxes are now
filled with scattering
media, the left box with fewer scattering centers then the right box. The
glucose concentration in each
box is the same. Light rays are launched into the media from a single light
source at the top of the
box and the light rays reaching the bottom of the box are recorded at two
sampler channels or
detectors. This is an example where different spatial filters are applied to
the two measurement
channels. As the light rays travel through the media they are scattered much
like the balls of the prior
example. As illustrated, the photons travel different distances based upon the
scattering
characteristics of the media. The relationship between the path lengths
traveled is heavily influenced
by the amount of scatter. For example, in the left side with more scatter, the
difference in pathiengths
traveled as observed by the two detectors is less than for the lower scatter
situation on the left side.
[0062] The spectral information recorded at each detector channel of this
multi-channel sampler
can be used to generate glucose prediction results. In this application, the
same predictor function is
applied to the signal or spectrum measured by each channel. The resulting
glucose predictions
effectively scale with the pathiength the photons have traveled and the actual
glucose concentration
14
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
of the media. As the objective of this process is to characterize the
scattering or pathlength of the
media, the contribution of the glucose concentration of the media needs to be
removed. The media
concentration of glucose can be effectively removed by examining the relative
difference between the
glucose predictions, an simple subtraction creates the relative difference.
Thus, the relative prediction
difference can be used to classify or characterize the media or tissue under
examination. As shown in
Figure 19, difference in the glucose prediction results for channel 1 and
channel 2 of the sampler can
be a diagnostic metric to characterize the scattering or pathlength
characteristics of the tissue sample.
This method is very powerful as it is a direct measure of the influence that
the media is imposing on
the prediction result. Stated differently, this analysis framework uses the
net effect of the path length
distribution changes on the predicted analyte concentration to characterize
the sample. In practice,
the analysis method determines the characterization of the media by
effectively using the same
system used for analyte measurement versus a secondary measurement system for
media
characterization. Specifically, the media characterization method uses the
same optical system,
similar processing methods, a similar predictor function, and similar level of
computational complexity.
The observation that relative differences in prediction results can be used
for media characterization
is extremely valuable and requires only an additional piece of spectral
information. This second piece
of spectral information should have a different functional dependence on the
scatering and absorbing
characteristic of the sample than the first piece of spectral information..
The fact that the media is
characterized by the relative difference in the prediction results removes any
requirements to know
the true glucose concentration of the sample.
[0063] The relative prediction difference method can be extended to other
analytes in the
sample. For example, alcohol diffuses throughout tissue and will be influenced
by changes in
pathiength. As alcohol absorbs differently than glucose, the influences of
path can be slightly different
than glucose but the basic concept that the measurement is sensitive to path
applies. Thus, the use
of relative prediction differences as a diagnostic function to characterize
the media can be extended to
multiple analytes in the sample. The use of diagnostics metrics from multiple
analytes increases the
information content available for tissue scattering characterization. Using an
image analogy, it
transitions the picture from black and white to color.
[0064] Figure 20 is a summary of the concept described above. Historically,
most noninvasive
glucose measurement systems have used a single source and detector. This
results in a single
spectra or singular piece of information and can be equated to a monocular
vision system with a
limited ability to determine pathiength. The expansion of the system to
multiple observation points
increases the information content and transitions the system to a binocular
system with the ability to
diagnose and characterize the effects of path length distribution changes that
result from variations in
absorbance and scattering across a set of samples. The extension of the
concept to include multiple
analytes adds an additional dimension to the information content and allows
for further tissue
characterization. In analogy terms, we think of the addition of multiple
analytes as adding color to a
black and white image, a dramatic increase in information content.
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
[0065] The discussion above describes a general framework where a prediction
function
optimized for a set of calibration samples is applied to measurements made on
a new sample
measured at two (or more) channels of a multi-channel sampler. The spectral
measurements made
at these channels differ in the subset of light rays collected from the
sample, such that the path length
distribution for these subsets of rays have different functional dependences
on the underlying
absorbance and scattering properties of the sample. Rather than deducing the
path length properties
directly from these multiple spectral measurement, this analysis framework
uses the net effect of the
path length distribution changes on the predicted analyte concentration to
characterize the sample.
Demonstration of Media Classification by Relative Prediction Difference
[0066] To demonstrate the above concept the tissue phantoms composed of
polystyrene beads
were sampled on a sampler with different source-detector separations. This
sampler is an example of
a multi-channel system that applies a spatial filter to light rays leaving the
sample. The four
measurement channels correspond to detector fibers spaced 300, 370, 460, and
625 m (center-to-
center) from the source fiber. A predictor function was developed using
spectral from all four source-
detector separations but only those samples have from scatter level 5. This
single predictor function
was then used to generate glucose prediction results on the remaining scatter
levels at two different
source detector separations (300 and 625 m). The difference between the
glucose predictions was
then calculated to generate a diagnostic metric for use in characterizing the
media. This diagnostic
metric was then plotted versus the scatter level of the sample upon which the
diagnostic metric was
calculated. Figure 21 demonstrates that the diagnostic metric enables the
identification of the correct
scatter level of the sample. In summary, the analysis framework using
predicted analyte concentration
differences does effectively enable characterization of the media.
Prediction function calibrated on a single-channel.
[0067] For comparison purposes the first method discussed applies single
channel calibration
and prediction process to a set of validation samples. The predictor function
was developed on
calibration samples from only a single channel of the multi-channel sampler
and glucose predictions
were generated on validation spectra acquired on the same channel as the
calibration spectra..
[0068] In this study the tissue phantoms were measured on multi-channel
sampler that uses up
to four rotational settings of a polarizing filter to define the measurement
channels. Figure 22a shows
the relationship between polarization angle and pathlength. Examination of the
data at a polarization
angle of 90 shows the degree of pathlength variation present in the samples.
Figure 22b shows a
histogram of the number of calibration samples used and their corresponding
scatter level.. The
scattering levels used were mid-scattering samples that includes scatter
levels 3 to 7.This calibration
and subsequent calibration models are developed in this manner to simulate the
expected
distributions of scattering levels in humans. Estimated path lengths observed
for these scattering
levels are reported by estimating the effective path length observed at the
absorbance peak centered
at 6900 cm"1 , which is a strong water absorbance feature. The effective path
length for this spectral
16
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
region is estimated by comparing its baseline-corrected absorbance to that of
the same peak in a I
mm cuvette of pure water. This crude metric is used for illustration purposes
and it is not used for
subsequent glucose predictions.,
[0069] In this first method the predictor function was calibrated,on a single
channel of spectral
measurements. In particular, all calibration spectra and validation spectra
were collected using a
polarizer angle of 90 degrees, which has the longest pathlength through the
scattering samples. The
glucose predictor function was calibrated with the PLS algorithms using near-
infrared spectral
absorbance between 4200 and 7200 cm"1.
[0070] Figure 23 shows characteristics of validation samples data in a similar
format to Figure
22. The validation set includes some samples at scatter level 5, which is at
the center of the
calibration set scattering levels as well as samples from scattering levels 3
and 6. The validation set
also included samples with scatter levels lower and higher then the
calibration samples, level 1, 2, 8
and 9. These samples were included to test prediction performance at the
limits, or outside the
scattering range included in the calibration set. Examination of Figure 23B at
a polarization angle of
90 shows the pathlength variation present in both the calibration samples and
validation samples.
[0071] Figure 24 compares predicted glucose values to their true
concentrations and presents
the standard error of prediction (SEP) at each scatter level. Consistent with
previous discussions,
measurement precision deteriorates when the calibration model is forced to
extrapolate beyond its
calibrated range of path length distributions. One average, the worst
predictions are observed for
scatter levels 1,2, 8 and 9. Thus, an object of the invention is to use the
ability to characterize the
media for the generation of more accurate glucose results.
Using the relative reference approach with a single prediction function to
classify new samples
[0072] In the first demonstration of the relative referencing concept will to
use the media
characterization capabilities in a classification framework. The application
of the concept applies a
single prediction function to samples collected on a multi-channel sampler to
classify new samples for
improved glucose predictions. At a high level, the steps are to build a single
prediction function on a
calibration set the includes and then to apply this prediction function to a
new sample observed on the
multi-channel sampler. This prediction function will produce a diagnostic
vector of predicted glucose
values for each channel of the sampler
dn =An,v bv
where dõ is an (number of channels by 1) diagnostic vector containing a
glucose prediction for each
sampler channel, An,,, is an absorbance matrix for a new sample (number of
channels by number of
wavelengths), and bõ is a prediction function (number of wavelengths by 1).
17
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
[0073] In one embodiment, the diagnostic vector for a new sample is used to
build a submodel
for this sample by selecting a subset of the calibration samples with similar
path length distributions.
In practice the steps are:
a. Measure the spectra of calibration samples on a multi-channel sampler with
n
channels.
b. Estimate a predictor function b,,,= (where the star indicates all channels
are used)
using an inverse model and a subset 'A' of the calibration set that includes
all or a
restricted range of path length variation and spectra acquired on two or more
channels of a multi-channel sampler.
c. Apply the prediction function b,,,= developed in Step (2) to the all
channels of all
calibration samples to produce a diagnostic vector for each calibration
sample.
d. Characterize the samples using one or more diagnostic metrics, m,
calculated from
the diagnostic vector. One example of a diagnostic metric, based on the
relative
reference approach is to subtract one element of the diagnostic vector from
another,
m=d, - d2
This diagnostic metric is equivalent to the relative referencing example in
Figure 21.
e. Save one or more diagnostic metrics for each calibration sample.
f. Measure a new sample on a multi-channel sampler and calculate its
diagnostic metric
or metrics
g. Select a subset'B' of calibration samples with similar diagnostic values to
the new
sample.
h. Estimate a predictor functions [bõ,, bv2, ... b,,,,] from subset'B' of
calibration samples
by building one model for each of, n, sampler channels.
i. Predict the new sample's concentration by applying predictor functions bõi,
bõ2, bv3,
and bõ4 the appropriate measurement channels of the new sample.
18
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
[0074] One example of this approach was applied the set of scattering tissue
phantoms
discussed previously. For step 1 of this example, the samples were measured on
a sampler with
different source -detector separations. This is a example of a multi-channel
sampler that applies a
spatial filter to light rays leaving the sample. The four measurement channels
correspond to detector
fibers spaced 300, 370, 460, and 625 m (center-to-center) from the source
fiber.
[0075] In step 2 the predictor function b,,,= was estimated with the PLS
algorithm applied to
spectra from all four channels of the sampler and the subset'A' included only
calibration samples
from scatter level 5. These absorbance spectra included all wavelengths (v)
between 4200 and 7200
cm"' in the near-infrared spectrum.
[0076] In step 3 the predictor function bv,. was used estimate glucose
concentrations for all
channels of the remaining calibration samples. This provided a four-element
diagnostic vector for all
sample in the full calibration set.
[0077] In step 4 the diagnostic metric was the difference between between
glucose
concentrations estimated with predictor function applied to spectra for the
shortest source-receiver
separation (element di of the diagnostic vector) and the longest source-
receiver separations (element
d4 of the diagnostic vector).
[0078] In step 5 the diagnostic vector or metric was saved for each
calibration sample.
[0079] Figure 21 illustrates the value of this diagnostic method applied to
tissue phantoms
across the entire range of scattering levels. This diagnostic metric alone can
accurately classify the
scattering of the tissue phantom into their nine respective levels.
[0080] In step 6 the diagnostic metric was calculate for validation samples
using the predictor
function bõ= calibrated in step 2.
[0081] In step 7 the calibration subset 'B' was selected by finding the 25
calibration samples with
the most similar diagnostic metrics.
[0082] In step 8 a set of predictor functions bõl, bV2, bV3, and bõ4 were
calibrated for each of the
four channels using calibration samples from subset 'B'.
[0083] In step 9 glucose concentrations estimate at each channel by applying
the channel-
specific prediction functions to the appropriate each model to the
corresponding channel of the new
sampler were averaged together.
[0084] Figure 25 shows that the predictive ability of a model built on samples
chosen with the
relative referencing approach described above a significantly better than
prediction results from a set
of randomly chosen samples.
19
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
[0085] While the example above uses a diagnostic vector of glucose
predictions, steps I to 6
could be repeated for other analytes, such that diagnostic vectors computed
with urea or ethanol
model could be concatenated to make a diagnostic vector with more elements.
For example a 12-
element diagnostic vector could be for these samples in step 3 by applying
three models (calibrated
for glucose, ethanol and, and urea) to spectra from each of the four channels
of the sampler.
[0086] Note that there are many possible diagnostics metrics that can be
calculated from the
diagnostic vector that can be applied in step 4 with mathematical combinations
of it elements. Note
there are similarity metrics other than the absolute value that can be applied
to a one or more
diagnostic metrics to find calibration samples that are similar to the new
sample. Examples
calculating the dot product between the two vectors, calculating a Mahalinobis
distance, and using the
k-nearest neighbors approach. For many more examples see Handbook of
Chemometrics and
Qualimetrics: Part B.
Using the relative reference metrics as a prediction model input.
[0087] In the previous section, the concept of relative referencing was used
in a classification
framework. Analyte prediction functions were applied to spectra collected on a
multi-channel sampler
to produce a diagnostic vector. In the next step, mathematical operations are
applied to this
diagnostic vector to produce one or more diagnostic metrics. These diagnostic
metrics are then
collectively used as a classification features to identify samples in the
calibration set which have
similar path length properties to the new sample.
[0088] Another related approach is to produce a diagnostic vector for a new
sample and then
use this vector alone, rather than an absorbance spectrum, as an input to a
second prediction model.
This two-model approach will be called the X-Y approach. The first step is to
build predictor functions
using X-models that calibrate the relationships between absorbance spectra
measured on each
channel of a multi-channel sample and the analyte. In this example, the X-
model step would provide
glucose prediction functions for each of the four channels of the polarizer
sampler, which will be
labeled as b,,,o , bv,50, bv,sa, and b,,,9o. Next, the diagnostic vector, d,
is generated by applying the four
prediction function to each of the four measurement channels to produce a 16-
element diagnostic
vector.
[0089] Figure 26 illustrates the framework for generating all 16 possible
predictions along with
the 16 sets of prediction that result from applying the prediction functions
calibrated on five middle
scattering levels to a set of samples containing all nine scattering levels.
Figure 27 shows that the
resulting glucose prediction errors are highly structured with respect to
scatter level.
[0090] The second step is to calibrate the Y-model, which uses the
interrelationship of the X-
model predictions to estimate an implicit correction for changes in the path
length distribution. The Y-
calibration uses diagnostic vectors from the X-model step for each calibration
sample as the data
matrix. In other words, a vector of prediction results for each sample
replaces the usual vector of
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
absorbance values for a sample in the calibration procedure. The relationship
between this data
matrix of estimated concentration (many of which are corrupted by changes in
the path length
distribution) and the true analyte concentration is established with a linear
regression to produce the
Y-model prediction function.
[0091] The determination of analyte concentration in a validation sample is
then estimated as a
two-step process. In the first step, the set (one for each sampler channel) of
X-model prediction
functions are applied, in all possible combinations, to the multi-channel
spectra to generate a
diagnostic vector of glucose predictions. In the second step, the Y-model
prediction function is
applied to this diagnostic vector to produce a single analyte prediction that
is corrected for distortions
due to changes in the sample's path length distributions. Figure 28 shows
results from an X-Y model
for glucose compared to the baseline case of a prediction function estimate
with PLS from one
channel of spectral data. The result of the X-Y model and the PLS model are
similar for scatter level
3 and 7, which are scatter level present in the calibration set. The X-Y model
has significantly better
measurement performance than PLS when applied to samples with scattering
properties outside the
calibrated space, such as scatter levels I and 9.
[0092] In this first example, all the X-models were calibrated for glucose.
This approach can also
be extended to include multiple analytes, such as adding urea and ethanol in
the first step (X-
models). The resulting diagnostic vector will then include concentration
values for more than one
analytes. The second step (Y-model) uses then uses predicted concentrations
for multiple analytes
as the input to a prediction function for a single analyte. For example, this
approach can use relative
reference error for glucose, urea, and ethanol to collectively predict glucose
in scattering samples.
The prediction results generated using the other analytes is shown in Figure
29.
[0093] The basic concept of creating diagnostic vectors from one modeling
process and using
the vectors as inputs into a second model has been disclosed above. The
implementation can take
many forms and a variety of calibration methods can be used to include neural
networks, non-linear
models, and other approximation and estimation techniques.
New Approach to Adaptive Model Selection using Prediction Differences
[0094] The adaptive modeling method is an attempt to overcome some general
limitations of
submodeling approach described previously or possible limitations associated
with the use of a
second prediction model as described in the previous section. A general
limitation of a sub-modeling
is it requires a set of samples that are reasonably similar to the new sample.
This approach can limit
the performance of a submodel for samples that require extrapolation beyond
the calibration set or
interpolation across sparse regions within the calibration set. As was shown
in Figure 24, these
samples are often the most difficult sample to predict.
[0095] The adaptive model approach starts with the assumption that the optimal
prediction
function for a sample with one path length distribution is not the optimal
model for another sample with
21
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
a different path length distribution, but the prediction functions share
similar attributes. Examination of
Figure 13 demonstrates that the general characteristics of these prediction
functions are similar but
that they have subtle differences as well. Furthermore, that the most
important model attributes for
interpolation or extrapolation can be derived by examining the set of valid
prediction functions (or
equivalently net analyte signals or regression vectors) rather than examining
the attributes of the raw
data from which they were constructed. In this construct, examination of
different prediction function
obtained from different media or media with different pathlength distributions
allows one to understand
the influence the media differences are imposing on the prediction function.
[0096] A practical application of this approach involves
a. Build a series of discrete calibrations submodels that include a single
channel and a
relatively narrow ranges of path length properties or scattering conditions.
For the
example data set, a model was built on each scattering level in the
calibration set
using samples from adjacent scattering levels if they were available. These
individual
models have limited performance due to the small number of samples in each
submodel but collectively they map the space of valid regression vectors for
this
system, or equivalently, locally-optimal net analyte signals. A sequence of
these local
models is shown in Figure 30.
b. The next step is to find a function that smoothly interpolates and
extrapolates the
geometric properties of these regression models. In the example shown, the
geometric properties of length and direction varied linearly with scatter
level. See
Figure 31. Thus a family of models can be created by progressively changing
the
contributions of the length vector and the direction vector contributions to
tune the
central model. In a more complex situation, a series of regression vectors can
be
decomposed through eigenvector decomposition such that differences in both
direction and length can be smoothly modeled.
[0097] The ability to progressively modify the predictor function allows the
estimation of predictor
function for samples with properties in between scatter levels. For example, a
prediction function
could be estimated for samples containing a scatter level between calibrated
scatter levels 3 and 4 by
equally weighting these two models. Similarly, a calibration function could be
estimated for samples
with higher or lower scattering level than the calibration set. The used of an
optimized model
minimizes the type of prediction errors seen in Figures 9, 10 and 11.
[0098] The next step is to select the optimal model for a set of validation
samples from this
larger, continuous family of models. An obvious metric would be to select the
most accurate model,
but this metric requires glucose reference values. A successful alternative is
constructed from the
knowledge that models mismatched to the scattering properties of the sample
result in degraded
prediction precision. Thus the correct family of models should produce similar
prediction values
across multiple observations. Using the approach of prediction consistency,
prediction values
generated from different channels can be compared. The prediction difference
between two such
22
CA 02597234 2007-08-08
WO 2006/086566 PCT/US2006/004608
models are minimized when the correct scattering model is applied. The process
of using prediction
consistency allows selection of the optimal predictor function by accounting
for the net effect of the
path length distribution of the media in which the measurement is being made.
This ability to select
the optimal model for a given media condition is critical as an optimized
model can out perform a
single un-optimized model. This approach is validated in Figure 32. The x-axis
is used to define the
data upon which the predictor function was generated. The y-axis is the
difference in the prediction
results at two channels. As shown in the figure, the sample being predicted
contains scatter
consistent with scatter level three. The predictor function developed from
media or a scattering level
most consistent with the media or scattering level of the validation sample
should generate the most
consistent prediction results, the lowest prediction difference and the most
accurate prediction.
Examination of the prediction differences demonstrates that the smallest
prediction differences are for
the predictor function generated from scatter level three calibration data.
Adjacent models have the
next lowest prediction differences while predictor functions developed from
dissimilar scatter levels
generate appreciable prediction differences. The results presented demonstrate
that the method does
enable one to select the best model for subsequent prediction. In practice the
two predictions are then
averaged together to estimate the analyte concentration. The performance of
the adaptive model
approach is summarized in Figure 33 for the validation data set. This approach
outperforms the PLS
calibration in terms of prediction accuracy and extrapolation abilities.
[0099] The method of determining the best prediction function by searching a
space of possible
prediction function with the subsequent select being driven by prediction
consistency across channels
can be implemented in many different methodologies. The above example should
simply be viewed
as one of many possible embodiments of this general method.
23