Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
1
MESURE DE PARAMETRES LIÉS A L'ÉCOULEMENT DE FLUIDES
DANS UN MATÉRIAU POREUX
[0001] La présente invention concerne la mesure de propriétés physiques
relatives à l'écoulement d'une phase fluide dans un matériau poreux.
[0002] Elle s'applique notamment aux matériaux présentant de très petits
diamètres de canaux d'écoulement à l'échelle du pore, c'est-à-dire aux
matériaux présentant une grande résistance à l'écoulement d'un fluide (inverse
de la perméabilité intrinsèque). Comme exemples non-limitatifs de ces
matériaux, on peut citer des roches des réservoirs de gaz ultra-compacts
("tight
gas reservoirs"), des roches de couvertures de sites potentiels de stockage,
des matériaux utilisés dans les dispositifs d'étanchéité, des matériaux
composites, etc.
[00031 L'écoulement d'un fluide à travers un milieu poreux dépend, à
l'échelle d'un bloc représentatif du matériau, de trois caractéristiques
physiques
intrinsèques au milieu qui sont :
- sa perméabilité liquide ou intrinsèque kl, exprimée en m2 ou plus
communément en D (darcy: 1 D = 0,987 x 10-12 m2) ;
- son coefficient de Klinkenberg b, exprimé en Pa, s'il s'agit d'un milieu peu
perméable et d'un écoulement de gaz à bas niveau de pression, ou son
coefficient de Forchheimer R, exprimé en m-1, aussi appelé facteur de
résistance inertiel, lorsqu'on s'intéresse à des niveaux de débits élevés
donnant lieu à des effets inertiels ;
- sa porosité ~, égale au rapport du volume des vides du matériau sur son
volume total.
[00041 Aucune méthode actuelle ne permet la détermination simultanée de
ces trois paramètres à l'aide d'une seule expérimentation. En particulier, la
porosité est souvent mesurée séparément des deux autres paramètres par une
méthode de pycnométrie (à l'hélium, au mercure, ...) ou de pesée.
[00051 Pour mesurer la perméabilité au gaz d'un matériau, on distingue des
méthodes en régime stationnaire et des méthodes en régime instationnaire.
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-2-
Voir par exemple J.A. Rushing et al., Klinkenberg-corrected permeability
measurements in tight gas sands: Steady-state versus unsteady-state
techniques, SPE 89867 1-11, 2004.
[0006 La méthode en régime stationnaire a pour inconvénient de requérir
un temps assez long avant d'obtenir le régime d'écoulement stationnaire pour
l'acquisition d'un point de mesure. Le temps au bout duquel ce régime
stationnaire est atteint varie avec l'inverse de k, et avec le carré de
l'épaisseur
de l'échantillon. Il atteint aisément plusieurs heures pour les très faibles
perméabilités. La détermination séparée de la perméabilité intrinsèque k, et
du
coefficient de Klinkenberg b nécessite plusieurs points de mesure et donc
l'obtention d'autant d'états stationnaires. Ceci peut devenir très long, de
sorte
que cette méthode est mal adaptée à la gamme des faibles perméabilités. Par
ailleurs, cette technique nécessite la mesure du débit de fluide, qui peut
s'avérer délicate lorsque la perméabilité est très faible.
[0007] Pour pallier ces inconvénients, une mesure en condition transitoire
est préférable. Typiquement, une expérience en condition instationnaire
consiste à enregistrer l'évolution de la pression différentielle AP(t) entre
les
extrémités de l'échantillon. Chaque extrémité de l'échantillon est connectée à
un réservoir respectif et l'une d'elles est initialement soumise à une
impulsion
de pression. Cette méthode est nommée "Pulse decay". Une variante où le
réservoir aval est de volume infini (atmosphère) est nommée "Draw down".
[00081 L'interprétation de AP(t) conduit à identifier la perméabilité du
milieu.
Fréquemment, la technique ne tient pas compte des effets Klinkenberg.
[0009] Dans le brevet US n 2 867 116, une méthode approchée a été
proposée pour déterminer expérimentalement la porosité, la perméabilité
apparente (c'est-à-dire incluant les effets Klinkenberg) et la perméabilité
intrinsèque. Dans ces travaux, kl, b et 4 sont déterminés de manière approchée
en réalisant trois fois la même expérience avec un rapport constant entre la
valeur de l'impulsion initiale de pression et la pression initiale de
l'échantillon.
La première expérience est conduite en relevant le temps de décroissance de
l'impulsion de pression jusqu'à une fraction donnée (par exemple 55%) de sa
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-3-
valeur initiale. La seconde expérience est identique à la première, mais
conduite en changeant simplement le niveau de pression de l'impulsion et la
pression initiale de l'échantillon de façon que l'écart entre eux soit le même
que
dans la première expérience. On relève encore le temps pour que l'impulsion
de pression ait diminué jusqu'à la même fraction (55%) de la valeur initiale.
La
troisième expérience est identique aux deux autres en modifiant le volume de
la chambre utilisée pour générer l'impulsion de pression. La détermination de
kl, b et ~ à partir de ces trois expériences est réalisée de manière approchée
en utilisant un abaque graphique et en exploitant un comportement linéaire
empirique. En fait, il est difficile d'estimer l'impact réel de ces
approximations
dans le cas général. En outre, on notera la difficulté expérimentale liée au
dispositif et au temps d'exécution nécessité par le conditionnement de
l'échantillon à des pressions différentes.
[0010] Dans "A method for the simultaneous determination of permeability
and porosity in low permeability cores", SPE 15379, 1-11, 1988, S.E. Haskett
et al. ont proposé une méthode de détermination de la perméabilité kl, les
effets Klinkenberg étant négligés, et de la porosité ~. La méthode nécessite
que l'expérience soit conduite jusqu'à l'équilibre final des pressions dans
les
réservoirs amont et aval. Elle repose sur la mesure au cours du temps de la
différence de pression entre les réservoirs amont et aval. Cette configuration
est peu précise et n'est pas optimale pour la détermination des paramètres.
[00111 Dans "A detailed analysis of permeability and Klinkenberg coefficient
estimation from unsteady-state pulse-decay or draw-down experiments", Symp.
Soc. Core Analysts, Calgary, 10-13 september, 5CA2007-08, 2007, Y. Jannot
et al. ont réexaminé la méthode "Pulse decay" sans hypothèses simplificatrices
particulières. Il a simplement été considéré que l'échantillon constitue une
matrice solide indéformable sous l'effet de l'écoulement du gaz de mesure, et
que l'écoulement du gaz est faiblement compressible, isotherme, rampant.
Dans ce contexte, le problème physique décrivant l'expérience de "Pulse
decay" dans le cas général s'exprime par:
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-4-
ax1(P+b)P] kP pour 0<x<e et t>0 (1)
avec les conditions initiales
P(0,0) = Poi (2)
P(x,0) = Pli pour x > 0 (3)
et les conditions aux limites :
kiS [P(0,t)+b]aP(0,t) = aP(0,t) (4)
V0 ax at
kiS [P(e,t)+b]aP(e,t)=-aP(e,t) (5)
Vl ax at
où : P est la pression à l'instant t et à la position x le long de
l'échantillon,
x = 0 correspondant à la face amont de l'échantillon, x = e à sa face
aval, l'impulsion de pression étant appliquée à t = 0 ;
S est la section de l'échantillon ;
e est la longueur de l'échantillon
V0 et V, sont respectivement les volumes du réservoir amont (haute
pression) et du réservoir aval (basse pression) communiquant avec
l'échantillon, où règnent initialement (à t = 0) des pressions respectives
PO et Pli;
est la viscosité dynamique du gaz, supposée constante.
[00121 En configuration "Draw down", la deuxième condition aux limites est
remplacée par une condition de Dirichlet classique : P(e,t) = Pl = Pli. On
suppose ici que l'échantillon est initialement à la pression ambiante avec
laquelle il est normalement à l'équilibre.
[00131 Un volume mort est nécessairement présent en amont de
l'échantillon, entre la vanne qui isole l'échantillon du réservoir amont et la
face
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-5-
amont de l'échantillon. Il est souhaitable d'avoir un volume V0 très petit
(idéalement de l'ordre du volume de pore dans l'échantillon) pour accroître la
sensibilité des mesures à la porosité ~, mais alors sa détermination précise,
pour prise en compte dans la condition (4), devient très délicate car elle
suppose de connaître alors le volume mort avec précision. L'existence de ce
volume mort a donc un impact important sur les valeurs estimées de k, et b. En
outre, l'ouverture de la vanne au moment où l'expérience de "Pulse decay"
débute produit une détente du fluide dans le volume mort qui provoque des
perturbations thermiques et hydrodynamiques observables mais dont il est
extrêmement difficile de rendre compte avec précision dans un modèle. Les
équations (1) à (5) ci-dessus n'intègrent pas ces effets thermiques et
hydrodynamiques.
[0014] Une erreur sur la valeur de la porosité 4 a un impact considérable
sur les valeurs estimées de la perméabilité k, et du coefficient de
Klinkenberg
b. Une estimation de qualité de ces deux paramètres requiert donc une
connaissance précise de 4 si cette quantité est fournie comme paramètre
d'entrée. Les techniques pycnométriques utilisées pour cela prennent du temps
et conduisent à une estimation de la porosité intrinsèque et non pas de la
porosité en contrainte (coefficient de stockage) généralement utile pour
l'analyse d'un matériau réel.
[0015] Il existe un besoin d'une méthode expérimentale permettant
d'améliorer l'estimation de la perméabilité k, et du coefficient de
Klinkenberg b
(pour les gammes de perméabilité faibles, remplacé par le coefficient de
Forchheimer pour les gammes de perméabilité fortes). Il est en outre
souhaitable de permettre d'estimer simultanément la porosité ~ à l'aide d'une
seule expérience.
[00161 Il est proposé un procédé d'estimation de paramètres physiques
d'un matériau, comprenant :
- placer un échantillon du matériau dans une cellule étanche de façon
qu'une face amont de l'échantillon communique avec un premier volume
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-6-
et qu'une face aval de l'échantillon communique avec un deuxième
volume;
- provoquer une modulation de pression dans le premier volume ;
- mesurer les variations au cours du temps de pressions respectives dans
le premier volume et dans le deuxième volume; et
- à l'aide d'une équation différentielle ayant pour paramètres la
perméabilité intrinsèque du matériau, la porosité du matériau et au moins
un autre coefficient propre au matériau et pour condition aux limites la
variation mesurée de la pression dans le premier volume, analyser
numériquement la variation mesurée de la pression dans le deuxième
volume pour estimer au moins la perméabilité intrinsèque et ledit autre
coefficient.
[00171 Pour pallier les difficultés liées au volume mort en amont de
l'échantillon, on ne considère plus la donnée initiale comme étant seulement
la
valeur d'une impulsion de pression P0i servant à simuler l'évolution de P(0,t)
pour effectuer l'inversion. Au contraire, on prévoit un réservoir de volume
fini
V1 du côté aval et on considère deux informations séparées toutes deux
mesurées: le signal de pression en amont P(0,t) = P0(t) et le signal de
pression
en aval P(1,t) = P1(t). Le signal P0(t) peut servir de signal d'entrée à
l'étape
d'analyse qui consiste en une inversion numérique d'équation différentielle,
effectuée sur le signal aval P1(t). Comme P0(t) n'est plus simulé, mais
mesuré,
il peut contenir des irrégularités liées à des événements thermiques, à
l'existence d'un volume mort, etc., sans que cela soit une source de
perturbation par rapport au modèle utilisé dans la procédure d'inversion.
[ooi8j L'autre coefficient propre au matériau estimé conjointement à sa
perméabilité intrinsèque k, est typiquement le coefficient de Klinkenberg b
lorsqu'on sait que le matériau étudié est dans une gamme basse de
perméabilité (inférieure à 10-16 m2 environ). Si la perméabilité est dans une
gamme plus élevée, l'autre coefficient peut être le coefficient de Forchheimer
R. Il peut exister une gamme de perméabilité où à la fois le coefficient de
Klinkenberg b et le coefficient de Forchheimer 0 sont susceptibles d'être pris
en
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-7-
compte dans le modèle.
[0019] Dans le cas où c'est le coefficient de Klinkenberg b qui est estimé
avec la perméabilité intrinsèque kl, l'étape d'analyse consiste en l'inversion
numérique de (1) effectuée sur le signal aval P1 (t). La condition à la limite
(4)
est remplacée par une condition de Dirichlet en pression P(0,t) = PO(t), où
PO(t)
est mesuré à l'aide d'un manomètre dans le premier volume VO. Le problème
physique ne dépend plus de VO, ni d'un volume mort qui n'a donc plus besoin
d'être connu.
[0020] La modulation de pression dans le premier volume n'est pas
appliquée de manière simplement instantanée, mais sur une échelle de temps
supérieure à celle d'une impulsion de pression. Elle l'est typiquement sur une
échelle de temps dépendant de la gamme de perméabilité du matériau mais
généralement supérieure à la minute. Cette modulation de pression dans le
premier volume peut notamment être provoquée par une succession
d'impulsions de pression.
[0021 Dans un mode de réalisation, l'analyse numérique des variations
des pressions mesurées comprend un suivi de l'évolution dans le temps de la
sensibilité réduite de la pression P1(t) mesurée dans le deuxième volume à la
perméabilité intrinsèque et de l'évolution dans le temps de la sensibilité
réduite
de P1(t) au coefficient de Klinkenberg ou de Forchheimer. Ceci permet de
vérifier que la modulation de pression a été appliquée dans le premier volume
de façon à ne pas laisser stabiliser le rapport entre ces deux sensibilités,
ce qui
ne permettrait pas d'estimer convenablement la perméabilité et le coefficient
en
question.
[0022] Dans un mode de réalisation préféré, l'analyse numérique des
variations des pressions mesurées PO(t), P1(t) est effectuée de façon à
estimer
la porosité 4 du matériau en plus de sa perméabilité intrinsèque k, et de son
coefficient de Klinkenberg b (ou de Forchheimer R).
[00231 Dans une expérience classique de type "Pulse decay", la sensibilité
de P1(t) à 4 devient rapidement constante, au bout d'un temps trop court pour
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-8-
que ce paramètre puisse être correctement estimé. Pour augmenter cette
sensibilité, il convient de multiplier les effets aux temps courts pour que
l'accumulation du fluide dans les pores du matériau se produise de manière
répétée sur la durée de l'expérience. Comme le procédé comprend une
mesure de PO(t) qui devient une donnée pour l'inversion effectuée sur P1(t),
toute variation de PO(t) imposée est possible. On génère donc une succession
d'impulsions de pression en amont de l'échantillon de manière à exciter le
comportement capacitif du système pour faciliter l'estimation de la porosité.
[00241 L'analyse numérique des variations des pressions mesurées peut
comprendre un suivi de l'évolution dans le temps de la sensibilité réduite de
la
pression P1(t) mesurée à la porosité. Ceci permet de vérifier que la
modulation
de pression a été appliquée dans le premier volume de façon à ne pas laisser
stabiliser cette sensibilité réduite à la porosité, ce qui ne permettrait pas
d'estimer convenablement la porosité ~.
[00251 Pour faciliter la convergence de l'estimation des paramètres, on peut
dans certains cas procéder à une pré-estimation de la perméabilité intrinsèque
k, et du coefficient de Klinkenberg b à l'aide des pressions mesurées dans des
intervalles de temps où la pression dans le deuxième volume varie
sensiblement linéairement.
[0026 Une réalisation avantageuse comporte alors un examen de
l'évolution dans le temps de la pression dans le deuxième volume. Lorsque cet
examen montre que la pression dans le deuxième volume varie de façon
sensiblement linéaire en fonction du temps, on laisse varier cette pression de
façon sensiblement linéaire pour acquérir des valeurs pour la pré-estimation
de
la perméabilité intrinsèque et du coefficient, puis on applique une nouvelle
impulsion de pression dans le premier volume.
[00271 D'autres particularités et avantages de la présente invention
apparaîtront dans la description ci-après d'un exemple de réalisation non
limitatif, en référence aux dessins annexés, dans lesquels :
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-9-
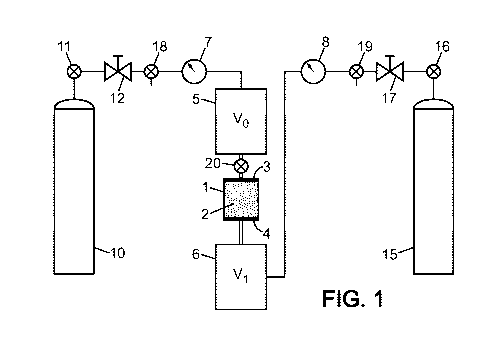
- la figure 1 est un schéma d'une installation utilisable pour mettre en
oeuvre un procédé d'estimation de paramètres physiques selon
l'invention ;
- la figure 2 est un graphique montrant des sensibilités réduites à la
perméabilité, au coefficient de Klinkenberg et à la porosité dans un
mode de réalisation du procédé ;
- la figure 3 est un graphique montrant l'évolution de la pression simulée
en aval de l'échantillon dans un exemple de mise en oeuvre du
procédé ;
- la figure 4 est un graphique montrant l'évolution des sensibilités
réduites à la perméabilité, au coefficient de Klinkenberg et à la porosité
dans l'exemple de la figure 3 ;
- la figure 5 est un graphique montrant l'évolution du rapport entre les
sensibilités réduites à la perméabilité et au coefficient de Klinkenberg
dans l'exemple de la figure 3 ;
- la figure 6 est un graphique montrant l'évolution du rapport entre les
sensibilités réduites à la perméabilité et à la porosité dans l'exemple de
la figure 3 ;
- les figures 7 à 10 sont des graphiques semblables à ceux des figures 3
à 6 dans un autre exemple de mise en oeuvre du procédé ;
- les figures 11 à 14 sont des graphiques semblables à ceux des figures
3 à 6 dans encore un autre exemple de mise en oeuvre du procédé ;
- les figures 15 et 16 sont des graphiques montrant l'évolution des
pressions simulées en amont et en aval de l'échantillon dans un cas de
test du procédé ;
- les figures 17 et 18 sont des graphiques montrant l'évolution des
pressions mesurées en amont et en aval de l'échantillon dans un essai
sur un échantillon de pin ;
- la figure 19 est un graphique montrant le résidu de pression en aval de
l'échantillon dans l'essai des figures 17 et 18, le résidu étant la
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-10-
différence entre la pression calculée par un modèle décrivant la
physique de l'essai et la pression mesurée lors de l'essai ;
- les figures 20 à 22 sont des graphiques semblables à ceux des figures
17 à 19 dans un premier essai sur un échantillon de roche ;
- les figures 23 à 25 sont des graphiques semblables à ceux des figures
17 à 19 dans un deuxième essai sur le même échantillon de roche ;
- les figures 26 à 28 sont des graphiques semblables à ceux des figures
17 à 19 dans un troisième essai sur le même échantillon de roche.
[00281 L'installation représentée sur la figure 1 comporte une cellule de
Hassler dans laquelle on place un échantillon 2 de matériau dont on cherche à
déterminer des paramètres physiques en présence d'un écoulement de fluide.
Sans que ceci soit limitatif, le fluide utilisé est un gaz tel que l'azote ou
l'hélium.
[0029] De façon connue, la cellule de Hassler se présente comme un
manchon dans lequel l'échantillon 2, de forme cylindrique de section S et de
longueur e, est enfermé de manière étanche afin de forcer l'écoulement du gaz
à travers la structure poreuse du matériau. L'échantillon 2 a une face amont 3
et une face aval 4 qui communiquent avec deux réservoirs 5, 6 dont les
volumes sont respectivement notés Vo et Vl.
[0030] Des manomètres 7, 8 permettent de mesurer les pressions régnant
dans les réservoirs 5, 6. Le gaz qu'on fait écouler à travers l'échantillon
provient d'une bouteille 10 reliée au volume amont Vo par l'intermédiaire
d'une
vanne 11 et d'un détendeur 12. Du côté aval, le volume V, est relié à une
bouteille de récupération 15 par l'intermédiaire d'une vanne 16 et d'un
détendeur 17. D'autres vannes 18, 19 sont prévues entre le détendeur 12 et le
volume amont Vo et entre le détendeur 17 et le volume aval V, pour faire
communiquer sélectivement les détendeurs avec les réservoirs 5, 6.
[0031) Une autre vanne 20 est placée entre le réservoir amont 5 et la
cellule de Hassler 1 afin de déclencher des impulsions de pression au niveau
de la face amont 3 de l'échantillon. Pour appliquer une première impulsion de
pression à l'échantillon 2, la vanne 19 est positionnée pour mettre le
réservoir
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-11-
aval 6 à une pression de départ Pl; (par exemple la pression atmosphérique)
alors que la vanne 20 est fermée. Une fois que l'équilibre de pression est
atteint, la vanne 19 est fermée. On ouvre les vannes 11, 18 et on règle le
détendeur 12 à la valeur de pression souhaitée pour l'impulsion. Le volume
amont Vo est ainsi rempli de gaz à la pression souhaitée. On ferme alors la
vanne 18 et on ouvre la vanne 20 afin d'appliquer l'impulsion de pression à
l'échantillon 2. A l'aide des manomètres 7 et 8, on observe alors la
décroissance de la pression dans le volume amont Vo et l'augmentation de
pression dans le volume aval Vl. L'évolution des pressions PO(t) et P1(t)
ainsi
mesurées est enregistrée afin d'être analysée numériquement. Pour appliquer
ultérieurement une autre impulsion de pression à l'échantillon 2, on règle le
détendeur 12 à la nouvelle valeur de pression souhaitée, on ouvre la vanne 18
pour remplir le volume Vo à la pression souhaitée, puis on la referme.
[0032] Avant l'application de la première impulsion de pression, la vanne 20
étant fermée, l'échantillon 2 est en équilibre avec le volume aval Vl, de
sorte
que la condition initiale (3) s'applique. Dans le cas où on peut négliger les
effets Forchheimer, le problème physique résolu numériquement pour
l'estimation des paramètres est alors le problème (1)-(3)-(4')-(5) suivant
ax i(P + b)aPi = k a- pour 0 < x < e et t>0 (1)
avec la condition initiale :
P(x,0) = Pl; pour x > 0 (3)
et les conditions aux limites :
P(0,t) = PO(t) pour t > 0 (4')
kIS [P(e,t)+b]aP(e,t)=-aP(e,t) (5)
Vl ax at
[00331 Dans l'expression de ce problème, la pression PO(t) en amont de
l'échantillon 2 est une donnée. Les paramètres physiques du matériau de
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-12-
l'échantillon 2 intervenant dans le système sont sa porosité ~, sa
perméabilité
intrinsèque kl, et son coefficient de Klinkenberg b.
[0034) La faisabilité de l'estimation de paramètres à partir d'un signal f(t)
peut être étudiée à l'aide d'une étude de sensibilité. Dans notre cas, on peut
par exemple s'intéresser au signal f(t) = P1(t). La sensibilité de f(t) à un
paramètre yr qu'on cherche à estimer est définie par a(t) . Pour des raisons
W
pratiques, on utilise plutôt la sensibilité réduite Ey, = yr f(t) , permettant
W
d'obtenir ces quantités en unités de pression. L'analyse de l'évolution de ces
quantités en fonction du temps permet un diagnostic sur la possibilité
d'estimer
le paramètre yr à partir du signal f(t). Cette estimation est possible si
- les variations de EY = yr f(t) sont significatives sur un intervalle de
W
temps suffisamment grand devant le pas d'échantillonnage temporel du
signal. Par significatives, on entend que E, est supérieure à la précision
de l'outil de mesure (capteurs de pression 7, 8) utilisé pour relever f(t) ;
- si plusieurs paramètres sont recherchés (par exemple kl, b, voire j), les
sensibilités réduites à tous ces paramètres doivent être décorrélées, ce
qui suppose qu'elles ne soient pas proportionnelles entre elles. Dans le
cas contraire, cela signifie que des variations observées sur f(t) ne
peuvent être indépendamment attribuables à l'un ou l'autre des
paramètres, rendant leur estimation simultanée impossible à partir d'un
seul signal f(t).
[0035] La figure 2 montre l'évolution dans le temps des sensibilités réduites
à la perméabilité kl, au coefficient de Klinkenberg b et à la porosité 4
calculées
dans le cas d'une seule impulsion de pression (type "Pulse decay") dans les
conditions suivantes : k, = 10-19 m2, b = 13,08 bar, 4 = 0,02, e = 5 cm,
diamètre
de l'échantillon d = 5 cm, Vo = 10-3 m3, V1 = 2,5.10-3 m3, avec une pression
initiale de 15 bar dans le volume amont Vo et de 1 bar dans le volume aval V1.
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-13-
Ces sensibilités ont été calculées à partir de signaux P1 (t) simulés à l'aide
du
modèle physique (1)-(3)-(4')-(5). On voit qu'au bout de quelques dizaines de
minutes, la sensibilité réduite E~ à la porosité se stabilise de sorte que
passé
ce délai, la mesure des pressions ne renseigne plus sur la valeur de la
porosité ~. Des mesures effectuées dans les conditions de la figure 2 peuvent
donc être insuffisantes pour déterminer la porosité ~. Néanmoins, elles
pourront être appropriées pour déterminer la perméabilité k, et le coefficient
de
Klinkenberg b si on connaît par ailleurs la valeur de la porosité ~. Ces
estimations de k, et b sont obtenues sans avoir à déterminer avec précision le
volume Vo et le volume mort associé du côté amont de l'échantillon 2, et en
s'affranchissant des irrégularités éventuelles sur PO(t) qui, étant mesurées,
n'ont plus besoin d'être calculées.
[0036 Pour augmenter la sensibilité à la porosité 4 et permettre son
estimation, il convient de multiplier les effets aux temps courts pour que
l'accumulation du gaz dans les pores du matériau se produise de manière
répétée sur toute la durée de l'expérience. Ceci est illustré ci-après à
l'aide de
trois exemples.
Exemple 1 (figures 3-6)
[00371 Dans cet Exemple, l'analyse de sensibilité a été conduite dans une
simulation sur un matériau de perméabilité intrinsèque k, = 10-17 m2, de
coefficient de Klinkenberg b = 2,49 bar, de porosité 4 = 0,02 sur une durée
d'expérimentation tf = 500 s. Trois impulsions de pression étaient appliquées
successivement, la première de 5 bar à t = 0, la seconde de 10 bar à t = tf/3
et
la troisième de 15 bar à t = 2tf/3. Le volume du réservoir amont 5 était
Vo = 10-3 m3 et celui du réservoir aval 6 était V, = 2,5.10-3 m3.
[00381 La figure 3 montre l'évolution dans le temps de la pression P1 (t) en
aval de l'échantillon. La figure 4 montre l'évolution dans le temps des
sensibilités réduites Eki, Yb et E~ de la pression P1 (t) à la perméabilité
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-14-
intrinsèque kl, au coefficient de Klinkenberg b et à la porosité ~. La figure
5
montre l'évolution dans le temps du rapport entre les sensibilités réduites
Eki,
Yb à la perméabilité intrinsèque k, et au coefficient de Klinkenberg b. La
figure 6
montre l'évolution dans le temps du rapport entre les sensibilités réduites
Eki,
E~ à la perméabilité intrinsèque k, et à la porosité
Exemple 2 (figures 7-10)
[00391 Dans cet Exemple, l'analyse de sensibilité a été conduite dans les
mêmes conditions que pour l'Exemple 1 sur un matériau de perméabilité
intrinsèque k, = 10-17 m2, de coefficient de Klinkenberg b = 2,49 bar, de
porosité 4 = 0,1 sur une durée d'expérimentation tf = 200 s. Les figures 7 à
10
sont des graphiques pour l'Exemple 2 semblables à ceux des figures 3 à 6.
Exemple 3 (figures 11-14)
[0040] Dans cet Exemple, l'analyse de sensibilité a été conduite dans les
mêmes conditions que pour les Exemples 1 et 2 sur un matériau de
perméabilité intrinsèque k, = 10-19 m2, de coefficient de Klinkenberg b =
13,08
bar, de porosité 4 = 0,02 sur une durée d'expérimentation tf = 13000 s. Les
figures 11 à 14 sont des graphiques pour l'Exemple 3 semblables à ceux des
figures 3 à 6.
[0041] Les trois Exemples montrent, sur trois matériaux différents, que les
remontées de pression P1(t) en aval de l'échantillon sont des quantités
mesurables même en ayant choisi un volume V1 relativement grand (2,5 litres).
Ce volume a été choisi exagérément grand pour bien souligner le fait qu'on
peut minimiser l'erreur relative sur sa mesure. Un choix de volume plus petit
conduit à des remontées plus significatives et on peut vérifier que les
sensibilités n'en sont pas affectées. Le choix d'un grand volume pour V1 n'est
pas motivé, comme dans la méthode "Draw down", par l'obtention d'une
grande variation de la pression moyenne au cours du temps. En effet, la
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-15-
variation de pression moyenne, très significative, est ici due aux impulsions
successives de pression.
[00421 Dans tous les cas, les sensibilités sont très significatives et bien
décorrélées deux à deux. Ceci permet une estimation simultanée des trois
paramètres kl, b et ~. On observe notamment, en comparant la figure 4, 8 ou
12 à la figure 2, que la modulation de la pression amont avec plusieurs
impulsions successives améliore nettement la sensibilité à la porosité
facilitant ainsi son estimation.
[0043] Pour illustrer la capacité du procédé à permettre l'estimation
simultanée des trois paramètres kl, b et ~, une série de tests a été effectuée
à
partir de signaux générés numériquement à l'aide du modèle physique, avec
Po; = 1 bar. Un bruit aléatoire donné par 6P0 = 0,01 x dP x s x Pomax/3 et
6P, = 0,01 x dP x s x P1max/3 a été superposé aux deux signaux simulés Po(t)
et P1 (t) de manière à mieux représenter une mesure réelle. Ces bruits sont
tels
que s est un nombre aléatoire d'écart type unité et dP est l'erreur sur Po(t)
et
P1 (t) (en % de la mesure). Le coefficient 3 a été pris de sorte que les
intervalles Po(t) 6P0 et P1(t) 6P, incluent 99,7% des valeurs si elles
avaient
été effectivement mesurées. Dans ces simulations, on a pris dP = 0,1%, ce qui
est une valeur typique d'un capteur de pression, sauf pour les cas 14, 15 et
16
pour lesquels on a pris dP = 1%.
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-16-
Cas ki b Vo V1 Poi dP N tf M
nO (m2) (bar) (%) (m3) (m3) (bar) (%) (s)
1 10-17 2,49 0,02 10-5 10-2 3 0,1 1000 1000 200
2 10-17 2,49 0,02 10-2 10-2 3 0,1 1000 1000 200
3 10-17 2,49 0,02 10-5 10-2 3 0,1 100 1000 200
4 10-17 2,49 0,02 10-5 10-2 3 0,1 1000 300 200
10-17 2,49 0,02 10-5 10-2 3 0,1 1000 1000 50
6 10-17 2,49 0,1 10-5 10-2 3 0,1 1000 1000 200
7 10-17 13,08 0,02 10-5 10-2 3 0,1 1000 100000 200
8 10-17 2,49 0,02 10-2 10-4 3 0,1 1000 1000 200
9 10-17 2,49 0,1 10-2 10-4 3 0,1 1000 1000 200
10-19 13,08 0,02 10-2 10-4 3 0,1 1000 10000 200
11 10-19 13,08 0,02 10-2 10-4 5 0,1 1000 10000 200
12 10-17 2,49 0,02 10-2 10-4 3 1 1000 1000 200
13 10-17 2,49 0,1 10-2 10-4 3 1 1000 1000 200
14 10-19 13,08 0,02 10-2 10-4 5 1 1000 10000 200
Tableau I
[00441 Les paramètres employés dans la série de test sont ceux indiqués
au Tableau I, y compris le nombre N de points de mesure des pressions Po(t)
et P1 (t), la durée tf de l'expérimentation et le nombre M de pas de
discrétisation
5 en espace sur l'épaisseur e de l'échantillon utilisés pour l'inversion du
problème
(1)-(3)-(4')-(5). Dans chaque cas, trois impulsions de pression amenant la
pression dans le réservoir amont à Poi, 2P0i et 3P0i étaient appliquées aux
instants 0, tf/3 et 2tf/3. La modulation de pression adoptée dans cette série
de
tests permet de qualifier la méthode de mesure dans ce cas de "Step Decay".
10 Les figures 15 et 16 montrent l'évolution des pressions Po(t) et P1 (t) en
bar
synthétisées en amont et en aval de l'échantillon dans le cas n 1.
[0045] Les résultats des inversions sont présentés dans le Tableau 11, avec
les écarts dki, db, d~ en % entre les valeurs de départ de ki, b et 4 et les
valeurs retrouvées par les calculs d'inversion.
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-17-
Cas k, dkI b db d~
nO (m2) (%) (bar) (%) (%) (%)
1 1,007.10-17 0,10 2,456 0,26 1,96 0,28
2 1,003.10-17 0,11 2,469 0,34 1,97 0,50
3 1,067.10-17 0,61 2,159 1,70 1,60 2,00
4 1,005.10-17 0,09 2,460 0,31 1,98 0,21
1,006.10-17 0,10 2,460 0,26 1,97 0,28
6 1,007.10-17 0,09 2,454 0,28 9,93 0,18
7 1,030.10-19 0,31 12,55 0,44 1,96 0,25
8 1,004.10-17 0,11 2,460 0,35 1,95 0,53
9 1,002.10-17 0,08 2,472 0,38 9,95 0,38
1,027.10-19 0,21 12,58 0,47 1,96 0,30
11 1,007.10-19 0,21 13,08 0,37 2,00 0,30
12 1,001.10-17 1,07 2,49 3,47 2,06 5,11
13 1,003.10-17 0,81 2,42 3,85 9,67 3,81
14 1,088.10-19 1,81 11,24 3,37 1,78 2,99
Tableau II
[OO461 Ces résultats amènent les conclusions suivantes :
- la précision des estimations est excellente (souvent meilleure que 1 %)
pour les trois paramètres estimés et reste tout à fait acceptable avec un
5 bruit de mesure de 1 % de la valeur maximale de la pression (cas n 12 à
14).
- la précision dépend peu du volume VO. Un volume de 0,1 à 10 litres, de
préférence de 0,1 à 1 litre, convient très bien ;
- le volume V1 doit être choisi pour que la remontée en pression soit
10 suffisante pour pouvoir être mesurée avec une bonne précision. Une
valeur de 0,1 litre conduit à des résultats satisfaisants dans le cas des
matériaux étudiés et est suffisamment élevée pour limiter l'erreur due au
volume mort à l'aval. Un volume V1 de 0,05 à 10 litres pourra
généralement être retenu ;
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-18-
- travailler à des niveaux de pressions supérieurs (5, 10 et 15 bar) conduit
à une meilleure précision dans le cas où b = 13,08 bar ;
- un nombre de points expérimentaux de 1000 semble adéquat, la
précision baissant quelque peu si on diminue ce nombre à 100 (cas n 3).
- l'allongement de la durée de l'expérience au-delà d'une certaine limite
n'améliore pas significativement la précision (comparaison des cas n 7
et 10).
- des durées de mesure acceptables pour l'estimation des trois paramètres
sont 20 minutes pour k, autour de 10-17 m2 et 3 heures pour k, autour de
10-19 m2. Il convient généralement d'appliquer la modulation de pression
dans le premier volume sur une échelle de temps de quelques dizaines
de minutes à quelques heures, et en tous cas supérieure à la minute. On
observera que la modulation de pression par une succession
d'impulsions est un cas particulier et que d'autres formes de modulation
sur une échelle de temps suffisante peuvent convenir pour la mise en
oeuvre de l'invention étant donné que le profil de pression en amont PO(t),
qui est mesuré, peut avoir une forme quelconque.
[00471 Un volume Vo relativement grand a pour avantage que la pression
PO(t) varie faiblement entre deux impulsions. Par ailleurs, si le volume V1
est
choisi suffisamment grand pour que la remontée de pression soit peu
significative devant P0, alors l'expérience se déroule en condition faiblement
instationnaire (quasi-stationnaire). Dans ces conditions, une pré-estimation
de
bonne qualité peut-être effectuée par simple régression linéaire sur les
portions
de P1(t) correspondant à chaque impulsion de pression. Cette pré-estimation
de bonne qualité permet d'assurer une convergence plus facile de l'estimation
sur l'intégralité du signal avec le modèle complet.
[00481 Une automatisation du déroulement de l'expérience peut être
utilisée. En effet, l'apparition d'un régime linéaire ou quasi-linéaire sur
P1(t)
pour chaque pulse de pression (figure 16) correspond à un régime quasi-
stationnaire avec perte de sensibilité de P1(t) à la porosité 4 (par
définition, en
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-19-
régime quasi-stationnaire, l'effet d'accumulation dans les pores de
l'échantillon
disparaît). L'expérience peut donc être conduite de telle sorte que chaque
impulsion de pression ait une durée permettant à P1 (t) d'atteindre un
comportement quasi-linéaire en fonction du temps. On laisse alors durer ce
régime quasi-linéaire sur une courte période permettant de procéder à une
bonne pré-estimation de ki et b. L'utilisation de volumes Vo et V,
suffisamment
grands permet ainsi un pilotage direct de l'expérience afin d'en optimiser la
durée tout en obtenant des résultats bien convergés.
[0049] Des essais de laboratoire ont été réalisés avec Vo = 1,02.10-3 m3 et
V, = 2,26.10-3 m3 et avec le protocole expérimental suivant :
- mise en place de l'échantillon 2 dans la cellule Hassler 1 ;
- mise sous pression de la chambre extérieure de la cellule Hassler ;
- fermeture de la vanne 20 et attente de l'équilibre ;
- ouverture de la vanne 18 et réglage du détendeur 12 pour obtenir
Po = Poil ;
- démarrage de l'enregistrement des pressions Po(t) et P1 (t) ;
- fermeture de la vanne 18 et ouverture de la vanne 20 ;
- réglage du détendeur 12 pour obtenir Po = Poil ;
- après un temps tl, ouverture de la vanne 18 pendant quelques secondes
- réglage du détendeur 12 pour obtenir Po = Poi3 ;
- après un temps t2, ouverture de la vanne 18 pendant quelques
secondes;
- après un temps t3, arrêt de l'enregistrement, ouverture de la vanne 19 et
démontage de l'échantillon 2.
[00501 Pour certains de ces essais, il a été procédé à une pré-estimation de
la perméabilité ki et du coefficient de Klinkenberg b de la façon suivante :
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-20-
- estimer les pentes des trois parties des courbes P1(t), assimilées à des
droites, correspondant aux impulsions de pression successives ;
- en déduire trois valeurs de la perméabilité apparente kg. On utilise pour
ces calculs des valeurs de Po et P1 égales à la demi-somme des valeurs
aux extrémités de chaque intervalle ;
- tracer les valeurs de kg en fonction de 1/Pmoy = 2/(PO+P1) et par
régression linéaire, obtenir classiquement une pré-estimation de k, et de
b, sachant que kg = kl.(1+b/Pmoy)
[00511 Ces valeurs pré-estimées de k, et b sont ensuite utilisées comme
valeurs de départ pour l'estimation finale de kl, b et 4 par inversion sur le
signal
complet P1(t), le signal P0(t) étant une donnée d'entrée, en utilisant le
modèle
physique (1)-(3)-(4')-(5).
Exemple 4 (figures 17-19)
[00521 Deux essais ont été réalisés suivant le protocole expérimental ci-
dessus sur un échantillon de bois de pin sec dont les caractéristiques
dimensionnelles sont d = 38,5 mm et e = 60 mm. La porosité (hors contraintes)
de l'échantillon a été mesurée par pycnométrie comme étant de 4 = 0,27.
[0O531 Dans le deuxième essai, la perméabilité k, et le coefficient de
Klinkenberg b étaient pré-estimés à 1,76.10-16 m2 et à 0,099 bar. Les
résultats
finaux de l'estimation sont indiqués au Tableau III, avec les écarts types
relatifs
6kl, 6b et 6~ sur les trois paramètres estimés simultanément.
Essai k, GkI b 6b
no (m2) (%) (bar) (%) (%)
1 1,64.10-16 0,045 0,230 0,98 0,257 0,38
2 1,70.10-16 0,038 0,187 1,14 0,252 0,39
Tableau III
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
[00541 Les évolutions des pressions mesurées P0(t) en bar et
OP1 (t) = P1 (t)-P,(0) en millibar sont représentées sur les figures 17-18. La
figure 19 montre le résidu sur P1 (t), en millibar, après estimation. Les
estimations sont d'excellente qualité comme en attestent les courbes P1 (t)
mesurée et estimée et surtout la courbe de résidu, et comme le confirment les
faibles écarts types relatifs 6k,' 6b, 6~.
Exemple 5 (figures 20-28)
[0055] Trois essais ont été réalisés suivant le protocole expérimental ci-
dessus sur une carotte de roche dont les caractéristiques dimensionnelles sont
d = 38 mm, e = 60,3 mm. La porosité (hors contraintes) de la carotte a été
mesurée par pycnométrie comme étant de 4 = 0,06.
[0056] La perméabilité k, et du coefficient de Klinkenberg b étaient pré-
estimés à 3,34.10-17 m2 et à 1,47 bar dans le deuxième essai et à 3,86.10-17
m2 et à 0,97 bar dans le troisième essai. Les résultats finaux de l'estimation
sont indiqués au Tableau IV.
Essai k, 6kl b 6b
n0 (m2) (%) (bar) (%) (%)
1 3,41.10-17 0,058 1,57 0,18 0,055 0,23
2 3,51.10-17 0,023 1,41 0,11 0,055 0,28
3 3,77.10-17 0,052 1,16 0,41 0,048 1,13
Tableau IV
[00571 Les évolutions des pressions mesurées P0(t) en bar et
AP1(t) = Pl(t)-P,(0) en millibar sont représentées sur les figures 20-21 pour
le
premier essai, sur les figures 23-24 pour le deuxième essai et sur les figures
26-27 pour le troisième essai. Les résidus sur P1 (t) après estimation, en
millibar, sont indiqués sur la figure 22 pour le premier essai, sur la figure
25
pour le deuxième essai et sur la figure 28 pour le troisième essai. Là aussi,
les
CA 02787771 2012-07-20
WO 2011/089367 PCT/FR2011/050123
-22-
estimations sont d'excellente qualité comme en attestent les courbes P1 (t)
mesurées et estimées et les courbes de résidus, et comme le confirment les
faibles écarts types relatifs 6k,' 6b, 6~.