PROCEDE ET DISPOSITIF POUR DETERMINER LA POSITION RELATIVE ENTRE DEUX RECEPTEURS ET UTILISATION DU DISPOSITIF POUR STABILISER DES CHARGES OSCILLANTES

METHOD AND APPARATUS FOR DETERMINING THE RELATIVE POSITION BETWEEN TWO RECEIVERS AND USE OF THE APPARATUS FOR STABILIZING SUSPENDED LOADS

Abrégé français

L'invention concerne un procédé et un dispositif pour déterminer les positions relatives entre deux récepteurs (10, 11) pour la navigation par satellites. Avec le procédé et le dispositif, des mesures de phase sur des signaux porteurs (3) d'un système de navigation par satellites (1) sont effectuées par les récepteurs (10, 11). La position relative des récepteurs (10, 11) est déterminée sur la base des mesures de code et de phase par une unité d'évaluation (14) en ce sens que les ambiguïtés de phase entières et le vecteur de distance (15) décrivant la position relative sont déterminés. À cette fin, l'unité d'évaluation (14) optimise une fonction d'évaluation qui contient, outre une première mesure pour évaluer les ambiguïtés de phase entières, une deuxième mesure par laquelle l'écart du vecteur de distance (15) décrivant la position relative et associé aux ambiguïtés de phase entières par rapport à un vecteur de distance de longueur déterminée est déterminé.

Abrégé anglais

The invention proposes a method and an apparatus for
determining the relative positions between two receivers
(10, 11) for satellite navigation. In the case of the
method and the apparatus, phase measurements are carried
out on carrier signals (3) of a satellite navigation system
(1) by the receivers (10, 11). An evaluation unit (14)
determines the relative position of the receivers (10, 11)
using the code and phase measurements by determining the
integer phase ambiguities and the distance vector (15)
which describes the relative position. For this purpose,
the evaluation unit (14) optimizes an evaluation function
which, in addition to a first measure for evaluating the
integer phase ambiguities, comprises a second measure which
is used to determine the difference between the distance
vector (15), which describes the relative position and is
assigned to the integer phase ambiguities, and a distance
vector of a predetermined length.

Revendications

29
Claims:
1. Method for determining the relative position between
two receivers (10, 11) for satellite navigation, in which
phase measurements on carrier signals (4) of a satellite
navigation system (1) are performed by the receivers (10,
11), and in which the relative position of the receivers
(10, 11) is determined by an evaluation unit (14) on the
basis of the phase measurements,
characterized in that
- integer phase ambiguities and a distance vector (15)
describing the relative position are determined by the
evaluation unit (14), by
- minimizing an evaluation function, which comprises
besides a first measure for evaluating the consistency of
the integer phase ambiguities with the phase measurements, a
second measure, that determines the deviation of the
distance vector (15), which describes the relative position
and is associated with the integer phase ambiguity, from a
distance vector of predetermined length.
2. Method according to claim 1,
- in which the real-valued phase ambiguities are initially
determined and then the integer phase ambiguities and the
first distance vector (15) describing the relative position
is determined by optimizing the evaluation function,
- in which the first measure for evaluating the integer
phase ambiguities comprises a norm, that determines the
deviation of the real-valued phase ambiguities from the
integer phase ambiguities, and
- in which the second measure comprises a norm, which
determines the deviation of the distance vector describing
the relative position and associated with the integer phase
ambiguities from the distance vector of predetermined
length.

30
3. Method according to claim 2,
- in which the distance vector of predetermined length is
determined by searching the one distance vector, which has a
predetermined length and the smallest distance to the
distance vector describing the relative position and
associated with the integer phase ambiguities, by means of a
search evaluation function.
4. Method according to claim 3,
in which the search evaluation function is a Lagrange
function.
5. Method according to claim 4,
in which the evaluation function is given by:
<IMG>
and in which the search evaluation function is given by:
<IMG>
with:
N: the vector of the integer phase ambiguities, for which
the evaluation function is optimized,
.xi..lambda.(N): the searched distance vector,
N: the vector of the estimated real-valued phase
ambiguities,
.xi.(N): the distance vector estimated on the basis of N
i: the previously known length of the searched distance
vector (15),
.lambda. : the Lagrange factor and
.SIGMA.: the respective covariance matrixes.
6. Method according to claim 1,

31
- in which the first measure for evaluating the integer
phase ambiguities comprises a norm that determines the
deviation of calculated phase values, which have been
calculated based on integer phase ambiguities and the
distance vector, from measured phase values, which have been
detected by code and phase measurements, and
- in which the second measure determines the deviation of a
norm of the distance vector from a predetermined length.
7. Method according to claim 6,
in which the first measure is connected to the second
measure by a coupling parameter that adjusts the influence
of the second measure on the determination of the integer
phase ambiguities and of the distance vector.
8. Method according to claim 7,
in which the evaluation function is given by:
<IMG>
with:
N: the vector of the integer phase ambiguities, for which
the evaluation function is optimized,
.xi.: the searched distance vector,
.PSI.: the vector of the measured values
H: the geometry matrix
A: the wavelength matrix,
µ : the coupling factor
l: the predetermined length of the searched distance
vector (15) and
.SIGMA.:the respective covariance matrix.
9. Method according to any one of claims 1 to 8,
in which the evaluation function is repeatedly evaluated for
various integer phase ambiguities.
10. Method according to claim 9,

32
in which the phase ambiguities to be evaluated are searched
by means of a search tree, whose branches correspond to
series of phase ambiguities and in which search tree
branches with a phase ambiguity or a length of the distance
vector beyond probability limits are excluded.
11. Method according to claim 10,
in which the probability limits are determined by the error
norm of the estimation of the real-valued phase ambiguities,
and in which a branch of the search tree is only prosecuted,
if the difference between the estimated length of the
distance vector (15) and its previously known value is
smaller than the standard deviation of the length estimation
of the distance vector (15) multiplied by a factor.
12. Method according to any one of claims 1 to 11,
in which at least one linear combination of phase
measurements is used, and in which the phase ambiguities of
the linear combination and the distance vector are searched
by evaluating the evaluation function.
13. Method according to claim 12,
in which the wavelength of the phase measurements is
increased by at least one geometry preserving linear
combination.
14. Method according to claim 13,
in which the ratio of the wavelength to the standard
deviation of the noise of the linear combination is
maximized by the at least one geometry preserving linear
combination.
15. Method according to any one of claims 12 to 14,
in which the linear combination includes code measurements.
16. Apparatus for determining a relative position between
at least two user devices comprising:

33
- at least two receivers (10, 11) which are disposed at a
distance and which perform code and phase measurements on
navigation signals, which the receivers (10, 11) receive
from satellites (2) of a satellite navigation system (1),
and
- an evaluation unit (14), which can determine a distance
vector (15) between the receivers (10, 11) on the basis of
the code and phase measurements,
characterized in that
the receivers (10, 11) and the evaluation unit (14) are
arranged for performing the method according to any one of
claims 1 to 15.
17. Use of the apparatus according to claim 16,
characterized in that
the distance vector determined by the apparatus is used as
an actual value for a control unit (15) for stabilizing a
suspended load (7), which is provided with one of both
receivers (10) and which is held by a carrier apparatus (6),
which is provided with the other one of both receivers (11).
18. Use according to claim 17,
in which the carrier apparatus (6) is a cargo helicopter or
a cargo crane.

Description

CA 02814882 2013-04-16
1
METHOD AND APPARATUS FOR DETERMINING THE RELATIVE POSITION
BETWEEN TWO RECEIVERS AND USE OF THE APPARATUS FOR
STABILIZING SUSPENDED LOADS
Description:
The invention relates to a method for determining the
relative position between two receivers for satellite
navigation, in which phase measurements on carrier signals
of the satellite navigation system are performed by the
receivers and in which the relative position of the
receivers is determined by an evaluation unit using code
and phase measurements.
The invention further relates to an apparatus for
determining the relative position between two receivers as
well as the use of the apparatus for stabilizing suspended
loads.
A method for determining the relative position between two
receivers is known from the publication GIORGI G.,
TEUNISSEN P., VERHAGEN S.: Reducing the Time-To-Fix for
Stand-Alone Single Frequency GNSS Attitude Determination,
Proc. of Intern. Techn. Meeting of the Inst. of Navigation
(ION-ITM), San Diego, January 2010. Determining a distance
vector describing the relative position between two
receivers basically comes down to solving a minimization
problem in the framework of a least square method. The
solution for the distance vector shall be found under the
constraint that the length of the distance vector has a
predetermined value. In the known method, the distance
vector is presented in polar coordinates. This, however,
results in strong non-linearities with respect to the
angles of the polar coordinates, that are overcome by
separating the distance vector in an initial estimate and
in a variation, which scales linearly with the angles.

CA 02814882 2013-04-16
2
Thus, the system of equations, which is non-linear with
respect to the angles of the polar coordinates, can be
linearized and be solved by conventional methods.
One drawback of the known method is that the linearization
can only be performed if the initial distance vector can be
determined with sufficient accuracy. That is the case, if
the length of the distance vector is significantly bigger
than the error on the initial absolute determination of the
positions of both receivers. If the distance vector has a
length greater 100 meters, that is usually the case.
TEUNISSEN, P.: Least-squares estimation of the integer
ambiguities, Invited lecture, Section IV, Theory and
Methodology, IAG General Meeting, Beijing, China, 1993
describes various methods for resolving phase ambiguities.
TEUNISSEN, P.: The least-squares ambiguity decorrelation
adjustment: a method for fast GPS ambiguity estimation, J.
of Geodesy, volume 70, pages 65-82, 1995 describes a
decorrelation method for resolving phase ambiguities.
HENKEL, P.: Bootstrapping with Multi-Frequency Mixed Code
Carrier Linear Combinations and Partial Integer
Decorrelation in the Presence of Biases, Proc. of the IAG
Scient. Assembly, Buenos Aires, Argentina, September 2009
studies code and phase combinations for improving the
resolution of phase ambiguities.
From EP 1 972 959 Al, various methods for resolving phase
ambiguities of linear combinations of carrier signals of a
satellite navigation system are known.
From WO 2009/125011, a method is further known for tracking
phases of a plurality of carrier signals.

CA 02814882 2013-04-16
3
Proceeding from this related prior art, the invention is
based on the object to provide an improved method for
determining the relative position between two receivers of
a satellite navigation system.
This object is achieved by an apparatus having the features
of the independent claim. Advantageous embodiments and
refinements are specified in claims dependent thereon.
In the method, the evaluation unit determines the integer
phase ambiguities and the distance vector describing the
relative position by minimizing an evaluation function,
which, in addition to a first measure for evaluating the
consistency of the integer phase ambiguities with the phase
measurements, comprises a second measure, which determines
the deviation of the distance vector, which describes the
relative position and is associated with the integer phase
ambiguities and whose length is not predetermined, from a
distance vector of a predetermined length. The method thus
determines the one distance vector, which, on the one hand,
corresponds as well as possible with known previous
knowledge, and which, on the other hand, is associated with
phase ambiguities, which are as much as possible consistent
with phase measurements. By such a method, the relative
position of both receivers can also be determined, if the
error on the determination of the absolute position of the
receivers is not negligible in view of the distance between
the receivers.
In one embodiment of the method, the real-valued phase
ambiguities are determined first and then the integer phase
ambiguities and the distance vector describing the relative
position, are determined by optimizing the evaluation
function. The first measure of the evaluation function
includes a norm, which can be used for determining the
variation of the real-valued phase ambiguities from the

CA 02814882 2013-04-16
4
integer phase ambiguities. The second measure further
includes a norm, which can be used for determining the
deviation of the distance vector, that is associated with
the integer phase ambiguities and whose length is not
predetermined, from the distance vector of predetermined
length. The method is therefore used for searching for the
one distance vector, whose associated integer valued phase
ambiguities is as close to the real-valued phase
ambiguities as possible and that coincides with the
predetermined distance vector as precisely as possible.
The method allows to determine the distance vector
accurately even without a precise previous knowledge on the
direction of the distance vector.
The accuracy in determining the distance vector can be
further enhanced, if it is additionally required that the
distance vector to be determined must have a previously
known length. This may be achieved, for instance, by using
a search evaluation function and searching for the one
distance vector, that comprises a predetermined length and
has the smallest distance to the distance vector, which is
associated with the integer phase ambiguities and whose
length is not predetermined. In this two-step method, the
real-valued phase ambiguities are initially estimated in a
first method step, and candidates for the integer phase
ambiguities are searched, which are within the error limits
of the real-valued phase ambiguities. In a second method
step, the distance vector to a selected candidate for the
integer phase ambiguities is determined, and a further
distance vector of previously known length is searched
such, that, using the search evaluation function, the one
distance vector is searched, that comprises the
predetermined length and the smallest distance to the
distance vector, which is associated with the integer phase
ambiguities and which has no predetermined length. As soon
as the searched distance vector has converged to a

CA 02814882 2013-04-16
particular distance vector, the evaluation function can be
evaluated. The second method step is repeated for all
candidates of the integer phase ambiguities. Among all
candidates for the integer phase ambiguities, the one
5 vector of the integer phase ambiguities is chosen as an
optimum, that minimizes the evaluation function together
with the associated distance vector.
The search evaluation function can be a Lagrange function,
that enforces a given length of the distance vector
associated with the integer phase ambiguities.
In an alternative embodiment of the method, the first
measure for evaluating the integer phase ambiguities
comprises a norm, by which a deviation of the measured code
and phase values from calculated code and phase values is
determined. The calculated code and phase values have been
calculated by means of the integer phase ambiguities and
the distance vector. The measured code and phase values,
however, have been detected in the control circuits of the
receiver (phase lock loop, delay lock loop) during the code
and phase measurements. In the modified embodiment of the
method, the second measure of the evaluation function
further comprises a deviation of a norm of the distance
vector from a predetermined length. The relative position
of both receivers can also be determined with high accuracy
using this method, even if the errors on the determination
of the absolute position of the receivers were not be
negligible in view of the distance.
If in the modified embodiment the first measure is
connected to the second measure by a coupling parameter, by
which the influence of the second measurement on the
determination of the integer phase ambiguities and the
distance can be adjusted, the predetermined length does not
need to be known exactly in advance.

CA 02814882 2013-04-16
6
In optimizing the evaluation function, advantageously,
various integer phase ambiguities are subsequently applied
to the evaluation function. The integer phase ambiguities
can then be selected by means of a search tree, whose
branches correspond to series of various phase ambiguities
and in which search tree branches with a phase ambiguity or
a length of the distance vector beyond error limits are
excluded.
The precision of the method can further be improved, if
linear combinations of the phase measurements are formed
and if phase ambiguities thereof are searched.
For further improving the accuracy, the ratio of the
wavelength to a standard deviation of the noise of the
linear combination is maximized by the geometry preserving
linear combination.
Additionally, it is also possible to combine the phase
measurements with code measurements for increasing the
wavelength of the linear combination of the phase
measurements and for thereby enhancing the reliability of
the estimates.
The method can be performed using an apparatus, that
comprises at least two receivers, which perform code and
phase measurements on navigation signals, and that is
provided with an evaluation unit, by which a distance
vector between the receivers can be determined. The
evaluation unit is thereby arranged for performing the
method.
Such an apparatus can be used for providing an actual value
for controlling a stabilization of a suspended load that is
provided with one of both receivers and that is held by a

CA 02814882 2013-04-16
7
carrier apparatus which is provided with the other one of
both receivers. In particular suspended loads , that are
held by a cargo helicopter or a cargo crane, can thereby be
stabilized.
Further advantages and properties of the present invention
are disclosed in the following description, in which
embodiments of the present invention are explained in
detail based on the drawing:
Figure 1 is a presentation of an apparatus for stabilizing
a suspended load;
Figure 2 shows a flow diagram of a method for determining
the relative position of two receivers of a
satellite navigation system;
Figure 3 shows a flow diagram of a further method for
determining the relative position of two
receivers of a satellite navigation system;
Figure 4 is a presentation of a search tree for selecting
integer phase ambiguities;
Figure 5 is a diagram, in which the probability for a
wrong resolution of the phase ambiguities for
various methods is depicted over several epochs;
Figure 6 is a diagram, in which the probability for a
wrong resolution of the phase ambiguities is
depicted over the length of the distance vector
for various methods; and
Figure 7 is a diagram, that shows the probability for a
wrong resolution of the phase ambiguities in case
of a multipath propagation.

CA 02814882 2013-04-16
8
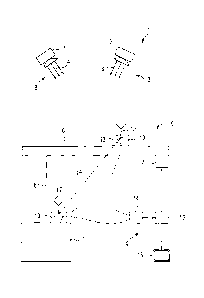
Figure 1 shows a satellite navigation system 1, that
comprises a number of satellites 2, that are situated in an
Earth's orbit. The satellites 2 emit navigation signals 3,
which are modulated on carrier signals 4. The carrier
signals 4 comprise in particular various wavelengths. By
linear combination of the carrier signals 4, various error
sources, like ionospheric errors, tropospheric errors or
instrumental errors, or other error sources can be
eliminated. The satellite navigation system 1 can be one
of the known conventional satellite navigation systems as
GPS, Galileo, Glonass, COMPASS, or any future satellite
navigation system.
Figure 1 further shows a load transport system 5, that
comprises an load carrier 6. The load carrier 6, for
instance, can be a crane, in particular a boom of a crane,
or a cargo helicopter. The load carrier 6 can be used for
transporting load 7, that are attached to the load carrier
6 by means of a holding cable 8 attached to the load
carrier 6. A problem associated with the transport of such
suspended load 7 is that oscillations of the load 7 can be
caused by side winds or by the motion of the load carrier
6. Thereby the placement of the load 7 can become
difficult. The load transport system 5 is therefore
provided with a load stabilization 9. The load
stabilization 9 comprises a first receiver 10 attached to
the load carrier 6 as well as a further receiver 11
attached to the load 7 or to the holding cable 8. The
receivers 10 and 11 are respectively provided with antennas
12 for the receiving navigation signals 3. The receivers
10 and 11 can further include a signal processing unit 13.
The signal processing unit 13 processes the navigation
signals 3 received by the antennas 12. This results in so
called code and phase measurements, whose measured values
are transferred to an evaluation unit 14 in a wire-bound or

CA 02814882 2013-04-16
9
wireless way. Using the phase measurements or using the
code and phase measurements, the evaluation unit 14
particularly calculates a distance vector 15 that
represents the relative position of both receivers 10 and
11. A control unit 16, that is provided with the distance
vector 15, can generate a control signal for a drive 17
based on the distance vector 15 and further actual values.
The control signal is used for moving the load carrier 6 in
a manner which diminishes the oscillation of the load 7 and
thereby stabilizes the load 7. In addition, it is
conceivable to present the actual relative position of the
load 7 and load carrier 6 on a monitor 18. The
presentation on a monitor 18 can also be used to control
the load carrier 6 manually instead of controlling the
drive 17 by the control unit 16, or to intervene manually
if there is a threatening danger.
In the embodiment shown in Figure 1, the receiver 10 is
shifted with respect to receiver 11 in a lateral direction.
In practice, it will though be advantageous to attach the
receiver 11 to the load carrier 6 in the region of the
location, in which the holding cable 8 is attached to the
load carrier 6 for facilitating the determination of the
length / of the distance vector 15. If the load carrier 6
is a cargo helicopter, the length / of the distance vector
15 will be about equal to the length of the holding cable
8. In a cargo crane, the length of the holding cable 8 and
therefore the length of the distance vector 15 can be
determined by using a revolution counter at the drum of the
holding cable 8.
For determining the distance vector 15 with sufficient
accuracy, among other things the phases of the carrier
signals 4 must be processed. The phases of the carrier
signals 4 may, however, be affected by phase ambiguities.
In principle, it is possible to determine the phase

CA 02814882 2013-04-16
ambiguities by a method such as the so called LAMBDA (=
Least-Squares Ambiguity Decorrelation Adjustment) method
that is described in the publication by TEUNISSEN cited in
the beginning. The short wavelength of the carrier signal
5 4, that is typically in the range of 19 cm, impedes a
reliable determination of the integer phase ambiguities due
to multipath propagation as well as unknown instrumental
errors in the order of magnitude of several centimeters.
10 For improving the resolution of the phase ambiguities,
previous knowledge on the length or the direction of the
distance vector 15 can be used.
The vector W of the code and phase measurements can be
written as:
= gd-ANd-b+ (1)
With the measurements IF, the geometry matrix H, the
unknown distance vector (= baseline), the wavelength
matrix di, the unknown integer phase ambiguities IV, the
unknown system errors b (= biases) and with the white
Gaussian measurement noise n11), wherein I is the
correlation matrix for the individual measurements. The
problem, to find the integer phase ambiguities PJ under the
constraint, that the associated distance vector comprises
the known length /, can be solved by a method of least
squares:
min ¨ H ¨ AN112-1 9 e R3, N E ZK with =1 (2)
wherein 1: is the number of integer phase ambiguities to be
determined, and thus equal to the number of carrier signals
4 multiplied by the number of satellites 2, from which the
receivers 10 and 11 receive satellite signals 4.

CA 02814882 2013-04-16
11
In the publication of GIORGI ET AL., cited in the
beginning, it was proposed to linearize the distance
vector. It was in particular proposed, to express the
distance vector in spherical coordinates:
cos(a)cos(0)
a
V-y) = 1 cos(a) sin(/3) with 7 = [ 0 1
sin(a) ( 3 )
Thereby, the problem of minimizing the least squares under
a constraint is transformed into a conventional problem of
minimizing the least squares without constraint:
min II* ¨ HV-y)¨ AN11_1, 7 E R2, NE ZK
-y,N (4)
But this problem is to a high degree non-linear.
Therefore, it was proposed to linearize the distance vector
around an initial estimate (,0):
(-Y)= ("70) C(70)A7 (5)
with
70 = [ao, Oor ( 6 )
and the Jacobi matrix
_
¨ sin(a0) cos(00) ¨ cos(ao) sin(00) -
Ceyo) = 1 = ¨ sin(a0) sin()30) cos(a0) cos(00)
cos(ao) 0
_ _ ( 7 )
The linearization results in a conventional problem of
least squares:

CA 02814882 2013-04-16
12
min ¨ HC(-yo)A-y ¨ e R2, N E ZK
^y,N
(8)
with
(9)
Thus, the non-linearity was eliminated by a linearization
with regard to a particular distance vector (/0).
The linearization of the distance vector requires a precise
initial estimation of the direction of the distance vector,
so that the angles of ao and ,30 can be fixed. The initial
estimation is generally sufficiently precise, if the
distance vector has a length greater 100 meters. In
connection with the positioning of loads 7 by load carriers
6 the distances are considerably smaller, since the length
of the holding cables 8 are significantly below 100 meters.
Therefore a linearization of the distance vector 15 is not
possible in the present case.
In addition, the length of the distance vector 15 may vary.
The holding cable 8 may be stretched for instance,
depending on the weight of the load 7.
In the following, two methods for resolving the phase
ambiguities are described, which need no linearization of
the distance vector 15.
A. Resolution of the Phase Ambiguities with Strong
Constraints
The conventional real-valued estimation N and an
estimation of (-1\7) can be used for formulating the problem
of minimizing the least squares as follows:

CA 02814882 2013-04-16
13
2 2
min N - N + min (N)-(N)
(10)
(N) )
Thus, the one integer phase ambiguities Nand the one
distance vector &Iõ are searched, which minimizes the
evaluation function, which is given in brackets in formula
(10).
The real-valued ambiguities are obtained by an orthogonal
projection of the measurements T on the space of II:
H
PIT=PIAN+P B+P/7 with 11HI H .1_ 7"7" =ki
(11)
A
An estimation according to the least square method then
results in a real-valued estimation of the phase
ambiguities:
1sT = (ATE-1A)-1ATE-141
(12)
Similarly the distance vector 7-) is obtained by an
estimation according to the least square method:
4-(N) = (HT E-1 H)_i HT E-1H(41 - AN)
(13)
The second term of the evaluation function which has to be
minimized according to expression (10) can also be
presented as Lagrange function with the Lagrange parameter
A:
2
2
30f(2) = (N)- +2( (N) _12)
(14)
EE-0v)
The minimization of PA) with respect to 42(V) results in
an estimation for the distance vector 15 as a function of

CA 02814882 2013-04-16
14
the Lagrange parameter A and the integer phase ambiguities
N:
2(N) = (N) (N)E71 ¨ 21) E-' (N)
(15)
(
This estimation of the distance vector of length / can be
introduced in the constraint for the distance:
,
(N) E7.1 _21)-1 ETI (N) ( 2 N) _12 = 0
(16)
¶.5
The unknown in equation (16) are the Lagrange parameter A
and the integer phase ambiguities N. This equation must
be resolved for the Lagrange parameter, which cannot be
done by an analytic expression. However, by using a
multidimensional Gauss-Newton-method, equation (16), can
efficiently be solved.
For each candidate of the integer vector of the phase
ambiguities N the Lagrange parameter A is determined
iteratively:
An+i = + J-1(2,75 N) = f (2õ)
(17)
with the Jacobi matrix:
N)=af(2,N)
(18)
aA,
and the Lagrange function:
2
fRoNM= (N) (N)E71 _21) E71 (N) -12
( n
(19)

CA 02814882 2013-04-16
The initial value for / is chosen to be 0. The iterative
calculation of 2 is performed as long as the value of 2 has
converged.
5 Figure 2 illustrates the flow of the method: In a first
step, the phase measurements 19 are performed on the
carrier signals 2. In parallel, the code measurements 20
can also be performed. By a linear combination 21,
combination signals can be formed from the phase measured
10 values and code measured values obtained from the phase
measurements 19 and code measurements 20. The combination
signals can also be formed by the phase measurements only.
For this combination signals an estimation 22 according to
equation (12) is performed for the phase ambiguities Ar,
15 which results in real-valued phase ambiguities N. As a
next step, a limitation 23 of the considered integer phase
ambiguities is made depending on an integrity factor K,
and a number of candidates /V is determined for the
integer phase ambiguities Pion the basis of the real-
valued phase ambiguities. A method that can be used for
the limitation 23 is described in more details in the
following. Among all considered integer phase ambiguities
a particular integer phase ambiguity is selected by a
selection 24. By a further estimation 25 according to
equation (13), the distance vector (N) is estimated for
the selected integer phase ambiguities. Afterwards an
iterative calculation 26 of A according to formulas (17) to
(19) is performed. After 2 has been converged, a
calculation 27 of 42(V) according to formula (15) is
carried out. An evaluation 28 of the evaluation function
according to formula (10) will follow. If the evaluation
function has not yet been evaluated for all candidates /V,
a candidate for the integer phase ambiguities is again
selected by the selection 25, and the subsequent method
steps are repeated until the calculation 28 of the
evaluation function. When the calculation 28 has been

CA 02814882 2013-04-16
16
performed for all candidates Ar for the integer phase
ambiguities, the one vector AT of the integer phase
ambiguities, for which the evaluation function according to
formula (10) yields the smallest value, can be selected by
_
a final selection 29. The associated distance vector 2(N)
can then be provided to the control unit 15 as an actual
value.
B. Resolving the Phase Ambiguities with Weak Constraints
In this method, the distance vector 15 need not necessarily
have the length L This is achieved in the evaluation
function by coupling the corresponding constraint only
weakly with the coupling parameter P.
In the present case, the evaluation function can be written
as:
2
J ( , N) = tli - IR ANIL, + ,u = ( _l)2 (20)
In this evaluation function, the first term represents the
weighted sum of squared errors (SSE) and the second term
represents the difference between the length of the
distance vector and a previously known length 1 of the
distance vector 15. The parameter A depends on the
reliability of the previous knowledge. A big value for A
indicates that the length value / is considered as
reliable, whereas a low value for A indicates, that the
length value 1 is considered as erroneous. There is an
essential difference between the coupling parameter A and
the Lagrange parameter A of the preceding method. In the
preceding method the Lagrange parameter A was calculated
iteratively for minimizing the evaluation function. The
coupling parameter A, however, is a priori set to express
the strength of the constraint. In the preceding method,

CA 02814882 2013-04-16
17
the found distance vector comprises exactly the length 1,
wherein in the present method the found distance vector may
have a length, which deviates from the length value 1.
The derivation of the evaluation function with respect to
the distance vector results in:
aJ
¨ = -2HT E-1(T - AN)+2HT 1-11R + ,u-1101 2( 4:1 - (21)
a4=
This equation cannot be solved for the distance vector in
closed form. The solution, however, can be found
iteratively using the Newton method of the steepest
gradient:
j2 OJ
n-F1 = C't a^2
(22)
with the second derivation of the evaluation function:
\\
a j2 gT
=2HTE-1H+2p= (23)
4a2,
As an initial value the estimation for according to
equation (13) can be used.
The flow of the method is illustrated in Figure 3: The
method starts with the same method steps as the method
illustrated in Figure 2. After the selection 25 an
iterative solution 30 of equation (21) is performed,
wherein the distance vector i(A) estimated in the
estimation 23 is used as initial value. The remaining
method steps correspond again to the method steps of the
method illustrated in Figure 2 with the exception that a

CA 02814882 2013-04-16
18
depending on the coupling parameter p is calculated
instead of a A depending on A.
C. Limitation of the Integer Phase Ambiguities
In the methods illustrated in Figures 2 and 3, before the
selection 24 of the integer phase ambiguities, the
limitation 23 is performed, which is described in detail in
the following.
The search for candidates for the integer phase ambiguities
aims at finding an integer candidate vector /V which
fulfils the condition:
= iS7112
.67 (24)
In practice the search space is limited by a given value:
11N¨ Ar112-1 < X2
E ¨
icr (25)
wherein X2 can be chosen to be equal to the error norm of
the sequential solution without constraints. Thus, it is
possible, to limit the search for candidates for the
integer phase ambiguities.
As described in the publications of TEUNISSEN mentioned in
the beginning, the error norm can also be expressed by
estimations for the integer errors as:
(Ni
11N - S r 11 - 1 = 2
N11 i-i (28)
with

CA 02814882 2013-04-16
19
k-1
= -1\4 Ea ¨-2
(g=11 = 1 ¨ [1Cr=l1 = 1])
j=1 (29)
and
k-1
2
cr,c,0_2 _ \--"` c-
k-1 iST'k NN1
j=1 (30)
wherein H in equation (29) refers to a truncation to the
nearest integer value.
The squared sum of the conditioned errors is now
transformed, wherein one term is kept on the left side and
the remaining terms are transferred to the right side.
This results in:
i-1 (N/ / 1)2 (Ni ¨ / 1)2
¨
< X2 E __________________________________________________
2 ____________________________________ 2 2
1=1 /=1+1
i-1 ( 2
N1 Ars /11,.. / 1
< X2 ¨
1=,
(31)
what enables an sequential search for the integer phase
ambiguities. The set of candidates for each integer phase
ambiguity Ni is therefore given by:
i-1 (N/ / 1 2
Cig x2
1=1 (32)
what provides a lower and an upper limit for Thus, a
sequential search tree for all components of the vector of

CA 02814882 2013-04-16
integer phase ambiguities having a error norm smaller than
2 can be constructed. The efficiency of the search can
further be improved by checking the length of the distance
vector in each branch of the search tree. A branch of the
5 search tree is only prosecuted, if the difference between
the estimated length of the distance vector 15 and its
previously known value is smaller than the standard
deviation of the length estimation of the distance vector
multiplied by an integrity factor K:
HIE(Nmi)11-11 5-- = C111411
(33)
with the estimation for the length of the distance vector
without constraints:
(Nmi) = arg min II* ¨ kg¨ ANm,111-1
(34)
and the partially fixed vector of the phase ambiguities
Nm-, = [ATI ... gm, I gm, 1 NK1
(35)
in which the first Afi phase ambiguities have already been
set to integer values and the remaining components are
still unknown. It is obvious, that the increasing number
of fixed phase ambiguities results in a smaller standard
deviation of the distance estimation. In consequence, the
distance limitation is becoming stronger with increasing
what results in an essential improvement of the search
efficiency.
The standard deviation of the length estimation in formula
(33) can further be calculated by:
a = Vcr? ______________ cr?
4
(36)

CA 02814882 2013-04-16
21
Figure 3 shows an example of a search tree 31. The search
tree comprises an initial node 32, to which is associated
with a possibility for selecting the first component of the
vector /IV of the candidates for the integer phase
ambiguities. The initial node 32 is followed in downward
direction by various nodal planes 33, from where nodes 34
can be selected for further components of the vectors of
phase ambiguities. Final nodes 35 are disposed on the
lowest nodal plane 33, in which the last component of the
vector ST of the phase ambiguities is fixed. The search
tree 31 therefore comprises various search tree branches
36, which extend respectively from the initial nodes 32 to
the final nodes 35, and which correspond to the various
possibilities to set the vector AT' of the phase
ambiguities.
The search tree is now processed as follows:
In a first step, the lower and the upper limit and
are determined, which can generally expressed as:
/-
2
= v
. ,i-1 %
= 0 -2 (37)
N
= N r N X2 -(38)
0-2
1=1
Is 1 m,
The first component /V1 is determined within the limits
and
< N < u
- r
(39)

CA 02814882 2013-04-16
22
In the example shown in Figure 4, there are three
possibilities for allocating ST,, since three search tree
branches 36 originate from initial node 32. Subsequently,
the three search tree branches 36 are checked for the
condition given in formula (33). In the present case, it is
particularly checked whether
(NM) - Ka(N)
(40)
is valid. The search tree branch 36 is only prosecuted, if
the condition (40) is met. In the present case only the
outer two search tree branches 36 are prosecuted.
In the next nodal plane 36, the integer values for the
component ST2 are selected, where for Sr2 shall apply:
N < N2 <u
(39)
^õ,r fir211
The selected four values of ST2 are then checked again,
whether the condition (33) is fulfilled.
(NM)-1 - (
41)
2 A,f2
In the example illustrated in Figure 4, only the two inner
search tree branches 36 are then maintained.
In the following nodal plane 33, the values for the
component Spi3 are selected, and subsequently the selected
values are again checked with respect to the condition
(33).
In the nodal plane 33 above the final nodes 35, the values
for ./Vic are finally selected, wherein:

CA 02814882 2013-04-16
23
< NI( <UAr ............................... K¨I
(42)
= ,K¨I Ku
The selected values 81K are checked again thereupon,
whether the selected values i\--Tic are fulfilling the
condition (33):
(Nivi) ¨/
(43)
j(Armic)
In the embodiment shown in Figure 4, only three search tree
branches 36 arrive at the final nodes 35. Insofar, only
three candidates for the integer phase ambiguities must be
evaluated.
D. Further Improvements with Multifrequency Combinations
of Code and Phase Measurements
The reliability of the resolving the phase ambiguities can
be further improved by multifrequency linear combinations
having long wavelength. The combinations can include code
,k
measurements l'u,rn -t
and phase measurements Am*k :
EarnArnouk,rn + ornpuk,.
m=i
(44)
,k
with the combined wavelength A, the phase coefficients 'I/071
Rk
and the code coefficients -'14,rn. The coefficients are
selected such that the phase ambiguities can maximally be
distinguished:
A
max D= max
am,i3m am,o,,, 2a
(45)

CA 02814882 2013-04-16
24
wherein further conditions must be fulfilled. Firstly, the
linear combination must preserve geometry:
E +Om = 1
m=1 (46)
and secondly, the linear combination of the phase
ambiguities of different wavelengths must be an integer
multiple of the combined wavelength:
EaAN = AN
m=1
(47)
which is equivalent to:
N=Ea-AmNn,
A
Jm (48)
Since Arm is unknown, but an integer number, jm must be an
integer number for obtaining an integer N. Transforming
this equation results in the phase coefficients:
am = in-tA
Am (49)
which depends on the integer coefficients jm and the
combined wavelength
M.
wo
A = _________________ ER
m=i
(50)
wherein CO0 is the combined phase coefficient:

CA 02814882 2013-04-16
Wçb =E am.
m=1 (51)
The multipath propagation and the instrumental errors can
often be recognized by deviations of the distance vector 15
5 and the weighted sum of the squared errors. Some
instrumental errors, however, can not be recognized by
means of distance deviations. If the integer phase
ambiguities are estimated by minimizing least squares
without constraints the following types of instrumental
10 errors cannot be detected:
bl = -11,6, and b2 = AAN (52)
wherein the first vector of the instrumental errors
15 corresponds to a positional deviation and the second vector
of the instrumental errors corresponds to a deviation of
the integer phase ambiguities. Both cases are relatively
unlikely. The resolution of the phase ambiguities and the
constraints reduces the set of instrumental errors that
20 cannot be recognized because:
(53)
25 E. Advantages
The resolution of the phase ambiguities and the constraints
has two essential advantages in comparison with a phase
resolution without constraints. On the one hand, the
resolution of the phase ambiguities becomes more reliable,
and, on the other hand, the estimation of the distance
vector becomes more accurate.
Figure 5 illustrates the advantage of resolving the phase
ambiguities under constraints using phase ambiguities of an

CA 02814882 2013-04-16
26
E1-E5 linear combination of double difference measurements
as an example, wherein only phase measurements with a
combined wavelength of 2\ = 78 cm have been processed. The
exact knowledge on the length of the distance vector
reduces the error probability for a wrong determination of
the phase ambiguities by several orders of magnitudes.
The error probability Pwf shown in Figure 5 is defined by:
K {1, if Nk #N
P = P(N # N) = liml f (N K) with f (N k) =
wf k-300
k=1 0, otherwise
(54)
and is determined by extensive Monte-Carlo simulations
based on the statistics of the estimation for the real-
valued phase ambiguities:
N =N (N , EA,. ) (55)
In the Monte-Carlo simulations, the vector of the true
ambiguities AT is initially set to an arbitrary value.
Afterwards, various real-valued phase ambiguities are
generated according to their probability distribution and
the method depicted in Figure 2 and 3 is applied. After
each passage through the method, it is determined, whether
the phase ambiguities have been resolved correctly. By
averaging over the results of the Monte-Carlo simulation
the error probability is then calculated.
It can be recognized from Figure 6 that resolving the phase
ambiguities with weak constraints is considerably better
than the other methods, while the length of the distance
vector 15 is not known from the outset. By resolving the
phase ambiguities with weak constraints, the search space
is limited, which results in a lower error rate in
comparison to resolving without constraints. Resolving

CA 02814882 2013-04-16
27
with weak constraint is also better than resolving with
strong constraint, since resolving with strong constraint
restricts the search space too severely. The integer
candidates for both resolutions with constraints where
selected among the ten best candidates, that had been
determined using the LAMBDA method. It can be recognized
from Figure 6 that the coupling factor A should be
selected according to the expected precision of the
predetermined value.
Figure 7 demonstrates that the resolution with weak
constraints is also advantageous in case of a stationary
multipath propagation. The diagram of Figure 7 was
generated by simulating the resolution of the phase
ambiguities in the presence of an instrumental error, which
was equivalent to multipath propagation and which had the
indicated standard deviation of a mean value free Gaussian
distribution.
The method described herein offers the possibility of
stabilizing the load 7 by determining the distance vector
15 between both receivers 10 and 11. In contrast to
conventional methods, this is also possible at cable
lengths below 100 meters.
Besides pure phase combinations, also code and phase
combinations can be used, for instance, an optimized E1-E5
linear combination with a combined wavelength of 3.285 m, a
noise level in the range of few centimeters and a
suppression of multipath errors of 12.6 dB.
It should further be noted that phase measurements can also
be difference or double difference measurements.
The method described herein can be used for determining one
single relative position. In a modified embodiment,

CA 02814882 2013-04-16
28
several relative distances are determined, between several
receivers, either stationary or attached to the load
carrier, and a further receiver in the vicinity of the
suspended load. Based on the determined relative positions
and the known relative position of the receivers, that are
stationary or attached to the load carrier, the position of
the receivers can be checked for consistency by
triangulation or the errors can be eliminated by averaging.
It should finally be pointed out that features and
characteristics described in conjunction with a particular
aspect, embodiment or example of the invention are to be
understood to be applicable to any other aspect, embodiment
or example described herein unless incompatible therewith.
It should further be pointed out in the end that throughout
the description and claims of this specification, the
singular encompasses the plural unless the context
otherwise requires. In particular, where the indefinite
article is used, the specification is to be understood as
contemplating plurality as well as singularity, unless the
context requires otherwise.

Dessin représentatif