Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
CA 02939561 2016-08-22
Methods And Systems For Implementing Dynamic Neural
Networks
Field of the Invention
[0001] The invention relates generally to computing using single or multi-
layer networks; and
more particularly to a system and method for providing feed-forward,
recurrent, and deep networks
that process dynamic signals using temporal filters and static or time-varying
nonlinearities.
Background
[0002] The majority of artificial neural networks (ANNs) in use today are
applied to static inputs
(e.g., images). However, processing dynamic inputs (e.g., movies, sound,
sensory feedback) is
critical for real-time interaction with the world in domains such as
manufacturing, auditory
processing, video processing, and robotics. Non-ANN prior art methods for
processing dynamic
inputs occasionally rely on future information for processing a current state.
This is sometimes called
"acausal" filtering, and is typically physically implemented using delays
(i.e. waiting until the
future information is available before computing a response). Other state-of-
the-art methods for
processing dynamic inputs include nonlinear filtering, in which the output is
not a linear function of
the input. Both of these kinds of filtering are challenging for ANNs to
realize. Currently, a dominant
approach to processing temporal information in ANNs is to employ Long, Short-
Term Memories
(LSTMs; see S. Hochreiter and J. Schmidhuber, Long short-term memory. Neural
Computation,
vol. 9, no. 8, pp. 1735-1780, Nov. 1997.). LSTMs rely solely on recurrent
connections to process
information over time with no synaptic filtering.
[0003] Another class of dynamic ANNs are those that employ "reservoir
computing" (RC; see M.
Lukogevielus and H. Jaeger, Reservoir computing approaches to recurrent neural
network training.
Computer Science Review, vol. 3, no. 3, pp. 127-149, Aug. 2009.). Reservoir
ANNs randomly
connect large numbers of nonlinear nodes (i.e., neurons) recurrently, and then
optimize (i.e., 'learn')
a linear readout to perform dynamic signal processing. A neuron is said to be
'spiking' if its output
consists of brief temporal pulses of output in response to its input. If the
nodes in the reservoir are
non-spiking (i.e., rate neurons), the method is called an Echo State Network
(ESN; see H. Jaeger,
1
CA 02939561 2016-08-22
The echo state approach to analysing and training recurrent neural networks.
German National
Research Center for Information Technology Technical Report, vol. 148, p. 34,
Jan. 2001.).
LSTMs and the majority of other ANNs use rate neurons. There are a variety of
methods for
determining the connection weights between neurons in these networks,
including gradient descent
on the output connection weights, the First-Order Reduced and Controlled Error
(FORCE; see D.
Sussillo and L. F. Abbott, Generating coherent patterns of activity from
chaotic neural networks.
Neuron, vol. 63, no. 4, pp. 544-557, Aug. 2009.) method on feedback
connections, and
unsupervised, error- driven Hebbian learning rules on the recurrent
connections. Like LSTMs,
ESNs and related methods rely solely on recurrent connections to process
information over time. If
the reservoir in an RC network uses spiking nodes, then the method is called a
Liquid State
Machine (LSM; see W. Maass, T. Natschlager, and H. Markram, Real- time
computing without
stable states: A new framework for neural computation based on perturbations.
Neural
Computation, vol. 14, no. 11, pp. 2531-2560, Nov. 2002.). Liquid state
machines are trained (i.e.,
optimized) in a similar manner to ESNs. Because of the spiking temporal
representation, LSMs
typically introduce a temporal filter (i.e., synapse) on the input to the
nodes. This is most commonly
a low-pass filter (i.e., decaying exponential), which smooths the spiking
input before driving the
neural non- linearity. LSMs usually use the same linear filter on all neurons,
and they are usually
first-order.
[0004] A different approach to building spiking and non-spiking dynamic neural
networks is the
Neural Engineering Framework (NEF; see C. Eliasmith and C. Anderson, Neural
engineering:
Computation, representation, and dynamics in neurobiological systems. MIT
Press, 2003.). In this
approach, the dynamics of the network are optimized to approximate a given
function. This can be
thought of as directly optimizing the "reservoir" in RC networks. The
optimization can be done
directly using a global optimizer, or during run-time using any of several
learning rules. These
networks usually assume a first-order low-pass temporal filter (i.e., synapse)
as well.
[0005] Prior art approaches to implementing dynamic neural networks either do
not have a
synaptic filter (e.g., LSTMs, ESNs), or pick a simple filter (e.g., LSMs, NEF
networks). These
approaches also assume that the same filter is used for the majority of
synapses in the model.
Summary
[0006] In a first aspect, some embodiments of the invention provide a method
for implementing
2
CA 02939561 2016-08-22
single or multi-layer, feed-forward or recurrent neural networks for dynamic
computations. The
method includes defining any node response function that either exhibits brief
temporal
nonlinearities for representing state over time, often termed 'spikes', or
exhibits a value at each
time step or over continuous time (i.e., `rates'). These response functions
are dynamic because they
accept input over time and produce output over time. For spiking neurons, the
nonlinearity is over
both time and state, whereas for rate neurons it is largely over state. The
method also includes
defining one or more temporal filters (i.e., synapses) on the input and/or
output of each node. These
synapses serve to filter the input/output signal in various ways, either
linearly or nonlinearly. This
structure is then used to determine connection weights between layers of nodes
for computing a
specified dynamic function. Specification of the function can be performed
either by writing it in
closed form, or by providing sample points.
[0007] In some cases, the initial couplings and connection weights are
determined using a neural
compiler. Connection weights can be further trained either with online or
offline optimization and
learning methods.
[0008] In a second aspect, some embodiments of the invention provide a system
for pattern
classification, data representation, or signal processing in neural networks.
The system includes one
or more input layers presenting a vector of one or more dimensions, as well as
zero or more
intermediate layers coupled via weight matrices to at least one of the input,
other intermediate, or
output layers, and one or more output layers generating a vector
representation of the data presented
at the input layer or computing a function of that data. Each layer comprises
a plurality of nonlinear
components, wherein each nonlinear component has zero or more temporal filters
on its input and
zero or more temporal filters on its output, with one or more filters
associated with each component,
and the component coupled to the layer's input and output by at least one
weighted coupling. The
output from each nonlinear component's temporal filter is weighted by the
connection weights of
the corresponding weighted couplings and the weighted outputs are provided to
the layer's output.
The input to each nonlinear component's temporal filter is weighted by the
connection weights of
the corresponding weighted couplings and the weighted and filtered inputs are
provided to the
component. The connection weights are determined using methods of the first
aspect.
[0009] In some cases, the input to the system is either discrete or continuous
in time and/or space.
3
CA 02939561 2016-08-22
[00010] In some cases, the input to the system can be scalar or a
multidimensional vector.
Brief Description of the Drawings
[00011] A preferred embodiment of the present invention will now be
specified in detail
with reference to the drawings.
[00012] FIG. 1 is a block diagram of layers and nonlinear elements in
accordance with an
example embodiment.
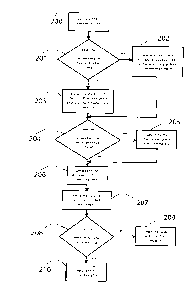
[00013] FIG. 2 is a diagram of the process involved in applying the method.
[00014] FIG. 3 shows an embodiment computing a 100ms delay with spiking
neurons.
[00015] FIG. 4 shows improved accuracy of these methods over state-of-the-
art methods.
[00016] FIG. 5 shows improved computational costs compared to state-of-the-
art methods.
[00017] FIG. 6 shows an embodiment computing the acausal derivative filter.
[00018] FIG. 7 shows an embodiment with a controllable delay.
[00019] FIG. 8 shows an embodiment computing ten different delays within
one network.
[00020] FIG. 9 shows results of computing the Fourier transform power, a
nonlinear
dynamic computation.
[00021] FIG. 10 shows trajectory generation using a controllable delay
bank.
[00022] FIG. 11 is a diagram of an abstract characterization of the system
with an arbitrary
synaptic filter.
[00023] FIG. 12 shows improved accuracy in delay computation by including
higher-order
synapses.
[00024] FIG. 13 is a diagram of an abstract decomposition of the system
into encoding and
decoding filters.
4
CA 02939561 2016-08-22
[00025] FIG. 14 shows the ability to determine the optimal distribution of
heterogeneous
synapses to minimize error in computing a derivative.
Description of Exemplary Embodiments
[00026] Herein, specific details are set forth in order to provide a
thorough understanding
of the exemplary embodiments described. However, it will be understood by
those of ordinary skill
in the art that the embodiments described herein may be practiced without
these specific details. In
other instances, well-known methods, procedures and components have not been
described in detail
so as not to obscure the embodiments generally described herein. Furthermore,
this description is
not to be considered as limiting the scope of the embodiments described herein
in any way, but
rather as merely describing the implementation of various embodiments as
presented here for
illustration.
[00027] The embodiments of the systems and methods described herein may be
implemented in hardware or software, or a combination of both. These
embodiments may be
implemented in computer programs executing on programmable computers, each
computer
including at least one processor, a data storage system (including volatile
memory or non-volatile
memory or other data storage elements or a combination thereof), and at least
one communication
interface.
[00028] Program code is applied to input data to perform the functions
described herein
and to generate output information. The output information is applied to one
or more output
devices, in known fashion.
[00029] Each program may be implemented in a high-level procedural or
object-oriented
programming or scripting language, or both, to communicate with a computer
system. Alternatively
the programs may be implemented in assembly or machine language, if desired.
The language may
be a compiled or interpreted language. Each such computer program may be
stored on a storage
media or a device (e.g., read-only memory (ROM), magnetic disk, optical disc),
readable by a
general or special purpose programmable computer, for configuring and
operating the computer
when the storage media or device is read by the computer to perform the
procedures described
herein. Embodiments of the system may also be considered to be implemented as
a non-transitory
CA 02939561 2016-08-22
computer-readable storage medium, configured with a computer program, where
the storage
medium so configured causes a computer to operate in a specific and predefined
manner to perform
the functions described herein.
[00030] Furthermore, the systems and methods of the described embodiments
are capable
of being distributed in a computer program product including a physical, non-
transitory computer
readable medium that bears computer useable instructions for one or more
processors. The medium
may be provided in various forms, including one or more diskettes, compact
disks, tapes, chips,
magnetic and electronic storage media, and the like. Non-transitory computer-
readable media
comprise all computer-readable media, with the exception being a transitory,
propagating signal.
The term non-transitory is not intended to exclude computer readable media
such as a volatile
memory or random access memory (RAM), where the data stored thereon is only
temporarily
stored. The computer useable instructions may also be in various forms,
including compiled and
non-compiled code.
[00031] It should also be noted that, as used herein, the wording "and/or"
is to mean
inclusive-or. That is, "X and/or Y" is intended to mean X or Y or both, for
example. As a further
example, "X, Y, and/or Z" is intended to mean X or Y or Z or any combination
thereof.
[00032] Embodiments described herein generally relate to a system and
method for
designing and implementing a feed-forward or recurrent neural network for
dynamic computation.
Such a system can be efficiently implemented on a wide variety of distributed
systems that include
a large number of nonlinear components whose individual outputs can be
combined together to
implement certain aspects of the system as will be described more fully herein
below.
[00033] Examples of nonlinear components that can be used in various
embodiments de-
scribed herein include simulated/artificial neurons, field-programmable gate
arrays (FPGAs),
graphics processing units (GPUs), configurations of analog components and
other physical
primitives including but not limited to transistors, and/or other parallel
computing systems.
Components of the system may also be implemented using a variety of standard
techniques such as
by using microcontrollers.
[00034] The systems described herein can be implemented in various forms
including soft-
ware simulations (using standard languages (e.g. Python, C, etc.) and more
specialized
6
CA 02939561 2016-08-22
implementations (e.g. Open Computing Language (OpenCL), Message Passing
Interface (MPI),
etc.), hardware, and/or any neuronal fabric. Examples of neuronal fabric
mediums that can be used
to implement the system designs described herein include Neurogrid (see S.
Choudhary, S. Sloan,
S. Fok, A. Neckar, Eric, Trautmann, P. Gao, T. Stewart, C. Eliasmith, and K.
Boahen, Silicon
neurons that compute, in International Conference on Artificial Neural
Networks, pp. 121-128,
2012.), SpiNNaker (see M. Khan, D. Lester, L. Plana, A. Rast, X. Jin, E.
Painkras, and S. Furber,
SpiNNaker: Mapping neural networks onto a massively-parallel chip
multiprocessor. IEEE, Jun.
2008.), and TrueNorth (see P. A. Merolla, J. V. Arthur, R. Alvarez-Icaza, A.
S. Cassidy, J. Sawada, F.
Akopyan, B. L. Jackson, N. Imam, C. Guo, Y. Nakamura, B. Brezzo, I. Vo, S. K.
Esser, R.
Appuswamy, B. Taba, A. Amir, M. D. Flickner, W. P. Risk, R. Manohar, and D. S.
Modha,
Artificial brains. A million spiking-neuron integrated circuit with a scalable
communication
network and interface. Science, vol. 345, no. 6197, pp. 668-673, Aug. 2014.).
As used herein the
term 'neuron' refers to spiking neurons, continuous rate neurons, and/or
components of any
arbitrary high-dimensional, nonlinear, distributed system.
[00035] To generate such systems, the system dynamics can be characterized
at a high level
of description, using available background information regarding function. A
low-level neural
network structure can then be employed that includes a specific filter, or
distribution of filters, on
the inputs to the neurons in the network, and analytically relate the two.
Subsequently, it is possible
to optimize the connections between the elements in the neural network to
accurately compute the
desired function using standard optimization methods. The challenge this
addresses is one of
identifying and efficiently exploiting low-level dynamics and network
structure at the functional
level for dynamic information processing.
[00036] FIG. 1 shows the general architecture of a layer of these networks.
Each layer
(100) consists of several nodes (101) that can be either spiking or non-
spiking. The overall network
structure can be quite varied, with layers connecting within or back to
themselves or to other layers
earlier in the network (102; recurrent networks), or to layers later than them
in the network.
Networks that connect only in one direction are called feed-forward networks.
Connections
between layers may also be quite varied, including full connectivity, local
connectivity,
convolutional connectivity, or any other connectivity pattern known in the
art. In addition, the
networks considered introduce an explicit temporal filtering, some examples of
which are denoted
7
CA 02939561 2016-08-22
by black boxes (103), into the network. This filtering can take a variety of
forms and be introduced
in a variety of ways in each layer, including but not limited to same and/or
different filters on
inputs and/or outputs on each neuron, same and/or different filters on inputs
and/or outputs on each
dimension of the layer input/output vector (104, 105). Regardless of the
topology, the overall
network takes some form of vector input which it converts via its weighted,
connected components
to a different vector output, possibly changing the dimensionality. This
figure represents the basic
structure of the layers comprising the networks considered here.
[00037] Referring now to FIG. 2, there is shown a method for implementing
single or
multi-layer, feed-forward or recurrent spiking neural network dynamic
computations.
[00038] At step 200, the method defines any node response function that
exhibits brief
temporal nonlinearities for representing state over time, i.e., 'spikes' or
node response functions
that elicit values at each time, i.e., 'rates'. There are a wide variety of
example spiking
nonlinearities in the literature, including the Hodgkin-Huxley neuron, the
Fitzhugh-Nagumo
neuron, the exponential neuron, the quadratic neuron, the theta neuron, the
integrate-and-fire neuron,
the leaky integrate-and-fire neuron, the Wilson neuron, and the Izhikevich
neuron, among others.
Similarly, there are a wide variety of example rate nonlinearities, such as
the family of sigmoidal
curves, the tanh function, and/or the rectified linear neuron. Various
hardware implementations of
these and other nonlinearities have also been proposed for generating spike-
like or rate-like
outputs, any of which can be employed.
[00039] Steps 201-203 determine a plurality of input and/or output filters
to be associated
with the layer inputs. There are a wide variety of filters in the literature,
many of which are
considered models of synaptic response, including the exponential decay `low-
pass', the delayed
low-pass, the alpha synapse, the double exponential synapse, and conductance-
based models.
These filters can be applied to each neuron input and/or output, or to each
dimension of the input
and/or output space being manipulated by the layer, and may be heterogeneous,
as indicated at steps
204, 205.
[00040] At step 206, the method determines the dynamic function that is to
be computed by
the network. This function can be specified in closed form or defined with a
set of example inputs
and/or outputs.
8
CA 02939561 2016-08-22
[00041] Step 207 includes employing the chosen network structure to compute
the specified
dynamic function by finding the correct input and output weights. The novel
approach proposed
here for finding the weights is described in detail for several example
embodiments below.
Optimization for the weights can be accomplished in a number of ways at step
208, including by
direction optimization (e.g., as sometimes used in the NEF), by optimization
based on example
simulations of the network as per step 210, or using any of a variety of
standard "learning rules" or
optimization methods specified in the literature as per step 209. The proposed
network
construction method shows how these optimization methods can be effectively
used for networks
with the structure specified. With this method the weights determined in step
four can be used in a
dynamically implemented spiking or rate neural network to compute the function
trained for. This
consists in running the dynamic neural model, where each neuron is connected
to others by the
input/output filters weighted by the connection weights determined during
optimization. As shown
in the example embodiments, this set of steps allows for good performance on a
wide variety of
difficult dynamic computations.
[00042] In this method the input/output filters can be discrete or
continuous. Many software
and hardware implementations use discrete time steps to simulate dynamical
systems or perform
computation over time. As shown in the example embodiments, this method can
account for discrete
or continuous filtering. Accounting for discrete filtering can significantly
improve the accuracy of
discrete time step implementations.
[00043] In this method the optimization performed to determine the
input/output weights
can be performed either offline or online, determined in any of a number of
ways. NEF methods
fall into the former class, are very efficient and have strong convergence
guarantees. In the example
embodiments this is the most common method employed. However, some example
embodiments
use offline methods that require simulation of the network. Other work has
shown how these same
networks can be optimized using online methods as well (e.g., see T. Bekolay,
Learning in large-
scale spiking neural networks, Master's Thesis, University of Waterloo, Sep.
2011.).
[00044] In this method the input/output weights can often be combined
between layers to
determine a single large connection weight matrix, as is more common in
standard neural networks.
This method can employ either factorized weights (i.e., separate input/output
weights) or non-
factorized weights (i.e., a single matrix). The optimization described can be
performed on either
9
CA 02939561 2016-08-22
factorized or non-factorized weights. Often factorized matrices are more
computationally efficient
to employ. The example embodiments use factorized matrices.
[00045] In this method the specified dynamic function can be continuously
or discretely
defined. Discretely defined functions are especially relevant for
implementation of these methods
in digital hardware and software.
[00046] In this method the specified dynamic function can be defined in a
wide variety of
ways. Most generally any linear or nonlinear differential equations in phase
space can be specified.
Identifying such systems can include, but is not limited to writing the
equations in closed form,
specifying a transfer function form, or providing a set of input/output point
pairs. Similarly, any
function specified as a pure delay or definable in terms of pure delays (e.g.,
a finite impulse
response filters) can be employed. Subsequent example embodiments demonstrate
a variety of
these methods, including pure delays and a variety of functions defined in
terms of pure delays,
including differentiation and computing spectral power.
[00047] In this method the specified dynamic function can be a controllable
pure delay or
definable in terms of a controllable pure delay. A controllable pure delay is
shown in an example
embodiment. This is a nonlinear filter that allows the amount of delay to
change as a function of its
input. As with non-controlled delays and linear filters, controlled delays can
be used to define an
extremely wide variety of nonlinear temporal filters.
[00048] In this method Pad& approximants can be used to implement the
specified dynamic
function, as can system identification methods. Fade approximants are a useful
means of providing
optimal approximations to filters defined over infinite states (like pure
delays). An example
embodiment demonstrates the use of this approximation for computing dynamic
functions.
Similarly, approximating complex dynamic functions can be performed by using
numerical
methods for system identification.
Example embodiment: Acausal filtering
[00049] Past work has not demonstrated a general approach to performing
acausal filtering
in such networks. An acausal filter is a dynamical system that requires
information from future
times to determine the value of the filtered signal at the current time.
Acausal filtering is important
for a wide variety of dynamic signal processing, including performing
differentiation, highpass
CA 02939561 2016-08-22
filtering, distortion reversal (and/or any other deconvolution), predicting
future states of the system,
among many others. Acausal filtering is closely related to prediction because
it requires making
estimates of future states. The methods described in this section address this
problem for dynamic
neural networks.
[00050] To perform acausal filtering, we need to know information that is
not yet available
to the system. Consequently, we wait for a period of time to gather sufficient
information, and then
compute the desired filter. To successfully pursue this approach, it is
essential to be able to compute
delayed versions of the input signal. Past work has not demonstrated how to
construct such delays
accurately and in general. We begin by addressing how to compute delays in
dynamic neural
networks.
[00051] Linear time-invariant (LTI) systems can be described by the state
equations:
[00052] k(t) = Ax(t) + Bu(t)
[00053] y(t) = Cx(t) + Du(t) (1)
[00054] where the time-varying vector x represents the system state, y the
output, u the
input, and the time-invariant matrices (A, B, C, D) fully define the system
dynamics. All causal
finite-order LTI systems can be written in this form.
Accurate delays
[00055] In many scenarios, the transfer function is a more useful
representation of the LTI
system. The transfer function is defined as ¨Y(s) Y where Y(s) and U(s) are
the Laplace transforms of
u(s
output y(t) and input u(t) respectively. The variable s denotes a complex
variable in the frequency
domain, while t is a non-negative real variable in the time domain. The
transfer function is related
to the state-space representation (1) by the following equation:
[00056] F(s) = ¨Y(s) = C(s1 ¨ A)-1B + D. (2)
u(s)
[00057] The transfer function for a pure delay of a seconds is:
[00058] F(s)_, e-s. (3)
11
CA 02939561 2016-08-22
[00059] A transfer function can be converted into state-space
representation using (2) if and
only if it can be written as a proper ratio of finite polynomials in s. The
ratio is proper when the
degree of the numerator does not exceed that of the denominator. In this case,
the output will not
depend on future input, and so the system is causal. The order of the
denominator corresponds to
the dimensionality of x, and therefore must be finite. Both of these
conditions can be interpreted as
physically realistic constraints where time may only progress forward, and
neural resources are
finite.
[00060] To approximate the irrational transfer function (3) as a ratio of
finite polynomials,
we use the Pade approximants of the exponential,
[00061] [pm e -as = QP(-as) (4)
Qq(as)
[00062] (2k(s)
(k\(p+q--0! si
I (p+q)! * (5)
[00063] This gives the optimal approximation for a transfer function with
order p in the
numerator and order q in the denominator. After choosing suitable values for p
< q, we can
numerically find a state-space representation (A, B, C, D) that satisfies (2)
using standard methods.
[00064] For the common case that p = q ¨ 1, we may bypass the need for any
numerical
methods by analytically finding a simple state-space representation. Consider
the Pade
approximants of (3) in the case where q ¨ 1 and q are the order of the
numerator and denominator,
respectively. We rewrite (4) by expanding (5) to get:
1g- 1(q71)(2q-i-iy(-Vaisi
[00065] [q ¨1/q]e-as = i=
(q.)(2q-1-waisi
i=0 I
1 ,g-1 (q-1).!
[00066] = ag(g_i)4.1=0
sq+ 1 e-i q! (2_1_01aisi
aq(q-1)! 1=0 (q-0!i!'
/q-1 CiSi
[00067] i=0
sq-FE7:01 disi
12
CA 02939561 2016-08-22
[00068] where di - q(2q-1-1)! ai-cl and ci =
[00069] This transfer function is readily converted into a state-space
representation in
controllable canonical form:
-dq-i -dq-2 === -C10\
[00070] A = 1 0 = = = 0
0
0 1 oJ
[00071] B = (1 0 === 0)T
[00072] c (cq_i cq_2 = = = co)
[00073] D = 0.
[00074] However, the factorials in di and c, may introduce numerical
issues. To simplify
implementation we scale the th dimension of x by -dp_i. This is achieved
without changing the
transfer function by multiplying the ill' entry in B by -dq_j, the entry in C
by -1/dq_i, and the
(i, jr entry in A by dq_i/dq_j, to obtain the equivalent state-space
representation,
-vo -120 = = = -vo
v1 0 = = = 0
[00075] A =
0
i 0 Vq-i 0
[00076] B = (-1,0 0 === 0)T
[00077] C = (wo
[00078] D = 0, (6)
[00079] where vi = (q+i)(q-i) and w,i = (-1)q(i+i) ¨, for i = 0...q - 1.
This follows from
noting that vo = dq_i and vi = dq_i_i/dq_i for i 1. This provides an exact
solution for the
Pade approximation of the delay.
[00080] With this description we can use the NEF methods to generate an
example
embodiment. FIG. 3 shows the results of performing a 100 ms delay on a random
10 Hz white noise
signal with 400 spiking neurons using a first-order low-pass synaptic filter
with a time constant of 5
ms. It is using a 4th-order approximation. The original input signal (300) is
delayed and decoded
13
CA 02939561 2016-08-22
(301) from the neural spikes generated by the recurrently connected neurons.
[00081]
Furthermore, these methods are significantly more accurate and far less
computationally expensive than other state-of-the-art methods. Specifically,
FIG. 4 demonstrates
that in a network of 500 neurons computing delays from 50-100 ms on 8 Hz white
noise, the NEF
methods (400) are 4x or more accurate than a liquid state machine (LSM), which
is the spiking
implementation of reservoir computing (401). Rate mode versions of NEF
compared to an echo
state network (ESN), which is the non-spiking implementation of reservoir
computing, have the
same accuracy. However, as shown in FIG. 5 spiking and rate NEF networks are a
factor 0(N)
cheaper to compute (500, 501), with N as the number of neurons, because of
their factored weight
matrices compared to reservoir methods (502,503).
[00082] Another
embodiment of the delay network allows us to introduce controlled delay
into the network by noting that in (6) all terms in the feedback A matrix are
a function of a.
Consequently, we can introduce an input that provides a on-the-fly,
controlling the delay online.
This input is encoded into the state-space x and the product is computed in
the recurrent
connection. FIG. 6 is the same as the previous embodiment, but with 2000
spiking neurons and a
controllable input. The original input signal (600) is delayed by an amount
controlled by the delay
input (601) which changes from 25 ms to 150 ms in steps of 25 ms in this
figure (delay length is
indicated by the shaded bars). The delayed signal (602) is decoded from the
neural spiking activity.
Acausal filtering examples
[00083] An
accurate method for generating a delayed version of a signal provides the
basis
for general acausal filtering. One embodiment of an acausal filtering network
is the network that
computes the derivative of the input signal. FIG. 7 shows the behaviour of a
400 neuron network
that implements the acausal differentiation transfer function F (s) = Ts using
a delay of 15 ms. The
input signal (700) and the ideal derivative filter (701) are shown along with
the decoded output
(702) of the spiking recurrent neural network computation of that filter using
a delay. Since the
output is spikes, we filter it with a low-pass filter. The end result is
therefore the highpass filter,
TS
F = -, which smooths out the derivative. In this example r = 50 ms.
[00084] This
embodiment network is one example of a general (acausal) deconvolution net-
work with the specific transfer function F(s) =
Deconvolution can be instantiated with any LTI
14
CA 02939561 2016-08-22
that one wishes to invert, provided the delayed inverse can be accurately
approximated.
[00085] To perform more complex acausal filtering, we need to generate many
delayed
versions of the input signal. It is known that any finite impulse response
filter can be approximated
by a weighted sum of delays. Consequently, another embodiment consists of
creating many
different delays in a network and weighting those to compute the filter. Such
a delay bank is very
flexible for computing a wide variety of dynamic functions using neural
networks. Determining the
output weights on the filter bank can be done using a wide variety of methods
that employ either
online or offline learning or optimization. More generally, such a filter bank
allows for nonlinear
combinations of delays and represented states.
[00086] FIG. 8 shows the output of a network instantiating a bank of delays
separated by
15 ms each. The input signal (800) is a 10 Hz white noise signal and the
output includes 9 delayed
versions of that signal (801), computed with 5400 spiking neurons using 3rd-
order delay
approximations.
[00087] An example embodiment that employs a filter bank and is performing
nonlinear
filtering is demonstrated in FIG. 9. This network is computing the power of
the Fourier transform at
frequencies (900) which is compared to the ideal computation (901). The input
signal is random
25 Hz white noise, and the network employs 22800 rate neurons with 20 delays
spaced by 20 ms
where p = q = 40.
[00088] The next embodiment we consider uses controlled delay and an
arbitrary filter to
perform trajectory generation is shown in FIG. 10. In this case, the input is
a delta function and the
output is an arbitrary trajectory over time, defined by the shape of the
filter. The input (1000)
causes the system to play back the trajectory (1001) using the delay bank. The
speed and size of
playback can be controlled by the delay input (1002) as shown. This example
shows the same
trajectory played 'big' and 'small' given the same delta function input, but
for a different delay
control input.
Example embodiment: Arbitrary synaptic filters
Method 1: Using Taylor series approximations
[00089] Past work has not shown how to account for arbitrary synaptic
filters in the
CA 02939561 2016-08-22
implemented neural network. The NEF has demonstrated how to account for the
special case of a
first-order low-pass filter. The methods described in this section address the
general problem. Some
of these modifications improve network accuracy and reduce the number of
network elements
needed to perform a given computation effectively. These modifications also
allow the efficient use
of a wider variety of discrete and continuous synaptic filters.
[00090] Referring
to FIG. 11 we consider appending some arbitrary transfer function G(s)
(1100) to the feedback, so as to replace the integrator! (1101) with 11(s) =
G(s)-1 (1102). This
system has transfer function C(-- I ¨ A)-1B + D = F (¨s() )= F(-11(9)), where
F(s) =
G (s) Gs
C(SI ¨ A)-1B D is the transfer function for (A, B, C, D).
[00091] To invert
the change in dynamics introduced by appending G(s), we must
compensate for the change of variables ¨ in the complex frequency domain. This
involves
finding the required F'(s) such that Fr is equal
to the desired transfer function, F(s). Then the
H (s
state-space representation of F'(s) provides (A', B', , Dr) which implement
the desired dynamics.
[00092] For
example, if we replace the integrator with a low-pass filter, so that h(t) =
-e T, and set G (s) to unity then:
[00093] F'(s) = C(sI ¨ (TA + I)) 1(TB) + D = C' (sI ¨ TA')-1Br + D',
[00094] which is
an alternative derivation of the mapping given by NEF methods.
However, this is the only form of H (s) solved for by the NEF. We extend this
result to apply to a
wider variety of filters. For instance, in the case of the alpha synapse model
where H(s) =
(i-Frs)2
we can show that:
-1
[00095] F'(s) = C (Nis/ ¨ (TA + 1)) (TB) + D.
[00096] Notably,
this embodiment is nonlinear in s. We can use the Taylor series expansion
[00097] Nrs = 1 + - (s ¨ 1) + o(s)
2
16
CA 02939561 2016-08-22
[00098] to linearize 'Is in our characterization of F'(s), giving
[00099] F'(s) = C(s/ ¨ (2TA + /))-1(2TB) + D.
[000100] Another example embodiment is the case of a discrete low-pass
filter with a z-
_dt
1-a
transform of H(z) = ¨, a , e T ,
z-a
[000101] F, ( ) z-a . F(z)
.-a)
[000102] .4=> F'(z) = F(z(l ¨ a) + a)
[000103] = e((z(1 ¨ a) + a)(I ¨ A)-113 + 13
[000104] = C(z/ ¨ ¨1 (A ¨ a/))-1 (-1 B) + T) (7)
1-a 1-a
(Af, /3 / , 0,5') ,_ (_i (A _ a!),_i
R,C,T)), where (A,171,C,b) is the result of discretizing (A,
\ 1-a 1-a
B, C, D) with time step dt. Discrete filters are particularly relevant for
hardware implementations
which are clocked at a specific frequency, and hence have a built in dt, or
software
implementations that use a time step to approximate continuous dynamics. This
embodiment can
make such implementations more accurate.
[000105] A further example embodiment is one which compensates for a
continuous feed-
back delay of ,8 seconds, by setting G (s) = els, then
[000106] F' (¨_--es ps) = F(s) <=> F1(s) = F (1 Wo(13s)) (8)
/3
[000107] where Wo(xex) = x is the principle branch of the Lambert-W
function, since
Fl(se) = F( 731 W0(flsefis) = F(s). In this case, since Wo is nonlinear in s,
the effect of the
change of variables on the required state-space representation will depend on
the desired transfer
function F.
[000108] For this embodiment we consider the case of a synapse modeled by a
low-pass
filter with a pure delay of )8 seconds, to account for possible transmission
time delays along
17
CA 02939561 2016-08-22
e A
presynaptic axons. In this instance, H(s) = T-s+ 1, and let d= Ter. We can
then show
[000109] F' (1-5 ) = F(s)
p f3
[000110] <=> F' (h's + e( )vs+ = F (es)
[000111] 4=> F' (13 s + = F(Wo(ds))
[000112] <=>
F'(s) = F (¨Wo(ds) ¨ (9)
)6'
[000113] So in the pure delay case when F(s) = e's is the desired transfer
function, let
a
c = eT and r = ¨a so that
-a(2:141,(ds)-
[000114] F'(s) = e T) = ce (10)
ds
-rWo(ds) = c (Wo(ds))r
[000115] is the required transfer function. Then we can numerically find
the Pade
approximants by using the Taylor series of (10).
F' (s) = c 0 r(i+r)i-1 (¨ds)i
[000116] (11)
[000117] As shown in FIG. 12 an instance of this embodiment can be used to
provide a
better approximation of an ideal delay (1200) if the synapses themselves
include a delay (1201),
than the previous embodiment that only assumed a first-order linear filter
(1202). Because the
synapses include a 10 ms delay, this result demonstrates that these methods
can be used to amplify
the low-level synaptic delay 10-fold, while resulting in an improvement of 3x
on normalized root-
mean-square error (NRMSE).
Method 2: Direct solution
[000118] Consider the Laplace transform of some k-order synapse:
[000119] H (s) = k
Ei=0 cist
[000120] We wish to implement the desired nonlinear dynamical system:
18
CA 02939561 2016-08-22
[000121] = f (x, u)
[000122] using this synaptic filter. Letting w(t) = f'(x, u) and observing
that in the actual
system x(t) = (w * h)(t), we can write these dynamics in the Laplace domain:
x(s)
[000123] = ____
w(s)
[000124] <=> W(s) = X(s) Vic_o
cisi = Elf_o ci [X(s)si]
[000125] since s is the differential operator. So the required function f'
(x, u) for the
recurrent connection, for any synapse, is:
[000126] f (x, u) = cix(0, (12)
[000127] where x(i) denotes the j1h derivative of x(t).
[000128] In the discrete case x[t + 11 = f (x, u):
[000129] f ' (x, Eix[t + i]. (13)
[000130] The proof for the discrete case is similar by use of the time-
shift operator with the
z-transform.
[000131] For the generalized alpha synapse (i.e., double exponential), we
find
1 1
[000132] H (s) =
(1- + 1)(1-2. 3 +1) T1r2s2+(r1+T2)s+1
[000133] = f i(x, = x + (-r1 + 7-2)k + r1r2it
äf(cu) .
[000134] -I- x (-t-i 1-2)f (x, + ir 2
(a f (x, u) f (x, af()
+ u)
[000135]
ax au
[000135] (14)
[000136] This approach requires us to differentiate the desired system. If
we are dealing with
linear systems, then we can do this analytically to obtain a closed-form
expression.
[000137] By induction it can be shown that:
19
CA 02939561 2016-08-22
[000138] x(i) = Aix +
[000139] Then by expanding and rewriting the summations:
[000140] f (x, = Vic_o cix(i)
[000141] = ci [Aix + B u(i)]
[000142] = (V_0 ciAt) x+ Ei.1_711 di). (15)
Recurrent Matrix Input Matrices
[000143] This gives a matrix form for any LT1 system with a k-order
synapse, provided we
can determine each u(i) for 0 <j <k¨ 1.
[000144] As a demonstration, we can apply the above formula to the
generalized alpha
synapse, giving the following expression for any linear system:
[000145] f (x, = (r1T2A2 + (r1 + 2)A + 1)x + (7-1 + T2 + T1T2A)Bu + x1r2BU.
Example embodiment: Synaptic heterogeneity
[000146] Past work has not shown how to take advantage of having a variety
of different
synaptic filters within the implemented network. The methods described in this
section address this
general problem. Some of these modifications improve network accuracy for
performing dynamic
computation.
[000147] Introducing heterogeneous filters into the NEF significantly
extends these methods.
As shown in FIG. 13 we can introduce an "encoding filter" Hi (1300) after the
standard NEF
encoder ei (1301) that is distinct for each neuron and provides a specific
processing of the time-
varying vector x(t) (1302). The filter signal projects through the neural
nonlinearity Gi (1303)
resulting in neural activity that is decoded with linear decoders di (1304)
and filtered by a standard
NEF filter H (1305). In essence we have factorized the dynamics into encoding
and decoding filters
in a manner analogous to the factorization of the weight matrix into decoders
and encoders in the
NEF.
CA 02939561 2016-08-22
[000148] In the NEF, there is a single synaptic filter per projection
between ensembles,
resulting in the encoding given by:
[000149] Si = Gi[< eih(t) *x(t) > +Ji].
[000150] where Oi is the neural activity (rates or spikes) from neuron i,
and Ji is a bias
current. Here we have introduced the notion of defining one or more synaptic
filter per neuron, as is
shown in FIG. 13, giving:
[000151] Si = Gi[hi(t) *< ex(t) > +Ji],
[000152] or per dimension in the input space
[000153] Si =- eihi(t) * x(t) > +Jib
[000154] where hi(t) is a vector of D filters applied to their respective
dimensions in the D-
dimensional input vector x(t). This provides a wider variety of "temporal
features" that are encoded
by the neural population, allowing us to extend the NEF in a manner that
provides better
implementation of a broad class of dynamical computation.
[000155] In our example embodiment, we use heterogeneous first-order linear
filters, but the
methods apply to any linear filters. Here, we employ these methods to compute
the differentiation
operator. Specifically, we approximate the filter H(s) = 21-s/(rs + 1). This
is the derivative s
multiplied by a low-pass 1/(Ts + 1) (to make it causal) and scaled by Zr for
normalization. We
simulate a network of 1000 spiking neurons with 15 Hz white noise input, and
vary the width of the
distribution for the time constants of the input filters for each neuron. The
time constants are picked
from an even distribution with a lower bound of 0.2 ms and an upper bound that
varies up to 10 ms.
FIG. 14 shows the results of these simulations, that demonstrate the
importance of having a variety
of time constants. Root mean-square-error (RMSE) is shown as a function of the
change in
distribution width (1400). In this instance, the optimal width is
approximately 6 ms. Notably, the
RMSE drops in half at the optimal value. Because there exists an optimal
value, it is clear that the
distribution is playing an important role (i.e., it is not merely because
longer synapses are being
introduced). Thus this extension to the NEF improves the ability of these
networks to compute
dynamical functions.
21
CA 02939561 2016-08-22
Discussion
[000156] The embodiments demonstrated here show the ability to compute a
variety of
linear and nonlinear dynamic functions, including accurate casual and acausal
filters. Examples
include specific applications to delays, discrete implementation,
spectrographic power, derivatives,
and Fourier transforms. Additional embodiments extend these results by showing
how to employ a
wide variety of synaptic filters, and how to exploit heterogeneous
distributions of synaptic filters.
[000157] The example results shown demonstrate that the methods described
in this
invention allow us to improve RMSE and computation time compared to state-of-
the-art
approaches, and also show the applicability of these methods to a wide variety
of neural networks,
both spiking and non-spiking, for performing dynamical computation.
[000158] The methods described here can be used to develop additional
embodiments not
described in detail. These include exploitation of intrinsic neuron dynamics,
such as using
intrinsically bursting neurons to more efficiently implement oscillatory
networks, or adapting
neurons to more efficiently and accurately compute differentiation. Similarly,
these methods can
support dynamic processing, such as prediction (which reduces to
differentiation for a wide variety
of cases, e.g., as is evident from the Taylor series expansion of functions).
Some of the examples
provided can be directly combined, such as using a controlled delay bank of
filters for trajectory
generation to produce useful networks. As well, the employment of nonlinear
synaptic filters and
nonlinear mixing of delays can be accomplished through direct applications of
these methods.
22