Note : Les descriptions sont présentées dans la langue officielle dans laquelle elles ont été soumises.
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Fast and Partition-Resilient Blockchains
CROSS REFERENCE TO RELATED APPLICATIONS
This application claims priority to U.S. Prov. App. No. 62/607,558, filed
December 19,
2017, and entitled FASTER BYZANTINE AGREEMENT IN PROPAGATION NETWORKS
WITH > 2/3 HONEST MAJORITY, and to U.S. Prov. App. No. 62/632,944, filed
February
20, 2018, and entitled ALGORAND, and to U.S. Prov. App. No. 62/643,331, filed
March
15, 2018, and entitled INCENTIVES AND TRANSACTION FEES IN ALGORAND, and
to U.S. Prov. App. No. 62/777,410, filed December 10, 2018, and entitled
VIRTUAL
BLOCKCHAIN PROTOCOLS FOR FAIR ELECTRONIC EXCHANGE, and to U.S. Prov.
App. No. 62/778,482, filed December 12, 2018, and entitled VIRTUAL BLOCKCHAIN
PROTOCOLS FOR FAIR ELECTRONIC EXCHANGE, which are all incorporated by
reference
herein.
TECHNICAL FIELD
This application relates to the field of electronic transactions and more
particularly to the
field of distributed public ledgers, securing the contents of sequence of
transaction blocks, and
the verification of electronic payments.
BACKGROUND OF THE INVENTION
A blockchain consists of an augmentable sequence of blocks: B1, B2,...,
wherein each block
consists of a number of transactions, the hash of the previous block, and
other data e.g., the
index of the block, time information, etc. Useful properties of a blockchain
are that (P1) there
is a unique block corresponding to each index 1, 2, ... , (P2) every user in
the system eventually
learns the content of every block, (P3) no one can alter the content or the
order of the blocks,
and (P4) any valid transactio will eventually enter a block in the chain.
Users can digitally sign messages, and thus each user possesses at least one
public key and
a corresponding secret key. In a blockchain, in general, one knows the public
keys but not
necessarily the user who owns it. Accordingly, we may identify a public key
with its owner.
Several blockchain systems require a block to be certified by the digital
signatures of
sufficiently many users in the system. In some systems such certifying users
belong to a fixed
set of users. In some other systems they belong to a dynamically changing set.
The latter is
preferrable, because an adversary would have a harder time to corrupt a
dynamically changing
set, particularly if the set is not only dynamic, but unpredictable as well.
A particularly effective way of selecting a set of users in a verifiable but
unpredictable
way is the cryptographic sortition technique is described in published PCT
patent application
PCT/U52017/031037, which is incorporated by reference herein. Here, a user i
belongs to a
set of users empowered to act in some step s during the production of block
number r based on
the result of a computation that i performs via a secret key of his, using
inputs s and r, and
possibly other inputs and other data (e.g., the fact that the user has joined
the system at least
k blocks before block r, for some given integer k). For instance, i's
computation may involve
i's digital signature, szr's, of such inputs, hashing szr's, and checking
whether the hash is less
than a given threshold t. (Indeed, like any other string, a hashed value can
be interpreted in
1
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
some standard way as a number.) In this case, CT tr's = Str's is defined to be
the credential of i for
step s about block r. Such credential proves to anyone that i is indeed
entitled to produce a
(preferably signed) message mzr's, his voting message for step s in round r,
in the process aimed
at producing block r. In fact, i's digital signatures can be checked by
anyone, and anyone can
hash a given value, and then check whether the result is indeed less than (or
equal to) a given
number.
A blockchain works by propagating messages (e.g., blocks, transactions, voting
messages,
digital signatures, etc). Typically, but not exclusively, messages are
propagated by gossiping
them in a peer-to-peer fashion, or via relays. Several blockchain systems
require the propagation
network to guarantee the delivery of messages propagated by every honest user
to other honest
users within a bounded delay. Some further require the users to have (almost)
aligned system
clocks, so that the users propagate messages in a synchronized way _________
e.g., the users enter
step 2 in the generation of block 100 at time 11:20:00am EST, the voting
messages for this step
are delivered by time 11:20:05am EST, and the users enter step 3 of block 100
then. A less
demanding and thus preferable requirement, as imposed by Algorand, is that the
users' clocks
have (almost) the same speed, but the actual times shown on the clocks can be
arbitrarily far
from each other. A user starts his own step s in the generation of block r
based on the messages
he has received from the propagation network, and ends it based on messages
received and how
long his own clock has advanced since he started this step.
When the propagation network satisfies this requirement, Algorand ensures that
the
adversary cannot prevent the blockchain from functioning properly (including
achieving
properties P1 _______________________________________________________________
P4). However, this relies on the adversary not attacking the propagation
network
itself. Such attacks include any effort the adversary may take in order to
violate the bounded
delay of message delivery for a sufficiently large amount of users __________
e.g., by partitioning the users
into two groups of equal size and controlling the message delivery channels
between them, so
that a message propagated by a user from group 1 may have indefinite delay
before reaching
any user in group 2.
It is thus desirable to weaken this requirement and provide blockchains and
electronic
money systems that do not suffer from the inefficiencies and insecurities of
known decentralized
approaches.
SUMMARY OF THE INVENTION.
According to the system described herein, an entity manages a transaction
system in which
transactions are organized in a sequence of blocks that are certified by
digital signatures of a
sufficient number of verifiers by the entity proposing a hash of a block B'
that includes new
valid transactions relative to a sequence of certified blocks B Br-
1- if no rth block Br has
been certified and by the entity proposing a hash of the block Br if the rth
block Br has been
verified by a sufficient number of other entities. A block may be certified by
the entity only in
response to confirming transactions for the block and confirming that the
block was constructed
and propagated by an entity entitled to construct and propagate the block. The
entity may
propose a hash value by digitally signing the hash value to provide a
digitally-signed version of
the hash value and the entity may propagate the digitally-signed version of
the hash value to a
network that includes other entities. If no rth block Br has been certified,
the entity may also
digitally sign and propagate the block B'. The entity may determine a quantity
Q from the
prior blocks and may use a secret key in order to compute a string S uniquely
associated with Q
and computes from S a quantity T that is S itself, a function of S, and/or a
hash value of S and
the entity may determine whether to propose a hash value by determining
whether T possesses
a given property. S may be a signature of Q under a secret key of the entity,
T may be a hash of
S and T may possess the given property if T is less than a given threshold.
The entity may be
2
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
part of a network of entities and a particular one of the entities may
construct and propagates
the block Br . The rth block Br may be determined to be certified by the
entity if the entity
receives an indication that at least a predetermined number of the entities
individually certify a
hash value corresponding to the rth block Br . In response to the entity
receiving the indication
that a predetermined number of the entities individually certified the rth
block Br , the entity
may increment r to begin adding additional blocks to the sequence of blocks.
The particular
one of the entities may be individually chosen by a predetermined number of
the entities to be a
leader. The rth block Br may be determined to be certifiable by the entity if
the entity receives
an indication that at least a predetermined number of the entities
individually verify receiving
an indication that the particular one of the entities has provided a hash
value corresponding to
the rth block Br to each of the predetermined number of the entities.
According further to the system described herein, an entity manages a
transaction system
in which transactions are organized in a sequence of certified blocks by the
entity receiving
a hash value of a block Br from an other entity that generated the block based
on new valid
transactions relative to a sequence of certified blocks B , . . . , Br-1,the
entity certifying the block
Br in response to a sufficient number of other entities having indicated
receipt of the hash value
of the block Br from the other entity and the hash value being valid for the
block Br , the entity
generating a new block B' based on new valid transactions relative to a
sequence of certified
blocks B ,... , Br-1- in response to an insufficient number of the other
entities indicating receipt
of the hash value of the block Br from the other entity, B' being different
from Br , and the
entity incrementing r to begin adding additional blocks to the sequence of
blocks in response
to the entity receiving the indication that a predetermined number of the
entities individually
certified the rth block Br or a predetermined number of the entities
individually certified the
new block B'. The blocks may be certified by digital signatures. New blocks
may be proposed
by different ones of the entities until receiving the indication that a
predetermined number
of the entities individually certified a previously proposed block. The entity
may provides an
indication that a new block should be generated in response to the hash value
not being valid
for the block Br . The entity may generate a new block B' based on new valid
transactions
relative to a sequence of certified blocks B ,.. . , Br-1- in response to a
sufficient number of the
other entities providing an indication that a new block should be generated.
The entity may
provide an indication that the hash value of the block Br should be propagated
in response to
a sufficient number of the other entities having indicated receipt of the hash
value of the block
Br from the other entity and the hash value being valid for the block Br .
According further to the system described herein, an entity verifies a
proposed hash value of
a new block Br of transactions relative to a given a sequence of blocks, B ,..
. , Br-1, without
access to the new block Br in a transaction system in which transactions are
organized in blocks
and blocks are certified by a set of digital signatures by having the entity
determine a quantity
Q from the prior blocks, having the entity compute a digital signature S of Q,
having the entity
compute from S a quantity T that is S itself, a function of S, and/or hash
value of S, having the
entity determine whether T possesses a given property, andfif T possesses the
given property,
having the entity verify the proposed hash value of the new block Br
independent of confirming
whether the proposed hash value corresponds to the new block Br . The entity
may propagate
the proposed hash value of the new block Br prior to receiving the new block
Br .
According furtheer to the system described herein, in a transaction system in
which
transactions are organized in blocks, a new block Br of valid transactions is
constructed, relative
to a sequence of prior blocks B , BI-, ... , Br-1, by having an entity
determine a quantity Q from
the prior blocks, having the entity use a secret key in order to compute a
string S uniquely
associated to Q, having the entity compute from S a quantity T that is S
itself, a function of
S, and/or a hash value of S, having the entity determine whether T possesses a
given property
3
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
and, if T possesses the given property, having the the entity compute a hash
value H of Br ,
digitally sign H and make available to others S, Br and a digitally signed
version of H. The
secret key may be a secret signing key corresponding to a public key of the
entity and S is a
digital signature of Q by the entity. T may be a binary expansion of a number
and satisfies
the given property if T is less than a given number p. S may be made available
by making S
deducible from Br . Each user may have a balance in the transaction system and
p may vary
for each user according to the balance of each user.
According further to the system described herein, selecting a subset of users
in a blockchain
system to verify a data string m relative to a sequence of prior blocks B ,...
, Br-1-, includes
causing at least some of the users to determine a quantity Q from the prior
blocks, causing at
least some of the users to compute a digital signature S of Q and other
information, causing at
least some of the users to determine a hash value of the digital signature,
causing at least some
of the users to compare the hash value to a pre-determined threshold, and
causing the subset
of the users to digitally sign m together with other information and make
available to others S
and a digitally signed version of m in response to the hash value being below
a pre-determined
threshold for each of the subset of users. The digital signature may be
credentialed if the hash
value is below a pre-determined threshold. Each user may have a balance in the
transaction
system and the pre-determined threshold may vary for each user according to
the balance of
each user. The pre-determined threshold for each user may be chosen to cause
the subset of the
users to contain a minimum number of the users. The data string m may be a
hash value of a
new block Br . The data string m may be verified by at least a given number of
credentialed
signatures of m.
According further to the system described herein, selecting a subset of users
in a blockchain
system to certify a new block Br relative to a sequence of prior blocks B ,...
, Br-1-, includes
causing at least some of the users to determine a quantity Q from the prior
blocks, causing at
least some of the users to compute a digital signature S of Q and other
information, causing at
least some of the users to determine a hash value of the digital signature,
causing at least some
of the users to compare the hash value to a pre-determined threshold, causing
the subset of
the users to determine Br is valid relative to B ,. .. , Br-1- in response to
the hash value being
below a pre-determined threshold for each of the subset of users and causing
the subset of the
users to digitally sign a hash value H of Br together with other information
and make available
to others S and a digitally signed version of H. A particular one of the users
may digitally sign
the new block Br only if the particular one of the users verifies information
provided in the
new block Br . Each user may have a balance in the transaction system and the
pre-determined
threshold may vary for each user according to the balance of each user. The
pre-determined
threshold for each user may be chosen to cause the subset of the users to
contain a minimum
number of the users. The block Br may be certified by at least a given number
of credentialed
signatures of H from users who have determined Br is valid relative to B ,...
, Br-1-.
According further to the system described herein, computer software, provided
in a non-
transitory computer-readable medium, includes executable code that implements
any of the
steps described herein.
The present invention dispenses with the requirement on the propagation
network's message
delivery delay for the security of certifying new blocks. A new block is first
prepared (e.g.,
proposed, propagated, and/or agreed upon by at least some users) and then it
is certified.
A user who has receive a newly constructed block, a hash value of a new block,
and/or
credentialed signatures within a desired time interval proceeds to verify
and/or certify the
new block. However, we wish to certify a new block even when messages
propagated in the
network may be indefinitely delayed. The certification of a block B guarantees
that certain
valuable properties apply to the block. A typical main property is to enable a
user, even a
4
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
user who has not participated to or observed the preparation of a block B, to
ascertain that B
has been added to the blockchain, or even that B is the rth block in the
blockchain. Another
valuable property (often referred to as finalization) guarantees that B will
not disappear from
the blockchain, due to a soft fork, even in the presence of a partition of the
communication
network on which the blockchain protocol is executed. A partition of the
network may cause
the users to be separated into multiple groups, with messages propagated from
one group not
reaching users in other groups. A partition may be resolved after an
indefinite amount of time,
after which the network again guarantees message delivery after bounded
delays.
Assume that a block B has been prepared, in any fashion and in any number of
steps.
Realizing that a block has been properly prepared requires time and effort,
and the verification
of various pieces of evidence. A certificate of B consists of a given number
of users' digital
signatures with valid credentials. Such a certificate of B vouches that the
users who have
produced such signatures have participated to or observed the preparation of
B. At least, it
vouches that, if one of the digital signatures of the certificate has been
produced by an honest
user, then that user has checked that B has been properly prepared.
In the system described herein, while a user is collecting evidences for one
block B being
properly prepared as the rth block in the blockchain relative to prior blocks
B ,. .. , Br-1-, the
user may construct and propose a new block B' as the rth block in the
blockchain relative to
B , ... , Br-1- if he has evidence that a certificate of B has not been
generated in the system. A
user proposes B' by determining a quantity Q from prior blocks, computing a
string S uniquely
associated to Q using a secret key, computing from S a quantity T that is S
itself, a function
of S, and/or a hash value of S, determining whether T possesses a given
property and, if T
possesses the given property, computing a hash value H' of B', digitally
signing H' and making
available to others S, B' and a digitally signed version of H'. The secret key
may be a secret
signing key corresponding to a public key of the entity and S is a digital
signature of Q by the
entity. T may be a binary expansion of a number and satisfies the given
property if T is less
than a given number p. S may be made available by making S deducible from B'.
Each user
may have a balance in the transaction system and p may vary for each user
according to the
balance of each user.
In the system described herein, while a user is collecting evidences for one
block B being
properly prepared as the rth block in the blockchain relative to prior blocks
B ,. .. , Br-1-, the
user may re-propose B as the rth block in the blockchain if he has evidence
that a certificate
of B may have been generated in the system but have not been made available to
him. A user
may re-propose B without having received B itself but rather having received a
given number of
users' digital signatures with valid credentials verifying a hash value of B.
A user may re-propose
B by determining a quantity Q from prior blocks, computing a string S uniquely
associated to
Q using a secret key, computing from S a quantity T that is S itself, a
function of S, and/or
a hash value of S, determining whether T possesses a given property and, if T
possesses the
given property, digitally signing a hash value H of B and making available to
others S and a
digitally signed version of H. The secret key may be a secret signing key
corresponding to a
public key of the entity and S is a digital signature of Q by the entity. T
may be a binary
expansion of a number and satisfies the given property if T is less than a
given number p. S
may be made available by making S deducible from B'. Each user may have a
balance in the
transaction system and p may vary for each user according to the balance of
each user.
Proposing new blocks and re-proposing existing blocks may happen indefinite
amount of
times during the generation of a rth block of the blockchain and may be
carried out by different
users. A block B may have more than one certificates generated from different
steps. However,
during the generation of a rth block of the blockchain, one and only one block
will have a
certificate and thus be considered by the users as the rth block of the
blockchain.
5
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
The efficiency of the system described herein derives from the following
facts. First, a
user i may verify and/or re-propose a hash value of a block B before the user
may receive
B itself. Second, a new block B' may be proposed as the rth block before all
users may have
collected evidence that a previously proposed block B as the rth block does
not have a certificate
generated in the system. Indeed, B' may be proposed as soon as one user has
collected such
evidence. Third, a previously proposed block B as the rth block of the
blockchain may be
re-proposed before all users may have collected evidence that a certificate
for B may have been
generated in the system but not made available to all. Indeed, B may be re-
proposed as soon
as one user has collected such an evidence.
An evidence may consists of a set of credentialed signatures properly formed
to verify a data
string m. Evidences for different purposes may consist of different numbers of
signatures. The
security of the system described herein derives from proper choices of pre-
determined thresholds
that users compare the hash values of their signatures to when verifying
different data strings,
and from proper choices of numbers of signatures sufficient to form evidences
for different
purposes. For instance, let p be the maximum percentage of malicious users in
the system.
Typically, malicious users are in a minority _______________________________
e.g., p < 1/3. Then the pre-determined threshold
t and the sufficient number n of signatures forming a certificate for a block
may be chosen so
that, with sufficiently high probability, (a) for any possible block value B,
there are n or more
credentialed signatures of honest users to form a certificate for B and (b) in
any certificate of
B, more than 2/3 of credentialed signatures belongs to honest users.
The system described herein is agnostic about whether ephemeral keys are used
in the
blockchain: when users propose new blocks, re-propose existing blocks, or
verify data strings,
the users may use long-term secret keys to generate credentialed signatures,
where the keys may
be used repeatedly during the life time of the system, or the users may use
ephemeral secret
keys where one key is used only once, or the users may use combinations of
long-term keys and
ephemeral keys.
As part of the system described herein, a user i may not only have a
credentialed signature
for participating in the generation of a block, but also a credentialed
signature with a weight
(essentially a credentialed signature associated with a number of votes).
Indeed, the weight of
i's credential signature for participating in the generation of a block may
depend on how much
money i has in the system. Indeed, rather than having a single pre-determined
threshold t for
all users for participating in block generation, each user i may have his own
threshold tz that
is higher the higher i's amount of money is. And a user i may have different
thresholds for
participating in block generation in different ways ________________________
e.g., proposing a new block, re-proposing
a block, or verifying a data string m of a specific format. For simplicity,
but without limitation
intended, we shall continue to describe our system treating a user i with a
weight-n credentialed
signature as n users, each having a (weight-1) credentialed signature.
Below, after quickly recalling the traditional Algorand system, we provide an
example of
the preferred embodiment, without any limitation intended, based on Algorand.
BRIEF DESCRIPTION OF THE DRAWINGS.
Embodiments of the system described herein are explained in more details in
accordance
with the figures of the drawings, which are briefly described as follows.
FIG. 1 is a schematic representation of a network and computing stations
according to an
embodiment of the system described herein.
FIG. 2 is a schematic and conceptual summary of the first step of Algorand
system, where
a new block of transactions is proposed.
FIG. 3 is a schematic and conceptual summary of the agreement and
certification of a new
block in the Algorand system.
6
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
FIG. 4 is a schematic diagram illustrating a Merkle tree and an authenticating
path for a
value contained in one of its nodes.
FIG. 5 is a schematic diagram illustrating the 8 Merkle trees corresponding to
the first 8
blocks constructed in a blocktree.
FIG. 6 is a schematic representation of a partitioned network and computing
stations
according to an embodiment of the system described herein.
DETAILED DESCRIPTION OF VARIOUS EMBODIMENTS.
The system described herein provides a mechanisms for distributing transaction
verification
and propagation so that no entity is solely responsible for performing
calculations to verify
and/or propagate transaction information. Instead, each of the participating
entities shares in
the calculations that are performed to propagate transaction in a verifiable
and reliable manner.
Referring to FIG. 1, a diagram 20 shows a plurality of computing workstations
22a-22c
connected to a data network 24, such as the Internet. The workstations 22a-22c
communicate
with each other via the network 24 to provide distributed transaction
propagation and
verification, as described in more detail elsewhere herein. The system may
accommodate
any number of workstations capable of providing the functionality described
herein, provided
that the workstations 22a-22c are capable of communicating with each other.
Each of the
workstations 22a-22c may independently perform processing to propagate
transactions to all
of the other workstations in the system and to verify transactions, as
described in more detail
elsewhere herein.
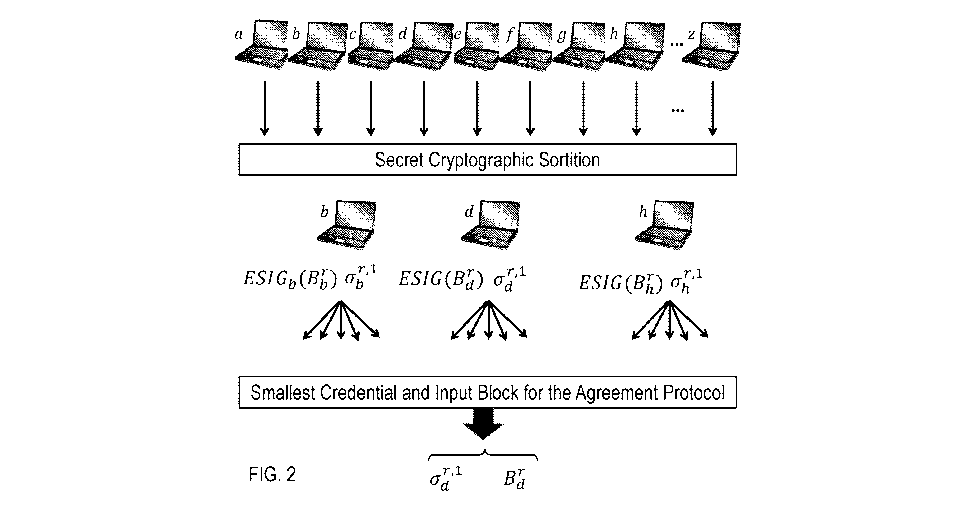
FIG. 2 diagrammatically and conceptually summarizes the first step of a round
r in the
Algorand system, where each of a few selected users proposes his own candidate
for the rth
block. Specifically, the step begins with the users in the system, a, ... , z,
individually undergo
the secret cryptographic sortition process, which decides which users are
selected to propose a
block, and where each selected user secretly computes a credential proving
that he is entitled to
produce a block. Only users b, d, and h are selected to propose a block, and
their respectively
r 1 r
computed credentials are o-b' ,a1, and o-hr'l. Each selected user i assembles
his own proposed
block, B"' , ephemerally signs it (i.e., digitally signs it with an ephemeral
key, as explained later
on), and propagates to the network together with his own credential. The
leader of the round
is the selected user whose credential has the smallest hash. The figure
indicates the leader to
be user d. Thus his proposed block, B, is the one to be given as input to the
Binary agreement
protocol.
FIG. 3 diagrammatically and conceptually summarizes Algorand's process for
reaching
agreement and certifying a proposed block as the official rth block, Br .
Since the first step
of Algorand consists of proposing a new block, this process starts with the
second step. This
step actually coincides with the first step of Algorand's preferred Byzantine
agreement protocol,
BA*. Each step of this protocol is executed by a different "committee" of
players, randomly
selected by secret cryptographic sortition (not shown in this figure).
Accordingly, the users
selected to perform each step may be totally different. The number of Steps of
BA* may vary.
Fig. 3 depicts an execution of BA* involving 7 steps: from Algorand's 2
through Algorand's
step 8. The users selected to perform step 2 are a, e, and q. Each user i E
{a, e, q} propagates
to the network his credential, CT tr that proves that i is indeed entitled to
send a message in
step 2 of round r of Algorand, and his message proper of this step, mzr's,
ephemerally signed.
Steps 3-7 are not shown. In the last step 8, the figure shows that the
corresponding selected
users, b, f, and x, having reached agreement on Br as the official block of
round r, propagate
their own ephemeral signatures of block Br (together, these signatures certify
Br ) and their
own credentials, proving that they are entitled to act in Step 8.
FIG. 4 schematically illustrates a Merkle tree and one of its autenticating
path. Specifically,
7
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Fig. 4.A illustrates a full Merkle tree of depth 3. Each node x, where x is
denoted by a binary
string of length < 3, stores a value vx. If x has length < 2, then vx = H(vxo,
vi). For the
Merkle tree of Fig. 4.a, Fig. 4.B illustrates the authenticating path of the
value v010.
FIG. 5 schematically illustrates the 8 Merkle trees, corresponding to the
first 8 blocks
constructed in a blocktree, constructed within a full binary tree of depth 3.
In Fig. 5.i, nodes
marked by an integer belong to Merkle tree T. Contents of nodes marked by i
(respectively, by
i) are temporary (respectively, permanent).
The description herein focuses on transactions that are payments and on
describing the
system herein as a money platform. Those skilled in the art will realize that
the system described
herein can handle all kinds of transactions as well.
The system described herein has a very flexible design and can be implemented
in various,
but related, ways. We illustrate its flexibility by detailing two possible
embodiments of its
general design. From them, those skilled in the art can appreciate how to
derive all kinds of
other implementations as well.
To facilitate understanding the invention, and allow to internal cross
reference of its various
parts, we organize its presentation in numbered and titled sections. The first
sections are
common to both of the detailed embodiments.
1 Introduction
Money is becoming increasingly virtual. It has been estimated that about 80%
of United States
dollars today only exist as ledger entries. Other financial instruments are
following suit.
In an ideal world, in which we could count on a universally trusted central
entity, immune
to all possible cyber attacks, money and other financial transactions could be
solely electronic.
Unfortunately, we do not live in such a world. Accordingly, decentralized
cryptocurrencies, such
as Bitcoin, and "smart contract" systems, such as Ethereum, have been
proposed. At the heart
of these systems is a shared ledger that reliably records a sequence of
transactions, as varied
as payments and contracts, in a tamperproof way. The technology of choice to
guarantee such
tamperproofness is the blockchain. Blockchains are behind applications such as
cryptocurrencies,
financial applications, and the Internet of Things. Several techniques to
manage blockchain-
based ledgers have been proposed: proof of work, proof of stake, practical
Byzantine fault-
tolerance, or some combination.
Currently, however, ledgers can be inefficient to manage. For example,
Bitcoin's proof-of-
work approach requires a vast amount of computation, is wasteful and scales
poorly. In addition,
it de facto concentrates power in very few hands.
We therefore wish to put forward a new method to implement a public ledger
that offers
the convenience and efficiency of a centralized system run by a trusted and
inviolable authority,
without the inefficiencies and weaknesses of current decentralized
implementations. We call
our approach Algorand, because we use algorithmic randomness to select, based
on the ledger
constructed so far, a set of verifiers who are in charge of constructing the
next block of valid
transactions. Naturally, we ensure that such selections are provably immune
from manipulations
and unpredictable until the last minute, but also that they ultimately are
universally clear.
Algorand's approach is quite democratic, in the sense that neither in
principle nor de facto
it creates different classes of users (as "miners" and "ordinary users" in
Bitcoin). In Algorand
"all power resides with the set of all users".
One notable property of Algorand is that its transaction history may fork only
with very
small probability (e.g., one in a trillion, that is, or even 10-18). Algorand
can also address some
legal and political concerns.
8
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
The Algorand approach applies to blockchains and, more generally, to any
method of
generating a tamperproof sequence of blocks. We actually put forward a new
method
alternative to, and more efficient than, blockchains that may be of
independent interest.
1.1 Bitcoin's Assumption and Technical Problems
Bitcoin is a very ingenious system and has inspired a great amount of
subsequent research.
Yet, it is also problematic. Let us summarize its underlying assumption and
technical problems
which are actually shared by essentially all cryptocurrencies that, like
Bitcoin, are based on
proof-of-work.
For this summary, it suffices to recall that, in Bitcoin, a user may own
multiple public keys
of a digital signature scheme, that money is associated with public keys, and
that a payment
is a digital signature that transfers some amount of money from one public key
to another.
Essentially, Bitcoin organizes all processed payments in a chain of blocks,
B1, B2,..., each
consisting of multiple payments, such that, all payments of B1, taken in any
order, followed by
those of B2, in any order, etc., constitute a sequence of valid payments. Each
block is generated,
on average, every 10 minutes.
This sequence of blocks is a chain, because it is structured so as to ensure
that any change,
even in a single block, percolates into all subsequent blocks, making it
easier to spot any
alteration of the payment history. (As we shall see, this is achieved by
including in each block
a cryptographic hash of the previous one.) Such block structure is referred to
as a blockchain.
Assumption: Honest Majority of Computational Power Bitcoin assumes that no
malicious entity (nor a coalition of coordinated malicious entities) controls
the majority of
the computational power devoted to block generation. Such an entity, in fact,
would be able
to modify the blockchain, and thus re-write the payment history, as it
pleases. In particular, it
could make a payment 0, obtain the benefits paid for, and then "erase" any
trace of 0.
Technical Problem 1: Computational Waste Bitcoin's proof-of-work approach to
block
generation requires an extraordinary amount of computation. Currently, with
just a few hundred
thousands public keys in the system, the top 500 most powerful supercomputers
can only muster
a mere 12.8% percent of the total computational power required from the
Bitcoin players. This
amount of computation would greatly increase, should significantly more users
join the system.
Technical Problem 2: Concentration of Power Today, due to the exorbitant
amount of
computation required, a user, trying to generate a new block using an ordinary
desktop (let
alone a cell phone), expects to lose money. Indeed, for computing a new block
with an ordinary
computer, the expected cost of the necessary electricity to power the
computation exceeds the
expected reward. Only using pools of specially built computers (that do
nothing other than
"mine new blocks"), one might expect to make a profit by generating new
blocks. Accordingly,
today there are, de facto, two disjoint classes of users: ordinary users, who
only make payments,
and specialized mining pools, that only search for new blocks.
It should therefore not be a surprise that, as of recently, the total
computing power for block
generation lies within just five pools. In such conditions, the assumption
that a majority of the
computational power is honest becomes less credible.
Technical Problem 3: Ambiguity In Bitcoin, the blockchain is not necessarily
unique.
Indeed its latest portion often forks: the blockchain may be say
B1, , Bk, Bik+2,
according to one user, and B1,
, Bk, N+1, N+2, N+3 according another user. Only after
9
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
several blocks have been added to the chain, can one be reasonably sure that
the first k 3
blocks will be the same for all users. Thus, one cannot rely right away on the
payments contained
in the last block of the chain. It is more prudent to wait and see whether the
block becomes
sufficiently deep in the blockchain and thus sufficiently stable.
Separately, law-enforcement and monetary-policy concerns have also been raised
about
Bitcoin.'
1.2 Algorand, in a Nutshell
Setting Algorand works in a very tough setting. Briefly,
(a) Permissionless and Permissioned Environments. Algorand works efficiently
and securely
even in a totally permissionless environment, where arbitrarily many users are
allowed to
join the system at any time, without any vetting or permission of any kind. Of
course,
Algorand works even better in a permissioned environment.
(b) Very Adversarial Environments. Algorand withstands a very powerful
Adversary, who can
(1) instantaneously corrupt any user he wants, at any time he wants, provided
that, in a
permissionless environment, 2/3 of the money in the system belongs to honest
user. (In a
permissioned environment, irrespective of money, it suffices that 2/3 of the
users are honest.)
(2) totally control and perfectly coordinate all corrupted users; and
(3) schedule the delivery of all messages, provided that each message m sent
by a honest
user reaches reaches all (or sufficiently many of) the honest users within a
time Arn, which
solely depends on the size of m.
Main Properties Despite the presence of our powerful adversary, in Algorand
= The amount of computation required is minimal. Essentially, no matter how
many users are
present in the system, each of fifteen hundred users must perform at most a
few seconds of
computation.
= A new block is generated quickly and will de facto never leave the
blockchain. That is,
Algorand's blockchain may fork only with negligible probability (i.e., less
than one in a trillion
or 10-18). Thus, users can relay on the payments contained in a new block as
soon as the
block appears.
= All power resides with the users themselves. Algorand is a truy
distributed system. In
particular, there are no exogenous entities (as the "miners" in Bitcoin), who
can control
which transactions are recognized.
'The (pseudo) anonymity offered by Bitcoin payments may be misused for money
laundering and/or the
financing of criminal individuals or terrorist organizations. Traditional
banknotes or gold bars, that in principle
offer perfect anonymity, should pose the same challenge, but the physicality
of these currencies substantially
slows down money transfers, so as to permit some degree of monitoring by law-
enforcement agencies.
The ability to "print money" is one of the very basic powers of a nation
state. In principle, therefore, the
massive adoption of an independently floating currency may curtail this power.
Currently, however, Bitcoin is
far from being a threat to governmental monetary policies, and, due to its
scalability problems, may never be.
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Algorand's Techniques.
1. A NEW AND FAST BYZANTINE AGREEMENT PROTOCOL. Algorand generates a new block
via an inventive cryptographic, message-passing, binary Byzantine agreement
(BA) protocol,
BA*. Protocol BA* not only satisfies some additional properties (that we shall
soon discuss),
but is also very fast. Roughly said, its binary-input version consists of a 3-
step loop, in which a
player i sends a single message m, to all other players. Executed in a
complete and synchronous
network, with more than 2/3 of the players being honest, with probability >
1/3, after each loop
the protocol ends in agreement. (We stress that protocol BA* satisfies the
original definition
of Byzantine agreement, without any weakenings.)
Algorand leverages this binary BA protocol to reach agreement, in our
different commu-
nication model, on each new block. The agreed upon block is then certified,
via a prescribed
number of digital signature of the proper verifiers, and propagated through
the network.
2. SECRET CRYPTOGRAPHIC SORTITION. Although very fast, protocol BA* would
benefit
from further speed when played by millions of users. Accordingly, Algorand
chooses the players
of BA* to be a much smaller subset of the set of all users. To avoid a
different kind of
concentration-of-power problem, each new block Br will be constructed and
agreed upon, via
a new execution of B A* , by a separate set of selected verifiers, SVr. In
principle, selecting
such a set might be as hard as selecting Br directly. We traverse this
potential problem
by a novel approach that we term secret cryptographic sortition. Sortition is
the practice of
selecting officials at random from a large set of eligible individuals.
(Sortition was practiced
across centuries: for instance, by the republics of Athens, Florence, and
Venice. In modern
judicial systems, random selection is often used to choose juries. Random
sampling has also
been advocated for elections.) In a decentralized system, of course, choosing
the random coins
necessary to randomly select the members of each verifier set SVr is
problematic. We thus
resort to cryptography in order to select each verifier set, from the
population of all users, in
a way that is guaranteed to be automatic (i.e., requiring no message exchange)
and random.
In a similar fashion we select a user, the leader, in charge of proposing the
new block Br , and
the verifier set SVr, in charge to reach agreement on the block proposed by
the leader. The
inventive system leverages some information, Qr-1, that is deducible from the
content of the
previous block and is non-manipulatable even in the presence of a very strong
adversary.
3. THE QUANTITY (SEED) Q. . We use the the last block Br ¨1 in the blockchain
in order to
automatically determine the next verifier set and leader in charge of
constructing the new block
Br . The challenge with this approach is that, by just choosing a slightly
different payment in
the previous round, our powerful Adversary gains a tremendous control over the
next leader.
Even if he only controlled only 1/1000 of the players/money in the system, he
could ensure that
all leaders are malicious. (See the Intuition Section 4.1.) This challenge is
central to all proof-
of-stake approaches, and, to the best of our knowledge, it has not, up to now,
been satisfactorily
solved.
To meet this challenge, we purposely construct, and continually update, a
separate
and carefully defined quantity, Qr , which provably is, not only
unpredictable, but also not
influentiable, by our powerful Adversary. We may refer to Qr as the rth seed,
as it is from Qr
that Algorand selects, via secret cryptographic sortition, all the users that
will play a special
role in the generation of the rth block. The seed Qr will be deducible from
the block Br ¨1 .
4. SECRET CREDENTIALS. Randomly and unambiguously using the current last
block, Br ¨1 , in
order to choose the verifier set and the leader in charge of constructing the
new block, Br , is not
enough. Since Br ¨1 must be known before generating Br , the last non-
influentiable quantity
11
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Qr-1 deducible from Br-1 must be known too. Accordingly, so are the verifiers
and the leader
in charge to compute the block Br . Thus, our powerful Adversary might
immediately corrupt
all of them, before they engage in any discussion about Br , so as to get full
control over the
block they certify.
To prevent this problem, leaders (and actually verifiers too) secretly learn
of their role,
but can compute a proper credential, capable of proving to everyone that
indeed have that role.
When a user privately realizes that he is the leader for the next block, first
he secretly assembles
his own proposed new block, and then disseminates it (so that can be
certified) together with
his own credential. This way, though the Adversary will immediately realize
who the leader
of the next block is, and although he can corrupt him right away, it will be
too late for the
Adversary to influence the choice of a new block. Indeed, he cannot "call
back" the leader's
message no more than a powerful government can put back into the bottle a
message virally
spread by WikiLeaks.
As we shall see, we cannot guarantee leader uniqueness, nor that everyone is
sure who
the leader is, including the leader himself! But, in Algorand, unambiguous
progress will be
guaranteed.
5. PLAYER REPLACEABILITY. After he proposes a new block, the leader might as
well "die"
(or be corrupted by the Adversary), because his job is done. But, for the
verifiers in SVr, things
are less simple. Indeed, being in charge of certifying the new block Br with
sufficiently many
signatures, they must first run Byzantine agreement on the block proposed by
the leader. The
problem is that, no matter how efficient it is, BA* requires multiple steps
and the honesty of
> 2/3 of its players. This is a problem, because, for efficiency reasons, the
player set of BA*
consists the small set SVr randomly selected among the set of all users. Thus,
our powerful
Adversary, although unable to corrupt 1/3 of all the users, can certainly
corrupt all members
of SW!
Fortunately we'll prove that protocol B A* , executed by propagating messages
in a peer-to-
peer fashion, is player-replaceable. This novel requirement means that the
protocol correctly and
efficiently reaches consensus even if each of its step is executed by a
totally new, and randomly
and independently selected, set of players. Thus, with millions of users, each
small set of players
associated to a step of BA* most probably has empty intersection with the next
set.
In addition, the sets of players of different steps of BA* will probably have
totally different
cardinalities. Furthermore, the members of each set do not know who the next
set of players
will be, and do not secretly pass any internal state.
The replaceable-player property is actually crucial to defeat the dynamic and
very powerful
Adversary we envisage. We believe that replaceable-player protocols will prove
crucial in lots
of contexts and applications. In particular, they will be crucial to execute
securely small sub-
protocols embedded in a larger universe of players with a dynamic adversary,
who, being able to
corrupt even a small fraction of the total players, has no difficulty in
corrupting all the players
in the smaller sub-protocol.
An Additional Property/Technique: Lazy Honesty A honest user follows his
prescribed
instructions, which include being online and run the protocol. Since, Algorand
has only modest
computation and communication requirement, being online and running the
protocol "in the
background" is not a major sacrifice. Of course, a few "absences" among honest
players, as
those due to sudden loss of connectivity or the need of rebooting, are
automatically tolerated
(because we can always consider such few players to be temporarily malicious).
Let us point
out, however, that Algorand can be simply adapted so as to work in a new
model, in which
honest users to be offline most of the time. Our new model can be informally
introduced as
12
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
follows.
Lazy Honesty. Roughly speaking, a user i is lazy-but-honest if (1) he follows
all his prescribed
instructions, when he is asked to participate to the protocol, and (2) he is
asked to participate
to the protocol only rarely, and with a suitable advance notice.
With such a relaxed notion of honesty, we may be even more confident that
honest people will
be at hand when we need them, and Algorand guarantee that, when this is the
case,
The system operates securely even if, at a given point in time,
the majority of the participating players are malicious.
2 Preliminaries
2.1 Cryptographic Primitives
Ideal Hashing. We shall rely on an efficiently computable cryptographic hash
function, H,
that maps arbitrarily long strings to binary strings of fixed length.
Following a long tradition, we
model H as a random oracle, essentially a function mapping each possible
string s to a randomly
and independently selected (and then fixed) binary string, H(s), of the chosen
length.
In our described embodiments, H has 256-bit long outputs. Indeed, such length
is short
enough to make the system efficient and long enough to make the system secure.
For instance,
we want H to be collision-resilient. That is, it should be hard to find two
different strings x and
y such that H(x) = H(y). When H is a random oracle with 256-bit long outputs,
finding any
such pair of strings is indeed difficult. (Trying at random, and relying on
the birthday paradox,
would require 2256/2 = 2128 trials.)
Digital Signing. Digital signatures allow users to to authenticate information
to each other
without sharing any sharing any secret keys. A digital signature scheme
consists of three fast
algorithms: a probabilistic key generator G, a signing algorithm S, and a
verification algorithm
V.
Given a security parameter k, a sufficiently high integer, a user i uses G to
produce a pair of
k-bit keys (i.e., strings): a "public" key pk, and a matching "secret" signing
key ski. Crucially,
a public key does not "betray" its corresponding secret key. That is, even
given knowledge of
pkz, no one other than i is able to compute sk, in less than astronomical
time.
User i uses sk, to digitally sign messages. For each possible message (binary
string) m,
first hashes m and then runs algorithm S on inputs H(m) and sk, so as to
produce the k-bit
string
sigpk,(m) S(H(m), ski) .2
The binary string sigpk,(m) is referred to as i's digital signature of m
(relative to pk,), and can
be more simply denoted by sigz(m), when the public key pk, is clear from
context.
Everyone knowing pk, can use it to verify the digital signatures produced by
i. Specifically,
on inputs (a) the public key pk, of a player i, (b) a message m, and (c) a
string s, that is, i's
alleged digital signature of the message m, the verification algorithm V
outputs either YES or
NO.
The properties we require from a digital signature scheme are:
1. Legitimate signatures are always verified: If s = sigz(m), then V(pk,,m,$)
= YES; and
2Since H is collision-resilient it is practically impossible that, by signing
m one "accidentally signs" a different
message a.
13
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
2. Digital signatures are hard to forge: Without knowledge of sk, the time to
find a string s
such that V(pk,,m,$) =Y ES, for a message m never signed by i, is
astronomically long.
(Following strong security requirements, this is true even if one can obtain
the signature of
any other message.)
Accordingly, to prevent anyone else from signing messages on his behalf, a
player i must keep
his signing key sk, secret (hence the term "secret key"), and to enable anyone
to verify the
messages he does sign, i has an interest in publicizing his key pk, (hence the
term "public key").
Signatures with Message Retrievability In general, a message m is not
retrievable from its
signature sigz(m). In order to virtually deal with digital signatures that
satisfy the conceptually
convenient "message retrievability" property (i.e., to guarantee that the
signer and the message
are easily computable from a signature, we define
S/Gpki (m) = (i, m, sigpk,(m)) and S IG,(m) = (i, m, sigz(m)), if pk, is
clear.
Unique Digital Signing. We also consider digital signature schemes (G, 5, V)
satisfying the
following additional property.
3. Uniqueness. It is hard to find strings pk', m, s, and s' such that
s s' and V (pk' , m, s) = V (pk' ,m, s') = 1.
(Note that the uniqueness property holds also for strings pk' that are not
legitimately
generated public keys. In particular, however, the uniqueness property implies
that, if one
used the specified key generator G to compute a public key pk together with a
matching
secret key sk, and thus knew sk, it would be essentially impossible also for
him to find two
different digital signatures of a same message relative to pk.)
Remarks
= FROM UNIQUE SIGNATURES TO VERIFIABLE RANDOM FUNCTIONS. Relative to a
digital
signature scheme with the uniqueness property, the mapping m
H(sigz(m)) associates to
each possible string m, a unique, randomly selected, 256-bit string, and the
correctness of
this mapping can be proved given the signature sigz(m).
That is, ideal hashing and digital signature scheme satisfying the uniqueness
property
essentially provide an elementary implementation of a verifiable random
function (VRF).
A VRF is a special kind of digital signature. We may write VRF (m) to indicate
such
a special signature of i of a message m. In addition to satisfy the uniqueness
property,
verifiable random functions produce outputs that are guaranteed to be
sufficiently random.
That is, V RF,(m) is essentially random, and unpredictable until it is
produced. By contrast,
SIC(m) need not be sufficiently random. For instance, user i may choose his
public key so
that SIC(m) always is a k-bit string that is (lexicographically) small (i.e.,
whose first few
bits could always be Os). Note, however, that, since H is an ideal hash
function, H(S/Gz(m))
will always be a random 256-bit string. In our preferred embodiments we make
extensive
use of hashing digital signatures satisfying the uniqueness property precisely
to be able to
associate to each message m and each user i a unique random number. Should one
implement
Algorand with VRFs, one can replace H(S/Gz(m)) with VRF,(m). In particular, a
user
i need not first to compute SIG,(m), then H(SIG,(m)) (in order, ______ say
to compare
H(S/Gz(m)) with a number p). He might directly compute V RF,(m). In sum, it
should be
14
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
understood that H(S/Gz(m)) can be interpreted as VRF,(m), or as a sufficiently
random
number, easily computed by player i, but unpredictable to anyone else,
unambiguously
associated to i and m.
= THREE DIFFERENT NEEDS FOR DIGITAL SIGNATURES. In Algorand, a user i
relies on digital
signatures for
(1) Authenticating i's own payments. In this application, keys can be "long-
term" (i.e.,
used to sign many messages over a long period of time) and come from a
ordinary signature
scheme.
(2) Generating credentials proving that i is entitled to act at some step s of
a round r. Here,
keys can be long-term, but must come from a scheme satisfying the uniqueness
property.
(3) Authenticating the message i sends in each step in which he acts. Here,
keys must be
ephemeral (i.e., destroyed after their first use), but can come from an
ordinary signature
scheme.
= A SMALL-COST SIMPLIFICATION. For simplicity, we envision each user i to
have a single long-
term key. Accordingly, such a key must come from a signature scheme with the
uniqueness
property. Such simplicity has a small computational cost. Typically, in fact,
unique digital
signatures are slightly more expensive to produce and verify than ordinary
signatures.
2.2 The Idealized Public Ledger
Algorand tries to mimic the following payment system, based on an idealized
public ledger.
1. The Initial Status. Money is associated with individual public keys
(privately generated
and owned by users). Letting pki, , pk 3 be the initial public keys and al,
, a3 their
respective initial amounts of money units, then the initial status is
So = (pki, ai), , (pk, a3) ,
which is assumed to be common knowledge in the system.
2. Payments. Let pk be a public key currently having a > 0 money units, pk'
another public
key, and a' a non-negative number no greater than a. Then, a (valid) payment
is a digital
signature, relative to pk, specifying the transfer of a' monetary units from
pk to pk', together
with some additional information. In symbols,
= S Gpk(pk, pk' , , I, H(1)),
where / represents any additional information deemed useful but not sensitive
(e.g., time
information and a payment identifier), and I any additional information deemed
sensitive
(e.g., the reason for the payment, possibly the identities of the owners of pk
and the pk',
and so on).
We refer to pk (or its owner) as the payer, to each pk' (or its owner) as a
payee, and to a'
as the amount of the payment 0.
Free Joining Via Payments. Note that users may join the system whenever they
want by
generating their own public/secret key pairs. Accordingly, the public key pk'
that appears
in the payment above may be a newly generated public key that had never
"owned" any
money before.
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
3. The Magic Ledger. In the Idealized System, all payments are valid and
appear in a tamper-
proof list L of sets of payments "posted on the sky" for everyone to see:
L = PAY1, PAY2, ,
Each block PAY r+1 consists of the set of all payments made since the
appearance of block
PAY. In the ideal system, a new block appears after a fixed (or finite) amount
of time.
Discussion.
= More General Payments and Unspent Transaction Output. More generally, if
a public key
pk owns an amount a, then a valid payment of pk may transfer the amounts a,
a'2,
respectively to the keys pei, , so long as E3 ,31 < a .
In Bitcoin and similar systems, the money owned by a public key pk is
segregated into
separate amounts, and a payment made by pk must transfer such a segregated
amount a
in its entirety. If pk wishes to transfer only a fraction a' < a of a to
another key, then it
must also transfer the balance, the unspent transaction output, to another
key, possibly pk
itself.
Algorand also works with keys having segregated amounts. However, in order to
focus on
the novel aspects of Algorand, it is conceptually simpler to stick to our
simpler forms of
payments and keys having a single amount associated to them.
= Current Status. The Idealized Scheme does not directly provide information
about the
current status of the system (i.e., about how many money units each public key
has). This
information is deducible from the Magic Ledger.
In the ideal system, an active user continually stores and updates the latest
status
information, or he would otherwise have to reconstruct it, either from
scratch, or from
the last time he computed it. (Yet, we later on show how to augment Algorand
so as to
enable its users to reconstruct the current status in an efficient manner.)
= Security and "Privacy". Digital signatures guarantee that no one can
forge a payment of
another user. In a payment 0, the public keys and the amount are not hidden,
but the
sensitive information I is. Indeed, only H(/) appears in 0, and since H is an
ideal hash
function, H(/) is a random 256-bit value, and thus there is no way to figure
out what I was
better than by simply guessing it. Yet, to prove what I was (e.g., to prove
the reason for
the payment) the payer may just reveal I. The correctness of the revealed I
can be verified
by computing H(/) and comparing the resulting value with the last item of 0.
In fact, since
H is collision resilient, it is hard to find a second value I' such that H(/)
= H(//).
2.3 Basic Notions and Notations
Keys, Users, and Owners Unless otherwise specified, each public key ("key" for
short) is
long-term and relative to a digital signature scheme with the uniqueness
property. A public key
i joins the system when another public key j already in the system makes a
payment to i.
For color, we personify keys. We refer to a key i as a "he", say that i is
honest, that i sends
and receives messages, etc. User is a synonym for key. When we want to
distinguish a key from
the person to whom it belongs, we respectively use the term "digital key" and
"owner".
Permissionless and Permissioned Systems. A system is permissionless, if a
digital key
is free to join at any time and an owner can own multiple digital keys; and
its permissioned,
otherwise.
16
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Unique Representation Each object in Algorand has a unique representation. In
particular,
each set {(x, y, z,...) : x E X,y E Y, z E Z, ...} is ordered in a pre-
specified manner: e.g., first
lexicographically in x, then in y, etc.
Same-Speed Clocks There is no global clock: rather, each user has his own
clock. User
clocks need not be synchronized in any way. We assume, however, that they all
have the same
speed.
For instance, when it is 12pm according to the clock of a user i, it may be
2:30pm according
to the clock of another user j, but when it will be 12:01 according to i's
clock, it will 2:31
according to j's clock. That is, "one minute is the same (sufficiently,
essentially the same) for
every user".
Rounds Algorand is organized in logical units, r = 0, 1,..., called rounds.
We consistently use superscripts to indicate rounds. To indicate that a non-
numerical
quantity Q (e.g., a string, a public key, a set, a digital signature, etc.)
refers to a round r, we
simply write Q. . Only when Q is a genuine number (as opposed to a binary
string interpretable
as a number), do we write Q(r), so that the symbol r could not be interpreted
as the exponent
of Q.
At (the start of a) round r > 0, the set of all public keys is PK' , and the
system status is
Sr = (i, 4r), .) :i E
where a(zr) is the amount of money available to the public key i. Note that PK
is deducible
from Sr, and that Sr may also specify other components for each public key i.
For round 0, PK is the set of initial public keys, and S is the initial
status. Both PK and
S are assumed to be common knowledge in the system. For simplicity, at the
start of round r,
so are PK1, , PK' and S1, , Sr .
In a round r, the system status transitions from Sr to Sr+1: symbolically,
Round r: Sr Sr+1.
Payments In Algorand, the users continually make payments (and disseminate
them in the
way described in subsection 2.7). A payment of a user i E PK' has the same
format and
semantics as in the Ideal System. Namely,
= SIG,(i, i', a, I, H(I)) .
Payment is individually valid at a round r (is a round-r payment, for
short) if (1) its
amount a is less than or equal to a,r), and (2) it does not appear in any
official payset PAY''
for r' < r. (As explained below, the second condition means that has not
already become
effective.
A set of round-r payments of i is collectively valid if the sum of their
amounts is at most
a (7') .
Paysets A round-r payset P is a set of round-r payments such that, for each
user i, the
payments of i in P (possibly none) are collectively valid. The set of all
round-r paysets is
PAY(r). A round-r payset P is maximal if no superset of P is a round-r payset.
We actually suggest that a payment also specifies a round p, = SIG,(p,i,i' ,
a, I, H(I)) ,
and cannot be valid at any round outside [p, p k], for some fixed non-negative
integer k.3
3This simplifies checking whether 0 has become "effective" (i.e., it
simplifies determining whether some payset
PAY' contains 0. When k = 0, if 0 = SIG, (r, , a, I, H(I)) , and 0 cl PAY',
then i must re-submit 0.
17
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Official Paysets For every round r, Algorand publicly selects (in a manner
described later
on) a single (possibly empty) payset, PAY', the round's official payset.
(Essentially, PAY'
represents the round-r payments that have "actually" happened.)
As in the Ideal System (and Bitcoin), (1) the only way for a new user j to
enter the system
is to be the recipient of a payment belonging to the official payset PAY of a
given round r;
and (2) PAY' determines the status of the next round, Sr-hi, from that of the
current round,
Sr. Symbolically,
PAY' : Sr S" 1.
Specifically,
1. the set of public keys of round r 1, PK" 1, consists of the union of PKr
and the set of
all payee keys that appear, for the first time, in the payments of PAY'; and
2. the amount of money a( r+1) that a user i owns in round r +1 is the sum of
az(r) i.e., the
amount of money i owned in the previous round (0 if i 0 PK') ________________
and the sum of amounts
paid to i according to the payments of PAYr. .
In sum, as in the Ideal System, each status Sr-hi is deducible from the
previous payment history:
PAY , ... ,PAYr.
2.4 Blocks and Proven Blocks
In Algorando, the block Br corresponding to a round r specifies: r itself; the
set of payments of
round r, PAYr; a quantity SIGer(Qr-1), to be explained, and the hash of the
previous block,
H(Br-1). Thus, starting from some fixed block B , we have a traditional
blockchain:
B1 = (1, PAY', Sicei (Q ), H(B )), B2 = (2, PAY2,Sice2(Q1), H(B1))= = = =
In Algorand, the authenticity of a block is actually vouched by a separate
piece of
information, a "block certificate" C E RTr , which turns Br into a proven
block, Br . The Magic
Ledger, therefore, is implemented by the sequence of the proven blocks,
B2, ...
Discussion As we shall see, CERTr consists of a set of digital signatures for
H(Br), those
of a majority of the members of SY", together with a proof that each of those
members indeed
belongs to SY". We could, of course, include the certificates CERTr in the
blocks themselves,
but find it conceptually cleaner to keep it separate.)
In Bitcoin each block must satisfy a special property, that is, must "contain
a solution
of a crypto puzzle", which makes block generation computationally intensive
and forks both
inevitable and not rare. By contrast, Algorand's blockchain has two main
advantages: it is
generated with minimal computation, and it will not fork with overwhelmingly
high probability.
Each block Bz is safely final as soon as it enters the blockchain.
2.5 Acceptable Failure Probability
To analyze the security of Algorand we specify the probability, F, with which
we are willing
to accept that something goes wrong (e.g., that a verifier set SY" does not
have an honest
majority). As in the case of the output length of the cryptographic hash
function H, also F is
a parameter. But, as in that case, we find it useful to set F to a concrete
value, so as to get a
more intuitive grasp of the fact that it is indeed possible, in Algorand, to
enjoy simultaneously
18
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
sufficient security and sufficient efficiency. To emphasize that F is
parameter that can be set as
desired, in the first and second embodiments we respectively set
F = 10-12 and F = 10-18 .
Discussion Note that 10-12 is actually less than one in a trillion, and we
believe that such a
choice of F is adequate in our application. Let us emphasize that 10-12 is not
the probability
with which the Adversary can forge the payments of an honest user. All
payments are digitally
signed, and thus, if the proper digital signatures are used, the probability
of forging a payment is
far lower than 10-12, and is, in fact, essentially 0. The bad event that we
are willing to tolerate
with probability F is that Algorand's blockchain forks. Notice that, with our
setting of F and
one-minute long rounds, a fork is expected to occur in Algorand's blockchain
as infrequently as
(roughly) once in 1.9 million years. By contrast, in Bitcoin, a forks occurs
quite often.
A more demanding person may set F to a lower value. To this end, in our second
embodiment
we consider setting F to 10-18. Note that, assuming that a block is generated
every second,
1018 is the estimated number of seconds taken by the Universe so far: from the
Big Bang to
present time. Thus, with F = 10-18, if a block is generated in a second, one
should expect for
the age of the Universe to see a fork.
2.6 The Adversarial Model
Algorand is designed to be secure in a very adversarial model. Let us explain.
Honest and Malicious Users A user is honest if he follows all his protocol
instructions, and
is perfectly capable of sending and receiving messages. A user is malicious
(i.e., Byzantine, in the
parlance of distributed computing) if he can deviate arbitrarily from his
prescribed instructions.
The Adversary The Adversary is an efficient (technically polynomial-time)
algorithm,
personified for color, who can immediately make malicious any user he wants,
at any time
he wants (subject only to an upperbound to the number of the users he can
corrupt).
The Adversary totally controls and perfectly coordinates all malicious users.
He takes all
actions on their behalf, including receiving and sending all their messages,
and can let them
deviate from their prescribed instructions in arbitrary ways. Or he can simply
isolate a corrupted
user sending and receiving messages. Let us clarify that no one else
automatically learns that a
user i is malicious, although i's maliciousness may transpire by the actions
the Adversary has
him take.
This powerful adversary however,
= Does not have unbounded computational power and cannot successfully forge
the digital
signature of an honest user, except with negligible probability; and
= Cannot interfere in any way with the messages exchanges among honest
users.
Furthermore, his ability to attack honest users is bounded by one of the
following assumption.
Honesty Majority of Money We consider a continuum of Honest Majority of Money
(HMM) assumptions: namely, for each non-negative integer k and real h> 1/2,
HHMk > h: the honest users in every round r owned a fraction greater than h of
all money
in the system at round r ¨ k.
19
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Discussion. Assuming that all malicious users perfectly coordinate their
actions (as if
controlled by a single entity, the Adversary) is a rather pessimistic
hypothesis. Perfect
coordination among too many individuals is difficult to achieve. Perhaps
coordination only
occurs within separate groups of malicious players. But, since one cannot be
sure about the
level of coordination malicious users may enjoy, we'd better be safe than
sorry.
Assuming that the Adversary can secretly, dynamically, and immediately corrupt
users is
also pessimistic. After all, realistically, taking full control of a user's
operations should take
some time.
The assumption HMMk > h implies, for instance, that, if a round (on average)
is
implemented in one minute, then, the majority of the money at a given round
will remain
in honest hands for at least two hours, if k = 120, and at least one week, if
k = 10, 000.
Note that the HMM assumptions and the previous Honest Majority of Computing
Power
assumptions are related in the sense that, since computing power can be bought
with money, if
malicious users own most of the money, then they can obtain most of the
computing power.
2.7 The Communication Model
We envisage message propagation __ i.e., "peer-to-peer gossip"4 ____________
to be the only means of
communication, and assume that every propagated message reaches almost all
honest users in a
timely fashion. We essentially assume that each message m propagated by honest
user reaches,
within a given amount of time that depends on the length of m, all honest
users. (It actually
suffices that m reaches a sufficiently high percentage of the honest users.)
The BA Protocol BA* in a Traditional Setting
As already emphasized, Byzantine agreement is a key ingredient of Algorand.
Indeed, it is
through the use of such a BA protocol that Algorand is unaffected by forks.
However, to be
secure against our powerful Adversary, Algorand must rely on a BA protocol
that satisfies
the new player-replaceability constraint. In addition, for Algorand to be
efficient, such a BA
protocol must be very efficient.
BA protocols were first defined for an idealized communication model,
synchronous complete
networks (SC networks). Such a model allows for a simpler design and analysis
of BA protocols.
Accordingly, in this section, we introduce a new BA protocol, BA*, for SC
networks and ignoring
the issue of player replaceability altogether. The protocol BA* is a
contribution of separate
value. Indeed, it is the most efficient cryptographic BA protocol for SC
networks known so far.
To use it within our Algorand protocol, we modify BA* a bit, so as to account
for our
different communication model and context.
We start by recalling the model in which BA* operates and the notion of a
Byzantine
agreement.
3.1 Synchronous Complete Networks and Matching Adver-
saries
In a SC network, there is a common clock, ticking at each integral times r =
1, 2, ...
4Essentially, as in Bitcoin, when a user propagates a message m, every active
user i receiving m for the first
time, randomly and independently selects a suitably small number of active
users, his "neighbors", to whom he
forwards m, possibly until he receives an acknowledgement from them. The
propagation of m terminates when
no user receives m for the first time.
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
At each even time click r, each player i instantaneously and simultaneously
sends a single
message m'z',3 (possibly the empty message) to each player j, including
himself. Each m'' is
correctly received at time click r 1 by player j, together with the identity
of the sender i.
Again, in a communication protocol, a player is honest if he follows all his
prescribed
instructions, and malicious otherwise. All malicious players are totally
controlled and perfectly
coordinated by the Adversary, who, in particular, immediately receives all
messages addressed
to malicious players, and chooses the messages they send.
The Adversary can immediately make malicious any honest user he wants at any
odd time
click he wants, subject only to a possible upperbound t to the number of
malicious players.
That is, the Adversary "cannot interfere with the messages already sent by an
honest user i",
which will be delivered as usual.
The Adversary also has the additional ability to see instantaneously, at each
even round,
the messages that the currently honest players send, and instantaneously use
this information
to choose the messages the malicious players send at the same time tick.
3.2 The Notion of a Byzantine Agreement
The notion of Byzantine agreement might have been first introduced for the
binary case, that is,
when every initial value consists of a bit. However, it was quickly extended
to arbitrary initial
values. By a BA protocol, we mean an arbitrary-value one.
Definition 3.1. In a synchronous network, let P be a n-player protocol, whose
player set is
common knowledge among the players, t a positive integer such that n> 2t 1. We
say that P
is an arbitrary-value (respectively, binary) (n, t)-Byzantine agreement
protocol with soundness
a E (0, 1) if, for every set of values V not containing the special symbol I
(respectively, for
V = {0,1}), in an execution in which at most t of the players are malicious
and in which
every player i starts with an initial value vz E V, every honest player j
halts with probability 1,
outputting a value out, E V U {I} so as to satisfy, with probability at least
a, the following two
conditions:
1. Agreement: There exists out E V U {I} such that out, = out for all honest
players i.
2. Consistency: if, for some value v E V, vz = v for all players i, then out =
V.
We refer to out as P's output, and to each out, as player i's output.
3.3 The BA Notation
In our BA protocols, a player is required to count how many players sent him a
given message
in a given step. Accordingly, for each possible value v that might be sent,
#:(v)
(or just #z(v) when s is clear) is the number of players j from which i has
received v in step s.
Recalling that a player i receives exactly one message from each player j, if
the number of
players is n, then, for all i and s, > #:(v) = n.
3.4 The New Binary BA Protocol BBA*
In this section we present a new binary BA protocol, BBA*, which relies on the
honesty of more
than two thirds of the players and is very fast: no matter what the malicious
players might
21
CA 03086361 2020-06-18
WO 2019/126311
PCT/US2018/066481
do, each execution of its main loop not only is trivially executed, but brings
the players into
agreement with probability 1/3.
In BBA*, each player has his own public key of a digital signature scheme
satisfying the
unique-signature property. Since this protocol is intended to be run on
synchronous complete
network, there is no need for a player i to sign each of his messages.
Digital signatures are used to generate a sufficiently common random bit in
Step 3. (In
Algorand, digital signatures are used to authenticate all other messages as
well.)
The protocol requires a minimal set-up: a common random string r, independent
of the
players' keys. (In Algorand, r is actually replaced by the quantity Qr.)
Protocol BBA* is a 3-step loop, where the players repeatedly exchange Boolean
values, and
different players may exit this loop at different times. A player i exits this
loop by propagating,
at some step, either a special value 0* or a special value 1*, thereby
instructing all players
to "pretend" they respectively receive 0 and 1 from i in all future steps.
(Alternatively said:
assume that the last message received by a player j from another player i was
a bit b. Then, in
any step in which he does not receive any message from i, j acts as if i sent
him the bit b.)
The protocol uses a counter y, representing how many times its 3-step loop has
been
executed. At the start of BBA*, y = 0. (One may think of 'y as a global
counter, but it
is actually increased by each individual player every time that the loop is
executed.)
There are n > 3t+1, where t is the maximum possible number of malicious
players. A binary
string x is identified with the integer whose binary representation (with
possible leadings Os) is
x; and lsb(x) denotes the least significant bit of x.
PROTOCOL BBA*
(COMMUNICATION) STEP 1. [Coin-Fixed-To-0 Step] Each player i sends bz.
1.1 If (0) > 2t +1, then i sets b, = 0, sends 0*, outputs out, = 0, and
HALTS.
1.2 If #(1) > 2t +1, then, then i sets I), = 1.
1.3 Else, i sets I), = 0.
(COMMUNICATION) STEP 2. [Coin-Fixed-To-1 Step] Each player i sends bz.
2.1 If Yq(1) > 2t +1, then i sets b, =1, sends 1*, outputs out, =1, and HALTS.
2.2 If Yq(0)> 2t +1, then i set b, =0.
2.3 Else, i sets b, =1.
(COMMUNICATION) STEP 3. [Coin-Genuinely-Flipped Step] Each player i sends b,
and SIG,(r,ry).
3.1 If e(0) > 2t 1, then i sets b, = 0.
3.2 If e(1)> 2t +1, then i sets I), = 1.
3.3 Else, letting S, = fj E N who have sent i a proper message in this step 3
1,
i sets I), = c lsb(minics, H(SIG,(r,-)/))); increases -y, by I; and returns to
Step I.
Theorem 3.1. Whenever n > 3t +1, BBA* is a binary (n,t)-BA protocol with
soundness I.
A proof of Theorem 3.1 can be found in https://people.csail.mit.edu/silvio/
SelectedScien-
tificPapers/DistributedComputation/BYZANTINEAGREEMENTMADETRIVIAL. 15 pdf.
22
CA 03086361 2020-06-18
WO 2019/126311
PCT/US2018/066481
3.5 Graded Consensus and the Protocol GC
Let us recall, for arbitrary values, a notion of consensus much weaker than
Byzantine agreement.
Definition 3.2. Let P be a protocol in which the set of all players is common
knowledge, and
each player i privately knows an arbitrary initial value v.
We say that P is an (n, t)-graded consensus protocol if, in every execution
with n players, at
most t of which are malicious, every honest player i halts outputting a value-
grade pair (vi, 9,2),
where g, E {0,1, 2}, so as to satisfy the following three conditions:
I. For all honest players i and j, gi ¨ 931 < 1.
2. For all honest players i and j, gt, 9,1 > 0 v3 = v3.
3. If v'1 = = = = = vn = v for some value v, then v, = v and g, = 2 for all
honest players i.
The following two-step protocol GC is a graded consensus protocol in the
literature. To
match the steps of protocol Algorand'i of section 4.1, we respectively name 2
and 3 the steps of
GC. (Indeed, the first step of A/gorand'i is concerned with something else:
namely, proposing
a new block.)
PROTOCOL GC
STEP 2. Each player i sends v't to all players.
STEP 3. Each player i sends to all players the string x if and only if #(x) >
2f 1.
OUTPUT DETERMINATION. Each player i outputs the pair (vi, g,) computed as
follows:
= If, for some x, #(x) > 2f 1, then v, = x and g, = 2.
= If, for some x, (x) > t 1, then v, = x and g, = 1.
= Else, v, = I and g, = 0.
Since protocol GC is a protocol in the literature, it is known that the
following theorem
holds.
Theorem 3.2. If n> 3f 1, then GC is a (n, t)-graded broadcast protocol.
3.6 The Protocol BA*
We now describe the arbitrary-value BA protocol BA* via the binary BA protocol
BBA* and
the graded-consensus protocol GC. Below, the initial value of each player i is
v.
PROTOCOL BA*
STEPS 1 AND 2. Each player i executes GC, on input et, so as to compute a pair
(v,, g,).
STEP 3, ... Each player i executes BBA* _______________________________ with
initial input 0, if g, = 2, and I otherwise
so as to compute the bit out,.
OUTPUT DETERMINATION. Each player i outputs v, if out, = 0, and I otherwise.
Theorem 3.3. Whenever n > 3t 1, BA* is a (n,t)-BA protocol with soundness I.
23
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Proof. We first prove Consistency, and then Agreement.
PROOF OF CONSISTENCY. Assume that, for some value v E V, viz = v. Then, by
property 3 of
graded consensus, after the execution of GC, all honest players output (v, 2).
Accordingly, 0 is
the initial bit of all honest players in the end of the execution of BBA*.
Thus, by the Agreement
property of binary Byzantine agreement, at the end of the execution of B A* ,
out, = 0 for all
honest players. This implies that the output of each honest player i in BA* is
v, = v. El
PROOF OF AGREEMENT. Since BBA* is a binary BA protocol, either
(A) out, = 1 for all honest player i, or
(B) out, = 0 for all honest player i.
In case A, all honest players output I in BA*, and thus Agreement holds.
Consider now case
B. In this case, in the execution of BBA*, the initial bit of at least one
honest player i is 0.
(Indeed, if initial bit of all honest players were 1, then, by the Consistency
property of BBA*,
we would have outi = 1 for all honest j.) Accordingly, after the execution of
GC, i outputs
the pair (v, 2) for some value v. Thus, by property 1 of graded consensus, gj
> 0 for all honest
players j. Accordingly, by property 2 of graded consensus, tt? = v for all
honest players j. This
implies that, at the end of BA*, every honest player j outputs v. Thus,
Agreement holds also
in case B. El
Since both Consistency and Agreement hold, BA* is an arbitrary-value BA
protocol. =
Protocol BA* works also in gossiping networks, and in fact satisfies the
player replaceability
property that is crucial for Algorand to be secure in the envisaged very
adversarial model.
The Player Replaceability of BBA* and BA* Let us now provide some intuition of
why
the protocols BA* and BBA* can be adapted to be executed in a network where
communication
is via peer-to-peer gossiping, satisfy player replaceability. For
concreteness, assume that the
network has 10M users and that each step x of BBA* (or BA*) is executed by a
committee of
10,000 players, who have been randomly selected via secret cryptographic
sortition, and thus
have credentials proving of being entitled to send messages in step x. Assume
that each message
sent in a given step specifies the step number, is digitally signed by its
sender, and includes the
credential proving that its sender is entitled to speak in that step.
First of all, if the percentage h of honest players is sufficiently larger
than 2/3 (e.g., 75%),
then, with overwhelming probability, the committee selected at each step has
the required 2/3
honest majority.
In addition, the fact that the 10,000-strong randomly selected committee
changes at each
step does not impede the correct working of either BBA* or BA*. Indeed, in
either protocol,
a player i in step s only reacts to the multiplicity with which, in Step s ¨
1, he has received
a given message m. Since we are in a gossiping network, all messages sent in
Step s ¨ 1 will
(immediately, for the purpose of this intuition) reach all users, including
those selected to play
in step s. Furthermore because all messages sent in step s ¨ 1 specify the
step number and
include the credential that the sender was indeed authorized to speak in step
s ¨ 1. Accordingly,
whether he happened to have been selected also in step s ¨ 1 or not, a user i
selected to play
in step s is perfectly capable of correctly counting the multiplicity with
which he has received
a correct step s ¨ 1 message. It does not at all matter whether he has been
playing all steps so
far or not. All users are in "in the same boat" and thus can be replaced
easily by other users.
24
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
4 Two Embodiments of Algorand
As discussed, at a very high level, a round of Algorand ideally proceeds as
follows. First, a
randomly selected user, the leader, proposes and circulates a new block. (This
process includes
initially selecting a few potential leaders and then ensuring that, at least a
good fraction of
the time, a single common leader emerges.) Second, a randomly selected
committee of users is
selected, and reaches Byzantine agreement on the block proposed by the leader.
(This process
includes that each step of the BA protocol is run by a separately selected
committee.) The
agreed upon block is then digitally signed by a given threshold (TH) of
committee members.
These digital signatures are propagated so that everyone is assured of which
is the new block.
(This includes circulating the credential of the signers, and authenticating
just the hash of the
new block, ensuring that everyone is guaranteed to learn the block, once its
hash is made clear.)
In the next two sections, we present two embodiments of the basic Algorand
design,
A/gorand'i and Algorand, that respectively work under a proper majority-of-
honest-users
assumption. In Section 7 we show how to adopts these embodiments to work under
a honest-
majority-of-money assumption.
Algorand'i only envisages that > 2/3 of the committee members are honest. In
addition, in
Algorand, the number of steps for reaching Byzantine agreement is capped at a
suitably high
number, so that agreement is guaranteed to be reached with overwhelming
probability within
a fixed number of steps (but potentially requiring longer time than the steps
of Algorand). In
the remote case in which agreement is not yet reached by the last step, the
committee agrees
on the empty block, which is always valid.
Algorand12 envisages that the number of honest members in a committee is
always greater
than or equal to a fixed threshold tH (which guarantees that, with
overwhelming probability,
at least 2/3 of the committee members are honest). In addition, Algorand12
allows Byzantine
agreement to be reached in an arbitrary number of steps (but potentially in a
shorter time than
Algorand).
Those skilled in the art will realize that many variants of these basic
embodiments can be
derived. In particular, it is easy, given Algorand, to modify A/gorand'i so as
to enable to reach
Byzantine agreement in an arbitrary number of steps.
Both embodiments share the following common core, notations, notions, and
parameters.
4.1 A Common Core
Objectives Ideally, for each round r, Algorand should satisfy the following
properties:
1. Perfect Correctness. All honest users agree on the same block Br .
2. Completeness I. With probability 1, the block Br has been chosen by a
honest user.
(Indeed a malicious user may always choose a block whose payset contains the
payments of just
his "friends".)
Of course, guaranteeing perfect correctness alone is trivial: everyone always
chooses the
official payset PAY to be empty. But in this case, the system would have
completeness 0.
Unfortunately, guaranteeing both perfect correctness and completeness 1 is not
easy in the
presence of malicious users. Algorand thus adopts a more realistic objective.
Informally, letting
h denote the percentage of users who are honest, h> 2/3, the goal of Algorand
is
Guaranteeing, with overwhelming probability, perfect correctness and
completeness close to h.
Privileging correctness over completeness seems a reasonable choice: payments
not processed
in one round can be processed in the next, but one should avoid forks, if
possible.
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Led Byzantine Agreement Disregarding excessive time and communication for a
moment,
perfect Correctness could be guaranteed as follows. At the start of round r,
each user i proposes
his own candidate block B. . Then, all users reach Byzantine agreement on just
one of the
candidate blocks. As per our introduction, the BA protocol employed requires a
2/3 honest
majority and is player replaceable. Each of its step can be executed by a
small and randomly
selected set of verifiers, who do not share any inner variables.
Unfortunately, this approach does not quite work. This is so, because the
candidate blocks
proposed by the honest users are most likely totally different from each
other. Indeed, each
honest user sees different payments. Thus, although the sets of payments seen
by different
honest users may have a lot of overlap, it is unlikely that all honest users
will construct a
propose the same block. Accordingly, the consistency agreement of the BA
protocol is never
binding, only the agreement one is, and thus agreement may always been reached
on I rather
than on a good block.
Algorand' avoids this problem as follows. First, a leader for round r, fr, is
selected. Then, fr
propagates his own candidate block, B. Finally, the users reach agreement on
the block they
actually receive from fr. Because, whenever fr is honest, Perfect Correctness
and Completeness
1 both hold, Algorand' ensures that fr is honest with probability close to h.
Leader Selection In Algorand's, the rth block is of the form
Br = (r, PAYr, H(Br-1).
As already mentioned in the introduction, the quantity Qr-1- is carefully
constructed so as to
be essentially non-manipulatable by our very powerful Adversary. (Later on in
this section, we
shall provide some intuition about why this is the case.) At the start of a
round r, all users
know the blockchain so far, B ,
, Br-1, from which they deduce the set of users of every prior
round: that is, PK1, , PKr-1. A potential leader of round r is a user i
such that
.H (SIG, (r, 1, Qr ¨1)) < p .
Let us explain. Note that, since the quantity Qr-1- is deducible from block Br-
1, because of
the message retrievability property of the underlying digital signature
scheme. Furthermore,
the underlying signature scheme satisfies the uniqueness property. Thus, SIG,
(r,1,Qr-1)
is a binary string uniquely associated to i and r. Accordingly, since H is a
random oracle,
H (SIG, (r, 1, Qr-1)) is a random 256-bit long string uniquely associated to i
and r. The
symbol "." in front of H (SIG, (r, 1, Qr-1)) is the decimal (in our case,
binary) point, so that
r,
.H (SIG, (r, 1, Qr-1)) is the binary expansion of a random 256-bit number
between 0 and
1 uniquely associated to i and r. Thus the probability that r, is less than or
equal to p is
essentially p.
The probability p is chosen so that, with overwhelming (i.e., 1 ¨ F)
probability, at least one
potential verifier is honest. (If fact, p is chosen to be the smallest such
probability.)
Note that, since i is the only one capable of computing his own signatures, he
alone can
determine whether he is a potential verifier of round 1. However, by revealing
his own credential,
SIG (r, 1, Qr-1), i can prove to anyone to be a potential verifier of round r.
The leader r is defined to be the potential leader whose hashed credential is
smaller that
the hashed credential of all other potential leader j: that is, H(oTer,'s) <
H(os).
Note that, since a malicious fr may not reveal his credential, the correct
leader of round r
may never be known, and that, barring improbable ties, r is indeed the only
leader of round r.
Let us finally bring up a last but important detail: a user i can be a
potential leader (and
thus the leader) of a round r only if he belonged to the system for at least k
rounds. This
26
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
guarantees the non-manipulatability of Qr and all future Q-quantities. In
fact, one of the
potential leaders will actually determine Q.
.
Verifier Selection Each step s > 1 of round r is executed by a small set of
verifiers, SV".
Again, each verifier i E SVr's is randomly selected among the users already in
the system k
rounds before r, and again via the special quantity Qr-1-. Specifically, i E
Picr¨k is a verifier
in SV", if
.H (SIG, (r, s,Qr-1)) < .
Once more, only i knows whether he belongs to SV",but, if this is the case, he
could prove it
by exhibiting his credential az" = H(SIGt (r,s,Qr-1)). A verifier i E SVr's
sends a message,
mtr's, in step s of round r, and this message includes his credential CT tr's
, so as to enable the
verifiers f the nest step to recognize that mtr's is a legitimate step-s
message.
The probability p' is chosen so as to ensure that, in SV", letting #good be
the number
of honest users and #bad the number of malicious users, with overwhelming
probability the
following two conditions hold.
For embodiment Algoran4:
(1) #good > 2 = #bad and
(2) #good 4 = #bad < 2n, where n is the expected cardinality of SV".
For embodiment Algorand12:
(1) #good > tH and
(2) #good +2#bad < 2tH, where tH is a specified threshold.
These conditions imply that, with sufficiently high probability, (a) in the
last step of the BA
protocol, there will be at least given number of honest players to digitally
sign the new block
Br (b) only one block per round may have the necessary number of signatures,
and (c) the
used BA protocol has (at each step) the required 2/3 honest majority.
Clarifying Block Generation If the round-r leader fr is honest, then the
corresponding
block is of the form
Br = (r, PAY, sic (Qr ¨1) H (Br-1)) ,
where the payset PAY r is maximal. (recall that all paysets are, by
definition, collectively valid.)
Else (i.e., if fr is malicious), Br has one of the following two possible
forms:
Br = (r, PAY, SIGt (Qr ¨1) H (Br ¨1)) and Br = BrE: (r,0, Q-1 H (Br ¨1)) .
In the first form, PAY r is a (non-necessarily maximal) payset and it may be
PAY r = 0; and i
is a potential leader of round r. (However, i may not be the leader fr . This
may indeed happen
if if fr keeps secret his credential and does not reveal himself.)
The second form arises when, in the round-r execution of the BA protocol, all
honest players
output the default value, which is the empty block BrE: in our application.
(By definition, the
possible outputs of a BA protocol include a default value, generically denoted
by I. See
section 3.2.)
Note that, although the paysets are empty in both cases, Br = (Qr
H (Br-1))
and BrE: are syntactically different blocks and arise in two different
situations: respectively, "all
went smoothly enough in the execution of the BA protocol", and "something went
wrong in the
BA protocol, and the default value was output".
Let us now intuitively describe how the generation of block Br proceeds in
round r of
Algorand/ . In the first step, each eligible player, that is, each player i E
PKr¨k , checks whether
27
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
he is a potential leader. If this is the case, then i is asked, using of all
the payments he has seen
so far, and the current blockchain, B ,
, Br-1, to secretly prepare a maximal payment set,
PAY:, and secretly assembles his candidate block, Br = (r, PAY:, SIG, (Qr-1-)
,H (Br-1)).
That,is, not only does he include in B, as its second component, the just
prepared payset, but
also, as its third component, his own signature of Qr-1, the third component
of the last block,
Br-1. Finally, he propagates his round-r-step-1 message, mrt'l, which includes
(a) his candidate
block B'z' , (b) his proper signature of his candidate block (i.e., his
signature of the hash of Br ,
and (c) his own credential 0-tr'l, proving that he is indeed a potential
verifier of round r.
(Note that, until an honest i produces his message mtr'1, the Adversary has no
clue that i is
a potential verifier. Should he wish to corrupt honest potential leaders, the
Adversary might as
well corrupt random honest players. However, once he sees mrt'l, since it
contains i's credential,
the Adversary knows and could corrupt i, but cannot prevent n4", which is
virally propagated,
from reaching all users in the system.)
In the second step, each selected verifier j E SVr'2 tries to identify the
leader of the round.
Specifically, j takes the step-1 credentials, , o-
tr'1, contained in the proper step-1 message
rntr'l he has received; hashes all of them, that is, computes H (o-zr ;1) ,
,H (o-tr'1); finds the
credential, o-re'l, whose hash is lexicographically minimum; and considers fri
to be the leader of
3
round r.
Recall that each considered credential is a digital signature of Qr-1, that
SIG, (r, 1, Qr-1)
is uniquely determined by i and Qr-1, that H is random oracle, and thus that
each
H(S/G3 (r, 1, Qr-1) is a random 256-bit long string unique to each potential
leader i of round
r.
From this we can conclude that, if the 256-bit string Qr-1 were itself
randomly and
independently selected, than so would be the hashed credentials of all
potential leaders of round
r. In fact, all potential leaders are well defined, and so are their
credentials (whether actually
computed or not). Further, the set of potential leaders of round r is a random
subset of the
users of round r ¨ k, and an honest potential leader i always properly
constructs and propagates
his message m13', which contains i's credential. Thus, since the percentage of
honest users is h,
no matter what the malicious potential leaders might do (e.g., reveal or
conceal their own
credentials), the minimum hashed potential-leader credential belongs to a
honest user, who is
necessarily identified by everyone to be the leader fr of the round r.
Accordingly, if the 256-bit
string Qr-1 were itself randomly and independently selected, with probability
exactly h (a) the
leader fr is honest and (b) 3 = fr for all honest step-2 verifiers j.
In reality, the hashed credential are, yes, randomly selected, but depend on
Qr-1, which is
not randomly and independently selected. A careful analysis, however,
guarantees that Qr-1 is
sufficiently non-manipulatable to guarantee that the leader of a round is
honest with probability
h' sufficiently close to h: namely, h'> h2 (1+ h ¨ h2). For instance, if h =
80%, then h'> .7424.
Having identified the leader of the round (which they correctly do when the
leader fr is
honest), the task of the step-2 verifiers is to start executing BA* using as
initial values what
they believe to be the block of the leader. Actually, in order to minimize the
amount of
communication required, a verifier j E SVr'2 does not use, as his input value
tt; to the Byzantine
protocol, the block B3 that he has actually received from .3 (the user j
believes to be the leader),
but the the leader, but the hash of that block, that is, tt; = H(B3). Thus,
upon termination
of the BA protocol, the verifiers of the last step do not compute the desired
round-r block Br ,
but compute (authenticate and propagate) H(Br). Accordingly, since H(Br) is
digitally signed
by sufficiently many verifiers of the last step of the BA protocol, the users
in the system will
realize that H(Br) is the hash of the new block. However, they must also
retrieve (or wait for,
since the execution is quite asynchronous) the block Br itself, which the
protocol ensures that
28
CA 03086361 2020-06-18
WO 2019/126311
PCT/US2018/066481
is indeed available, no matter what the Adversary might do.
Asynchrony and Timing A/gorand'i and Algoranc112 have a significant degree of
asynchrony.
This is so because the Adversary has large latitude in scheduling the delivery
of the messages
being propagated. In addition, whether the total number of steps in a round is
capped or not,
there is the variance contribute by the number of steps actually taken.
As soon as he learns the certificates of B ,. , Br-1, a user i computes Qr-1
and starts
working on round r, checking whether he is a potential leader, or a verifier
in some step s of
round r.
Assuming that i must act at step s, in light of the discussed asynchrony, i
relies on various
strategies to ensure that he has sufficient information before he acts.
For instance, he might wait to receive at least a given number of messages
from the verifiers
of the previous step (as in Alg oranciii), or wait for a sufficient time to
ensure that he receives
the messages of sufficiently many verifiers of the previous step (as in
Algoranc112).
The Seed Cr and the Look-Back Parameter k Recall that, ideally, the quantities
Qr should random and independent, although it will suffice for them to be
sufficiently non-
manipulatable by the Adversary.
At a first glance, we could choose Qr-1 to coincide with H (PAYr-1). An
elementary
analysis reveals, however, that malicious users may take advantage of this
selection mechanism.5
Some additional effort shows that myriads of other alternatives, based on
traditional block
quantities are easily exploitable by the Adversary to ensure that malicious
leaders are very
frequent. We instead specifically and inductively define our brand new
quantity Qr so as to be
able to prove that it is non-manipulatable by the Adversary. Namely,
Qr
H(S/aer (V-1), r), if Br is not the empty block, and Qr H (Qr-1 , r)
otherwise.
The intuition of why this construction of Qr works is as follows. Assume for a
moment that
Qr-1 is truly randomly and independently selected. Then, will so be Qr? When
fr is honest
the answer is (roughly speaking) yes. This is so because
H(S/Ger(=),r) {0, 1}256 {0, 1}256
is a random function. When fr is malicious, however, Qr is no longer
univocally defined from
Qr-1 and fr . There are at least two separate values for Qr . One continues to
be Qr
H (S aer(Qr-1) , r), and the other is H(Qr-1, r). Let us first argue that,
while the second
5We are at the start of round r ¨ 1. Thus, Qr-2 = PAYr-2 is publicly known,
and the Adversary privately
knows who are the potential leaders he controls. Assume that the Adversary
controls 10% of the users, and
that, with very high probability, a malicious user w is the potential leader
of round r ¨1. That is, assume that
H (SIGõ, (r ¨ 2, 1, Qr-2)) is so small that it is highly improbable an honest
potential leader will actually be
the leader of round r ¨ 1. (Recall that, since we choose potential leaders via
a secret cryptographic sortition
mechanism, the Adversary does not know who the honest potential leaders are.)
The Adversary, therefore, is
in the enviable position of choosing the payset PAY' he wants, and have it
become the official payset of round
r ¨ 1. However, he can do more. He can also ensure that, with high
probability, (*) one of his malicious users
will be the leader also of round r, so that he can freely select what PAY r
will be. (And so on. At least for a
long while, that is, as long as these high-probability events really occur.)
To guarantee (*), the Adversary acts
as follows. Let PAY' be the payset the Adversary prefers for round r ¨ 1.
Then, he computes H(PAY') and
checks whether, for some already malicious player z,
H(PAY')) is particularly small, that is, small
enough that with very high probability z will be the leader of round r. If
this is the case, then he instructs w
to choose his candidate block to be B,r-1 = (r ¨ 1, PAY', H (Br-2). Else, he
has two other malicious users x
and y to keep on generating a new payment 0', from one to the other, until,
for some malicious user z (or even
for some fixed user z) H (SIG. (PAY' U {0})) is particularly small too. This
experiment will stop quite quickly.
And when it does the Adversary asks w to propose the candidate block Bzr-1 =
(r ¨ 1, PAY' U {0}, H (Br-2)).
29
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
choice is somewhat arbitrary, a second choice is absolutely mandatory. The
reason for this is
that a malicious fr can always cause totally different candidate blocks to be
received by the
honest verifiers of the second step.6 Once this is the case, it is easy to
ensure that the block
ultimately agreed upon via the BA protocol of round r will be the default one,
and thus will not
contain anyone's digital signature of Qr-1. But the system must continue, and
for this, it needs
a leader for round r. If this leader is automatically and openly selected,
then the Adversary will
trivially corrupt him. If it is selected by the previous Qr-1 via the same
process, than fr will
again be the leader in round r +1. We specifically propose to use the same
secret cryptographic
sortition mechanism, but applied to a new Q-quantity: namely, H(Qr-1, r). By
having this
quantity to be the output of H guarantees that the output is random, and by
including r as the
second input of H, while all other uses of H have either a single input or at
least three inputs,
"guarantees" that such a Qr is independently selected. Again, our specific
choice of alternative
Qr does not matter, what matter is that fr has two choice for Qr, and thus he
can double his
chances to have another malicious user as the next leader.
The options for Qr may even be more numerous for the Adversary who controls a
malicious
tr. For instance, let x, y, and z be three malicious potential leaders of
round r such that
H (o-xr4) <H (ar4) <H (0-zr'1)
and H (o-zr'1) is particulary small. That is, so small that there is a good
chance that H (o-zr'1)
is smaller of the hashed credential of every honest potential leader. Then, by
asking x to hide
his credential, the Adversary has a good chance of having y become the leader
of round r ¨ 1.
This implies that he has another option for Qr: namely, H (SIGy (Qr-1) r).
Similarly, the
Adversary may ask both x and y of withholding their credentials, so as to have
z become the
leader of round r ¨ 1 and gaining another option for Qr: namely, H (51-Gz (Qr-
1) r).
Of course, however, each of these and other options has a non-zero chance to
fail, because
the Adversary cannot predict the hash of the digital signatures of the honest
potential users.
A careful, Markov-chain-like analysis shows that, no matter what options the
Adversary
chooses to make at round r ¨ 1, as long as he cannot inject new users in the
system, he cannot
decrease the probability of an honest user to be the leader of round r 40 much
below h.
This is the reason for which we demand that the potential leaders of round r
are users already
existing in round r ¨ k. It is a way to ensure that, at round r ¨ k, the
Adversary cannot
alter by much the probability that an honest user become the leader of round
r. In fact, no
matter what users he may add to the system in rounds r ¨ k through r, they are
ineligible to
become potential leaders (and a fortiori the leader) of round r. Thus the look-
back parameter
k ultimately is a security parameter. (Although, as we shall see in section
??, it can also be a
kind of "convenience parameter" as well.)
Ephemeral Keys Although the execution of our protocol cannot generate a fork,
except with
negligible probability, the Adversary could generate a fork, at the rth block,
after the legitimate
block r has been generated.
Roughly, once Br has been generated, the Adversary has learned who the
verifiers of each
step of round r are. Thus, he could therefore corrupt all of them and oblige
them to certify a
new block Br . Since this fake block might be propagated only after the
legitimate one, users
that have been paying attention would not be fooled.7 Nonetheless, B would be
syntactically
correct and we want to prevent from being manufactured.
6For instance, to keep it simple (but extreme), "when the time of the second
step is about to expire", r could
directly email a different candidate block B, to each user i. This way,
whoever the step-2 verifiers might be, they
will have received totally different blocks.
7Consider corrupting the news anchor of a major TV network, and producing and
broadcasting today a
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
We do so by means of a new rule. Essentially, the members of the verifier set
SW"' of a
step s of round r use ephemeral public keys pktr's to digitally sign their
messages. These keys
are single-use-only and their corresponding secret keys skr's are destroyed
once used. This way,
if a verifier is corrupted later on, the Adversary cannot force him to sign
anything else he did
not originally sign.
Naturally, we must ensure that it is impossible for the Adversary to compute a
new key
and convince an honest user that it is the right ephemeral key of verifier i E
SW"' to use in
step s.
4.2 Common Summary of Notations, Notions and Parameters
Notations
= r > 0: the current round number.
= s> 1: the current step number in round r.
= Br: the block generated in round r.
= PKr: the set of public keys by the end of round r ¨ 1 and at the
beginning of round r.
= Sr: the system status by the end of round r ¨ 1 and at the beginning of
round r.8
= PAYr: the payset contained in B.
= fr: round-r leader. fr chooses the payset PAY of round r (and determines
the next Qr).
= Qr: the seed of round r, a quantity (i.e., binary string) that is
generated at the end of
round r and is used to choose verifiers for round r 1. Qr is independent of
the paysets
in the blocks and cannot be manipulated by fr
= SVr's: the set of verifiers chosen for step s of round r.
= SVr: the set of verifiers chosen for round r, SVr = Us>iSVr's.
= MSVr,s and HSVr's: respectively, the set of malicious verifiers and the
set of honest
verifiers in SW's. MSVr's U HSVr's = SVr's and MSVr's n HSVr's = 0.
= ni E Z+ and n E Z+: respectively, the expected numbers of potential leaders
in each SVr'1,
and the expected numbers of verifiers in each SW's, for s > 1.
Notice that n1 << n, since we need at least one honest honest member in SVr,i,
but at
least a majority of honest members in each SW"' for s > 1.
= h E (0,1): a constant greater than 2/3. h is the honesty ratio in the
system. That is, the
fraction of honest users or honest money, depending on the assumption used, in
each PK'
is at least h.
= H: a cryptographic hash function, modelled as a random oracle.
= I: A special string of the same length as the output of H.
= F E (0,1): the parameter specifying the allowed error probability. A
probability < F is
considered "negligible", and a probability > 1 ¨ F is considered
"overwhelming".
= Ph E (0,1): the probability that the leader of a round r, fr , is honest.
Ideally ph = h. With
the existence of the Adversary, the value of ph will be determined in the
analysis.
newsreel showing secretary Clinton winning the last presidential election.
Most of us would recognize it as a
hoax. But someone getting out of a coma might be fooled.
81n a system that is not synchronous, the notion of "the end of round r ¨1"
and "the beginning of round
r" need to be carefully defined. Mathematically, PK' and S' are computed from
the initial status S and the
blocks B', ...,B'.
31
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
= k E Z+: the look-back parameter. That is, round r ¨ k is where the
verifiers for round r
are chosen from ____ namely, SVr c pKr¨k.a
= /31 E (0,1): for the first step of round r, a user in round r ¨ k is
chosen to be in SVr,1 with
probability pi
= p E (0, 1): for each step s > 1 of round r, a user in round r ¨ k is chosen
to be in SVr's
with probability p ________
= CERTr: the certificate for B. It is a set of tH signatures of H(Br) from
proper verifiers
in round r.
= Br (Br ,CERTr) is a proven block.
A user i knows Br if he possesses (and successfully verifies) both parts of
the proven block.
Note that the CERTr seen by different users may be different.
= Tzr: the (local) time at which a user i knows B. In the Algorand protocol
each user has
his own clock. Different users' clocks need not be synchronized, but must have
the same
speed. Only for the purpose of the analysis, we consider a reference clock and
measure the
players' related times with respect to it.
= art's and t3tr's: respectively the (local) time a user i starts and ends
his execution of Step s
of round r.
= A and A: essentially, the upper-bounds to, respectively, the time needed
to execute Step 1
and the time needed for any other step of the Algorand protocol.
Parameter A upper-bounds the time to propagate a single 1MB block.
Parameter A upperbounds the time to propagate one small message per verifier
in a Step
s > 1.
We assume that A <4,\.
Notions
= Verifier selection.
For each round r and step s > 1, SV"
E PK" : .H(SIGt(r,s,Qr-1)) < pl.
Each user i E PK" privately computes his signature using his long-term key and
decides
whether i E SVr's or not. If i E SVr's, then SIG,(r,s,Qr-1) is i's (r, s)-
credential,
compactly denoted by o-tr's.
For the first step of round r, SVr,1 and atr'l are similarly defined, with p
replaced by pl.
The verifiers in SVr,1 are potential leaders.
= Leader selection.
User i E SVr,1 is the leader of round r, denoted by fr , if H(a4) < H (ar'l)
for all potential
leaders j E SVr,i. Whenever the hashes of two players' credentials are
compared, in the
unlikely event of ties, the protocol always breaks ties lexicographically
according to the
(long-term public keys of the) potential leaders.
By definition, the hash value of player r's credential is also the smallest
among all users
in PK". Note that a potential leader cannot privately decide whether he is the
leader or
not, without seeing the other potential leaders' credentials.
Since the hash values are uniform at random, when SVr'i is non-empty, r always
exists
and is honest with probability at least h. The parameter n1 is large enough so
as to ensure
that each SVr'i is non-empty with overwhelming probability.
9Strict1y speaking, "r ¨ k" should be "max{0, r ¨ k}".
32
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
= Block structure.
A non-empty block is of the form Br = (r, PAY', S/Ge,(Qr-1), H(Br-1)), and an
empty
block is of the form BEr = (r, 0, Qr H (Br-1)).
Note that a non-empty block may still contain an empty payset PAY', if no
payment
occurs in this round or if the leader is malicious. However, a non-empty block
implies that
r 1
the identity of fr , his credential cte,' and SIG(Q1) have all been timely
revealed. The
protocol guarantees that, if the leader is honest, then the block will be non-
empty with
overwhelming probability.
= Seed Q.
.
If Br is non-empty, then Qr H (S IG.e,(Qr-1),r), otherwise Qr H(Qr-1,r).
Parameters
= Relationships among various parameters.
________ The verifiers and potential leaders of round r are selected from the
users in PK",
where k is chosen so that the Adversary cannot predict Qr-1 back at round r ¨
k ¨ 1
with probability better than F: otherwise, he will be able to introduce
malicious users
for round r ¨ k, all of which will be potential leaders/verifiers in round r,
succeeding
in having a malicious leader or a malicious majority in SV" for some steps s
desired
by him.
________ For Step 1 of each round r, n1 is chosen so that with overwhelming
probability,
SVr'l 0.
= Example choices of important parameters.
________ The outputs of H are 256-bit long.
________ h = 80%, ni = 35.
A = 1 minute and A = 15 seconds.
= Initialization of the protocol.
The protocol starts at time 0 with r = 0. Since there does not exist "B-1" or
"CERT-1",
syntactically B-1 is a public parameter with its third component specifying Q-
1, and all
users know B-1 at time 0.
5 A lgorand'i
In this section, we construct a version of Algorancli working under the
following assumption.
HONEST MAJORITY OF USERS ASSUMPTION: More than 2/3 of the users in each PK are
honest.
In Section 7, we show how to replace the above assumption with the desired
Honest Majority
of Money assumption.
5.1 Additional Notations and Parameters
Notations
= m E Z+: the maximum number of steps in the binary BA protocol, a multiple
of 3.
33
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
= Lr <m/3: a random variable representing the number of Bernoulli trials
needed to see a
1, when each trial is 1 with probability
and there are at most m/3 trials. If all trials
fail then Lr m/3. Lr will be used to upper-bound the time needed to generate
block B.
= tH 23n +1: the number of signatures needed in the ending conditions of
the protocol.
= C ERT': the certificate for Br . It is a set of tH signatures of H(Br) from
proper verifiers
in round r.
Parameters
= Relationships among various parameters.
________ For each step s> 1 of round r, n is chosen so that, with
overwhelming probability,
IHSVr'sl> 21M SVr,s1 and IHSVr's1+ LIIMSVrl< 2n.
The closer to 1 the value of h is, the smaller n needs to be. In particular,
we use
(variants of) Chernoff bounds to ensure the desired conditions hold with
overwhelming
probability.
________ m is chosen such that Lr <m/3 with overwhelming probability.
= Example choices of important parameters.
F =10-12.
________ n c=--' 1500, k = 40 and m = 180.
5.2 Implementing Ephemeral Keys in Algorandi
1
As already mentioned, we wish that a verifier i E SVr's digitally signs his
message mrz's of step
s in round r, relative to an ephemeral public key pk, using an ephemeral
secrete key skr's
that he promptly destroys after using. We thus need an efficient method to
ensure that every
user can verify that pk,r's is indeed the key to use to verify i's signature
of mzr's. We do so by a
(to the best of our knowledge) new use of identity-based signature schemes.
At a high level, in such a scheme, a central authority A generates a public
master key,
PMK, and a corresponding secret master key, SMK. Given the identity, U, of a
player U,
A computes, via SMK, a secret signature key sku relative to the public key U,
and privately
gives sku to U. (Indeed, in an identity-based digital signature scheme, the
public key of a user
U is U itself!) This way, if A destroys SMK after computing the secret keys of
the users he
wants to enable to produce digital signatures, and does not keep any computed
secret key, then
U is the only one who can digitally sign messages relative to the public key
U. Thus, anyone
who knows "U's name", automatically knows U's public key, and thus can verify
U's signatures
(possibly using also the public master key PMK).
In our application, the authority A is user i, and the set of all possible
users U coincides
with the round-step pair (r, s) in __ say S = {i} x {r'
,r' 106} X {1, ,m 3}, where
r' is a given round, and m 3 the upperbound to the number of steps that may
occur within a
round. This way, pks (i, r, s), so that everyone seeing i's signature SIG",
s(Mt") can, with
overwhelming probability, immediately verify it for the first million rounds r
following r'.
In other words, i first generates PMK and SMK. Then, he publicizes that PMK is
i's
master public key for any round r E , 106], and uses SMK to privately
produce and store
the secret key sktr's for each triple (i, r, s) E S. This done, he destroys
SMK. If he determines
that he is not part of SV", then i may leave sktr's alone (as the protocol
does not require that
he aunthenticates any message in Step s of round r). Else, i first uses skr's
to digitally sign his
,
message m,rs , and then destroys sky.
34
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Note that i can publicize his first public master key when he first enters the
system. That
is, the same payment that brings i into the system (at a round r' or at a
round close to r'),
may also specify, at i's request, that i's public master key for any round r E
[r', r' 106] is
PMK _____ e.g., by including a pair of the form (PMK, [r', r' 106]).
Also note that, since m 3 is the maximum number of steps in a round,
assuming that a
round takes a minute, the stash of ephemeral keys so produced will last i for
almost two years.
At the same time, these ephemeral secret keys will not take i too long to
produce. Using an
elliptic-curve based system with 32B keys, each secret key is computed in a
few microseconds.
Thus, if m 3 = 180, then all 180M secret keys can be computed in less than
one hour.
When the current round is getting close to r' 106, to handle the next
million rounds, i
generates a new (PMK', SMK') pair, and informs what his next stash of
ephemeral keys is by
for example _________________________________________________________________
having SIG,(PMK',[r' 106 1, r' 2 = 106 1]) enter a new block, either
as a separate "transaction" or as some additional information that is part of
a payment. By so
doing, i informs everyone that he/she should use PMK' to verify i's ephemeral
signatures in
the next million rounds. And so on.
(Note that, following this basic approach, other ways for implementing
ephemeral keys
without using identity-based signatures are certainly possible. For instance,
via Merkle trees.1 )
Other ways for implementing ephemeral keys are certainly possible __________
e.g., via Merkle trees.
5.3 Matching the Steps of Algorand' with those of BA*
As we said, a round in Algorand'i has at most m 3 steps.
STEP 1. In this step, each potential leader i computes and propagates his
candidate block B,
together with his own credential, o-zr'l.
Recall that this credential explicitly identifies i. This is so, because atr'l
= SIGt(r,1,Qr-1).
Potential verifier i also propagates, as part of his message, his proper
digital signature of
H(Bfl. Not dealing with a payment or a credential, this signature of i is
relative to his
r
ephemeral public key pk1; : that is, he propagates sigpk ,i(H(R;)).
Given our conventions, rather than propagating B'z' and sigpk i(H(Bn), he
could have
,
propagated S/Gpk,i(H(Bn). However, in our analysis we need to have explicit
access to
sig ,i(H(Bn).
STEPS 2. In this step, each verifier i sets f'; to be the potential leader
whose hashed credential
is the smallest, and B'z' to be the block proposed by et'. Since, for the sake
of efficiency, we
wish to agree on H(Br), rather than directly on Br i propagates the message he
would have
propagated in the first step of BA* with initial value et = H(Bn. That is, he
propagates
v't, after ephemerally signing it, of course. (Namely, after signing it
relative to the right
ephemeral public key, which in this case is pktr'2.) Of course too, i also
transmits his own
credential.
Since the first step of BA* consists of the first step of the graded consensus
protocol GC,
Step 2 of A/gorand' corresponds to the first step of GC.
' In this method, i generates a public-secret key pair (pC's , skr's) for each
round-step pair (r, s) in say
r', , r' 1061 x {1,
, m 3}. Then he orders these public keys in a canonical way, stores the jth
public key
in the jth leaf of a Merkle tree, and computes the root value R,, which he
publicizes. When he wants to sign a
message relative to key pks , i not only provides the actual signature, but
also the authenticating path for plsr's
relative to R,. Notice that this authenticating path also proves that pls's is
stored in the jth leaf. Form this
idea, the rest of the details can be easily filled.
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
STEPS 3. In this step, each verifier i E SVr'2 executes the second step of
BA*. That is, he
sends the same message he would have sent in the second step of GC. Again, i's
message is
ephemerally signed and accompanied by i's credential. (From now on, we shall
omit saying
that a verifier ephemerally signs his message and also propagates his
credential.)
STEP 4. In this step, every verifier i E SVr'4 computes the output of GC, (v,,
g,), and
ephemerally signs and sends the same message he would have sent in the third
step of
BA*, that is, in the first step of BBA*, with initial bit 0 if g, = 2, and 1
otherwise.
STEP s = 5, ... , m 2. Such a step, if ever reached, corresponds to step s
¨1 of BA*, and thus
to step s ¨ 3 of BBA*.
Since our propagation model is sufficiently asynchronous, we must account for
the possibility
that, in the middle of such a step s, a verifier i E SVr's is reached by
information proving
him that block Br has already been chosen. In this case, i stops his own
execution of round
r of Algorand', and starts executing his round-(r 1) instructions.
Accordingly, the instructions of a verifier i E SVr's, in addition to the
instructions
corresponding to Step s ¨ 3 of BBA*, include checking whether the execution of
BBA*
has halted in a prior Step s'. Since BBA* can only halt is a Coin-Fixed-to-0
Step or in a
Coin-Fixed-to-1 step, the instructions distinguish whether
A (Ending Condition 0): ¨ 2 0 mod 3, or
B (Ending Condition 1): s' ¨ 2 1 mod 3.
In fact, in case A, the block Br is non-empty, and thus additional
instructions are
necessary to ensure that i properly reconstructs Br, together with its proper
certificate
CERTr. In case B, the block Br is empty, and thus i is instructed to set Br =
BrE: =
(r,0,Qr-1,H(Br-1)), and to compute CERTr.
If, during his execution of step s, i does not see any evidence that the block
Br has already
been generated, then he sends the same message he would have sent in step s¨ 3
of BBA*.
STEP Tri 3. If, during step m 3, i E SVr'm+3 sees that the block Br was
already generated
in a prior step s', then he proceeds just as explained above.
Else, rather then sending the same message he would have sent in step m of
BBA*, i is
instructed, based on the information in his possession, to compute Br and its
corresponding
certificate CERTr.
Recall, in fact, that we upperbound by m 3 the total number of steps of a
round.
5.4 The Actual Protocol
Recall that, in each step s of a round r, a verifier i E SVr's uses his long-
term public-secret key
pair to produce his credential, az"
SIG,(r,s,Qr-1), as well as SIG, (Qr-1) in case s = 1.
Verifier i uses his ephemeral secret key sktr's to sign his (r, s)-message
mtr's. For simplicity,
when r and s are clear, we write esig,(x) rather than sigpv,. (x) to denote
i's proper ephemeral
signature of a value x in step s of round r, and write ESIGi(x) instead of
S/Gpij,s(x) to denote
(i,x,esigz(x)).
Step 1: Block Proposal
Instructions for every user i E PKr¨k: User i starts his own Step 1 of round r
as soon as
he knows Br-1.
36
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
= User i computes Qr-1 from the third component of Br-1 and checks whether
i E SVr'1 or
not.
= If i SW,1, then i stops his own execution of Step 1 right away.
= If i E SVr'1, that is, if i is a potential leader, then he collects the
round-r payments that
have been propagated to him so far and computes a maximal payset PAY: from
them.
Next, he computes his "candidate block" _8'; = (r, PAY, SIG,(Qr-1), H (Br-1)).
Finally,
he computes the message
r 1 r
Tnz' = (Br, esigz(H(R;)), o-zr '1 ), destroys his ephemeral secret key sk1z' ,
and then propagates
r,1
.
Remark. In practice, to shorten the global execution of Step 1, it is
important that the
(r,1)-messages are selectively propagated. That is, for every user i in the
system, for the first
(r,1)-message that he ever receives and successfully verifies," player i
propagates it as usual.
For all the other (r,1)-messages that player i receives and successfully
verifies, he propagates
it only if the hash value of the credential it contains is the smallest among
the hash values of
the credentials contained in all (r,1)-messages he has received and
successfully verified so far.
Furthermore, as suggested by Georgios Vlachos, it is useful that each
potential leader i also
r 1
propagates his credential
separately: those small messages travel faster than blocks, ensure
timely propagation of the mir'l's where the contained credentials have small
hash values, while
make those with large hash values disappear quickly.
"That is, all the signatures are correct and both the block and its hash are
valid although i does not check
whether the included payset is maximal for its proposer or not.
37
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Step 2: The First Step of the Graded Consensus Protocol GC
Instructions for every user i E PKr¨k: User i starts his own Step 2 of round r
as soon as
he knows Br-1.
= User i computes Qr-1 from the third component of Br-1 and checks whether
i E SVr'2 or
not.
= If i SVr'2 then i stops his own execution of Step 2 right away.
= If i E SVr'2, then after waiting an amount of time t2 A A, i acts as
follows.
1. He finds the user such that H(OTer'1) < H (0-r:1) for all credentials ar:1
that are part of
the successfully verified (r, 1)-messages he has received so far.12
r 1
2. If he has received from a valid message me' = (Be,7e esige(H (Bn r
), af'1),13 then i sets
v = H (Br )* otherwise i sets v' I.
3. i computes the message mir'2 (E S G
ir'2),14 destroys his ephemeral secret key
skir'2, and then propagates mir'2.
Step 3: The Second Step of GC
Instructions for every user i E PKr¨k: User i starts his own Step 3 of round r
as soon as
he knows Br-1 .
= User i computes Qr ¨1 from the third component of Br-1 and checks whether
i E SVr'3 or
not.
= If i SVr,3, then i stops his own execution of Step 3 right away.
= If i E SVr'3, then after waiting an amount of time t3 t2 2A = 3A A, i
acts as follows.
r 1. If there exists a value v'
I such that, among all the valid messages mi2 he
has received, more than 2/3 of them are of the form (E S IG J(v), ar:2),
without any
contradiction,15 then he computes the message mir'3
(ESIGi(21),CTir'3). Otherwise,
he computes mri''3 (ESiGi(i),
2. i destroys his ephemeral secret key skir'3, and then propagates mir'3.
Step 4: Output of GC and The First Step of BB A*
Instructions for every user i E PKr¨k: User i starts his own Step 4 of round r
as soon as
he knows Br-1.
12Essentially, user i privately decides that the leader of round r is user L.
13Again, player L's signatures and the hashes are all successfully verified,
and PAY/ in BT is a valid payset for
round r __ although i does not check whether PAY/ is maximal for f or not.
14The message mir'2 signals that player i considers v,' to be the hash of the
next block, or considers the next
block to be empty.
15That is, he has not received two valid messages containing ESIG,(v') and a
different ESIG3(v") respectively,
from a player j. Here and from here on, except in the Ending Conditions
defined later, whenever an honest player
wants messages of a given form, messages contradicting each other are never
counted or considered valid.
38
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
= User i computes Qr-1 from the third component of Br-1 and checks whether
i E SVr''I or
not.
= If i SVr,4, then i his stops his own execution of Step 4 right away.
= If i E SVr'4, then after waiting an amount of time t4 t3 2A = 5A A, i
acts as follows.
1. He computes vz and gz, the output of GC, as follows.
(a) If there exists a value v' I such that, among all the valid messages mr'3
he has
received, more than 2/3 of them are of the form (ES/G3(e), ar'3), then he sets
II and gt 2.
(b) Otherwise, if there exists a value v' I such that, among all the valid
messages
mr,3 he has received, more than 1/3 of them are of the form (ESIG3(0,0-ir'3),
then he sets v3 v' and gt 1.16
(c) Else, he sets v3 H (Bn and gt 0.
2. He computes bz, the input of BRA*, as follows:
bt 0 if gt = 2, and bt 1 otherwise.
3. He computes the message Mrt'Ll = (ESiGt (10 , ESIG z(vz), rT:'4), destroys
his ephemeral
secret key sktr'4, and then propagates mir'4.
Step s, 5 < s < m 2, s ¨ 2 0 mod 3: A Coin-Fixed-To-0 Step of B B A*
Instructions for every user i E PKr¨k: User i starts his own Step s of round v
as soon as
he knows Br-1.
= User i computes Qr-1 from the third component of Br-1 and checks whether i E
SVr's.
= If i SVr,s, then i stops his own execution of Step s right away.
= If i E SVr's then he acts as follows.
¨ He waits until an amount of time ts ts_, 2A = (2s ¨ 3)A A has passed.
¨ Ending Condition 0: If, during such waiting and at any point of time, there
exists a
string v I and a step s' such that
(a) 5 < s' < s, s' ¨ 2 0 mod 3 ________ that is, Step s' is a Coin-Fixed-To-0
step,
(b) i has received at least tH =
1 valid messages mr.i's'-1 = (ES/G3(0),
ES/G3(v), 0_ ir,s')
¨1. 17
, and
(c) i has received a valid message mir'l = (B; , esig 3 (H (BD), 0- 3r4) with
v = H (B; ),
then, i stops his own execution of Step s (and in fact of round v) right away
without
propagating anything; sets Br = B;; and sets his own C E RTr to be the set of
messages mr-1.2' of sub-step (b).18
16It can be proved that the v' in case (b), if exists, must be unique.
17Such a message from player j is counted even if player i has also received a
message from j signing for 1.
Similar things for Ending Condition 1. As shown in the analysis, this is done
to ensure that all honest users
know B within time A from each other.
18User i now knows B' and his own round r finishes. He still helps propagating
messages as a generic user,
but does not initiate any propagation as a (r, s)-verifier. In particular, he
has helped propagating all messages
in his C E RT' , which is enough for our protocol. Note that he should also
set b, 0 for the binary BA protocol,
but b, is not needed in this case anyway. Similar things for all future
instructions.
39
CA 03086361 2020-06-18
WO 2019/126311
PCT/US2018/066481
¨ Ending Condition I: If, during such waiting and at any point of time, there
exists a
step s' such that
(a') 6 < < s, s' ¨ 2 1 mod 3 ______________________________________________
that is, Step s' is a Coin-Fixed-To-1 step, and
(b') i has received at least tH valid messages mr.'s'-1 = (ES/G3(1),
ES/G3(v3),
3
as'l)19 ,
then, i stops his own execution of Step s (and in fact of round r) right away
without
propagating anything; sets Br = BEr; and sets his own CERT to be the set of
messages mr,s'-1 of sub-step (b').
¨ Otherwise, at the end of the wait, user i does the following.
He sets vz to be the majority vote of the vi's in the second components of all
the valid
,s-1
mr 's he has received.
He computes bz as follows.
If more than 2/3 of all the valid Mir's-1's he has received are of the form
(ES/G3(0), ES/G3 (V3), air's-1), then he sets I), O.
Else, if more than 2/3 of all the valid mir's¨i's he has received are of the
form
(ES/G(1), ES/G3 (v3), ctri's-1), then he sets I), 1.
Else, he sets b = U.
He computes the message mrz's (ES/G,(1),), E S
, destroys his ephemeral
secret key sks, and then propagates m.
Step s, 6 < s <m 2, s ¨ 2 1 mod 3: A Coin-Fixed-To-1 Step of B B A*
Instructions for every user i E PKr¨k: User i starts his own Step s of round r
as soon as
he knows
= User i computes Qr-1 from the third component of Br-1 and checks whether
i E SVr's or
not.
= If i SV", then i stops his own execution of Step s right away.
= If i E SVr's then he does the follows.
¨ He waits until an amount of time ts (2s ¨ 3)A A has passed.
¨ Ending Condition 0: The same instructions as Coin-Fixed-To-0 steps.
¨ Ending Condition I: The same instructions as Coin-Fixed-To-0 steps.
¨ Otherwise, at the end of the wait, user i does the following.
He sets vz to be the majority vote of the vi 's in the second components of
all the valid
Mr,s-1s,3 he has received.
He computes I), as follows.
If more than 2/3 of all the valid mr's-1's he has received are of the form
(ES/G3 (0), ES/G3 (v3), oTs-1), then he sets I), U.
Else, if more than 2/3 of all the valid mri's-1's he has received are of the
form
(ES/G3(1),ES/G3 (v3), a''), then he sets bz 1.
191n this case, it does not matter what the vi's are.
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Else, he sets b = 1.
He computes the message mrz's (ES/G,(1),), E S Gz(Vz), Us), destroys his
ephemeral
secret key skir's, and then propagates ms.
Step s, 7 < s <m 2, s ¨ 2 2 mod 3: A Coin-Genuinely-Flipped Step of BBA*
Instructions for every user i E PKr¨k: User i starts his own Step s of round r
as soon as
he knows Br-1.
= User i computes Qr-1 from the third component of Br-1 and checks whether
i E SV" or
not.
= If i E SV", then i stops his own execution of Step s right away.
= If i E SV" then he does the follows.
¨ He waits until an amount of time ts (2s ¨ 3)A A has passed.
¨ Ending Condition 0: The same instructions as Coin-Fixed-To-0 steps.
¨ Ending Condition I: The same instructions as Coin-Fixed-To-0 steps.
¨ Otherwise, at the end of the wait, user i does the following.
He sets vz to be the majority vote of the vi's in the second components of all
the valid
Mr,s¨l's he has received.
3
He computes bt as follows.
If more than 2/3 of all the valid Mr's-1's he has received are of the form
(ESIG3(0),ESIG3(V3), o-ir's-1), then he sets bt U.
Else, if more than 2/3 of all the valid mir's¨l's he has received are of the
form
(ES/G(1), ES/G3 (v3), ctir's-1), then he sets bt 1.
Else, let SVr's be the set of (r, s-1)-verifiers from whom he has received a
valid
r,s-1 r's-1
message m I), isb(miniESV"
. He sets _i H(o-i)).
,
He computes the message mtr's (ES/Gz(bz), E SIGt(Vt),0-tr's), destroys his
ephemeral
secret key sky, and then propagates ms.
Step m 3: The Last Step of BBA* 20
Instructions for every user i E PKr¨k: User i starts his own Step m 3 of
round r as soon
as he knows Br-1.
= User i computes Qr-1 from the third component of Br-1 and checks whether
i E ST7r,"2+3
or not.
= If i E ST7r,n2+3, then i stops his own execution of Step m 3 right
away.
= If i E ST7r,m+3 then he does the follows.
20With overwhelming probability BBA* has ended before this step, and we
specify this step for completeness.
41
CA 03086361 2020-06-18
WO 2019/126311
PCT/US2018/066481
¨ He waits until an amount of time tm+3 tm+2 2A = (2m 3)A A has passed.
¨ Ending Condition 0: The same instructions as Coin-Fixed-To-0 steps.
¨ Ending Condition I: The same instructions as Coin-Fixed-To-0 steps.
¨ Otherwise, at the end of the wait, user i does the following.
He sets out, 1 and Br B.
He computes the message Mir'rn+3 = (ESIG,(out,),ESIG,(H(Br)), 0-tr" 3),
destroys
his ephemeral secret key skir'm+3, and then propagates mir'ru+3 to certify
B.21
Reconstruction of the Round-r Block by Non-Verifiers
Instructions for every user i in the system: User i starts his own round v as
soon as he
knows Br-1, and waits for block information as follows.
¨ If, during such waiting and at any point of time, there exists a string v
and a step s' such
that
(a) 5 < < m 3 with s' ¨ 2 0 mod 3,
r ¨1 r ¨1
(b) i has received at least tH valid messages m; =
(ES/G3(0), ES/G3(v), o-3' ), and
(c) i has received a valid message mir'l = esigi (H (B;)), air4) with v = H
(B;),
then, i stops his own execution of round v right away; sets Br = B; ; and sets
his own
CERT to be the set of messages mr's'-1 of sub-step (b).
¨ If, during such waiting and at any point of time, there exists a step s'
such that
(a') 6<8' < m 3 with s' ¨ 2 1 mod 3, and
r ¨1 r
(b') i has received at least tH valid messages m3' = (ES/G3(1),
ES/G3(v3), o- ¨13' ),
then, i stops his own execution of round v right away; sets Br = BEr; and sets
his own
CERT' to be the set of messages mr's'-1 of sub-step (b').
¨ If, during such waiting and at any point of time, i has received at least tH
valid messages
r,m+3
= (ESIG3(1),ESIG3(H(Ber)), air'711+3), then i stops his own execution of round
v
M3
right away, sets Br = BEr, and sets his own CERT' to be the set of messages
m3r'ru+3 for 1
and H(BEr).
6 Algorand'2
In this section, we construct a version of Algorand' working under the
following assumption.
HONEST MAJORITY OF USERS ASSUMPTION: More than 2/3 of the users in each PKr
are
honest.
In Section 7, we show how to replace the above assumption with the desired
Honest Majority
of Money assumption.
21A certificate from Step m 3 does not have to include ES/G,(out,). We
include it for uniformity only: the
certificates now have a uniform format no matter in which step they are
generated.
42
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
6.1 Additional Notations and Parameters for Algorand2
Notations
= p, E Z+: a pragmatic upper-bound to the number of steps that, with
overwhelming
probability, will actually taken in one round. (As we shall see, parameter p,
controls how
many ephemeral keys a user prepares in advance for each round.)
= _Lir: a random variable representing the number of Bernoulli trials
needed to see a 1, when
each trial is 1 with probability
Lr will be used to upper-bound the time needed to
generate block B.
= tH: a lower-bound for the number of honest verifiers in a step s> 1 of
round r, such that
with overwhelming probability (given n and p), there are > tH honest verifiers
in SW,s.
Parameters
= Relationships among various parameters.
________ For each step s> 1 of round r, n is chosen so that, with
overwhelming probability,
IHSW,s1 > tH and IHSV"1+21MSV"I <2tH.
Note that the two inequalities above together imply IHSV"1 > 21MSVrl: that is,
there is a 2/3 honest majority among selected verifiers.
The closer to 1 the value of h is, the smaller n needs to be. In particular,
we use
(variants of) Chernoff bounds to ensure the desired conditions hold with
overwhelming
probability.
= Specific choices of important parameters.
F =10-18.
________ n ,^,f, 4000, tH ,^,f, 0.69n, k = 70.
6.2 Implementing Ephemeral Keys in Alg rand/2
Recall that a verifier i E SVr's digitally signs his message mrz's of step s
in round r, relative to
an ephemeral public key pk,r's, using an ephemeral secrete key skr's that he
promptly destroys
after using. When the number of possible steps that a round may take is capped
by a given
integer we have already seen how to practically handle ephemeral keys. For
example, as we
have explained in A/gorand'i (where p, = m 3), to handle all his possible
ephemeral keys, from
a round r' to a round r' 106, i generates a pair (PMK, SMK), where PMK
public master
key of an identity based signature scheme, and SMK its corresponding secret
master key. User
i publicizes PMK and uses SMK to generate the secret key of each possible
ephemeral public
key (and destroys SMK after having done so). The set of i's ephemeral public
keys for the
relevant rounds is S = fil x {r',
, r' 106} x {1, , i}. (As discussed, as the round r' 106
approaches, i "refreshes" his pair (PMK, SMK).)
In practice, if p, is large enough, a round of Algoranc112 will not take more
than p, steps. In
principle, however, there is the remote possibility that, for some round r the
number of steps
actually taken will exceed
When this happens, i would be unable to sign his message mzr's for
any step s > ,a, because he has prepared in advance only p, secret keys for
round r. Moreover,
he could not prepare and publicize a new stash of ephemeral keys, as discussed
before. In fact,
to do so, he would need to insert a new public master key PMK' in a new block.
But, should
round r take more and more steps, no new blocks would be generated.
However, solutions exist. For instance, i may use the last ephemeral key of
round r,
as follows. He generates another stash of key-pairs for round r _____________
e.g., by (1) generating another
master key pair (PMK, SMK); (2) using this pair to generate another, say, 106
ephemeral
43
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
¨r, +1 ¨r, 106
keys, sk, , . . . ,
, corresponding to steps p, 1, ..., 106 of round r; (3) using sk,r'11
to digitally sign PMK (and any (r, ,u)-message if i E ST/T'A), relative to
pk,r41; and (4) erasing
SMK and sk,r41. Should i become a verifier in a step ,a+s with s E
{1,...,106}, then i digitally
¨r,
signs his (r, p, s)-message mzr'11 s relative to his new key pk s,
= (i, r, p s). Of course, to
verify this signature of i, others need to be certain that this public key
corresponds to i's new
public master key PMK. Thus, in addition to this signature, i transmits his
digital signature
of PMK relative to pk,r41.
Of course, this approach can be repeated, as many times as necessary, should
round r
continue for more and more steps! The last ephemeral secret key is used to
authenticate a new
master public key, and thus another stash of ephemeral keys for round r. And
so on.
6.3 The Actual Protocol Algorand'2
Recall again that, in each step s of a round r, a verifier i E SV" uses his
long-term public-
secret key pair to produce his credential, az"
SIGt(r, s, Q'), as well as SIG t (Qr-1) in
case s = 1. Verifier i uses his ephemeral key pair, (pktr's, sktr's), to sign
any other message m
that may be required. For simplicity, we write esigt(m), rather than
sigpv,s(m), to denote i's
proper ephemeral signature of m in this step, and write ES/G (m) instead of
S/Gpv,s(m)
(i, m, esigt(m)).
Step 1: Block Proposal
Instructions for every user i E PKr¨k: User i starts his own Step 1 of round r
as soon as
he has CERT'', which allows i to unambiguously compute H(B1) and Q'.
= User i uses Qr ¨1 to check whether i E SVr'l or not. If i SVr'1, he does
nothing for Step
1.
= If i E SW,1, that is, if i is a potential leader, then he does the
following.
(a) If i has seen B ,
, Br-1 himself (any B = B can be easily derived from its hash
value in C E RT3 and is thus assumed "seen"), then he collects the round-r
payments
that have been propagated to him so far and computes a maximal payset PAY:
from
them.
(b) If i hasn't seen all B , , Br-1 yet, then he sets PAY: =0.
(c) Next, i computes his "candidate block" .0; = (r, PAY,SIGt(Qr-1), H (Br-
1)).
(c) Finally, i computes the message mzr'l = (Br, esigt(H(M), atr"), destroys
his ephemeral
secret key sktr'1, and then propagates two messages, mir'1 and (S/Gt(Qr-1),
o1),
separately but simultaneously.22
Selective Propagation
To shorten the global execution of Step 1 and the whole round, it is important
that the (r, 1)-
messages are selectively propagated. That is, for every user j in the system,
22When i is the leader, S/G1(CI-1) allows others to compute Qr = H(SIG,(Qr
1),r)=
44
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
= For the first (r, 1)-message that he ever receives and successfully
verifies,23 whether it
contains a block or is just a credential and a signature of Qr-1, player j
propagates it
as usual.
= For all the other (r, 1)-messages that player j receives and successfully
verifies, he propagates
it only if the hash value of the credential it contains is the smallest among
the hash values
of the credentials contained in all (r, 1)-messages he has received and
successfully verified
so far.
r = However, if j receives two different messages of the form mi'1 from the
same player i,24 he
discards the second one no matter what the hash value of i's credential is.
Note that, under selective propagation it is useful that each potential leader
i propagates
his credential
separately from m1:25 those small messages travel faster than blocks, ensure
timely propagation of the mir'l's where the contained credentials have small
hash values, while
make those with large hash values disappear quickly.
Step 2: The First Step of the Graded Consensus Protocol GC
Instructions for every user i E PKr¨k: User i starts his own Step 2 of round r
as soon as
he has CE RTr-1.
= User i waits a maximum amount of time t2 = A A. While waiting, i acts
as follows.
r
1. After waiting for time 2A, he finds the user such that H(o1-f' ) < H(o1)
for all
credentials Cir:1 that are part of the successfully verified (r, 1)-messages
he has received
so far.26
2. If he has received a block B', which matches the hash value H (Br ¨1) con-
tained in C ERTr-1 ,27 and if he has received from
a valid message mt.'1 =
(BT , esige(H (BD), <1,28 then i stops waiting and sets t/i (H (BD ,).
3. Otherwise, when time t2 runs out, i sets t/i I.
4. When the value of t/i has been set, i computes Qr ¨1 from CERT'l and checks
whether
i E .9Vr'2 or not.
5. If i E SVr'2 i computes the message m7'2 = (ES/Gi(Vii), ari'2),29 destroys
his ephemeral
r 2 r 2
secret key ski' , and then propagates
. Otherwise, i stops without propagating
anything.
23That is, all the signatures are correct and, if it is of the form mr,'1,
both the block and its hash are valid
although j does not check whether the included payset is maximal for i or not.
24Which means i is malicious.
25We thank Georgios Vlachos for suggesting this.
26Essentially, user i privately decides that the leader of round r is user f.
270f course, if CERTr-1 indicates that Br-1 = B:-1, then i has already
"received" Br-1 the moment he has
CERTr-1.
28Again, player L's signatures and the hashes are all successfully verified,
and PAY/ in H; is a valid payset for
round r ____________________________________________________________________
although i does not check whether PAW' is maximal for or not. If BT contains
an empty payset,
then there is actually no need for i to see Br-1 before verifying whether BT
is valid or not.
29The message m,,r'2 signals that player i considers the first component of v,
to be the hash of the next block,
or considers the next block to be empty.
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Step 3: The Second Step of GC
Instructions for every user i E PKr¨k: User i starts his own Step 3 of round v
as soon as
he has CERT'l.
= User i waits a maximum amount of time t3 t2 2A = 3A A. While waiting,
i acts as
follows.
1. If there exists a value v such that he has received at least tH valid
messages mir'2 of
the form (ES/G3(v), cr3r'2), without any contradiction,30 then he stops
waiting and sets
VI = V.
2. Otherwise, when time t3 runs out, he sets v" = I.
3. When the value of v" has been set, i computes Qr-1 from CERT'l and checks
whether
i E SVr'3 or not.
4. If i E SVr'3, then i computes the message mr3 = (ESiGt(V/), a:'3), destroys
his
r r
ephemeral secret key sk,3, , and then propagates m,3i . Otherwise, i stops
without
propagating anything.
Step 4: Output of GC and The First Step of BBA*
Instructions for every user i E PKr¨k: User i starts his own Step 4 of round v
as soon as
he finishes his own Step 3.
= User i waits a maximum amount of time 2A.31 While waiting, i acts as
follows.
1. He computes v3 and gt, the output of GC, as follows.
(a) If there exists a value v" I such that he has received at least tH valid
messages
mr'3 = (ES/G3 (V/), ar'3), then he stops waiting and sets v3 vi and g, 2.
r r,3
(b) If he has received at least tH valid messages Tri3'3 = (ES/G3 (I), o-3 ),
then he
stops waiting and sets v3 I and g, 0.32
(c) Otherwise, when time 2A runs out, if there exists a value v"
I such that he
has received at least [41 valid messages mr'3 = (ES/G3 (e) o-r'3) then he sets
3 3
Vz= V/ and g, 1.33
(d) Else, when time 2A runs out, he sets v3 I and g, 0.
2. When the values v3 and g, have been set, i computes bz, the input of BBA*,
as follows:
b, 0 if g, = 2, and b, 1 otherwise.
3. i computes Qr-1 from CERT'l and checks whether i E SVr'4 or not.
4. If i E SVr'4, he computes the message mir'4
(ES/G,(1),), ES/Gz(vz), atr'4), destroys
r 4 r 4
his ephemeral secret key sk,' , and propagates mi' . Otherwise, i stops
without
propagating anything.
30That is, he has not received two valid messages containing ESIG,(v) and a
different ESIG1(1)) respectively,
from a player j. Here and from here on, except in the Ending Conditions
defined later, whenever an honest player
wants messages of a given form, messages contradicting each other are never
counted or considered valid.
31Thus, the maximum total amount of time since i starts his Step 1 of round r
could be Li t3 2A = 5A A.
32Whether Step (b) is in the protocol or not does not affect its correctness.
However, the presence of Step (b)
allows Step 4 to end in less than 2A time if sufficiently many Step-3
verifiers have "signed I."
331t can be proved that the v' in this case, if exists, must be unique.
46
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Step s, 5 < s < m 2, s ¨ 2 0 mod 3: A Coin-Fixed-To-0 Step of BBA*
Instructions for every user i E PKr¨k: User i starts his own Step s of round v
as soon as
he finishes his own Step s ¨1.
= User i waits a maximum amount of time 2A.34 While waiting, i acts as
follows.
¨ Ending Condition 0: If at any point there exists a string v I and a
step s' such
that
(a) 5 < s' < s, s' ¨ 2 0 mod 3 ________ that is, Step s' is a Coin-Fixed-To-0
step,
(b) i has received at least tH valid messages
r,s' ¨1
= (ESIGi(0), ESIGi(V), Or'-1),35 and
711./
(c) i has received a valid message (S/Gi(Qr-1), ar.'1) with j being the second
component of v,
then, i stops waiting and ends his own execution of Step s (and in fact of
round v)
right away without propagating anything as a (v, s)-verifier; sets H(B) to be
the first
r component of v; and sets his own CERT' to be the set of messages ms'-1 i'
of step
(b) together with (S/Gi(Qr-1), 1) .36
¨ Ending Condition I: If at any point there exists a step s' such that
(a') 6 < s' < s, s' ¨ 2 1 mod 3 _______ that is, Step s' is a Coin-Fixed-To-1
step, and
(b') i has received at least tH valid messages mr's'-1 = (ES/G(1), ES/Gi(vi),
3
r ,s' ¨1) 37
then, i stops waiting and ends his own execution of Step s (and in fact of
round v)
right away without propagating anything as a (v, s)-verifier; sets Br = BEr;
and sets
his own CERT to be the set of messages mr's'-1 of sub-step (b').
¨ If at any point he has received at least tH valid mr.'s l's of the form
(ES/G(1), ES/Gi(Vi), Ts-1), then he stops waiting and sets bi 1.
¨ If at any point he has received at least tH valid mr's l's of the form
(ES/Gi(0), ESIGi(Vi), 0-3r.'s-1), but they do not agree on the same v, then he
stops
waiting and sets bi 0.
¨ Otherwise, when time 2A runs out, i sets bi 0.
¨ When the value bi has been set, i computes Qr from CERT'l and checks whether
i E SVr's.
¨ If i E SW's, i computes the message 'mri's = (ES/Gi(bi), ES IGi(Vi), air's)
with vi
being the value he has computed in Step 4, destroys his ephemeral secret key
sky,
and then propagates mir's. Otherwise, i stops without propagating anything.
34Thus, the maximum total amount of time since i starts his Step 1 of round r
could be ts ts_i 2A =
(2s ¨ 3)A A.
35Such a message from player j is counted even if player i has also received a
message from j signing for 1.
Similar things for Ending Condition 1. As shown in the analysis, this is to
ensure that all honest users know
CERT' within time A from each other.
36User i now knows H(B) and his own round r finishes. He just needs to wait
until the actually block B' is
propagated to him, which may take some additional time. He still helps
propagating messages as a generic user,
but does not initiate any propagation as a (r, s)-verifier. In particular, he
has helped propagating all messages
in his CERT', which is enough for our protocol. Note that he should also set
b, 0 for the binary BA protocol,
but b, is not needed in this case anyway. Similar things for all future
instructions.
37In this case, it does not matter what the vj's are.
47
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Step s, 6 < s < m 2, s ¨ 2 1 mod 3: A Coin-Fixed-To-1 Step of BB A*
Instructions for every user i E PKr¨k: User i starts his own Step s of round r
as soon as
he finishes his own Step s ¨1.
= User i waits a maximum amount of time 2A. While waiting, i acts as
follows.
¨ Ending Condition 0: The same instructions as in a Coin-Fixed-To-0 step.
¨ Ending Condition I: The same instructions as in a Coin-Fixed-To-0 step.
¨ If at any point he has received at least tH valid mr's l's of the form
(ES/G3(0), ES/G3 (v3), ctri's 1
then he stops waiting and sets bt 0.38
¨ Otherwise, when time 2A runs out, i sets bt 1.
¨ When the value I), has been set, i computes Qr from C ERT'l and checks
whether
i E SV".
¨ If i E SVr's, i computes the message mzr's = (ES/G,(1),), E S IG,(Vt) az")
with vz being
the value he has computed in Step 4, destroys his ephemeral secret key skr's,
and then
propagates Tris. Otherwise, i stops without propagating anything.
Step s, 7 < s <m 2, s ¨ 2 2 mod 3: A Coin-Genuinely-Flipped Step of BB A*
Instructions for every user i E PKr¨k: User i starts his own Step s of round r
as soon as
he finishes his own step s ¨ 1.
= User i waits a maximum amount of time 2A. While waiting, i acts as
follows.
¨ Ending Condition 0: The same instructions as in a Coin-Fixed-To-0 step.
¨ Ending Condition I: The same instructions as in a Coin-Fixed-To-0 step.
¨ If at any point he has received at least tH valid mr's¨l's of the form
(ES/G3(0), ES/G3 (v3), ar's-1
then he stops waiting and sets bt U.
¨ If at any point he has received at least tH valid mr's¨l's of the form
(ES/G3(1), ES/G3 (v3), ar's-1
then he stops waiting and sets bt 1.
¨ Otherwise, when time 2A runs out, letting SVtr's 1 be the set of (r, s¨ 1)-
verifiers from
whom he has received a valid message Mr's-1 i sets b = lsb(min ESV r' s_i H
(ar's-1)).
,
¨ When the value bt has been set, i computes Qr from C ERT'l and checks
whether
i E SV".
¨ If i E SVr's i computes the message mzr's = (ES/Gz(bz), ESIGt(Vt) az") with
vz being
the value he has computed in Step 4, destroys his ephemeral secret key sk, and
then
propagates mir's. Otherwise, i stops without propagating anything.
Remark. In principle, as considered in subsection 6.2, the protocol may take
arbitrarily many
steps in some round. Should this happens, as discussed, a user i E SV" with s
> p, has
exhausted his stash of pre-generated ephemeral keys and has to authenticate
his (r, s)-message
mrt's by a "cascade" of ephemeral keys. Thus i's message becomes a bit longer
and transmitting
these longer messages will take a bit more time. Accordingly, after so many
steps of a given
round, the value of the parameter A will automatically increase slightly. (But
it reverts to the
original A once a new block is produced and a new round starts.)
38Note that receiving tH valid (r, s ¨ 1)-messages signing for 1 would mean
Ending Condition 1.
48
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Reconstruction of the Round-r Block by Non-Verifiers
Instructions for every user i in the system: User i starts his own round r as
soon as he has
= i follows the instructions of each step of the protocol, participates the
propagation of all
messages, but does not initiate any propagation in a step if he is not a
verifier in it.
= i ends his own round r by entering either Ending Condition 0 or Ending
Condition 1 in
some step, with the corresponding CERT'.
= From there on, he starts his round r +1 while waiting to receive the
actual block Br (unless
he has already received it), whose hash H(Br) has been pinned down by CERT'.
Again,
if CERT indicates that Br = BE' , the i knows Br the moment he has CERT'.
7 Protocol Algorand' with Honest Majority of Money
We now, finally, show how to replace the Honest Majority of Users assumption
with the much
more meaningful Honest Majority of Money assumption. The basic idea is (in a
proof-of-stake
flavor) "to select a user i E Picr¨k to belong to SV" with a weight (i.e.,
decision power)
proportional to the amount of money owned by i."39
By our HMM assumption, we can choose whether that amount should be owned at
round
r ¨k or at (the start of) round r. Assuming that we do not mind continual
participation, we opt
for the latter choice. (To remove continual participation, we would have opted
for the former
choice. Better said, for the amount of money owned at round r ¨ k ¨ 2, 000.)
There are many ways to implement this idea. The simplest way would be to have
each
key hold at most 1 unit of money and then select at random n users i from
Picr¨k such that
1.
The Next Simplest Implementation
The next simplest implementation may be to demand that each public key owns a
maximum
amount of money M, for some fixed M. The value M is small enough compared with
the total
amount of money in the system, such that the probability a key belongs to the
verifier set of
more than one step in __ say _______________________________________________
k rounds is negligible. Then, a key i E Pick, owning an
amount of money ci,r) in round r, is chosen to belong to SW,' if
(r)
.H (SIG, (r, s, Qr-1)) < p az ______________________ .
And all proceeds as before.
A More Complex Implementation
The last implementation "forced a rich participant in the system to own many
keys".
An alternative implementation, described below, generalizes the notion of
status and
consider each user i to consist of K +1 copies (i, v), each of which is
independently selected to
be a verifier, and will own his own ephemeral key (pk, sk) in a step s of a
round r. The
value K depends on the amount of money a(zr) owned by i in round r.
Let us now see how such a system works in greater detail.
--
39We should say PKk2,000 '
so as to replace continual participation. For simplicity, since one may wish
to
require continual participation anyway, we use PK'-k as before, so as to carry
one less parameter.
49
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Number of Copies Let n be the targeted expected cardinality of each verifier
set, and let
az(r) be the amount of money owned by a user i at round v. Let .Ar be the
total amount of
money owned by the users in PKr-k at round v, that is,
Ar = >_: C4r) .
tEPKr-k
If i is an user in PK", then i's copies are (i, 1), , (i, K 1), where
[n = a(r)
K=
Ar
EXAMPLE. Let n = 1, 000, Ar = 109, and o,r) = 3.7 millions. Then,
K=
[103 = (3.7 = 106)]
= [3.7] =3 .
109
Verifiers and Credentials Let i be a user in PK" with K 1 copies.
r For each v = 1,
, K, copy (i, v) belongs to SVr's automatically. That is, i's credential is
o- 's
S Gt((i, v), r, s , Qr-1), but the corresponding condition becomes .H(o-tr'vs)
< 1, which is
always true.
For copy (i, K 1), for each Step s of round v, i checks whether
.H (SIGt((i, K 1), v, S,Qr-1)) < aCr) - K .
- Ar
If so, copy (i, K 1) belongs to SV". To prove it, i propagates the credential
r,1
EXAMPLE. As in the previous example, let n = 1K, or) = 3.7M, K = 1B, and i has
4
copies: (i, 1),
, (i, 4). Then, the first 3 copies belong to SW,' automatically. For the 4th
one,
conceptually, Algorand' independently rolls a biased coin, whose probability
of Heads is 0.7.
Copy (i, 4) is selected if and only if the coin toss is Heads.
(Of course, this biased coin flip is implemented by hashing, signing, and
comparing as we
have done all along in this application so as to enable i to prove his
result.)
Business as Usual Having explained how verifiers are selected and how their
credentials
are computed at each step of a round v, the execution of a round is similar to
that already
explained.
8 Algorand with the Assumption of No Network
Partition
Essentially, in Algorand, blocks are gnerated in rounds. In a round v,
(1) A properly credentialed leader proposes a new block and then
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
(2) Properly credentialed users run, over several steps, a proper Byzantine
agreement (BA)
protocol on the block proposed.
The preferred BA protocol is BA*. The block proposal step can be considered
step 1, so
that the steps of BA* are 2, 3,...
Only a proper user i, randomly selected among the users in the system, is
entitled to send
r,s
a message mt in step s of round r. Algorand is very fast and secure because
such a user i
checks whether he is entitled to speak. If this is the case, user i actually
obtains a proof, a
credential. If it is his turn to speak in step s of round r, i propagates in
the network both his
credential, az" and his digitally signed message tri:'s. The credential proves
to other users that
they should take in consideration the message mtr's.
A necessary condition for user i to be entitled to speak in step s of round r
is that he was
already in the system a few rounds ago. Specifically, k rounds before round r,
where k is a
parameter termed the 'look-back' parameter. That is, to be eligible to speak
in round r, i must
belong to Pick, the set of all public keys/users already in the system at
round r ¨ k. (Users
can be identified with their public keys.) This condition is easy to verify in
the sense that it is
derivable from the blockchain.
The other condition is that
H(S/Gt(r, s, Qr-1)) < p
where p is a given probability that controls the expected number of verifiers
in SW'', that is,
the set of users entitled to speak in step s of round r. If this condition is
satisfied, then i's
credential is defined to be
az" SIGt(r, s, Qr
Of course, only i can figure out whether he belongs to ST7r,s. All other
users, who lack knowledge
of i's secret signing key, have no idea about it. However, if i E SV", then i
can demonstrate
that this is the case to anyone by propagating his credential az" given the
blockchain so far.
Recall in fact that (1) Qr-1 is easily computable from the previous block, Br-
1, although
essentially unpredictable sufficiently many blocks before, and (2) anyone can
verify i's digital
signatures (relative to his long-term key in the system).
Recall that, in the versions of Algorand so far, new blocks are proposed only
once in a round
r, __ that is, in step 1. The BA protocol has the users reach consensus on
one of them (or the
empty block), and does not further propose new blocks or re-propose blocks
that have already
been proposed for round r. When the network is not partitioned and the upper-
bounds for the
time to propagate messages are met, the users reach consensus efficiently and
securely.
9 Algorand Resilient Against Network Partition
Let us describe a new embodiment of Algorand, Algorand2, that dispenses the
assumption of
no network partition. We present the new protocol under the Honest Majority of
Users (HMU)
assumption. Using the same approach as in Section 7, the HMU assumption can be
replaced
with the Honest Majority of Money (HMM) assumption.
9.1 Communication Model
When the network is not partitioned, small messages take time A to propagate
to all honest
users, and blocks take time A to propagate to all honest users, as before.
When the network is
partitioned into more than one groups of users, the adversary determines
whether a message m
propagated by a user from one group will be delivered to users in other
groups, who in other
51
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
groups will receive m, and when they will receive m. A network partition may
be resolved at an
indefinite time in the future and messages propagated during the partition are
delivered to all
users after the partition is resolved. For simplicity, but without limitation
intended, we describe
the new embodiment assuming messages propagated during a network partition are
delivered
to all users immediately after the partition is resolved. For example, if a
network partition lasts
from time t1 to time t2, and let M be the set of messages propagated during
the partition, then
all users receive messages in M by time t2. Those skilled in the art will
realize that the system
described herein can handle other situations where messages in M take certain
amount of time
to reach all users or are re-propagated by users who have received them.
9.2 Choices of Parameters
The expected committee size n and the threshold tH are chosen according to the
following
conditions. Let PK be the set of users, HPK and MPK respectively the set of
honest and
malicious users. Let HPKi be an arbitrary subset of HPK with half the size.
When each
user i E PK is selected independently and randomly with probability p = *, let
HSVi and
MSV respectively be the set of selected ones from HPKi and MPK. Then with
overwhelming
probability,
1HSV
11 1MSVI<tH.
Moreover, let HSV be the set of selected ones from HPK. Then with overwhelming
probability,
IHSV1 > tH.
Note that the above two conditions imply IHSV1 > 21MSVI.
For example, when h = 80% and PK is large enough, we may choose n = 3, 500 and
tH = 2, 625.
9.3 General Structure
Rounds. The protocol generates one block every round. A round consists of
periods 1, 2, ...
and a period consists of steps 1, 2, .... At any moment in time, each user i
is working on exactly
one round-period pair. In particular, we use r.p to refer to period p of round
r.
In step 1 of period 1, users propose new blocks. In step 1 of following
periods, users propose
new blocks or re-propose blocks that have been proposed in earlier periods.
Committees. Each step s of period r.p has a committee chosen by cryptographic
self-
selection, denoted by SW,P,s. We use the same look-back parameter as in
Section 4.1, denoted
by k. For example, k = 70. A user i is eligible to be selected in round-r
committees if i E PKr-k.
The committee for Step 1 of each period has expected size n1 (e.g., 35) and
all other committees
have expected size n. Committee members for Step 1 are referred to as
potential leaders.
Note that for simplicity, but without limitation intended, we describe the new
embodiment
herein with the same expected committee size n for all steps other than step 1
of each period.
Those skilled in the art will realize that different committees may have
different sizes and can
appreciate how to derive all kinds of other implementations as well.
Keys. All credentials for cryptographic self-selection are signed with users'
long-term keys for
a digital signature scheme with unique signatures, so are the random seeds Qr
specified in the
blocks. All other messages are signed using ephemeral keys of corresponding
steps. In general
we will use SIG(m) to denote user i's signature for message m, without
specifying the keys.
52
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Note that for simplicity, but without limitation intended, we describe the new
embodiment
herein with ephemeral keys. Those skilled in the art can appreciate how to
derive other
implementations with message-credentialed blockchains, including using
techniques introduced
in existing versions of Algorand.
Definition 9.1. Credential: User i's credential o-ir'P's for a round r, period
p and step s is
S Gz(Qr , r, p, s).
A committee member for a step always propagates his corresponding credential
together with
his message for that step, and we will not explicitly mention the propagation
of credentials.
Definition 9.2. Leader: The leader fr.p for period r.p is the user arg
m-nd Esvr=P=1 H (CT tr 'P'1) =
When a user i identifies his own leader for period r.p, i sets
tz,r..p to be the user
arg mind E H (CT dr'P'1), where Si is the set of potential leaders from which
i has received valid
credentials.
Definition 9.3. Valid block: We call a block proposed during round r valid if
and only if all
its transactions are valid with respect to blocks B ,
, = = = , Br-1 and the seed Qr specified by it
follows the rules of the protocol.
Voting Messages. The committee members generate three types of voting
messages.
Definition 9.4. Cert-vote: User i's cert-vote for a value v for period r.p is
the signature
SIG,(v,"cert",r.p).
We say a user i cert-votes a value v for period r.p when he propagates
SIGz(v,"cert",r.p).
Definition 9.5. Soft-vote: User i's soft-vote for a value v for period r.p is
the signature
SIGz(v,"soft",r.p).
We say a user i soft-votes a value v for period p when he propagates
SIGz(v,"so ft" ,r.p).
Definition 9.6. Next-vote: User i's next-vote for a value v for period r.p and
step s is the
signature SIG,(v,"next",r.p.$).
We say a user i next-votes a value v when he propagates
SIGz(v,"next",r.p.$).40
The values v that will be voted upon are either values in the range of the
hash function H
or a special symbol I of the same length but outside the range of H.41-
Timers. Each user i keeps a timer clock, which he resets to 0 every time he
starts a new
period. As long as i remains in the same period, clock keeps counting. The
users' individual
timers do not need to be synchronized or almost synchronized. The only
requirement is that
they have the same speed.
40In each period, the soft-votes are generated only in one step, and so are
the cert-votes. Thus they do not
need to specify the corresponding step. The next-votes may be generated in
multiple steps and need to specify
the step numbers.
41The block structure in this manuscript is the same as in existing versions
of Algorand, with the header of a
block B, Header(B), containing everything in B except the actual payset. As in
the original protocol, we can
ask the potential leaders to propagate the headers of their proposed blocks
together with the hashes, to allow
users to start a round r +1 before seeing the actual block B. In this case, v
and I are of the same length as
possible hash-header pairs. We will ignore the headers in the protocol
description below.
53
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
9.4 The Actual Protocol Algorand2
In the protocol below, blocks and potential leaders' credentials from
different periods are
selectively propagated as in Section 5.
Round r, Period 1
The following are period 1 instructions for a generic user i. If user i is not
in the committee
of a specific step, he still computes his vote in that step, but does not
propagate it.
The moment user i starts his own round-r, he starts Period 1 and resets clock,
to 0.
STEP 1: [Block Proposal] User i does the following when clock, = 0.
= If i is a potential leader, then he prepares his proposed block Br",
which contains his
signature S/G,(Qr-1,r) to define his proposed seed r 1
He propagates H(B,' ), and
right after also propagates the block itself.
STEP 2: [The Filtering Step] User i does the following when clock, = 2A.
= He identifies his leader i,r.p and soft-votes his leader's proposed
block hash.43
STEP 3: [The Certifying Step] Let T A A. User i does the following when
clock, E (2, T).
= If i sees a valid block B, together with tH soft-votes for H(B), then i cert-
votes H(B).
STEP 4: [The First Finishing Step] User i does the following when clock, = T.
= If i has cert-voted some value v in Step 3,44 then he next-votes v;
= Else he next-votes I.
STEP 5: [The Second Finishing Step] User i does the following when clock, E
[T, T L), where
L equals, say, 50A.45
= If i sees a valid block B, together with tH soft-votes for H(B), then i
next-votes H(B).
STEPS s > 6: [Consecutive Finishing Steps]
= If s is even then i follows the same voting instruction as in Step 4 when
clock, =
T (s ¨ 4)L/2.
= Else (i.e., s is odd), i follows the same voting instruction as in Step 5
when clock, E
[T (s ¨ 5)L/2, T (s ¨ 3)L/2).
42That is, Q = r)).
43It's not required that i has seen the actual block before soft-voting.
44If i is not in SV''1'3, he may still have cert-voted some v "for himself",
without propagating his vote.
45If the Adversary cannot corrupt users dynamically, then it is enough to have
Step 5 lasting till time oo and
no further steps, as in the permissioned version of our protocol. Future steps
are used to ensure that the protocol
recovers after a partition is resolved, even if the Adversary has pocketed all
Step 4 and Step 5 messages and
corrupted all Step 4 and Step 5 committee members so that they cannot resend
their messages after the partition.
A smaller L helps speeding up partition resolution in the worst case, while a
larger L reduces the amount of
messages that need to be re-propagated once the partition is resolved.
54
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Round r, Period p> 2
The following are period-p instructions for a generic user i. Again, if user i
is not in the
committee of a specific step, he still computes his vote in the step but does
not propagate it.
User i starts period p the moment he receives tH next-votes for some value v
(which might
be equal to I) for the same step s of period p ¨ 1, and only if he has not yet
started a period
> p. User i sets his starting value for period p, sty, to v. The moment i
starts period p, he
finishes all previous periods and resets clock i to 0.
STEP 1: [Block Proposal] If user i is a potential leader, then he does the
following when clock =
0.
= If i has seen tH next-votes for I for the same step s of period p ¨ 1,46
then i proposes
a new block Bir'P, which defines his proposed seed qz: as H(Qr-1, 0.47 He
propagates
H(B"), and right after also propagates the block itself;
= Else (i.e., i only received tH next-votes for some v I for the same
period s of period
p ¨ 1, and stli) = v), i proposes stli) by propagating it;48
STEP 2: [The Filtering Step] User i does the following when clock = 2A.
= If i has seen tH next-votes for I for the same step s of period p ¨ 1,49
then i identifies
his leader fi,p for period p and soft-votes the value v proposed by tim;
= Else (i.e., i only received tH next-votes for v I for the same
step s of period p ¨ 1,
and stP = v), i soft-votes stP.
STEP 3: [The Certifying Step] User i does the following when clock i E (2A,
T), T = A A.
= If i sees a valid block B, together with tH soft-votes for H(B), then i
cert-votes H(B).
STEP 4: [The First Finishing Step] User i does the following when clock i = T.
= If i has cert-voted some value v in Step 3, then he next-votes v;
= Else if i has seen tH next-votes for I for the same steps of period p¨ 1,
he next-votes I.
= Else he next-votes stP
i =
STEP 5.1: [The Second Finishing Step] User i does the following when clock i E
[T,T L).
= If i sees a valid block B, together with tH soft-votes for H(B), then i
next-votes H(B).
STEP 5.2: [The Second Finishing Step] User i does the following when clock i E
[T,T L).5
= If i has not cert-voted in Step 3 and he sees tH next-votes for I for the
same step s of
period p ¨ 1, then i next-votes I.
461n extreme cases, a user i may simultaneously see tH next-votes for I and tH
next-votes for some v I for
period p ¨1. He is free to set his starting value to either I or v in this
case, but the Block Proposal step always
gives priority to I.
47That is, a newly proposed block for a period p> 2 is as if there were no
leader for it, and the corresponding
seed Q is defined in the same way as in the original Algorand protocol when B'
is the empty block.
481n this case, enough honest users have seen a valid block B such that v =
H(B), and it is not required that
i herself has seen B.
49Note that these votes may reach i during his time (0, 2)], thus i's starting
value is not necessarily I.
50Steps 5.1 and 5.2 are made into different steps so that they have different
committees.
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
STEPS s > 6: [Consecutive Finishing Steps]
= If s is even then i follows the same voting instruction as in Step 4 when
clock =
T (s ¨ 4)L/2.
= Else (i.e., s is odd), i follows the same voting instructions as in Steps
5.1 and 5.2 in
parallel when clock E [T (s ¨ 5)L/2, T (s ¨ 3)L/2).
Changing Rounds
Instructions for every user i E PK:
= At any point while i is working on a round r, if i sees a string v I and
a period T.' .p with
> r such that
¨ i has received at least tH cert-votes for v for period r'.p,51 and
¨ i has received the block header corresponding to v,52
then i cert-votes v for period r'.p,53 sets his own CERTr' to be the set of
cert-votes for v
and starts round r' 1.
Referring to FIG. 6, a diagram 20' shows a first plurality of computing
workstations 22a-
22c connected to a first portion 24' of a data network, such as the Internet,
and a second
plurality of computing workstations 22a'-22c' connected to a second portion
24" of the data
network. The workstations 22a-22c communicate with each other via the first
portion 24' of the
network and the workstations 22a'-22c' communicate with each other via the
second portion
24" of the network. However, unlike the diagram 20 of FIG. 1, the workstations
22a-22c do not
communicate with the workstations 22a'-22c' because the network has been
partitioned into the
first part 24' and the second part 24" by a partition mechanism 26. The
partition mechanism
26 could be any mechanism that suppresses communication between the parts 24',
24" of the
network. Note that the partition mechanism 26 could be purposefully inserted
into the network
by an adversary or could occur due to unanticipated network interruption
caused by natural
or man-made phenomena, such as a power outage or a network switching error. In
the system
described herein, each of the workstations 22a-22c, 22a'-22c' performs the
steps set forth above,
but the first plurality of workstations 22a-22c does not communicate with the
second plurality
of workstations 22a'-22c'. That is, each of the entities 22a-22c manages a
transaction system
locally within the part 24' while each of the entities 22a'-22c' manages a
transaction system
locally within the part 24". Only one of the parts 24', 24", at most, has
enough users (entities)
to generate certified blocks. After the partition mechanism 26 is removed and
the parts 24', 24"
converge to a single network (like the network 24, discussed above in
connection with FIG. 1),
all of the workstations 22a-22c, 22a'-22c' communicate with each other and are
able to resume
operation at the same point (block) of the chain. After the partition
mechanism 26 is removed,
each of the entities 22a-22c, 22a'-22c' manages a single transaction system in
the network where
all of the entities 22a-22c, 22a'-22c' communicate with each other.
51A cert-vote from a player j is counted even if player i has also received a
message from j cert-voting for a
different value for the same period. As shown in the analysis, this is to
ensure that all honest users know CERT
within time A from each other.
52The header defines the seed Q'' and, as mentioned earlier, strictly speaking
the header is part of v itself.
53For the theoretical analysis it is not necessary for i to propagate his
vote, because he ,already helped
propagating the tH cert-votes he received. However, having i propagate his
vote when i E SV" 'P'3 helps other
users see a certificate faster in reality.
56
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
Analysis. Even when the network is partitioned, the new embodiment remains
secure that
is, at most one block is certified for each round r. At a high level, this is
because honest users
cert-vote at most once in each period of round r, and the choices of the
committee size n and
the threshold tH guarantee that in each period r.p, at most one hash value
H(B) of a valid block
B can get a certificate. To see it from a different direction, assume a period
r.p has generated
tH cert-votes for one valid block B and tH cert-votes for another valid block
B' relative to
B , ... , Br-1-, then the conditions for how n and tH are chosen imply that at
least one honest
user has cert-voted for the hash values of both B and B', which contradicts
the fact that an
honest user cert-votes at most once in period r.p.
If in some period r.p, a valid block B has gotten a certificate _______ that
is, at least tH cert-votes
for its hash value H(B), then in all future periods p' > p (if they are ever
reached), B will
be the only block that may get a certificate in period r.p'. Indeed, an honest
user does not
next-vote for I in period r.p if he has cert-voted for H(B) in r.p. Thus by
the same choices
of n and tH, in no step s > 4 of period r.p will there be tH next-votes for I
or for any other
value v H(B). So an honest user moves to period r.(p 1) only if he has
received at least tH
next-votes for H(B). Accordingly, H(B) will be the only value that is (re-
)proposed in step 1 of
period r.(p 1), the only value that honest users will soft-vote for in step
2 of period r.(p 1),
and consequently the only value they will cert-vote in step 3 and next-vote in
step s > 4 of
period r.(p 1). By an inductive argument, the same is true for all
consecutive periods.
Notice that, when the network is partitioned, B having gotten a certificate in
a period
r.p does not mean that the honest users will receive the certificate. Indeed,
during a network
partition an adversary controls how messages are delivered in the system. He
may, for example,
allow all messages to be delivered properly except the cert-votes, where he
does not allow cert-
votes from one group of users to be delivered to other groups. Nevertheless, B
having gotten
a certificate implies that enough honest users have cert-voted for it and will
not next-vote for
anything else, which prevents any other block from being certified in period
r.p and any future
period.
The efficiency of the new embodiment comes from two parts. First, when the
network is not
partitioned, consensus about the rth block is reached quickly. Indeed, if the
leader of step 1 of
period r.1 is honest, then all honest users immediately cert-vote for his
proposed block B, B
has gotten a certificate after step 3 of period r.p, and all honest users
finish round r afterward.
Similarly, if round r has reached a period p> 2 and the leader f for period p
is honest, then
the block newly proposed or re-proposed by f is certified in step 3 and all
honest users finish
round r afterward. This is so because, if f has seen tH next-votes for I from
period p ¨ 1 and
proposed a new block, then those next-votes will reach all honest users within
time A and they
will all soft-vote for L's proposal. Otherwise, f has only seen tH next-votes
for the hash H(B)
of a valid block B from period p ¨ 1 and has re-proposed H(B). All honest
users' starting
values of period p are either I or H(B), and no matter which is the case, they
soft-vote for
H(B) _______________________________________________________________________
because they are following the leader's proposal in the former case, and
because they
are voting for their own starting values in the latter case.
Moreover, if a certificate for some valid block B is generated in a period
r.p, then all honest
users finish round r soon after that. This is so because, if at least tH cert-
votes for B come from
honest users, then all honest users will receive them within time A and will
finish round r with
B being the rth block. If any set of tH cert-votes for B contains at least one
malicious user,
the malicious users may choose to not send their cert-votes and the honest
users do not receive
a certificate for B right away. However, the choices of n and tH ensure that a
certificate for B
contain at least one honest user i, and i has received tH soft-votes for B
before he cert-voted
it. Since i propagated these soft-votes and the network is not partitioned,
all honest users will
receive them within time A and will next-vote for H(B) in step 5.1.
Accordingly, all honest
57
CA 03086361 2020-06-18
WO 2019/126311 PCT/US2018/066481
users start period r.(p 1) with starting value H(B) and will soft-vote for
it in step 2 of period
r.(p 1), regardless whether the leader of period r.(p +1) is honest or not.
As a result, honest
users will cert-vote for H(B) in step 3, B now has a certificate from honest
users, and all honest
users will receive them and finish round r within time A.
The choices of the seeds Qr and the cryptographic sortition used in the new
embodiment
ensure that each period p of round r has an honest leader with high
probability, as in the
original Algorand protocol, and the missing detailed analysis about the new
embodiment's
efficiency when there is no network partition follow from there.
Second, after the network partition is resolved, the protocol will recover and
reach consensus
quickly. Indeed, if some honest users have received a certificate for a block
B in round r during
the partition and moved to round r 1, then once the partition is resolved
all honest users will
receive such a certificate for B and move to round r 1. Moreover, let p be
the furthest period
in round r 1 where an honest user i has reached during the partition. Then
all the next-votes
that allowed i to move to period (r 1).p will reach other honest users after
the partition is
resolved, and they will also move to period (r +1).p. The protocol will then
continue from there
as usual, following the same analysis as when there is not network partition.
If no honest user
moved from round r to round r 1 during the partition, then all honest users
are in the same
round but perhaps different periods. In this case, let p be the furthest
period in round r where
an honest user i has reached during the partition. Similarly, after the
partition is resolved, all
the next-votes that allowed i to move to period r.p will reach other honest
users and they will
also move to period r.p. Again the protocol will continue from there as usual.
To summarize, the new embodiment is secure and does not soft-fork even when
the network
is partitioned. It generates block efficiently when the network is not
partitioned, and recovers
quickly after a network partition is resolved.
10 Scope
Note that the mechanism described herein is applicable to other blockchain
systems where it
is desirable to prevent more than one blocks are certified during a network
partition and to
restore liveness quickly after a partition is resolved. Thus, the system
described herein may be
adapted to other blockchain schemes, even schemes that do not relate directly
to currency.
The system described herein may be adapted to be applied to and combined with
mechanisms
set forth in any or all of PCT/US2017/031037, filed on May 4, 2017, 15/551,678
filed August
17, 2017, 16/096,107 filed on October 24, 2018, PCT/U52018/053360 filed on
September 28,
2018, PCT/U52018/054311 filed on October 4, 2018, 62/632,944 filed on February
20, 2018,
62/643,331 filed on March 15, 2018, 62/777,410 filed on December 10, 2018, and
62/778,482
filed on December 12, 2018, all of which are incorporated by reference herein.
Software implementations of the system described herein may include executable
code that
is stored in a computer readable medium and executed by one or more
processors. The computer
readable medium may be non-transitory and include a computer hard drive, ROM,
RAM, flash
memory, portable computer storage media such as a CD-ROM, a DVD-ROM, a flash
drive, an
SD card and/or other drive with, for example, a universal serial bus (USB)
interface, and/or any
other appropriate tangible or non-transitory computer readable medium or
computer memory
on which executable code may be stored and executed by a processor. The system
described
herein may be used in connection with any appropriate operating system.
Other embodiments of the invention will be apparent to those skilled in the
art from a
consideration of the specification or practice of the invention disclosed
herein. It is intended
that the specification and examples be considered as exemplary only, with the
true scope and
58
CA 03086361 2020-06-18
WO 2019/126311
PCT/US2018/066481
spirit of the invention being indicated by the following claims.
59